Public Traffic Congestion Estimation Using an Artificial Neural Network
Abstract
1. Introduction
2. Literature Review
2.1. Traffic Congestion Estimation
2.2. Transport Network Optimization
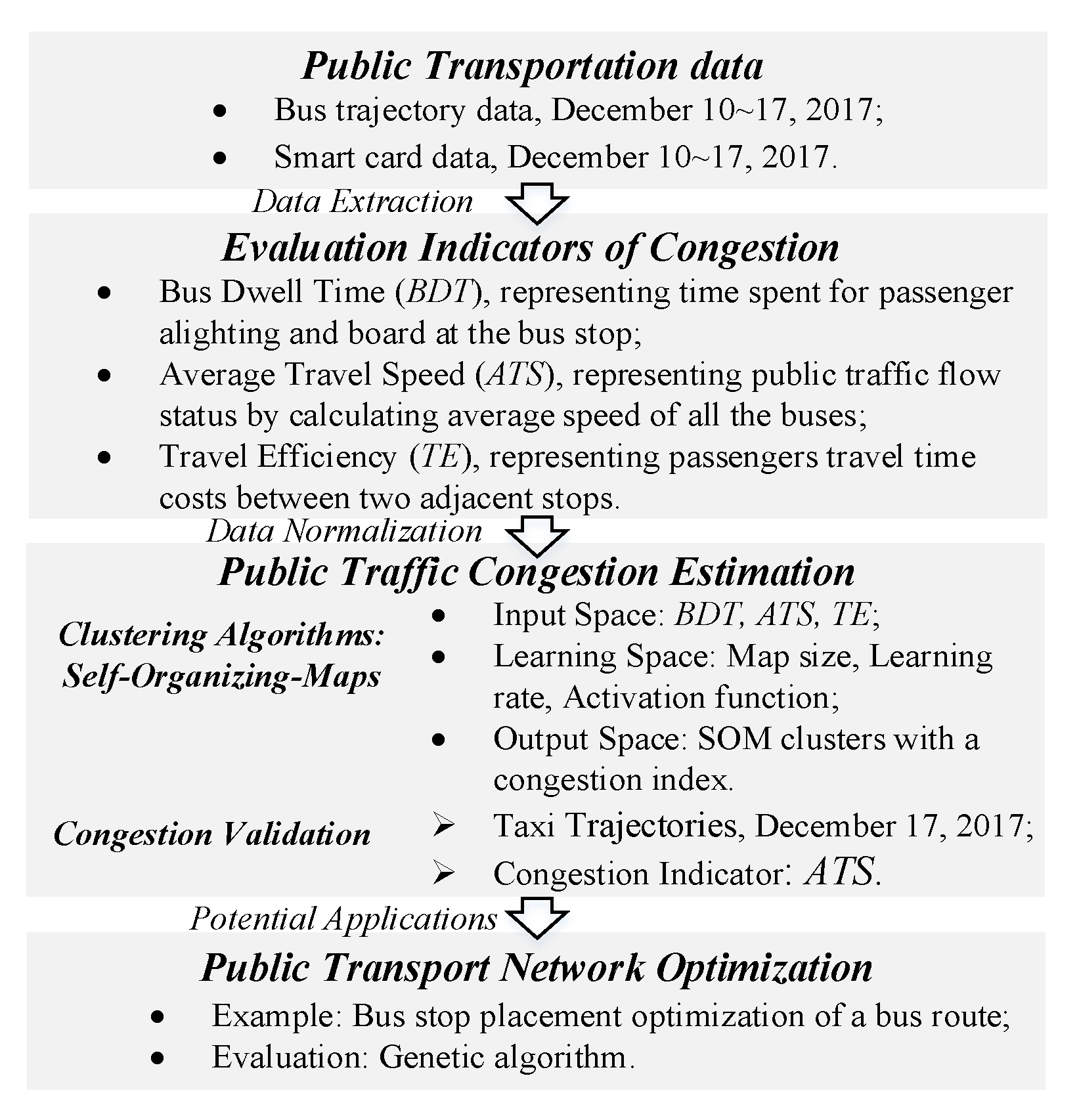
3. Methodology
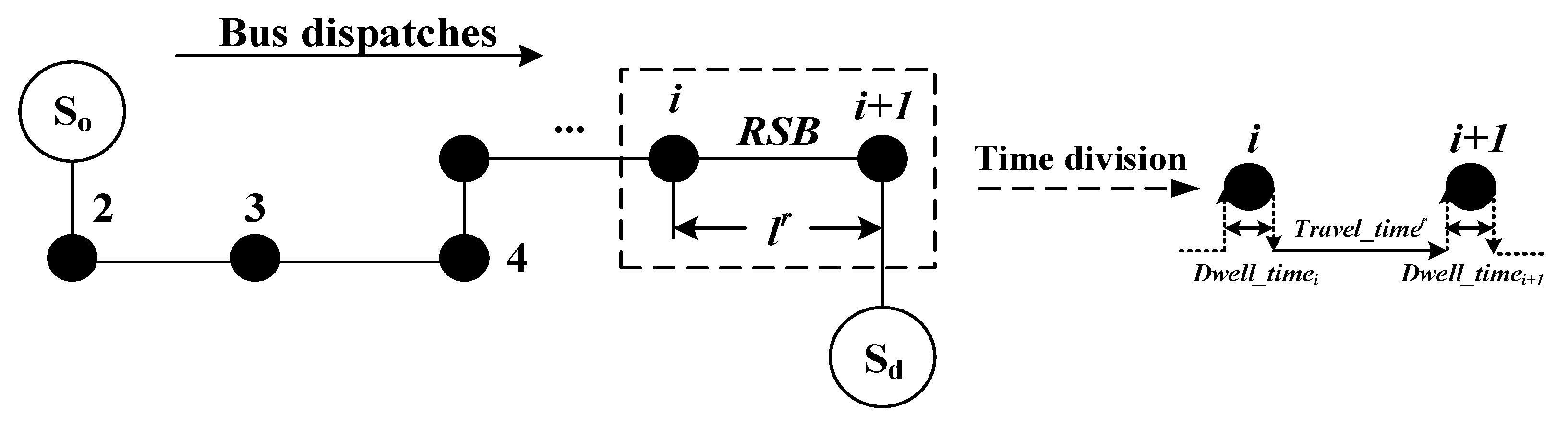
3.1. Definitions
- So, Sd – Terminal bus stops of a bus line.
- RSB – One road segment between adjacent bus stops of a bus line.
- i – The index of the bus stops.
- – Length of RSB r.
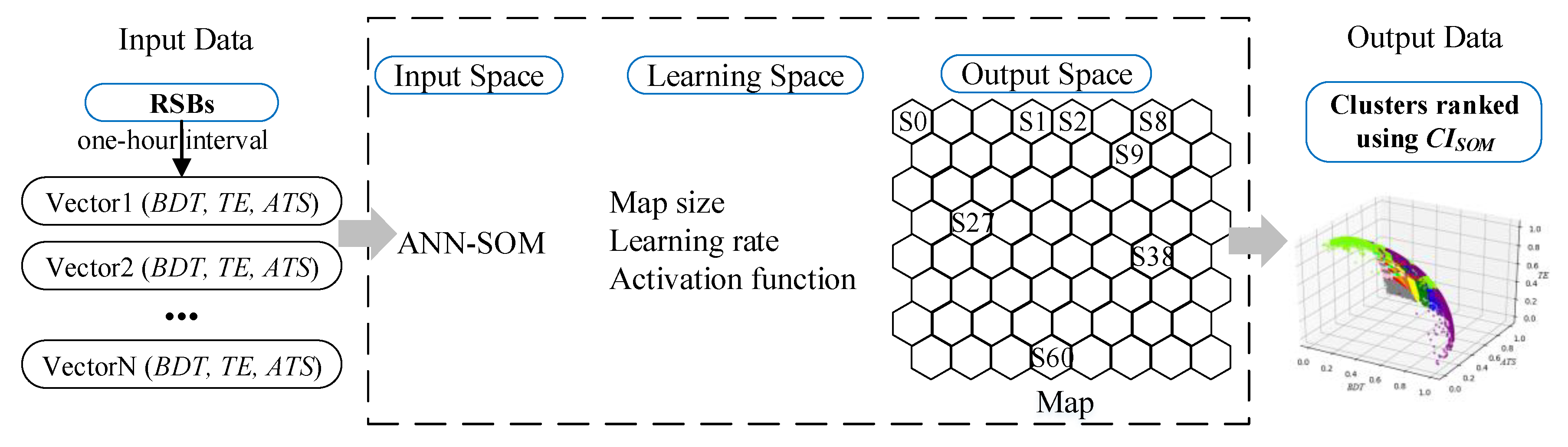
3.2. Congestion Estimation using an Artificial Neural Network
- (1)
- Initialization: Choose random values for the initial weights wi, and normalize the input vectors and weights.where x = [x1,…,xm]∈Rm represents an input vector, ||.|| represents the Euclidean norm, and M is the number of neurons.
- (2)
- Winner Finding: Find the winner neuron n, using the minimum Euclidean distance between vector x’ and weights w i’, according to Equation (5):
- (3)
- Update Weights: Adjust the weights of the winner and its neighbors at time t+1, and renormalize the weights after learning:where represents the topological neighborhood function of the winner neuron n at time t, is a positive constant called the ‘‘learning-rate’’, ri and rj are the location vectors of nodes i and j, respectively. represents the width of the kernel. The weights are updated at each time step.
- (4)
- Algorithm stop condition: Both and will decay over time. The algorithm will stop when or the prespecified number of epochs is reached.
4. Case Study
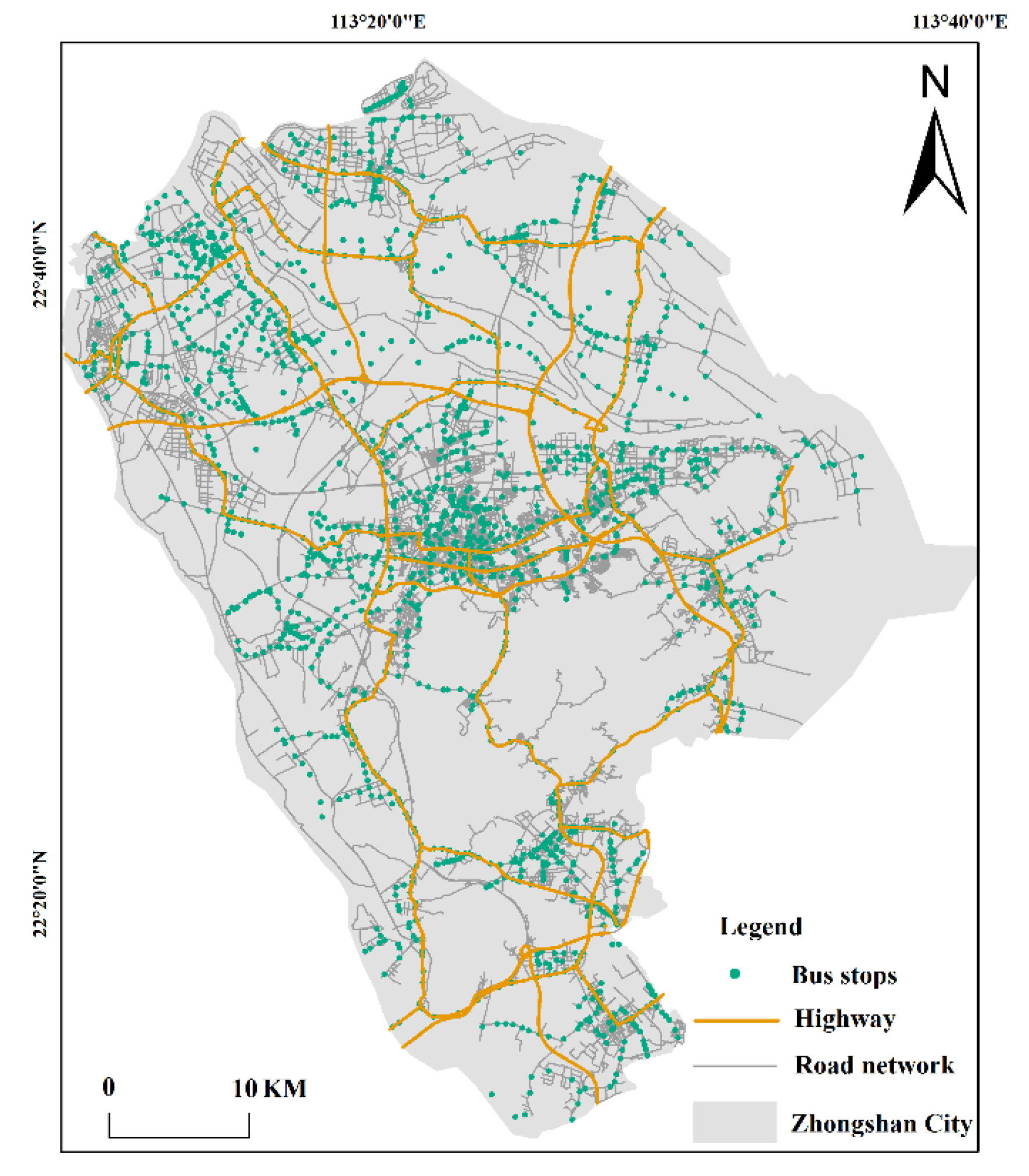
4.1. Data
4.1.1. Data Description
4.1.2. Data Preprocessing
4.2. Congested RSB Estimation and Validation
4.2.1. SOM Algorithm Results
4.2.2. Validation
5. Discussion
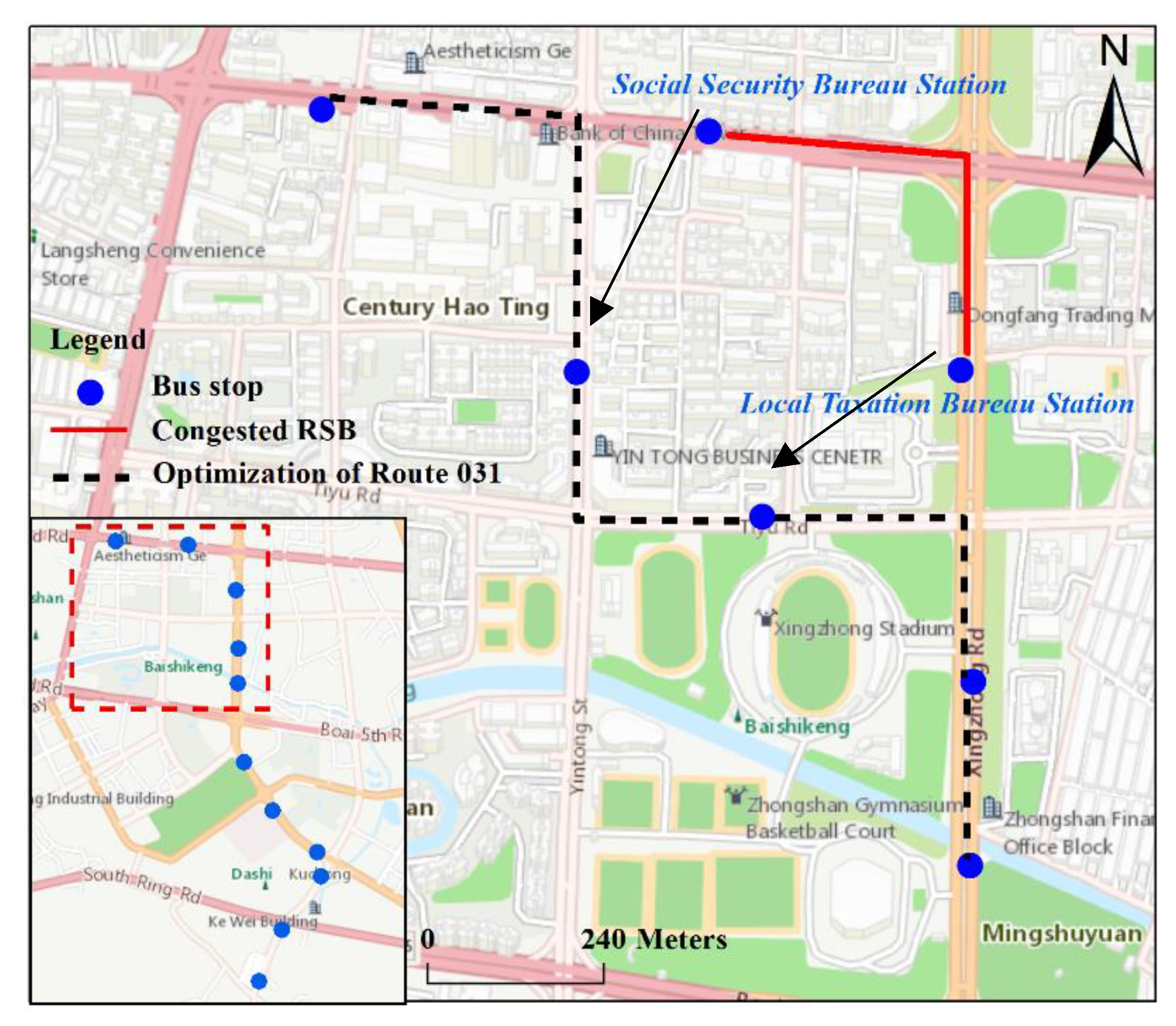
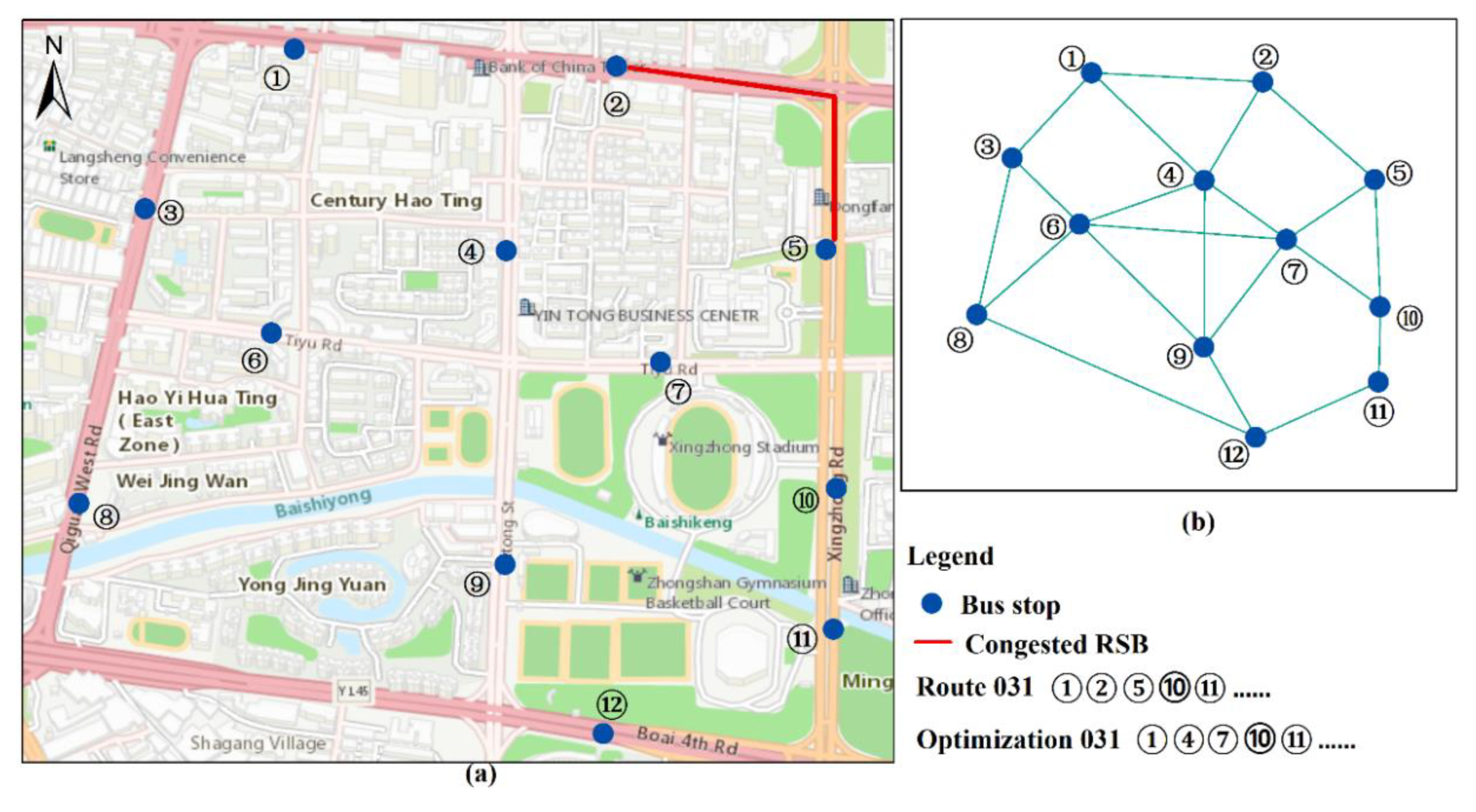
5.1. An Example of PTN Optimization based on Congested RSBs
5.2. Optimization Results Evaluating using Genetic Algorithm
5.2.1. Genetic Algorithm
- (1)
- (2)
- Initialization: In the initial step, each route was set as the shortest path between a selected pair of nodes according to the passenger travel time. Using the greedy algorithm from Nayeem et al. [48], we generated pairs of nodes i and j with high dsij values, which is the number of passengers that receive direct services between nodes i and j.where N is the set of nodes along the shortest path of nodes (i, j), and dmn is the passenger travel demand per time unit between nodes i and j.
- (3)
- Crossover: In the crossover operation, each gene in the individual represents a bus route. We decided at each index of the individual which one is used to perform the crossover operation between two randomly selected parents based on a given probability Pswap.
- (4)
- Mutation: Mutation is a GA operator with the goal to replace a randomly chosen gene by new genes (bus routes) in the population. Mutation usually operates with a quite small probability, which creates a slight modification of the population.
5.2.2. Results of Genetic Algorithm
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tirachini, A.; Hensher, D.A.; Rose, J.M. Multimodal pricing and optimal design of urban public transport: The interplay between traffic congestion and bus crowding. Transport. Res. B-Meth. 2014, 61, 33–54. [Google Scholar] [CrossRef]
- Ibeas, Á.; Dell Olio, L.; Alonso, B.; Sainz, O. Optimizing bus stop spacing in urban areas. Transport. Res. E-Log. 2010, 46, 446–458. [Google Scholar] [CrossRef]
- Ibarra-Rojas, O.J.; Delgado, F.; Giesen, R.; Muñoz, J.C. Planning, operation, and control of bus transport systems: A literature review. Transport. Res. B-Meth. 2015, 77, 38–75. [Google Scholar] [CrossRef]
- Fan, W.; Machemehl, R.B. Optimal Transit Route Network Design Problem with Variable Transit Demand: Genetic Algorithm Approach. J. Transp. Eng. 2006, 132, 40–51. [Google Scholar] [CrossRef]
- LeBlanc, L.J. Transit system network design. Transp. Res. Part B Methodol. 1988, 22, 383–390. [Google Scholar] [CrossRef]
- Chakroborty, P. Genetic Algorithms for Optimal Urban Transit Network Design. Comput-Aided. Civ. Inf. 2003, 18, 184–200. [Google Scholar] [CrossRef]
- Mesbah, M.; Sarvi, M.; Currie, G. Optimization of Transit Priority in the Transportation Network Using a Genetic Algorithm. IEEE T. Intell. Transp. 2011, 12, 908–919. [Google Scholar] [CrossRef]
- Gao, P.; Liu, Z.; Tian, K.; Liu, G. Characterizing Traffic Conditions from the Perspective of Spatial-Temporal Heterogeneity. ISPRS Int. J. Geo.-Inf. 2016, 5, 34. [Google Scholar] [CrossRef]
- Nguyen-Phuoc, D.Q.; Currie, G.; De Gruyter, C.; Kim, I.; Young, W. Modelling the net traffic congestion impact of bus operations in Melbourne. Transport. Res. A-Pol. 2018, 117, 1–12. [Google Scholar] [CrossRef]
- Tirachini, A. The economics and engineering of bus stops: Spacing, design and congestion. Transport. Res. A-Pol. 2014, 59, 37–57. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Meng, M.; Rau, A. Impact of Different Bus Stop Designs on Bus Operating Time Components. J. Public. Transport. 2017, 20, 104–118. [Google Scholar] [CrossRef]
- Daraio, C.; Diana, M.; Di Costa, F.; Leporelli, C.; Matteucci, G.; Nastasi, A. Efficiency and effectiveness in the urban public transport sector: A critical review with directions for future research. Eur. J. Oper. Res. 2016, 248, 1–20. [Google Scholar] [CrossRef]
- Chen, B.Y.; Lam, W.H.K.; Sumalee, A.; Li, Q.; Li, Z. Vulnerability analysis for large-scale and congested road networks with demand uncertainty. Transport. Res. A-Pol. 2012, 46, 501–516. [Google Scholar] [CrossRef]
- Zheng, Y.; Capra, L.; Wolfson, O.; Yang, H. Urban Computing: Concepts, Methodologies, and Applications. ACM Trans. Intell. Syst. Technol. 2014, 5, 1–55. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.; Han, J.; Wang, E.; Chen, W.; Yue, L. Efficient traffic congestion estimation using multiple spatio-temporal properties. Neurocomputing 2017, 267, 344–353. [Google Scholar] [CrossRef]
- An, S.; Yang, H.; Wang, J. Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories. ISPRS Int. J. Geo.-Inf. 2018, 7, 128. [Google Scholar]
- Jenelius, E.; Koutsopoulos, H.N. Travel time estimation for urban road networks using low frequency probe vehicle data. Transport. Res. B-Meth. 2013, 53, 64–81. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, J.; Li, W.; Gu, T.; Shi, W. Exploring traffic congestion correlation from multiple data sources. Pervasive. Mob. Comput. 2017, 41, 470–483. [Google Scholar] [CrossRef]
- Yu, Q.; Luo, Y.; Chen, C.; Zheng, X. Road Congestion Detection Based on Trajectory Stay-Place Clustering. ISPRS Int. J. Geo.-Inf. 2019, 8, 264. [Google Scholar] [CrossRef]
- Wang, Q.; Wan, J.; Yuan, Y. Locality constraint distance metric learning for traffic congestion detection. Pattern Recogn. 2018, 75, 272–281. [Google Scholar] [CrossRef]
- Farber, S.; Marino, M.G. Transit accessibility, land development and socioeconomic priority: A typology of planned station catchment areas in the Greater Toronto and Hamilton Area. J. Transp. Land Use 2017, 10, 879–902. [Google Scholar] [CrossRef]
- Kong, X.; Xu, Z.; Shen, G.; Wang, J.; Yang, Q.; Zhang, B. Urban traffic congestion estimation and prediction based on floating car trajectory data. Future Gener. Comp. Sy. 2016, 61, 97–107. [Google Scholar] [CrossRef]
- Xu, L.; Yue, Y.; Li, Q. Identifying Urban Traffic Congestion Pattern from Historical Floating Car Data. In Proceedings of the 13th COTA International Conference of Transportation Professionals (CICTP), Shenzhen, China, 13–16 August 2013; pp. 2084–2095. [Google Scholar]
- He, F.; Yan, X.; Liu, Y.; Ma, L. A Traffic Congestion Assessment Method for Urban Road Networks Based on Speed Performance Index. In Proceedings of the 6th International Conference on Green Intelligent Transportation System and Safety (GITSS), Beijing, China, 2–6 July 2015; pp. 425–433. [Google Scholar]
- Litman, T. Evaluating Public Transit Benefits and Costs; Victoria Transport Policy Institute: Victoria, BC, Canada, 2015. [Google Scholar]
- Ceder, A.A.; Butcher, M.; Wang, L. Optimization of bus stop placement for routes on uneven topography. Transport. Res. B-Meth. 2015, 74, 40–61. [Google Scholar] [CrossRef]
- Li, H.; Bertini, R.L. Assessing a Model for Optimal Bus Stop Spacing with High-Resolution Archived Stop-Level Data. Transport. Res. Rec. 2009, 2111, 24–32. [Google Scholar] [CrossRef]
- Chien, S.I.; Qin, Z. Optimization of bus stop locations for improving transit accessibility. Transport. Plan Techn. 2004, 27, 211–227. [Google Scholar] [CrossRef]
- Ruiz, M.; Segui-Pons, J.M.; Mateu-LLadó, J. Improving Bus Service Levels and social equity through bus frequency modelling. J. Transp. Geogr. 2017, 58, 220–233. [Google Scholar] [CrossRef]
- Nikolić, M.; Teodorović, D. A simultaneous transit network design and frequency setting: Computing with bees. Expert. Syst. Appl. 2014, 41, 7200–7209. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Hu, L.; Yang, Y.; Lee, L.H. A Data-Driven and Optimal Bus Scheduling Model With Time-Dependent Traffic and Demand. Ieee. T. Intell. Transp. 2017, 18, 2443–2452. [Google Scholar] [CrossRef]
- Yu, B.; Kong, L.; Sun, Y.; Yao, B.; Gao, Z. A bi-level programming for bus lane network design. Transport. Res. C-Emer. 2015, 55, 310–327. [Google Scholar] [CrossRef]
- Bagloee, S.A.; Sarvi, M.; Ceder, A. Transit priority lanes in the congested road networks. Public Transport 2017, 9, 571–599. [Google Scholar] [CrossRef]
- Delmelle, E.M.; Li, S.; Murray, A.T. Identifying bus stop redundancy: A gis-based spatial optimization approach. Comput. Environ. Urban. 2012, 36, 445–455. [Google Scholar] [CrossRef]
- Tirachini, A. Bus dwell time: The effect of different fare collection systems, bus floor level and age of passengers. Transp. A 2013, 9, 28–49. [Google Scholar] [CrossRef]
- Weng, J.; Wang, C.; Huang, H.; Wang, Y.; Zhang, L. Real-time bus travel speed estimation model based on bus GPS data. Adv. Mech. Eng. 2016, 8, 756467438. [Google Scholar] [CrossRef]
- Kohonen, T. Learning Vector Quantization. In Self-Organizing Maps; Kohonen, T., Ed.; Springer: Berlin, Heidelberg, 1995; pp. 175–189. [Google Scholar]
- Ruiz-Aguilar, J.J.; Turias, I.J.; Jiménez-Come, M.J. A novel three-step procedure to forecast the inspection volume. Transport. Res. C-Emer. 2015, 56, 393–414. [Google Scholar] [CrossRef]
- Li, Z.; Han, Z.; Xin, J.; Luo, X.; Su, S.; Weng, M. Transit oriented development among metro station areas in Shanghai, China: Variations, typology, optimization and implications for land use planning. Land Use Policy 2019, 82, 269–282. [Google Scholar] [CrossRef]
- Shieh, S.; Liao, I. A new approach for data clustering and visualization using self-organizing maps. Expert. Syst. Appl. 2012, 39, 11924–11933. [Google Scholar] [CrossRef]
- Olawoyin, R.; Nieto, A.; Grayson, R.L.; Hardisty, F.; Oyewole, S. Application of artificial neural network (ANN)–self-organizing map (SOM) for the categorization of water, soil and sediment quality in petrochemical regions. Expert. Syst. Appl. 2013, 40, 3634–3648. [Google Scholar] [CrossRef]
- OSM. Overhead Lines und Underground Cables. © Openstreetmap Contributors, Open Database License (ODbL). Available online: https://www.openstreetmap.org/copyright. (accessed on 6 September 2018).
- Nassir, N.; Hickman, M.; Ma, Z. Activity detection and transfer identification for public transit fare card data. Transportation 2015, 42, 683–705. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organising Maps; Springer: Berlin, Germany, 2001. [Google Scholar]
- Zhang, K.; Sun, D.; Shen, S.; Zhu, Y. Analyzing spatiotemporal congestion pattern on urban roads based on taxi GPS data. J. Transp. Land Use 2017, 10, 675–694. [Google Scholar] [CrossRef]
- Wu, H.; Liu, L.; Yu, Y.; Peng, Z.; Jiao, H.; Niu, Q. An Agent-based Model Simulation of Human Mobility Based on Mobile Phone Data: How Commuting Relates to Congestion. ISPRS Int. J. Geo.-Inf. 2019, 8, 313. [Google Scholar] [CrossRef]
- Guler, S.I.; Gayah, V.V.; Menendez, M. Bus priority at signalized intersections with single-lane approaches: A novel pre-signal strategy. Transport. Res. C-Emer. 2016, 63, 51–70. [Google Scholar] [CrossRef]
- Nayeem, M.A.; Rahman, M.K.; Rahman, M.S. Transit network design by genetic algorithm with elitism. Transport. Res. C-Emer. 2014, 46, 30–45. [Google Scholar] [CrossRef]
- Nikolić, M.; Teodorović, D. Transit network design by Bee Colony Optimization. Expert. Syst. Appl. 2013, 40, 5945–5955. [Google Scholar] [CrossRef]
- Dou, M.; Gu, Y.; Xu, G. Social awareness of crisis events: A new perspective from social-physical network. Cities 2020, 99, 102620. [Google Scholar] [CrossRef]
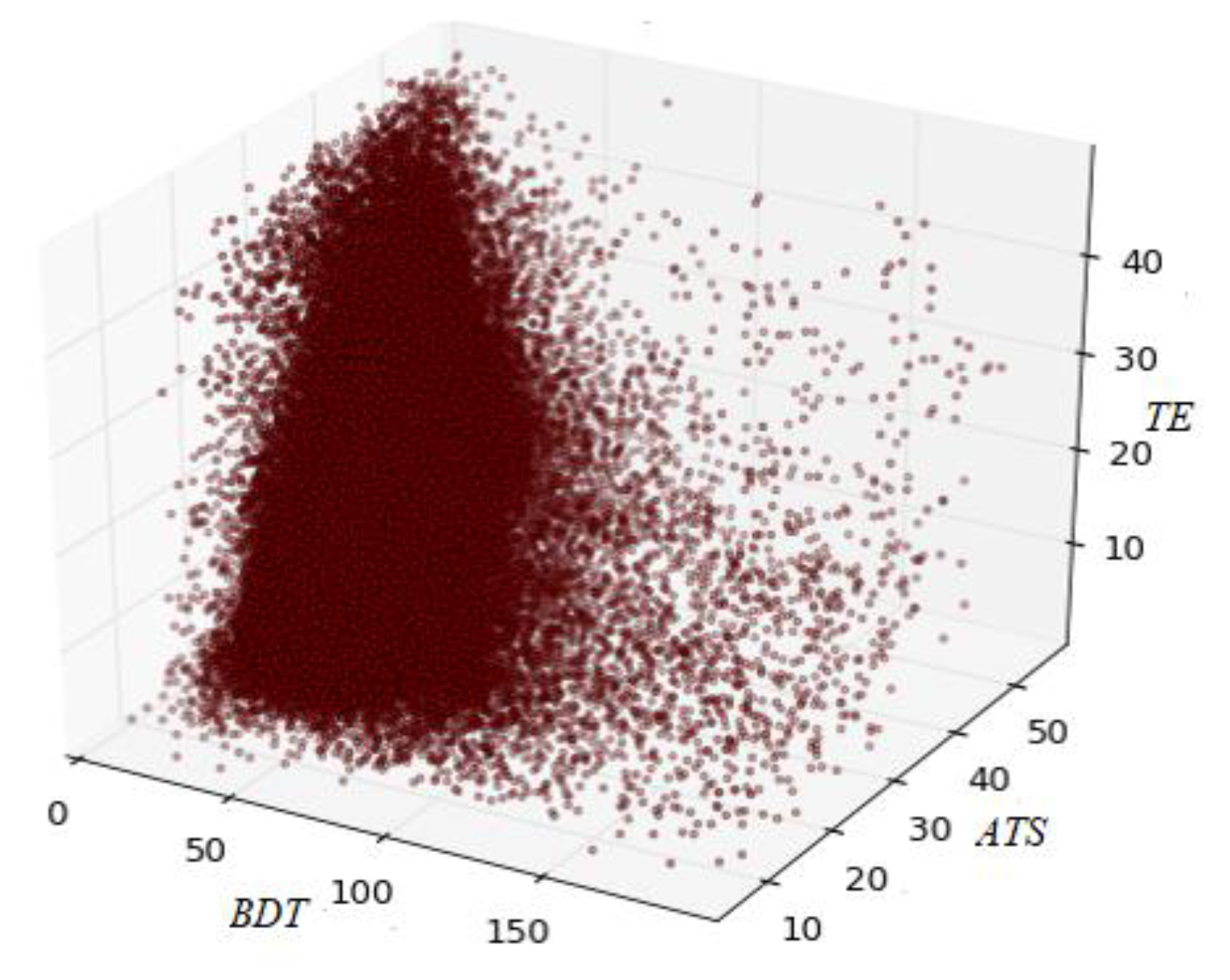
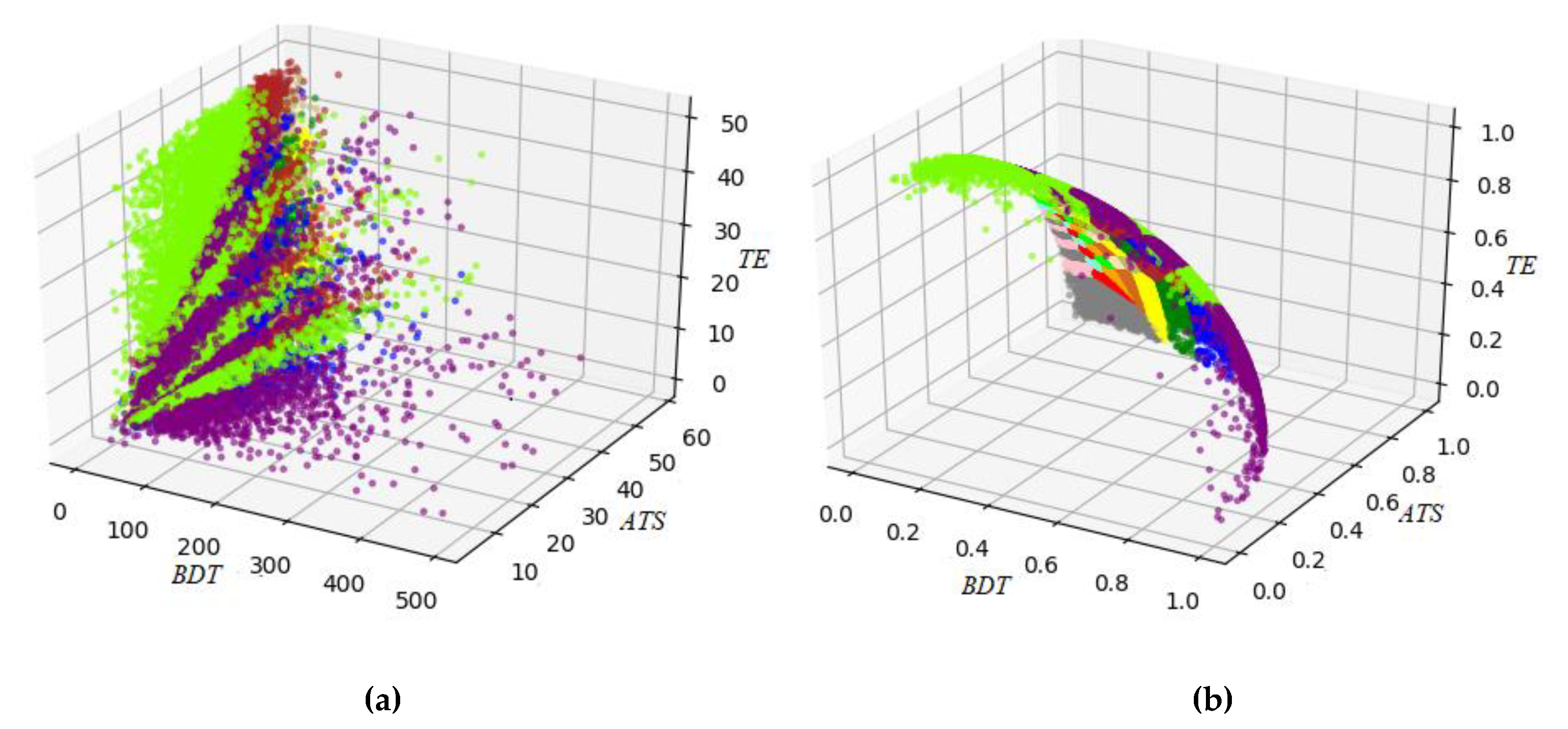
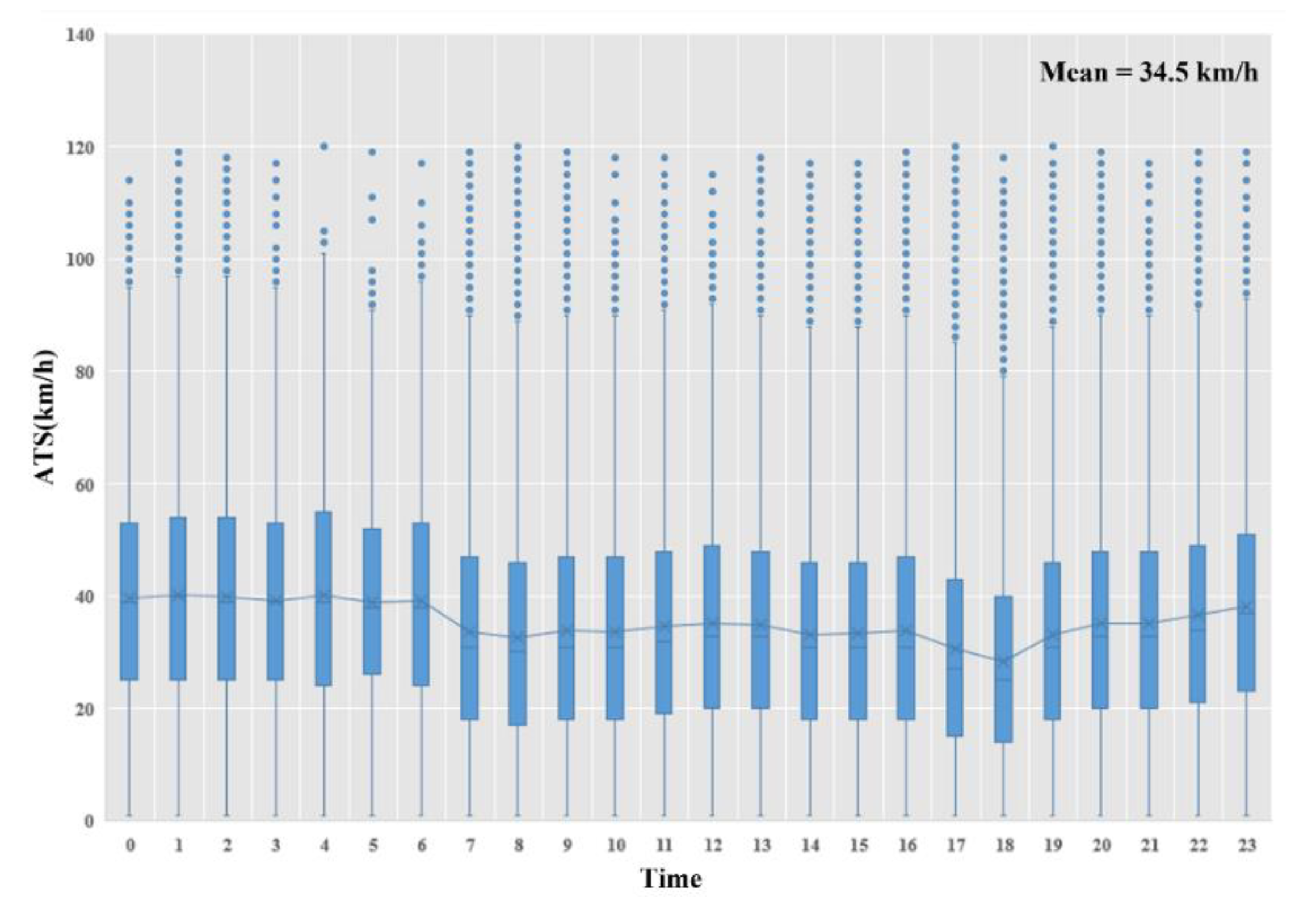
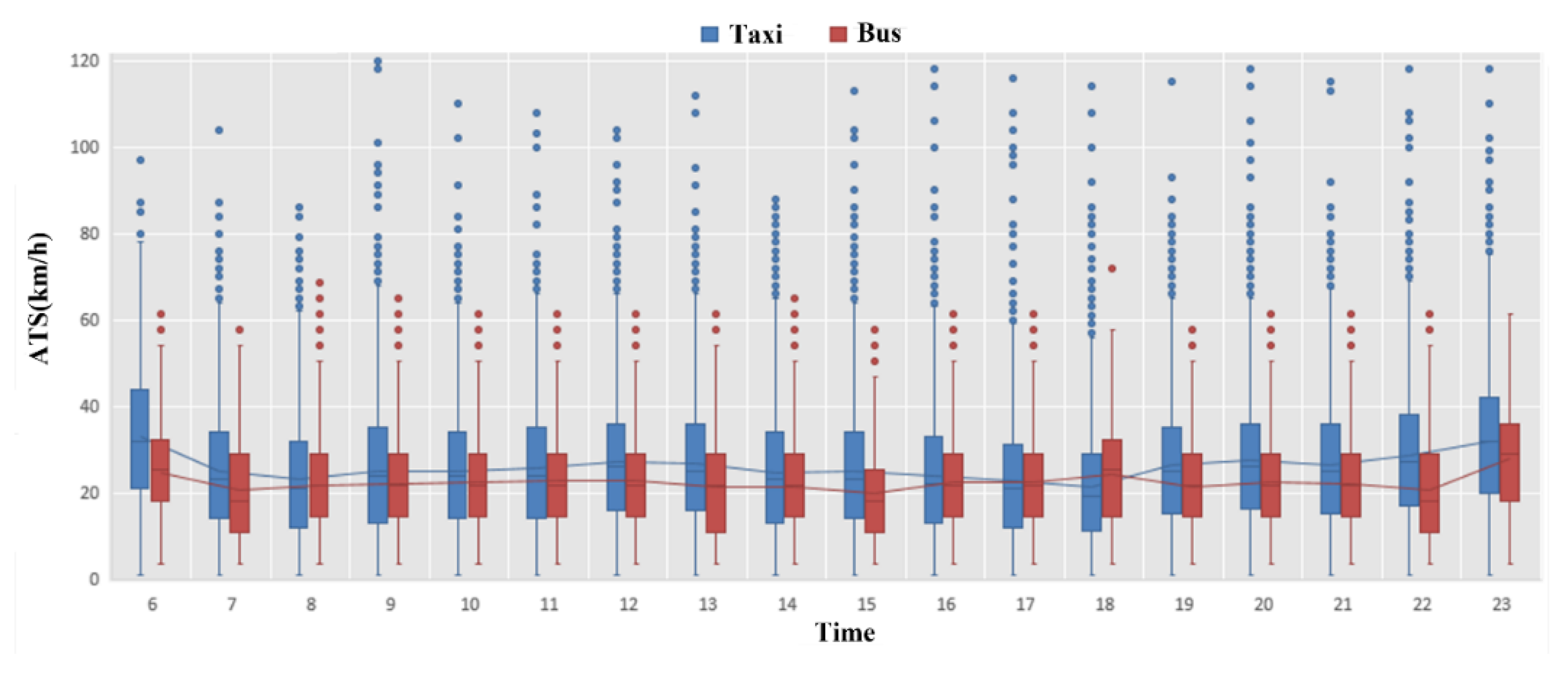

| Bus Stops of the RSB | Time | BDT | TE | ATS | Vector ID |
|---|---|---|---|---|---|
| ChangHong, Minke East | 6 | 0.29542 | 0.32698 | 0.08765 | 1 |
| 7 | 0.20095 | 0.38456 | 0.07612 | 2 | |
| 8 | 0.18994 | 0.31269 | 0.08438 | 3 | |
| … | … | … | … | … | |
| 22 | 0.19742 | 0.28761 | 0.07946 | 17 | |
| 23 | 0.24765 | 0.33097 | 0.08611 | 18 |
| ID | Card ID | Time | Route | Terminal ID | Bus ID |
|---|---|---|---|---|---|
| 1 | 920197793 | 2017/12/11 07:48:02 | 013 | 10026091 | T37925 |
| 2 | 920197876 | 2017/12/11 09:58:01 | 037 | 10029006 | T24273 |
| 3 | 920006217 | 2017/12/11 14:47:05 | 500 | 10024273 | T29006 |
| ID | Bus ID | Time | Longitude | Latitude | Direction | Speed(km/h) |
|---|---|---|---|---|---|---|
| 1 | T37925 | 2017/12/11 07:48:02 | 113.3108008 | 22.4562057 | 46 | 18.00 |
| 2 | T24273 | 2017/12/11 09:58:01 | 113.3203278 | 22.5557728 | 0 | 21.60 |
| 3 | T29006 | 2017/12/11 14:47:05 | 113.3255081 | 22.5612011 | 325 | 25.20 |
| Card ID | Bus ID | Boarding Time/Stop | Alighting Time/Stop | Dist. | Time | Route |
|---|---|---|---|---|---|---|
| 920197793 | T37925 | 07:48:02/Sanjia Village | 08:02:13/Huabai Center | 2170m | 851s | 013 |
| 920197876 | T24273 | 09:58:01/Chang Hong | 10:10:22/Yangjiao Kou | 1750m | 722s | 037 |
| MAP Size | Normalize LOG | |
|---|---|---|
| TE | QE | |
| 4∗4 | 0.018 | 1.034 |
| 5∗5 | 0.053 | 1.047 |
| 6∗6 | 0.012 | 0.854 |
| 7∗7 | 0.043 | 0.976 |
| 8∗8 | 0.001 | 0.743 |
| 9∗9 | 0.028 | 0.712 |
| 10∗10 | 0.003 | 0.651 |
| Cluster ID | BDT | TE | ATS | CISOM |
|---|---|---|---|---|
| 0 | 0.38692 | −0.21598 | −0.08499 | −0.08595 |
| 1 | 0.24895 | −0.29926 | −0.08056 | −0.13087 |
| 8 | 0.27386 | −0.24104 | −0.17600 | −0.14318 |
| 2 | 0.17297 | −0.32527 | −0.07892 | −0.23122 |
| 9 | 0.19913 | −0.31212 | −0.14586 | −0.25885 |
| Route | Bus Stops of the Congested RSBs | Congested Periods |
|---|---|---|
| 013 | (Minke West, Zhongshan North Railway) | 07:00-09:00, 18:00-22:00 |
| 013 | (Dongming Garden, Daxinxinduhui) | 07:00-08:00 |
| 013 | (Daxinxinduhui, Sanjia Village) | 07:00-08:00, 18:00-19:00 |
| 013 | (Sanjia Village, Liantang Road) | 07:00-09:00, 18:00-22:00 |
| 013 | (Liantang Road, Zhongshan People’s Hospital) | 07:00-11:00, 17:00-22:00 |
| 013 | (Zhongshan People’s Hospital, Huabai Market) | 07:00-09:00 |
| 037 | (ChangHong, Minke East) | 07:00-09:00, 18:00-19:00 |
| 001 | (Torch College, FanZhong) | 11:00-12:00 |
| 015 | (Sun Yat-sen University, HouXing) | 08:00-09:00 |
| 031 | (Social Security Bureau, Local Taxation Bureau) | 07:00-11:00, 14:00-19:00 |
| Congestion Level | Congestion Characteristic | Example Route |
|---|---|---|
| Level 1 | Recurring congestion during commuting hours | 037 |
| Level 2 | Chronic congestion on one RSB | 031 |
| Level 3 | Chronic congestion on Multi-RSBs | 013 |
| Index | Route |
| 0 | 1-3-6-9-12-11 |
| 1 | 1-2-5-10-11 |
| 2 | 5-2-1-3-8 |
| 3 | 1-4-9-12 |
| Number of Routes | Route Description |
|---|---|
| 4 | 5-2-1-3-8-12 |
| 1-4-7-10-11-12 | |
| 1-3-6-9-12-11 | |
| 5-2-4-6-8-12 | |
| 5 | 8-3-1-4-7-10 |
| 3-1-4-7-10-11 | |
| 12-9-4-1-3-8 | |
| 9-6-3-1-2-5 | |
| 1-3-6-7-10-11 | |
| 6 | 12-8-3-1-2-5 |
| 1-3-6-9-12-11 | |
| 3-6-7-10-11-12 | |
| 1-4-7-10-11-12 | |
| 8-3-1-4-9-12 | |
| 5-2-1-3-8-12 | |
| Optimization of route 013 | 1-4-7-10-11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Y.; Wang, Y.; Dong, S. Public Traffic Congestion Estimation Using an Artificial Neural Network. ISPRS Int. J. Geo-Inf. 2020, 9, 152. https://doi.org/10.3390/ijgi9030152
Gu Y, Wang Y, Dong S. Public Traffic Congestion Estimation Using an Artificial Neural Network. ISPRS International Journal of Geo-Information. 2020; 9(3):152. https://doi.org/10.3390/ijgi9030152
Chicago/Turabian StyleGu, Yanyan, Yandong Wang, and Shihai Dong. 2020. "Public Traffic Congestion Estimation Using an Artificial Neural Network" ISPRS International Journal of Geo-Information 9, no. 3: 152. https://doi.org/10.3390/ijgi9030152
APA StyleGu, Y., Wang, Y., & Dong, S. (2020). Public Traffic Congestion Estimation Using an Artificial Neural Network. ISPRS International Journal of Geo-Information, 9(3), 152. https://doi.org/10.3390/ijgi9030152





