Soil Mapping Based on Globally Optimal Decision Trees and Digital Imitations of Traditional Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Site
2.2. Proposed Approach for Soil Mapping
- Stability: determined via an analysis of the dispersion of the number of branches and via expert analysis for 10 runs of an algorithm;
- Complexity: the number of conditions in the trees;
- Notional consistency: expert-based interpretation of one tree of each algorithm;
- The mean and minimum prior probabilities of proper classification were calculated as the mean and minimum number of properly classified points of a class from the training sample set in each tree terminal node divided by the total number of properly and improperly classified points in the same node;
- Spatial uncertainty in pixels: the mean probability of the most likely class for 10 runs of an algorithm;
- Map accuracy assessment: overall, the producer’s, user’s, and kappa accuracy [48]. The overall accuracy shows the number of similar depicted pixels in the predicted and reference maps multiplied by the total number of pixels. The producer’s accuracy represents the number of pixels that were depicted as part of the same class multiplied by the total number of that class’s pixels in the reference map. The user’s accuracy is the number of pixels that were depicted in the similar class but multiplied by the total number of that class’s pixels in the predicted map. The producer’s accuracy is associated with the error of misclassification, and the user’s accuracy is dedicated to the error of over-classification. The Cohen’s kappa index represents the overall accuracy considering the possibility of the agreement occurring by chance: , where po is the relative observed agreement among raters (identical to overall accuracy), and pe is the hypothetical probability of chance agreement, using the observed data to calculate the probabilities of each observer randomly seeing each category. For k categories, N observations to categorize and nki the number of times rater i predicted category k: .
3. Results
- The addition of more accurate covariate maps to the analysis;
- manual tree correction;
- change in qualitative rules;
- change in quantitative rules;
- manual soil map unit correction.
4. Discussion
- The laborious manual work associated with producing two forms of soil rules as a general classification tree and soil-specific rule chains. A possible solution is using a package with an interface that allows one to make adjustments as easily as possible. Moreover, this method should permit automatic transformations between classification trees and chains of rules.
- The significant changes in the classification trees when using updated covariate maps. This can be overcome by using more sophisticated statistical methods of finding classification rules and incorporating prior soil knowledge into the search for rules.
- The mapping of soil classes when we need to map continuous soil properties or soil functions. Compliance with other methodologies provides a solution for this problem. In that case, the proposed framework offers an interface with legacy soil maps.
- Statistical improvements of the classification tree algorithm’s accuracy.
5. Conclusions
- The overall accuracy of the soil maps in the study area was 59%, 67%, and 87% for EVTREE, CART, and Random Forest, respectively. The prediction accuracy of EVTREE for the study area was slightly lower than that for CART and substantially lower than that for Random Forest. After reducing the size of the sample set from 5001 to 1785 points, the accuracy remained the same for EVTREE (59%), decreased for CART (61%), and decreased substantially for Random Forest (62%). With a sample set of 1000 points, the Random Forest algorithm failed to run, and EVTREE and CART realized similar accuracy to 1785 points. The reduced sample sets covered all soils and most soil formation factor features of the original entire sample set. Therefore, the quality of soil classification under EVTREE was much less dependent on the size of the sample set.
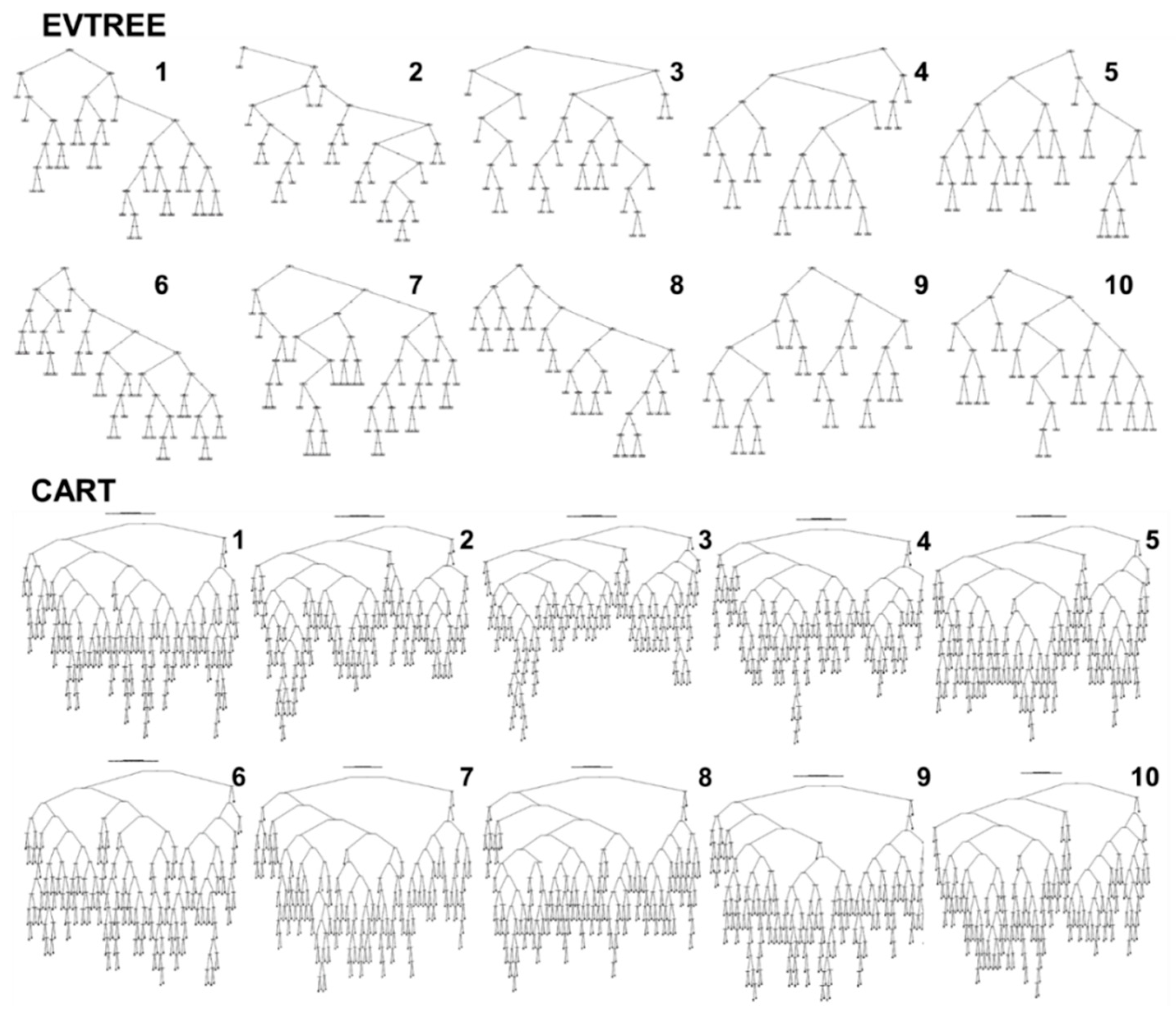
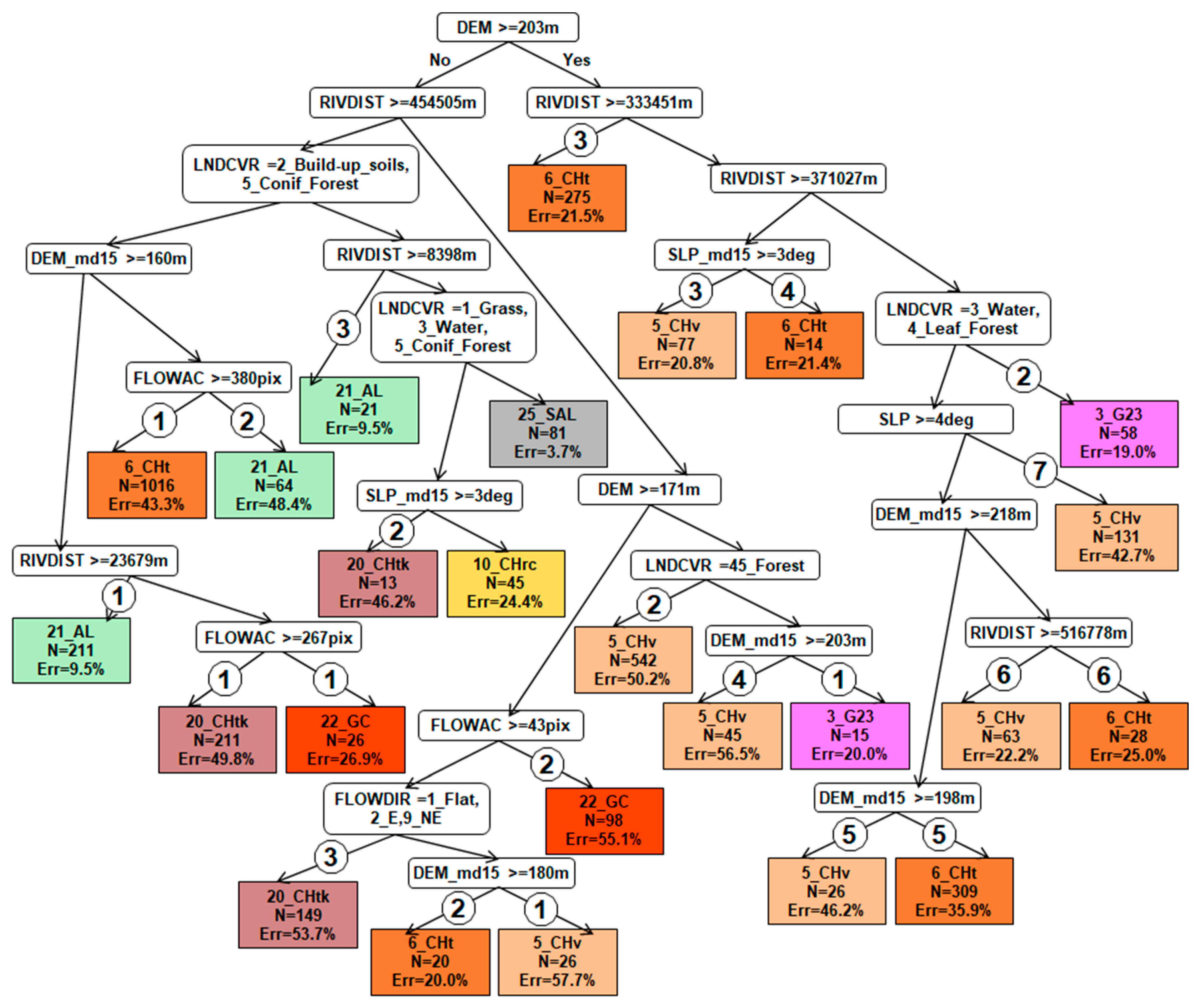
- The mean size of the trees in the study area constructed by EVTREE included 24 conditions, compared to the 154 conditions for the trees constructed by CART. The compact decision trees that were constructed by EVTREE were convenient for both quantitative quality assessment and expert-based notional tracing.
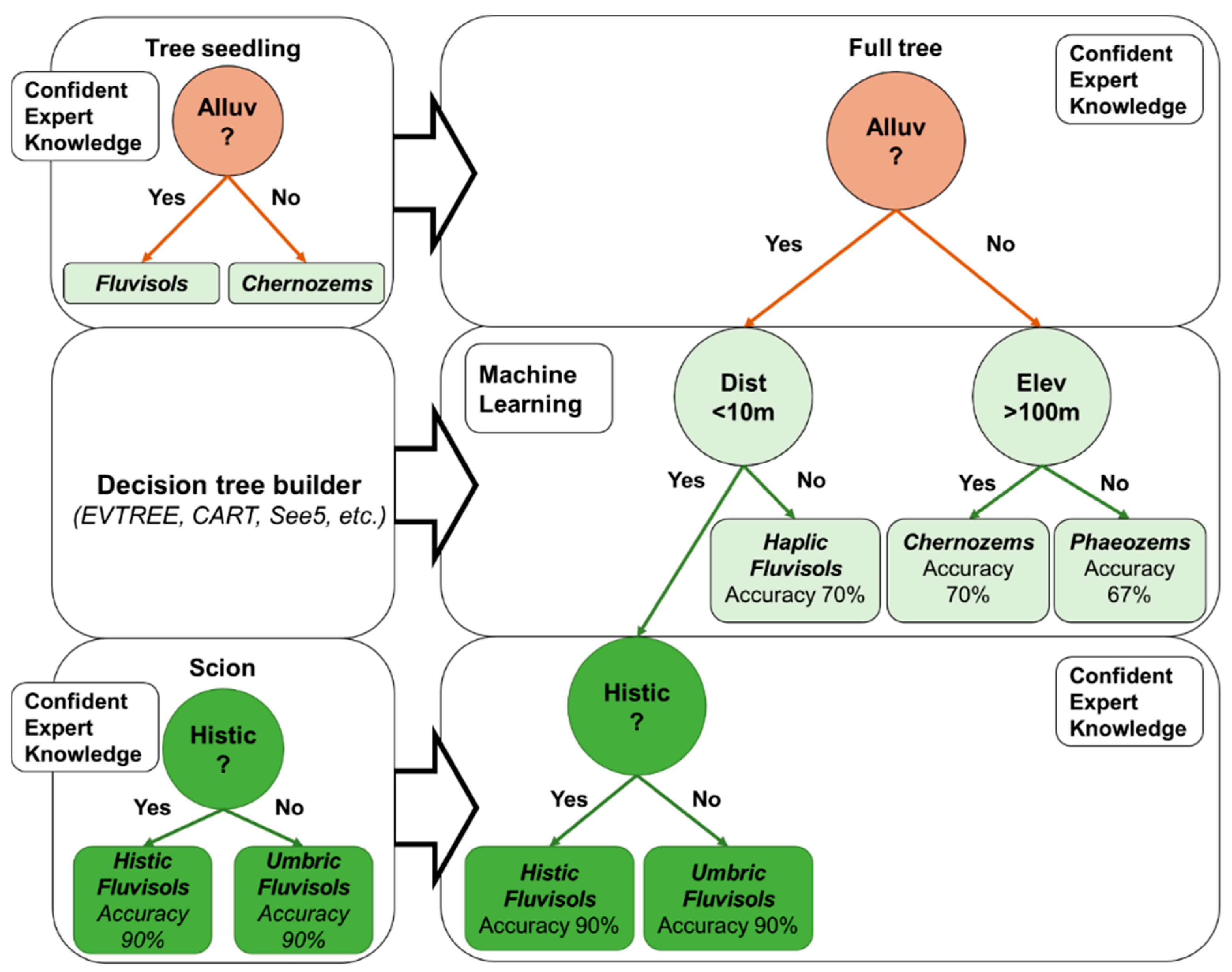
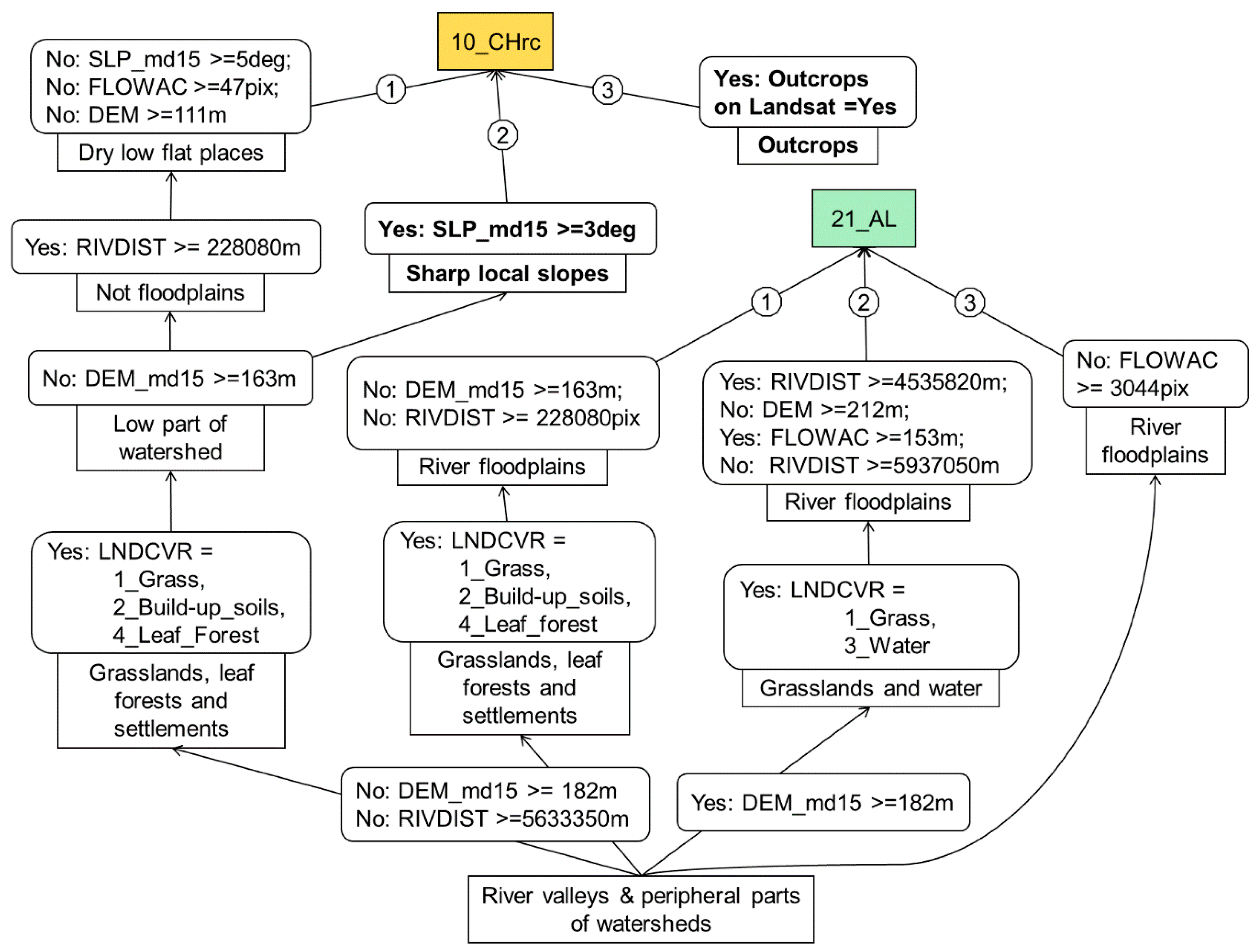
- The soil maps that were created using EVTREE had much higher notional consistency than the maps created using CART. The rules formulated by EVTREE for the delineation of Fluvisols and Phaeozems were much more direct than those formulated by CART. The direct models constructed by EVTREE for soil mapping are suitable for full or partial extrapolation to distant territories in the world with similar environmental conditions.
- The R package is required for the manual “constparty” decision tree model corrections, which can correct conditions and labels. The features for selecting tree branches and linking the tree with the associated soil map for the online monitoring of changes will be useful.
- We developed a digital soil mapping framework that imitates the process of traditional soil mapping and incorporates qualitative knowledge about soil geography into the quantitative rules for soil delineation. This model in the form of a decision tree can be expertly analyzed, and improvements can be made to the covariate list and notional consistency of the model.
- Challenges include the development of an easy-to-use and fast visual tree editor, automatic transformation of the classification trees to soil-specific rule chains, automatic statistical incorporation of prior soil knowledge in the process of tree building, and compliance with other methods for mapping continuous soil properties and soil functions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arrouays, D.; McBratney, A.B.; Minasny, B.; Hempel, J.W.; Heuvelink, G.B.M.; MacMillan, R.A.; McKenzie, N.J. The GlobalSoilMap Project Specifications. In GlobalSoilMap: Basis of the Global Spatial Soil Information System; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Arrouays, D.; Richer-de-Forges, A.C.; McBratney, A.B.; Hartemink, A.E.; Minasny, B.; Savin, I.; Lagacherie, P. The GlobalSoilMap project: Past, present, future, and national examples from France. Dokuchaev Soil Bull. 2018, 95, 3–23. [Google Scholar] [CrossRef]
- Arrouays, D.; Savin, I.; Leenaars, J.; McBratney, A.B. (Eds.) GlobalSoilMap—Digital Soil Mapping from Country to Globe; CRC Press: London, UK, 2017. [Google Scholar]
- Lagacherie, P.; McBratney, A.B. Chapter 1. Spatial soil information systems and spatial soil inference systems: Perspectives for digital soil mapping: Review article. Digital Soil Mapping. An introductory perspective. Dev. Soil Sci. 2007, 31, 137–150. [Google Scholar]
- Arrouays, D.; Leenaars, J.G.; Richer-de-Forges, A.C.; Adhikari, K.; Ballabio, C.; Greve, M.; Heuvelink, G. Soil legacy data rescue via GlobalSoilMap and other international and national initiatives. GeoResJ 2017, 14, 1–19. [Google Scholar] [CrossRef]
- Grunwald, S.; Thompson, J.A.; Boettinger, J.L. Digital soil mapping and modeling at continental scales: Finding solutions for global issues. Soil Sci. Soc. Am. J. 2011, 75, 1201–1213. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Guevara, M.A. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [Green Version]
- Lagacherie, P. Digital soil mapping: To state-of-the-art. In Digital Soil Mapping with Limited Data; Springer: Dordrecht, The Netherlands, 2008; pp. 3–14. [Google Scholar]
- McBratney, A.B.; de Gruijter, J.; Bryce, A. Pedometrics Timeline. Geoderma 2019, 338, 568–575. [Google Scholar] [CrossRef]
- Mulder, V.L.; De Bruin, S.; Schaepman, M.E.; Mayr, T.R. The use of remote sensing in soil and terrain mapping—A review. Geoderma 2011, 162, 1–19. [Google Scholar] [CrossRef]
- Qi, F.; Zhu, A.X. Knowledge discovery from soil maps using inductive learning. Int. J. Geogr. Inf. Sci. 2003, 17, 771–795. [Google Scholar] [CrossRef]
- Angelini, M.E.; Heuvelink, G.B.M.; Kempen, B.; Morrás, H.J.M. Mapping the soils of an Argentine Pampas region using structural equation modeling. Geoderma 2016, 281, 102–118. [Google Scholar] [CrossRef]
- Bui, E.N.; Henderson, B.L.; Viergever, K. Knowledge discovery from models of soil properties developed through data mining. Ecol. Modeling 2006, 191, 431–446. [Google Scholar] [CrossRef]
- McBratney, A.B.; Santos, M.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Zhogolev, A.V. A comparison of SoilGRIDs with the Disaggregated State Soil Map of Russia. In GlobalSoilMap—Digital Soil Mapping from Country to Globe; CRC press: London, UK, 2017; pp. 49–52. [Google Scholar]
- Odgers, N.P.; Sun, W.; McBratney, A.B.; Minasny, B.; Clifford, D. Disaggregating and harmonising soil map units through resampled classification trees. Geoderma 2014, 214, 91–100. [Google Scholar] [CrossRef]
- Pásztor, L.; Laborczi, A.; Takács, K.; Szatmári, G.; Bakacsi, Z.; Szabó, J. DOSoReMI as the National Implementation of GlobalSoilMap for the Territory of Hungary. In GlobalSoilMap—Digital Soil Mapping from Country to Globe; CRC Press: London, UK, 2017; pp. 17–22. [Google Scholar]
- Caubet, M.; Dobarco, M.R.; Arrouays, D.; Minasny, B.; Saby, N.P.A. Merging country, continental and global predictions of soil texture: Lessons from ensemble modeling in France. Geoderma 2019, 337, 99–110. [Google Scholar] [CrossRef]
- Chinilin, A.V.; Savin, I.Y. The large-scale digital mapping of soil organic carbon using machine learning algorithms. Dokuchaev Soil Bull. 2018, 91, 46–62. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random Forest as a generic framework for predictive modelling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Angelini, M.E.; Heuvelink, G.B.M.; Kempen, B. Multivariate mapping of soil with structural equation modeling. Eur. J. Soil Sci. 2017, 68, 575–591. [Google Scholar] [CrossRef] [Green Version]
- Zhu, A.; Cheng-Zhi, Q.; Peng, L.; Fei, D. Digital soil mapping for smart agriculture: The SoLIM method and software platforms. Rudn J. Agron. Anim. Ind. 2018, 13, 317–335. [Google Scholar] [CrossRef]
- Zhu, A.X.; Band, L.E.; Dutton, B.; Nimlos, T.J. Automated soil inference under fuzzy logic. Ecol. Modeling 1996, 90, 123–145. [Google Scholar] [CrossRef]
- Qi, F.; Zhu, A.X. Comparing three methods for modeling the uncertainty in knowledge discovery from area-class soil maps. Comput. Geosci. 2011, 37, 1425–1436. [Google Scholar] [CrossRef]
- Zhogolev, A.V.; Savin, I.Y. Automated updating of medium-scale soil maps. Eurasian Soil Sci. 2016, 49, 1241–1249. [Google Scholar] [CrossRef]
- Bui, E.N. Data-driven Critical Zone science: A new paradigm. Sci. Total Environ. 2016, 568, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.X.; Minasny, B.; Malone, B.P.; McBratney, A.B. Pedology and Digital Soil Mapping (DSM). Eur. J. Soil Sci. 2019, 70, 216–235. [Google Scholar] [CrossRef]
- Padarian, J.; Morris, J.; Minasny, B.; McBratney, A.B. Pedotransfer Functions and Soil Inference Systems; Springer: Berlin/Heidelberg, Germany, 2018; pp. 195–220. [Google Scholar]
- Lagacherie, P. Formalisation des Lois de Distribution des Sols Pour Automatiser la Cartographie Pédologique à Partir d’un Secteur Pris Comme Reference. Master’s Thesis, Université de Montpellier, Institut National de la Recherche Agronomique, Montpellier, France, 1992. [Google Scholar]
- Therneau, T.M.; Atkinson, E.J. An Introduction to Recursive Partitioning Using the RPART Routines. 2018. Available online: https://cran.r-project.org/web/packages/rpart/vignettes/longintro.pdf (accessed on 28 February 2019).
- Grubinger, T.; Zeileis, A.; Pfeiffer, K.P. Evtree: Evolutionary Learning of Globally Optimal Classification and Regression Trees in R. J. Stat. Softw. 2014, 61, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Balestriero, R.; Baraniuk, R. A spline theory of deep learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 374–383. [Google Scholar]
- Chimatapu, R.; Hagras, H.; Starkey, A.; Owusu, G. Explainable AI and Fuzzy Logic Systems. In International Conference on Theory and Practice of Natural Computing; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–20. [Google Scholar]
- Savin, I.Y. Computer-Based Imitation of Soil Mapping. Digital Soil Mapping: Theoretical and Experimental Investigations; V.V. Dokuchaev Soil Science Institute: Moscow, Russia, 2012; pp. 26–34. (In Russian) [Google Scholar]
- Egorov, V.V.; Fridland, V.M.; Ivanova, E.N.; Rozov, N.N. Classification and Diagnostics of Soils of the Soviet Union; Kolos: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Shishov, L.L.; Tonkonogov, V.D.; Lebedeva, I.I.; Gerasimova, V.I. (Eds.) Classification and Diagnostic System of Russian Soils; Oikumena: Smolensk, Russia, 2004. (In Russian) [Google Scholar]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2006; World Soil Resources Reports 103; FAO: Rome, Italy, 2006. [Google Scholar]
- Ilyina, L.P.; Mihailova, R.P.; Simakova, M.S.; Shubina, I.G. Compilation of the Regional Medium-Scale Soil Maps with Representation of Patterns of Soil Cover; V.V. Dokuchaev Soil Science Institute: Moscow, Russia, 1990. [Google Scholar]
- Soil Survey Staff. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Surveys, 2nd ed.; Agriculture Handbook, 436; Natural Resources Conservation Service: Washington, DC, USA; U.S. Department of Agriculture: Washington, DC, USA, 1999.
- Zinck, J.A. Physiography and Soils. In Soil Survey Courses. International Institute for Aerospace and Earth Sciences; ITC: Enschede, The Netherlands, 1988. [Google Scholar]
- Hengl, T. Finding the right pixel size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Zhu, A.X.; Zhang, L.; Tang, G.A. Drainage basin object-based method for regional-scale landform classification: A case study of loess area in China. Phys. Geogr. 2018, 39, 523–541. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-filled SRTM for the Globe Version 4. Available online: http://srtm.csi.cgiar.org (accessed on 28 February 2019).
- Qin, C.Z.; Zhu, A.X.; Pei, T.; Li, B.L.; Scholten, T.; Behrens, T.; Zhou, C.H. An approach to computing topographic wetness index based on maximum downslope gradient. Precis. Agric. 2011, 12, 32–43. [Google Scholar] [CrossRef]
- Hengl, T.; Maathuis, B.H.P.; Wang, L. Geomorphometry in ILWIS. Dev. Soil Sci. 2009, 33, 309–331. [Google Scholar]
- Hothorn, T.; Zeileis, A. Partykit: A modular toolkit for recursive partytioning in R. J. Mach. Learn. Res. 2015, 16, 3905–3909. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and regression trees. Wadsworth Int. Group 1984, 37, 237–251. [Google Scholar]
- Rossiter, D.G.; Zeng, R.; Zhang, G.L. Accounting for taxonomic distance in accuracy assessment of soil class predictions. Geoderma 2017, 292, 118–127. [Google Scholar] [CrossRef] [Green Version]


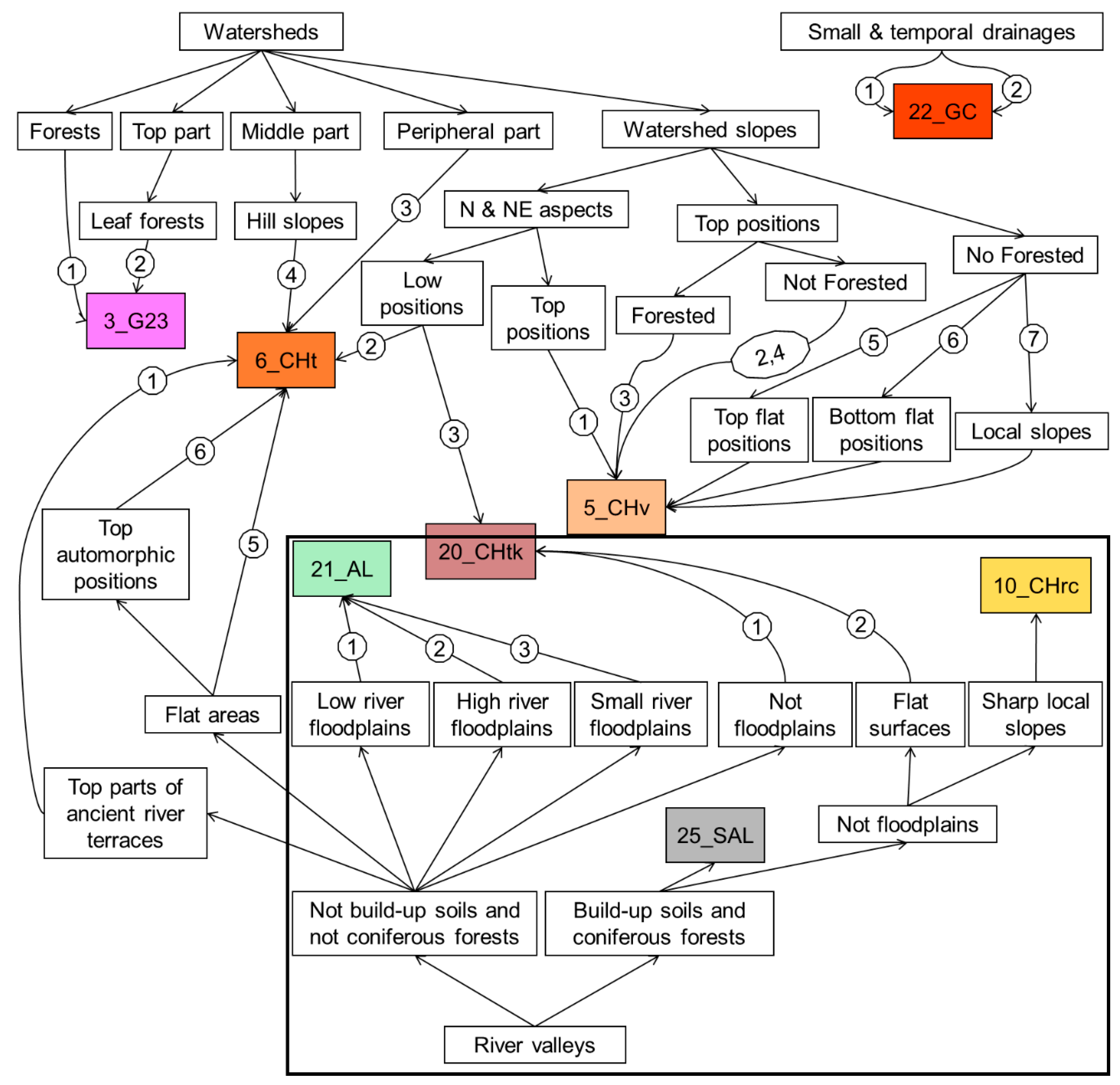
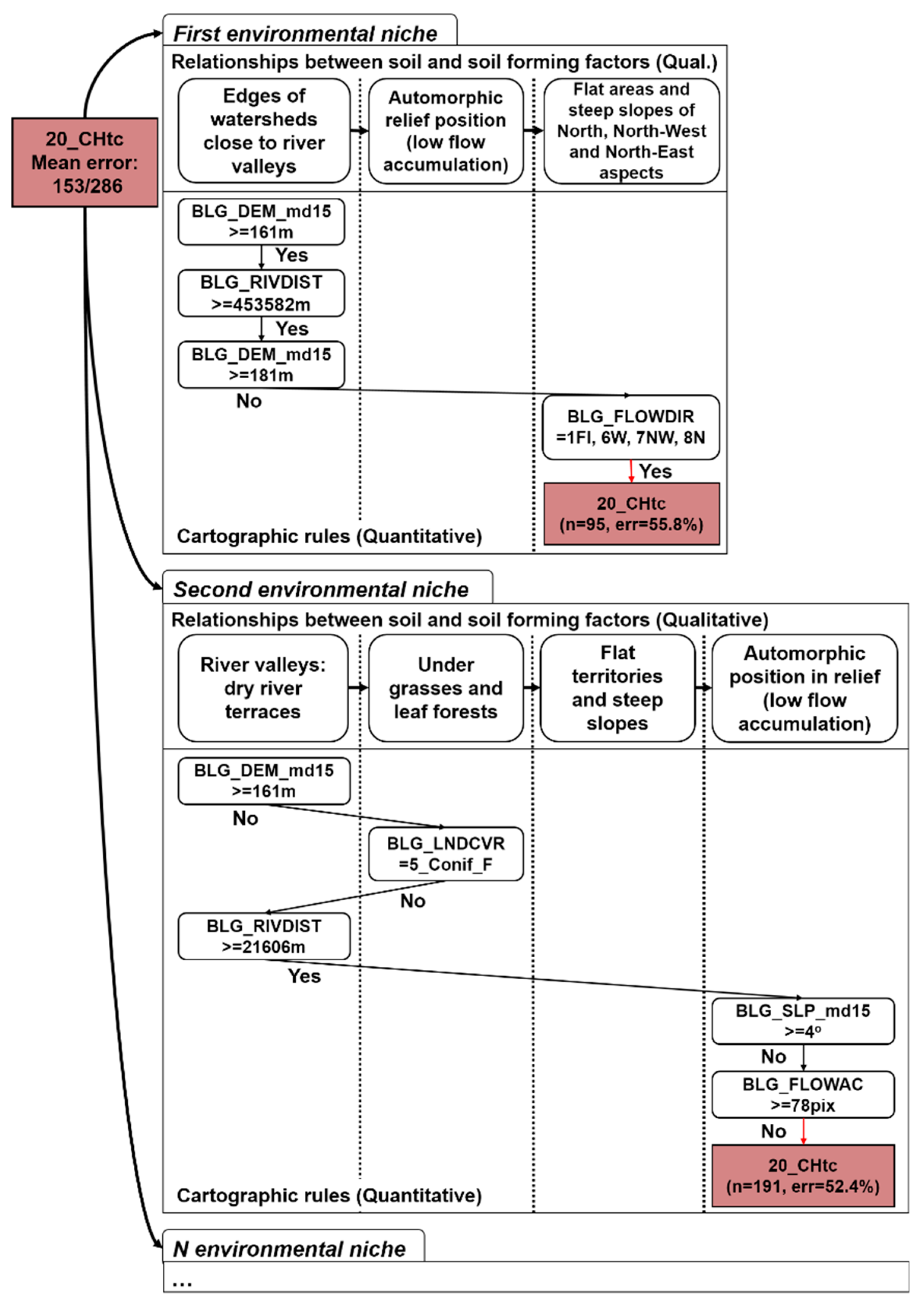

| Soil name in RCS1977 Classification [35] | Soil Name in RCS2004 Classification [36] | Soil Name in WRB2006 Classification [37] | Main Soil Forming Factors |
|---|---|---|---|
| Chernozems Typical (CHt) | Agrochernozem Migrational-Mycelial | Voronic Chernozems Pachic | flat interfluve on watersheds and riverine flat interfluves |
| Chernozems Leached (CHv) | Agrochernozems Clay-Illuvial | Voronic Chernozems Pachic | depressions of flat interfluves |
| Chernozems Residual-Calcareous (CHrc) | Agrochernozems Textural-Carbonate | Leptic Chernozems | steep slopes with calcareous sediment |
| Chernozems Podzolic (CHo) | Agrochernozems Podzolic Clay-Illuvial | Luvic Phaeozems | flat interfluves where oak forests were cut 1–2 hundred years ago |
| Grey and Dark Grey forest (G23) | Grey and Dark Grey soils | Greyic Phaeozems Albic | under oak forests |
| Meadow Chernozems (CHl) | Agro-Dark-humus Gley soils | Voronic Chernozems Pachic | ancient alluvial terraces |
| Sod Alluvial (SAL) | Sod Alluvial Laminate | Haplic Fluvisols | floodplain terraces, floodplains with lightly drained water–glacial deposits |
| Alluvial Meadow (AL) | Alluvial Dark-humus soils | Umbric Fluvisols Oxyaquic | river valleys |
| Gully complex (GC) | Gully complex | - | beams, ravines, and valleys of small rivers |
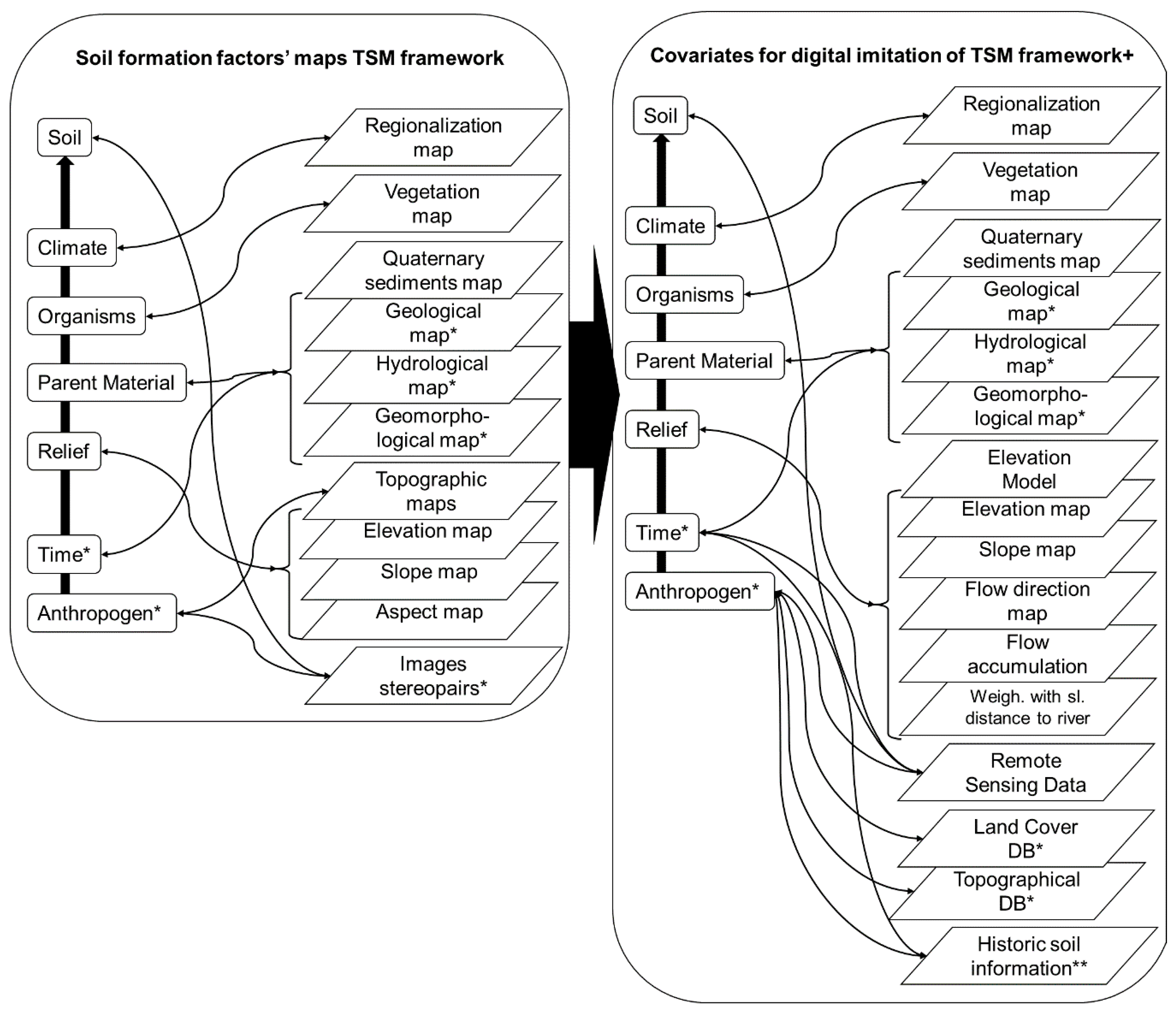
| Traditional Soil Mapping Framework [25,38] | Digital Soil Mapping Framework Using the Proposed Approach |
|---|---|
|
|
| № | Covariate | Basic Data | Method of Preparation |
|---|---|---|---|
| 1 | Elevation map (DEM) | DEM SRTM v.4.1 | Original data [43] |
| 2 | Elevation map median filtered through fifteen pixels (DEM_md15) | DEM SRTM v.4.1 | Median filtration [25] |
| 3 | Slope map (SLP) | DEM SRTM v.4.1 | Calculation [25] |
| 4 | Flow direction map (FLOWDIR) | Calculation [25] | |
| 5 | Slope map median filtered through fifteen pixels (SLP_md15) | Median filtration [25] | |
| 6 | Flow direction map median filtered through fifteen pixels (FLOWDIR_md15) | Median filtration [25] | |
| 7 | Weighted with slope distance to rivers (RIVDIST) | Calculation [25] | |
| 8 | Flow accumulation (FLOWAC) | Calculation of the number of input pixels of any outlet | |
| 9 | Vegetation map: coniferous forest, leaf forest, water, built-up area, cropping areas and grasslands, and peat bogs (LNDCVR) | Landsat 8OLI | Classification via the Random Forest algorithm using a prepared sample set |
| 10 | Type of quaternary sediments (QGEOL) | Quaternary sediment map at a scale of 1:500,000 (based on maps at a scale of 1:200,000) | Manual vectorization |
| Soil Model | Mean prior Probability, % | Minimum Prior Probability, % | Mean Number of Conditions | Stability (Expert) | Notional Consistency (Expert) | Comments (Expert) |
|---|---|---|---|---|---|---|
| EVTREE | 62.2 | 32.4 | 24 | ++/− | High | correct Fluvisols delineation |
| CART | 60.8 | 27.2 | 155 | +/−− | Medium | overlearned for Fluvisols and Phaeozems |
| Random Forest 1 | not applied to ensemble methods 1 | not applied to ensemble methods 1 | →∞ | not applied to ensemble methods 1 | not applied to ensemble methods 1 | overlearned for Fluvisols |
| Soil Model | Overall Accuracy, % | Producer’s Accuracy, % | User’s Accuracy, % | Kappa |
|---|---|---|---|---|
| EVTREE | 59 | 56 | 65 | 0.45 |
| CART | 67 | 56 | 63 | 0.55 |
| Random Forest | 87 | 81 | 91 | 0.83 |
| Soil Model | Overall Accuracy, % | Producer’s Accuracy, % | User’s Accuracy, % | Kappa |
|---|---|---|---|---|
| EVTREE | 59 | 49 | 61 | 0.45 |
| CART | 61 | 53 | 55 | 0.49 |
| Random Forest | 62 | 51 | 71 | 0.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhogolev, A.; Savin, I. Soil Mapping Based on Globally Optimal Decision Trees and Digital Imitations of Traditional Approaches. ISPRS Int. J. Geo-Inf. 2020, 9, 664. https://doi.org/10.3390/ijgi9110664
Zhogolev A, Savin I. Soil Mapping Based on Globally Optimal Decision Trees and Digital Imitations of Traditional Approaches. ISPRS International Journal of Geo-Information. 2020; 9(11):664. https://doi.org/10.3390/ijgi9110664
Chicago/Turabian StyleZhogolev, Arseniy, and Igor Savin. 2020. "Soil Mapping Based on Globally Optimal Decision Trees and Digital Imitations of Traditional Approaches" ISPRS International Journal of Geo-Information 9, no. 11: 664. https://doi.org/10.3390/ijgi9110664
APA StyleZhogolev, A., & Savin, I. (2020). Soil Mapping Based on Globally Optimal Decision Trees and Digital Imitations of Traditional Approaches. ISPRS International Journal of Geo-Information, 9(11), 664. https://doi.org/10.3390/ijgi9110664






