Large Common Plansets-4-Points Congruent Sets for Point Cloud Registration
Abstract
1. Introduction
2. Related Work
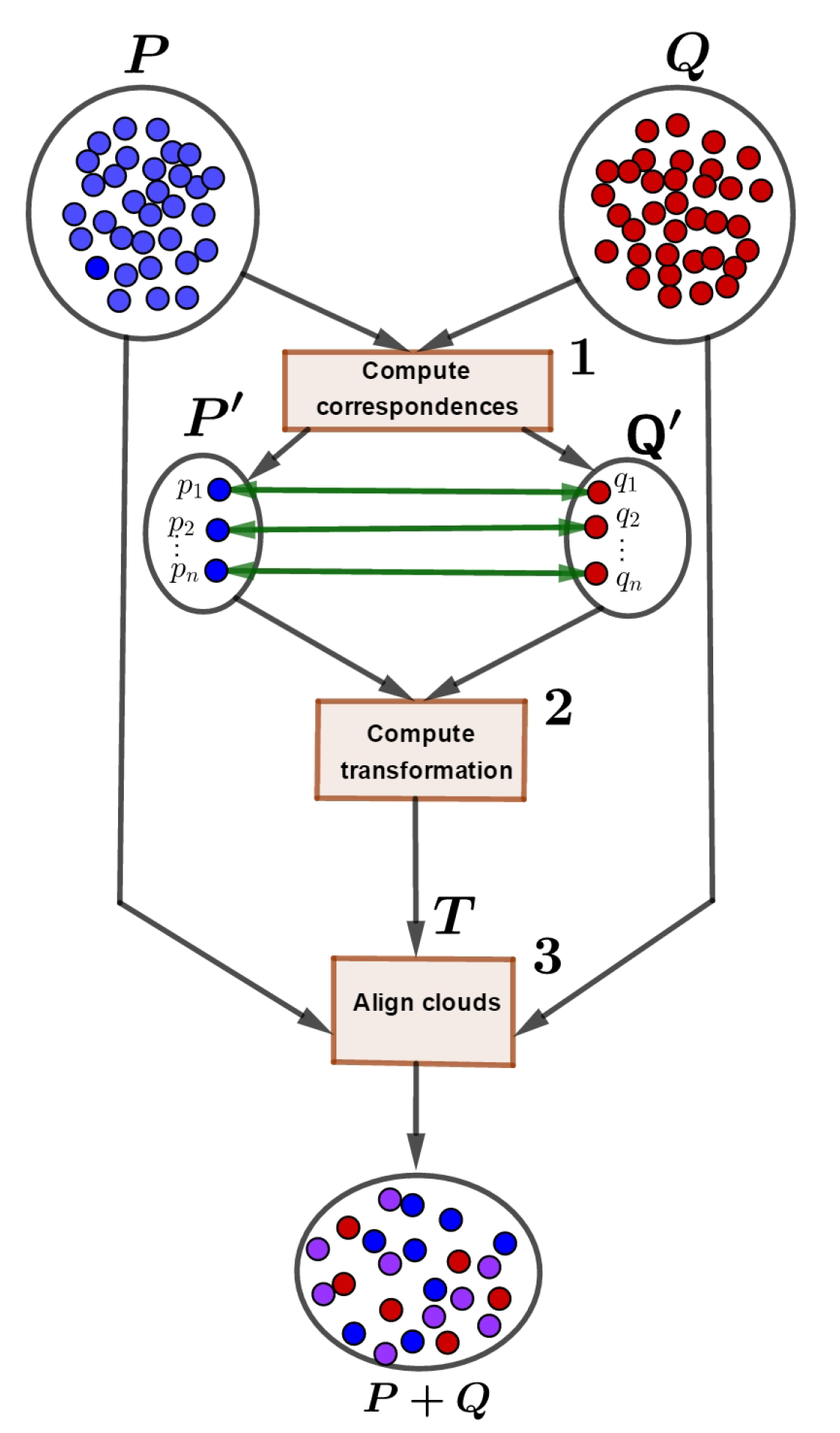
- Initialize registration parameters (Rotation, Translation, Scale) and registration error.
- For each point in the P, find the corresponding closest point in Q.
- Compute registration parameters, given the point correspondences obtained in step 2.
- Apply the alignment to P
- Compute the registration error between the currently aligned P and Q
- If error > threshold and max iterations has not been reached return to step 2 with new P.
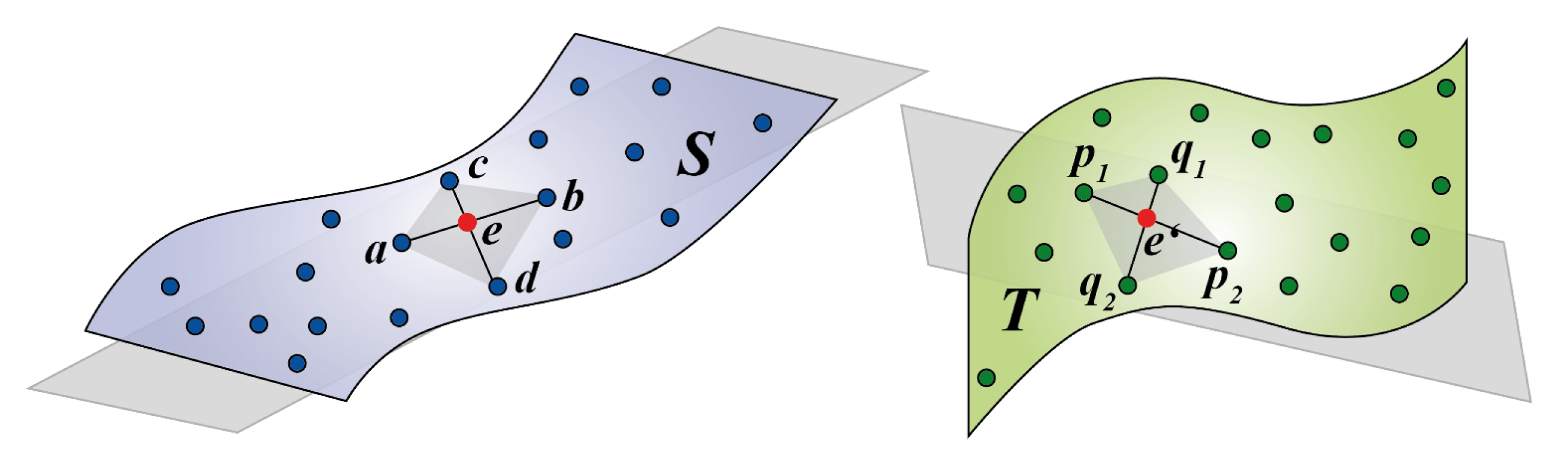
- Select a set of 4 coplanar points B in S
- Find the congruent bases U of B into T within an approximation level
- For each find the best rigid transform ,
- Find , such that
- If then = and
- Repeat the process from step 2 L times
- return
3. Large Common Plansets-4PCS (LCP-4PCS)
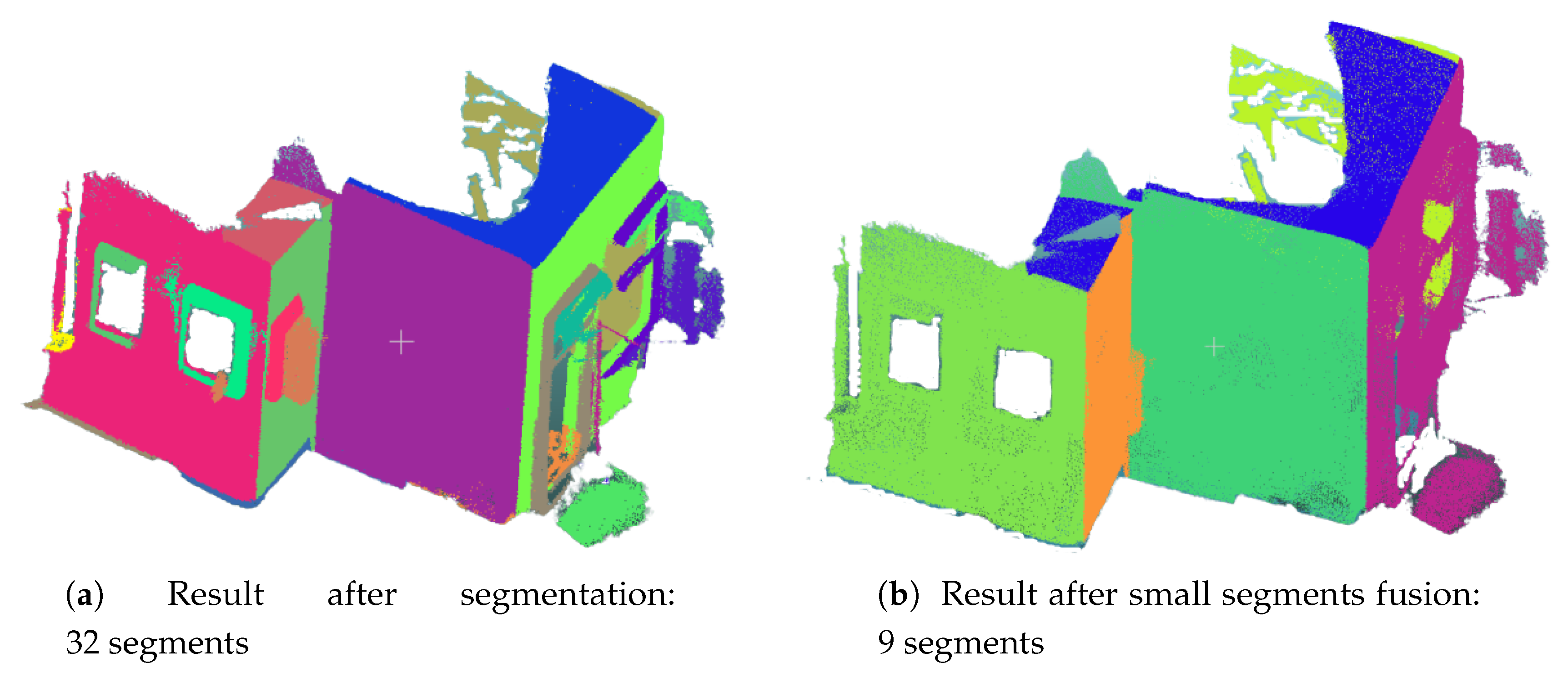
- In cases where the overlap levels between the entities to be merged are very low. A relatively large increase in the number of maximum iterations sometimes leads to good results. However, the execution time increases considerably.
- In cases where overlapping portions between the point clouds to be merged are concentrated in a relatively small part of the entities. An increase in the number of iterations does not improve the results.
| Algorithm 1 LCP-4PCS Given two point clouds P and Q in arbitrary initial positions, an approximation level, an overlapping threshold and a maximal iteration. |
|
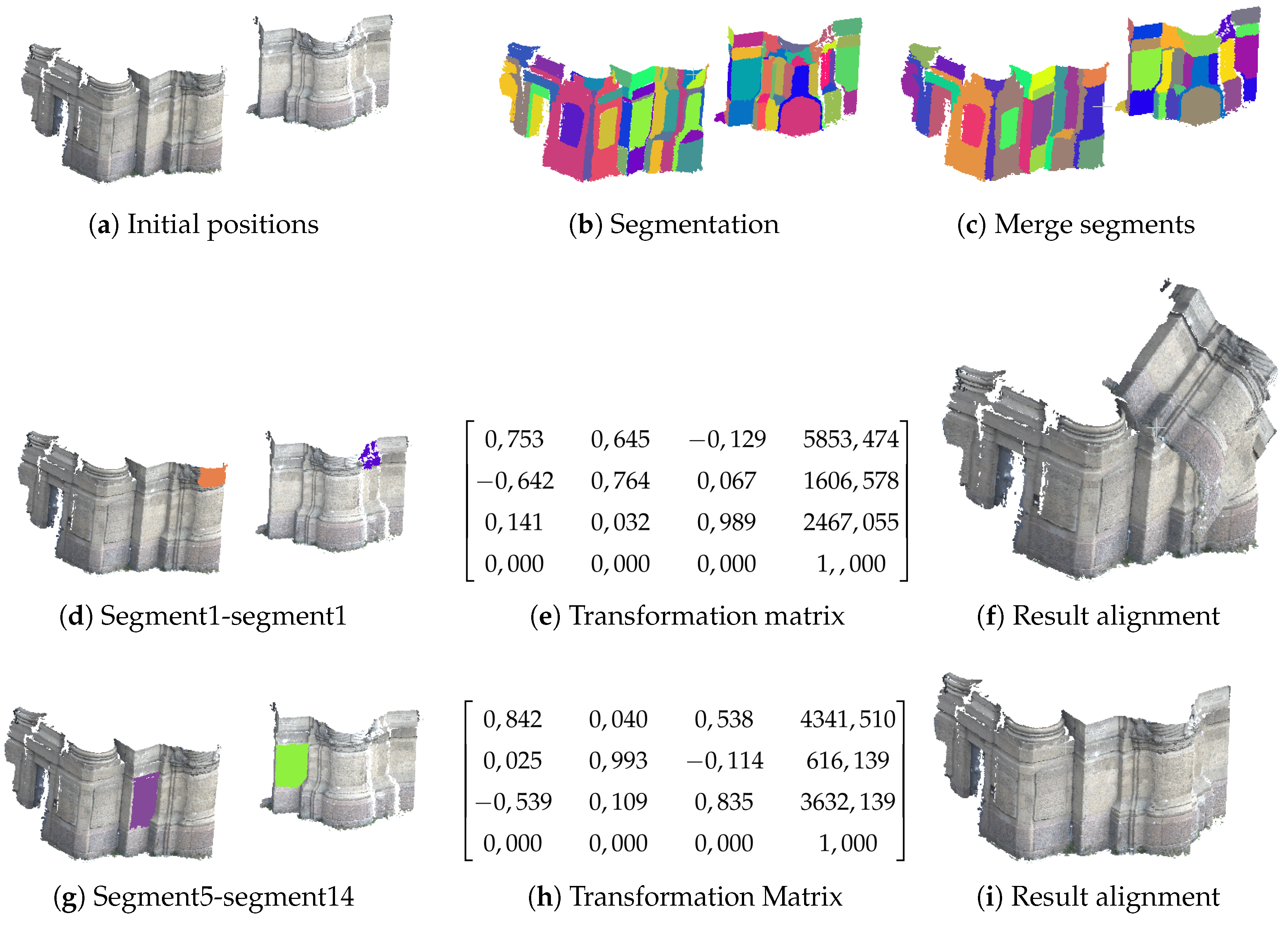
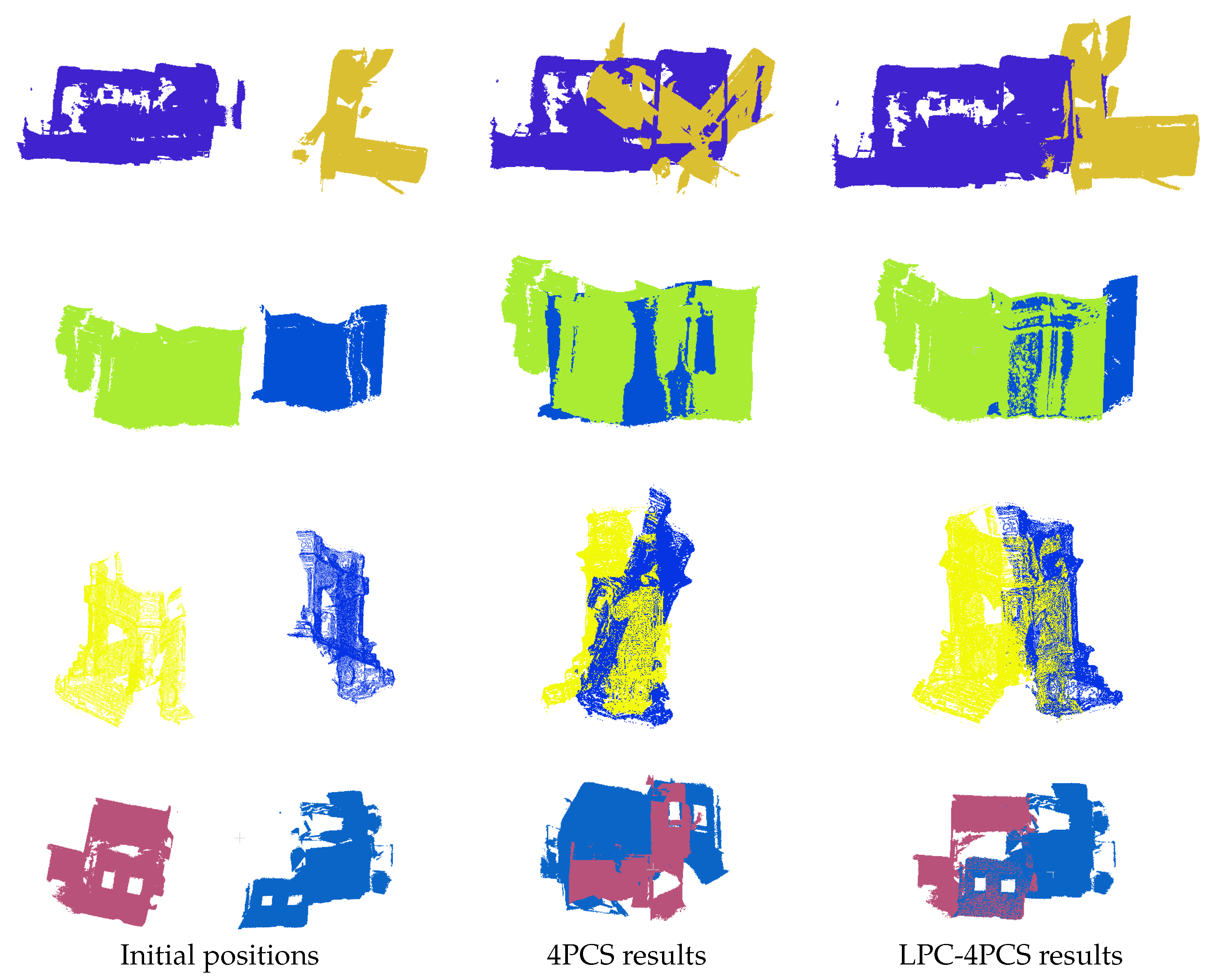
4. Experiments and Results
4.1. Data and Implementation
4.2. Tests and Comparisons
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bosché, F.; Forster, A.; Valero, E. 3D Surveying Technologies and Applications: Point Clouds and Beyond; Heriot-Watt University: Edinburgh, UK, 2015. [Google Scholar]
- Daneshmand, M.; Helmi, A.; Avots, E.; Noroozi, F.; Alisinanoglu, F.; Arslan, H.; Gorbova, J.; Haamer, R.; Ozcinar, C.; Anbarjafari, G. 3D Scanning: A Comprehensive Survey. Scand. J. For. Res. 2018, 30, 73–86. [Google Scholar]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-Points Congruent Sets for Robust Pairwise Surface Registration. In Proceedings of the 35th International Conference on Computer Graphics and Interactive Techniques (SIGGRAPH’08) Interactive Techniques (SIGGRAPH’08), Los Angeles, CA, USA, 11–15 August 2008; Volume 27. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for Registration of 3D Shapes. In Proceedings of the SPIE1611, Sensor Fusion IV: Control Paradigms and Data Structure, Boston, MA, USA, 12–15 November 1992; pp. 239–255. [Google Scholar]
- Horn, B. Closed-Form Solution of Absolute Orientation Using Unit Quaternions. J. Opt. Soc. A 1987, 4, 629–642. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R. A Review of Point Cloud Registration Algorithms for Mobile Robotics. Found. Trends Robot. 2015, 4, 1–104. [Google Scholar] [CrossRef]
- Mellado, N.; Mitra, N.J.; Aiger, D. Super 4PCS: Fast Global Pointcloud Registration via Smart Indexing. Comput. Graph. Forum 2014, 33. [Google Scholar] [CrossRef]
- Huang, J.; Kwok, T.H.; Zhou, C. V4PCS: Volumetric 4PCS Algorithm for Global Registration. J. Mech. Des. 2017, 139. [Google Scholar] [CrossRef]
- Nguyen, A.; Le, B. 3D point cloud segmentation: A survey. In Proceedings of the 2013 6th IEEE Conference on Robotics, Automation and Mechatronics (RAM), Manila, Philippines, 12–15 November 2013; pp. 225–230. [Google Scholar] [CrossRef]
- Limberger, F.; Oliveira, M. Real-time detection of planar regions in unorganized point clouds. Pattern Recognit. 2015, 48. [Google Scholar] [CrossRef]
- Grilli, E.; Menna, F.; Remondino, F. A review of point clouds segmentation and classification algorithms. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W3, 339–344. [Google Scholar] [CrossRef]
- Huber, D.; Hebert, M. Fully Automatic Registration Of Multiple 3D Data Sets. Image Vis. Comput. 2003, 21, 637–650. [Google Scholar] [CrossRef]
- Tazir, M.L.; Gokhool, T.; Checchin, P.; Malaterre, L.; Trassoudaine, L. CICP: Cluster Iterative Closest Point for Sparse-Dense Point Cloud Registration. Robot. Auton. Syst. 2018, 108. [Google Scholar] [CrossRef]
- Rangaprasad, A.S.; Zevallos, N.; Vagdargi, P.; Choset, H. Registration with a small number of sparse measurements. Int. J. Robot. Res. 2019, 38, 1403–1419. [Google Scholar] [CrossRef]
- Holz, D.; Ichim, A.; Tombari, F.; Rusu, R.; Behnke, S. Registration with the Point Cloud Library—A Modular Framework for Aligning in 3-D. IEEE Robot. Autom. Mag. 2015, 22, 110–124. [Google Scholar] [CrossRef]
- Faugeras, O.; Hebert, M. The Representation, Recognition, and Locating of 3-D Objects. Int. J. Robot. Res. IJRR 1986, 5, 27–52. [Google Scholar] [CrossRef]
- CloudCompare. GPL Software. 2019. Version 2.10.3. Available online: https://cloudcompare.org/ (accessed on 28 June 2020).
- Schroeder, W.; Martin, K.; Lorensen, B. The Visualization Toolkit, 4th ed.; Kitware: Clifton Park, NY, USA, 2009; ISBN 978-1-930934-19-1. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, W.; Lu, K.Q.; Wei, Y.D.; Chen, Z.C. A New Method for Registration of 3D Point Sets with Low Overlapping Ratios. Procedia CIRP 2015, 27, 202–206. [Google Scholar] [CrossRef]
- He, Y.; Liang, B.; Yang, J.; Li, S.; He, J. An Iterative Closest Points Algorithm for Registration of 3D Laser Scanner Point Clouds with Geometric Features. Sensors 2017, 17, 1862. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Moral, E.; Rives, P.; Arevalo, V.; González-Jiménez, J. Scene Structure Registration for Localization and Mapping. Robot. Auton. Syst. 2015, 75. [Google Scholar] [CrossRef]
- Forstner, W.; Khoshelham, K. Efficient and Accurate Registration of Point Clouds with Plane to Plane Correspondences. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2165–2173. [Google Scholar] [CrossRef]
- Li, X.; Guskov, I. Multiscale Features for Approximate Alignment of Point-based Surfaces. In Proceedings of the Symposium on Geometry Processing, Vienna, Austria, 4–6 July 2005; pp. 217–226. [Google Scholar]
- Gelfand, N.; Mitra, N.; Guibas, L.; Pottmann, H. Robust Global Registration. In Proceedings of the Symposium on Geometry Processing, Vienna, Austria, 4–6 July 2005. [Google Scholar]
- Biber, P.; Straßer, W. The Normal Distributions Transform: A New Approach to Laser Scan Matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003)(Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 3, pp. 2743–2748. [Google Scholar] [CrossRef]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan Registration for Autonomous Mining Vehicles Using 3D-NDT. J. Field Robot. 2007, 24, 803–827. [Google Scholar] [CrossRef]
- Rusu, R.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar] [CrossRef]
- Rusu, R.; Blodow, N.; Marton, Z.; Beetz, M. Aligning Point Cloud Views using Persistent Feature Histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar] [CrossRef]
- Ambühl, C.; Chakraborty, S.; Gärtner, B. Computing Largest Common Point Sets under Approximate Congruence. In European Symposium on Algorithms; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1879, pp. 52–63. [Google Scholar] [CrossRef]
- Dagum, L.; Menon, R. OpenMP: An Industry-Standard API for Shared-Memory Programming. Comput. Sci. Eng. IEEE 1998, 5, 46–55. [Google Scholar] [CrossRef]
- Balado Frias, J.; Díaz Vilariño, L.; Arias, P.; Gonzalez, H. Automatic classification of urban ground elements from mobile laser scanning data. Autom. Constr. 2018, 86, 226–239. [Google Scholar] [CrossRef]



| Dataset | Scan1 | Scan2 | Time(s) | |||
|---|---|---|---|---|---|---|
| Number Segments before Fusion | Number Segments after Fusion | Number Segments before Fusion | Number Segments after Fusion | Time before Fusion | Time after Fusion | |
| Camertronix | 27 | 14 | 11 | 8 | 179 | 107 |
| Valentino | 34 | 21 | 19 | 14 | 75 | 44 |
| Charlottebügerturm | 43 | 25 | 37 | 22 | 162 | 91 |
| Buro | 32 | 9 | 11 | 6 | 173 | 98 |
| Flurzimmer | 27 | 18 | 6 | 5 | 74 | 49 |
| Dataset | Size(x1000) | 4PCS | LCP-4PCS | ||||
|---|---|---|---|---|---|---|---|
| Scan1 | Scan2 | Aligned Samples (%) | Time (s) | Aligned Samples (%) | Number Aligned Segments | Time (s) | |
| Camertronix | 1,708,126 | 1,281,042 | 528 | 141 | 17.2 | 3 | 107 |
| Valentino | 82,259 | 75,533 | 507 | 108 | 223 | 2 | 44 |
| Charlottebürgerturm | 1,218,731 | 1,132,942 | 998 | 165 | 208 | 8 | 91 |
| Buro | 1,447,277 | 1,051,268 | 673 | 125 | 191 | 2 | 98 |
| Flurzimmer | 95,804 | 89,378 | 494 | 93 | 157 | 2 | 49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fotsing, C.; Nziengam, N.; Bobda, C. Large Common Plansets-4-Points Congruent Sets for Point Cloud Registration. ISPRS Int. J. Geo-Inf. 2020, 9, 647. https://doi.org/10.3390/ijgi9110647
Fotsing C, Nziengam N, Bobda C. Large Common Plansets-4-Points Congruent Sets for Point Cloud Registration. ISPRS International Journal of Geo-Information. 2020; 9(11):647. https://doi.org/10.3390/ijgi9110647
Chicago/Turabian StyleFotsing, Cedrique, Nafissetou Nziengam, and Christophe Bobda. 2020. "Large Common Plansets-4-Points Congruent Sets for Point Cloud Registration" ISPRS International Journal of Geo-Information 9, no. 11: 647. https://doi.org/10.3390/ijgi9110647
APA StyleFotsing, C., Nziengam, N., & Bobda, C. (2020). Large Common Plansets-4-Points Congruent Sets for Point Cloud Registration. ISPRS International Journal of Geo-Information, 9(11), 647. https://doi.org/10.3390/ijgi9110647





