Evaluation of the Space Syntax Measures Affecting Pedestrian Density through Ordinal Logistic Regression Analysis
Abstract
1. Introduction
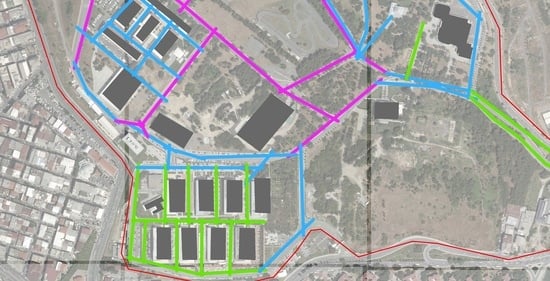
2. Study Area
3. Materials and Methods
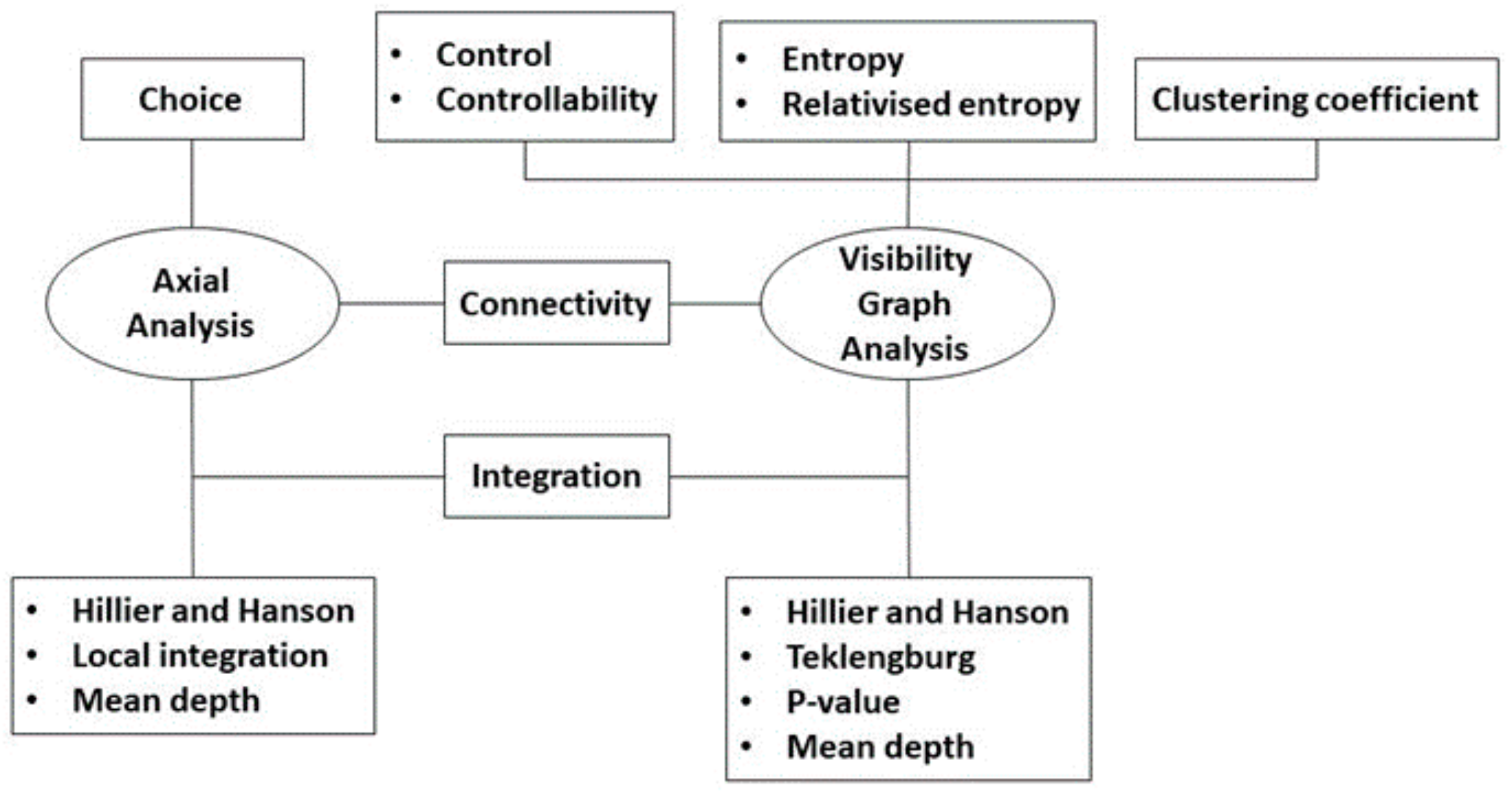
3.1. AA and VGA Measures
3.2. Determining the Most Proper Measure
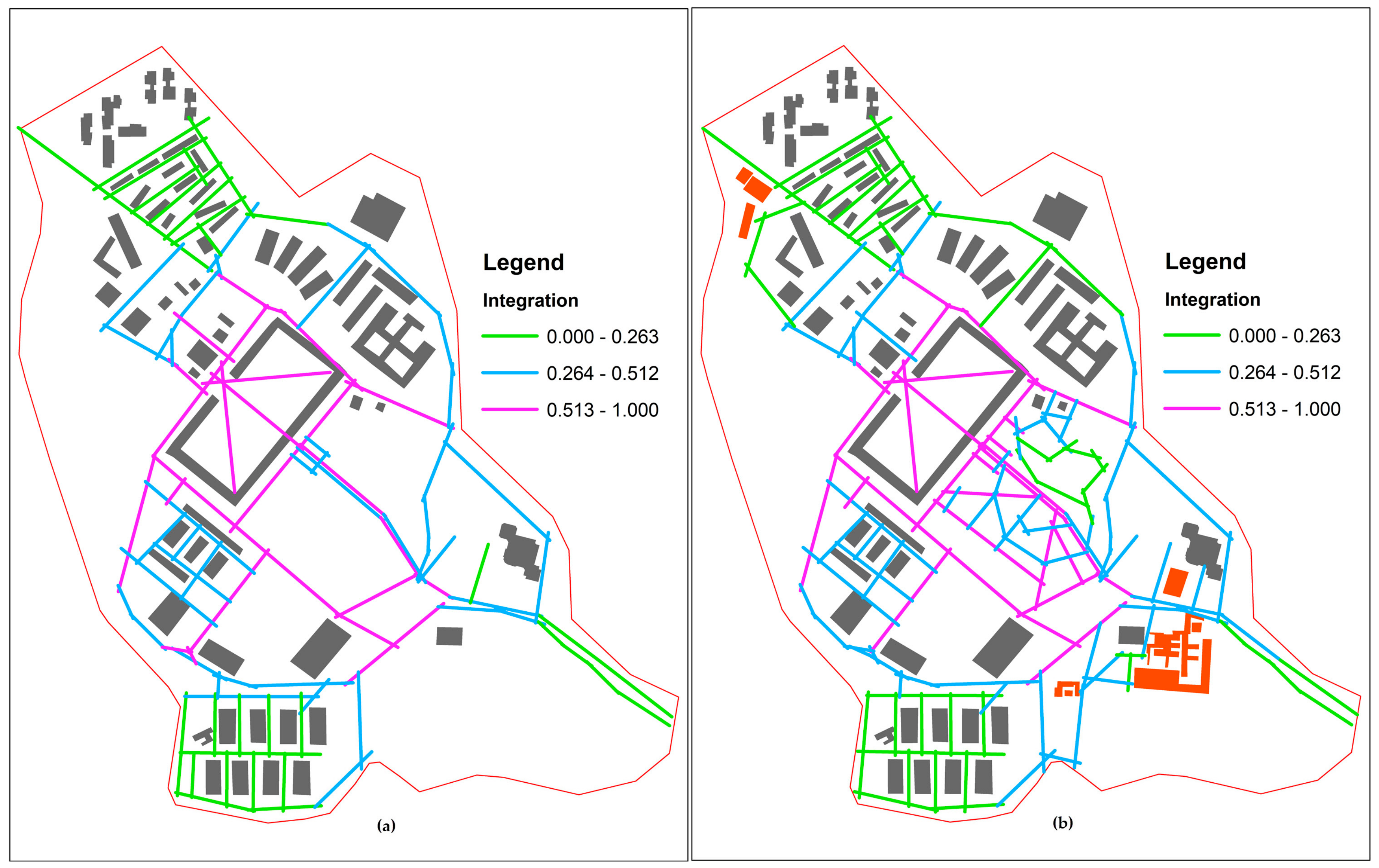
3.3. Analysing the Effect of Master Plan
4. Results
4.1. Calculated Values for Measures
4.2. Ordinal Logistic Regression Analysis
4.3. Evaluation of Current and Master Plan Datasets
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seneviratne, P.N.; Morrall, J.F. Analysis of factors affecting the choice of route of pedestrians. Trans. Plan. Technol. 1985, 10, 147–159. [Google Scholar] [CrossRef]
- Hillier, B.; Penn, A.; Hanson, J.; Grajewski, T.; Xu, J. Natural movement: Or, configuration and attraction in urban pedestrian movement. Environ. Plan. B Plan. Des. 1993, 20, 29–66. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.J.; Molnar, P.; Vicsek, T. Simulation of pedestrian crowds in normal and evacuation situations. In Pedestrian Evacuation Dynamics, 1st ed.; Schreckenberg, M., Sharma, S.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 21, pp. 21–58. ISBN 978-3-642-07658-9. [Google Scholar]
- Kim, S.; Choi, J.; Kim, Y. Determining the sidewalk pavement width by using pedestrian discomfort levels and movement characteristics. KSCE J. Civ. Eng. 2011, 15, 883. [Google Scholar] [CrossRef]
- Asadi-Shekari, Z.; Moeinaddini, M.; Shah, M.Z. A pedestrian level of service method for evaluating and promoting walking facilities on campus streets. Land Use Policy 2014, 38, 175–193. [Google Scholar] [CrossRef]
- Larrañaga, A.M.; Rizzi, L.I.; Arellana, J.; Strambi, O.; Cybis, H.B.B. The influence of built environment and travel attitudes on walking: A case study of Porto Alegre, Brazil. Int. J. Sustain. Trans. 2016, 10, 332–342. [Google Scholar] [CrossRef]
- Dovey, K.; Pafka, E. What is walkability? The urban DMA. Urban Stud. 2019, 57, 93–108. [Google Scholar] [CrossRef]
- Ericson, J.D.; Chrastil, E.R.; Warren, W.H. Space syntax visibility graph analysis is not robust to changes in spatial and temporal resolution. Environ. Plan. B Urban Anal. City Sci. 2020, in press. [Google Scholar] [CrossRef]
- Hillier, B. The art of place and the science of space. World Arch. 2005, 11, 96–102. [Google Scholar]
- Jacoby, K. What is space syntax? Does the Urban Form of the City Affect the Level of Burglary and Crime. Master’s Thesis, Architectures et Villes Face Ala Mondialisation, Royal Institute of Architecture, Stockholm, Sweden, June 2006. [Google Scholar]
- Turner, A.; Doxa, M.; O’sullivan, D.; Penn, A. From isovists to visibility graphs: A methodology for the analysis of architectural space. Environ. Plann. B Plan Urban Anal. City Sci. 2001, 28, 103–121. [Google Scholar] [CrossRef]
- Lerman, Y.; Omer, I. The effects of configurational and functional factors on the spatial distribution of pedestrians. In Geographic Information Science at the Heart of Europe, 1st ed.; Vandenbroucke, D., Bucher, B., Crompvoets, J., Eds.; Springer International Publishing: Cham, Switzerland, 2013; pp. 383–398. ISBN 978-3-319-03280-1. [Google Scholar]
- Monokrousou, K.; Giannopoulou, M. Interpreting and predicting pedestrian movement in public space through space syntax analysis. Procedia Soc. Behav. Sci. 2016, 223, 509–514. [Google Scholar] [CrossRef]
- Ahmed, B.; Hasan, R.; Maniruzzaman, K.M. Urban morphological change analysis of Dhaka city, Bangladesh, using space syntax. ISPRS Int. J. Geoinf. 2014, 3, 1412–1444. [Google Scholar] [CrossRef]
- Hajrasouliha, A.; Yin, L. The impact of street network connectivity on pedestrian volume. Urban Stud. 2015, 52, 2483–2497. [Google Scholar] [CrossRef]
- Liu, P.; Xiao, X.; Zhang, J.; Wu, R.; Zhang, H. Spatial configuration and online attention: A space syntax perspective. Sustainability 2018, 10, 221. [Google Scholar] [CrossRef]
- Jabbari, M.; Fonseca, F.; Ramos, R. Combining multi-criteria and space syntax analysis to assess a pedestrian network: The case of Oporto. J. Urban Des. 2018, 23, 23–41. [Google Scholar] [CrossRef]
- Desyllas, J.; Duxbury, E. Axial maps and visibility graph analysis. In Proceedings of the 3rd International Space Syntax Symposium, Atlanta, GA, USA, 7–11 May 2001; Volume 27, p. 27.1-27.13. [Google Scholar]
- Hölscher, C.; Brösamle, M.; Vrachliotis, G. Challenges in multilevel wayfinding: A case study with the space syntax technique. Environ. Plan. B Plan. Des. 2012, 39, 63–82. [Google Scholar] [CrossRef]
- Heitor, T.; Nascimento, R.; Tomé, A.; Medeiros, V. Accessible Campus: Space syntax for universal design. In Proceedings of the 9th International Space Syntax Symposium, Seoul, Korea, 31 October–3 November 2013. [Google Scholar]
- Bendjedidi, S.; Bada, Y.; Meziani, R. Urban plaza design process using space syntax analysis. Int Rev. Spat. Plan. Sustain. Dev. 2019, 7, 125–142. [Google Scholar] [CrossRef]
- Koutsolampros, P.; Sailer, K.; Varoudis, T.; Haslem, R. Dissecting Visibility Graph Analysis: The metrics and their role in understanding workplace human behaviour. In Proceedings of the 12th International Space Syntax Symposium, Beijing, China, 8–13 July 2019; Volume 12. [Google Scholar]
- Pagkratidou, M.; Galati, A.; Avraamides, M. Do environmental characteristics predict spatial memory about unfamiliar environments? Spat. Cogn. Comput. 2020, 20, 1–32. [Google Scholar] [CrossRef]
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: Cambridge, UK, 1984; ISBN 978-0-521-23365-1. [Google Scholar]
- Turner, A.; Penn, A.; Hillier, B. An algorithmic definition of the axial map. Environ. Plan. B Plan. Des. 2005, 32, 425–444. [Google Scholar] [CrossRef]
- Bafna, S. Space syntax: A brief introduction to its logic and analytical techniques. Environ. Behav. 2003, 35, 17–29. [Google Scholar] [CrossRef]
- Portugali, J.; Meyer, H.; Stolk, E.; Tan, E. Complexity Theories of Cities Have Come of Age: An Overview with Implications to Urban Planning and Design; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Turner, A.; Penn, A. Making isovists syntactic: Isovist integration analysis. In Proceedings of the 2nd International Symposium on Space Syntax, Brasilia, Brazil, 29 March–2 April 1999. [Google Scholar]
- Turner, A. Angular analysis. In Proceedings of the 3rd International Symposium on Space Syntax, Atlanta, GA, USA, 7–11 May 2001; pp. 1–30. [Google Scholar]
- Turner, A. Depthmap: A program to perform visibility graph analysis. In Proceedings of the 3rd International Symposium on Space Syntax, Atlanta, GA, USA, 7–11 May 2001; pp. 12–31. [Google Scholar]
- Gil, J.; Varoudis, T.; Karimi, K.; Penn, A. The space syntax toolkit: Integrating depthmapX and exploratory spatial analysis workflows in QGIS. In Proceedings of the SSS 2015-10th International Space Syntax Symposium, Space Syntax Laboratory, The Bartlett School of Architecture, University College London, London, UK, 3–7 July 2015; Volume 10. [Google Scholar]
- Hillier, B. Space Is the Machine: A Configurational Theory of Architecture; Space Syntax: London, UK, 2007. [Google Scholar]
- Goldsberry, K.; Duvall, C.S.; Howard, P.H.; Stevens, J.E. Visualizing nutritional terrain: A geospatial analysis of pedestrian produce accessibility in Lansing, Michigan, USA. Geocarto Int. 2010, 25, 485–499. [Google Scholar] [CrossRef]
- Cao, K.; Liu, M.; Wang, S.; Liu, M.; Zhang, W.; Meng, Q.; Huang, B. Spatial Multi-Objective Land Use Optimization toward Livability Based on Boundary-Based Genetic Algorithm: A Case Study in Singapore. ISPRS Int. J. Geo-Inf. 2020, 9, 40. [Google Scholar] [CrossRef]
- Yenisetty, P.T.; Bahadure, P. Measuring Accessibility to Various ASFs from Public Transit using Spatial Distance Measures in Indian Cities. ISPRS Int. J. Geo-Inf 2020, 9, 446. [Google Scholar] [CrossRef]
- Teklenburg, J.A.F.; Timmermans, H.J.P.; Van Wagenberg, A.F. Space syntax: Standardised integration measures and some simulations. Environ. Plan. B Plan. Des. 1993, 20, 347–357. [Google Scholar] [CrossRef]
- De Arruda Campos, M.B.; Fong, P.S. A proposed methodology to normalise total depth values when applying the visibility graph analysis. In Proceedings of the 4th International Space Syntax Symposium, London, UK, 17–19 June 2003. [Google Scholar]
- Hillier, B.; Burdett, R.; Peponis, J.; Penn, A. Creating life: Or, does architecture determine anything? Arch. Behav. 1987, 3, 233–250. [Google Scholar]
- Vaughan, L.; Grajewski, T. Space Syntax Observation Manual; University College London: London, UK, 2001. [Google Scholar]
- Petrasova, A.; Hipp, J.A.; Mitasova, H. Visualization of Pedestrian Density Dynamics Using Data Extracted from Public Webcams. ISPRS Int. J. Geo-Inf. 2019, 8, 559. [Google Scholar] [CrossRef]
- Cambra, P.; Moura, F.; Gonçalves, A. On the correlation of pedestrian flows to urban environment measures: A Space Syntax and Walkability Analysis comparison case. In Proceedings of the 11th Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017; pp. 1–21. [Google Scholar]
- Heiman, G. Basic Statistics for the Behavioral Sciences; Cengage Learning: Boston, MA, USA, 2000. [Google Scholar]
- De Smith, M.J.; Goodchild, M.F.; Longley, P. Geospatial Analysis: A Comprehensive Guide to Principles, Techniques and Software Tools; Troubador Publishing Ltd.: Kibworth Harcourt, UK, 2007. [Google Scholar]
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Agresti, A. Categorical Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 482. [Google Scholar]
- Anderson, J.A. Regression and ordered categorical variables. J. R. Stat. Soc. Ser. B (Methodol.) 1984, 46, 1–22. [Google Scholar] [CrossRef]
- Liao, T.F. Interpreting Probability Models: Logit, Probit, and Other Generalized Linear Models (No. 101); Sage: Thousand Oaks, CA, USA, 1994. [Google Scholar]
- Norris, C.M.; Ghali, W.A.; Saunders, L.D.; Brant, R.; Galbraith, D.; Faris, P. Ordinal regression model and the linear regression model were superior to the logistic regression models. J. Clin. Epid. 2006, 59, 448–456. [Google Scholar] [CrossRef]
- Backhaus, K.; Erichson, B.; Plinke, W.; Weiber, R. Multivariate Analysemethoden; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Schendera, C.F. Regressionsanalyse Mit SPSS; Walter de Gruyter: Berlin, Germany, 2011. [Google Scholar]
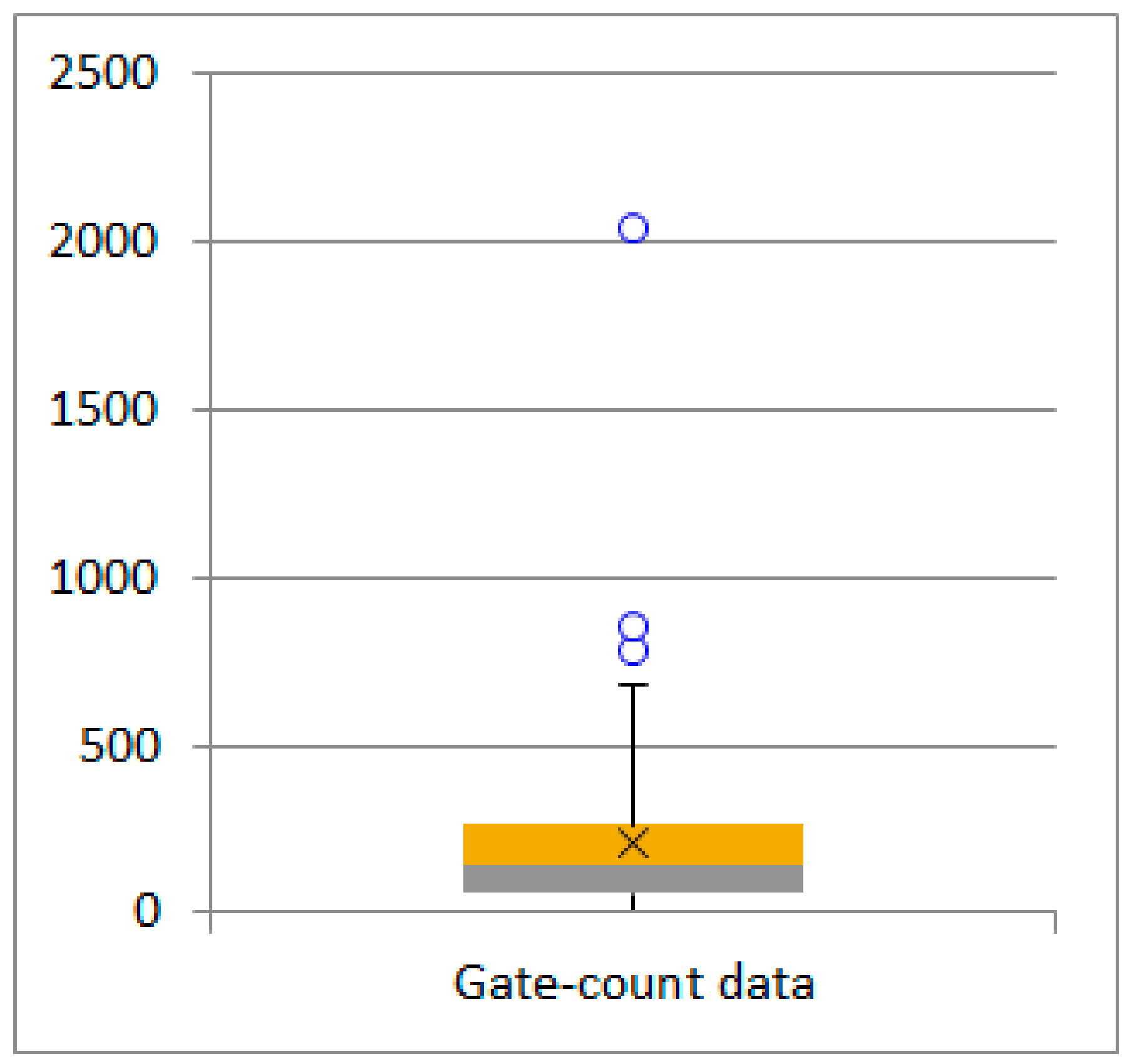
| Obs. Gates | ||||||
|---|---|---|---|---|---|---|
| 1 | 0.639 | 0.211 | 0.627 | 7.39 | 0 | 1 |
| 2 | 1.310 | 2.396 | 1.730 | 4.12 | 1219 | 4 |
| 3 | 1.063 | 2.081 | 1.526 | 4.84 | 306 | 3 |
| 4 | 1.527 | 3.339 | 2.117 | 3.67 | 4474 | 7 |
| 5 | 1.063 | 2.021 | 1.417 | 4.84 | 786 | 3 |
| 6 | 1.131 | 2.396 | 1.620 | 4.61 | 852 | 4 |
| 7 | 0.941 | 1.571 | 1.400 | 5.34 | 1051 | 2 |
| 8 | 0.759 | 2.081 | 1.451 | 6.38 | 407 | 3 |
| 9 | 0.906 | 1.833 | 1.289 | 5.51 | 538 | 3 |
| 10 | 0.992 | 1.379 | 1.175 | 5.12 | 785 | 2 |
| 11 | 1.201 | 2.212 | 1.456 | 4.40 | 2708 | 4 |
| 12 | 1.361 | 2.081 | 1.672 | 4.00 | 2309 | 3 |
| 13 | 1.015 | 1.896 | 1.364 | 5.02 | 1153 | 3 |
| 14 | 1.255 | 2.933 | 1.750 | 4.25 | 1411 | 6 |
| 15 | 1.319 | 3.476 | 1.820 | 4.09 | 2856 | 8 |
| 16 | 1.037 | 1.819 | 1.381 | 4.94 | 133 | 2 |
| 17 | 0.910 | 2.218 | 1.347 | 5.48 | 596 | 4 |
| 18 | 0.979 | 1.774 | 1.330 | 5.17 | 622 | 3 |
| 19 | 0.823 | 1.698 | 1.089 | 5.96 | 72 | 3 |
| 20 | 0.923 | 1.274 | 1.197 | 5.42 | 168 | 2 |
| 21 | 0.796 | 1.819 | 1.405 | 6.13 | 471 | 2 |
| 22 | 0.720 | 3.923 | 1.729 | 6.67 | 739 | 8 |
| Obs. Gates | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 16.0 | 1.0 | 1.36 | 1.7 | 7457 | 1.1 | 0.4 | 1.4 | 1.9 | 0.8 | |
| 2 | 17.1 | 1.0 | 1.49 | 1.7 | 8211 | 1.1 | 0.5 | 1.3 | 1.9 | 0.7 | |
| 3 | 14.0 | 1.0 | 1.24 | 1.8 | 8146 | 1.1 | 0.5 | 1.6 | 1.8 | 0.8 | |
| 4 | 16.0 | 1.0 | 1.35 | 1.7 | 7308 | 1.0 | 0.4 | 1.4 | 2.0 | 0.7 | |
| 5 | 10.9 | 0.9 | 0.95 | 2.0 | 3107 | 1.0 | 0.2 | 1.3 | 2.3 | 0.7 | |
| 6 | 10.8 | 0.9 | 0.93 | 2.1 | 2890 | 0.5 | 0.2 | 1.3 | 2.3 | 0.7 | |
| 7 | 12.5 | 0.9 | 1.06 | 1.9 | 2363 | 1.0 | 0.1 | 0.9 | 2.6 | 0.4 | |
| 8 | 10.1 | 0.9 | 0.86 | 2.2 | 1460 | 1.2 | 0.1 | 1.1 | 2.5 | 0.6 | |
| 9 | 14.5 | 1.0 | 1.25 | 1.8 | 6939 | 1.0 | 0.4 | 1.5 | 1.9 | 0.7 | |
| 10 | 17.0 | 1.0 | 1.46 | 1.7 | 7914 | 1.1 | 0.4 | 1.3 | 1.9 | 0.7 | |
| 11 | 16.8 | 1.0 | 1.43 | 1.7 | 7630 | 1.1 | 0.4 | 1.3 | 2.0 | 0.7 | |
| 12 | 18.0 | 1.0 | 1.53 | 1.7 | 8464 | 1.2 | 0.5 | 1.3 | 1.9 | 0.7 | |
| 13 | 13.0 | 0.9 | 1.10 | 1.9 | 4599 | 0.8 | 0.3 | 1.3 | 2.2 | 0.6 | |
| 14 | 13.5 | 0.9 | 1.17 | 1.9 | 6071 | 1.0 | 0.4 | 1.5 | 2.0 | 0.8 | |
| 15 | 10.7 | 0.9 | 0.90 | 2.1 | 1759 | 0.9 | 0.1 | 1.1 | 2.5 | 0.5 | |
| 16 | 10.1 | 0.9 | 0.87 | 2.2 | 2189 | 0.7 | 0.2 | 1.3 | 2.4 | 0.6 | |
| 17 | 11.8 | 0.9 | 1.02 | 2.0 | 3389 | 0.9 | 0.2 | 1.3 | 2.3 | 0.8 | |
| 18 | 9.5 | 0.9 | 0.81 | 2.3 | 675 | 0.3 | 0.0 | 1.0 | 2.7 | 0.5 | |
| 19 | 9.4 | 0.9 | 0.80 | 2.3 | 943 | 0.6 | 0.1 | 1.1 | 2.6 | 0.6 | |
| 20 | 14.2 | 0.9 | 1.22 | 1.8 | 7224 | 1.2 | 0.4 | 1.6 | 1.9 | 0.7 | |
| 21 | 10.0 | 0.9 | 0.86 | 2.2 | 1677 | 0.8 | 0.1 | 1.2 | 2.5 | 0.5 | |
| 22 | 10.8 | 0.9 | 0.93 | 2.1 | 1351 | 0.9 | 0.1 | 0.9 | 2.7 | 0.4 | |
| JNB | Class | Min. Limit | Max. Limit | Num. of Data | GVF |
|---|---|---|---|---|---|
| 1st | low | 9 | 262 | 106 | 0.823 |
| medium | 284 | 856 | 25 | ||
| high | 2040 | 2040 | 1 | ||
| 2nd | low | 9 | 154 | 75 | 0.870 |
| medium | 159 | 370 | 44 | ||
| high | 414 | 676 | 10 |
| Variables | Types | Classes | Num. of Data | Percentage | |
|---|---|---|---|---|---|
| Dependent | Pedestrian density | Ordinal | low | 75 | 56.8% |
| medium | 44 | 33.3% | |||
| high | 13 | 9.8% | |||
| Independents | Periods | Nominal | T1(08:30–10:30) | 31 | 23.5% |
| T2(10:30–12:30) | 40 | 30.3% | |||
| T3(12:30–14:30) | 29 | 22.0% | |||
| T4(14:30–16:30) | 32 | 24.2% | |||
| Measures | Continuous | Covariates data (Table 1 and Table 2) | 100.0% | ||
| Measures | Significance (p-Value) | |
|---|---|---|
| Model Fit | Test of Parallel Lines | |
| 0.005 | 0.170 | |
| 0.095 | 0.841 | |
| 0.090 | 0.294 | |
| 0.021 | 0.126 | |
| 0.024 | 0.277 | |
| 0.111 | 0.941 | |
| 0.110 | 0.937 | |
| 0.106 | 0.941 | |
| 0.107 | 0.939 | |
| 0.112 | 0.942 | |
| 0.102 | 0.940 | |
| 0.037 | 0.776 | |
| 0.776 | 0.940 | |
| 0.107 | 0.632 | |
| 0.108 | 0.857 | |
| 0.107 | 0.183 | |
| Variables | Estimate (ß) | Wald (w) | Odds Ratio (eβ) | Significance (p) | |
|---|---|---|---|---|---|
| Dependent Variable | low | 1.967 | 4.680 | 0.031 | |
| medium | 4.064 | 17.475 | 0.000 | ||
| Independent Variables | 2.132 | 6.930 | 8.432 | 0.008 | |
| T1 | −0.966 | 3.546 | 0.060 | ||
| T2 | −1.058 | 4.696 | 0.347 | 0.030 | |
| T3 | −0.069 | 0.020 | 0.888 | ||
| Variables | Estimate (ß) | Wald (w) | Odds Ratio (eβ) | Significance (p) | |
|---|---|---|---|---|---|
| Dependent Variable | low | −2.383 | 4.797 | 0.029 | |
| medium | −0.321 | 0.088 | 0.766 | ||
| InDependent Variables | −0.416 | 4.256 | 0.660 | 0.039 | |
| T1 | −0.942 | 3.428 | 0.064 | ||
| T2 | −1.069 | 4.861 | 0.343 | 0.027 | |
| T3 | −0.092 | 0.035 | 0.852 | ||
| Variables | Estimate (ß) | Wald (w) | Odds Ratio (eβ) | Significance (p) | |
|---|---|---|---|---|---|
| Dependent Variable | Low | 0.059 | 0.023 | 0.879 | |
| medium | 2.117 | 22.033 | 0.000 | ||
| InDependent Variables | 0.000 | 3.398 | 0.065 | ||
| T1 | −0.949 | 3.493 | 0.062 | ||
| T2 | −1.080 | 4.988 | 0.340 | 0.026 | |
| T3 | −0.101 | 0.042 | 0.837 | ||
| Variables | Estimate (ß) | Wald (w) | Odds Ratio (eβ) | Significance (p) | |
|---|---|---|---|---|---|
| Dependent Variable | low | −1.501 | 3.453 | 0.063 | |
| medium | 0.545 | 0.456 | 0.499 | ||
| InDependent Variables | −1.273 | 2.639 | 0.104 | ||
| T1 | −0.915 | 3.311 | 0.069 | ||
| T2 | −1.150 | 5.688 | 0.317 | 0.017 | |
| T3 | −0.181 | 0.138 | 0.711 | ||
| Years | Number of Axial Lines | Mean of the Integration | Paired Samples | Means | p-Value |
|---|---|---|---|---|---|
| 2019 | 96 | 0.388 | 96 | 0.388 | 0.002 |
| Master | 137 | 0.356 | 0.370 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hacar, Ö.Ö.; Gülgen, F.; Bilgi, S. Evaluation of the Space Syntax Measures Affecting Pedestrian Density through Ordinal Logistic Regression Analysis. ISPRS Int. J. Geo-Inf. 2020, 9, 589. https://doi.org/10.3390/ijgi9100589
Hacar ÖÖ, Gülgen F, Bilgi S. Evaluation of the Space Syntax Measures Affecting Pedestrian Density through Ordinal Logistic Regression Analysis. ISPRS International Journal of Geo-Information. 2020; 9(10):589. https://doi.org/10.3390/ijgi9100589
Chicago/Turabian StyleHacar, Özge Öztürk, Fatih Gülgen, and Serdar Bilgi. 2020. "Evaluation of the Space Syntax Measures Affecting Pedestrian Density through Ordinal Logistic Regression Analysis" ISPRS International Journal of Geo-Information 9, no. 10: 589. https://doi.org/10.3390/ijgi9100589
APA StyleHacar, Ö. Ö., Gülgen, F., & Bilgi, S. (2020). Evaluation of the Space Syntax Measures Affecting Pedestrian Density through Ordinal Logistic Regression Analysis. ISPRS International Journal of Geo-Information, 9(10), 589. https://doi.org/10.3390/ijgi9100589