1. Introduction
Algorithms for the concavity-convexity detection of vertices of spatial objects are the basis of many graphics algorithms, including test algorithms [
1,
2,
3,
4,
5], orientation and convexity-concavity determination algorithm for simple polygons [
6,
7], and computer graphics processing [
8,
9]. The commonly used vertex concavity-convexity detection algorithms for polygons include the convex hulls [
10], angle [
11], left-right-point [
12], vector area [
13], cross product [
14], slope [
15], and extremity vertices sequence methods [
16]. Among these, the angle, left-right-point, and vector area methods use the inherent properties of simple polygons for algorithm design, while the cross product, ray, slope, and extremity vertices sequence methods tremendously reduce the algorithmic complexity during the identification of the concavity-convexity of fixed points of simple polygons. Nonetheless, the currently available studies on vertex concavity-convexity detection mostly concentrate on two-dimensional (2D) polygons, and studies on the detection of vertex concavity-convexity of three-dimensional (3D) spatial polyhedrons are rarely reported. With the rapid development of field, such as 3D modeling and artificial intelligence, the need for a concavity-convexity detection algorithm for vertices in multi-dimensional conditions is becoming increasingly important and urgent.
This paper introduces geometric algebra into the vertex concavity-convexity detection of spatial objects based on the computation principle of the cross product method for determining the vertex concavity-convexity of a simple polygon. Taking advantage of the fact that the outer product computation in geometric algebra possesses unified and clear geometric implications among spaces with different dimensionalities, the limitation that the cross product in the Euclidean space can only be applied between vectors is eliminated, and a detection method for the vertex concavity-convexity of simple polygons and polyhedrons that is based on the outer product computation is proposed. Moreover, on the basis of the proposed detection method, a vertex concavity-convexity detection algorithm framework for both 2D and 3D objects is proposed that is universal for spaces with various dimensionalities; therefore, the detection method of vertex concavity-convexity of different dimensional objects is unified.
The structure of this paper is organized, as follows.
Section 2 proposes relative basic theories and a technology roadmap for this paper.
Section 3 presents the main methodology for vertex concavity-convexity detection on basis of geometric algebra. In
Section 4, a simple application is presented to verify the feasibility of methods that are proposed in this paper. Finally, conclusions and discussion are drawn, on the basis of the previous sections and some issues for future study.
2. Basic Idea
As the first person to propose geometric algebra, William K. Clifford combines Grassmann algebra with Hamilton’s quaternion algebra to yield Clifford’s geometric algebra, which is also referred to as Clifford algebra [
17]. Geometric algebra presents higher representation and computation capabilities when compared with conventional linear algebra. Geometric algebra can directly perform algebraic operations that are based on the representation of spatial objects, i.e., it deals with a geometric problem in an algebraic manner [
18]. This results in greater intuitiveness and simplicity. Simultaneously, the coordinate independence and the dimension independence of geometric algebra provide a mathematical basis for the unified expression and spatial analysis and operation of complex objects in 3D space [
19,
20]. Hestenes and Li et al. develop the conformal geometric algebra (CGA) that is based on Clifford geometric algebra, which further expands the application range of geometric algebra [
21,
22]. The CGA has been extensively applied in multiple fields, such as computer geometrics [
23,
24], computer vision [
25,
26,
27], and multidimensional geographical spatial analysis [
28,
29,
30,
31,
32,
33].
The cross product algorithm is one of the most frequently used methods among the existing vertex concavity-convexity detection algorithms for 2D polygons. The algorithm uses the directional characteristics of the cross product result vector to determine the concavity-convexity of a vertex. However, the cross product in the Euclidean space is only valid among vectors and it cannot be applied in spaces with other dimensionalities, which limits the applicability of the cross product method, such that the vertex concavity-convexity detection algorithms that are based on the cross product are only applicable to plane polygons. For the conformal geometric space, the outer product is a basic operation for dimensionality expansion. It possesses a unified and clear geometric implication across spaces with varied dimensionalities and it lays the theoretical foundation for the implementation of multi-dimensional universal spatial geometric analysis and computation based on the outer product.
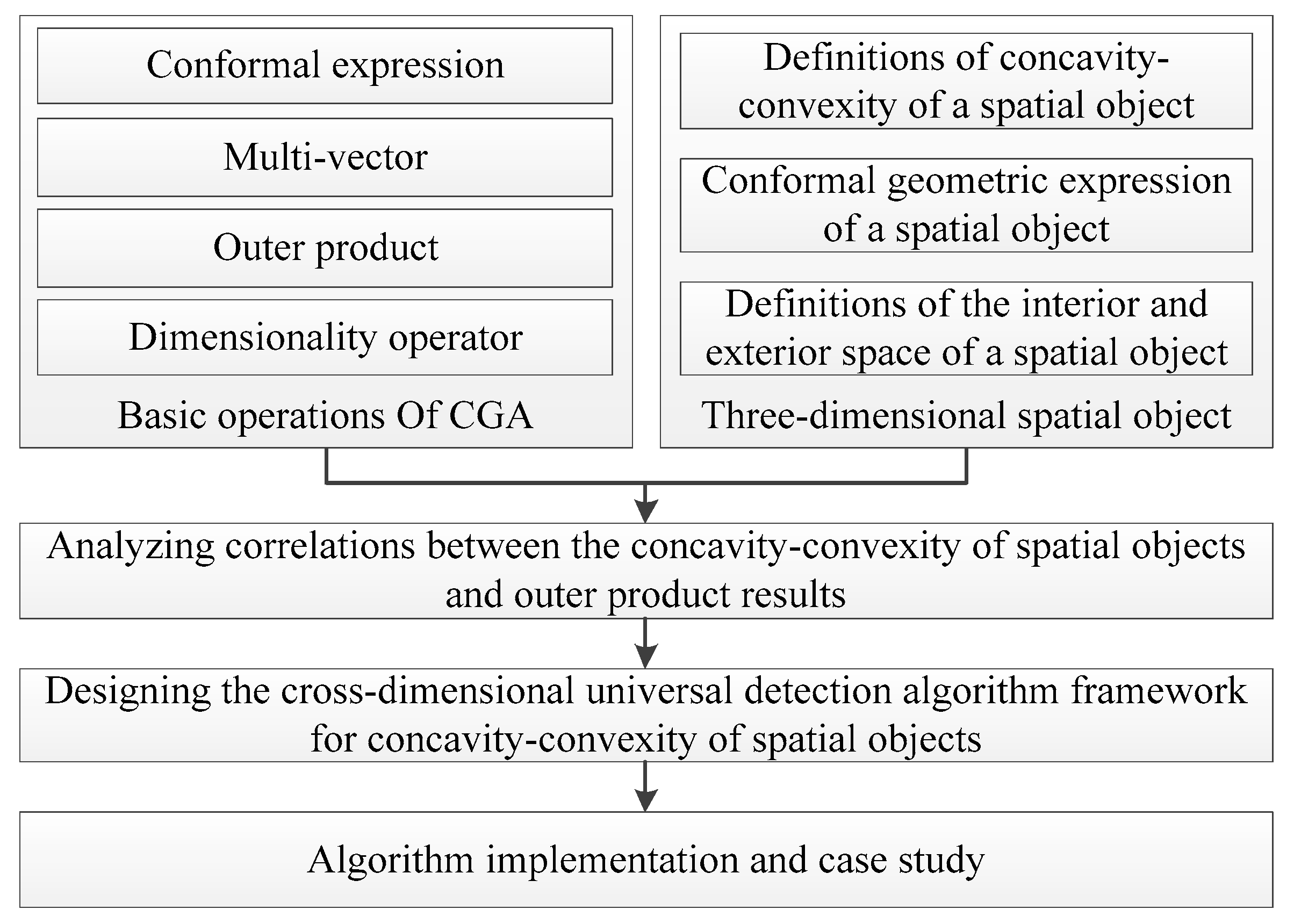
The overall framework of this study is illustrated in
Figure 1, some concepts relevant to vertex concavity-convexity of a spatial object are defined based on the conformal expression of an object in 3D space, the correlations among the outer product operation results, the topological space of the spatial object, and its vertex concavity-convexity using basic concepts in geometric algebra, such as the outer product operation, dimensionality analysis, and multi-vector structure in the conformal space, are analyzed and a computation framework for the vertex concavity-convexity detection of objects in 3D space is proposed. The vertex concavity-convexity detection method that is proposed in this paper takes full advantage of the fact that the outer product operation in conformal space has a uniform and definite geometric meaning in all geometric spaces. The method can be used for the traditional vertex concavity-convexity detection in a 2D space; however, it can also be applied to vertex concavity-convexity detection in a 3D space, which indicates that the proposed algorithm possesses cross-dimensional universality.
3. Methodology
3.1. Definitions Relevant to Vertex Concavity-Convexity Detection
The range of the spatial object of interest and relevant concepts should be first clearly defined prior to carrying out vertex concavity-convexity detection for a spatial object. Herein, the spatial object includes simple polygons and polyhedrons, which are described in Definitions 1 and 2, respectively.
Definition 1. If there exist n straight lines in the 3D space that are non-overlapping, non-intersecting and coplanar, among which any pair of adjacent lines is not collinear and no more than two adjacent lines are concurrent, and then the polygon enclosed by such n straight lines is a simple polygon.
Definition 2. If there exist n planar polygons in the 3D space that are non-overlapping and non-intersecting, among which any pair of adjacent polygons is non-coplanar and no more than two adjacent polygons share a common edge, which is always the longest line for both polygons, and then the polyhedron enclosed by such n polygons is a simple polyhedron.
On the basis of the aforementioned definitions of simple polygons and simple polyhedrons, Definition 3 defines the interior angle of them.
Definition 3. The interior angle of a simple polygon refers to the intersection angle inside the polygon formed by two adjacent edges of the simple polygon. The interior angle of a simple polyhedron is defined as the intersection angle inside the polyhedron that was formed by two adjacent surfaces of the simple polyhedron.
From Definitions 1 and 2, it can be deduced that the interior angle of a simple polygon or polyhedron must be less than π. The vertex concavity-convexity can then be identified with respect to the interior angles of simple polygons and simple polyhedrons, which is stated in detail in Definitions 4 and 5.
Definition 4. If the interior angle formed by two adjacent edges of a simple polygon exceeds π, then the vertex shared by these two adjacent is a concave point; otherwise, it is a convex point.
Definition 5. If the interior angle that is formed by two adjacent surfaces of a simple polyhedron exceeds π, then the two vertexes of the edge shared by these two adjacent surfaces are concave points; otherwise, they are convex points.
3.2. Outer Product Operation
The outer product is one of the basic operations in geometric algebra. The outer product in conformal space can be expanded to all spaces with various dimensionalities, having a unified and definitive geometric implication across multiple spaces with varied dimensionalities, unlike the cross product in Euclidean space that can only be applied between vectors. The definition of the outer product is presented as Definition 6.
Definition 6. if and
are any two linear independent blades in space (a symbol for a category system of algebra, in which denotes Euclidean space, denotes Homogeneous space, and denotes Conformal space) [18], where and are their corresponding dimensions, and then the outer product between them is defined, as follows:where and
are modulus operation, θ is an angle between two blades, is used for determining the size of the outer product resulting object, is the dimension space operation of the outer product, and is the dimension of the outer product space. When ,
the result of the outer product is zero. From Formula (1), higher dimensional geometric objects can be directly constructed by the lower dimensional geometric objects via the outer product. For instance, outer product between two linear independent one-dimensional vectors results in a 2D vector. The outer product operation satisfies the inverse commutative law. The result of the outer product calculation has directivity that is reflected in the symbol of the calculation result. Geometric objects constructed in different outer product order with the same vectors are equal in size, but opposite in direction. The outer product operation also satisfies the linear correlation. The result of outer product is equal to zero if the blades involved in the outer product are linearly correlated.
3.3. CGA Expression for Geometric Objects Based on Outer Product
The points in 3D Euclidean space can be transformed to CGA by the following definition.
Definition 7. if is a point in Euclidean space , then the corresponding expression of point CP in CGA is as follows:where , and
are the five basis vectors in CGA, denotes the origin of reference coordinates with coefficient 1, and denotes the infinity point. In the conformal space, the boundary lines’ geometric information is represented by an outer product among its two boundary points and an infinity point. Definition of boundary lines’ CGA expression is explained as follows.
Definition 8. If and are two boundary points in space, CL is a boundary line constructed by the and , and if boundary line in the CGA space is represented by the , where 〈4〉 indicates that the boundary line corresponds to the 3D subspace in the conformal space, the conformal expression of the boundary line is defined, as follows: Geometric information of boundary surfaces can be represented by outer product among three composing conformal points and an infinity point in CGA space, as shown in definition 9.
Definition 9. If CF is a boundary surface in space, , and are three boundary points of CF. If denotes the boundary surface’s CGA expression in conformal space, the 〈4〉 represents the four-dimensional subspace in the corresponding CGA space, and then the conformal expression of the boundary surface is defined, as follows: 3.4. Correlations between the Outer Product Results and the Spatial Topology of the Geometric Object
Different from the cross product in Euclidean space that can only be applied between vectors, in the conformal space, the outer product possesses the identical geometric implication among all of the spaces with varied dimensionalities. Accordingly, the topological properties of the outer product results in the conformal space can be used to study the determination method for the interior and the exterior spaces of polygons and the boundary surface orientation of polyhedrons. Theorems 1 and 2 summarize the details.
Theorem 1. Let q be an arbitrary point in the conformal space. Afterwards, P1, P2, …, Pn are coplanar points sequenced counterclockwise, which form the simple polygon A. Point q and Polygon A are coplanar. In the case that all of the outer product operation results between q and all edges of A are non-zero and the signs of the coefficients are the same, Point q is located inside Polygon A. If there is a zero in the outer product operation results between q and all edges of A and the signs of all non-zero coefficients are the same, then Point q is on the boundary of Polygon A. If the signs of the outer product operation results between q and all edges of A are not the same, Point q is located outside Polygon A.
Theorem 2. Let q be an arbitrary point in the conformal space and B is an arbitrary simple polyhedron in the conformal space. q is located inside the polyhedron in the case that the outer product operation results between q and all boundary surfaces of B are non-zero and the signs of the coefficients are the same. If there is a zero in the outer product operation results between q and all boundary surfaces of B and the signs of all non-zero coefficients are the same, Point q is on the boundary surface of the polyhedron. If the signs of the outer product operation results between q and all boundary surfaces of B are not the same, then q is located outside the polyhedron.
As complex mathematical derivation is involved in proving the correlations between the outer product result and the topological relationships of spatial objects, as stated in Theorems 1 and 2. This study focuses on the application of this characteristic to determine the vertex concavity-convexity of spatial objects; thus, the proofs of the theorems are not presented here. Specific theoretic details have been well-stated in the relevant literature [
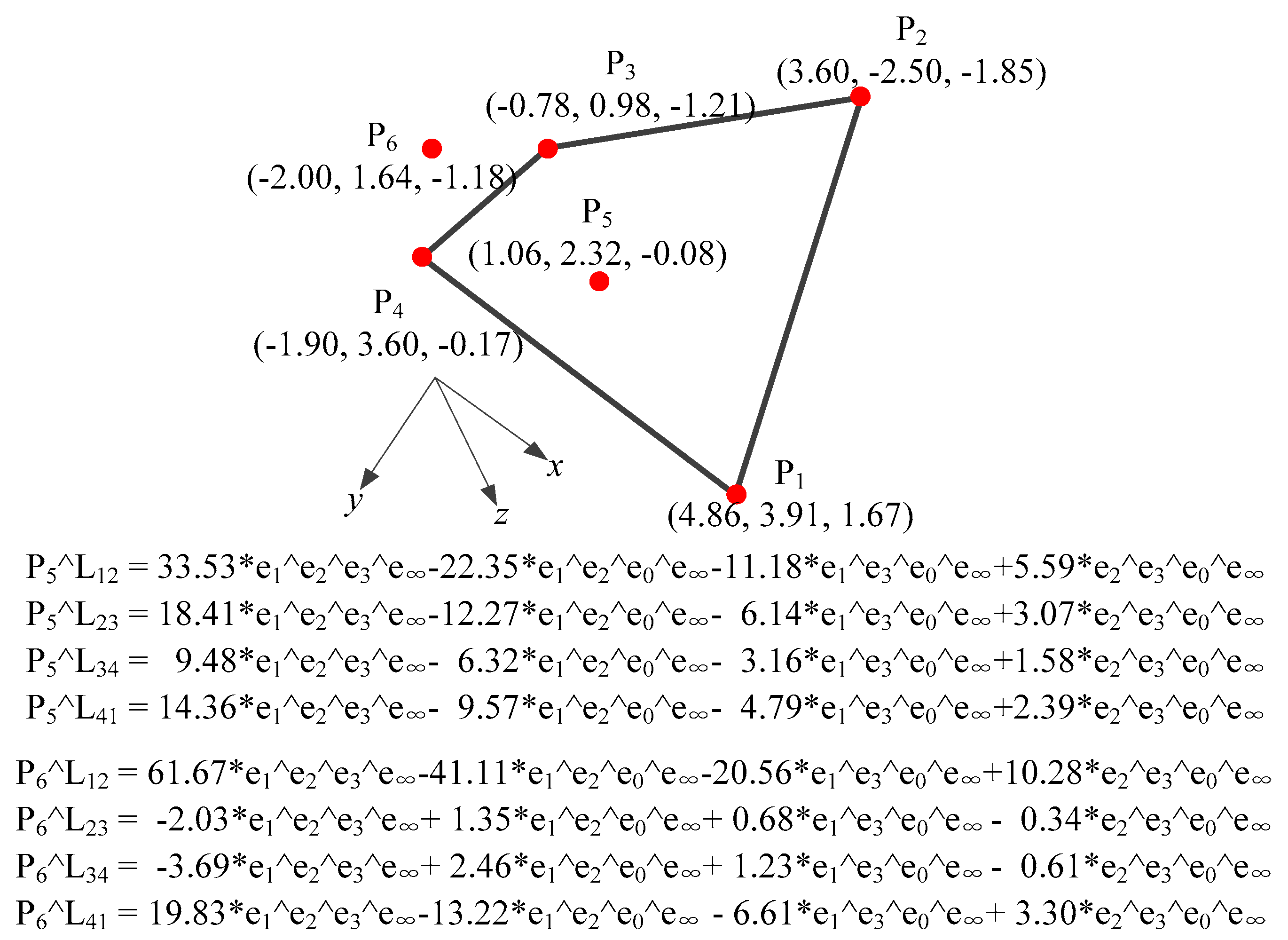
19]. Hereafter, the simple polygon illustrated in
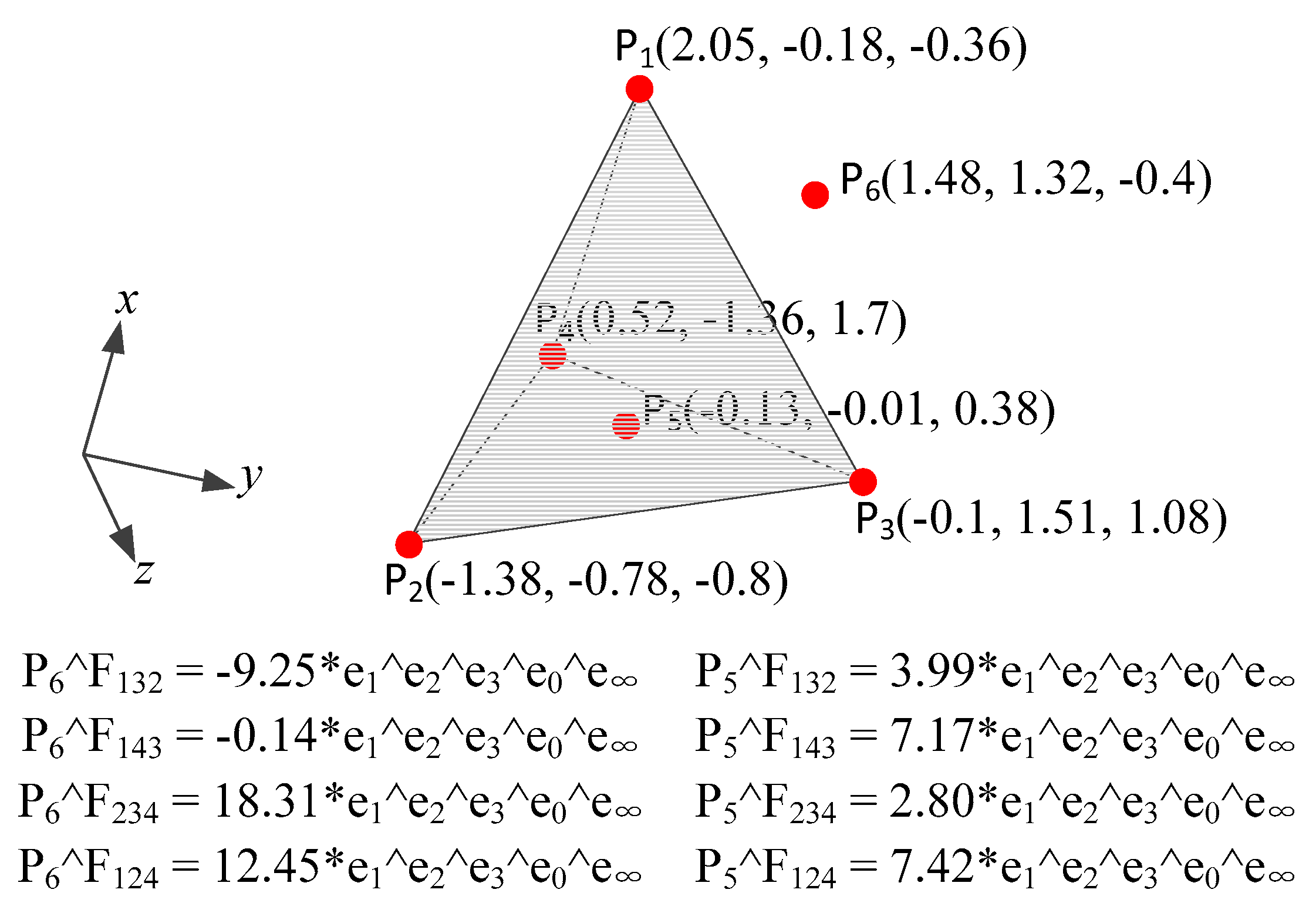
Figure 2 and simple polyhedron illustrated in
Figure 3 are used as examples for presenting the application cases of the topological space decision rules of spatial objects in Theorems 1 and 2.
In
Figure 2 and
Figure 3, Points
P5 and
P6 are located inside and outside the spatial object, respectively. According to the outer product results between the two points and the boundaries of the spatial object, the signs of the resulting coefficients of the cross product are consistent for the outer product between the point inside the spatial object and the boundary object; for the outer product between the point outside the spatial object and the boundary object, the signs of the resulting coefficients of the cross product are inconsistent.
3.5. Interior Space Detection of Spatial Objects Based on the Outer Product
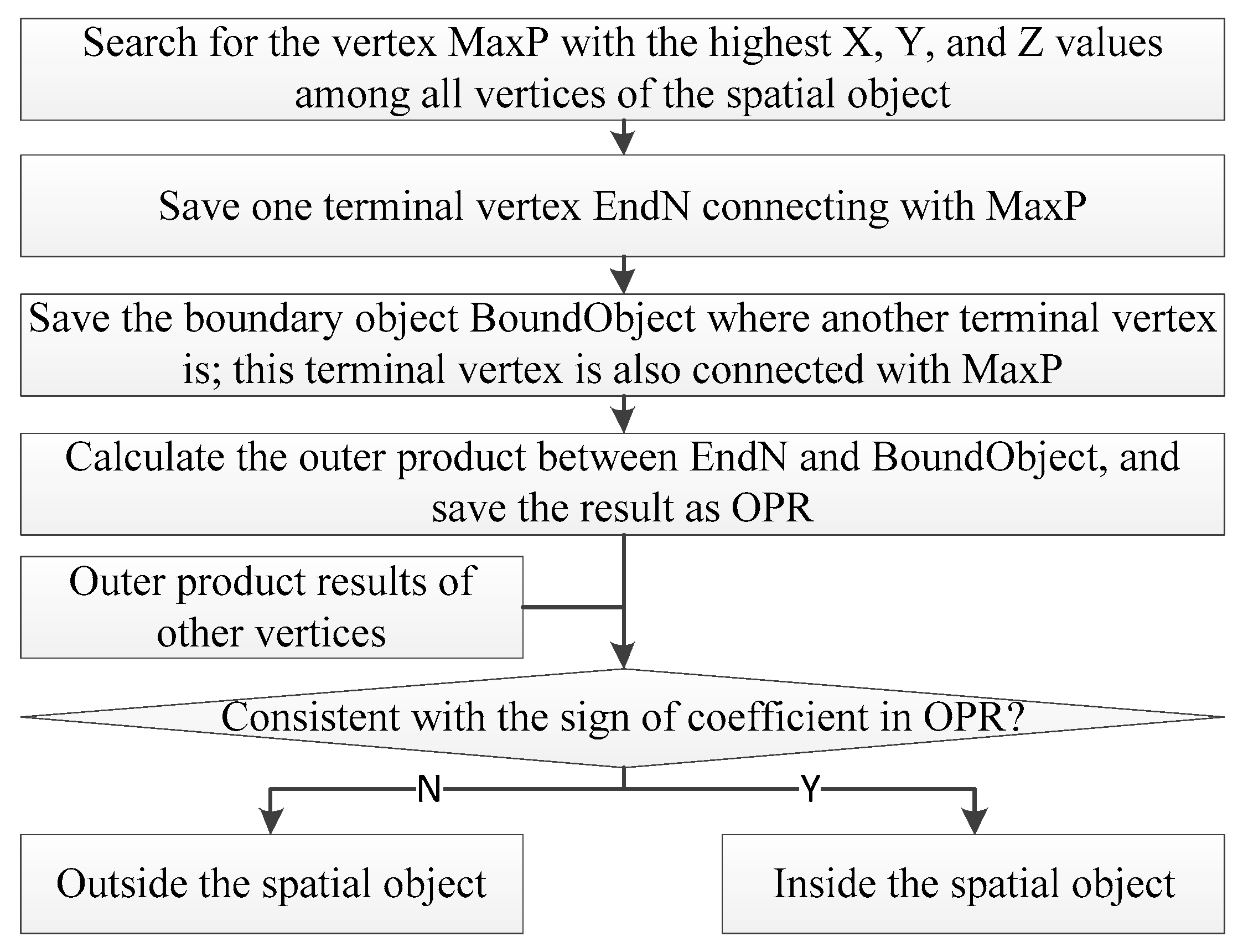
In this paper, a method that is able to rapidly locate the interior space of simple polygons and simple polyhedrons in a 3D space is developed based on the discovered correlation characteristics between the sign of the coefficients of the outer product results and the topological space of the spatial object.
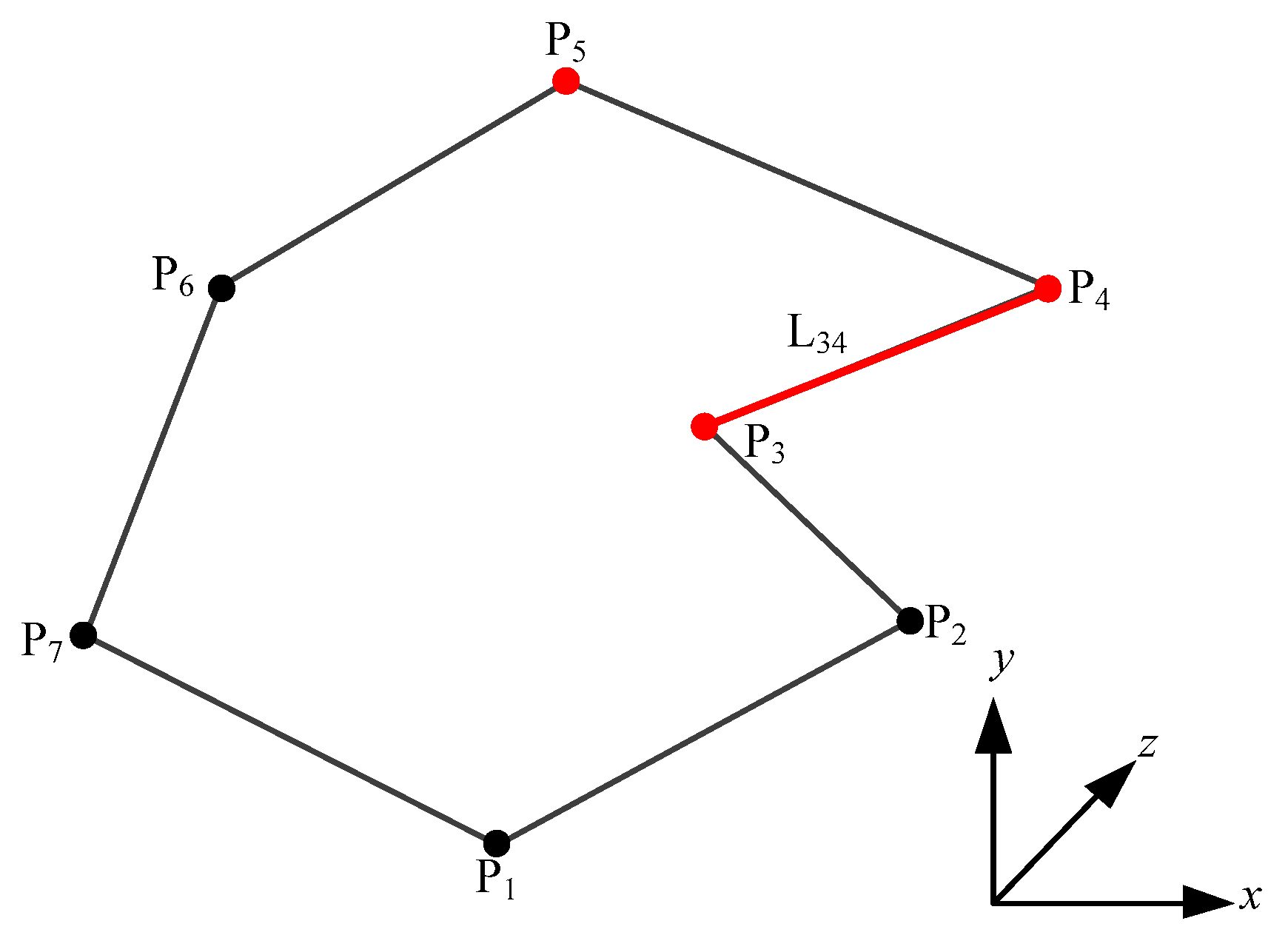
Figure 4 shows the algorithm flow. Using the simple polygon that is shown in
Figure 5 as an example, the algorithm principle of determining the interior space of spatial objects that is based on the result of the outer product is demonstrated. The algorithm first searches for the convex vertex of the spatial object, specifically, to look for the vertex with the highest coordinate value along the X-axis (e.g.,
P4 in
Figure 5). The one with the highest Y-axis and Z-axis values are searched if multiple vertices are found with the same X-axis value. The resultant vertex is inevitably a convex vertex. Moreover, the outer product between any terminal vertex connecting the convex vertex (
P5 in
Figure 5) and the boundary object, where the other terminal vertex at Edge
L34 of
P3 (
Figure 5), OPResult, is computed. Finally, the signs of the coefficients of the outer product between an arbitrary spatial point and the boundary of the polygon are used as criteria to determine whether it is inside the polygon. If the sign of the coefficient of the outer product of a spatial point and the polygon boundary is consistent with that of OPResult, then this spatial point is located within the interior of the polygon. This method can detect the interior space for both two-dimensional simple polygons and three-dimensional simple polyhedrons.
3.6. Multi-Dimensional Unified Concavity-Convexity Detection for Spatial Objects
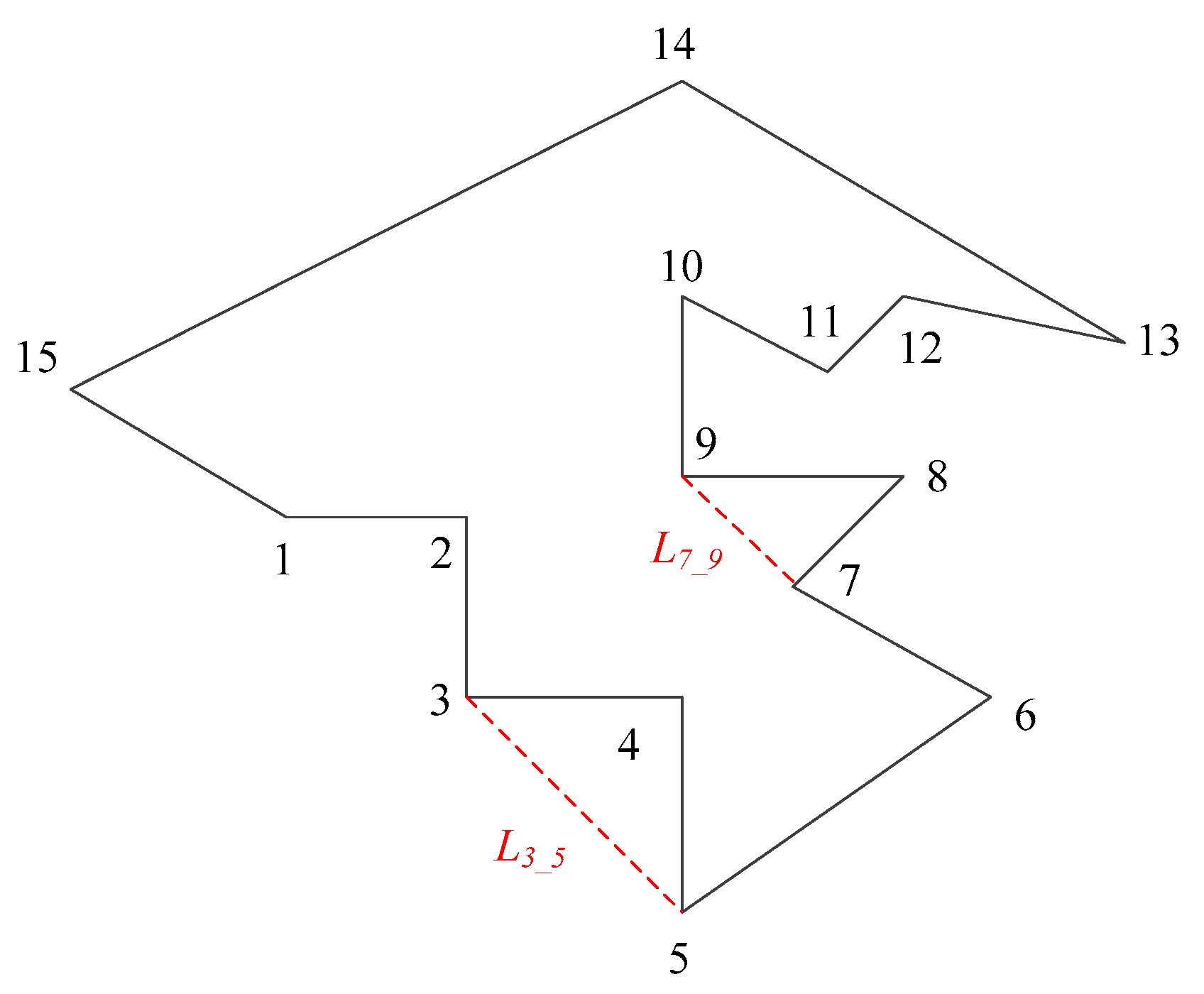
In this paper, a vertex concavity-convexity detection method for spatial objects based on the outer product is developed on the basis of the orientation characteristics contained in the outer product in conformal space and their correlations with the topological space of the spatial object. The simple polygon that is shown in
Figure 6 is used as an example to elaborate the proposed method. The core algorithm includes the following four steps:
(1) Identification of the interior space of a polygon: Calculate the outer product of any vertex of the polygon and any boundary object that does not include this vertex, and record the signs of the coefficients of the outer product result in IdentifyDirect, which is used as the criterion for defining the interior and exterior space of the polygon. If consistency is found between the signs of coefficients of the outer product of another point and IdentifyDirect, this point is located inside the polygon; otherwise, it is outside the polygon.
(2) Generation of new boundaries relevant to the to-be-detected vertex: Identify all terminal vertices that are connected to the to-be-detected vertex (Points 8 and 4), and use these identified vertices to generate several planes (or straight lines) that are not coplanar (or collinear). Subsequently, save the conformal expressions of all created planes (or lines) into the IdentifyObjects set (e.g., Edge
L7_9 created by Points 7 and 9 connected to Point 8, and Edge
L3_5 generated by Points 3 and 5 connected to Point 4, in
Figure 6).
(3) Topological analysis of the to-be-detected vertex: For each IObject from the IdentifyObjects set, the outer product of this IObject and the to-be-detected vertex is calculated to determine whether or not the signs of coefficients of the outer product are consistent with those saved in IdentifyDirect. If they are consistent, the to-be-detected vertex is located inside the new boundary (Point 4 in
Figure 6). Otherwise, the to-be-detected vertex is located outside the new boundary (Point 8 in
Figure 6).
(4) Concavity-convexity determination: If the to-be-detected vertex is located outside the generated new boundary, then this vertex is a convex vertex (Point 8 in
Figure 6); otherwise, it is a concave vertex (Point 4 in
Figure 6).
The presented vertex concavity-convexity detection method for spatial objects based on the outer product can be applied to determine the vertex concavity-convexity of both simple polygons and simple polyhedrons since the outer product in the conformal space has definitive and unified geometric implications across all spaces with varied dimensionalities; therefore, the multi-dimensional unified vertex concavity-convexity detection algorithm for objects in 3D space is achieved.
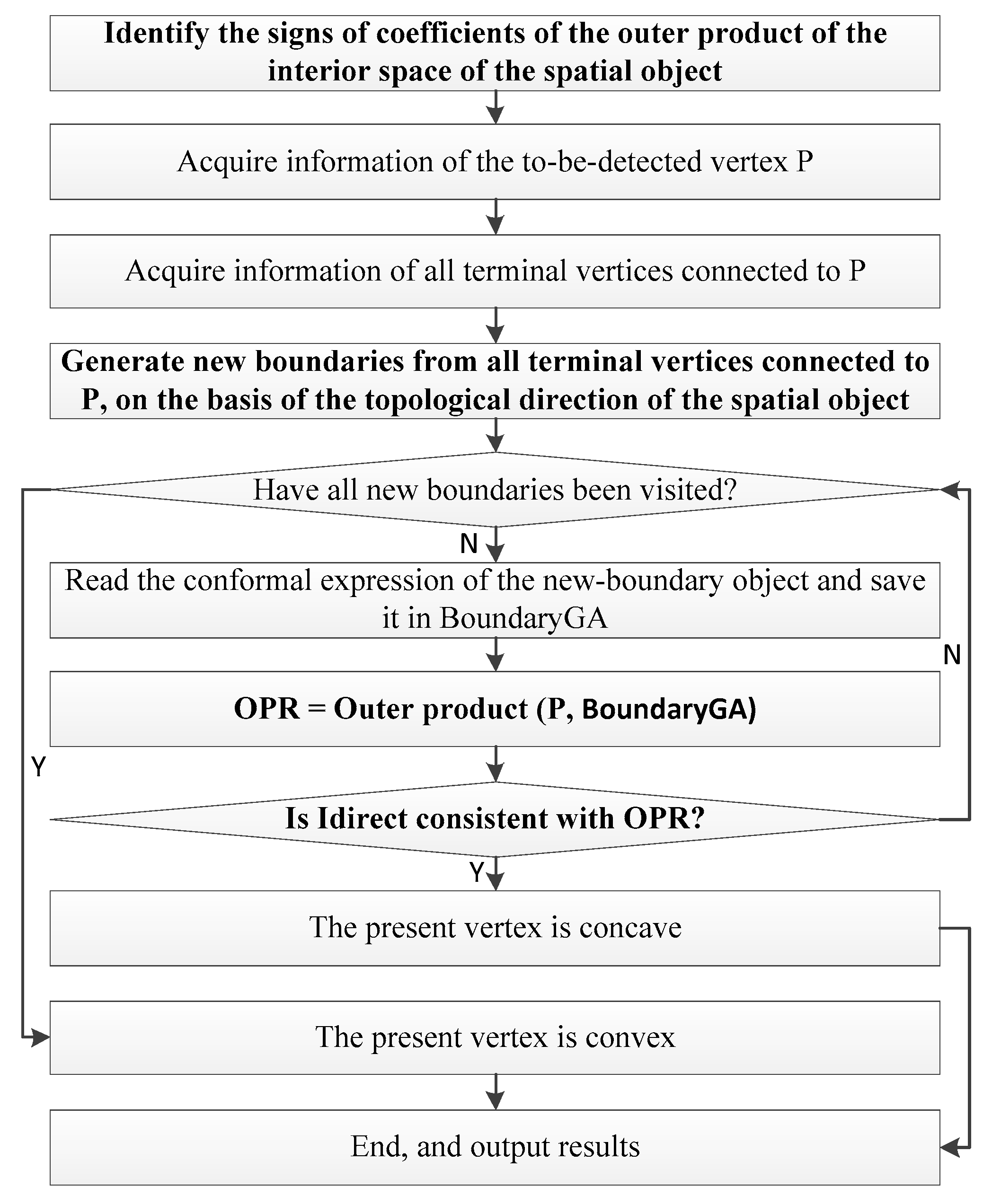
Figure 7 presents the detailed algorithm framework, in which the core steps of the algorithm framework are highlighted with a bold font.
4. Case Studies
The detection method for simple polygons was elaborated in the method section. Hence, in the following case study section, we mainly focus on the vertex concavity-convexity detection of simple polyhedrons in 3D space.
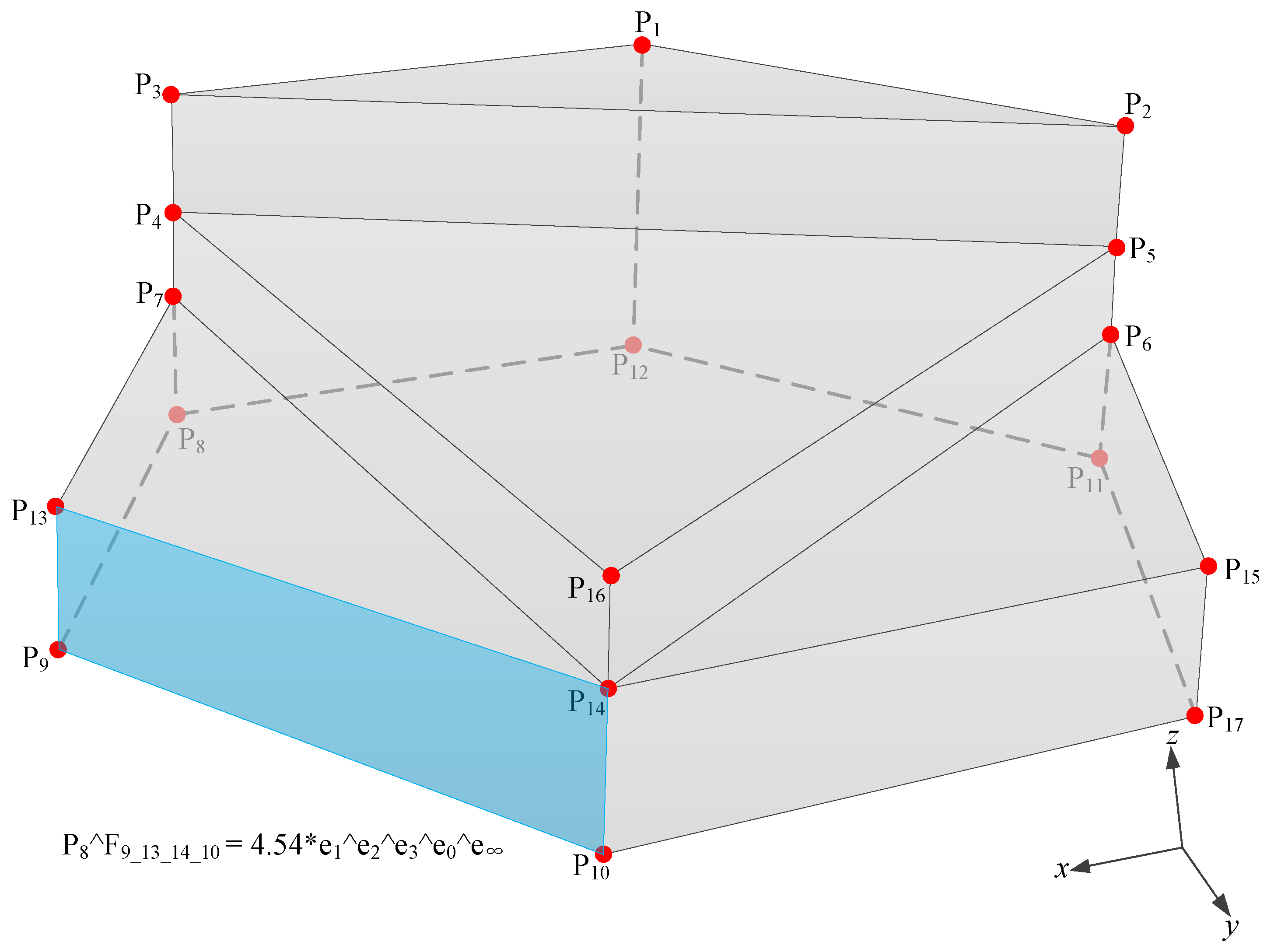
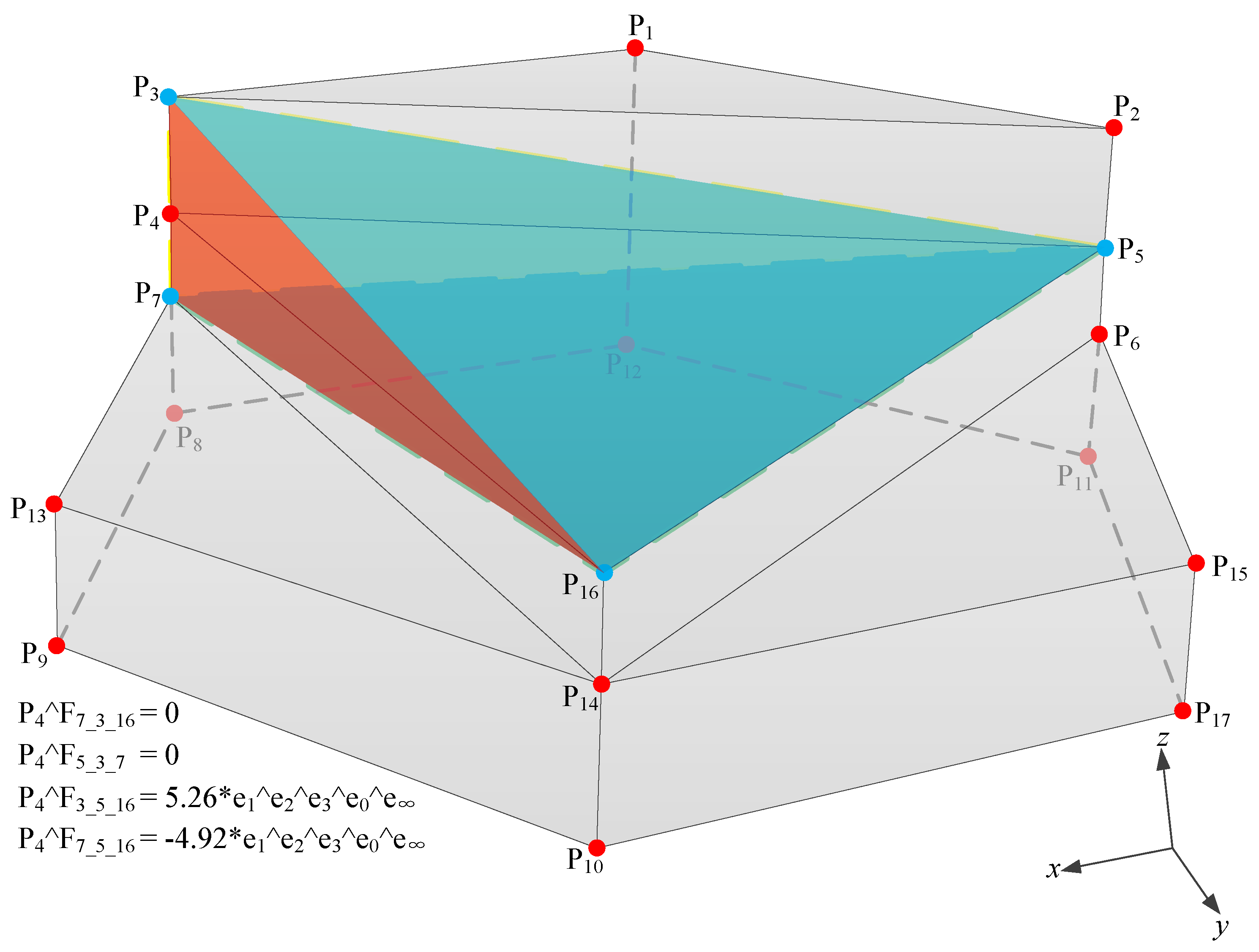
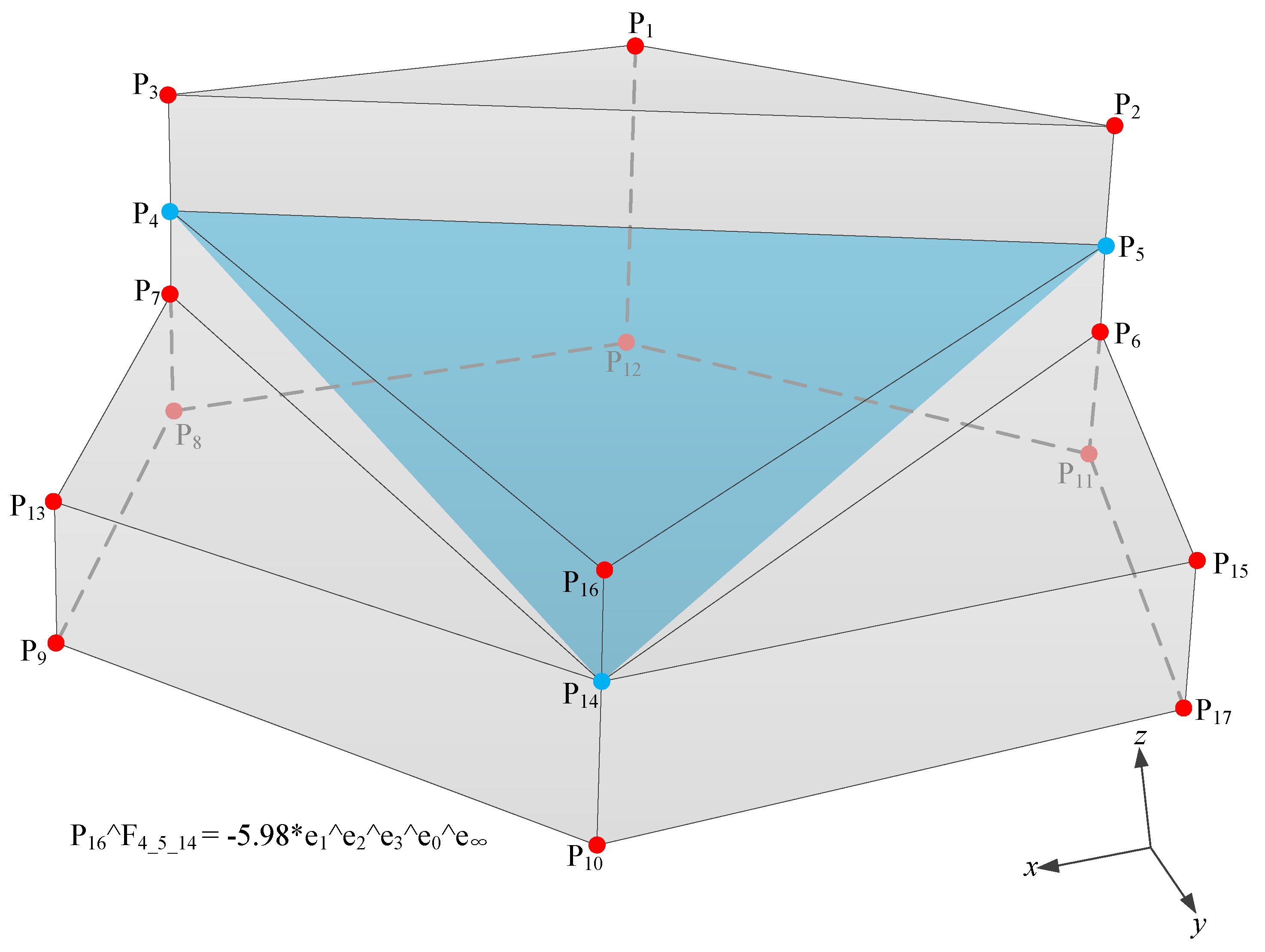
The simple 3D polyhedron that is shown in
Figure 8 is used as an example to verify the proposed algorithm for multidimensional unified vertex concavity and convexity detection. Points
P4 and
P16 are the to-be-detected vertices. According to the algorithm framework (
Figure 7), the core algorithm to detect vertex concavity-convexity of a simple polyhedron includes the following four steps:
(1) First, calculate the outer product of the interior space of the simple polyhedron in
Figure 8 and identify the signs of the coefficients of the outer product. Specifically, the extreme point
P9 is identified, and
P8 is randomly chosen from vertices connected to
P9 as the reference point, and Surface
F9_13_14_10 to which
P9 belongs is chosen as the reference surface. The outer product of
P8 and
F9_13_14_10 is computed and
Figure 8 shows the result.
(2) Second, identify the terminal nodes directly connected with the to-be-detected vertex, e.g.,
P3,
P5,
P7, and
P16 connected to
P4 in
Figure 9 and
P4,
P5, and
P14 connected to
P16 in
Figure 10, and generate new boundary surfaces
F7_3_16,
F5_3_7,
F3_5_16,
F7_5_16, and
F4_5_14 according to the topological rules of the polyhedron.
(3) Third, calculate the outer product of the to-be-detected vertex and the newly generated boundary surface.
Figure 9 and
Figure 10 show detailed results.
(4) Finally, determine whether the signs of the coefficients of the outer product of the to-be-detected vertex are consistent with those of the interior space of the polyhedron, and subsequently determine the concavity-convexity of the vertex.
5. Conclusions and Discussion
This study investigates the detection method for the interior space of spatial objects and the correlations between the vertex concavity-convexity of a spatial object and the outer products, since the outer product in geometric algebra possesses unified and definitive implications among all spaces with varied dimensionalities. Subsequently, the algorithm framework for vertex concavity-convexity detection for spatial objects based on the outer product is proposed, and this framework is capable of detecting vertex concavity-convexity for both simple polygons and polyhedrons. Therefore, this multi-dimensional unified vertex concavity-convexity detection algorithm for spatial objects in 3D space is verified.
The research findings of this paper enrich the algorithms for vertex concavity-convexity detection for 2D polygons and unify the algorithms for vertex concavity-convexity detection for 2D polygons and 3D polyhedrons. More importantly, the introduction of geometric algebra into vertex concavity-convexity detection and other relevant topology-based detections allows for us to fully take advantage of the coordinate independence and dimension independence of geometric algebra in the calculation of geometric relations of spatial objects and perform in-depth research on other graphics and topological relations, including detecting convex/concave edges of objects in 3D space. CGA’s advantage in geometric computation and multidimensional unified will make be a great help for computer image processing in simplifying calculation complexity and improving calculation efficiency.
Author Contributions
Conceptualization, Pengcheng Yin and Di Hu; Data curation, Jiyi Zhang, Xiying Sun and Chengyan Wu; Methodology, Pengcheng Yin, Jiyi Zhang and Zhifeng Shi; Software, Di Hu and Zhifeng Shi. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant number 41771421, 41601417), Land and Resources Science and Technology Project of Jiangsu Province (Grant number. 2018055), and Nantong Key Laboratory Project (grant number CP12016005).
Acknowledgments
We thank anonymous reviewers and editors for their helpful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, J.; Gao, M.; Wang, S. Orientation, Convexity-Concavity and Inclusion Test Algorithms for Polygons. In Proceedings of the 2009 International Conference on Information Technology & Computer Science, Kiev, Ukraine, 25–26 July 2009; IEEE Computer Society: Washington, DC, USA, 2009. [Google Scholar]
- Li, W.; Ong, E.T.; Xu, S.; Hung, T. A Point Inclusion Test Algorithm for Simple Polygons. In Proceedings of the Computational Science and Its Applications—ICCSA 2005, International Conference, Singapore, 9–12 May 2005; Part I. Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Wu, H.; Gong, J.; Li, D.; Shi, W. An algebraic algorithm for point inclusion query. Comput. Graph. 2000, 24, 517–522. [Google Scholar] [CrossRef]
- Li, J.; Wang, W.; Wu, E. Point-in-polygon tests by convex decomposition. Comput. Graph. 2007, 31, 636–648. [Google Scholar] [CrossRef]
- Hormann, K.; Agathos, A. The point in polygon problem for arbitrary polygons. Comput. Geom. 2001, 20, 131–144. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Y.; Gao, M.; Wang, S. An Algorithm for Determining the Orientation and Convexity-Concavity of Simple Polygons. In Proceedings of the 2009 First International Workshop on Education Technology and Computer Science, Wuhan, China, 7–8 March 2009; Volume 2, pp. 463–467. [Google Scholar]
- Wu, C. Determining Convexo-Concave Vertices of Polygon By Topological Mapping. J. Comput. Aided Des. Comput. Graph. 2002, 14, 810–814. [Google Scholar]
- Amato, N. Approximate Convex Decomposition of Polyhedra. Comput. Aided Geom. Des. 2008, 25, 503–522. [Google Scholar]
- Lien, J.-M.; Amato, N.M. Approximate convex decomposition of polygons. Comput. Geom. 2006, 35, 100–123. [Google Scholar] [CrossRef]
- Zhou, P. An algorithm for determining convexo-concave vertices of an arbitrary polygon. J. Softw. 1995, 6, 276–279. [Google Scholar]
- Xu, R.; Zhang, Z. An algorithm for rapidly determining the convexity-concavity of the vertices of an arbitrary polygon. J. Huazhong Univ. Sci. Technol. 1997, 25, 103–104. [Google Scholar]
- Zhou, P. Computational Geometry: Algorithm Design and Analysis; Tsinghua University Press: Beijing, China, 2006. [Google Scholar]
- Feito, F.; Torres, J.C.; Ureña, A. Orientation, simplicity, and inclusion test for planar polygons. Comput. Graph. 1995, 19, 595–600. [Google Scholar] [CrossRef]
- Jin, W.; Tang, W.; Tang, R. A fast algorithm for determining the convexity-concavity of vertices of simple polygon. J. Eng. Graph. 1998, 1, 66–70. [Google Scholar]
- Pang, M.; Lu, Z. An algorithm for rapidly identifying convexo-concave vertices of simple polygon based on comparing the slopes of two adjacent edge vectors. J. Eng. Graph. 2004, 3, 71–77. [Google Scholar]
- Zhao, J.; Zhang, G.; Qu, S. Orientation and convexity-concavity identification for polygons using extremity vertices sequence. J. Eng. Graph. 2007, 1, 55–59. [Google Scholar]
- Clifford, W.K. APPlieations of Grassmann’s extensive algebra. Am. J. Math. 1878, 1, 350–358. [Google Scholar] [CrossRef]
- Dorst, L.; Fontijne, D.; Mann, S. Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2007. [Google Scholar]
- Yuan, L.; Yu, Z.; Luo, W.; Zhou, L.; Lü, G. A 3D GIS Spatial Data Model Based on Conformal Geometric AIgebra. Sci. China Earth Sci. 2011, 54, 101–112. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Yin, P.-C.; Li, G.; Gu, H.-H.; Zhao, H.; Fu, J.-C. 3D Cadastral Data Model Based on Conformal Geometry Algebra. ISPRS Int. J. Geo-Inf. 2016, 5, 20. [Google Scholar] [CrossRef]
- Li, H.B. Invariant Algebras and Geometric Reasoning; World Scientific: Singapore, 2008. [Google Scholar]
- Li, H.B.; Hestenes, D.; Rockwood, A. Generalized Homogeneous Coordinates for Computational Geometry, Geometric Computing with Clifford Algebra; Springer: Berlin, Germany, 2001; pp. 27–59. [Google Scholar]
- Penvass, C.; Lasenby, J. A Unified Description of Multiple View Geometry, Geometric Computing with Clifford Algebra; Springer: Berlin, Germany, 2001. [Google Scholar]
- Cameron, J.; Lasenby, J. Oriented conformal geometric algebra. In Proceedings of the 7th International Conference on Clifford Algebras and Their Applications in Mathematical Physics ICCA7, Toulouse, France, 19–29 May 2005. [Google Scholar]
- Lasenby, J.; Bayro-Corrochano, E.; Lasenby, A.; Sommer, G. A new methodology for computing invariants in computer vision. In Proceedings of the 13th International Conference on Pattern Recognition, Institute of Electrical and Electronics Engineers (IEEE), ICPR 96, Vienna, Austria, 25–29 August 1996. [Google Scholar]
- Lasenby, J.; Fitzgerald, W.; Doran, C. New Geometric Methods for Computer Vision: An Application to Structure and Motion Estimation. Int. J. Comput. Vis. 1998, 26, 191–213. [Google Scholar] [CrossRef]
- Penvass, C. Applications of Geometric Algebra in Computer Vision. Ph.D. Thesis, Cambridge University, Cambridge, UK, 2000. [Google Scholar]
- Yuan, L.; Yu, Z.; Luo, W.; Yi, L.; Lu, G. Multidimensional-unified topological relations computation: A hierarchical geometric algebra-based approach. Int. J. Geogr. Inf. Sci. 2014, 28, 2435–2455. [Google Scholar] [CrossRef]
- Yuan, L.; Yu, Z.; Chen, S.; Luo, W.; Wang, Y.; Lu, G. CAUSTA: Clifford Algebra-based Unified Spatio-Temporal Analysis. Trans. GIS 2010, 14, 59–83. [Google Scholar] [CrossRef]
- Yuan, L.; Yu, Z.; Luo, W.; Hu, Y.; Feng, L.; Zhu, A.-X. A Hierarchical Tensor-Based Approach to Compressing, Updating and Querying Geospatial Data. IEEE Trans. Knowl. Data Eng. 2015, 27, 312–325. [Google Scholar] [CrossRef]
- Yu, Z.; Luo, W.; Hu, Y.; Yuan, L.; Zhu, A.-X.; Lu, G. Change detection for 3D vector data: A CGA-based Delaunay–TIN intersection approach. Int. J. Geogr. Inf. Sci. 2015, 29, 2328–2347. [Google Scholar] [CrossRef]
- Luo, W.; Hu, Y.; Yu, Z.; Yuan, L.; Lü, G. A Hierarchical Representation and Computation Scheme of Arbitrary-dimensional Geometrical Primitives Based on CGA. Adv. Appl. Clifford Algebras 2017, 27, 1977–1995. [Google Scholar] [CrossRef]
- Luo, W.; Yu, Z.; Yuan, L.; Hu, Y.; Zhu, A.-X.; Lü, G. Template-based GIS computation: A geometric algebra approach. Int. J. Geogr. Inf. Sci. 2017, 31, 2045–2067. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).