Transparent Collision Visualization of Point Clouds Acquired by Laser Scanning
Abstract
:1. Introduction
2. Collision Visualization Targets
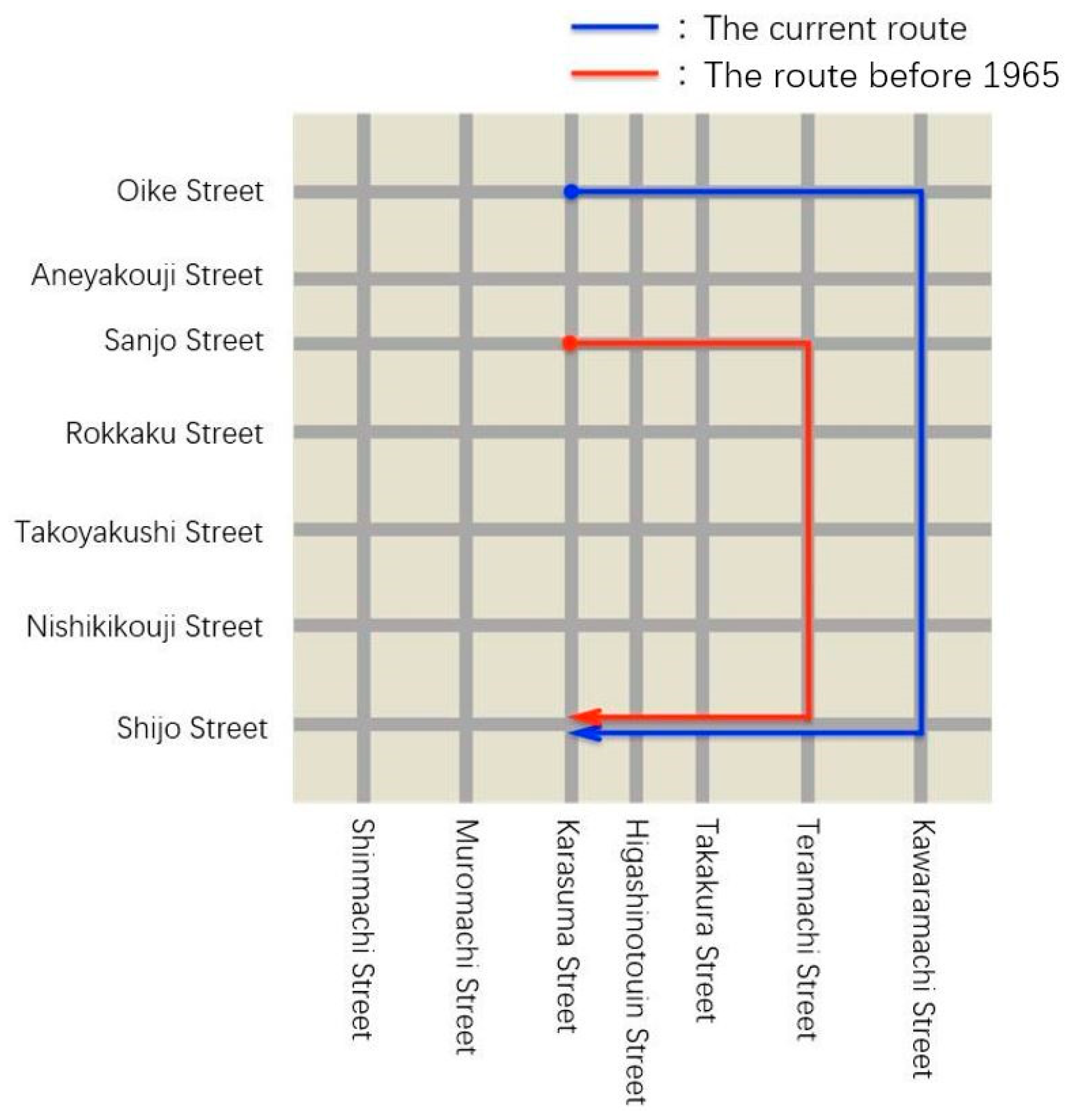
2.1. Project of Reviving the Original Procession Route of the Festival Float
2.2. Engineering Plants Simulation
3. Proposed Method
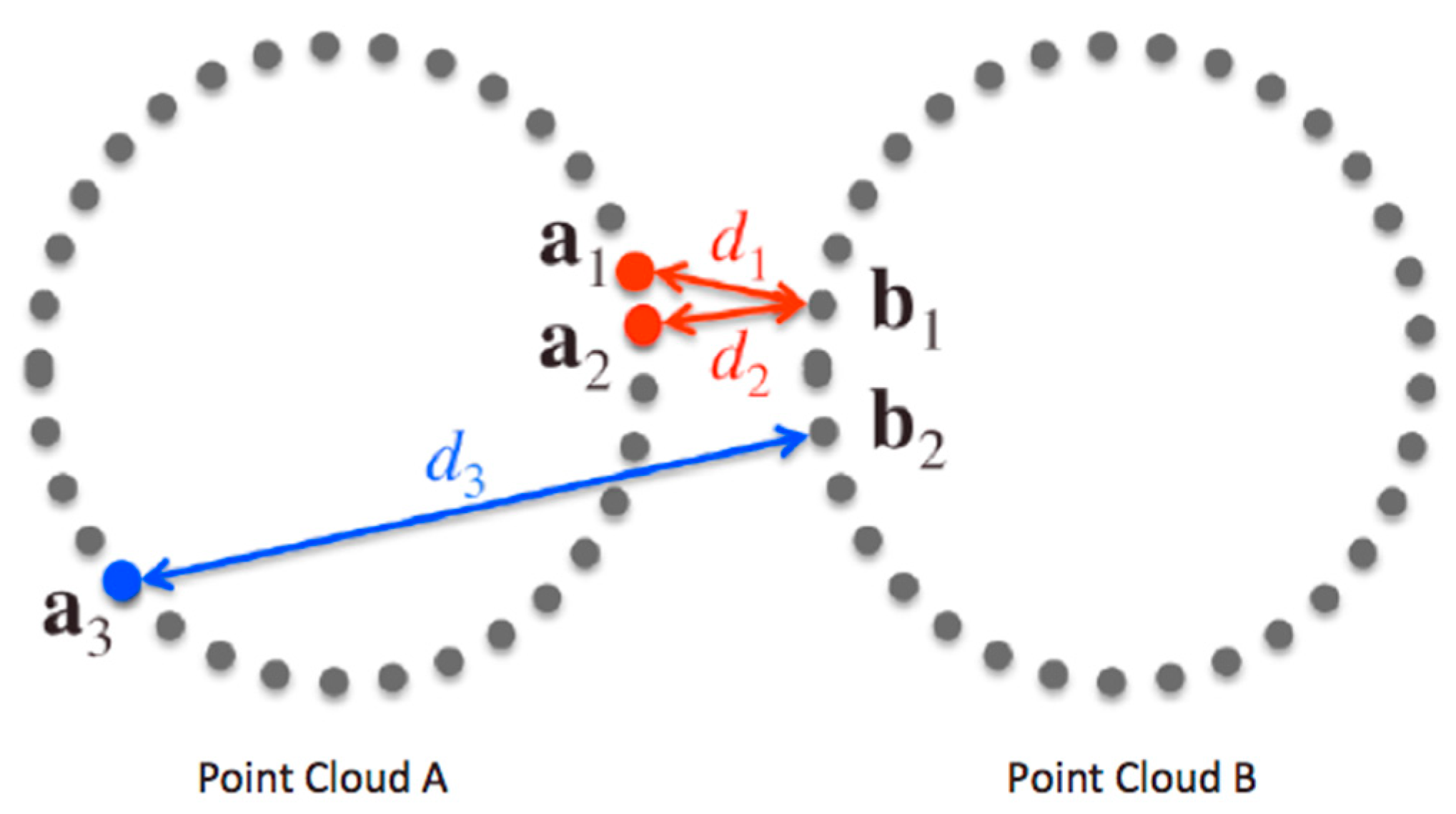
3.1. Assignment of Color and Opacity to Points
- For a point ai in point cloud A, perform the nearest neighbor search and find its nearest neighboring point bj(ai) in point cloud B (see Figure 3).
- Calculate the inter-point distance d (ai, bj(ai)) between points ai and bj(ai).
- If d (ai, bj(ai)) is less than or equal to a threshold value, ε, then assign a proper collision area color and collision area opacity to ai. If d (ai, bj(ai)) is larger than ε and less than or equal to a proper non-small distance dmax, then assign a proper high collision risk area color and high collision risk area opacity to ai. (In the current work, ε is set to 1/100 or 1/500 of the bounding-box diameter of the scene that consists of point clouds A and B. When considering collisions with electric wires, the smaller value of 1/500 works better. dmax is set to 1/10 of the bounding box.)
- Execute Steps 1–3 for all points in A. Repeat the same for the points in B if the points in B should also be assigned colors.
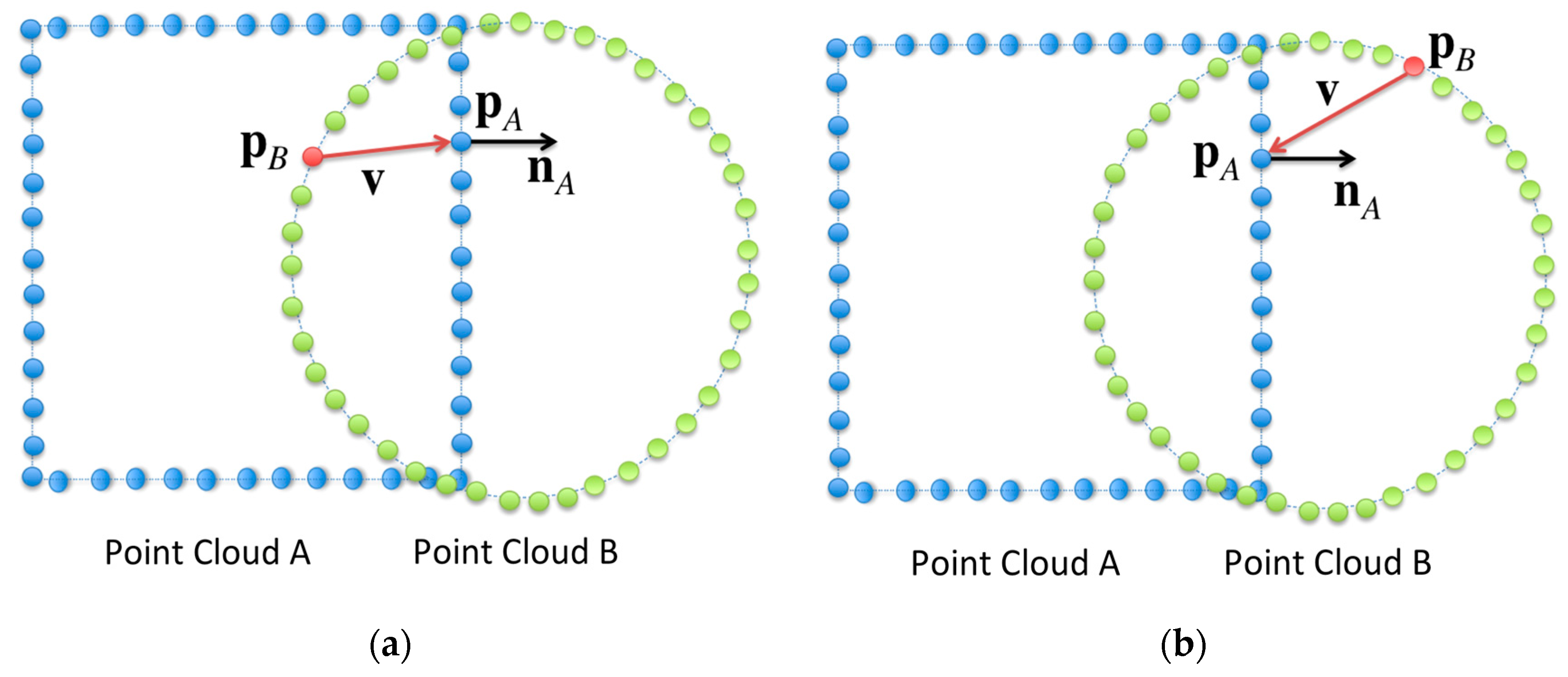
3.2. Visualization of Deep Collisions
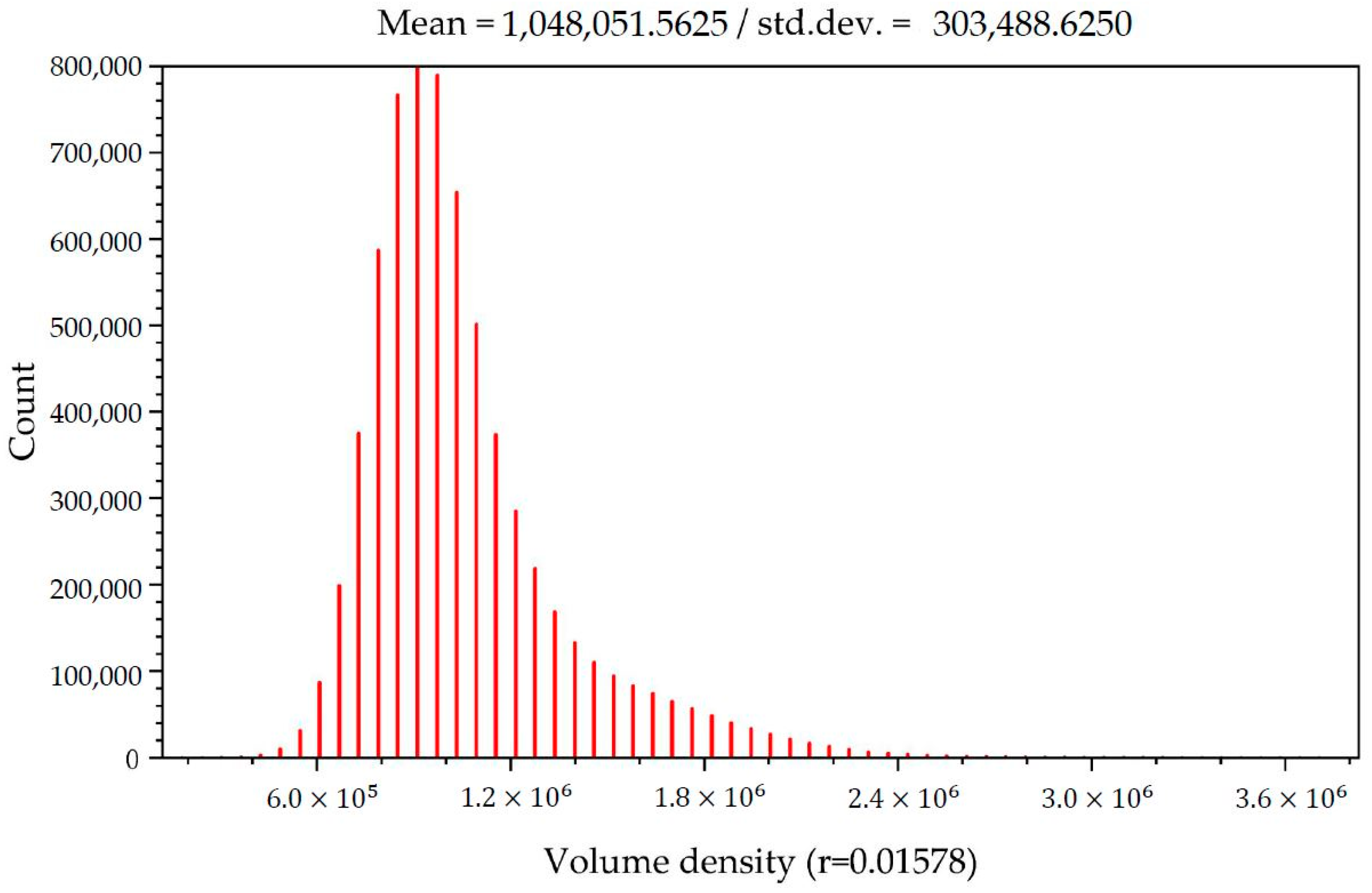
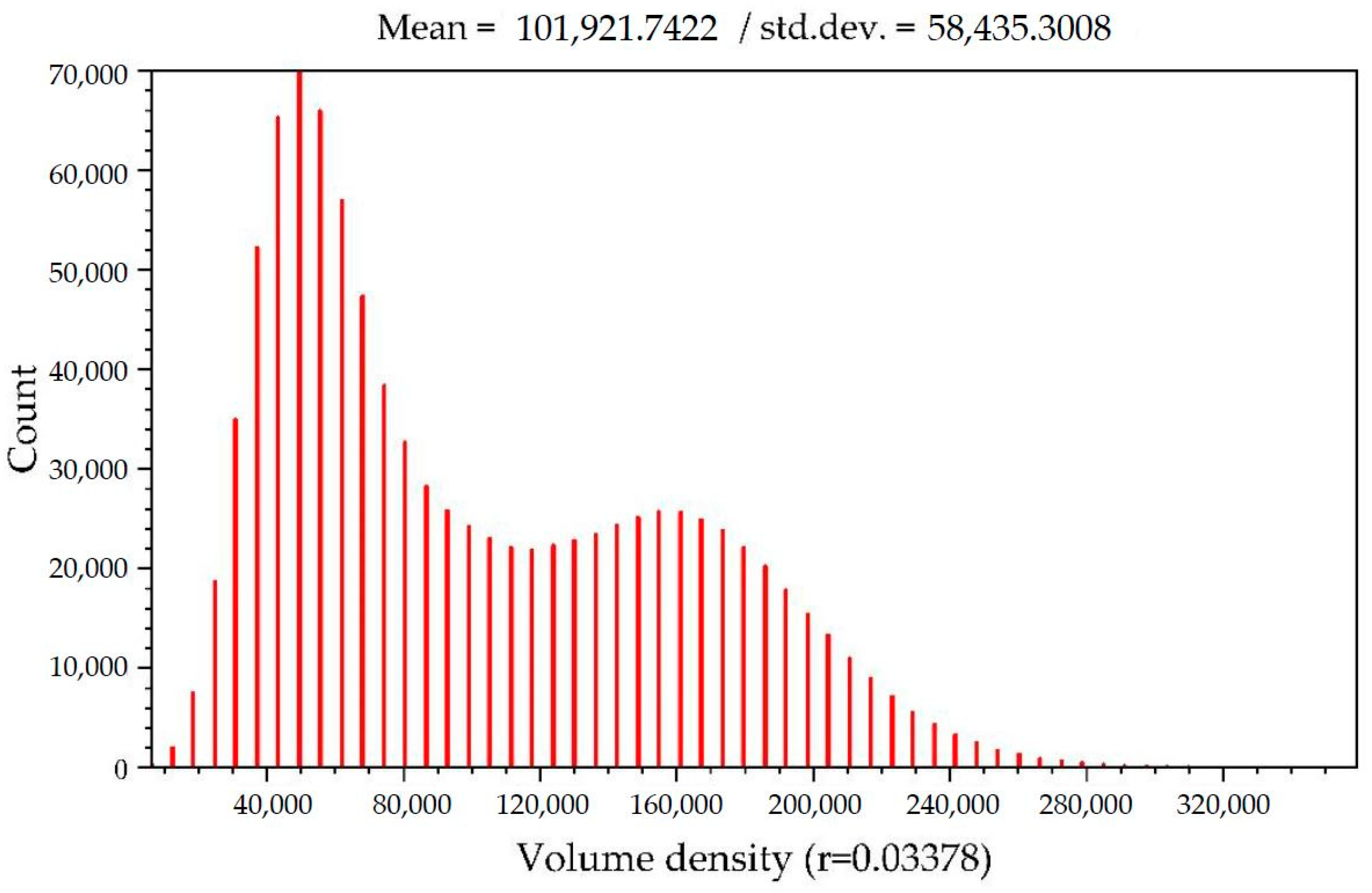
3.3. Realization of the Collision Area Opacity and the High Collision Risk Area Opacity Based on Stochastic Point-Based Transparent Rendering
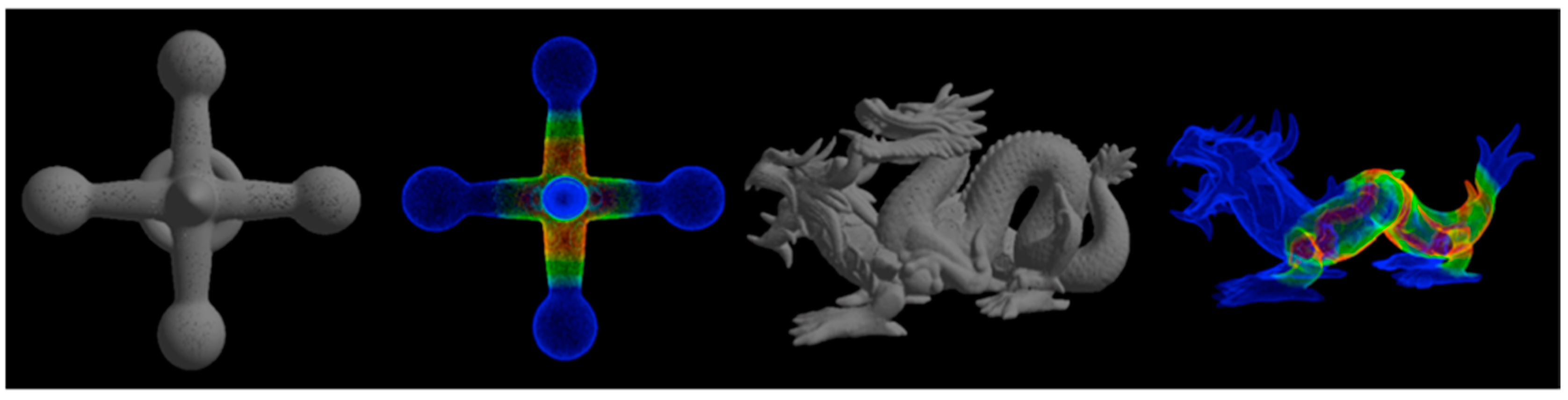
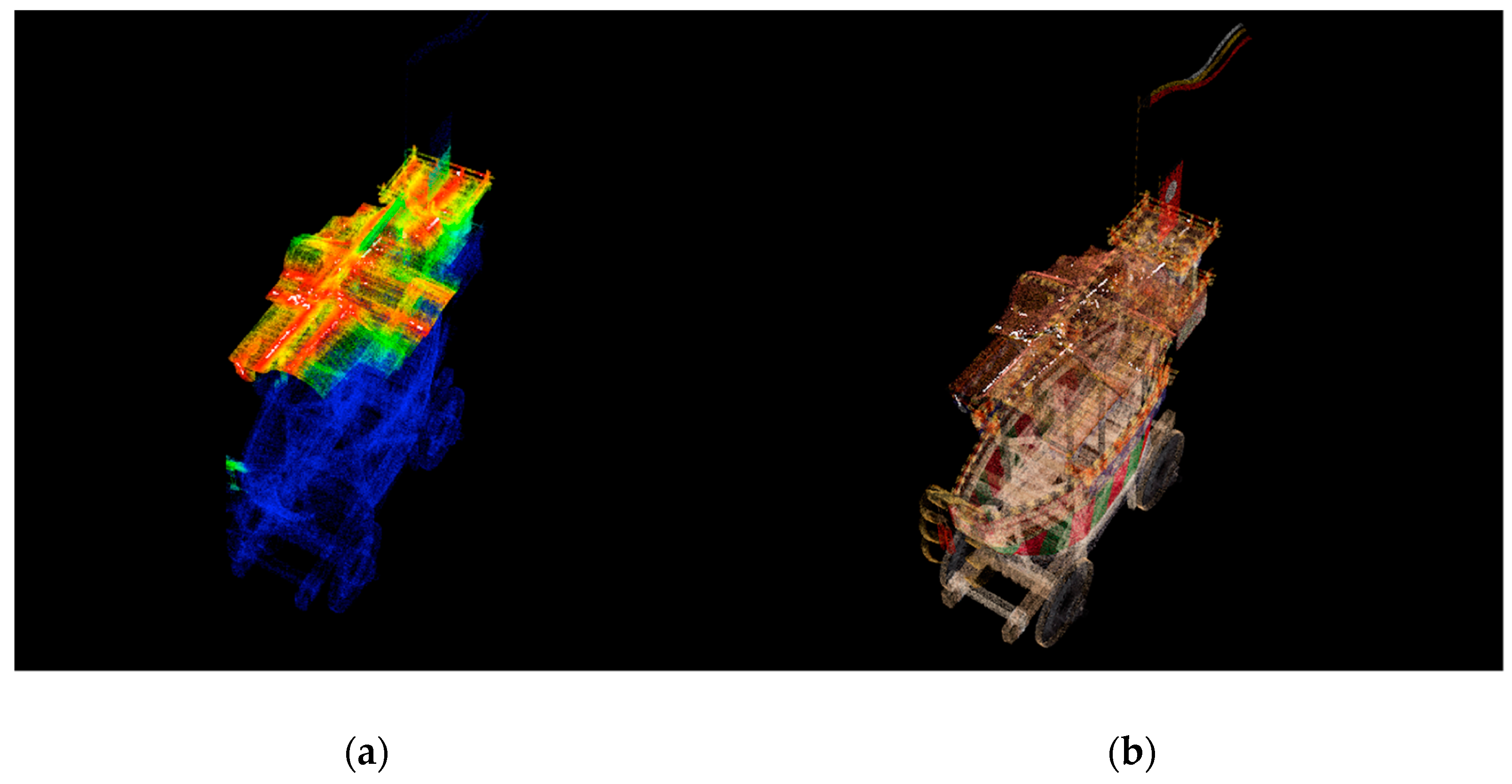
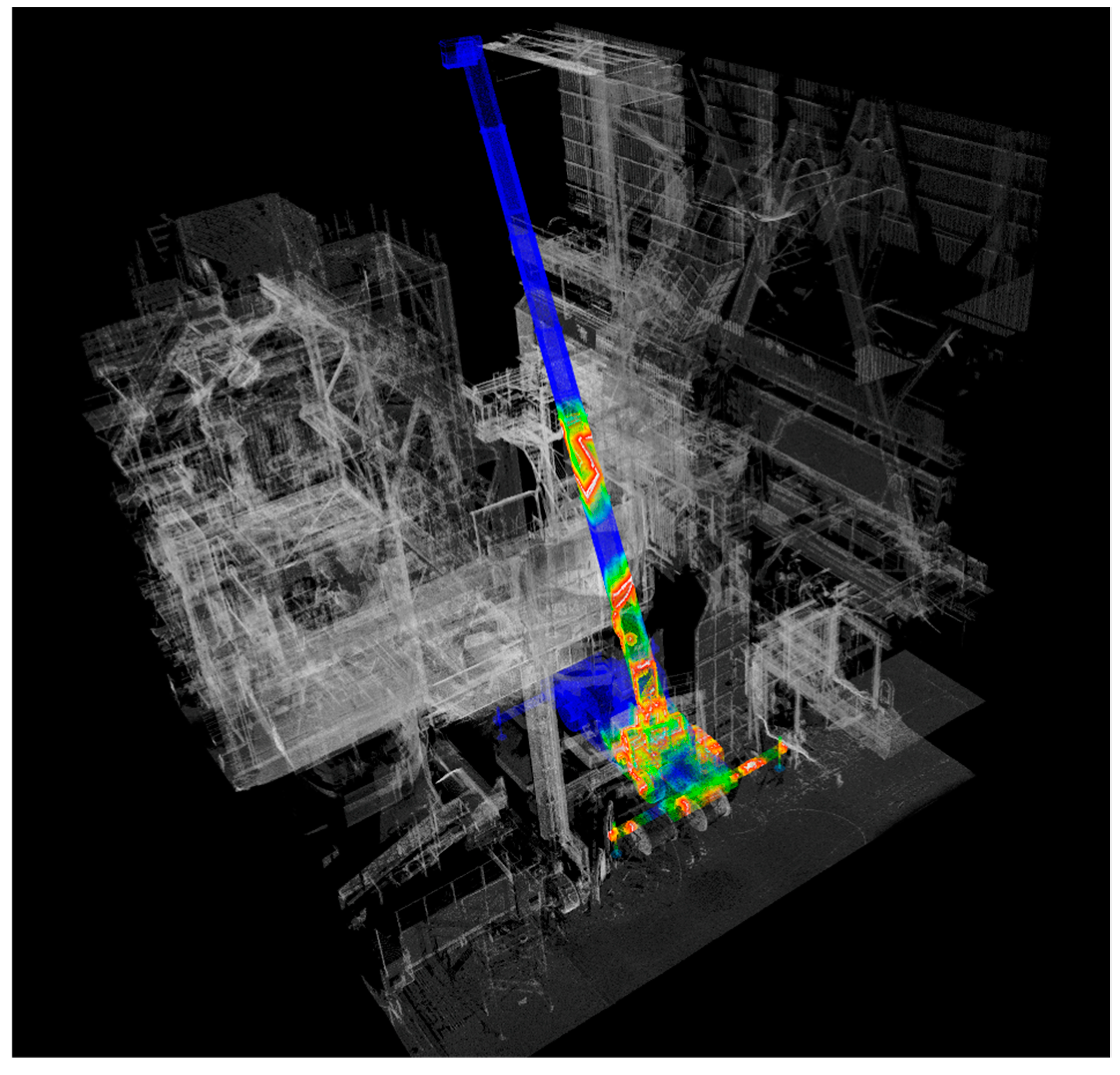
4. Experimental Results
4.1. Collision Detection Simulation of the Ofune-Hoko Float Along its Original Procession Route
4.2. Results of the Engineering Plant Simulation
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giorgini, M.; Aleotti, J. Visualization of AGV in Virtual Reality and Collision Detection with Large Scale Point Clouds. In Proceedings of the 2018 IEEE 16th International Conference on Industrial Informatics (INDIN), Porto, Portugal, 18–20 July 2018. [Google Scholar]
- Patil, A.K.; Kumar, G.A.; Kim, T.-H.; Chai, Y.H. Hybrid approach for alignment of a pre-processed three-dimensional point cloud, video, and CAD model using partial point cloud in retrofitting applications. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718766452. [Google Scholar] [CrossRef]
- Riveiro, B.; Morer, P.; Arias, P.; De Arteaga, I. Terrestrial laser scanning and limit analysis of masonry arch bridges. Constr. Build. Mater. 2011, 25, 1726–1735. [Google Scholar] [CrossRef]
- Boulaassal, H.; Landes, T.; Grussenmeyer, P.; Tarsha-Kurdi, F. Automatic Segmentation of Building Facades Using Terrestrial Laser Data; ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007; HAL: Espoo, Finland, 2007; pp. 65–70. [Google Scholar]
- Alshawabkeh, Y.; Haala, N. Integration of digital photogrammetry and laser scanning for heritage documentation. Int. Arch. Photogramm. Remote Sens. 2004, 35, B5. [Google Scholar]
- Adam, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. H-RANSAC: A hybrid point cloud segmentation combining 2D and 3D data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2018, 4, 1–8. [Google Scholar] [CrossRef]
- Niwa, T.; Masuda, H. Interactive Collision Detection for Engineering Plants based on Large-Scale Point-Clouds. Comput.-Aided Des. Appl. 2016, 13, 511–518. [Google Scholar] [CrossRef]
- Li, W.; Shigeta, K.; Hasegawa, K.; Li, L.; Yano, K.; Tanaka, S. Collision Visualization of a Laser-Scanned Point Cloud of Streets and a Festival Float Model used for the Revival of a Traditional Procession Route. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 255–261. [Google Scholar] [CrossRef]
- Dos Anjos, R.K.; Pereira, J.M.; Oliveira, J.F. Collision detection on point clouds using a 2.5+ D image-based approach. J. WSCG 2012, 20, 145–154. [Google Scholar]
- Figueiredo, M.; Oliveira, J.; Araujo, B.; Pereira, J. An efficient collision detection algorithm for point cloud models. In Proceedings of the 20th International Conference on Computer Graphics and Vision, St. Petersburg, Russia, 20–24 September 2010; pp. 43–44. [Google Scholar]
- Hermann, A.; Drews, F.; Bauer, J.; Klemn, S.; Roennau, A.; Dillmann, R. Unified GPU voxel collision detection for mobile manipulation planning. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 4154–4160. [Google Scholar]
- Ioannides, M.; Magnenat-Thalmann, N.; Fink, E.; Zarnic, R.; Yen, A.Y.; Quak, E. (Eds.) Digital Heritage: Progress in Cultural Heritage. In Proceedings of the Documentation, Preservation, and Protection 5th International Conference, EuroMed 2014, Limassol, Cyprus, 3–8 November 2014; Proceedings (Lecture Notes in Computer Science). Springer: Berlin, Germany, 2014. [Google Scholar]
- Klein, J.; Zachmann, G. Point cloud collision detection. In Computer Graphics Forum; Blackwell Publishing, Inc.: Oxford, UK; Boston, MA, USA, 2004; Volume 23, pp. 567–576. [Google Scholar]
- Pan, J.; Sucan, A.; Chitta, S.; Manocha, D. Real-time collection detection and distance computation on point cloud sensor data. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 3593–3599. [Google Scholar]
- Pan, J.; Chitta, S.; Manocha, D. Probabilistic Collision Detection between Noisy Point Clouds Using Robust Classification. In Robotics Research (Volume 100 of the Series Springer Tracts in Advanced Robotics); Springer: Champaign, IL, USA, 2016; pp. 77–94. [Google Scholar]
- Radwan, M.; Ohrhallinger, S.; Wimmer, M. Efficient Collision Detection While Rendering Dynamic Point Clouds. In Proceedings of the Graphics Interface Conference on Canadian Information Processing Society, Montreal, QC, Canada, 7–9 May 2014; p. 25. [Google Scholar]
- Schauer, J.; Nuchter, A. Efficient point cloud collision detection and analysis in a tunnel environment using kinematic laser scanning and KD Tree search. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 289–295. [Google Scholar] [CrossRef]
- Gross, M.H.; Pfister, H. (Eds.) Point-Based Graphics. Series in Computer Graphics; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2007. [Google Scholar]
- Sainz, M.; Pajarola, R. Point-based rendering techniques. Comput. Graph. 2004, 28, 869–879. [Google Scholar] [CrossRef]
- Kobbelt, L.; Botsch, M. A survey of point-based techniques in computer graphics. Comput. Graph. 2004, 28, 801–814. [Google Scholar] [CrossRef]
- Discher, S.; Richter, R.; Döllner, J. Concepts and Techniques for Web-based Visualization and Processing of Massive 3D Point Clouds with Semantics. Graph. Models 2019, 104, 101036. [Google Scholar] [CrossRef]
- Tanaka, S.; Hasegawa, K.; Okamoto, N.; Umegaki, R.; Wang, S.; Uemura, M.; Okamoto, A.; Koyamada, K. See-Through Imaging of Laser-scanned 3D Cultural Heritage Objects based on Stochastic Rendering of Large-Scale Point Clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 73–80. [Google Scholar] [CrossRef]
- Zhang, Y.; Pajarola, R. Image composition for singlepass point rendering. Comput. Graph. 2007, 31, 175–189. [Google Scholar] [CrossRef]
- Zwicker, M.; Pfister, H.; van Baar, J.; Gross, M. EWA splatting. IEEE TVCG 2002, 8, 223–238. [Google Scholar] [CrossRef]
- Kyoto Visualization System (KVS). Available online: https://github.com/naohisas/KVS (accessed on 18 September 2019).
- Point Cloud Library (PCL). Available online: http://pointclouds.org/ (accessed on 18 September 2019).
- OpenGL Utility Toolkit (GLUT). Available online: https://www.opengl.org/resources/libraries/glut/ (accessed on 18 September 2019).
- OpenGL Extension Wrangler Library (GLEW). Available online: http://glew.sourceforge.net/ (accessed on 18 September 2019).
- Doria, D.; Radke, R.J. Filling large holes in lidar data by inpainting depth gradients. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Sahay, P.; Rajagopalan, A.N. Geometric inpainting of 3D structures. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–2 June 2015. [Google Scholar]













| Data | Points | Time for Collision Detection [sec] | Time for Visualization [sec] |
|---|---|---|---|
| Hub | 2.5 × 105 | 5.03 | 0.68 |
| Dragon | 4.39 × 105 | 7.56 | 1.74 |
| Sanjo Street | 6.56 × 106 | 10.17 | |
| Sanjo Street (Ground removed) | 3.49 × 106 | 4.16 | |
| Ofune-hoko | 6.74 × 106 | 21.85 | 12.21 |
| Plant | 9.05 × 106 | 19.88 | |
| Crane vehicle | 9.9 × 105 | 13.97 | 2.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Shigeta, K.; Hasegawa, K.; Li, L.; Yano, K.; Adachi, M.; Tanaka, S. Transparent Collision Visualization of Point Clouds Acquired by Laser Scanning. ISPRS Int. J. Geo-Inf. 2019, 8, 425. https://doi.org/10.3390/ijgi8090425
Li W, Shigeta K, Hasegawa K, Li L, Yano K, Adachi M, Tanaka S. Transparent Collision Visualization of Point Clouds Acquired by Laser Scanning. ISPRS International Journal of Geo-Information. 2019; 8(9):425. https://doi.org/10.3390/ijgi8090425
Chicago/Turabian StyleLi, Weite, Kenya Shigeta, Kyoko Hasegawa, Liang Li, Keiji Yano, Motoaki Adachi, and Satoshi Tanaka. 2019. "Transparent Collision Visualization of Point Clouds Acquired by Laser Scanning" ISPRS International Journal of Geo-Information 8, no. 9: 425. https://doi.org/10.3390/ijgi8090425
APA StyleLi, W., Shigeta, K., Hasegawa, K., Li, L., Yano, K., Adachi, M., & Tanaka, S. (2019). Transparent Collision Visualization of Point Clouds Acquired by Laser Scanning. ISPRS International Journal of Geo-Information, 8(9), 425. https://doi.org/10.3390/ijgi8090425





