Japanese Lexical Variation Explained by Spatial Contact Patterns
Abstract
1. Introduction
1.1. Motivation
1.2. Background
1.3. Aims of the Research
- A series of models estimating contact potential:
- -
- before the time of infrastructural development, using network of least cost paths based on digital elevation models (DEM),
- -
- at present, using today’s road network for calculating travel distances and travel times
- -
- independent of time, using the great circle distances between localities.
- A model estimating the potential influence between communities based on their population density and an inverse-distance association similar to the law of gravity.
- Finally, we test the separating effect of administrative boundaries, on the one hand the administrative system of domains (Japanese: han) used in the Edo-era (1603–1868), which are deemed to have affected the language variation before the LAJ respondents’ age of mother tongue acquisition, due to restriction of free movement [79], and on the other hand their modern counterpart, the prefectures (Japanese: ken).
2. Materials and Methodology
2.1. Dialect Data: The Linguistic Atlas of Japan
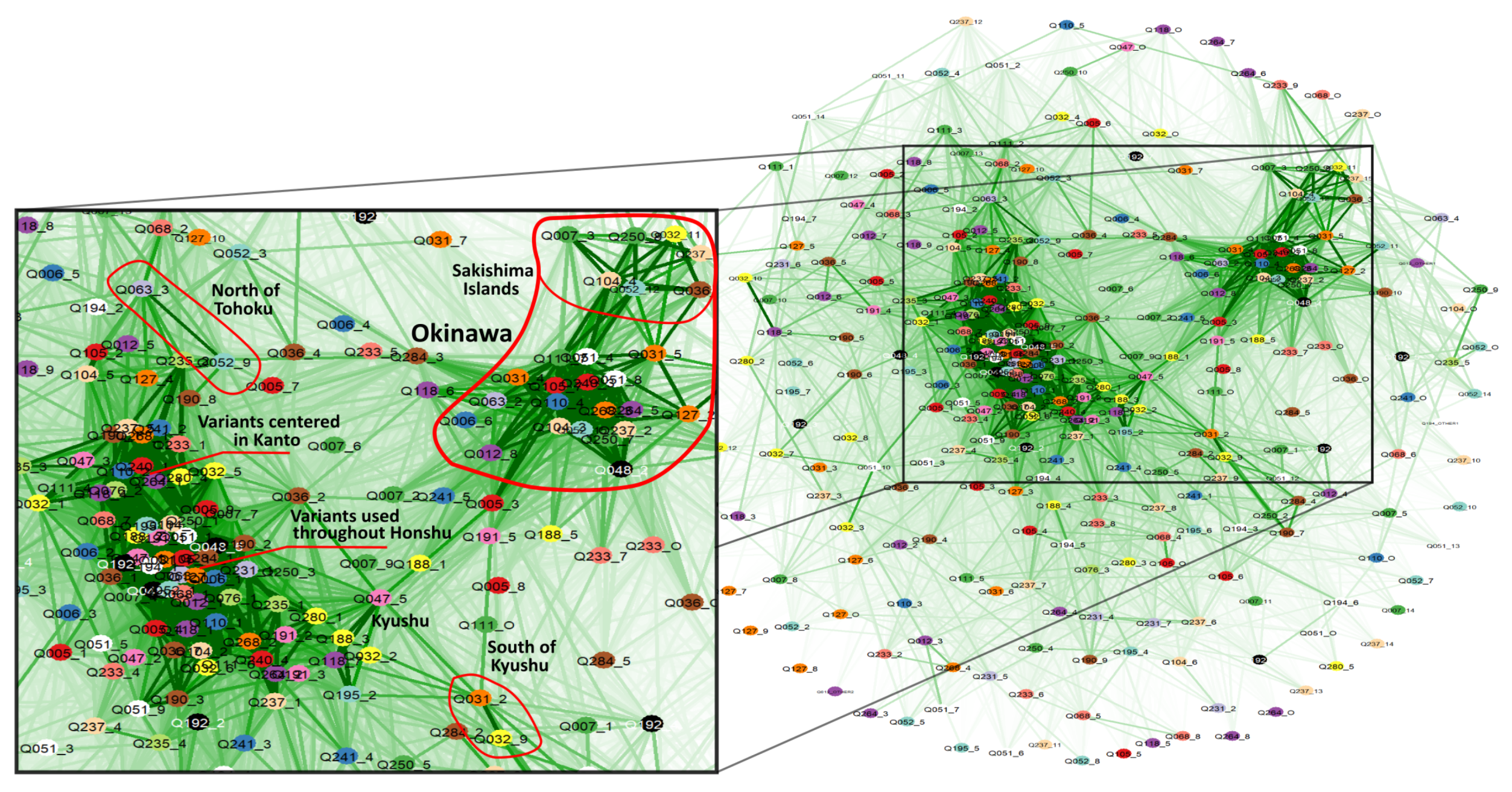
2.2. Categorisation of the Dialect Data: Overlap Analysis
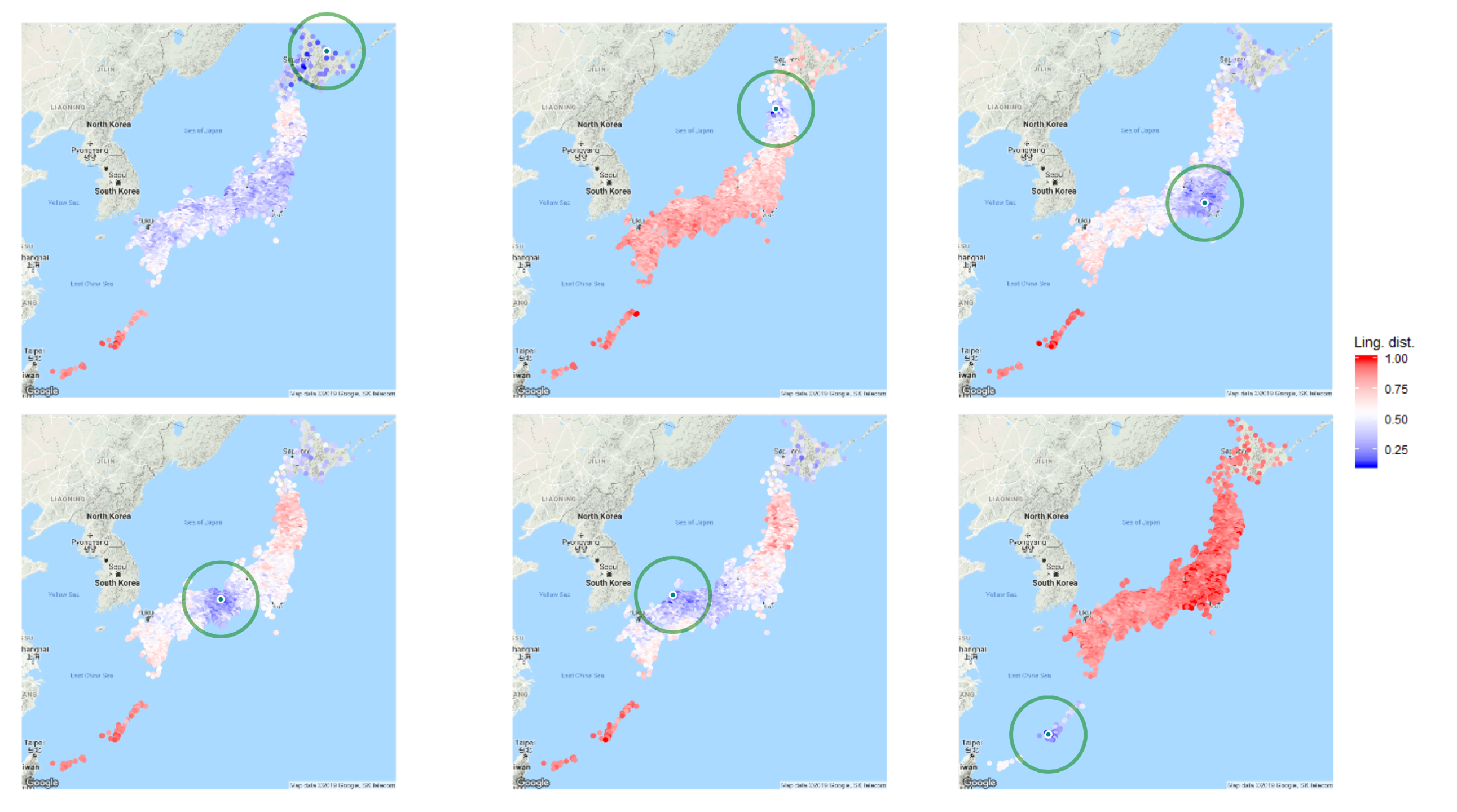
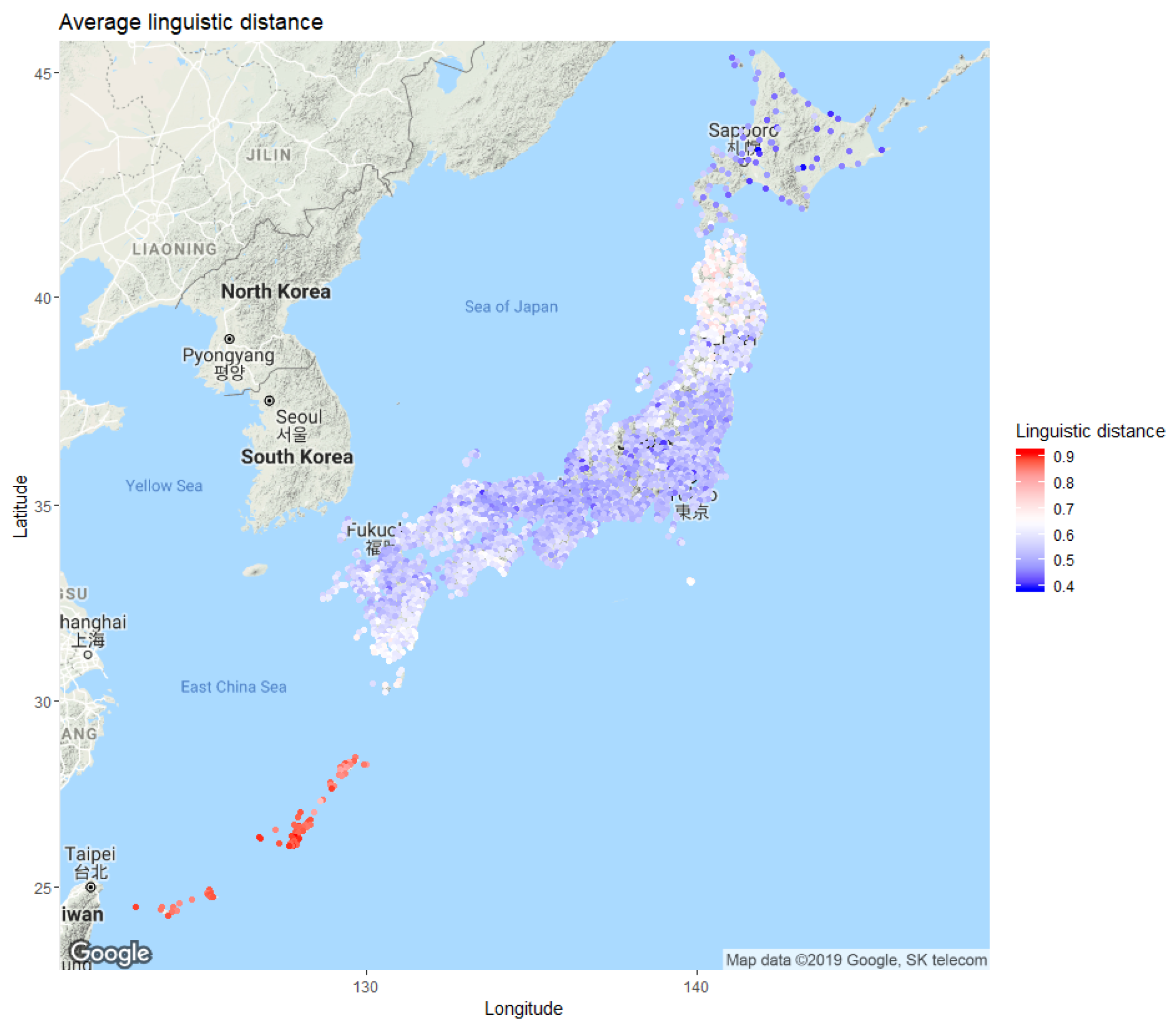
2.3. Linguistic Distance: Quantifying the Dialect Variation across Localities
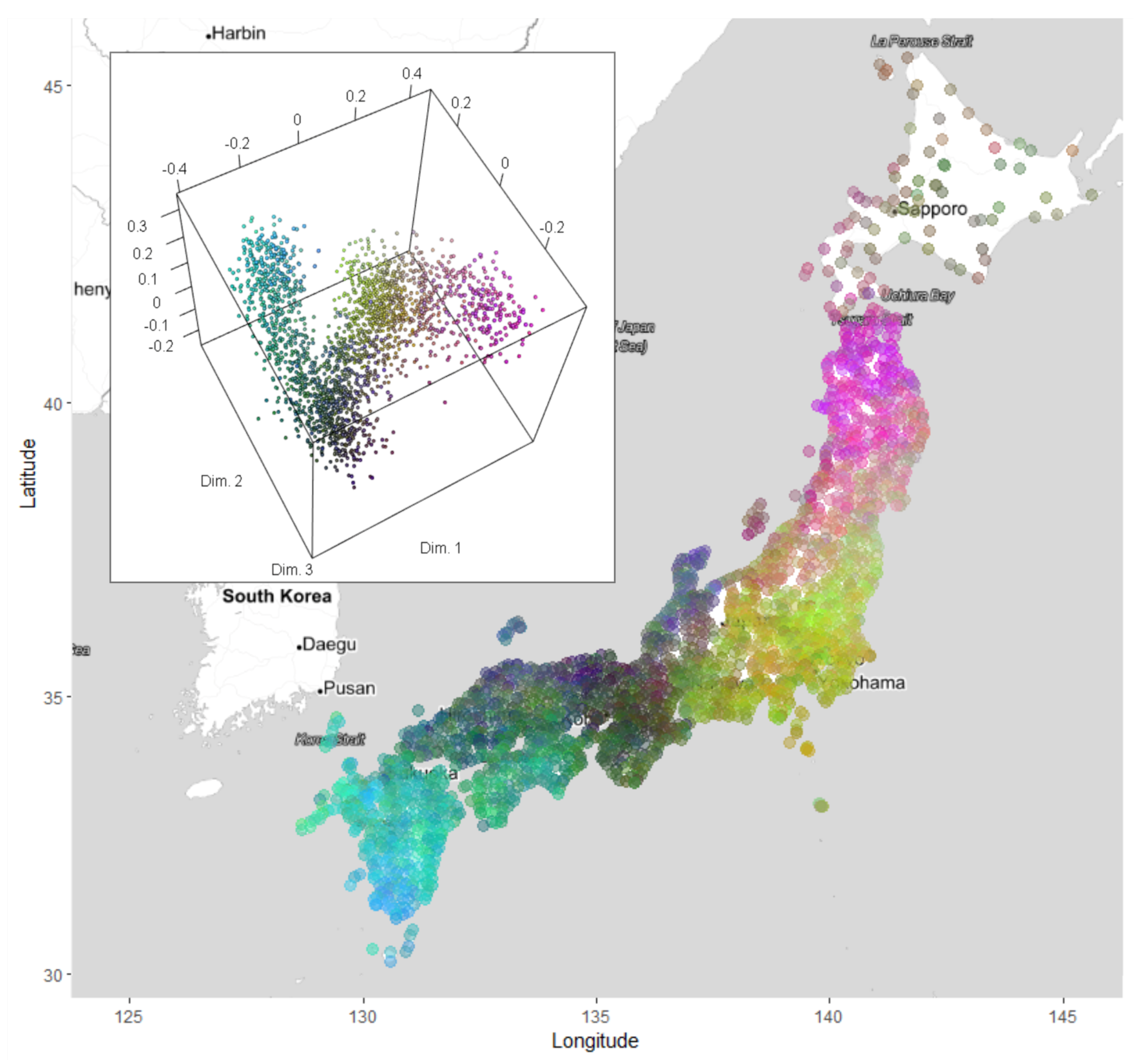
2.4. Discovering the Spatial Association of Linguistic Distance by Multidimensional Scaling
2.5. Estimating the Dialect Contact Potential
2.5.1. Great Circle Distance
2.5.2. Travel Distance
2.5.3. Travel Times
2.5.4. Least Cost Paths and Hiking Times
2.5.5. Linguistic ’Gravity’ Index
2.6. Explaining Linguistic Variation through Administrative Boundaries
- Both localities are located in the same domain or prefecture (termed ‘within’ group) and
- the localities are separated by domain or prefectural boundaries (termed ‘separated’ group).
3. Results and Interpretation
3.1. Association Across Linguistic Variants Disregarding Space
3.2. Linguistic Distances Mapped
3.3. Dialectal Variation in Space
3.4. Correlations with Spatial Measurements
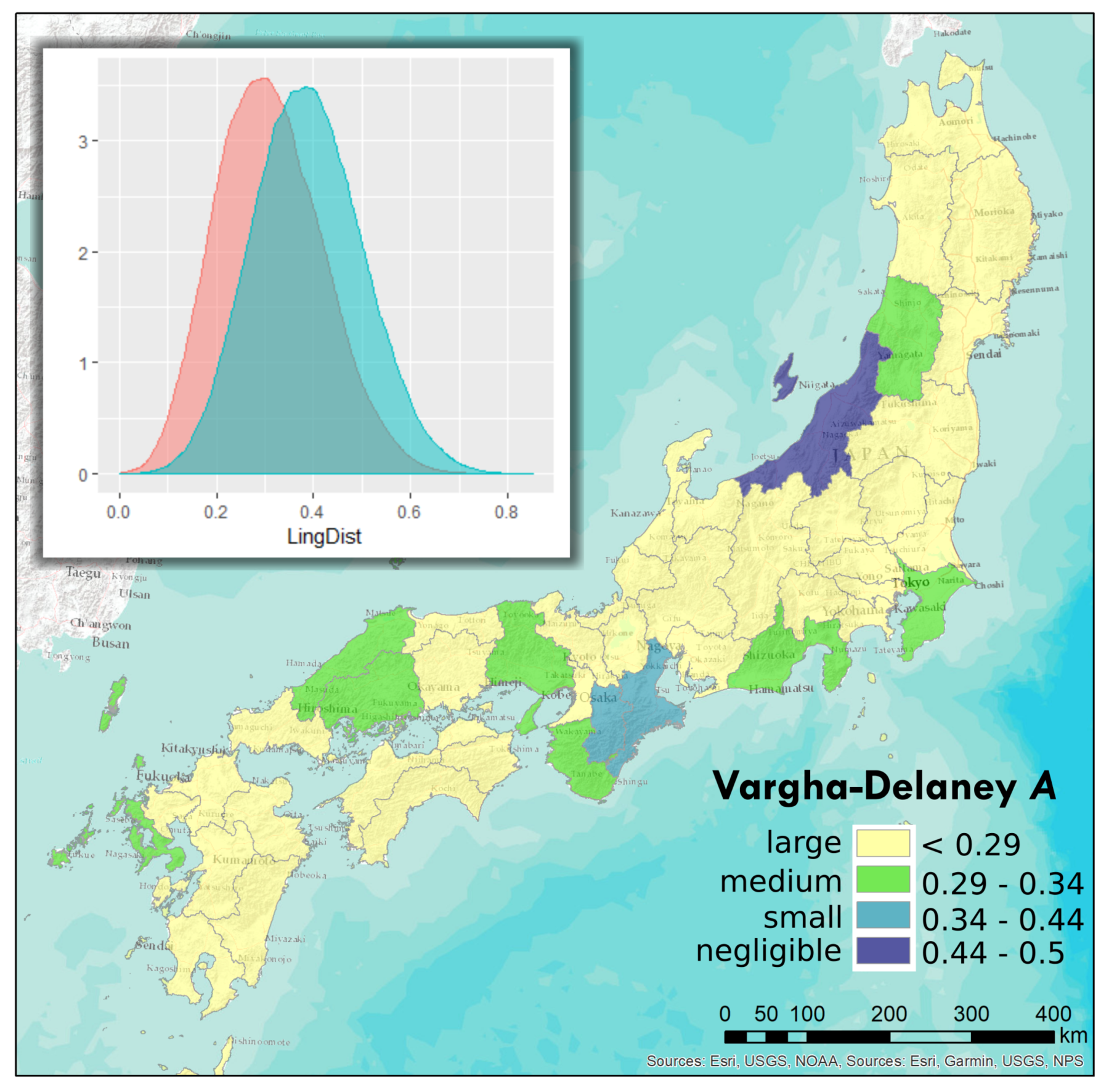
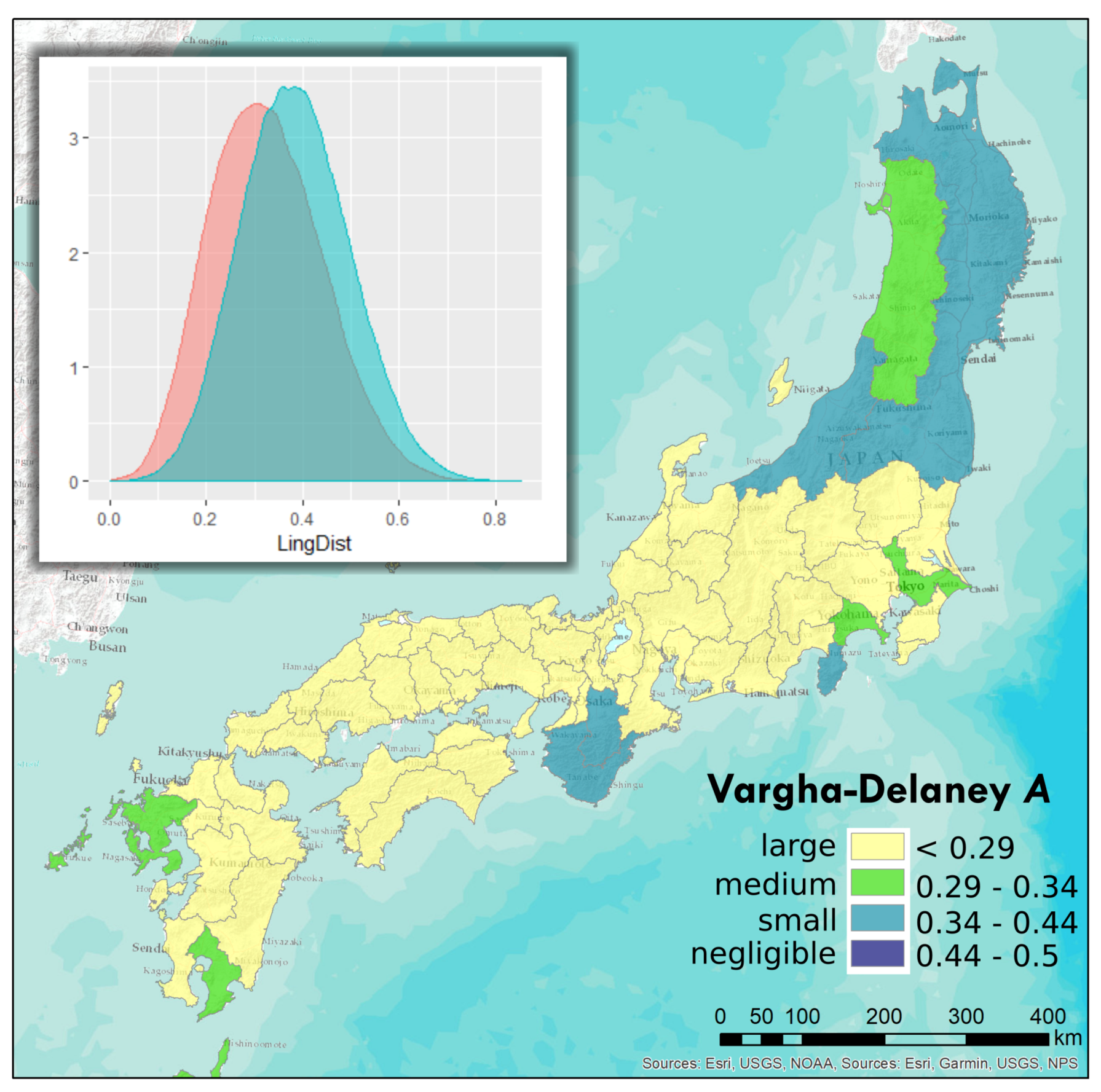
3.5. Effects of Administrative Boundaries
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GCD | Great Cirlce Distance |
| HT | Hiking Time (along least cost paths) |
| LAJ | Linguistic Atlas of Japan |
| LAJDB | Linguistic Atlas of Japan DataBase |
| MDS | MultiDimensional Scaling |
| NLRI | National Language Research Institute |
| NINJAL | National Institute of Japanese Language and Linguistics |
| OSRM | Open Source Routing Machine |
| TD | Travel Distance |
| TLGI | Trudgill’s Linguistic Gravity Index |
| TT | Travel Time |
References
- Lameli, A.; Purschke, C.; Rabanus, S. Digitaler Wenker-Atlas (DiWA). In Regionale Variation des Deutschen—Projekte und Perspektiven; Kehrein, R., Lameli, A., Rabanus, S., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2015; pp. 127–154. [Google Scholar]
- Rosch, E.H. Natural Categories. Cogn. Psychol. 1973, 4, 328–350. [Google Scholar] [CrossRef]
- Lakoff, G. Women, Fire, and Dangerous Things: What Categories Reveal about Thought; University of Chicago Press: Chicago, IL, USA; London, UK, 1987. [Google Scholar]
- Hinskens, F.; Auer, P.; Kerswill, P. The Study of Dialect Convergence and Divergence: Conceptual and Methodological Considerations. In Dialect Change: Convergence and Divergence in European Languages; Auer, P., Hinskens, F., Kerswill, P., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 1–48. [Google Scholar] [CrossRef]
- Bowern, C. Relatedness as a Factor in Language Contact. J. Lang. Contact 2013, 6, 411–432. [Google Scholar] [CrossRef]
- Schreier, D. Language in Isolation, and its Implications for Variation and Change. Linguist. Lang. Compass 2009, 3, 682–699. [Google Scholar] [CrossRef]
- Fagyal, Z.; Swarup, S.; Escobar, A.M.; Gasser, L.; Lakkaraju, K. Centers and Peripheries: Network Roles in Language Change. Lingua 2010, 120, 2061–2079. [Google Scholar] [CrossRef]
- Lee, S.; Hasegawa, T. Oceanic Barriers Promote Language Diversification in the Japanese Islands. J. Evol. Biol. 2014, 27, 1905–1912. [Google Scholar] [CrossRef]
- Bloomfield, L. Language; Holt, Rinehart & Winston: New York, NY, USA, 1933. [Google Scholar]
- Hägerstrand, T. The Propagation of Innovation Waves. In Lund Studies in Geography, Series B; Royal University of Lund, Department of Geography: Lund, Sweden, 1952. [Google Scholar]
- Trudgill, P. Linguistic Change and Diffusion: Description and Explanation in Sociolinguistic Dialect Geography. Lang. Soc. 1974, 2, 215–246. [Google Scholar] [CrossRef]
- Britain, D. Space and Spatial Diffusion. In Language and Space: An International Handbook of Linguistic Variation; Chambers, J.K., Trudgill, P., Schilling-Estes, N., Eds.; Blackwell: Oxford, UK, 2002; pp. 603–637. [Google Scholar] [CrossRef]
- De Vriend, F.; Giesbers, C.; van Hout, R.; Ten Bosch, L. The Dutch-German Border: Relating Linguistic, Geographic and Social Distances. Int. J. Humanit. Arts Comput. 2008, 2, 119–134. [Google Scholar] [CrossRef]
- Huisman, J.L.A.; Majid, A.; van Hout, R. The Geographical Configuration of a Language Area Influences Linguistic Diversity. PLoS ONE 2019, 14, e0217363. [Google Scholar] [CrossRef]
- Onishi, T. On the Relationship of the Degrees of Correspondence of Dialects and Distances. Languages 2019, 4, 37. [Google Scholar] [CrossRef]
- Limper, J.; Pheiff, J.; Williams, A. REDE SprachGIS: A Geographic Information System for Linguists. In Handbook of the Changing World Language Map; Springer: Berlin, Germany, 2019; pp. 1–30. [Google Scholar] [CrossRef]
- Hoch, S.; Hayes, J. Geolinguistics: the Incorporation of Geographic Information Systems and Science. Geogr. Bull. 2010, 51, 23–36. [Google Scholar]
- Labov, W. The Social Motivation of a Sound Change. Word 1963, 19, 273–309. [Google Scholar] [CrossRef]
- Bailey, G.; Wilke, T.; Tillery, J.; Sand, L. The Apparent Time Construct. Lang. Var. Chang. 1991, 3, 241–264. [Google Scholar] [CrossRef]
- Kokuritsu Kokugo Kenkyûjo [National Language Research Institute (NLRI)], Nihon gengo chizu [Linguistic Atlas of Japan]; Printing Bureau, Ministry of Finance: Tokyo, Japan, 1966–1974.
- Gooskens, C. Norwegian Dialect Distances Geographically Explained. In Proceedings of the Second International Conference on Language Variation in Europe ICLAVE, Uppsala, Sweden, 12–14 June 2003; Volume 2, pp. 195–206. [Google Scholar]
- Bouckaert, R.R.; Lemey, P.; Dunn, M.; Greenhill, S.J.; Alekseyenko, A.V.; Drummond, A.J.; Gray, R.D.; Suchard, M.A.; Atkinson, Q.D. Mapping the Origins and Expansion of the Indo-European Language Family. Science 2012, 337, 957–960. [Google Scholar] [CrossRef]
- Matsumae, H.; Savage, P.E.; Ranacher, P.; Blasi, D.E.; Currie, T.E.; Sato, T.; Tajima, A.; Brown, S.; Stoneking, M.; Shimizu, K.K.; et al. Exploring Deep-time Relationships between Cultural and Genetic Evolution in Northeast Asia. bioRxiv 2019, 513929. [Google Scholar] [CrossRef]
- Ladd, D.R.; Roberts, S.G.; Dediu, D. Correlational Studies in Typological and Historical Linguistics. Annu. Rev. Linguist. 2015, 1, 221–241. [Google Scholar] [CrossRef]
- Derungs, C.; Sieber, C.; Glaser, E.; Weibel, R. Dialect Borders—Political Regions are Better Predictors than Economy or Religion. Digit. Scholarsh. Humanit. 2019. [Google Scholar] [CrossRef]
- Séguy, J. La relation entre la distance spatiale et la distance lexicale. Rev. De Linguist. Rom. 1971, 35, 335–357. [Google Scholar]
- Goebl, H. Dialektometrie: Prinzipien und Methoden des Einsatzes der Numerischen Taxonomie im Bereich der Dialektgeographie; Verlag der Osterreichischen Akademie der Wissenschaften: Vienna, Austria, 1982. [Google Scholar]
- Nerbonne, J. Mapping Aggregate Variation. In Language and Space. An International Handbook of Linguistic Variation. Vol 1. Theories and Methods; Mouton de Gruyter: Berlin, Germany; New York, NY, USA, 2010; pp. 476–495. [Google Scholar]
- Wieling, M.; Nerbonne, J. Advances in Dialectometry. Annu. Rev. Linguist. 2015, 1, 243–264. [Google Scholar] [CrossRef]
- Nerbonne, J. Data-Driven Dialectology. Lang. Linguist. Compass 2009, 3, 175–198. [Google Scholar] [CrossRef]
- Levenshtein, V.I. Binary Codes Capable of Correcting Deletions, Insertions and Reversals. Dokl. Akad. Nauk SSSR 1965, 163, 845–848. [Google Scholar]
- Kessler, B. Computational Dialectology in Irish Gaelic. In Proceedings of the 7th Conference of the European Chapter of the Association for Computational Linguistics, Dublin, Ireland, 27–31 March 1995; pp. 60–66. [Google Scholar]
- Heeringa, W. Measuring Dialect Pronunciation Differences Using Levenshtein Distance. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2004. [Google Scholar]
- Goebl, H. “Stammbaum” und “Welle”. Z. Für Sprachwiss. 1983, 2, 3–44. [Google Scholar]
- Kumagai, Y. Development of a Way to Visualize and Observe Linguistic Similarities on a Linguistic Atlas. In Working Papers from NWAV Asia-Pacific 2; National Institute for Japanese Language and Linguistics: Tokyo, Japan, 2013. [Google Scholar]
- Haag, K. Die Mundarten des Oberen Neckar-und Donaulandes (Schwäbisch-Alemannisches Grenzgebiet: Baarmundarten); Buchdruckerei Hutzler: Reutlingen, Germany, 1898. [Google Scholar]
- Maurer, F. Oberrheiner, Schwaben, Südalemannen: Räume und Kräfte im Geschichtlichen Aufbau des Deutschen Südwestens; Hünenburg: Strassburg, France, 1942. [Google Scholar]
- Kurath, H. Studies in Area Linguistics; Indiana University Press: Bloomington, Indiana; London, UK, 1972. [Google Scholar]
- Heeringa, W.; Nerbonne, J. Dialect Areas and Dialect Continua. Lang. Var. Chang. 2001, 13, 375–400. [Google Scholar] [CrossRef]
- Embleton, S. Multidimensional Scaling as a Dialectometrical Technique: Outline of a Research Project. In Contributions to Quantitative Linguistics; Köhler, R., Berger, B.B., Eds.; Springer: Dordrecht, The Netherlands, 1993; pp. 267–276. [Google Scholar]
- Spruit, M.R. Measuring Syntactic Variation in Dutch Dialects. Lit. Linguist. Comput. 2006, 21, 493–505. [Google Scholar] [CrossRef]
- Kellerhals, S. Dialektometrische Analyse und Visualisierung von Schweizerdeutschen Dialekten auf Verschiedenen Linguistischen Ebenen. Ph.D. Thesis, Universität Zürich, Zürich, Switzerland, 2014. [Google Scholar]
- Shackleton, R.G.J. English-American Speech Relationships: A Quantitative Approach. J. Engl. Linguist. 2005, 33, 99–160. [Google Scholar] [CrossRef]
- Nerbonne, J. Identifying Linguistic Structure in Aggregate Comparison. Lit. Linguist. Comput. 2006, 21, 463–475. [Google Scholar] [CrossRef]
- Pröll, S.M. Detecting Structures in Linguistic Maps—Fuzzy Clustering for Pattern Recognition in Geostatistical Dialectometry. Lit. Linguist. Comput. 2013, 28, 108–118. [Google Scholar] [CrossRef]
- Pröll, S.M.; Pickl, S.; Spettl, A. Latente Strukturen in geolinguistischen Korpora. In Deutsche Dialekte. Konzepte, Probleme, Handlungsfelder. Akten des 4. Kongresses der Internationalen Gesellschaft für Dialektologie des Deutschen (IGDD) in Kiel. (Zeitschrift für Dialektologie und Linguistik, Beihefte, 158.); Elmentaler, M., Hundt, M., Schmidt, J.E., Eds.; Steiner: Stuttgart, Germany, 2014; pp. 247–258. [Google Scholar]
- Prokić, J.; Nerbonne, J. Recognising Groups among Dialects. Int. J. Humanit. Arts Comput. 2008, 1, 153–172. [Google Scholar] [CrossRef]
- Grieve, J.; Speelman, D.; Geeraerts, D. A Statistical Method for the Identification and Aggregation of Regional Linguistic Variation. Lang. Var. Chang. 2011, 23, 1–29. [Google Scholar] [CrossRef]
- Holman, E.W.; Schulze, C.; Stauffer, D.; Wichmann, S. On the Relation between Structural Diversity and Geographical Distance among Languages: Observations and Computer Simulations. Linguist. Typol. 2007, 11, 393–421. [Google Scholar] [CrossRef]
- Wright, S. Isolation by Distance. Genetics 1943, 28. [Google Scholar] [CrossRef]
- Nerbonne, J.; Kleiweg, P. Toward a Dialectological Yardstick. J. Quant. Linguist. 2007, 14, 148–167. [Google Scholar] [CrossRef]
- Szmrecsanyi, B. Geography is Overrated. In Dialectological and Folk Dialectological Concepts of Space—Current Methods and Perspectives in Sociolinguistic Research on Dialect Change; Hansen, S., Schwarz, C., Stoeckle, P., Streck, T., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2012; pp. 215–231. [Google Scholar]
- Jeszenszky, P.; Stoeckle, P.; Glaser, E.; Weibel, R. Exploring Global and Local Patterns in the Correlation of Geographic Distances and Morphosyntactic Variation in Swiss German. J. Linguist. Geogr. 2017, 5, 86–108. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Shackleton, R.G.J. Phonetic Variation in the Traditional English Dialects: A Computational Analysis. J. Engl. Linguist. 2007, 35, 30–102. [Google Scholar] [CrossRef]
- Inoue, F. Year of First Attestation of Standard Japanese Forms and Gravity Centre by Railway Distance. Dialectol. et. Geoling 2009, 17, 118–133. [Google Scholar] [CrossRef]
- Stanford, J.N. One Size Fits All? Dialectometry in a Small Clan-based Indigenous Society. Lang. Var. Chang. 2012, 24, 247–278. [Google Scholar] [CrossRef]
- Lameli, A.; Nitsch, V.; Südekum, J.; Wolf, N. Same Same but Different: Dialects and Trade. Ger. Econ. Rev. 2015, 16, 290–306. [Google Scholar] [CrossRef]
- Gooskens, C. Travel Time as a Predictor of Linguistic Distance. Dialectol. et Geolinguist. 2005, 13, 38–62. [Google Scholar] [CrossRef]
- Van Gemert, I. Het Geografisch Verklaren van Dialectafstanden met een Geografisch Informatiesysteem (GIS). Master’s Thesis, Rijksuniversiteit Groningen, Groningen, The Netherlands, 2002. [Google Scholar]
- Nerbonne, J.; Heeringa, W. Geographic Distributions of Linguistic Variation Reflect Dynamics of Differentiation. In Roots: Linguistics in Search of its Evidential Base; Featherston, S., Sternefeld, W., Eds.; Mouton de Gruyter: New York, NY, USA, 2007; pp. 267–297. [Google Scholar]
- Kürschner, S.; Gooskens, C. Verstehen nah Verwandter Varietäten über Staatsgrenzen Hinweg. In Dynamik des Dialekts—Wandel und Variation; Akten des 3. Kongresses der Internationalen Gesellschaft für Dialektologie des Deutschen (IGDD); Glaser, E., Schmidt, J.E., Frey, N., Eds.; Steiner: Stuttgart, Germany, 2011. [Google Scholar]
- Pickl, S. Probabilistische Geolinguistik. Ph.D. Thesis, University of Salzburg, Salzburg, Austria, 2013. [Google Scholar]
- Scholz, J.; Lampoltshammer, T.J.; Bartelme, N.; Wandl-Vogt, E. Spatial-temporal Modeling of Linguistic Regions and Processes with Combined Intermediate and Crisp Boundaries. In Progress in Cartography: EuroCarto 2015; Gartner, G., Jobst, M., Huang, H., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 133–151. [Google Scholar] [CrossRef]
- Yanagita, K. Kagyuukou [On the Dialectal Lexicon of Snail]; Tokoshoin: Tokyo, Japan, 1930. [Google Scholar]
- Mase, Y. The Distribution and the Interpretation of the Dialect of ’mompe’ (Some Kind of Trousers) in a Mountain Village. Kokugogaku 1964, 59, 40–52. [Google Scholar]
- Fukushima, C. Interplay of Phonological, Morphological, and Lexical Variation: Adjectives in Japanese Dialects. Languages 2019, 4, 31. [Google Scholar] [CrossRef]
- Tanaka, A. Hyôjungo: Kotoba no Komichi [Standard Language: A Lane of Speech]; Seibundô Shinkôsha: Tokyo, Japan, 1991. [Google Scholar]
- Takada, M. Kotoba no chiri: Nihon gengo chizu kara [Geography of Words, Kyuushuu District: An Observation by Using the LAJ]. Gengo Seikatsu 1969, 216, 30–38. [Google Scholar]
- Hondo, H. Gendai Hyoujun Nihongo no Bunpu: Nihon Gengo Chizu de Mite [Distribution of Modern Standard Japanese: An Observation by Using the LAJ]. In Sato Shigeru Kyoju Taikan Kinen Ronshu Kokugogaku; Sato, S., Ed.; Ohfusha: Tokyo, Japan, 1980; pp. 479–498. [Google Scholar]
- Kasai, H. Hyoujun gokei no zenkoku bunpu [Nationwide Distribution of Standard Forms]. Gengo Seikatsu 1981, 354, 52–54. [Google Scholar]
- Ichii, T. Hougen to Keiryou Bunseki [Dialect and Quantitative Analysis]; Shintensha: Tokyo, Japan, 1993. [Google Scholar]
- Inoue, F. Keiryouteki Hougen Kukaku [Quantitative Dialect Division]; Meiji Shoin: Tokyo, Japan, 2001. [Google Scholar]
- Inoue, F. Hyōjun-go shiyōsotsu to tetsudō kyori ni miru komyunikēshon no chiri-teki yōin [Geographical Factors of Communication on the Basis of Usage Rate of the Standard Japanese Forms and Railway Distance]. Jpn. J. Lang. Soc. 2004, 7, 19–29. [Google Scholar] [CrossRef]
- Kumagai, Y. Developing the Linguistic Atlas of Japan Database and Advancing Analysis of Geographical Distributions of Dialects. In the Future of Dialects. Selected Papers from Methods in Dialectology XV; Cote, M.H., Knooihuizen, R., Nerbonne, J., Eds.; Language Science Press: Berlin, Germany, 2016; pp. 333–362. [Google Scholar] [CrossRef]
- Inoue, F.; Kasai, H. Dialect Classification by Standard Japanese Forms. Jpn. Quant. Linguist. 1989, 39, 220–235. [Google Scholar]
- Lee, S.; Hasegawa, T. Bayesian Phylogenetic Analysis Supports an Agricultural Origin of Japonic Languages. Proc. R. Soc. B Biol. Sci. 2011, 278, 3662–3669. [Google Scholar] [CrossRef]
- Tojo, M. Prolegomena. In Japanese Dialectology; Yoshikawakobunkan: Tokyo, Japan, 1954; pp. 3–86. [Google Scholar]
- Hamano, K. Rekishi Jinkōgaku de Yomu Edo Nihon [Historical Demographics of the Edo-era Japan]; Yoshikawa Koubunkan: Tokyo, Japan, 2011. [Google Scholar]
- Chambers, J.K.; Trudgill, P. Dialectology, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998; p. 198. [Google Scholar]
- Magué, J.P. Semantic Changes in Apparent Time. In Proceedings of the 32nd Annual Meeting of the Berkeley Linguistics Society, Berkeley, CA, USA, 12 February 2006. [Google Scholar]
- Willis, D. Investigating Geospatial Models of the Diffusion of Morphosyntactic Innovations: the Welsh Strong Second-person Singular Pronoun chdi. J. Linguist. Geogr. 2017, 5, 41–66. [Google Scholar] [CrossRef]
- Longobardi, G.; Guardiano, C. Evidence for Syntax as a Signal of Historical Relatedness. Lingua 2009, 119, 1679–1706. [Google Scholar] [CrossRef]
- Uiboaed, K.; Hasselblatt, C.; Lindström, L.; Muischnek, K.; Nerbonne, J. Variation of Verbal Constructions in Estonian Dialects. Lit. Linguist. Comput. 2013, 28, 42–62. [Google Scholar] [CrossRef][Green Version]
- Epskamp, S.; Schmittmann, V.D.; Borsboom, D. Qgraph: Network Visualizations of Relationships in Psychometric Data. J. Stat. Softw. 2012, 48. [Google Scholar] [CrossRef]
- Kretzschmar, W.A. Variation in the Traditional Vowels of the Eastern States. Am. Speech 2012, 87, 378–390. [Google Scholar] [CrossRef]
- Scherrer, Y.; Leemann, A.; Kolly, M.J.; Werlen, I. Dialäkt Äpp—A Smartphone Application for Swiss German Dialects with Great Scientific Potential. In Proceedings of the 7th SIDG Congress—Dialect 2.0, Vienna, Austria, 23–28 July 2012; p. 29. [Google Scholar]
- Meng, X.L.; Rosenthal, R.; Rubin, D.B. Comparing Correlated Correlation Coefficients. Psychol. Bull. 1992, 111, 172–175. [Google Scholar] [CrossRef]
- Diedenhofen, B.; Musch, J. cocor: A Comprehensive Solution for the Statistical Comparison of Correlations. PLoS ONE 2015, 10, e0121945. [Google Scholar] [CrossRef]
- Nychka, D.; Furrer, R.; Paige, J.; Sain, S. Fields: Tools for Spatial Data; R Package Version 9.6; University Corporation for Atmospheric Research: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Giraud, T. osrm: Interface Between R and the OpenStreetMap-Based Routing Service OSRM, R Package Version 3.2.0; CRAN; 2019. Available online: https://github.com/rCarto/osrm (accessed on 4 August 2019).
- Tobler, W.R. Three Presentations on Geographical Analysis and Modeling: Non- Isotropic Geographic Modeling; Speculations on the Geometry of Geography; and Global Spatial Analysis (93-1); Technical Report; UC Santa Barbara: Santa Barbara, California1993. [Google Scholar]
- Magyari-Sáska, Z.; Dombay, S. Determining Minimum Hiking Time Using DEM. Geogr. Napoc. 2012, VI, 124–129. [Google Scholar]
- Casson, L. Speed under Sail of Ancient Ships. Trans. Proc. Am. Philol. Assoc. 1951, 82, 136–148. [Google Scholar]
- Saito, Y. Navigation Area of the Kitamae, Oshu and Okusuji Vessels in the 19th Century [19 Seiki ni Okeru Kitamaebune, Bishuukaisen (Utsumi Bune), Okusuji Kaisen no Koukai-Ken]; Tohoku Electric Power [Tohoku Denryoku]: Sendai, Miyagi Prefecture, Japan, 2004. [Google Scholar]
- Vargha, A.; Delaney, H.D. A Critique and Improvement of the CL Common Language Effect Size Statistics of McGraw and Wong. J. Educ. Behav. Stat. 2000, 25, 101–132. [Google Scholar] [CrossRef]
- Mangiafico, S.S. Summary and Analysis of Extension Program Evaluation in R; Rutgers Cooperative Extension: New Brunswick, NJ, USA, 2016; Volume 125, pp. 16–22. [Google Scholar]
- Jones, P.J.; Mair, P.; McNally, R.J. Visualizing Psychological Networks: A Tutorial in R. Front. Psychol. 2018, 9, 1–12. [Google Scholar] [CrossRef]
- Goebl, H. Dialektometrie; Österreichische Akademie der Wissenschaften: Vienna, Austria, 1982. [Google Scholar]
- Hudson, M. The Linguistic Prehistory of Japan: Some Archaeological Speculations. Anthropol. Sci. 1994, 102, 231–255. [Google Scholar] [CrossRef]
- Hikosaka, Y. Nihongo hōgen ni Okeru Ishi Suiryōhyōgen no Kōshō to Bunka [Expressing will in Japanese Dialects: Discussion and Differentiation of Speculative Expressions]. In Japanese Language Research 9—Topological Research of the Present Age; Sato, K., Ed.; Meiji Shoin: Tokyo, Japan, 2002; Volume 9. [Google Scholar]
- Fujiwara, Y. The Seto Inland Sea Language Scrolls: Volume I; Hiroshima Dialect Research Institute: Hiroshima, Japan, 1974. [Google Scholar]
- Torchiano, M. effsize: Efficient Effect Size Computation; R Package Version 0.7.4; CRAN; 2018; Available online: https://zenodo.org/record/1480624#.XXIGMnERX4F (accessed on 4 September 2019). [CrossRef]
- Onishi, T. (Ed.) Shin Nihon Gengo Chizu [New Linguistic Atlas of Japan: NLJ]; Asakura Shoten: Tokyo, Japan, 2016. [Google Scholar]
- Cheshire, J.A.; Longley, P.A.; Yano, K.; Nakaya, T. Japanese Surname Regions. Pap. Reg. Sci. 2014, 93, 539–555. [Google Scholar] [CrossRef]
- Sound Archives at the Institute for Musicology. In Hungaricana (zti.hungaricana.hu/en/); Institute for Musicology at the Hungarian Academy of Sciences: Budapest, Hungary, 2019.
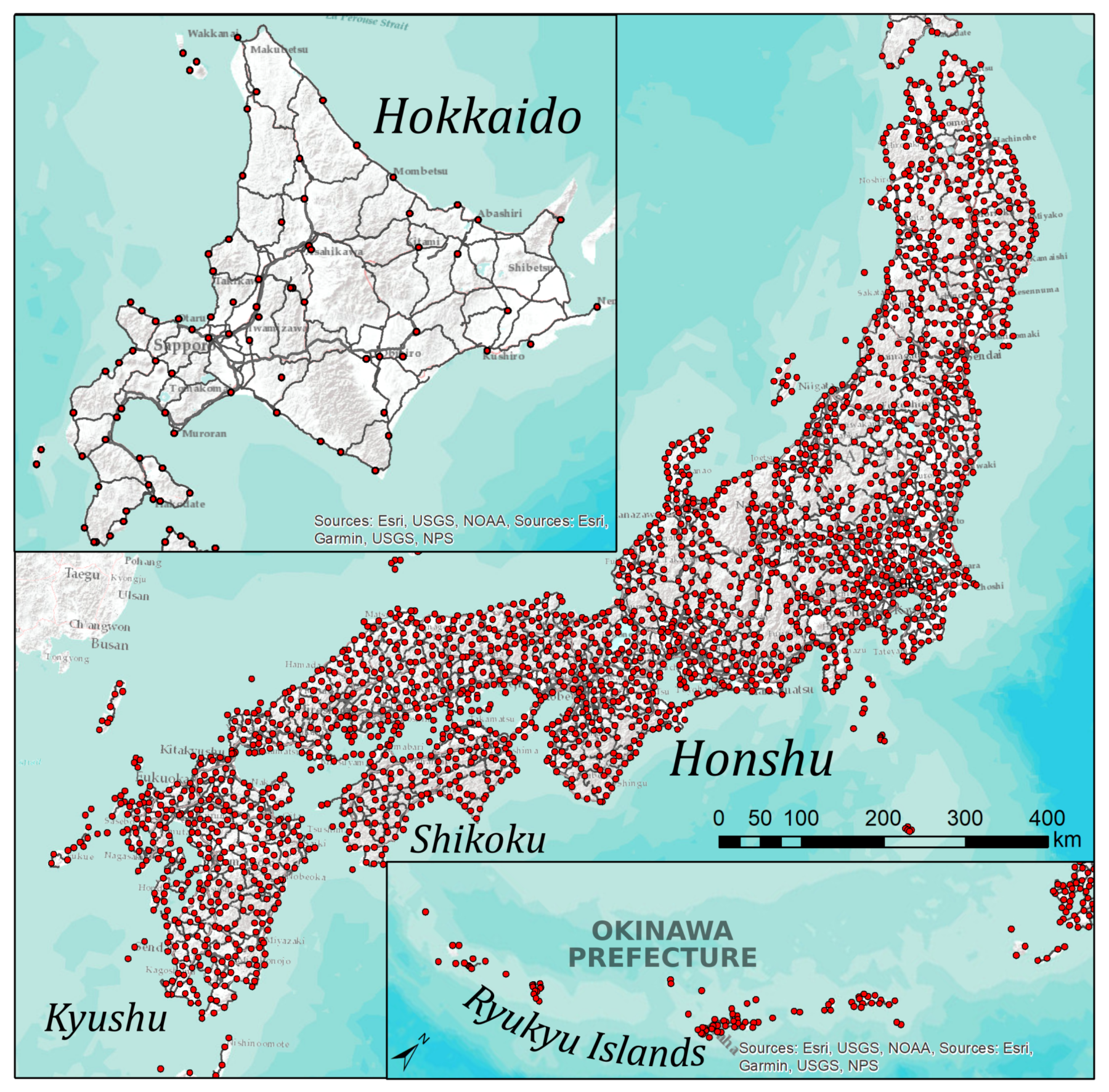
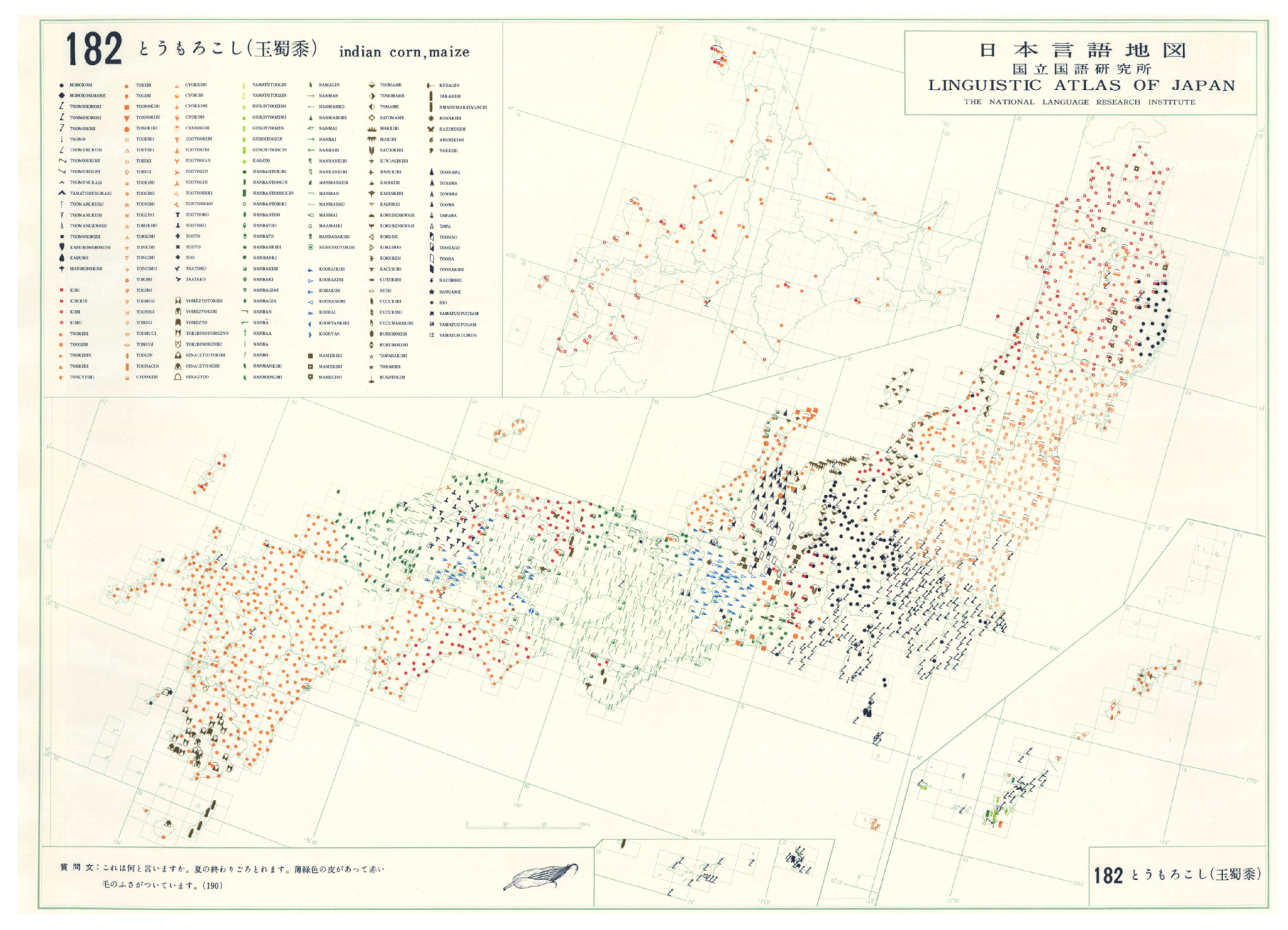

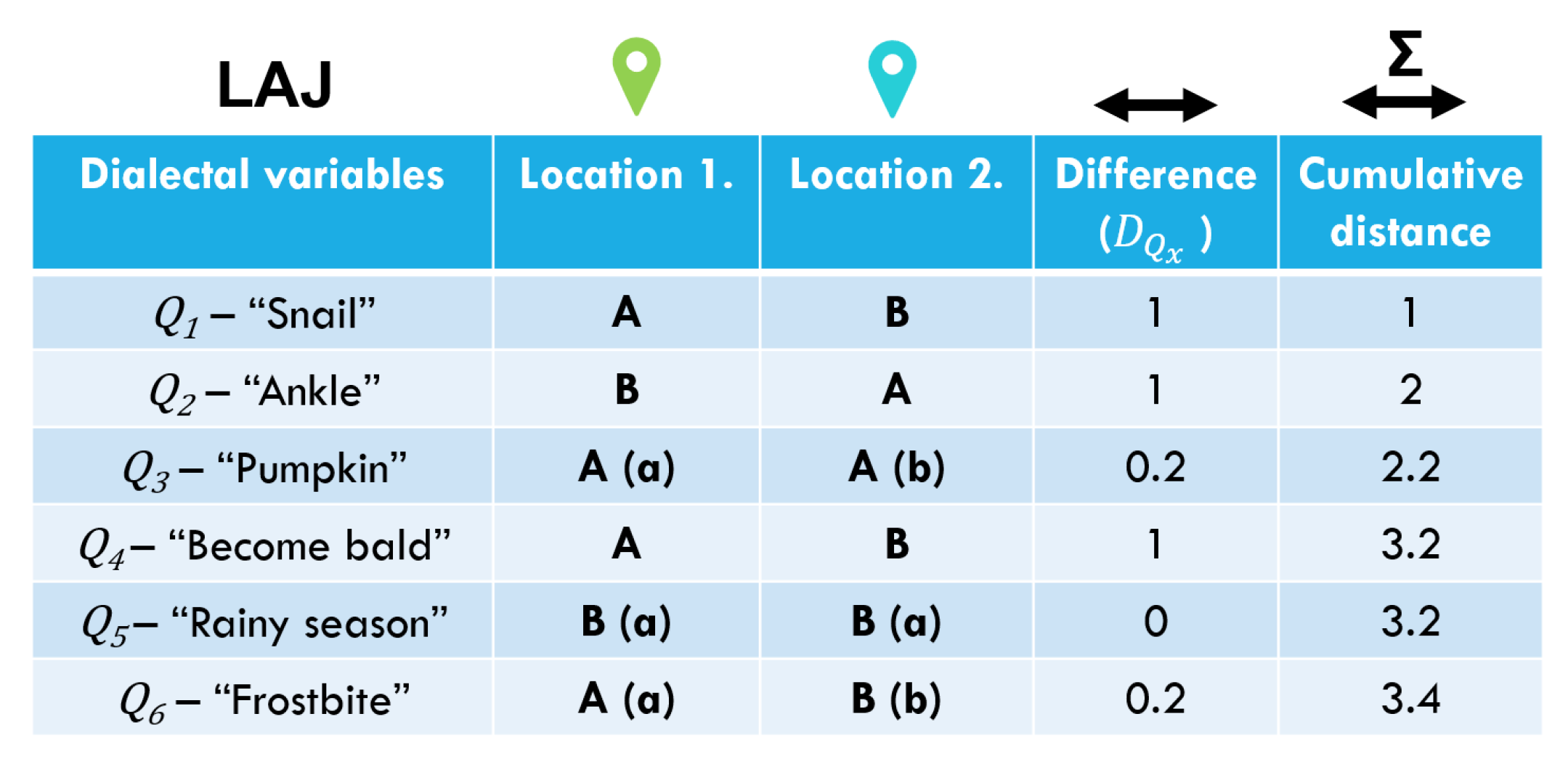
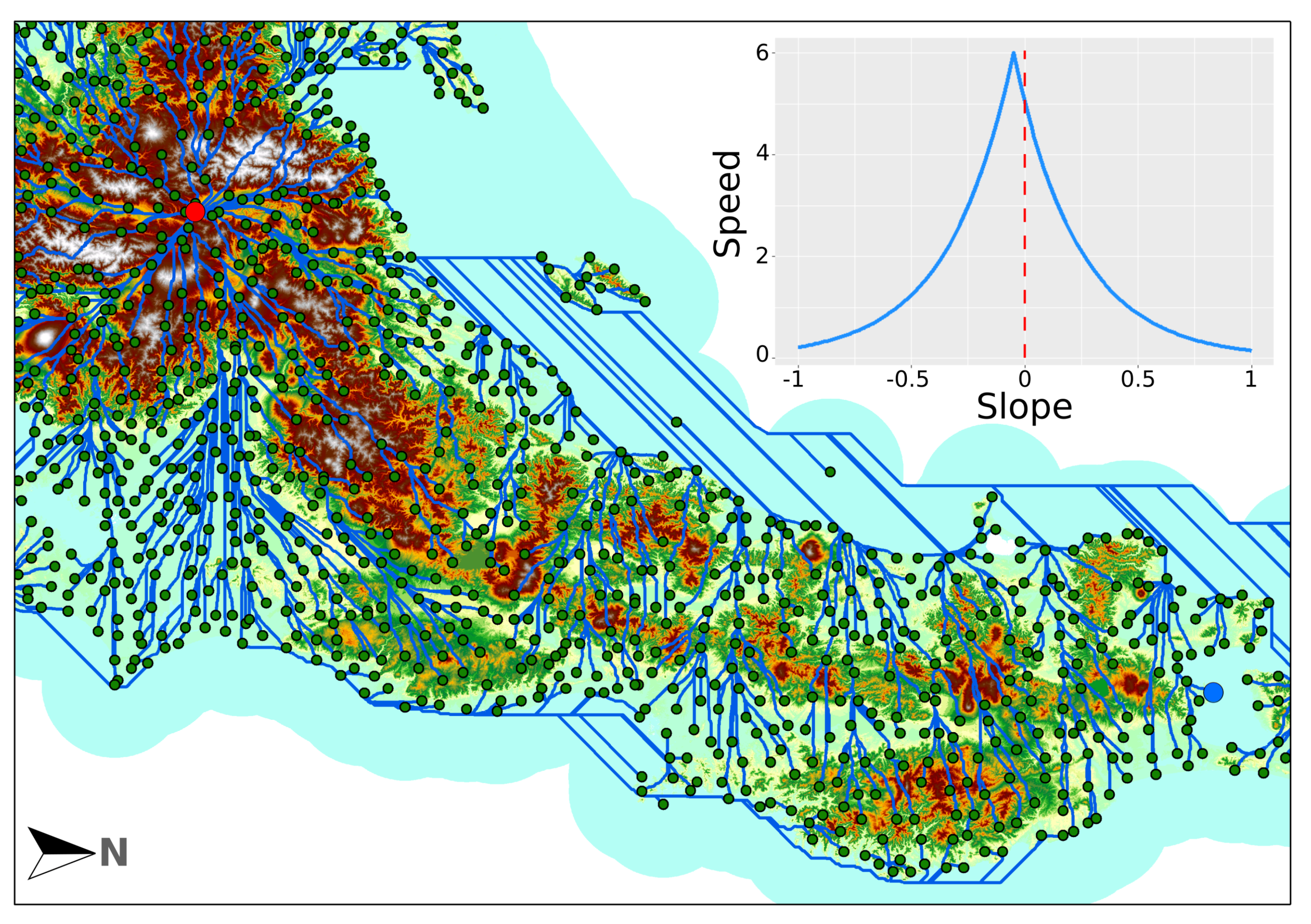
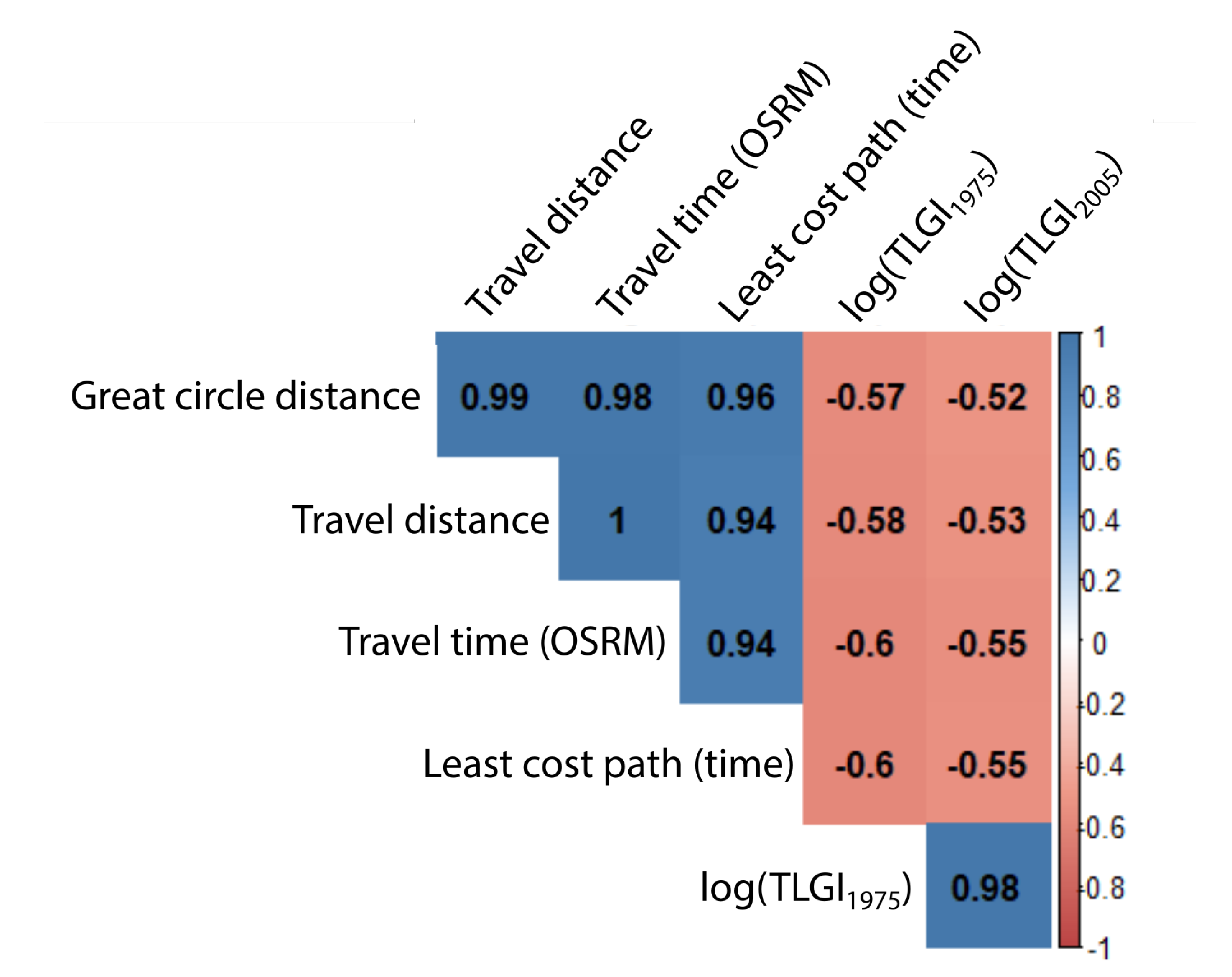
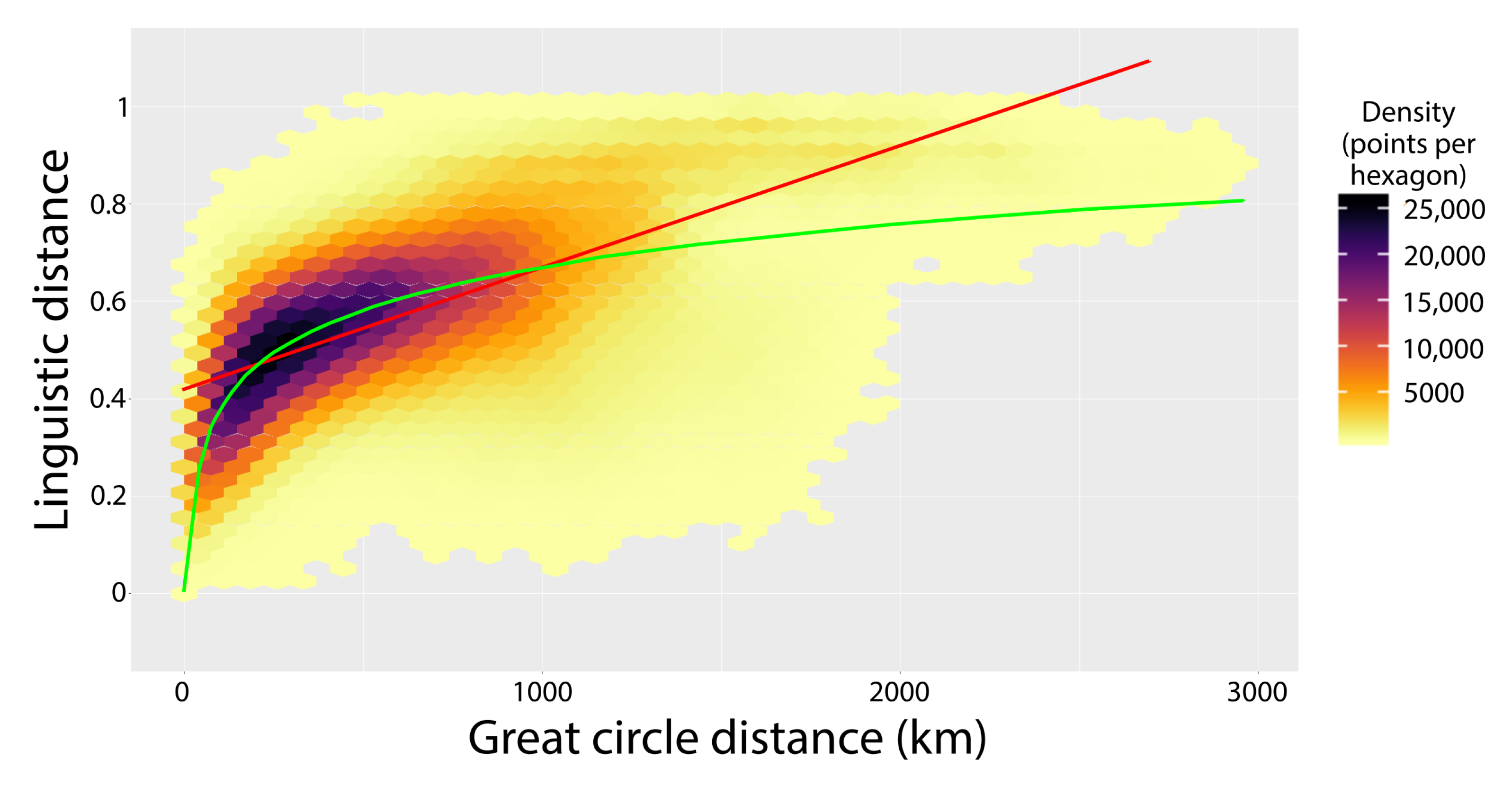
| Entire Area (2400) | L | Hokkaido (83) | Honshu (1666) | HSK (2125) | Shikoku (141) | Kyushu (318) | Okinawa (82) | |
|---|---|---|---|---|---|---|---|---|
| GCD | 0.6462 | 0.6672 | 0.2487 | 0.6488 | 0.6673 | 0.7391 | 0.7237 | 0.6999 |
| log(GCD) | 0.6714 | 0.7048 | 0.2339 | 0.6876 | 0.7037 | 0.7824 | 0.7544 | 0.7718 |
| TD * | 0.6613 | 0.6613 | 0.2564 | 0.6713 | 0.6606 | 0.7602 | 0.7246 | 0.3902 |
| log(TD) * | 0.7058 | 0.7057 | 0.2441 | 0.7126 | 0.7055 | 0.7943 | 0.7561 | 0.4139 |
| TT ** | 0.5322 | 0.6681 | 0.1773 | 0.5023 | 0.6675 | 0.5456 | 0.5493 | 0.7573 |
| log(TT) ** | 0.6717 | 0.7087 | 0.2782 | 0.6622 | 0.7072 | 0.6923 | 0.7357 | 0.7454 |
| HT | 0.5836 | 0.6718 | 0.2177 | 0.6605 | 0.6719 | 0.7548 | 0.6786 | 0.5739 |
| log(HT) | 0.6078 | 0.6834 | 0.2115 | 0.669 | 0.6845 | 0.7693 | 0.664 | 0.6848 |
| TLGI1975 | −0.5078 | −0.5188 | −0.3539 | −0.4919 | −0.5182 | −0.6454 | −0.5498 | −0.6078 |
| TLGI2005 | −0.4695 | −0.4862 | −0.3407 | −0.4627 | −0.4855 | −0.606 | −0.4966 | −0.584 |
| Boundary Type | Distance Cut-off (km) | Vargha-Delaney A | Interpreted Effect Size |
|---|---|---|---|
| Prefectures (47) | 200 | 0.2607 | large |
| Prefectures (47) | 150 | 0.3045 | medium |
| Prefectures (47) | 100 | 0.3473 | small |
| Prefectures (47) | 50 | 0.3793 | small |
| Domains (68) | 200 | 0.5387 | negligible |
| Domains (68) | 150 | 0.3513 | small |
| Domains (68) | 100 | 0.3725 | small |
| Domains (68) | 50 | 0.4079 | small |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeszenszky, P.; Hikosaka, Y.; Imamura, S.; Yano, K. Japanese Lexical Variation Explained by Spatial Contact Patterns. ISPRS Int. J. Geo-Inf. 2019, 8, 400. https://doi.org/10.3390/ijgi8090400
Jeszenszky P, Hikosaka Y, Imamura S, Yano K. Japanese Lexical Variation Explained by Spatial Contact Patterns. ISPRS International Journal of Geo-Information. 2019; 8(9):400. https://doi.org/10.3390/ijgi8090400
Chicago/Turabian StyleJeszenszky, Péter, Yoshinobu Hikosaka, Satoshi Imamura, and Keiji Yano. 2019. "Japanese Lexical Variation Explained by Spatial Contact Patterns" ISPRS International Journal of Geo-Information 8, no. 9: 400. https://doi.org/10.3390/ijgi8090400
APA StyleJeszenszky, P., Hikosaka, Y., Imamura, S., & Yano, K. (2019). Japanese Lexical Variation Explained by Spatial Contact Patterns. ISPRS International Journal of Geo-Information, 8(9), 400. https://doi.org/10.3390/ijgi8090400





