1. Introduction
In 2009, Typhoon Morakot brought extensive rainfall, causing numerous landslides in southern Taiwan. An official report [
1] documented that 769 individuals died or went missing directly or indirectly because of these landslides, and that approximately US
$526 million was lost due to damage to the agriculture, forestry, and fishery industries. Of particular note, a riverside village called Xiaolin (sometimes spelled Shiaolin or Hsiaolin) was destroyed by the landslides from a devastating landslide nearby, which led to approximately 500 fatalities. After this event, a large number of studies have concentrated on detecting, characterizing, assessing, and modeling landslide events in areas such as Xiaolin Village and the Kaoping watershed in the interest of identifying methods to mitigate or minimize the effect of similar disasters in the future. For example, Mondini et al. [
2] and Mondini and Chang [
3] have utilized spectral and geo-environmental information to detect landslide areas. Deng et al. [
4] and Tsai et al. [
5] have determined the extent and analyzed the topographic and environmental characteristics of landslides using satellite images and spatial analysis. From a geological or geotechnical viewpoint, Tsou et al. [
6] and Wu et al. [
7] have explored the relationship between rainfall duration, geological structures, soil types, geo-morphological features, and other similar variables. In addition, Chen et al. [
8] estimated the average landslide erosion rate, and Chang et al. [
9] modeled the spatial occurrence of landslides between 2001 and 2009.
Modeling landslide susceptibility is a critical and forward task within the framework of landslide hazard and risk management [
10,
11,
12]. It is used to assess the likelihood (0 to 1) or degree (e.g., low, moderate, and high) of landslide occurrence in an area with given local terrain attributes [
13]. Traditionally, modeling methods can be classified into three main categories [
14,
15,
16] of approaches: deterministic [
17,
18,
19], heuristic [
20,
21], and statistical [
22,
23,
24,
25,
26,
27]. A review of the literature indicates that continuing improvements in remote sensing and geographic information systems (GIS) have led to the incorporation of machine learning (and data mining) models for the evaluation of regional landslide susceptibility; examples include decision tree [
28,
29,
30], rough set [
31,
32], support vector machine [
16,
33], neural network [
16,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43], fuzzy theory [
35,
44,
45,
46,
47,
48], neural fuzzy systems [
35,
42,
49,
50,
51], and entropy- and evolution-based algorithms [
15,
38,
52,
53]. Some related works have also considered using various composite strategies based on previous approaches to achieve a specific purpose [
45,
47,
54]. A number of studies in the literature have compared different methods and various results obtained from modeling landslide susceptibility for different study sites and collected data [
16,
30,
35,
38,
42,
43,
44,
55,
56,
57]. However, no general consensus has yet been reached concerning which is the best procedure and algorithm for evaluating landslide susceptibility [
57,
58].
With improved temporal, spatial, and spectral resolutions of remote sensing observations, the automatic or semiautomatic approaches are widely used to detect landslide areas during a single triggering event using pixel-based [
2,
3,
59,
60,
61] and object-oriented [
62,
63,
64,
65] strategies to produce landslide inventories (databases). Then, the susceptibility assessment using an event-based landslide inventory [
25,
66], landslide hazard, and vulnerability and risk assessments in the framework of landslide hazard and risk management can be further made [
66]. To maintain the quality of these subsequent tasks, landslide susceptibility modeling must be studied and explored further.
Petschko et al. [
67] identified three uncertainty issues when constructing data-driven landslide susceptibility models (i.e., statistical and machine-learning-based approaches): input data, constructed models, and susceptibility maps. Landslide inventory and factors are the major input data. The spatial resolution, scale, type, and accuracy of the landslide inventory, and various landslide related factors are also important [
12]. Some input data may be produced subjectively, and the experience of the digitizer and measurement errors or imprecision in data processing can be sources of parametric uncertainty [
11,
12,
68,
69,
70]. Therefore, the quality assurance/quality control (QA/QC) assessment of all input data is an essential part of the process of reducing data uncertainties. Brenning [
71] and Guzzetti et al. [
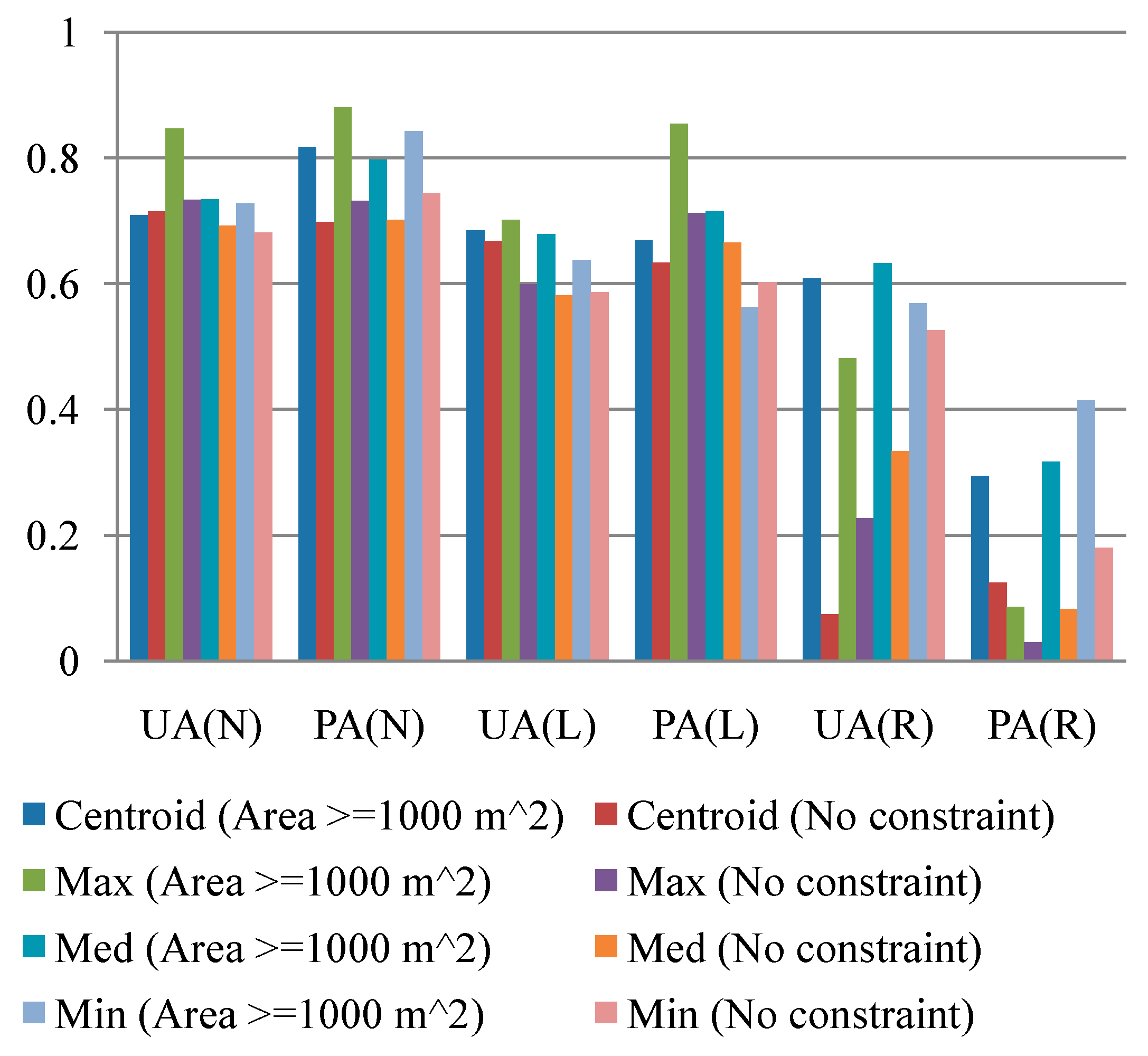
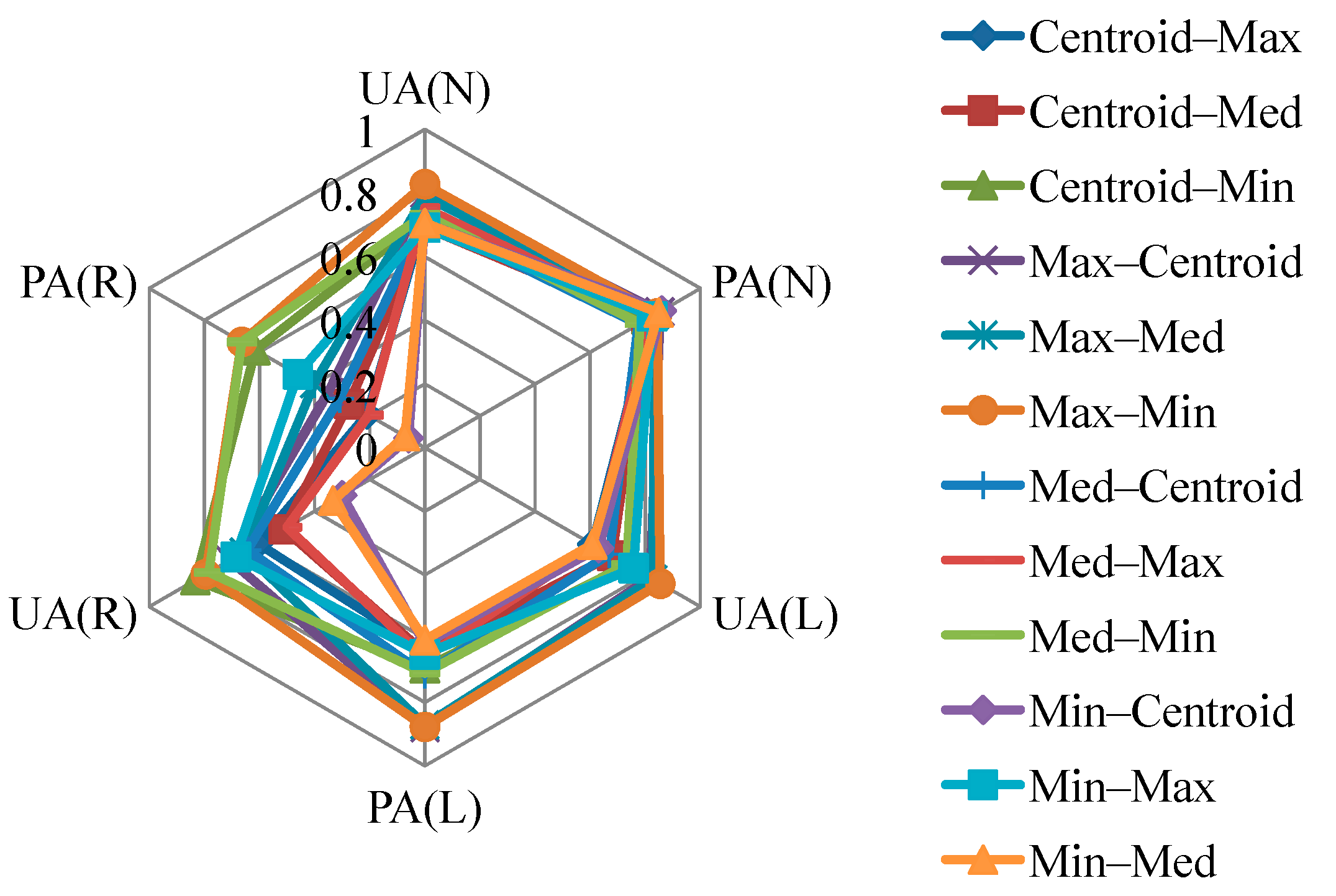
72] have discussed some cases for the evaluation of the uncertainty of landslide susceptibility models. Statistical indices commonly used to verify a model or classifier performance include overall accuracy, kappa coefficient, precision (also called user’s accuracy (UA)), recall (also called producer’s accuracy (PA)), and receiver operating characteristics (ROCs) curve. The quality of a landslide susceptibility map depends on the input data and selected algorithm or model. The mapping results are also affected by the analytical unit (e.g., grid cell, slope, or terrain units) and thresholds and number of degrees for discretizing the likelihood of landslide occurrences [
67,
73].
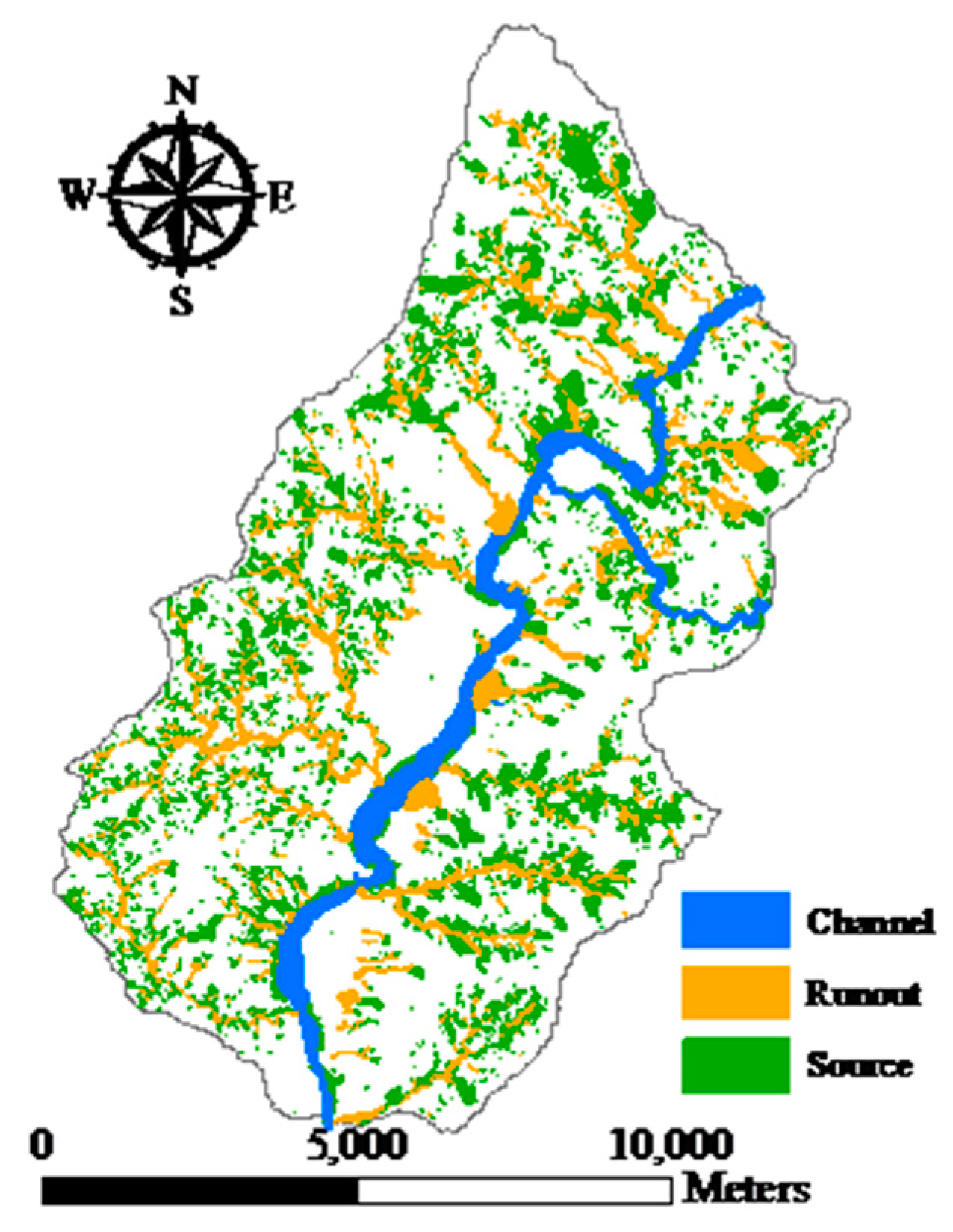
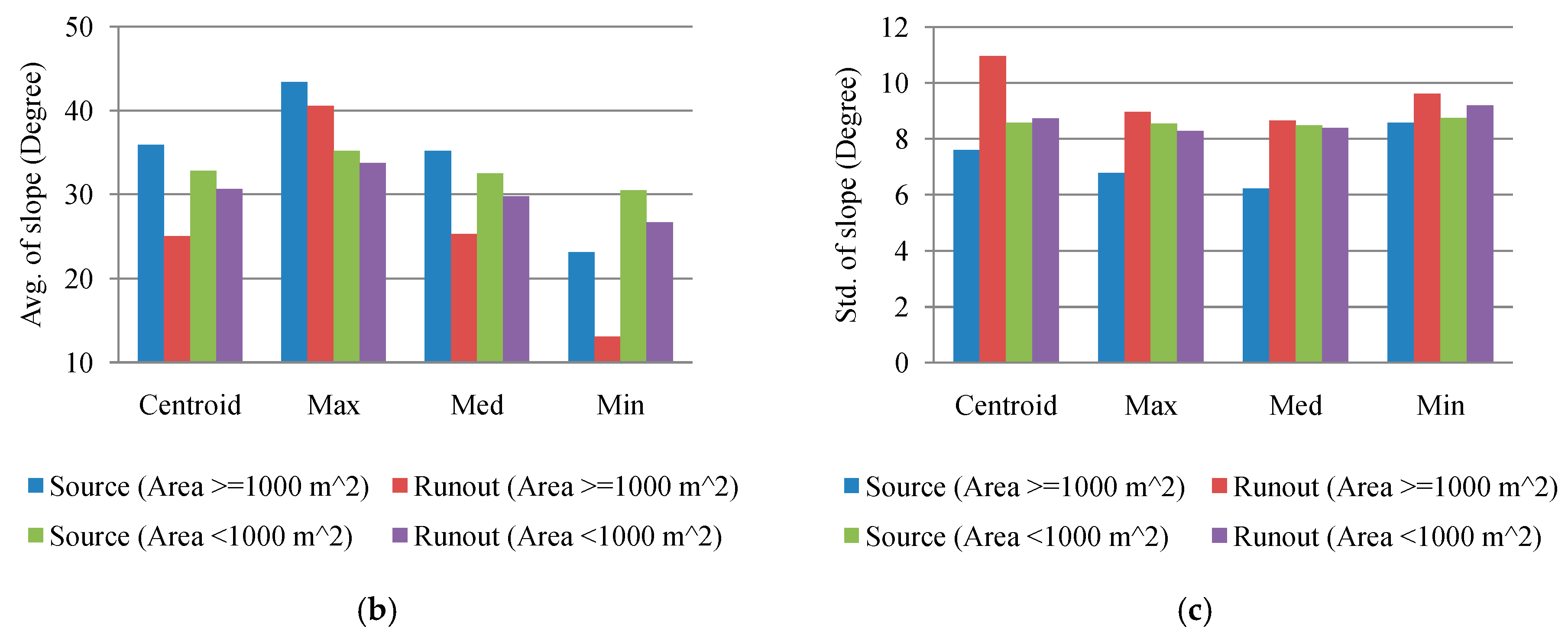
From a geotechnical viewpoint, three major features are typical of natural terrain landslides, and these were highlighted by Dai and Lee [
74]. The source area is defined as the surface of the rupture comprising the main scarp and the scarp floor. The landslide trail downslope of the source area is predominately produced by transport of the landslide mass, although erosion and deposition may also occur. The deposition fan is where the majority of the landslide mass is deposited. The term run-out generally describes the downslope displacement of failed geo-materials by landslides and is used to indicate the landslide trail and deposition fan [
2]. In general, landslide areas detected by automatic and semiautomatic algorithms from remotely-sensed images might include run-out regions, unless these have been removed manually by comparison with stereo aerial photos and other auxiliary data. However, these run-out areas should be excluded from the landslide area because they are caused by a different mechanism. Mixing landslide areas with run-out features might reduce the reliability of a landslide susceptibility model.
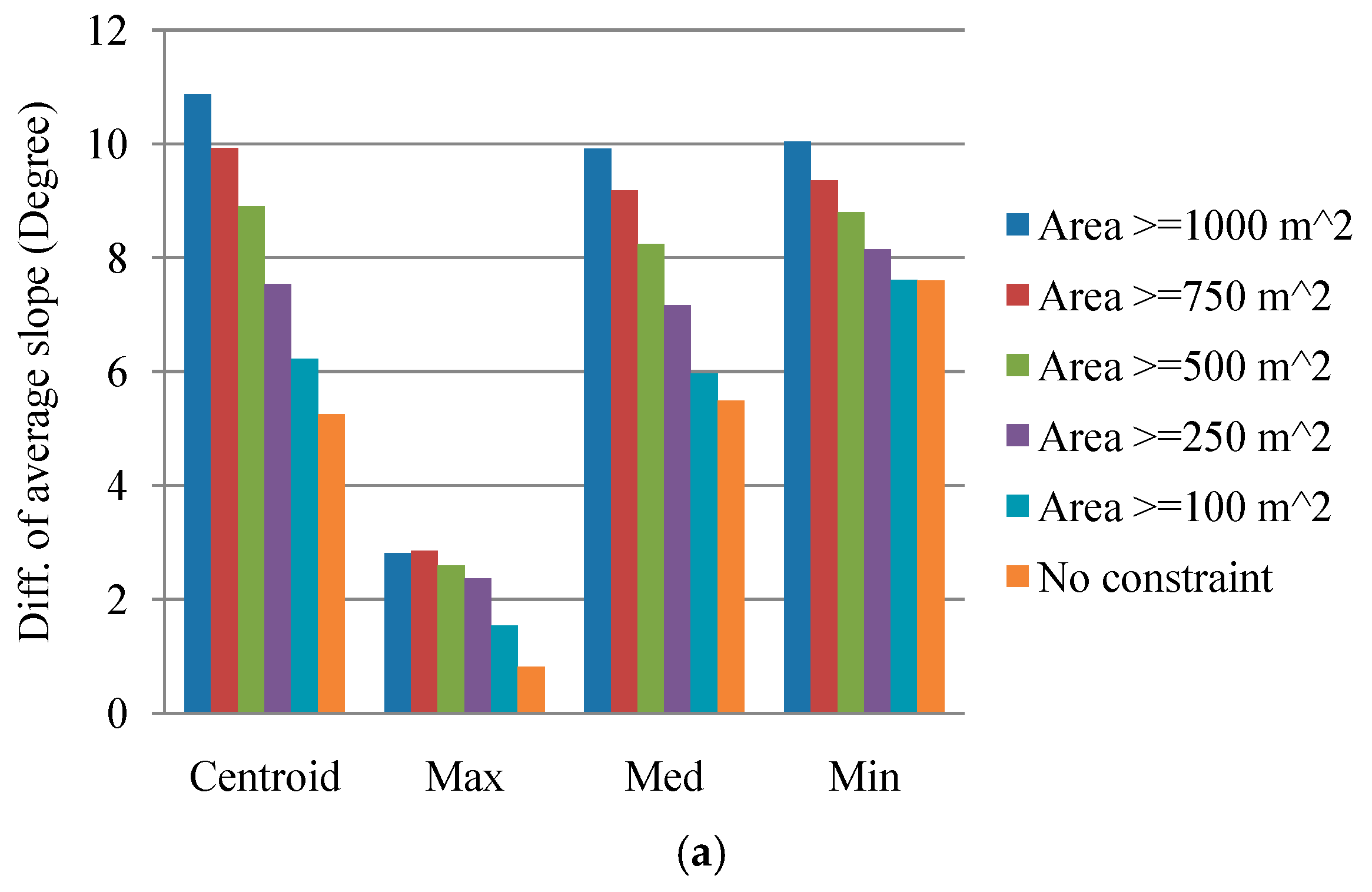
Selecting a suitable sampling strategy is crucial for transforming the landslide inventory and factors into formats that can be imported as samples to construct a data-driven landslide susceptibility model. It also affects the subsequent results and maps. Hussin et al. [
75] summarized the four sampling strategies most commonly used to extract landslide samples for data-driven landslide susceptibility modeling and mapping. These include, (1) the sampling of single pixels extracted from each landslide inventory polygon using the centroid or statistical method [
76,
77]; (2) extraction of all the pixels within landslide inventory polygons [
67], which increases computational loading in modeling; (3) selection of pixels on and around the landslide crown-line, which is called the main scrap upper edge (MSUE) approach [
14]; and (4) choosing the pixels within a buffer polygon around the upper landslide scarp area, which is referred to as the seed-cell approach [
77] and was proposed by Suzen and Doyuran [
78]. Several studies have compared the effectiveness of various sampling strategies [
77,
79,
80] and concluded that there could be some extraction and registration problems when using centroid pixels [
75]. In addition, results based on the MSUE and seed-cell approaches might be subjective and performed manually in some cases.
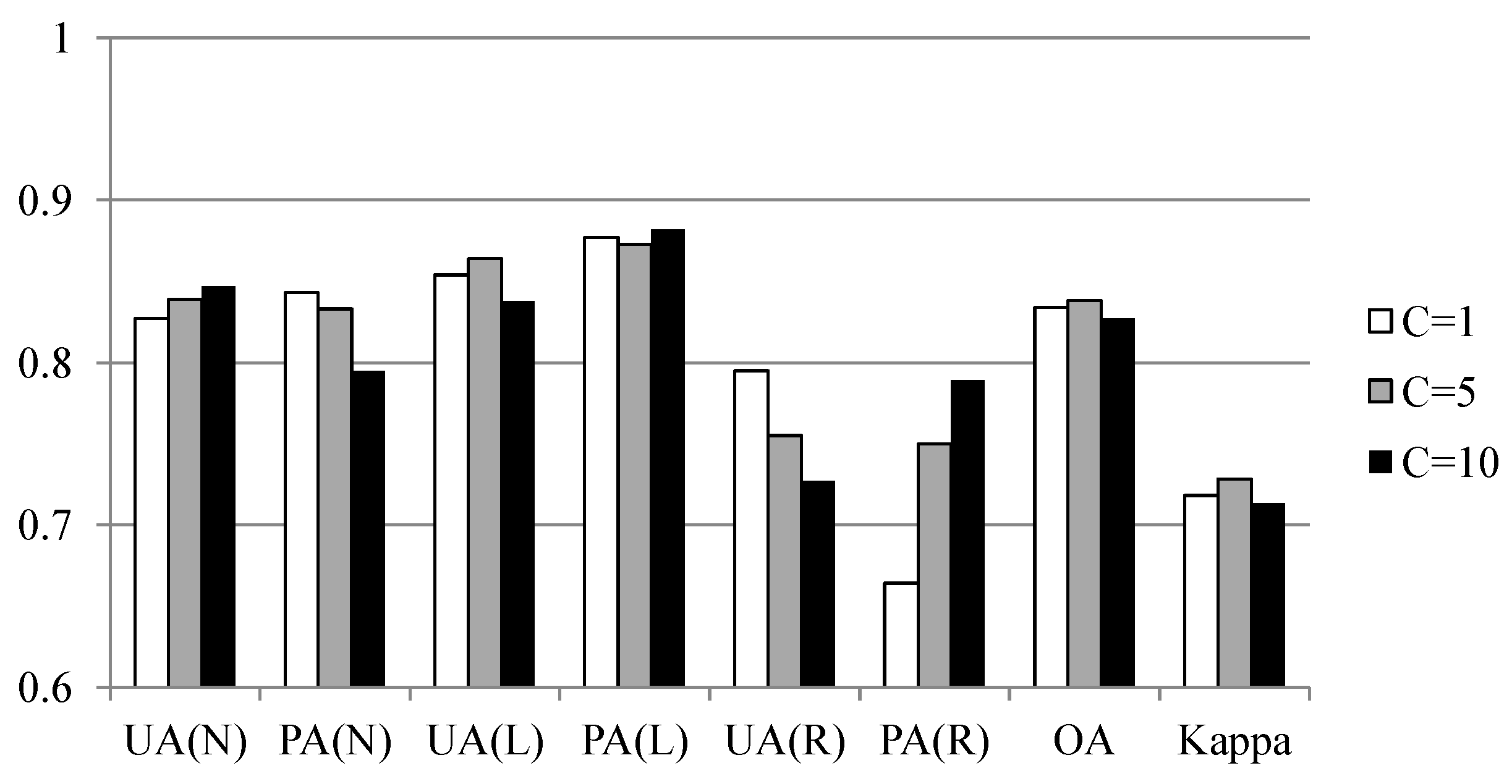
Selecting a proper algorithm to construct a landslide susceptibility model is also a critical task. The random forests (RF) algorithm has received increasing attention due to (1) excellent accuracy [
81], (2) fast processing [
82,
83], (3) few parameter settings [
84,
85], (4) high-dimension data analysis ability [
86,
87], and (5) insensitivity to imbalanced training data [
88]. Fewer studies have investigated the performance of the RF algorithm in landslide susceptibility modeling [
71,
89] than have evaluated the performance of statistical methods such as logistic regression. On the other hand, to address the problem of unbalanced results, the construction of models with extreme false alarm (commission error) or missing (omission error) predictions, the cost-sensitive analysis can be applied to adjust the decision boundary and improve modeling [
90,
91,
92] (i.e., the cut value that determines landslide and non-landslide).
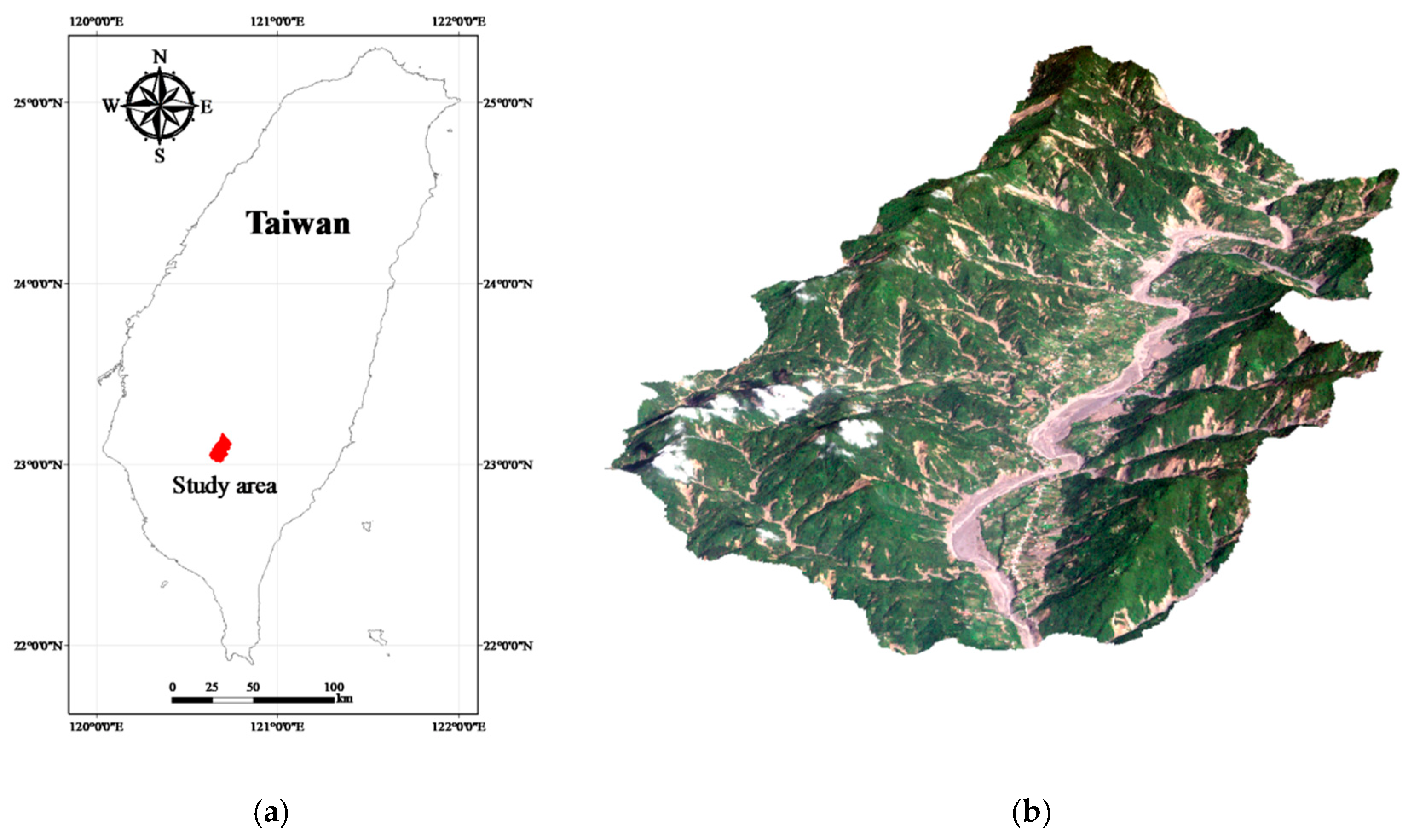
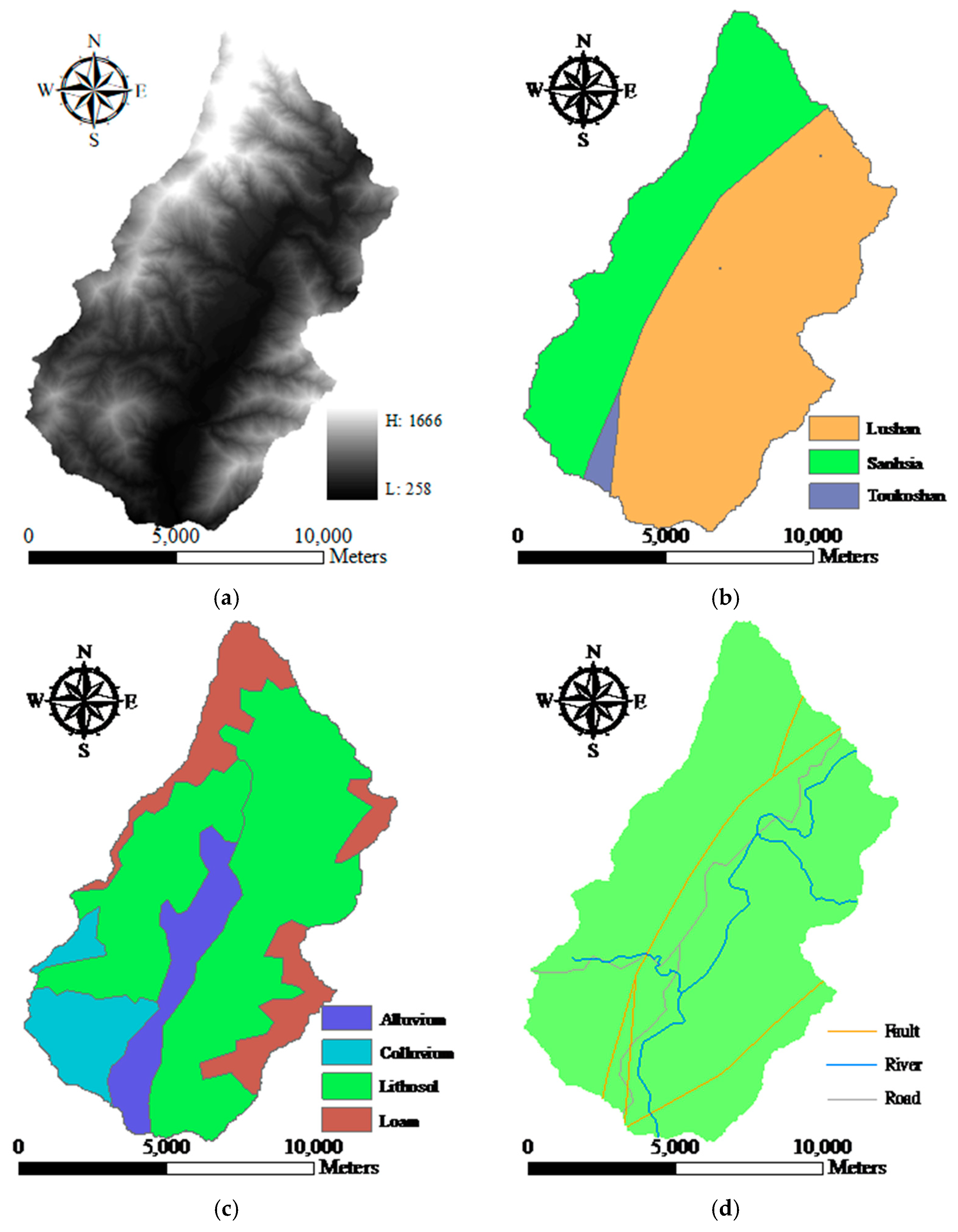
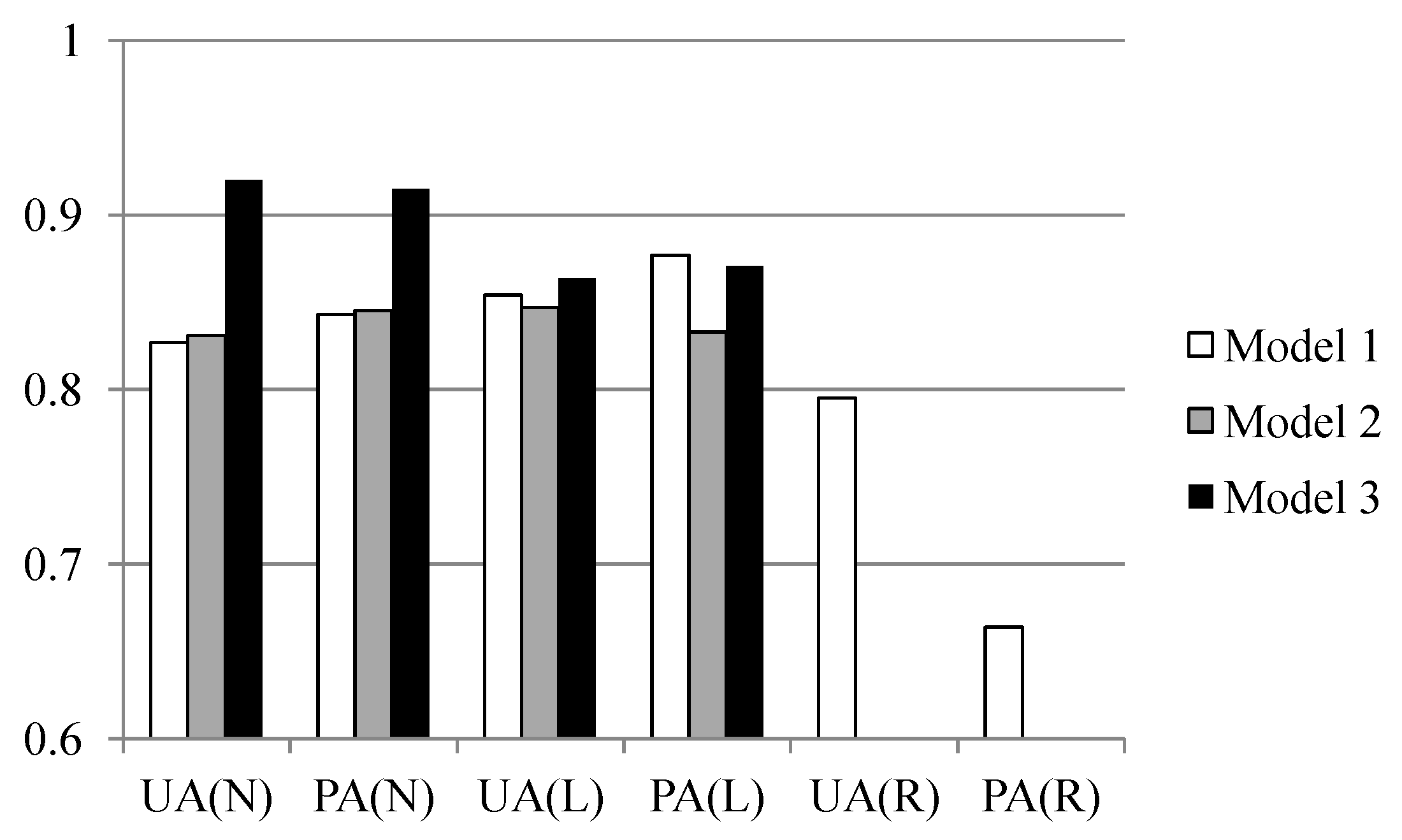
This study explored two modeling issues that may cause uncertainty in landslide susceptibility assessment when different sampling strategies are applied. The first issue is that extracted attributes within a landslide polygon can be varied by taking the sample from different topographic locations. Ideally, a landslide sampling point represents the geo-environmental characteristics at the location of the landslide initiation point. Previous studies have used different sampling strategies, such as taking samples from the centroid point of landslide polygons, but the effect has not been clarified yet. The second issue is the mixing problem of landslide inventory; here, landslide features detected by automatic or semiautomatic algorithms from remotely-sensed data generally include source and run-out features, unless the run-out portion can be removed manually with stereo aerial photo interpretation and other auxiliary data. The hill slope mechanism of run-out involves transportation and deposition, which differ from slope failure and erosion from landslides. For modeling purposes; therefore, a landslide model constructed using mixed samples may cause uncertainty. The landslide event induced by Typhoon Morakot in 2009 in southern Taiwan was selected as the study case. The definition of landslide in this study describes the downslope movement of soil, rock, and organic masses under the influence of gravity, as well as the landform that results from such movement [
93], ignoring the size of the materials.
Two experiments were designed to explore these sampling issues. The first experiment entailed the application of different sampling operators for the extraction of attributes from the centroid, maximum slope, median slope, and minimum slope of landslide and run-out. In the second experiment, this study categorized the run-out samples into the following: (1) An independent (run-out) class, (2) a run-out combined with landslide (source) class, and (3) a run-out combined with non-landslide class. RF was selected to perform landslide susceptibility modeling with geo-spatial data (i.e., remote sensing and GIS data) on the basis of the grid mapping unit, which is a popular and simple analytic format. In addition, this study combined cost-sensitive analysis with RF to adjust the decision boundary of constructed models and thereby reduce extremely high false alarm or missing errors.
4. Discussion
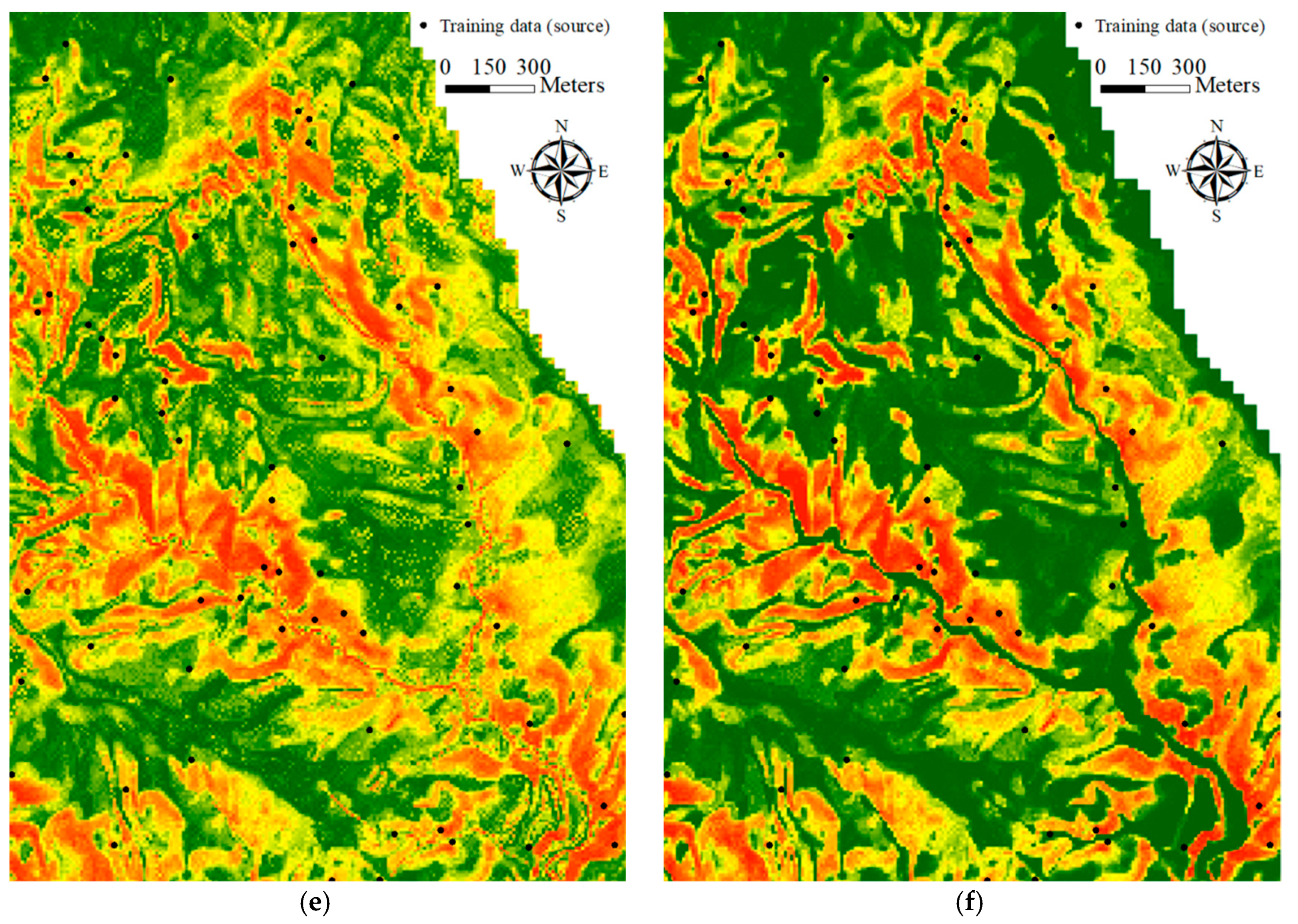
The effectiveness of automatic statistical sampling methods and cost-sensitive analysis as well as the influence of the run-out area were demonstrated for the study site. These achievements also reveal the significance of landslide inventory in which the considered classes and completeness affect the quality and development of consequent tasks within the landslide risk assessment and management framework. More precisely, the run-out area and topological relationship may be considered independent categories in the landslide records when producing a landslide inventory. The primary limitation of this study is that the constructed models are only suited to the regional scale and may be difficult to apply to other sites. In other words, the outcomes are empirical rather than knowledge based. The landslide susceptibility determined in this study is the spatial likelihood of landslide occurrence instead of the probability. The reason for this is that general data-driven (include data mining) algorithms directly explore the relationship between the collected landslide factors and inventory, and the generalization of these outcomes is a general rule that should be further evaluated. However, the study cases demonstrated the feasibility of the proposed procedure, suggesting that the developed procedure can be used for other sites. The generated landslide susceptibility maps can also be used for land planning, disaster insurance, and rescue purposes.
Previous works have focused on the modeling of landslide and non-landslide labels with ratios of 1:1 to 1:10 [
100]. However, the effect of number of run-out samples in the landslide susceptibility modeling process has not been discussed. Regarding the class ratio of classes, this study utilized all the landslide source and run-out samples extracted from the landslide inventory. The amount of non-landslide samples was set to be equal to the sum of the landslide source and run-out classes. Perhaps the impact of the number of samples and labels can be examined further in future.
Landslide inventory is a critical factor in the landslide risk assessment and management framework, and its labels (i.e., landslide source, run-out, and non-landslide), completeness, and topological relationships will increase the value to subsequent tasks. It may be of interest for future research to apply object-oriented classification [
62,
63] to preserve the completeness and topological relationships of landslide-affected regions and to develop a semi-automatic or automatic approach to further extract run-out areas from these regions and generate the complete landslide inventory. After that, the run-out patterns derived from the landslide susceptibility models may be adequate for further evaluating related parameters such as run-out distance and damage corridor width, as described in Dai et al. [
10]. Finally, future research may also examine the effect of the quality, number of classes (labels), and sample ratios of landslide susceptibility models on the consequent tasks within the landslide risk assessment and management framework.