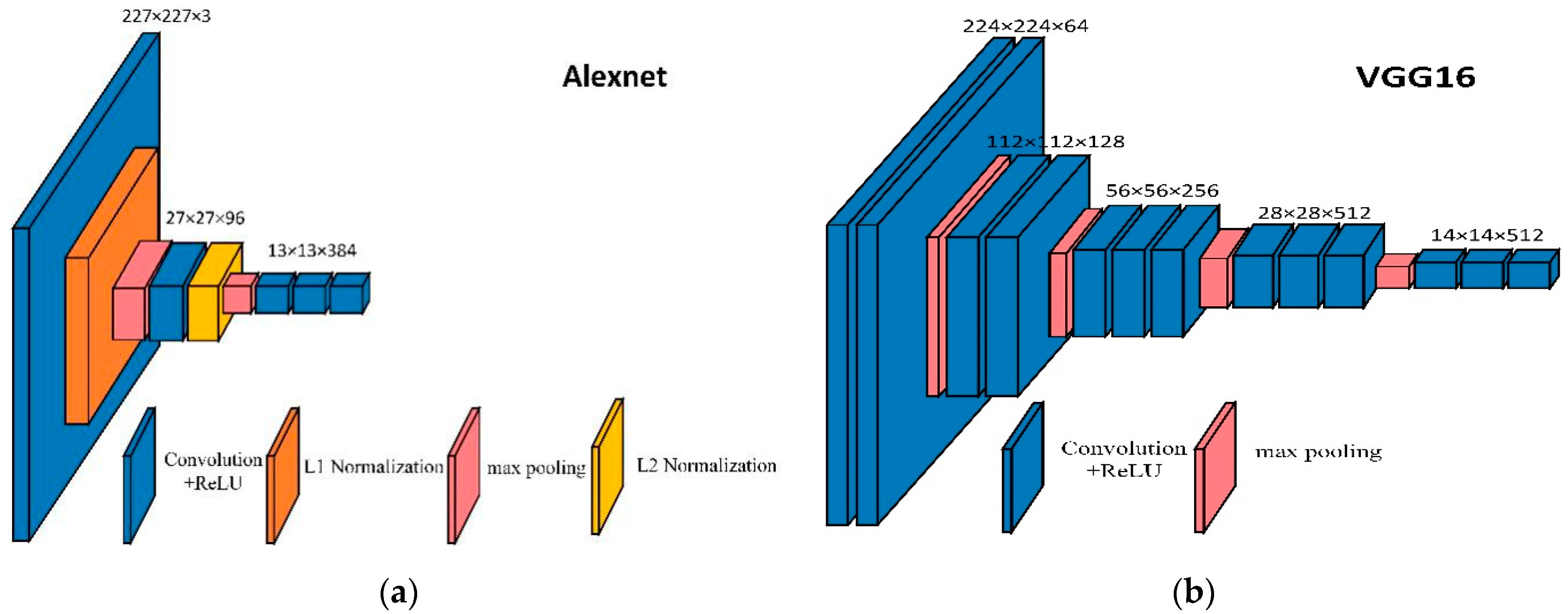
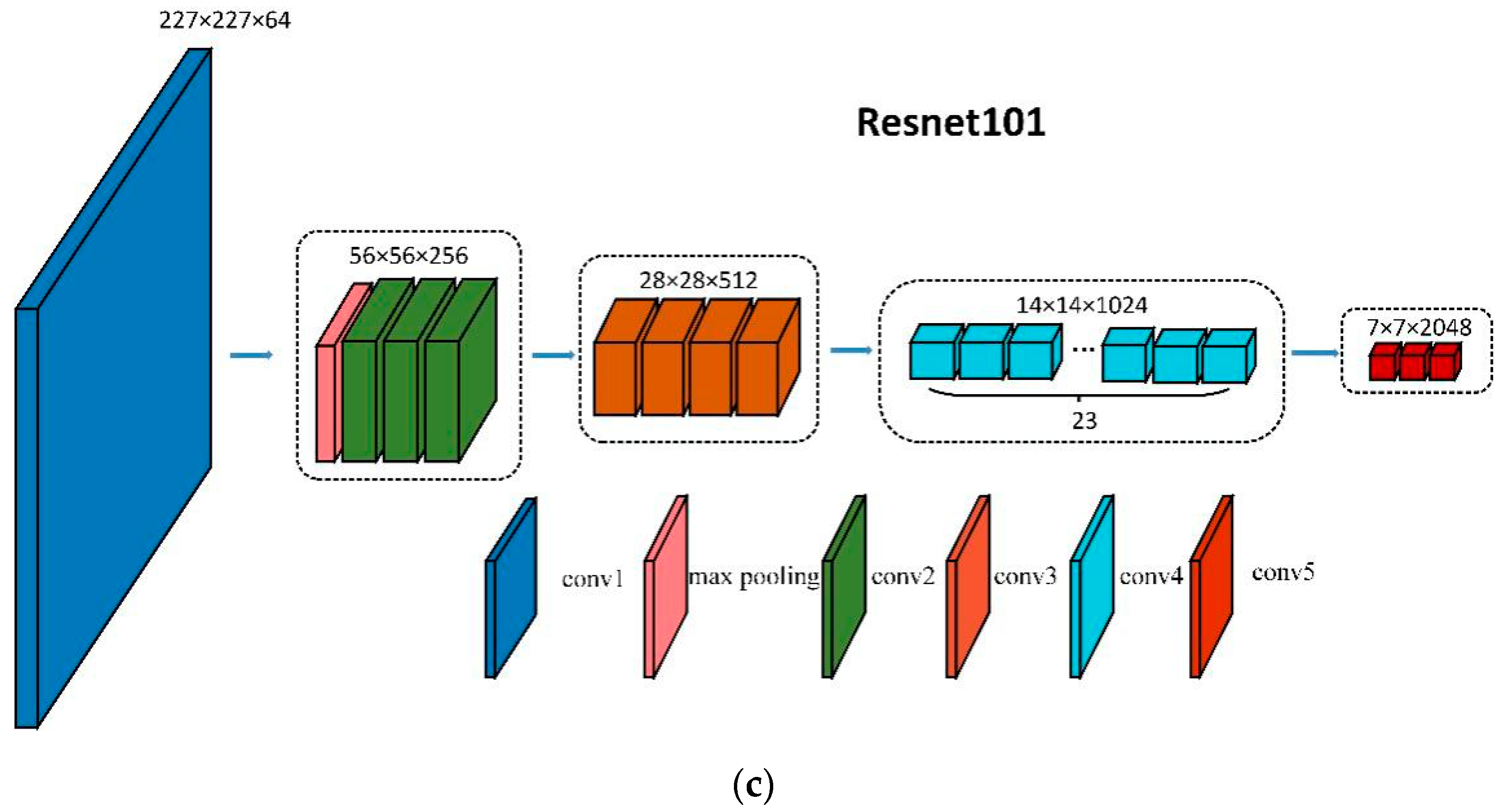
1. Introduction
The goal of instance-image retrieval is to quickly and automatically search images that are same or similar, with the query image from a large but unordered database, and return the results to users, according to related ranking. Convolutional Neural Network (CNN), as a tool for deep learning [
1], has made great breakthroughs in terms of computer vision. As a category of CNN model, a pre-trained CNN model is one pass where the success lies in feature extraction and encoding steps. ResNet and GoogleNet in pre-trained networks have won the challenges of ImageNet Large Scale Visual Recognition (ILSVRC) in 2014 and 2015. Though the pre-trained CNN model has achieved remarkable retrieval performance, the fine-tuning of current CNN models on the specified training sets still needs to improve. When using a fine-tuned CNN model, image-level descriptors are typically generated end-to-end, and the network will produce a final visual representation without the need for additional explicit encoding or merging steps. Fine-tuning the CNN model includes fine-tuning for datasets and network-oriented fine-tuning. The datasets used to fine-tune the network are crucial for learning high-resolution CNN features. This is because ImageNet merely provides class labels for images, which can be classified by pre-trained CNN models. However, it is difficult to distinguish images of the same classification. So, it is necessary to train task-oriented datasets by fine-tuning the CNN model. The fine-tuned structures of CNN model fall into two main categories: classification-based networks and verification-based networks. Classification-based networks are trained to classify landmarks into predefined categories. A verification-based fine-tuning network applies a Siamese network combined with a pairwise loss function or a triple loss function, which can significantly improve the adaptability of the network [
2], but the training data needs to be further annotated. The first fine-tuning method requires much manual work to collect images and mark them as specific architectural categories, which improves the accuracy of retrieval. However, its formula is closer to the image classification rather than the expected attributes of instance retrieval. Another method uses a geotagged image database to perform training by separating matching and non-matching pairs, and directly optimizes the similarity metric to be applied in the final task [
3]. In this process, metric learning plays a key role.
Within the frameworks of metric learning, loss functions form the key component and current works have proposed various loss functions in which contrastive loss masters the interactional relationships among pairwise data points, with similarity and dissimilarity as a case in point [
4]. Triplet losses have also been intensively studied [
5,
6], with an anchor point, a similar (positive) data point and dissimilar (negative) data point constituting a triplet. Triplet losses aim to learn a distance metric, where the anchor point closes to the similar data point, rather than the dissimilar ones through a margin. The model of triplet loss training has significant randomness when selecting samples, and it takes a long time, which leads to relatively large intra-class spacing, and it also has weak generalization ability from training to testing. Therefore, the quadruplet network [
7], the triplet loss with batch hard mining (TriHard loss) [
8] and the mining network of marginal sample [
9] came into existence. However, these conjoined networks usually rely on a simple network structure. The network architecture involves the collection and aggregation of regions. Its accuracy and robustness of image retrieval is low, and more importantly, the existing metric learning network is characterized by shortening the distance between the query image and positive samples, meanwhile widening the distance towards negative samples. The same value is adopted in the distance setting between the sample and the query image. However, not all negative samples have the same dissimilarity with the query image. Thus, designing a new CNN network and learning strategies are important for making the most of training data.
In this work, we focus on learning to rank (L2R) problems that have well-matched image retrieval tasks. We found that deep learning methods lag behind existing techniques. This is due to the insufficient supervised learning of particular tasks for processing instance-level images [
10]. The CNN-based retrieval method usually distinguishes different semantic categories by learning local features extracted by pre-trained network on ImageNet, ready for classification tasks. However, the disadvantage is that the intra-class differences are relatively large. We propose a solution tailored to such problems to retrieve the heavy training process.
Our main contributions are as follows:
We propose a novel multiple loss-based ranking to learn discriminative embeddings. In contrast with current losses, we firstly incorporate learning to rank, which learns image features according to their true ranking; besides, we propose a learning of sorted information of every sample, in order to preserve the similarity structure inside it. This avoids the shortcomings that the intra-class data distribution might be dropped due to separate negative pairs into equal distance in the embedding space.
We use both hard non-matching examples, also referring to negative examples, and hard-matching examples, namely positive examples prepared for the training of CNN model, and also select samples according to their similarity between the query image and examples, so as to enhance training efficiency.
We achieve state-of-the-art performance on three benchmarks, i.e., Oxford Buildings [
11], Paris [
12], and Holiday [
13].
The following sections of this paper are organized as follows.
Section 2 discusses related works.
Section 3 describes the algorithm framework and its details.
Section 4 summarizes the main contributions and evaluates the proposed method of learning to rank and multiple loss (LRML) by a series of experiments.
Section 5 reviews and concludes the major points.
2. Related Work
We discuss related works revolving around our main contributions, i.e., the image retrieval based on CNN model, the fine-tuned network and the deep Metric Learning algorithm.
A. CNN-Based Image Retrieval.
More recent approaches to image retrieval replace the low-level hand-crafted features with deep convolutional descriptors obtained from convolutional neural networks (CNNs), typically pre-trained on large-scale datasets such as the ImageNet, forming compact image representations, so as to present a promising direction. Early approaches to applying CNNs for image retrieval included methods that set the fully-connected layer activations to be the global image descriptors [
1,
14]. Husain proposes a global descriptor REMAP based on CNN, which learns and aggregates the hierarchical structure of deep features from multiple CNN layers, and learns discriminative features which are mutually-supportive and complementary at various semantic levels of visual abstraction [
15]. Perronnin and Jegou et al. aggregated deep convolutional descriptors to form image signatures using Fisher Vectors (FV) [
16], Vector of Locally Aggregated Descriptors (VLAD) [
17] and alternatives [
18,
19,
20]. Tolias et al. [
21] have proposed R-MAC to produce a global descriptor by aggregating the activation features of a CNN. One step further is the weighted sum pooling of Kalantidis et al. [
22], which can also be seen as a way to perform transfer learning. Popular encodings such as BoW, BoW-CNN and Fisher vectors are adapted in the context of CNN activations in the work of Kalantidis et al. [
22], Mohedano et al. [
23] and Ong et al. [
24], respectively. In image retrieval, the query expansion is used to enhance the image retrieval efficiency [
25,
26,
27]. Shen [
28] proposed using a small number of training images to learn low-dimensional subspaces, by preserving neighbor-reversibility (NR) correlation to enhance training efficiency.
In this work, we propose that by adding large visual code books [
20,
29] and spatial verification [
28,
29], CNN can control the image retrieval tasks by outweighing state-of-the-art methods and have achieved a higher maturity level.
B. Finetuning for Retrieval.
In this study, we treat instance retrieval as a metric learning problem, i.e., the Euclidean distance well captures the similarity on the basis that an image embedding is learned. Metric learning by representative architectures employ matching and non-matching pairs to perform training and be applicable for the task. Here, the annotations have become striking, e.g., for classification, only an object category label is needed, while labels per image pair are needed for particular objects. There may exist huge differences when comparing two images of the same object, e.g., images of buildings from different viewpoints. So, it is necessary to fine-tune the CNN model, based on task-oriented datasets. Presently, through minimizing classification errors, ImageNet datasets [
30] are used by employed networks trained for image classification. Babenko et al. [
14] have further retrained such networks by using a dataset closer to the target task. They conducted training with object classes that match particular landmarks/buildings. They achieved significant improvement with the performance on standard benchmark tests. Although obtaining achievements, there are still differences in terms of utilized layers and the truly optimized ones during learning. Much manual effort is required in building up such training datasets. Recently, geotagged datasets with time stamps have equipped weakly-supervised finetuning with a triplet network [
3]. Two images are easily classified as non-matching if they are taken far from each other, while the most similar images are considered as matching examples. In the latter, the current representation of the CNN basically defines similarity. The above presents a new approach, trying end-to-end finetuning for image retrieval especially for the task of geo-localization. The used training images are currently more concerned with the final task. Our point of difference is finding matching and non-matching image pairs in an automatic way. Moreover, matching examples are derived on the basis of 3D reconstructions, allowing for more challenging examples. We also select positive examples by using local features and geometric verification [
31]. We have a fully automatic method which starts from manually cleaned datasets of landmarks, so as to avoid exhaustive evaluation by using landmarks of the datasets, instead of the geometry.
C. Deep Metric Learning.
The goal of deep metric learning is to learn an optimal metric to minimize the distance between similar images. The typical architecture used for metric learning is two-branch Siamese [
32,
33] and the triplet network [
5,
34]. These methods can complete the image retrieval by shortening the absolute distance of the matching pair and widening the relative distance of the non-matching pair. The traditional triplet network randomly extracts three pictures from the training data. Although this method is simple, most of the extracted images pairs are simple and easy to distinguish. If a large number of trained image pairs are simple, then it is not conducive to better representation of the network [
31]. Based on the triplet networks, a training-based batch hard mining-TriHard Loss comes into being. Its core idea is to select a positive sample farthest from the query image for each training batch, and a closest negative sample and query picture to form a triple. TriHard’s loss effect is better than the traditional triple loss function [
31], which only considers the relative distance between positive and negative samples. In comparison, Chen introduced a quadruplet loss, which only considers the absolute distance between positive and negative samples. The quadruplet loss has increased inter-class variations and reduced intra-class variations, which allows the model to achieve better representations [
7]. Xiao designed the margin sample mining loss (MSML)-LSTM architecture with contrastive loss, which is a metric learning method that introduces batch hard mining. However, Varior ignores the influence of parameters in quadruple loss and adopts a more generalized form to represent the quadruplet loss. In summary, the TriHard loss prepares a triple for each image in the batch, and the MSML loss only picks the hardest positive sample pair and the hardest negative pair to carry out loss calculation, which is a hard-positive sample that is more difficult than TriHard. It considers both the relative distance and the absolute distance, and introduces a metric learning method of batch hard mining [
22].
4. Experimental Results and Analysis
In this section, we illustrate the training process and a detailed procedure of implementation. We will discuss the implementation details of our training process, assess he different components of our model, and compare the experimental results with the current techniques.
4.1. Data Collection
4.1.1. Acquisition of Training Datasets
We adopt the training dataset constructed by Schonberger et al. [
35]. The dataset includes 7.4 million images, which are searched and downloaded by Flickr, with popular landmarks throughout the world. The dataset uses bag-of-word model (BoW) and structure-from-motion (SfM) to reconstruct the 3D model, and uses a method exempt from manual annotation to automatically obtain a large dataset with a query image, a positive image, and a cluster with serial number. There is a total of 91,642 training images in the dataset, and 98 cluster images identical or nearly identical to the test dataset can be excluded through image retrieval based on BoW. About 20,000 images are selected as query images, 181,697 pairs of positive images, and 551 training clusters, including more than 163,000 from original datasets, by the minimum hash and spatial verification methods mentioned in the clustering procedure [
27]. The original datasets contain all the images of the Oxford5k and Paris6k datasets.
4.1.2. Selection of Training Datasets
In this paper, we create a tuple dataset (Xq, Xi), where q is the query image, i is a positive image that matches the query image, and these tuples are used to make image pairs for later training.
Selection of positive images: During the training process, several sets of images are randomly selected from positive image pairs. The annotated positive image pairs from the training dataset will be treated as positive images inside the training sets. In [
27], the acquisition of a positive sample is through the following three methods.
CNN descriptor distance: The positive image refers to those with the lowest descriptor distance to the query, formally:
The GPS coordinates of the positive image are the same as the query. Consequently, the images that are chosen will get a small loss since they already have small descriptor distance. Thus, the drawback is that the network is not forced to dramatically change and learn by the matching examples.
Maximum inliers. The positive image is chosen by 3D information, which is independent of the CNN descriptor. Thus, the image has the largest number of co-observed 3D points with the chosen query. That is:
The number of features with spatial verifications between the two images correspond with this measure, which commonly applies to ranking in BoW-based retrieval. Since this measure is not influenced by the representation of the CNN model, it requires delivering more challenging positive examples.
Relaxed inliers. The positive image pair is randomly selected from a set of images, rather than use a pool of images captured with similar positions of the camera. This image shares a sufficient number of co-observed points with the query image, and does not show extreme scale changes. This positive image is:
In (6), the scale changes between the two images are reflected from scale (i,q). The harder matching examples selected by this method are guaranteed to ensure the depiction of the same object. We proposed three different methods to exhibit the queries and their corresponding positive ones. The relaxed method is conducive to increase more diversified viewpoints.
Selection of negative images: We select negative examples from clusters that differ from the query image. In the process of training the dataset, we use the training parameters and test methods used by Radenović to extract the image features in the dataset. Here, we use the VGG16 as fine-tuning network, and adopt Generalized-Mean (GeM) pooling to extract salient features, learning whitening to reduce dimensionality and average query expansion to improve retrieval accuracy. By calculating the Euclidean distance between the extracted query image and the feature vector of the images in the dataset, we randomly select a number of negative examples in the training dataset as the pool of low correlation images. In each round of training, we first select the same N image clusters with the smallest Euclidean distance corresponding to the feature vector of the query image. As shown in the
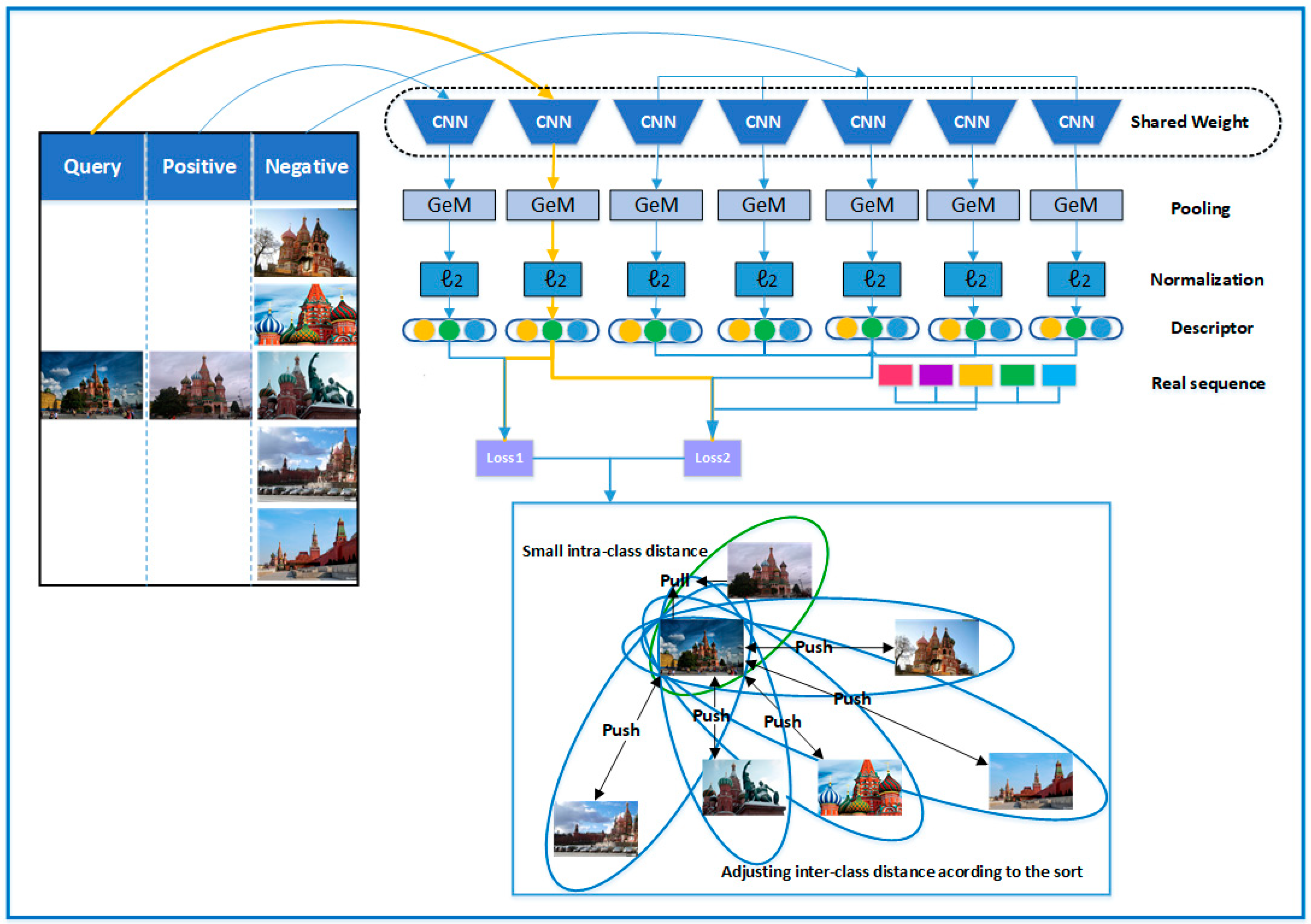
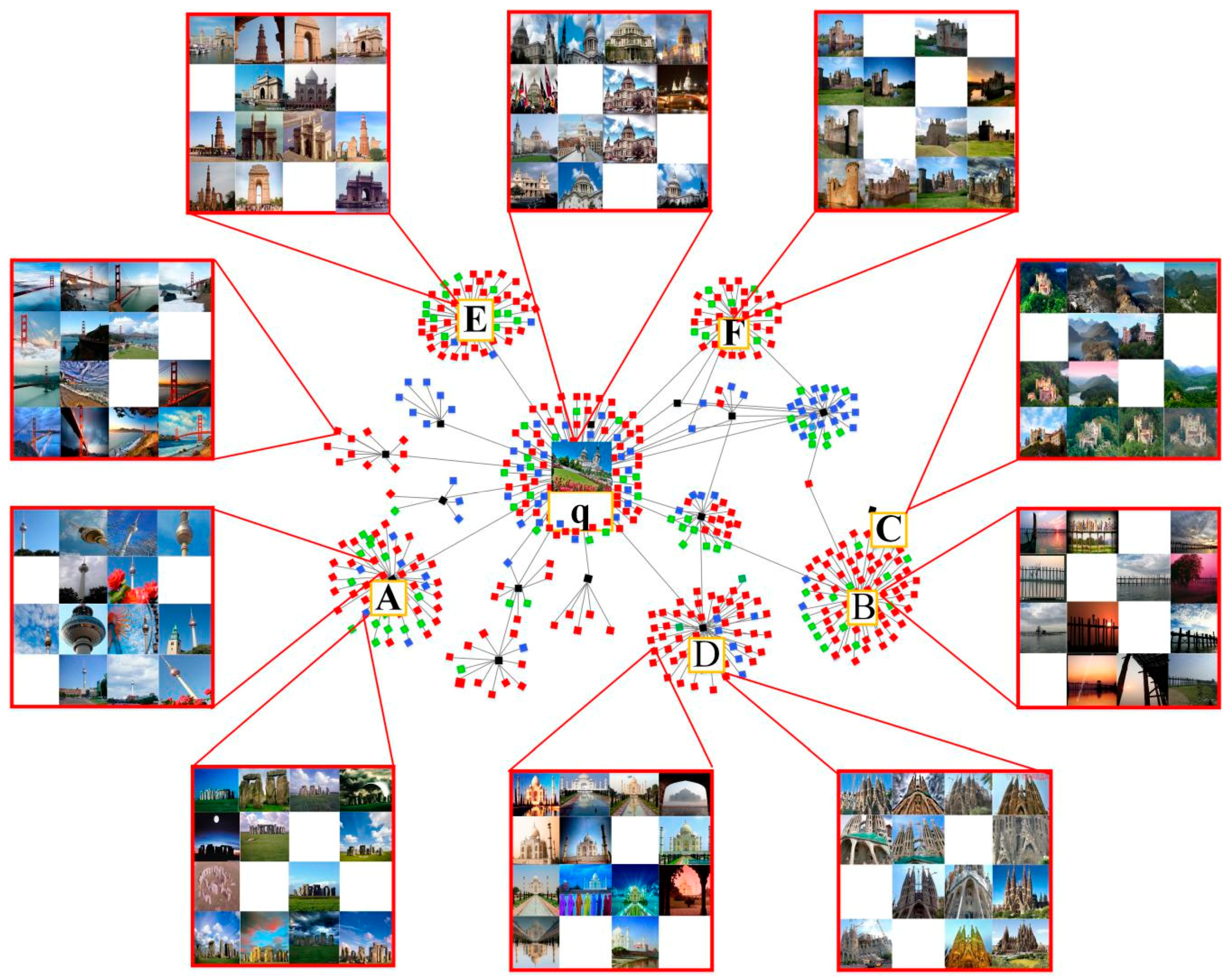
Figure 3, q is the query image, and the clusters where A, B, C, D, and E locate are negative clusters that observe far Euclidean distance to the query image. Suppose we choose A, B, C, D, E as negative examples. If we want to select 5 low correlation negative examples, then we first consider image A, and if image A is not in the query cluster q, or in the positive example clusters, then image A is used as a low correlation image listed in the input set of query image q. Similarly, image B is also marked with low correlation in the input set of images. For image C, although there exists large distance of Euclidean distance between its feature vector and the feature vector of the query image, image C and image B belong to one labeled cluster. So, image C, as a low correlation image, is not taken in the negative image set of the query image q. Images D, E, and F are taken as low correlation images to q. When the number of the required image equals to N, the low correlation image is no longer selected, so image G and other images will no longer be considered.
4.1.3. Acquisition of the Real Sequence
For each selected low correlation image, A, B, C, D, E, F for the query image Q, as shown in
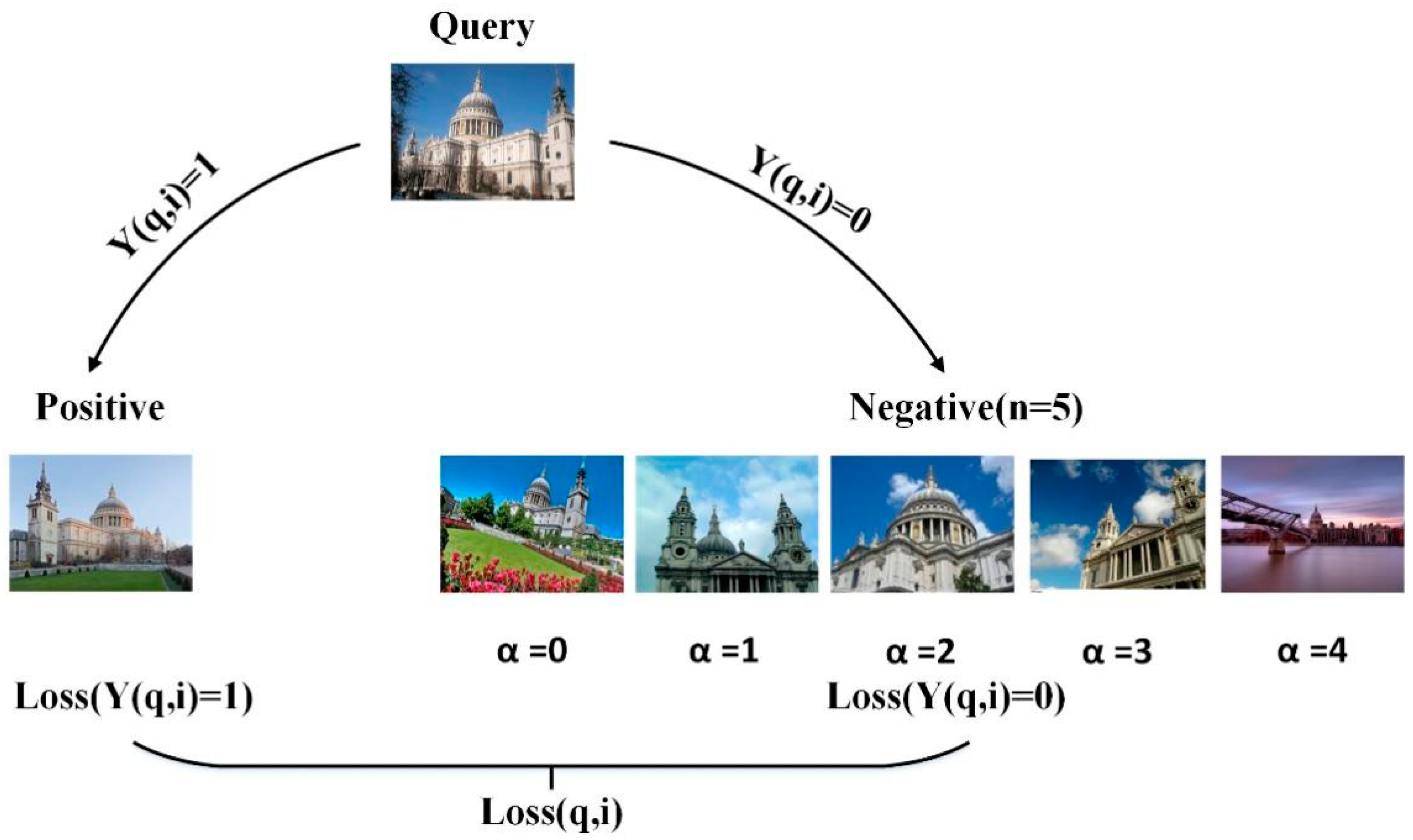
Figure 4, we extract the corresponding vectors a’, b’, c’, d’, e’, f’ in a benchmark sort. We calculate the Euclidean distance between them and the query image features, and rank them according to their Euclidean distance to the query image feature vector, the obtained serial number is the ordinal value of the negative correlation image in the loss function, and the obtained sequence is the real ranking sequence of negative examples for the query image. In
Figure 5, we present examples of query images and the real ranking sequence. As seen in the figure, the leftmost column is the query image, followed by the negative samples sorted by similarity. From left to right, the similarity decreases. In
Figure 6, we show a visual representation of the loss function calculation after the real sequence is obtained.
4.2. Implementation Details
To train the proposed model, we use the pytorch deep learning architecture to train this multiple loss deep network model based on L2R. In order to perform the fine-tuning of networks, we initialize the convolutional layers of AlexNet, VGG 16 and ResNet101, all trained by Adam, and the Adam algorithm is based on the loss function for each parameter. The first moment estimate and the second moment estimate of the gradient are dynamically adjusted for the learning rate of each parameter. Since the network pre-training parameters [
36] are used, the learning rate equal to lr = 1 × 10
−6, for the AlexNet network is used during training. The learning rate equal to lr = 7 × 10
−7 for the VGG16 and Resnet101 networks, momentum 0.9, margin τ for multiple loss 0.7 for AlexNet, 1.25 for VGG and ResNet, justified by the increase in the dimensionality of the embedding. All of the images in the training set have been resized to a maximum size of 362 × 362 under the premise of ensuring the original aspect ratio. The training results take the experimental data obtained during the 30 epochs.
The experimental environment is intel(R) i7-8700, GPU with 11GB of memory, NVIDIA(R) 2080Ti graphics card, driver version 419**, operating system Ubuntu 18.04 LTS, pytorch version v1.0.0, CUDA version 10.0, cudnn version 7.5.
4.3. Evaluation Metrics
To evaluate the effect of multiple loss, based on L2R in instance-level image retrieval, we test our method on four standard datasets: the Oxford 5k building dataset [
11], the Paris 6k dataset [
12], the INRIA Holidays dataset [
13]. We combine these datasets with 100k distractors from Oxford 100kd for larger scale evaluation. We crop the query images by adding the bounding box and follow the standard evaluation protocol on the Oxford and Paris datasets. Then we feed the cropped image into the CNN model, and the entire query image for Holiday and UKB is fed as input. To measure the search results, we uniformly use the standards provided on the dataset website, namely calculating mean Average Precision (mAP) of the search results. The mAP value is calculated as shown in Equation (7):
where AP(q) is mAP of the results of the query image compared with the benchmark annotations in the dataset.
Single-scale evaluation. The image dimensionality input into the CNN is limited to 1024 × 1024 pixels. In the experiments, no post-processing of vectors is used, if not specifically stated.
Multi-scale evaluation. We only use multi-scale representation during test time. The input images are re-sized into a different size, then multiple inputs are fed into the network, and finally the global descriptors are combined from multiple scales into a single descriptor. Baseline average pooling is compared with GeM pooling, the parameter of which equals the value that was learned in the network of global pooling layer. In this respect, the learning whitening is through final multiple scale image descriptors. In the experiment, we use single scale evaluation, if not specifically stated otherwise.
4.4. Contributions of Add LRML into Contrastive Loss Network
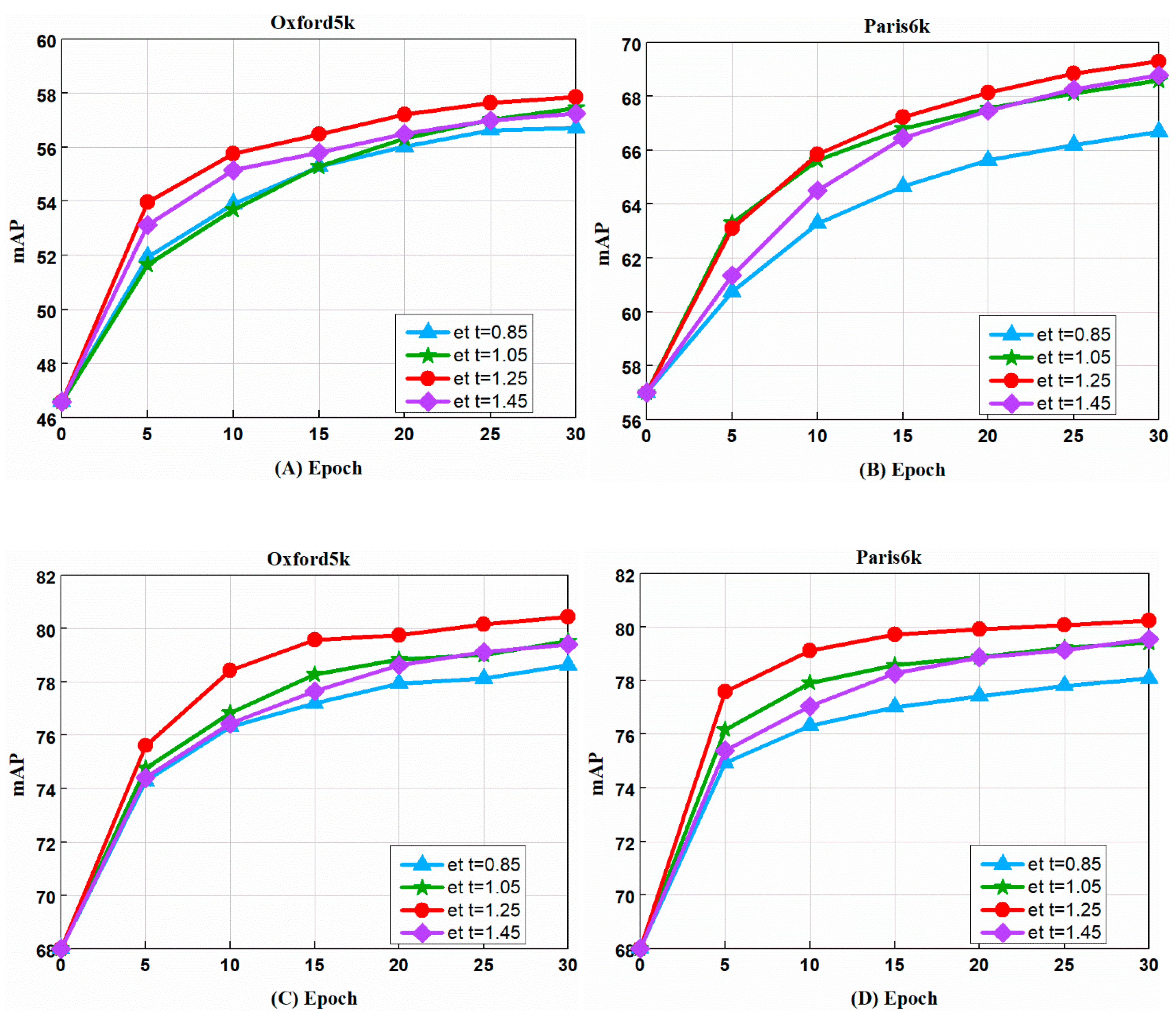
4.4.1. Margin Parameter Selection
We trained the model with margin parameter
at different values to evaluate our network performance. Choosing different margin parameter
can find the optimal parameters suitable for different datasets. The results are shown in
Figure 7. The data shown in
Figure 7A,B is trained under AlexNet, while
Figure 7C,D presents data trained by the VGG. The results show that whatever is in Oxford5k or in Paris6k, the best results appear when
= 1.25. Through the image we observe that in our model, the image retrieval performance will be improved to some extent with the increase of
, but when the value of
is too large, the distance between the matching pairs with high similarity will be furthered. However, when
is too small, some negative samples with certain similarities, such as bad samples, will be discarded. This is because fewer samples involved will lead to poor training results. The key to image retrieval based on L2R is to find the range of distance between all samples and query pictures. For the remainder of this article, we use
= 1.25 in all network and datasets.
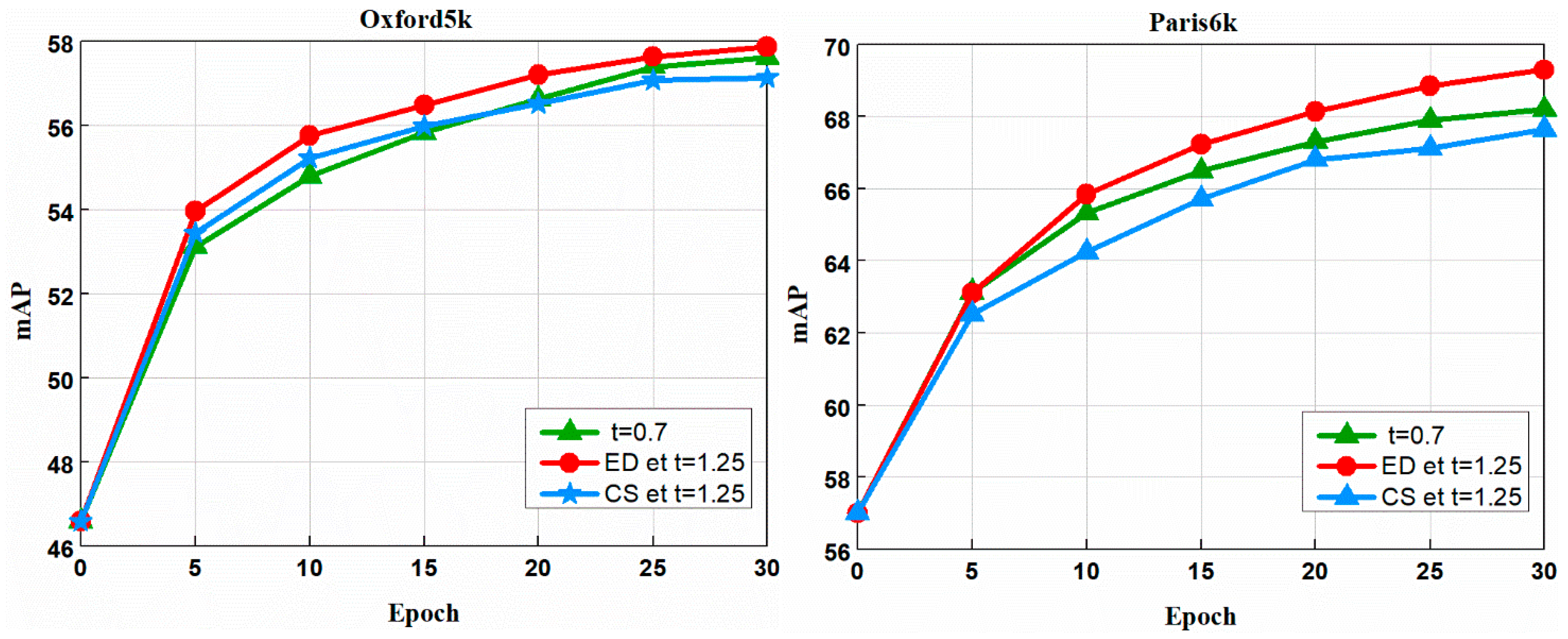
4.4.2. Comparison of Different Loss Functions
We use the large number of training pairs generated in [
27] as training data. Compared with [
3,
5,
38,
39], we find that the contrastive loss has a more powerful convergence function than the triplet loss. Here we compare our multi-loss based on L2R with the current contrastive loss used in [
40]. In this experiment, to better observe the impact of ranking accuracy on the proposed model, we use the cosine similarity and the Euclidean distance to measure the similarity between the query image and the images in the training datasets, and obtain two lists with different ranking. The values in the two lists are brought into the function to train the model. We show the results in
Figure 8, where ED represents the similarity measured by Euclidean distance, CS represents that the measurement of trained datasets ranking is cosine similarity, and ED refers to the experimental results of the multiple loss based on L2R. The corresponding
values are obtained by conducting contrastive loss. It can be seen from the comparison that the performance of image retrieval using our multiple loss function is significantly better than that of contrastive loss function. In addition, we also find that the results in real sequence obtained from Euclidean distance are generally better than those ranked by cosine similarity. This fully demonstrates that multiple loss based on L2R performs better than contrastive loss, and plays a key role in the process of real sequencing of datasets.
4.5. Design Choices of LRML Network
4.5.1. Pooling Methods
We evaluate the impact of different pooling layers on our network and find the pooling method that best fits our network model. Theoretically, when p is 2.32, the performances of GeM is the best. Here we set the value of p to 2.32. We present the results in
Table 2. By observing the data in the table, we see that the pooling performance of GeM and the maximum pooling are always better than the current average pooling, whether it is on Oxford5k or Paris6k. So, in the next experiment of this paper, we combine maximum pooling or GeM with other steps and choose the best combination by comparing the experimental results.
4.5.2. Learned Projections
In the experiment, we compare the previous whitening methods and the newly proposed method of learned discriminative whitening (Lw). The results are shown in
Table 3 without post-processing, but with PCAw [
40] and Lw [
27]. Our experimental results prove that PCAw lowers down the performance, while Lw generally obtains the best performance in the majority of tests and never achieves the worst performance in comparison with others. This complies with the experimental results found by Radenović [
27].
During the finetuning process, an additional experiment is conducted to append a whitening layer at the end of the network. By this means, whitening is learned in an end-to-end manner, combined with convolutional filters and the same training data in batch-mode. Specifically, Lw achieves 58 on AlexNet MAC, and 67.74 mAP on both Oxford5k and Paris6k. In contrast, on the same network, GeM achieves 67.04 mAP on Oxford5k and 72.4 mAP on Paris6k, respectively. In view of these findings, we combined Lw and GeM, because they are trained in a much faster and more effective manner.
4.5.3. Dimensionality of Final Image Vector and Its Impact
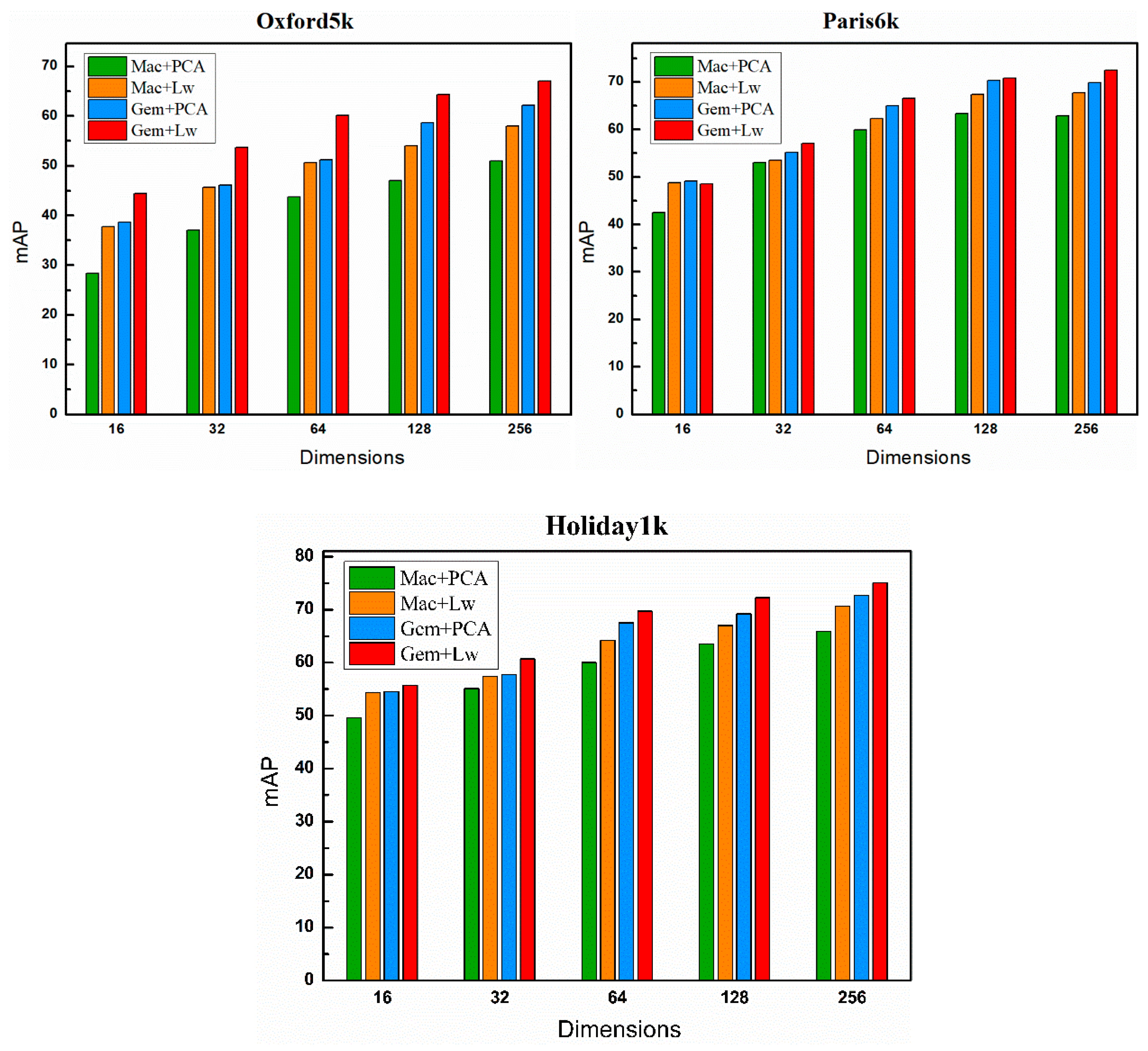
We compared the performance of cross-combination of Mac pooling, GeM pooling, PCA whitening and Lw whitening in different dimensions. The performance of image retrieval in image vector from 16 to 256 is shown in
Figure 9.
As can be seen from
Figure 9, no matter what the combination, the higher the dimension, the better the performance. In the same dimension, when using the same pooling method, the effect of Lw whitening outweighs the others, and achieves even better results when co-functioning with GeM. Overall, when the dimension is 256, the combination of GeM pooling and Lw whitening has the best performance.
4.5.4. Efficiency
In order to verify the advantages of our proposed LRML algorithm model in terms of training speed, in this part of the experiment, we compare the training time of this model with other classical metric learning models. We run the experiment on intel(R) i7-8700, GPU with 11GB of memory, operating system Ubuntu 18.04 LTS. In the testing phase, we use VGG16 and ResNet101 as the basic network and calculate training time on the datasets.
Table 4 shows the training efficiency of the five methods.
As can be seen from the figure, the training time with our method is shorter than those by Triplet loss and Quadruplet loss, because we use a two-branch network, and the structure is simple. The sample pairs in Lifted Struct are selected in mini-batches, and our method is to choose within the entire data set, so in terms of time, our method has an advantage over Lifted Struct. Compared to contrastive loss, we not only use the same branch structure, but also add a pair of samples based on this sorting operations. This makes our training time slightly longer than contrastive loss, but our outcome is much better. In general, our approach is demonstrated to be the most effective.
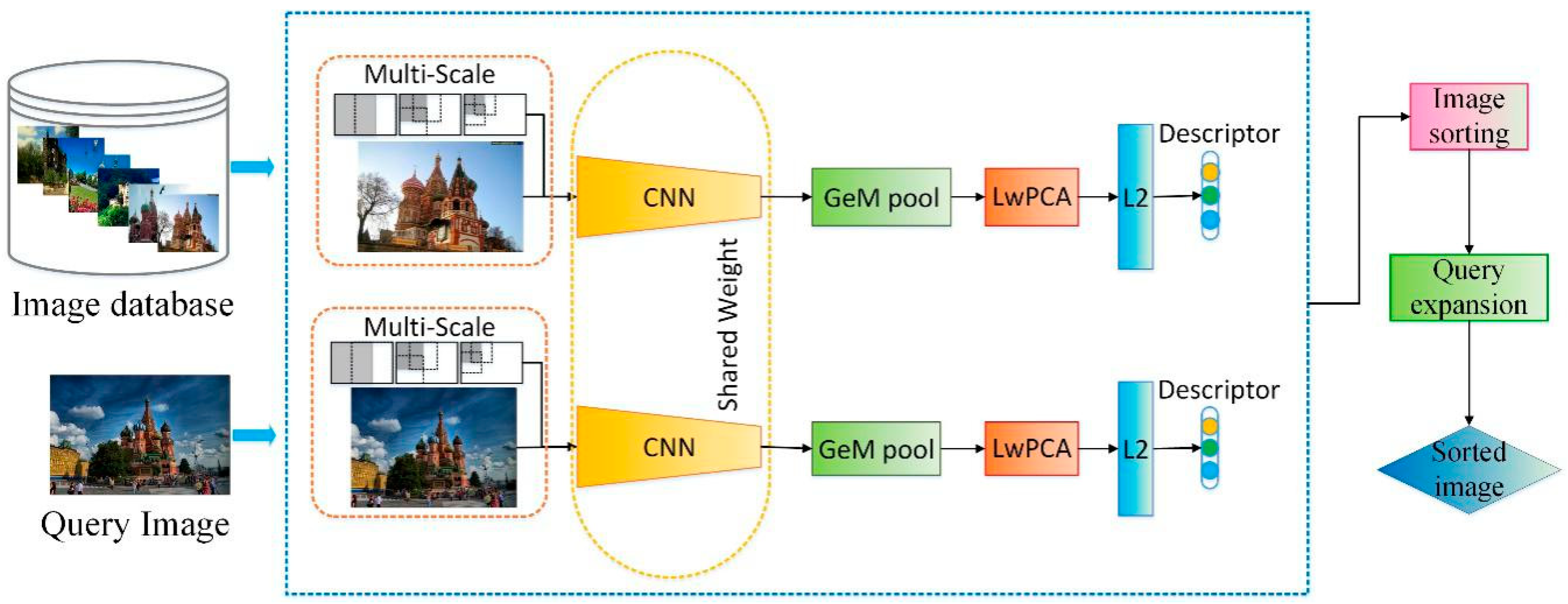
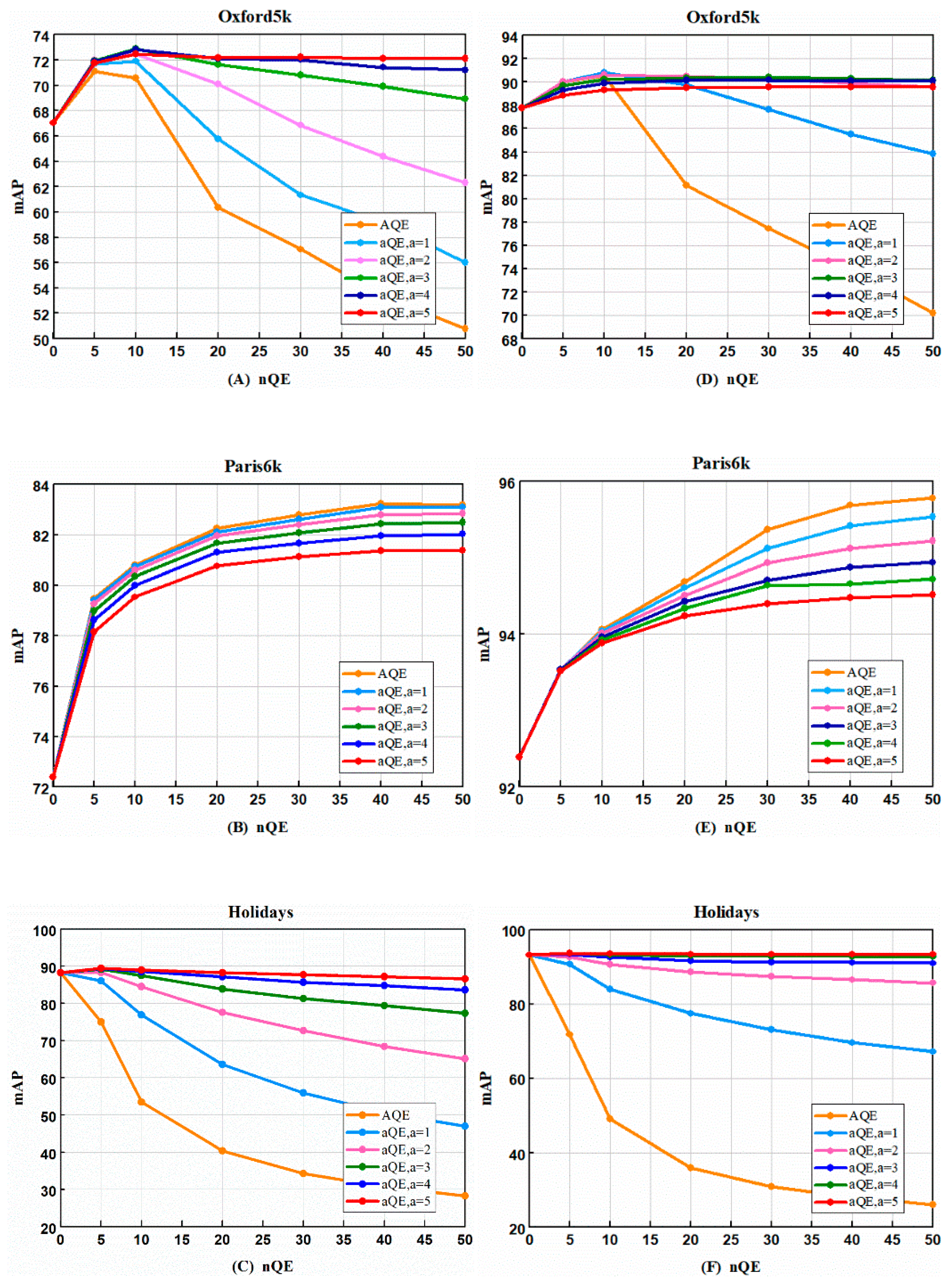
Query expansion is a post-processing technology that can effectively improve retrieval performance. It works as follows: in the initial query phase, the feature vector is adopted, and the returned top k results are obtained through the query. The current results will probably experience space verification phase, in which we discard results that do not match the query image. The remaining results are then summed with the original query and experience renormalization. Finally, a second query is performed by combining the descriptors to generate a final list of retrieved images. Query expansion usually leads to a significant increase the level of accuracy. The existing query expansion methods include the average query expansion (AQE) and the weighted (α) query expansion αQE. We used the AlexNet and ResNet to test on the Oxford5k, Paris6k, and Holiday datasets, and the result is shown in
Figure 10. The results on AlexNet are shown in
Figure 10A–C. The test results are shown in
Figure 10D–F on ResNet. We compare the two query expansion methods, and the experimental results are consistent with that found in [
27]. The AQE performs very differently on the Oxford5k, Paris6k and Holiday datasets. It performs more prominently on Paris6k, but unstable on the Oxford5k and Holiday datasets. When n = 10, the accuracy rates drop sharply, while αQE is stable on three datasets. We finally set a = 5 and nQE = 50 on Oxford5k and Holiday datasets, and set a = 0 and nQE = 50 on Paris6k datasets.
4.6. Experimental Results and Comparison
4.6.1. Comparison with the State of the Art
To comprehensively evaluate the localization performance of our trained LRML model, we have extensively compared the results with the latest performance of compact image representation and methods for query expansion. The results of the fine-tuning network based on the multiple loss are summarized together with the results currently published in
Table 5. When using deep networks to compact representation, the better performance on Paris is inherited by the nature of the pre-trained networks; the LRML model with ResNet achieves 87.9 on Oxford5k, 93.3 on Holiday and 93.8 on Paris6k. Using the architectures of VGG and ResNet has achieved most advanced scores on both Paris and Holiday. When using the architecture of ResNet to conduct initialization, the proposed method is superior to the state-of-the-art in all datasets. Notably, the result of GeM+VGG16 [
27] on Oxford5k is 87.9, and 83.3 on Oxford105k, better than our results, that is, 83.2 on Oxford5k and 78.6 on Oxford105k. The reason is probably because in training datasets, the differences between the negative samples are limited, with fewer VGG16 network layers. Thus, it is difficult to extract effective features based on ranking sequence. However, when the framework of ResNet is adopted, with the datasets on Oxford5k and Oxford105k, our results are 87.9 and 84.8 respectively, which still outperform those on GeM [
27], namely 87.8 and 84.6. When we use VGG19 as the experimental network, the results are better than those on VGG16, which proves one of our hypotheses, that is, the limitation on the number of layers of networks restricts feature extraction.
We have also evaluated how our model fares on the occasion of combining an updated query expansion method by Radenović. This method applies in addition to the current methods and uses information from the closest neighbors in the gallery, so as to improve the ranking results. As shown in
Table 5, our proposed method performs well and demonstrates similar improvements to those achieved by Radenović [
27]. After adding re-ranking and query expansion, the results on ResNet still achieve the best performance. Specifically, the final LRML model with ResNet achieves 92.0 on Oxford5k, 89.5 on Holiday and 96.7 on Paris6k. In accordance with the current results, the results of VGG16 on Oxford5k and Oxford105k are 90.0 and 86.9, and the results of VGG19 on Oxford5k and Oxford105k are 90.8 and 87.9, respectively, which are lower than the results of GeM+VGG [
27], with 91.9 on Oxford5k and 89.6 on Oxford105k. But the counterpart results on Paris and Holiday are 94.2 and 92.1, surpassing the other methods under the same conditions.
Table 5 also indicates that our method is robust in terms of the size of irrelevant training data. We trained our method with different sizes of training data from the Flickr100k distractor images. The experiment was performed on the two large-scale datasets, i.e., Oxford 105k, Paris106k and Holiday101k. The experimental results indicate that the mAP score of our method is almost unchanged with the training size. The results indicate that our method is robust in terms of training size when this is learned from irrelevant data.
4.6.2. Visualization of Image Retrieval
We use the existing ResNet network and the already trained network that joins the multiple loss function to search images on Oxford. As shown in
Figure 11, the first column is the query images, and the following two lines behind each query image introduce the Top-20 query results. The first line includes the image retrieval result by using off-the-shelf ResNet architecture, and the second line reflects the retrieval result of the trained network after leveraging multiple loss function. By comparing the first three groups of queries, it can be found that some error images appear in the image search of ResNet, which are circled in red. As observed from the two sets of queries, under the condition that all image search results are correct, ours are uniform and highly consistent with the similarity of the query images. In contrast, the effect of ResNet search is not that integrated. Overall, our model has significantly improved the retrieval performance.
5. Conclusions
In this paper, we proposed a new metric learning loss called multiple loss based on L2R. For contrastive loss, triple loss, and quadruple loss, we can use multiple examples simultaneously to improve the robustness of the model. In our method, we calculate a distance sequence, choose the maximum positive distance and the different negative pairwise distances after adjusting the threshold to calculate the final loss. In this way, the ranking-based multiple loss trains the network using a dissimilar positive image and multiple negative images, selected from different clusters, thus sharing different similarities with the query image. We used VGG16 and ResNet101 as the base model to perform some comparative experiments with different metric losses.
The comparison shows that our multiple loss network based on L2R has achieved the top performance. We have then compared our approach to some of the most advanced methods available today. On several benchmark datasets, including Oxford, Paris, and Holiday, our approach shows better performance than those methods.
In the future, we will investigate other ways to improve the performance of images retrieved, such as increasing the number of negative samples for better feature extraction. Furthermore, we will expand our work by building up a more effective network architecture where a positive sample sorting sequence is introduced to improve multiple loss. This makes the proposed architecture obtain robustness in image processing, and also extracts some high-level cues, so as to accurately retrieve images.