An Attention-Based Spatiotemporal Gated Recurrent Unit Network for Point-of-Interest Recommendation
Abstract
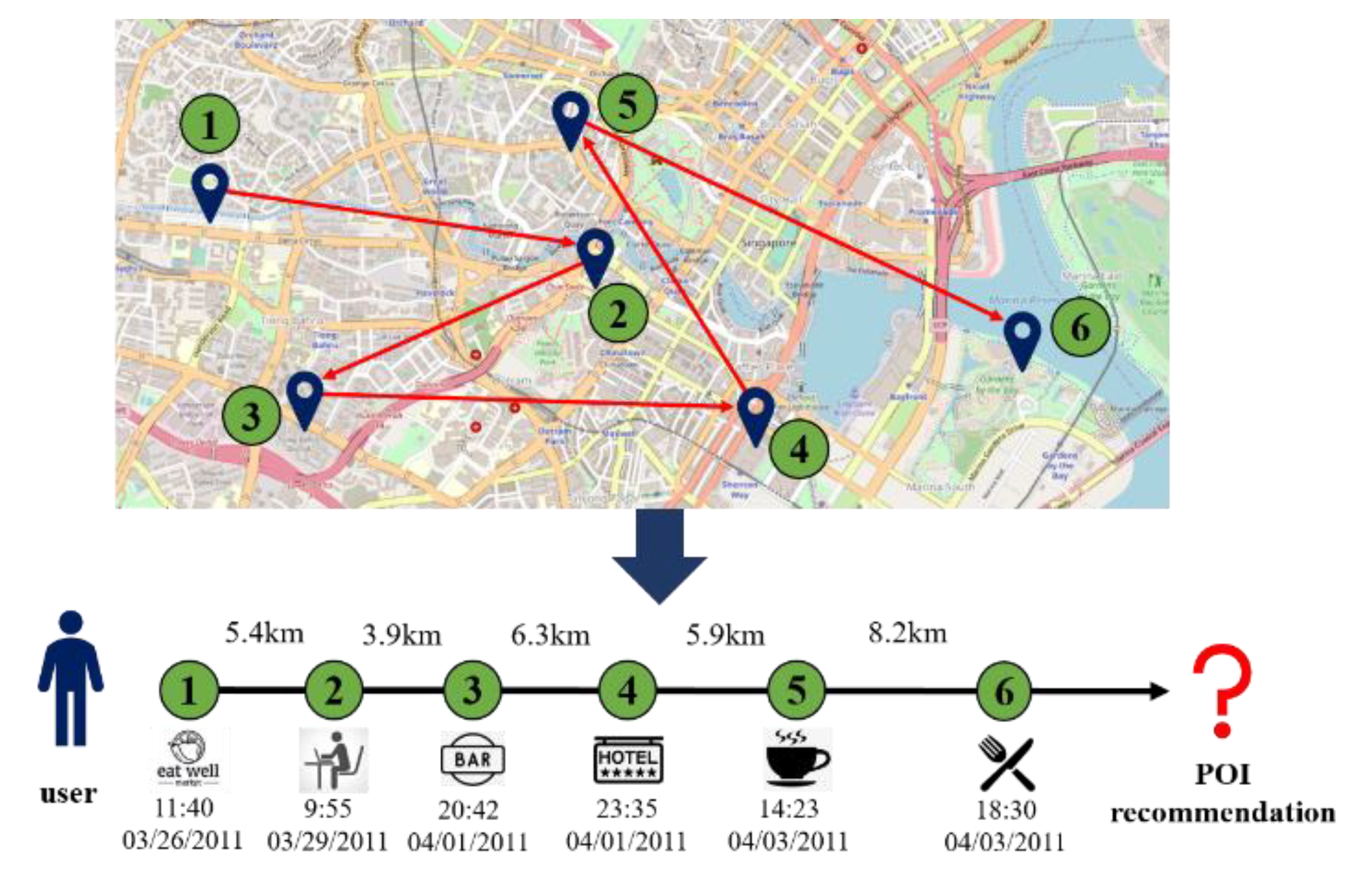
:1. Introduction
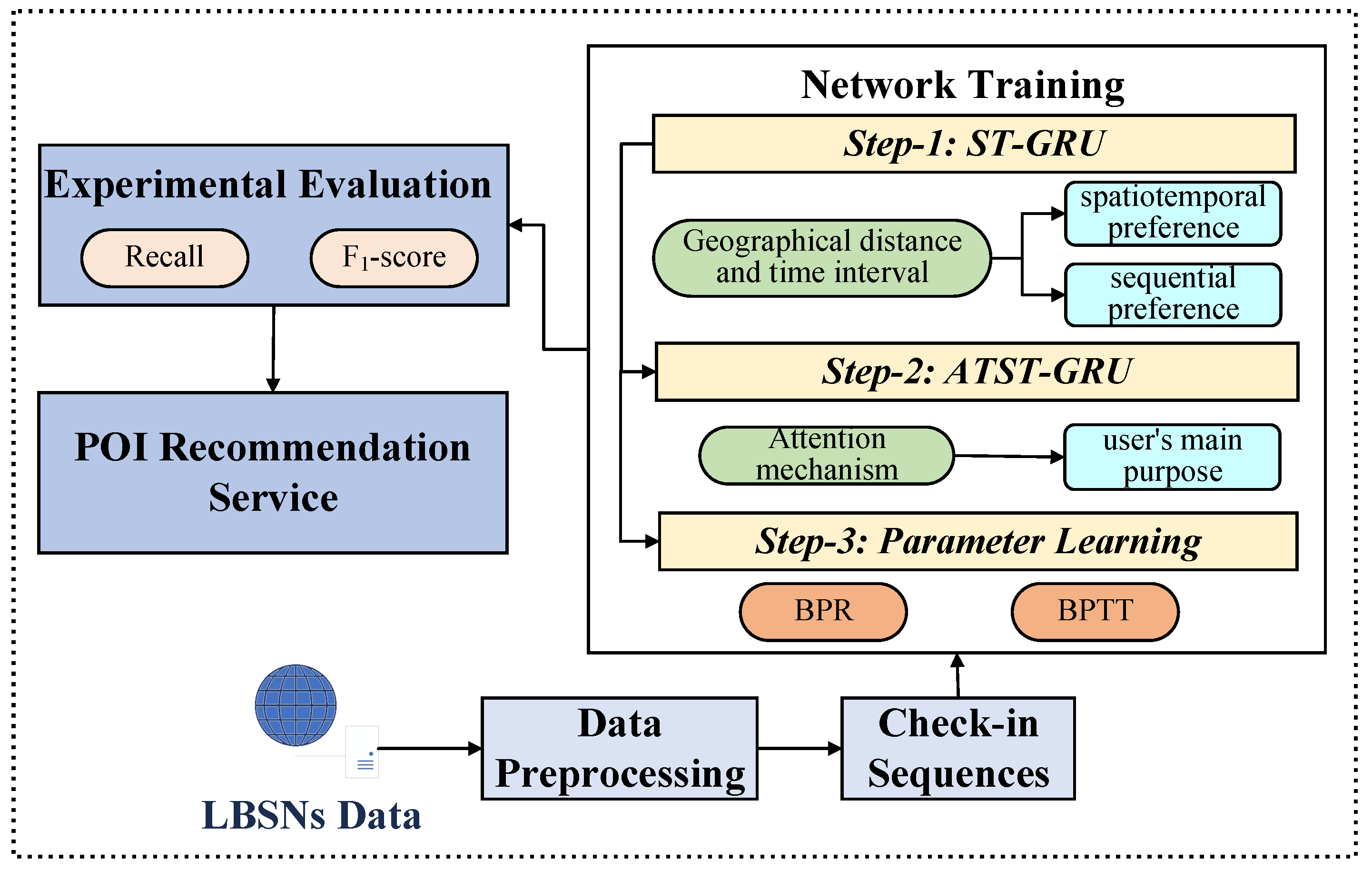
- A novel spatiotemporal gated recurrent unit (ST-GRU) network model is proposed in this paper, which combines continuous values of spatial and temporal contexts information into GRU network naturally to capture the user’s spatiotemporal preferences and alleviate the problems of data heterogeneity and sparsity;
- An attention-based method is introduced to ST-GRU network for POI recommendation, named ATST-GRU model. This can automatically pay more attention to critical information and extract the user’s main purpose, which significantly strengthens the user’s long-term interest;
- Extensive experiments on two real-world datasets show that ATST-GRU is effective and outperforms state-of-the-art methods significantly.
2. Related Work
2.1. Collaborative Filtering Based Methods
2.2. Markov Chain Based Methods
2.3. Deep Learning Based Methods
3. Proposed ATST-GRU Model
3.1. Problem Statement
3.2. Gated Recurrent Unit
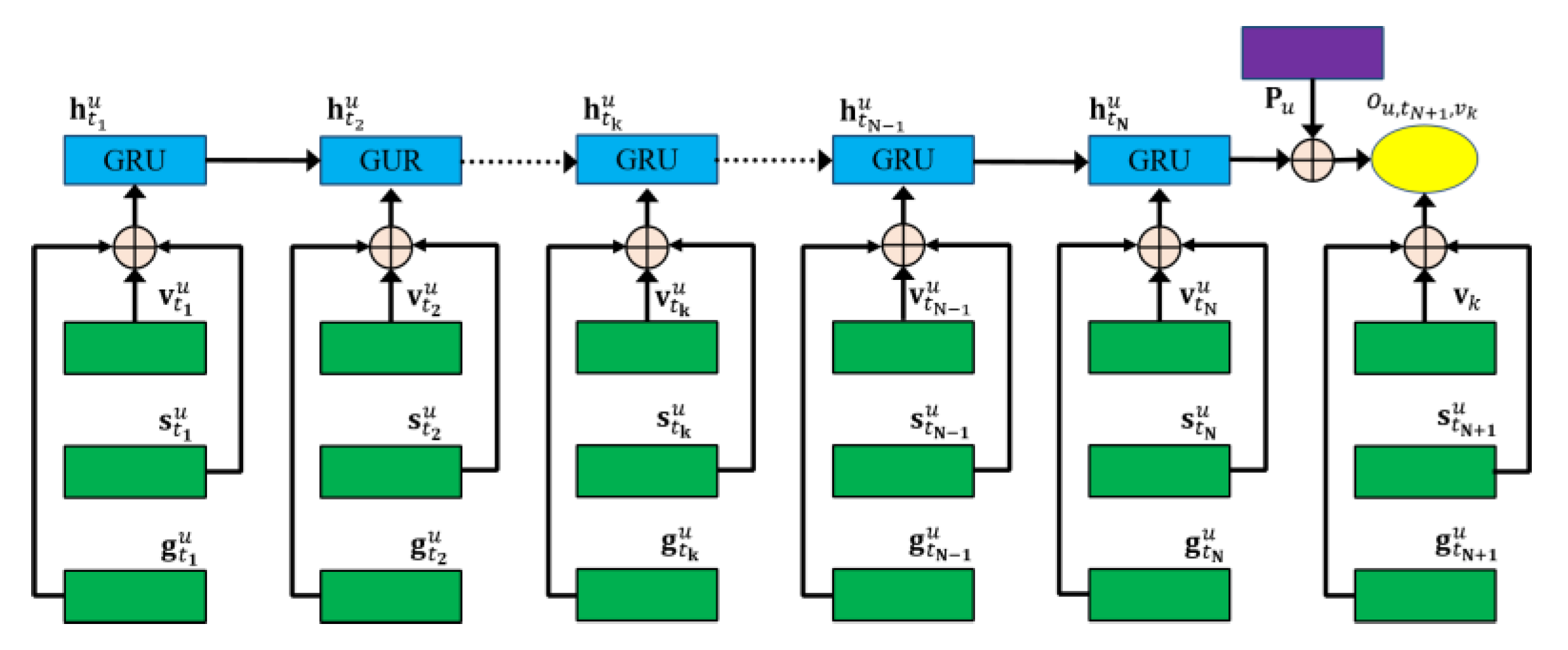
3.3. Spatiotemporal GRU Network
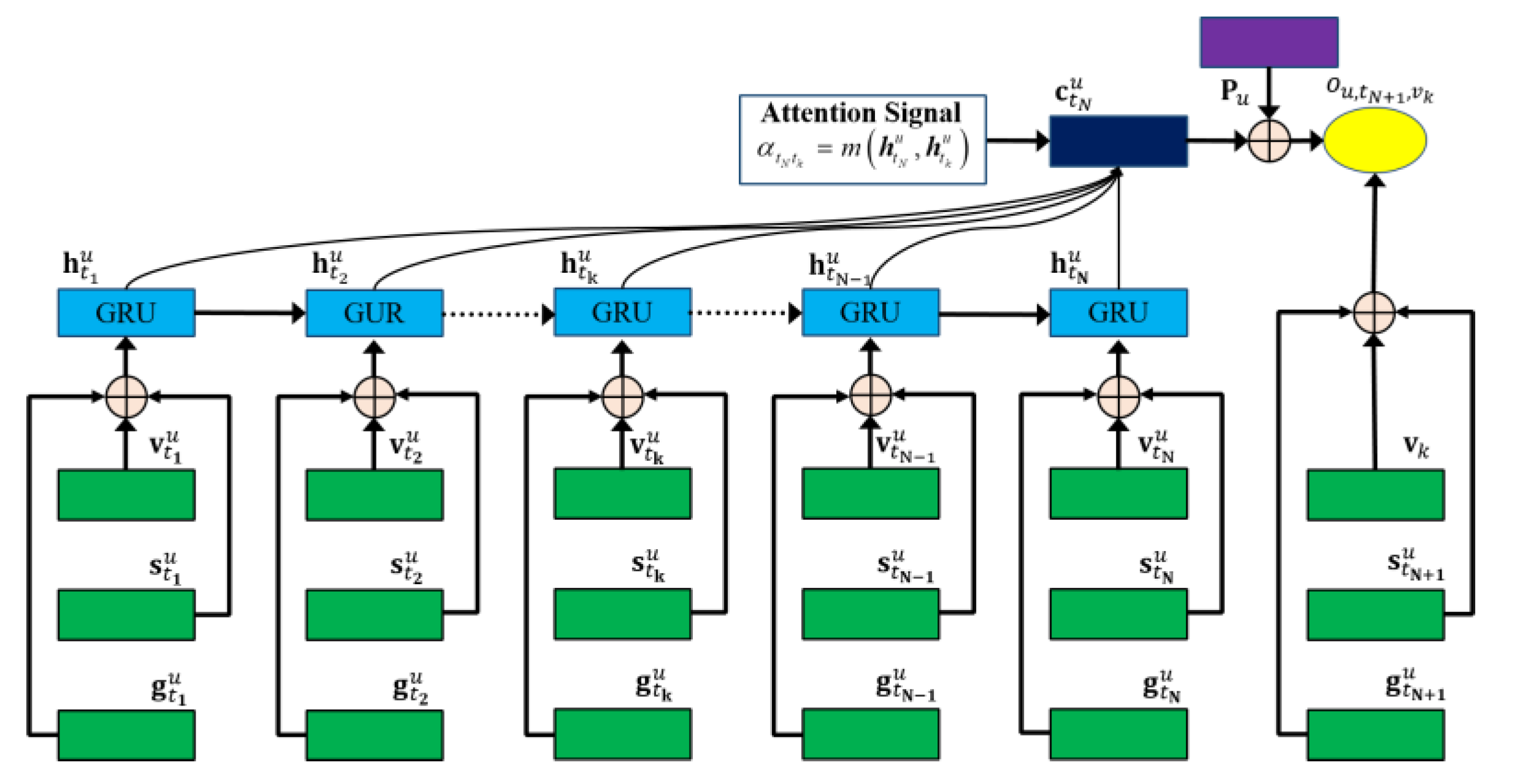
3.4. Attention-Based Spatiotemporal GRU Network
3.5. Network Learning
| Algorithm 1: ATST-GRU |
| Input: historical check-in sequences . Output: model parameters . //construct training instances For each user u in P do For each check-in sequence do Get the set of negative samples ; For each check-in activity in do Compute the embedded vector ; Compute the spatial contexts vector ; Compute the temporal contexts vector ; End for Add a training instance into D; End for End for Initialize the parameter set ; repeat For each user u in P do Randomly select a batch of instances from ; Update by minimizing the object with End for until convergence; return |
4. Experimental Results and Analysis
4.1. Experimental Settings
4.1.1. Datasets
4.1.2. Baseline Methods
- BPR [26]. This method is a generic optimization criterion and learning algorithm for personalized ranking, and we applied BPR in POI recommendation;
- GRU [19]. GRU network is a more robust variant of RNN which work better in capturing long term dependencies, and we applied GRU in POI recommendation;
- FPMC-LR [3]. This method is a state-of-the-art Markov chain method that models personalized sequential transitions for POI recommendation;
- PRME-G [52]. This method is a state-of-the-art metric embedding method for POI recommendation, which integrates geographical influence and sequential information;
- Rank-GeoFM [35]. It is a state-of-the-art ranking-based factorization model for POI recommendation, which incorporates the geographical influence and temporal influence;
- ST-RNN [8]. This is a state-of-the-art RNN-based model for successive POI recommendation. It incorporates both local temporal and spatial transition context within the RNN architecture;
- DeepMove [66]: It is a state-of-the-art attentional RNN model which capture the sequential transitions by jointly embedding the multiple factors.
4.1.3. Evaluation Metrics
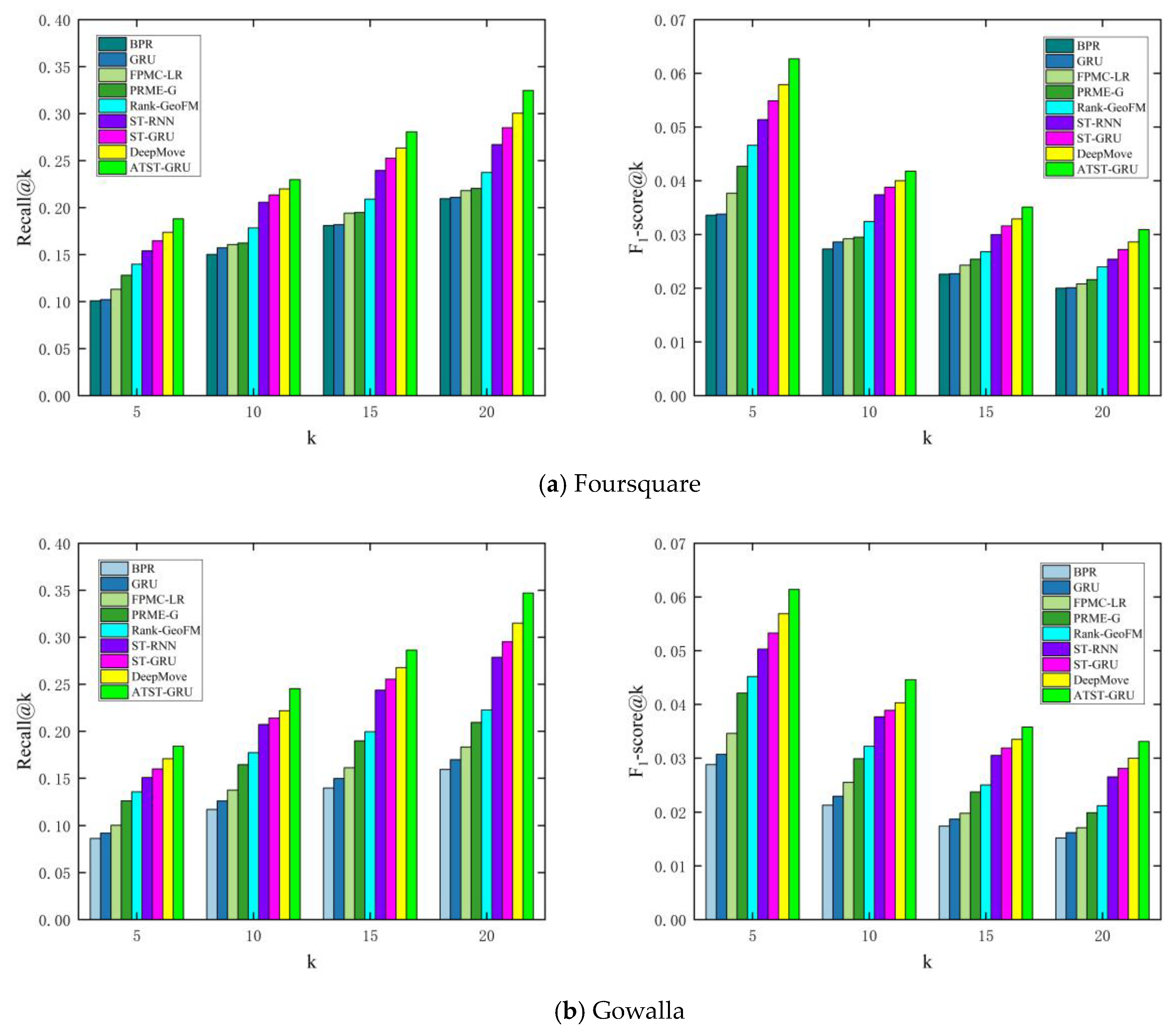
4.2. Comparison and Results
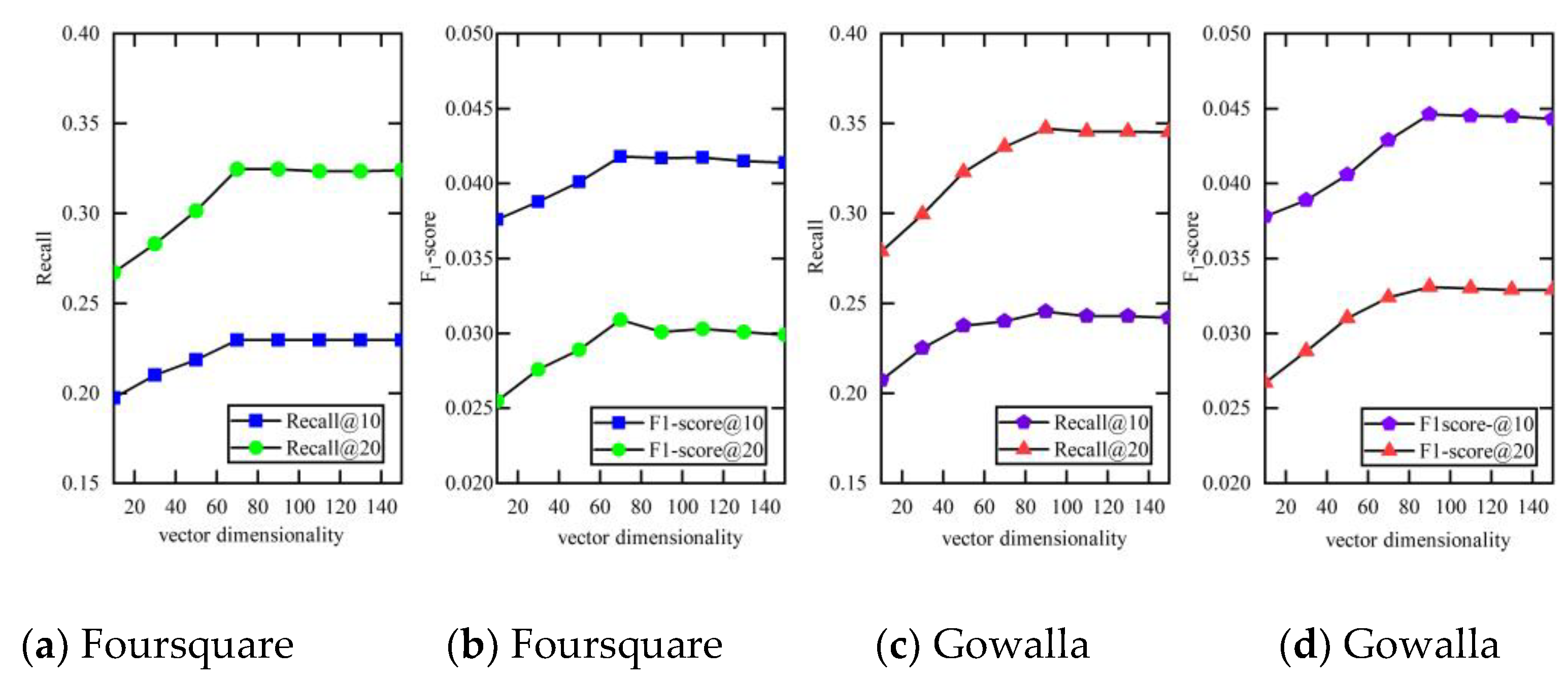
4.3. Influence of Embedding Dimension Size
4.4. Influence of Different Spatial and Temporal Window Widths
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, H.; Tang, J.; Liu, H. Exploring social-historical ties on location-based social networks. In Proceedings of the Sixth International AAAI Conference on Weblogs and Social Media, Dublin, Ireland, 4–7 June 2012. [Google Scholar]
- Yuan, Q.; Cong, G.; Ma, Z.; Sun, A.; Thalmann, N.M. Time-aware point-of-interest recommendation. In Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 28 July–1 August 2013; pp. 363–372. [Google Scholar]
- Cheng, C.; Yang, H.; Lyu, M.R.; King, I. Where you like to go next: Successive point-of-interest recommendation. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–19 August 2013. [Google Scholar]
- Cheng, C.; Yang, H.; King, I.; Lyu, M.R. Fused matrix factorization with geographical and social influence in location-based social networks. In Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012. [Google Scholar]
- Ye, M.; Yin, P.; Lee, W.C.; Lee, D.L. Exploiting geographical influence for collaborative point-of-interest recommendation. In Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval, Beijing, China, 24–28 July 2011; pp. 325–334. [Google Scholar]
- Cai, L.; Xu, J.; Liu, J.; Pei, T. Integrating spatial and temporal contexts into a factorization model for POI recommendation. Int. J. Geogr. Inf. Sci. 2018, 32, 524–546. [Google Scholar] [CrossRef]
- Yin, H.; Sun, Y.; Cui, B.; Hu, Z.; Chen, L. LCARS: A location-content-aware recommender system. In Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining, Chicago, IL, USA, 11–14 August 2013; pp. 221–229. [Google Scholar]
- Liu, Q.; Wu, S.; Wang, L.; Tan, T. Predicting the next location: A recurrent model with spatial and temporal contexts. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- He, J.; Li, X.; Liao, L.; Song, D.; Cheung, W.K. Inferring a personalized next point-of-interest recommendation model with latent behavior patterns. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence. Phoenix, Arizona USA, 12-17 February 2016. [Google Scholar]
- Anagnostopoulos, A.; Atassi, R.; Becchetti, L.; Fazzone, A.; Silvestri, F. Tour recommendation for groups. Data Min. Knowl. Discov. 2017, 31, 1157–1188. [Google Scholar] [CrossRef]
- Ayala-Gómez, F.; Daróczy, B.Z.; Mathioudakis, M.; Benczúr, A.; Gionis, A. Where could we go? Recommendations for groups in location-based social networks. In Proceedings of the 2017 ACM on Web Science Conference, Troy, New York, NY, USA, 25–28 June 2017; pp. 93–102. [Google Scholar]
- Lian, D.; Zhao, C.; Xie, X.; Sun, G.; Chen, E.; Rui, Y. GeoMF: Joint geographical modeling and matrix factorization for point-of-interest recommendation. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 831–840. [Google Scholar]
- Gan, M.; Gao, L. Discovering Memory-Based Preferences for POI Recommendation in Location-Based Social Networks. ISPRS Int. J. Geo Inf. 2019, 8, 279. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Cho, E.; Myers, S.A.; Leskovec, J. Friendship and mobility: User movement in location-based social networks. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 1082–1090. [Google Scholar]
- Ye, J.; Zhu, Z.; Cheng, H. What’s your next move: User activity prediction in location-based social networks. In Proceedings of the 2013 SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 171–179. [Google Scholar]
- Williams, R.J.; Zipser, D. A learning algorithm for continually running fully recurrent neural networks. Neural Comput. 1989, 1, 270–280. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Duives, D.C.; Wang, G.; Kim, J. Forecasting pedestrian movements using recurrent neural networks: An application of crowd monitoring data. Sensors 2019, 19, 382. [Google Scholar] [CrossRef]
- Quadrana, M.; Cremonesi, P.; Jannach, D. Sequence-aware recommender systems. ACM Comput. Surv. (CSUR) 2018, 51, 66. [Google Scholar] [CrossRef]
- Cui, Q.; Tang, Y.; Wu, S.; Wang, L. Distance2Pre: Personalized Spatial Preference for Next Point-of-Interest Prediction. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Macau, China, 14–17 April 2019; pp. 289–301. [Google Scholar]
- Hidasi, B.; Karatzoglou, A.; Baltrunas, L.; Tikk, D. Session-based recommendations with recurrent neural networks. arXiv 2015, arXiv:1511.06939, 2015. [Google Scholar]
- Mnih, V.; Heess, N.; Graves, A. Recurrent models of visual attention. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2204–2212. [Google Scholar]
- Wang, S.; Hu, L.; Cao, L.; Huang, X.; Lian, D.; Liu, W. Attention-based transactional context embedding for next-item recommendation. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; pp. 452–461. [Google Scholar]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative Filtering for Implicit Feedback Datasets. In Proceedings of the 8th IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Wang, H.; Terrovitis, M.; Mamoulis, N. Location recommendation in location-based social networks using user check-in data. In Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 November 2013; pp. 374–383. [Google Scholar]
- Koren, Y. Factorization meets the neighborhood: A multifaceted collaborative filtering model. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 426–434. [Google Scholar]
- Liu, B.; Fu, Y.; Yao, Z.; Xiong, H. Learning geographical preferences for point-of-interest recommendation. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 1043–1051. [Google Scholar]
- Gao, H.; Tang, J.; Hu, X.; Liu, H. Exploring temporal effects for location recommendation on location-based social networks. In Proceedings of the 7th ACM Conference on Recommender Systems, Hong Kong, China, 12–16 October 2013; pp. 93–100. [Google Scholar]
- Zhao, S.; Zhao, T.; Yang, H.; Lyu, M.R.; King, I. STELLAR: Spatial-temporal latent ranking for successive point-of-interest recommendation. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Zhao, S.; Zhao, T.; King, I.; Lyu, M.R. Geo-teaser: Geo-temporal sequential embedding rank for point-of-interest recommendation. In Proceedings of the 26th International Conference on World Wide Web Companion. International World Wide Web Conferences Steering Committee, Perth, Australia, 3–7 April 2017; pp. 153–162. [Google Scholar]
- Li, X.; Cong, G.; Li, X.L.; Pham, T.A.N.; Krishnaswamy, S. Rank-geofm: A ranking based geographical factorization method for point of interest recommendation. In Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, Santiago, Chile, 9–13 August 2015; pp. 433–442. [Google Scholar]
- Huang, L.; Ma, Y.; Liu, Y.; Sangaiah, A.K. Multi-modal Bayesian embedding for point-of-interest recommendation on location-based cyber-physical–social networks. Future Gener. Comput. Syst. 2017. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, D.; Yu, Z.; Wang, Z. A sentiment-enhanced personalized location recommendation system. In Proceedings of the 24th ACM Conference on Hypertext and Social Media, Paris, France, 1–3 May 2013; pp. 119–128. [Google Scholar]
- Liu, B.; Xiong, H.; Papadimitriou, S.; Fu, Y.; Yao, Z. A general geographical probabilistic factor model for point of interest recommendation. IEEE Trans. Knowl. Data Eng. 2014, 27, 1167–1179. [Google Scholar] [CrossRef]
- Kefalas, P.; Manolopoulos, Y. A time-aware spatio-textual recommender system. Expert Syst. Appl. 2017, 78, 396–406. [Google Scholar] [CrossRef]
- Ren, X.; Song, M.; Haihong, E.; Song, J. Context-aware probabilistic matrix factorization modeling for point-of-interest recommendation. Neurocomputing 2017, 241, 38–55. [Google Scholar] [CrossRef]
- Levandoski, J.J.; Sarwat, M.; Eldawy, A.; Mokbel, M.F. Lars: A location-aware recommender system. In Proceedings of the 2012 IEEE 28th International Conference on Data Engineering, Arlington, VA, USA, 1–5 April 2012; pp. 450–461. [Google Scholar]
- Kurashima, T.; Iwata, T.; Hoshide, T.; Takaya, N.; Fujimura, K. Geo topic model: joint modeling of user’s activity area and interests for location recommendation. In Proceedings of the Sixth ACM International Conference on Web Search and Data Mining, Rome, Italy, 4–8 February 2013; pp. 375–384. [Google Scholar]
- Zhang, J.D.; Chow, C.Y. TICRec: A probabilistic framework to utilize temporal influence correlations for time-aware location recommendations. IEEE Trans. Serv. Comput. 2015, 9, 633–646. [Google Scholar] [CrossRef]
- Zhang, J.D.; Chow, C.Y. iGSLR: Personalized geo-social location recommendation: A kernel density estimation approach. In Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 November 2013; pp. 334–343. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Schmidt-Thieme, L. Factorizing personalized markov chains for next-basket recommendation. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 811–820. [Google Scholar]
- Mathew, W.; Raposo, R.; Martins, B. Predicting future locations with hidden Markov models. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, PA, USA, 5–8 September 2012; pp. 911–918. [Google Scholar]
- Chen, M.; Liu, Y.; Yu, X. NLPMM: A next location predictor with markov modeling. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Tainan, Taiwan, 13–16 May 2014; pp. 186–197. [Google Scholar]
- Zhang, C.; Zhang, K.; Yuan, Q.; Zhang, L.; Hanratty, T.; Han, J. Gmove: Group-level mobility modeling using geo-tagged social media. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1305–1314. [Google Scholar]
- Natarajan, N.; Shin, D.; Dhillon, I.S. Which app will you use next: collaborative filtering with interactional context. In Proceedings of the 7th ACM Conference on Recommender Systems, Hong Kong, China, 12–16 October 2013; pp. 201–208. [Google Scholar]
- Chen, J.; Wang, C.; Wang, J. A personalized interest-forgetting markov model for recommendations. Proceedings of Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Wang, H.; Shen, H.; Ouyang, W.; Cheng, X. Exploiting POI-Specific Geographical Influence for Point-of-Interest Recommendation. In Proceedings of the IJCAI, Stockholm, Sweden, 13–19 July 2018; pp. 3877–3883. [Google Scholar]
- Feng, S.; Li, X.; Zeng, Y.; Cong, G.; Chee, Y.M.; Yuan, Q. Personalized ranking metric embedding for next new POI recommendation. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 3111–3119. [Google Scholar]
- Yang, C.; Bai, L.; Zhang, C.; Yuan, Q.; Han, J. Bridging collaborative filtering and semi-supervised learning: A neural approach for poi recommendation. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1245–1254. [Google Scholar]
- Chen, Y.; Fan, R.; Yang, X.; Wang, J.; Latif, A. Extraction of urban water bodies from high-resolution remote-sensing imagery using deep learning. Water 2018, 10, 585. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Tang, J.; Shu, K.; Ranganath, S.; Liu, H. What your images reveal: Exploiting visual contents for point-of-interest recommendation. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 391–400. [Google Scholar]
- Chen, Y.; Fan, R.; Bilal, M.; Yang, X.; Wang, J.; Li, W. Multilevel cloud detection for high-resolution remote sensing imagery using multiple convolutional neural networks. ISPRS Int. J. Geo Inf. 2018, 7, 181. [Google Scholar] [CrossRef]
- Ding, R.; Chen, Z. RecNet: A deep neural network for personalized POI recommendation in location-based social networks. Int. J. Geogr. Inf. Sci. 2018, 32, 1631–1648. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, H.; Xu, C.; Feng, J.; Wang, T.; Bian, J.; Liu, T.Y. Sequential click prediction for sponsored search with recurrent neural networks. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec, QC, Canada, 27–31 July 2014. [Google Scholar]
- Zhao, P.; Zhu, H.; Liu, Y.; Li, Z.; Xu, J.; Sheng, V.S. Where to Go Next: A Spatio-temporal LSTM model for Next POI Recommendation. arXiv 2018, arXiv:1806.06671. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Xu, K.; Ba, J.; Kiros, R.; Cho, K.; Courville, A.; Salakhudinov, R.; Bengio, Y. Show, attend and tell: Neural image caption generation with visual attention. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2048–2057. [Google Scholar]
- Chen, J.; Zhang, H.; He, X.; Nie, L.; Liu, W.; Chua, T.S. Attentive collaborative filtering: Multimedia recommendation with item-and component-level attention. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Shinjuku, Tokyo, Japan, 7–11 August 2017; pp. 335–344. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Feng, J.; Li, Y.; Zhang, C.; Sun, F.; Meng, F.; Guo, A.; Jin, D. Deepmove: Predicting human mobility with attentional recurrent networks. In Proceedings of the 2018 World Wide Web Conference on World Wide Web, Lyon, France, 23–27 April 2018; pp. 1459–1468. [Google Scholar]
| Notation | Explanation |
|---|---|
| , , , | user, POI, location, time |
| , , | set of users, set of POIs, set of locations |
| latent representation of user | |
| POI visited by user at time point | |
| the hidden vector of GRU units | |
| candidate state of GRU units | |
| , | reset gate vector and update gate vector of GRU units |
| check-in sequence of user | |
| , | set of weight matrices for a GRU network |
| set of bias vectors for a GRU network | |
| predicted probability that visits POI at | |
| sigmoid function | |
| attention weight factors | |
| , | vector representations of spatial and temporal intervals |
| Dataset | #Users | #POIs | #Check-ins | Sparsity |
|---|---|---|---|---|
| Foursquare | 2321 | 5596 | 194,108 | 99.18% |
| Gowalla | 10,162 | 24,237 | 456,967 | 99.88% |
| Dataset | Window | 6 h | 12 h | 24 h | 48 h | 60 h |
|---|---|---|---|---|---|---|
| Foursquare | 0.1 km | 0.3215 | 0.3205 | 0.3106 | 0.3032 | 0.3011 |
| 0.3 km | 0.3201 | 0.3247 | 0.3009 | 0.3105 | 0.3093 | |
| 0.5 km | 0.3126 | 0.3133 | 0.3211 | 0.3119 | 0.3042 | |
| Gowalla | 0.1 km | 0.3158 | 0.3301 | 0.3325 | 0.3471 | 0.3412 |
| 0.3 km | 0.3192 | 0.3215 | 0.3298 | 0.3392 | 0.3317 | |
| 0.5 km | 0.3204 | 0.3287 | 0.3153 | 0.3266 | 0.3255 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Liu, J.; Wang, J.; Xu, S.; Han, H.; Chen, Y. An Attention-Based Spatiotemporal Gated Recurrent Unit Network for Point-of-Interest Recommendation. ISPRS Int. J. Geo-Inf. 2019, 8, 355. https://doi.org/10.3390/ijgi8080355
Liu C, Liu J, Wang J, Xu S, Han H, Chen Y. An Attention-Based Spatiotemporal Gated Recurrent Unit Network for Point-of-Interest Recommendation. ISPRS International Journal of Geo-Information. 2019; 8(8):355. https://doi.org/10.3390/ijgi8080355
Chicago/Turabian StyleLiu, Chunyang, Jiping Liu, Jian Wang, Shenghua Xu, Houzeng Han, and Yang Chen. 2019. "An Attention-Based Spatiotemporal Gated Recurrent Unit Network for Point-of-Interest Recommendation" ISPRS International Journal of Geo-Information 8, no. 8: 355. https://doi.org/10.3390/ijgi8080355
APA StyleLiu, C., Liu, J., Wang, J., Xu, S., Han, H., & Chen, Y. (2019). An Attention-Based Spatiotemporal Gated Recurrent Unit Network for Point-of-Interest Recommendation. ISPRS International Journal of Geo-Information, 8(8), 355. https://doi.org/10.3390/ijgi8080355






