High-Performance Overlay Analysis of Massive Geographic Polygons That Considers Shape Complexity in a Cloud Environment
Abstract
1. Introduction
2. Relevant Work
2.1. Shape Complexity
2.2. Overlay Analysis
3. Methodology
3.1. Basic Overlay Analysis Algorithm Running on Each Computing Node.
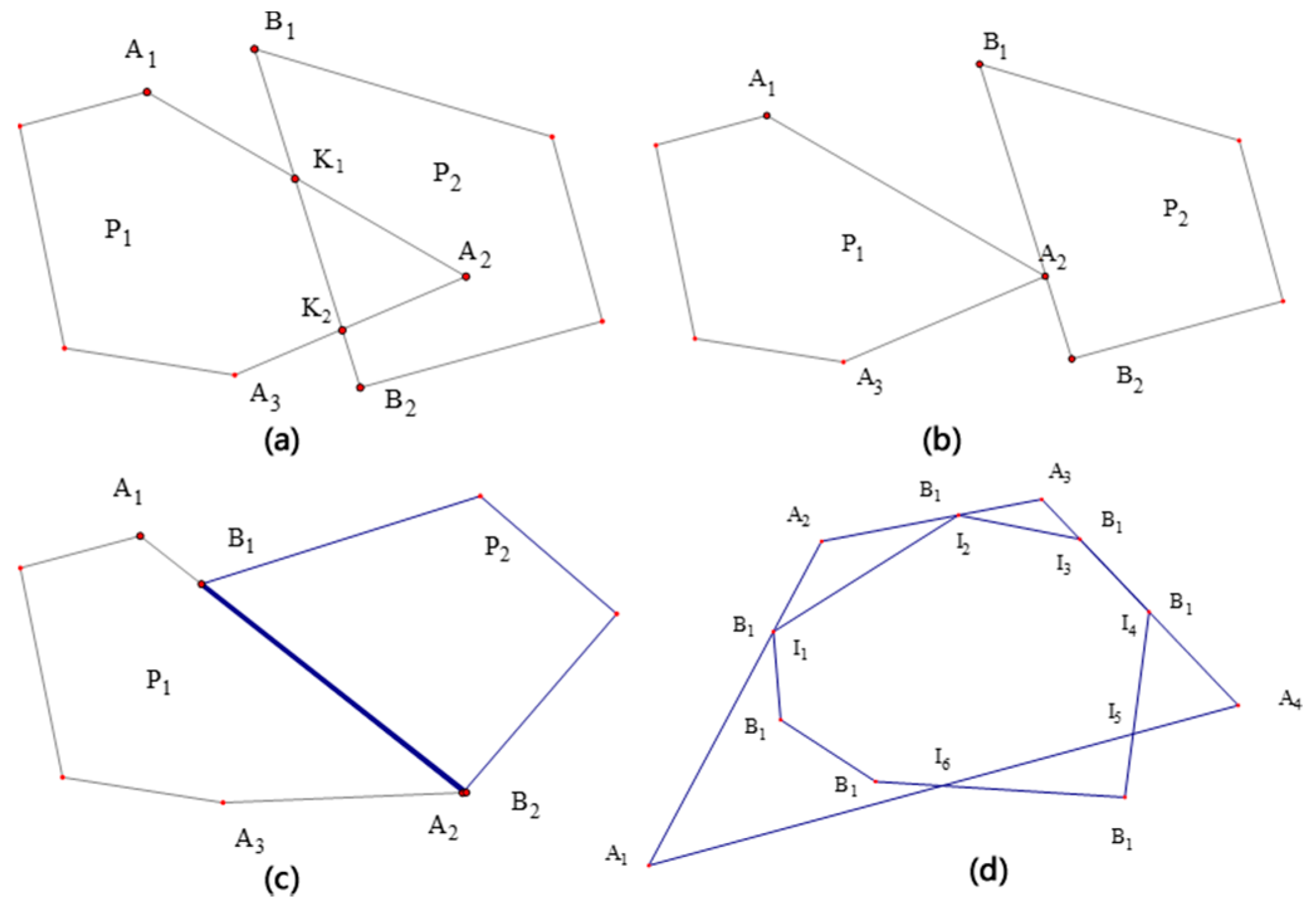
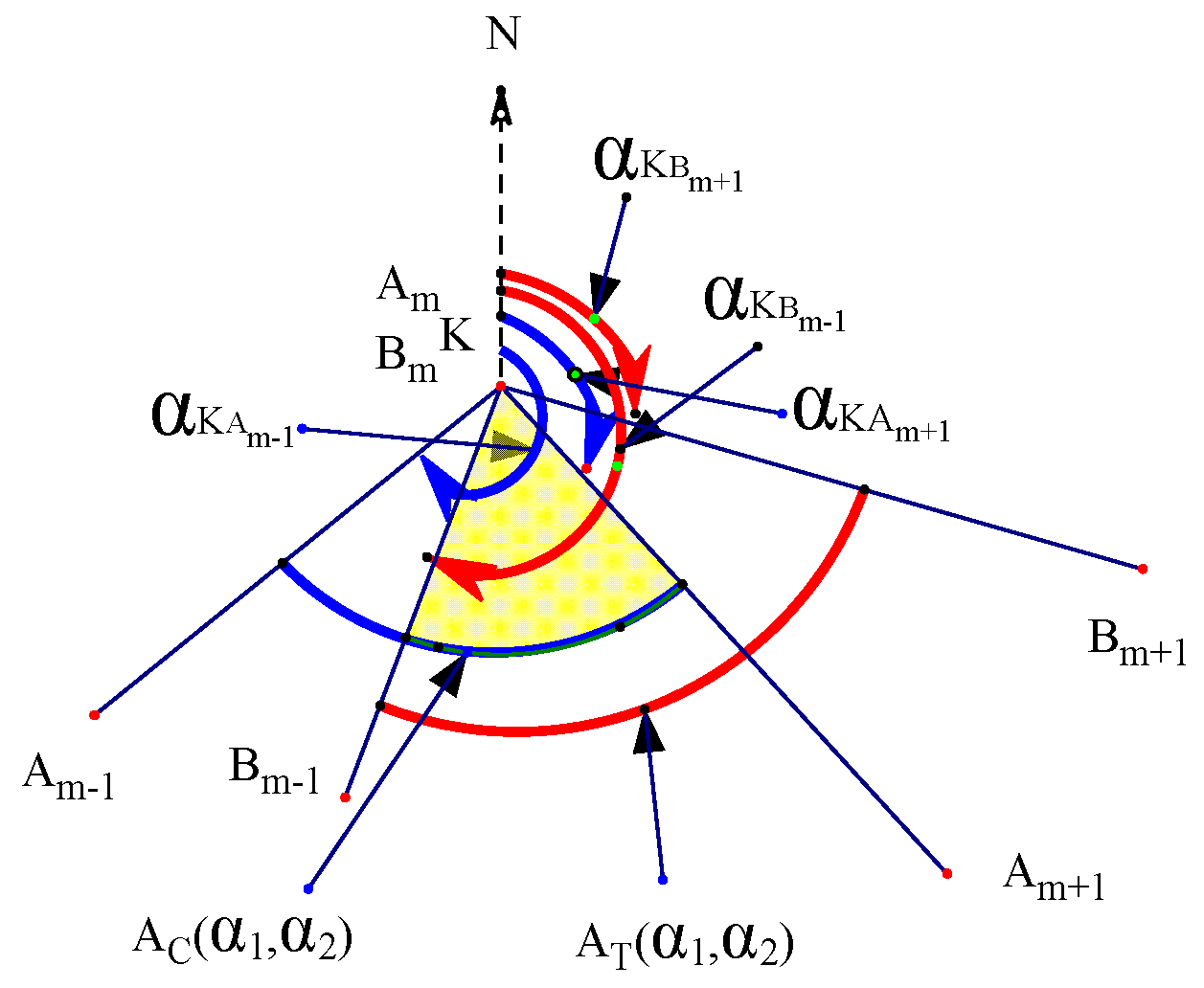
3.1.1. Hormann Algorithm and Improvement of Intersection Degeneration Problem.
- Calculating the intersections of the clipped and target polygons
- Judging the entry and exit of the intersection point by the vector line segment (judging the entry or exit point of the intersection point) and adding the entry point to the vertex sequence of the clipping result polygon
- Comparing the azimuth intervals of the degenerated vertices of the intersection points and adding the overlapping vertices of the azimuth intervals to the vertex sequence of the clipping result polygon
- Forming a new polygon (clipping result) in accordance with the sequence of vertices
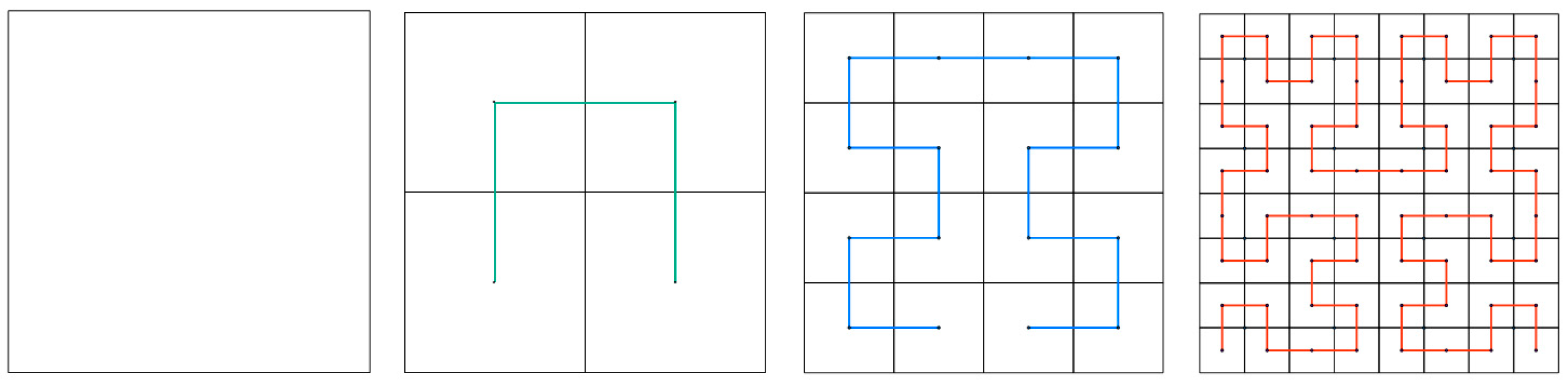
3.1.2. Effect of Shape Complexity on Parallel Clipping Efficiency
3.2. Data Balancing and Partitioning Method that Considers Polygon Shape Complexity
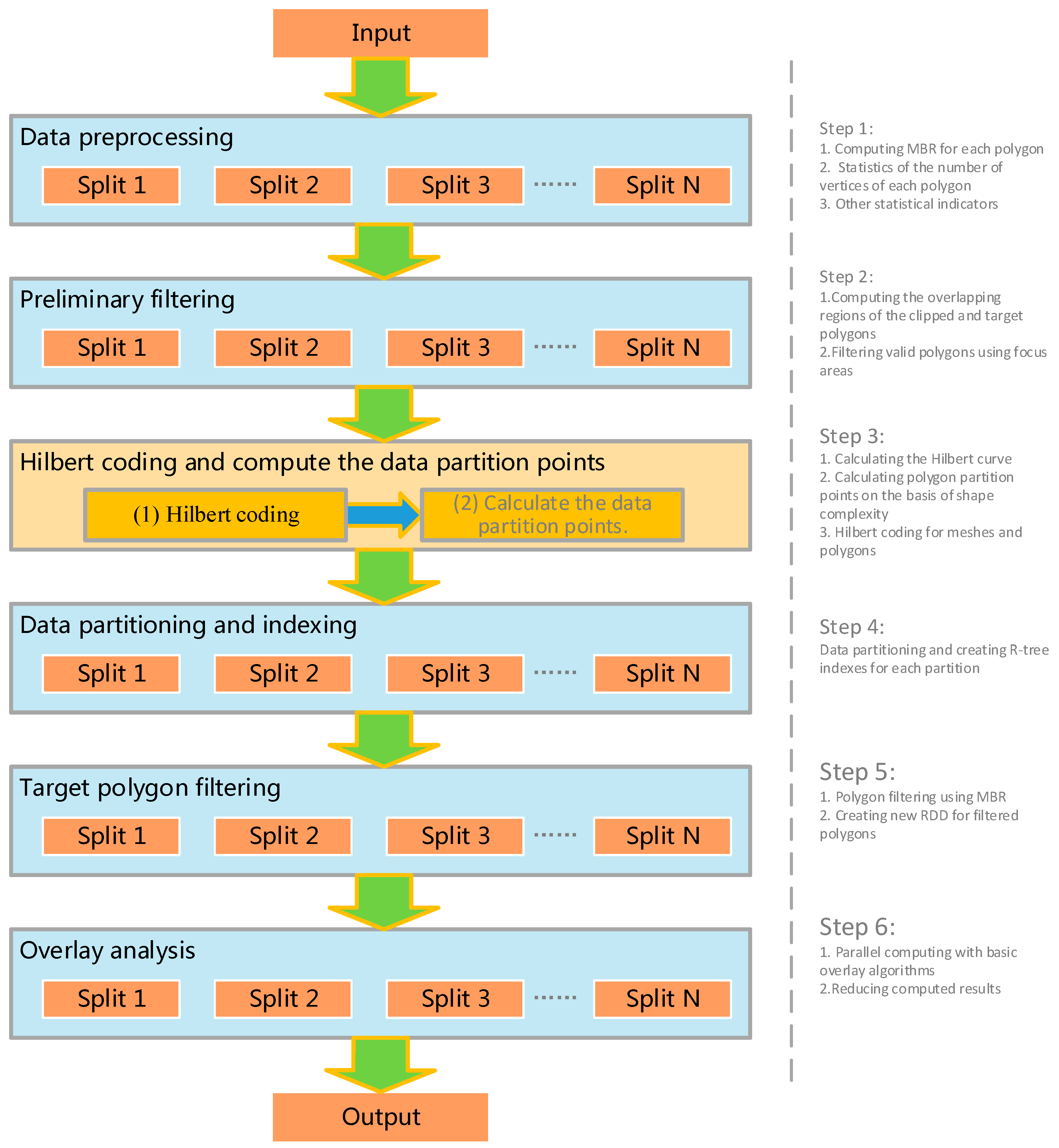
3.2.1. Data Partitioning and Loading Strategy
- (1)
- Determine the order of the Hilbert curve, generate the Hilbert grid and the Hilbert curve, number the Hilbert curve sequentially, and obtain the Hilbert grid coding set,
- (2)
- Calculate the polygon MBR center point, find its corresponding mesh, and use the Hilbert coding of the mesh as the Hilbert coding of the polygon to obtain the Hilbert coding set of the polygon,
- (3)
- In accordance with the number of computing nodes M, divide the Hilbert coding set of the polygons into M partitions, and calculate the start–stop coding of the Hilbert coding of polygons in each partition.
- (4)
- Merge the grids of the Hilbert partitions to obtain partition polygons
3.2.2. R-tree Index Construction
3.3. Process Design of Distributed Parallel Overlay Analysis
3.4. Algorithmic Analysis
4. Experimental Study
4.1. Experimental Design
4.1.1. Computing Equipment
4.1.2. Experimental Data
4.1.3. Experimental Scene
- How much better will Spark parallel computing improve the performance of overlay analysis compared to desktop software?
- How much better is the performance of the parallel overlay analysis algorithm proposed in this paper compared with the direct use of the spark computing paradigm?
- How much influence does the complexity difference of a geographic polygon have on parallel overlay analysis?
4.2. Test Process and Results
4.2.1. Compare the Performance Differences of Four Modes: ArcMap, Spark_original, Spark_NoComlexity and Spark_improved
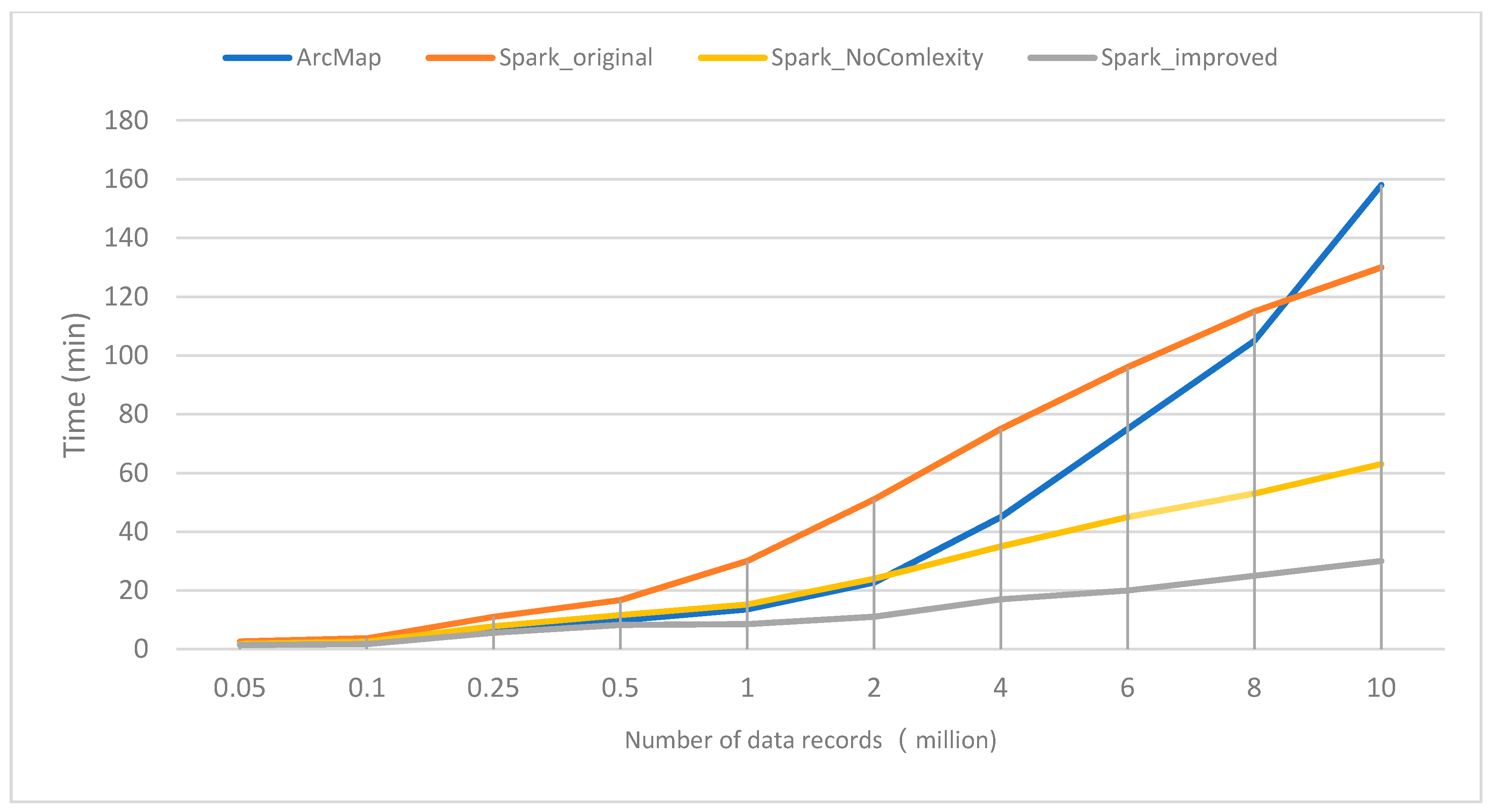
- (1)
- When the number of polygons is less than 10 million, the efficiency of Spark_original mode is even lower than that of ArcMap mode. When the number of polygons is more than 50,000, the time-consumption of the Spark_improved mode is less than that of the ArcMap mode. When the number of polygons exceeds 1 million, ArcMap mode consumes twice as much time as the Spark_improved mode. As the amount of data increases, the time-consumption of the ArcMap mode increases dramatically, and the time-consumption curve of Spark_improved mode is still relatively flat.
- (2)
- The efficiency of Spark_original mode is lower than that of Spark_improved mode, and the more polygons there are, the more obvious it is. This shows that the efficiency of overlay analysis using Spark directly is very low, and the algorithm optimization must be carried out according to the characteristics of spatial data and geographical calculation.
- (3)
- By comparing the time-consumption curves, Spark_improved takes almost half as much time as Spark_NoComlexity, which is better than I thought. I think it may be related to my experimental data: in Section 4.1.2, I have found that there are many polygons with high shape complexity in the experimental data. Maybe many big polygons are partitioned into the same computational partition, which leads to data skew.
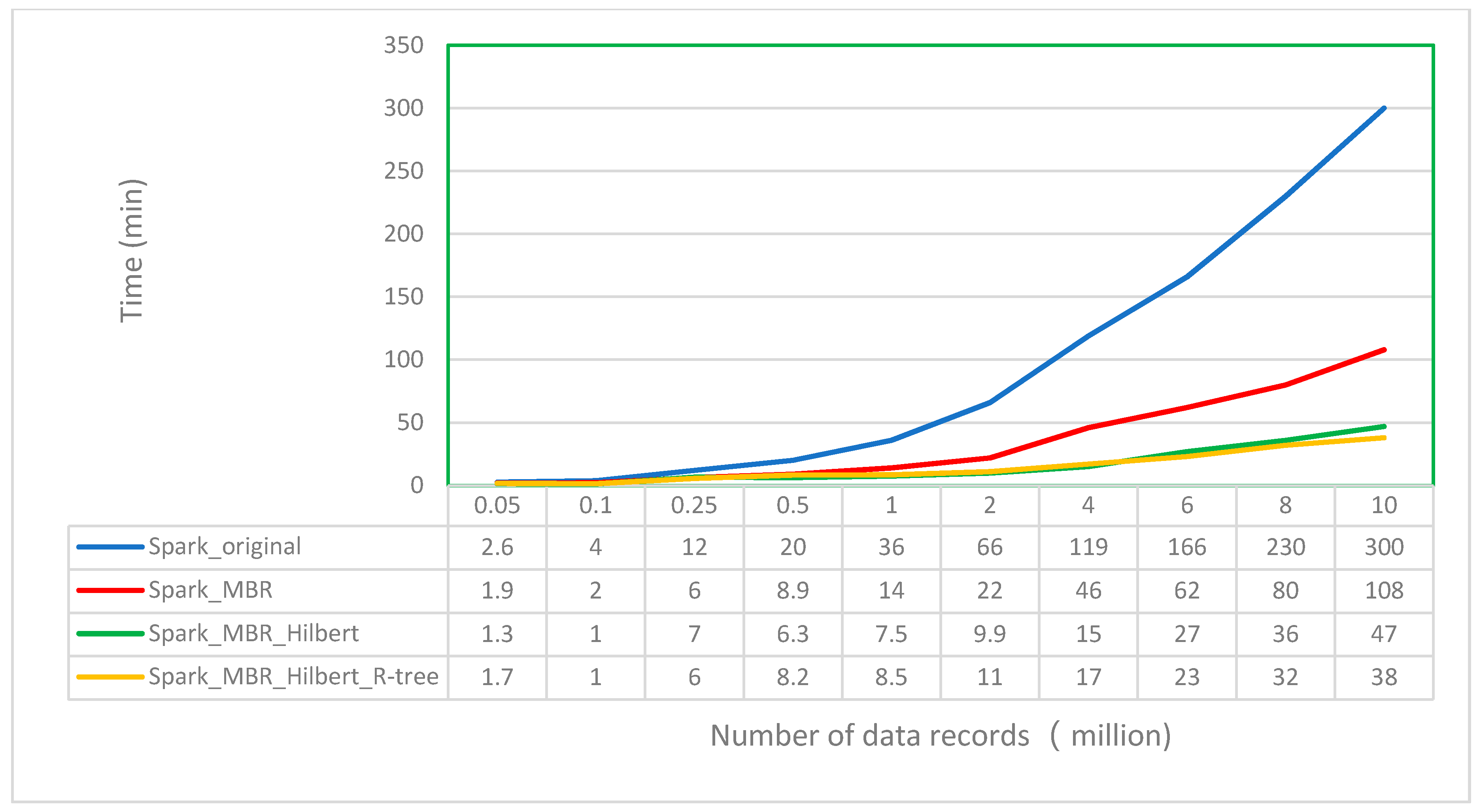
4.2.2. Compare the Performance Differences of Four Modes: Spark_original, Spark_MBR, Spark_MBR_Hilbert and Spark_MBR_Hilbert_R-tree
- (1)
- After only adopting the MBR filtering strategy, the efficiency of overlay computation is increased by two to four times. Therefore, this strategy filters a large number of invalid overlay computations. Specific efficiency improvement is related to the size, shape, and spatial distribution of polygons in the target and clipped layers.
- (2)
- The Hilbert partitioning algorithm based on polygon graphic complexity is used to allocate the data of each computing node. When the amount of data reaches millions, the computing performance can be doubled. As the data amount increases, the computational performance advantage becomes more evident. The experimental data verify that the spatial aggregation characteristics of Hilbert partitioning that considers polygon complexity can considerably improve spatial analysis algorithms.
- (3)
- Index construction can generally improve the efficiency of data access, but index construction itself can result in a certain amount of computational overhead. After adding the R-tree index strategy based on the first two steps, the overlay calculation time of each order of magnitude increases slightly when the amount of data is less than 5 million. When the amount of data exceeds 5 million, the overlay calculation time decreases compared with the case without the R-tree index. Therefore, the data access time saved after the R-tree index is established offsets the time consumed by the index itself.
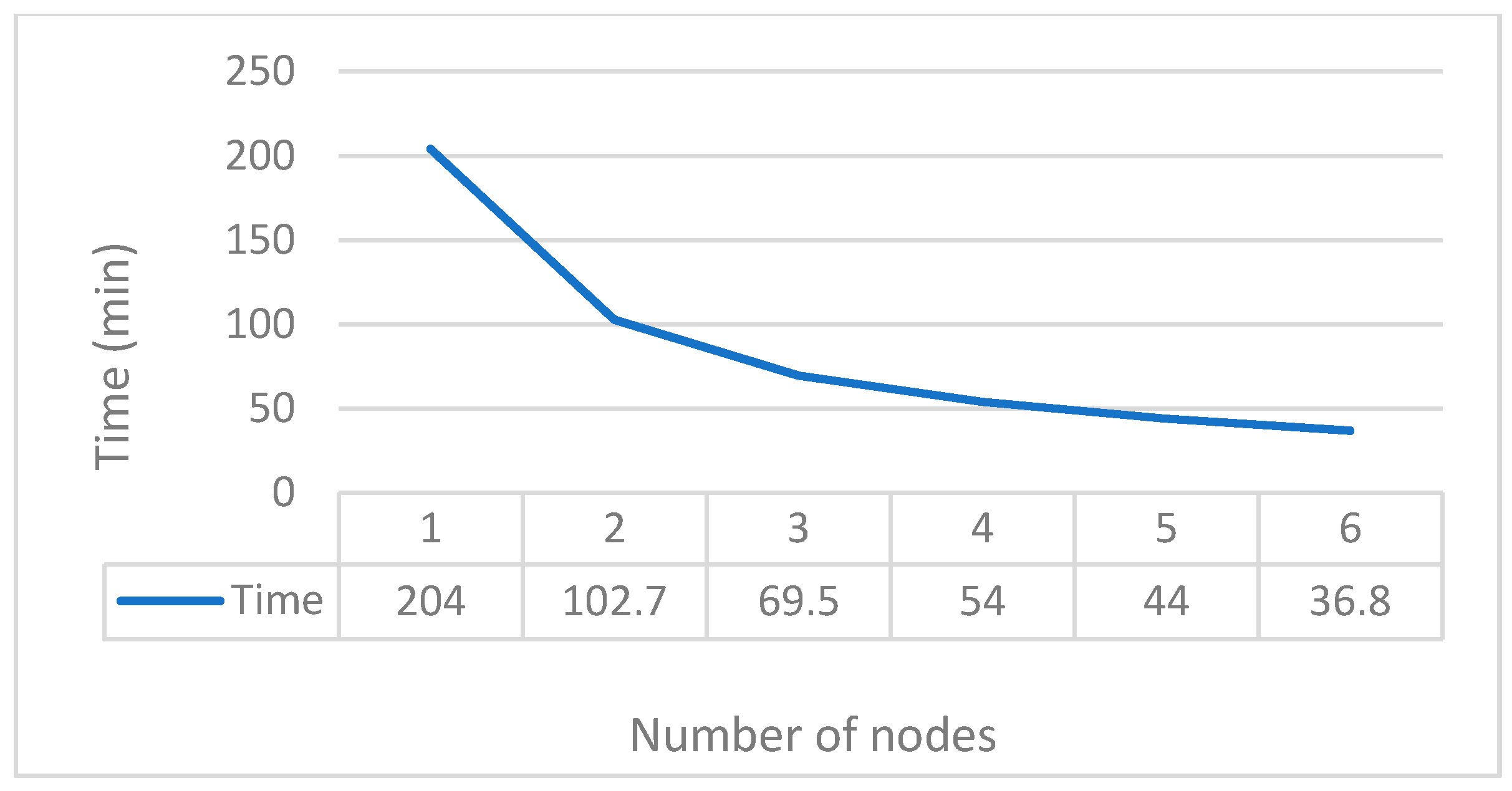
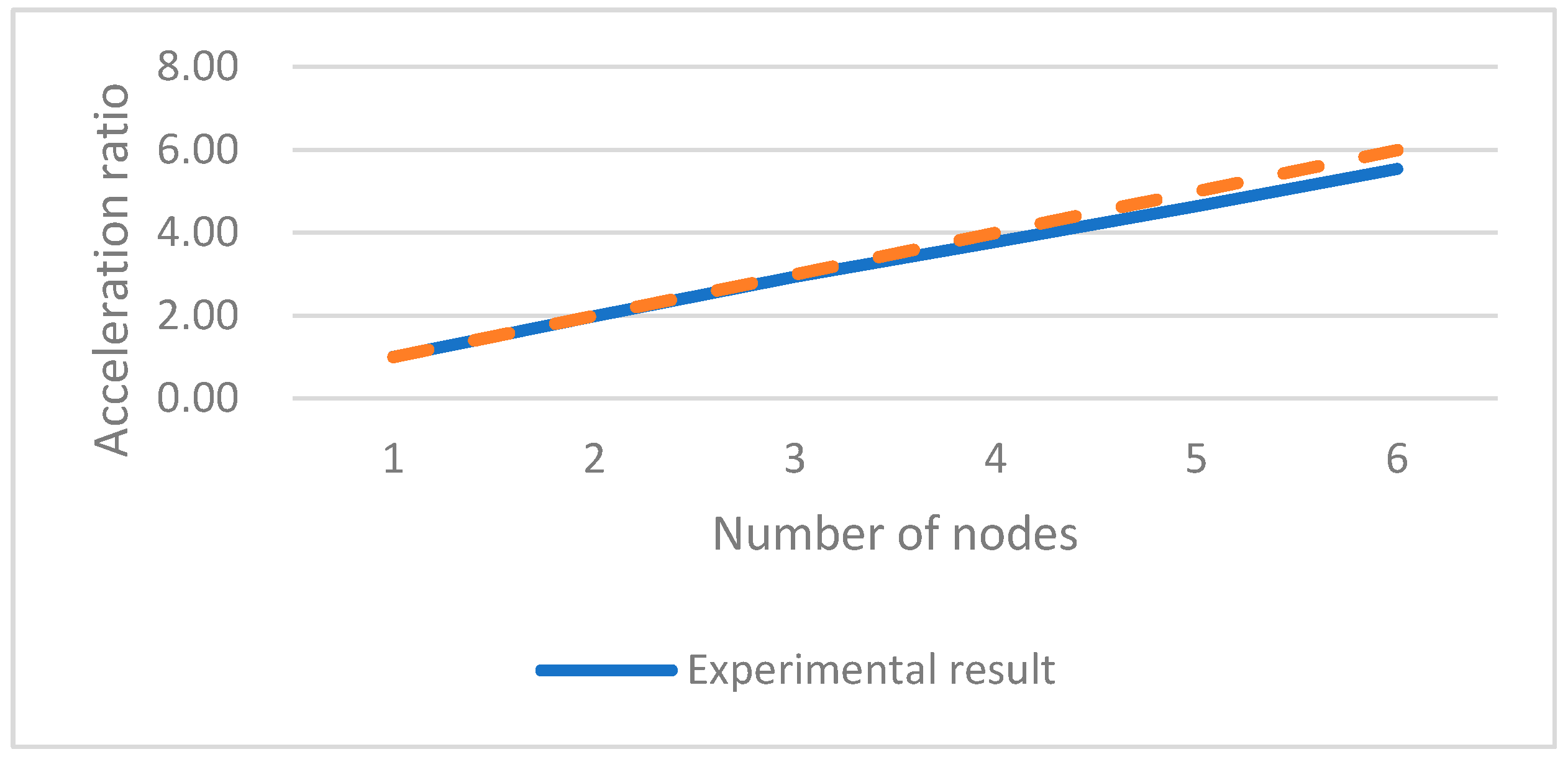
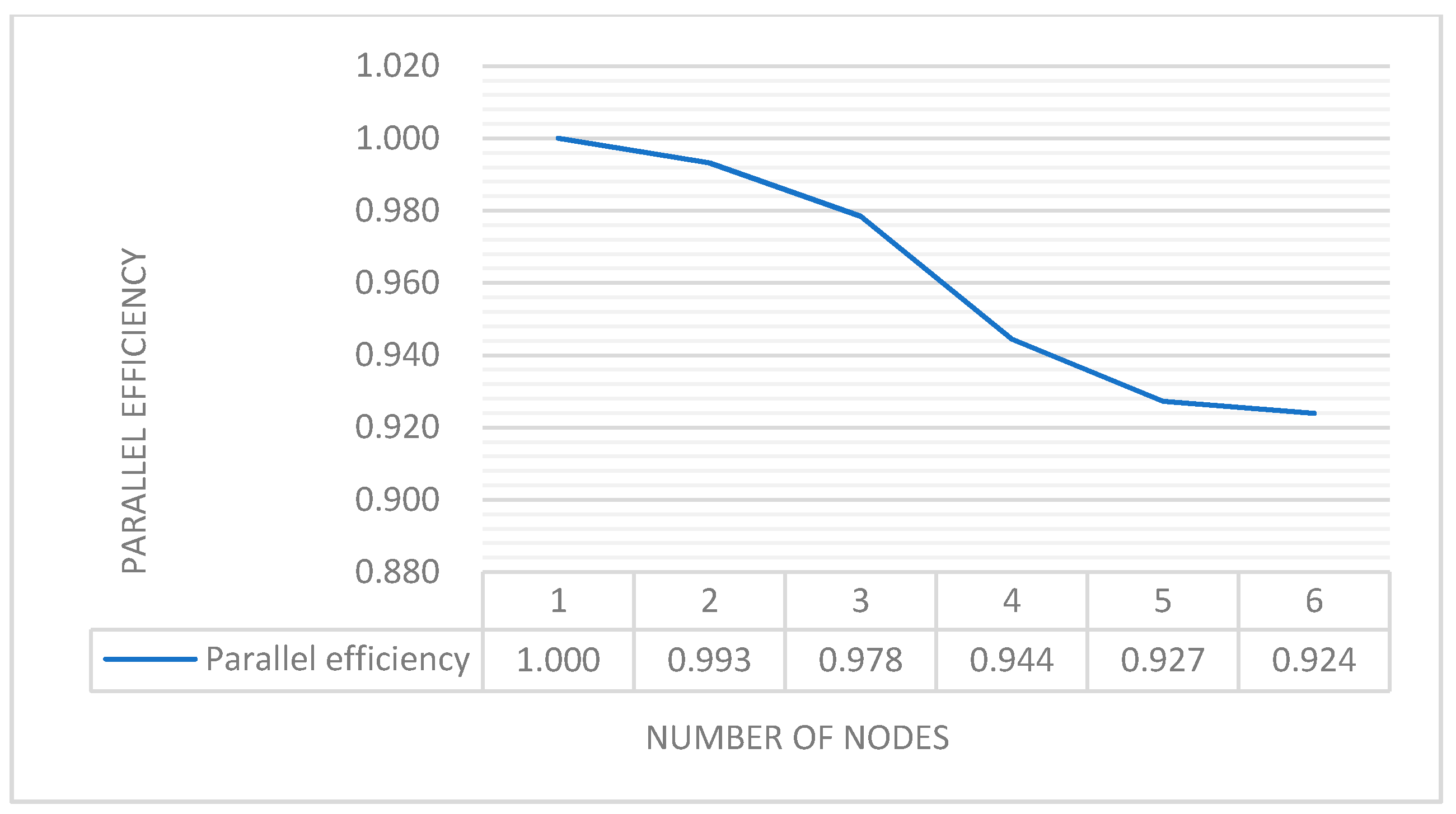
4.2.3. Cluster Acceleration Performance Testing of the Proposed Algorithm
4.3. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Zhong, E.; Lu, H.; Guo, H.; Long, L. An effective algorithm for lines and polygons overlay analysis using uniform spatial grid indexing. In Proceedings of the 2015 2nd IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services (ICSDM), Fuzhou, China, 8–10 July 2015; pp. 175–179. [Google Scholar]
- Puri, S.; Prasad, S.K. Efficient parallel and distributed algorithms for GIS polygonal overlay processing. In Proceedings of the 2013 IEEE International Symposium on Parallel & Distributed Processing, Workshops and Phd Forum, Cambridge, MA, USA, 20–24 May 2013; pp. 2238–2241. [Google Scholar]
- van Kreveld, M.; Nievergelt, J.; Roos, T.; Widmayer, P. Algorithmic Foundations of Geographic Information Systems; Springer: New York, NY, USA, 1997; Volume 1340. [Google Scholar]
- Li, Q.; Li, D. Big data GIS. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 641–644. [Google Scholar]
- Li, D.R.; Cao, J.J.; Yuan, Y. Big data in smart cities. Sci. China Inf. Sci. 2015, 58, 108101. [Google Scholar] [CrossRef]
- Yang, C.; Goodchild, M.; Huang, Q.; Nebert, D.; Raskin, R.; Xu, Y.; Bambacus, M.; Fay, D. Spatial cloud computing: How can the geospatial sciences use and help shape cloud computing? Int. J. Digit. Earth 2011, 4, 305–329. [Google Scholar] [CrossRef]
- Greiner, G.; Hormann, K. Efficient clipping of arbitrary polygons. ACM Trans. Graph. (TOG) 1998, 17, 71–83. [Google Scholar] [CrossRef]
- Rossignac, J. Shape complexity. Vis. Comput. 2005, 21, 985–996. [Google Scholar] [CrossRef]
- Day, H. Evaluations of subjective complexity, pleasingness and interestingness for a series of random polygons varying in complexity. Percept. Psychophys. 1967, 2, 281–286. [Google Scholar] [CrossRef]
- Tilove, R.B. Line/polygon classification: A study of the complexity of geometric computation. IEEE Comput. Graph. Appl. 1981, 1, 75–88. [Google Scholar] [CrossRef]
- Chen, Y.; Sundaram, H. Estimating complexity of 2D shapes. In Proceedings of the 2005 IEEE 7th Workshop on Multimedia Signal Processing, Shanghai, China, 30 October–2 November 2005; pp. 1–4. [Google Scholar]
- Huang, C.-W.; Shih, T.-Y. On the complexity of point-in-polygon algorithms. Comput. Geosci. 1997, 23, 109–118. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Peitgen, H.-O.; Jürgens, H.; Saupe, D. Chaos and Fractals: New Frontiers of Science; Springer Science & Business Media: New York, NY, USA, 1992. [Google Scholar]
- Faloutsos, C.; Kamel, I. Beyond uniformity and independence: Analysis of R-trees using the concept of fractal dimension. In Proceedings of the Thirteenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database Systems, Minneapolis, MN, USA, 24–27 May 1994; pp. 4–13. [Google Scholar]
- Brinkhoff, T.; Kriegel, H.-P.; Schneider, R.; Braun, A. Measuring the Complexity of Polygonal Objects. In Proceedings of the ACM-GIS, Baltimore, MD, USA, 1–2 December 1995; p. 109. [Google Scholar]
- Bryson, N.; Mobolurin, A. Towards modeling the query processing relevant shape complexity of 2D polygonal spatial objects. Inf. Softw. Technol. 2000, 42, 357–365. [Google Scholar] [CrossRef]
- Ying, F.; Mooney, P.; Corcoran, P.; Winstanley, A.C. A model for progressive transmission of spatial data based on shape complexity. Sigspat. Spec. 2010, 2, 25–30. [Google Scholar] [CrossRef]
- Weiler, K.; Atherton, P. Hidden surface removal using polygon area sorting. ACM SIGGRAPH Comput. Graph. 1977, 11, 214–222. [Google Scholar] [CrossRef]
- Vatti, B.R. A generic solution to polygon clipping. Commun. ACM 1992, 35, 56–63. [Google Scholar] [CrossRef]
- Wang, H.; Chong, S. A high efficient polygon clipping algorithm for dealing with intersection degradation. J. Southeast Univ. 2016, 4, 702–707. [Google Scholar]
- Zhang, S.Q.; Zhang, C.; Yang, D.H.; Zhang, J.Y.; Pan, X.; Jiang, C.L. Overlay of Polygon Objects and Its Parallel Computational Strategies Using Simple Data Model. Geogr. Geo-Inf. Sci. 2013, 29, 43–46. [Google Scholar]
- Chen, Z.; Ma, L.; Liang, W. Polygon Overlay Analysis Algorithm Based on Monotone Chain and STR Tree in the Simple Feature Model. In Proceedings of the 2010 International Conference on Electrical & Control Engineering, Wuhan, China, 25–27 June 2010. [Google Scholar]
- Wang, J. An Efficient Algorithm for Complex Polygon Clipping. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 369–372. [Google Scholar]
- Guest, M. An overview of vector and parallel processors in scientific computation. J. Comput. Phys. Commun. 1989, 57, 560. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Liao, H.; Li, C. Improving the performance of GIS polygon overlay computation with MapReduce for spatial big data processing. Clust. Comput. 2015, 18, 507–516. [Google Scholar] [CrossRef]
- Zheng, Z.; Luo, C.; Ye, W.; Ning, J. Spark-Based Iterative Spatial Overlay Analysis Method. In Proceedings of the 2017 International Conference on Electronic Industry and Automation (EIA 2017), Suzhou, China, 23–25 June 2017. [Google Scholar]
- Xiao, Z.; Qiu, Q.; Fang, J.; Cui, S. A vector map overlay algorithm based on distributed queue. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 6098–6101. [Google Scholar]
- Eldawy, A.; Mokbel, M.F. A demonstration of spatialhadoop: An efficient mapreduce framework for spatial data. Proc. VLDB Endow. 2013, 6, 1230–1233. [Google Scholar] [CrossRef]
- Eldawy, A.; Alarabi, L.; Mokbel, M.F. Spatial partitioning techniques in SpatialHadoop. Proc. VLDB Endow. 2015, 8, 1602–1605. [Google Scholar] [CrossRef]
- Eldawy, A.; Mokbel, M.F. Spatialhadoop: A mapreduce framework for spatial data. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Korea, 13–17 April 2015; pp. 1352–1363. [Google Scholar]
- Lenka, R.K.; Barik, R.K.; Gupta, N.; Ali, S.M.; Rath, A.; Dubey, H. Comparative analysis of SpatialHadoop and GeoSpark for geospatial big data analytics. In Proceedings of the 2016 2nd International Conference on Contemporary Computing and Informatics (IC3I), Noida, India, 14–17 December 2016; pp. 484–488. [Google Scholar]
- Yu, J.; Wu, J.; Sarwat, M. GeoSpark: A cluster computing framework for processing large-scale spatial data. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2015; pp. 1–4. [Google Scholar]
- Yu, J.; Wu, J.; Sarwat, M. A demonstration of GeoSpark: A cluster computing framework for processing big spatial data. In Proceedings of the 2016 IEEE 32nd International Conference on Data Engineering (ICDE), Helsinki, Finland, 16–20 May 2016; pp. 1410–1413. [Google Scholar]
- Yu, J.; Zhang, Z.; Sarwat, M. Spatial data management in apache spark: The geospark perspective and beyond. Geoinformatica 2019, 23, 37–78. [Google Scholar] [CrossRef]
- Luitjens, J.; Berzins, M.; Henderson, T. Parallel space-filling curve generation through sorting: Research Articles. Concurr. Comput. Pract. Exp. 2010, 19, 1387–1402. [Google Scholar] [CrossRef]
- Kim, K.-C.; Yun, S.-W. MR-Tree: A cache-conscious main memory spatial index structure for mobile GIS. In Proceedings of the International Workshop on Web and Wireless Geographical Information Systems, Goyang, Korea, 26–27 November 2004; pp. 167–180. [Google Scholar]
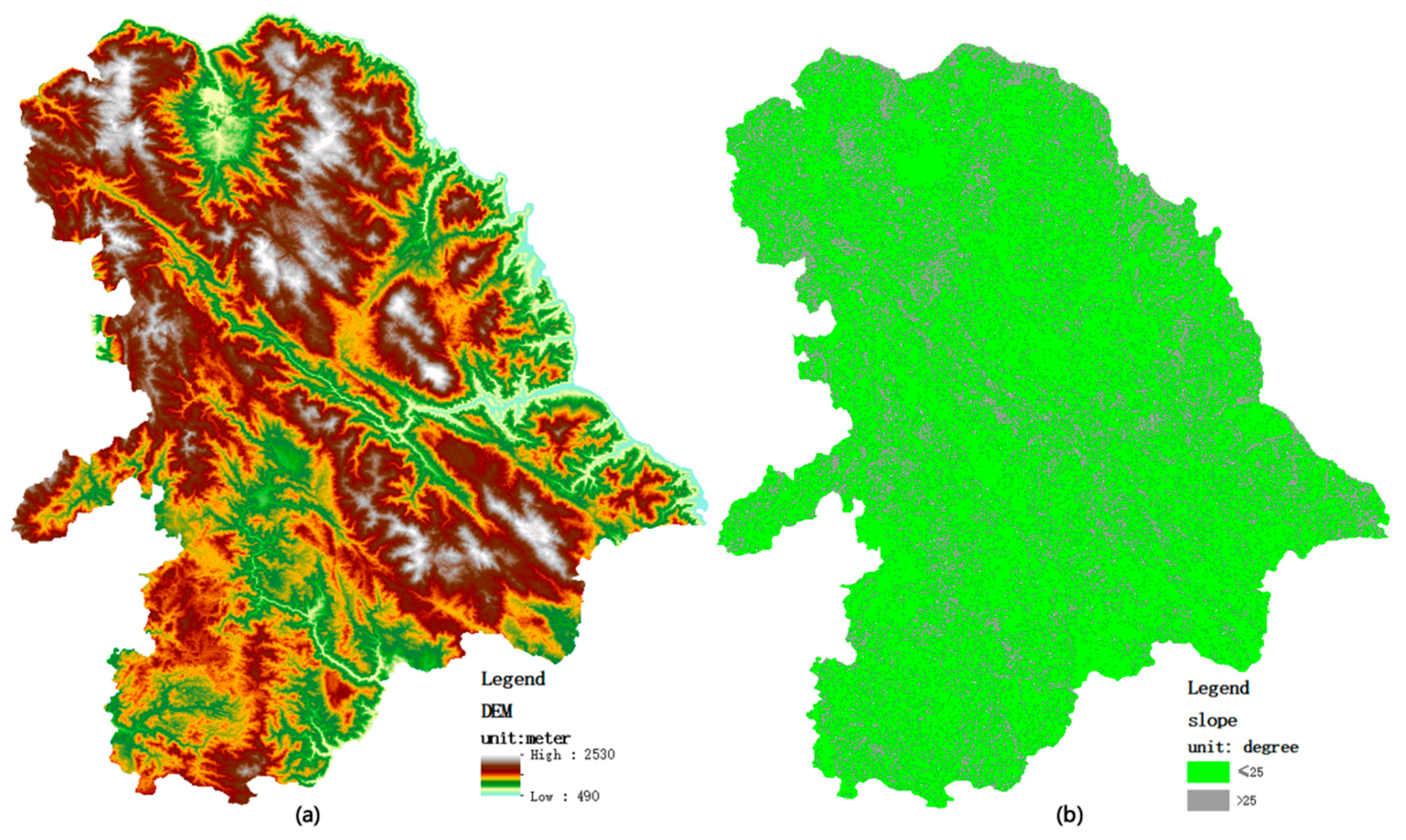
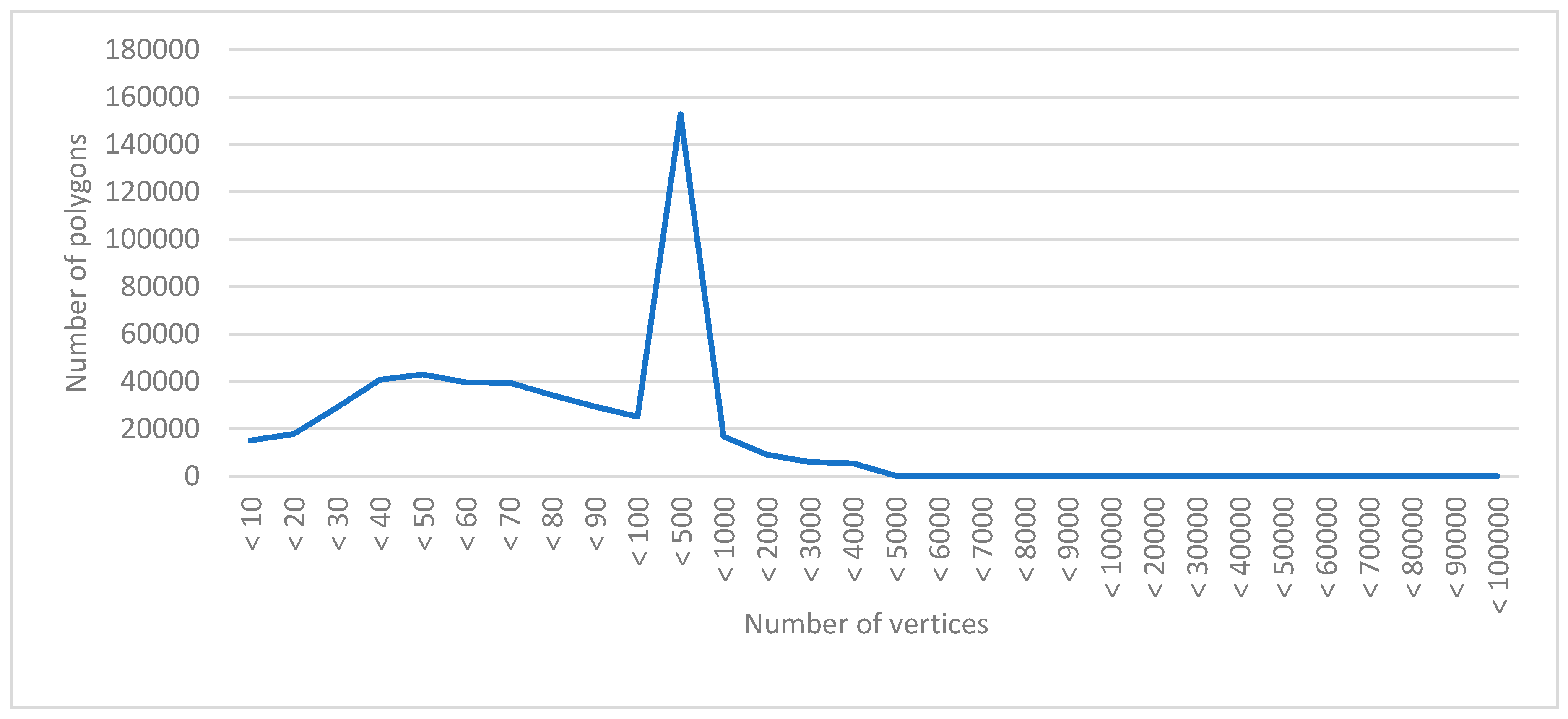
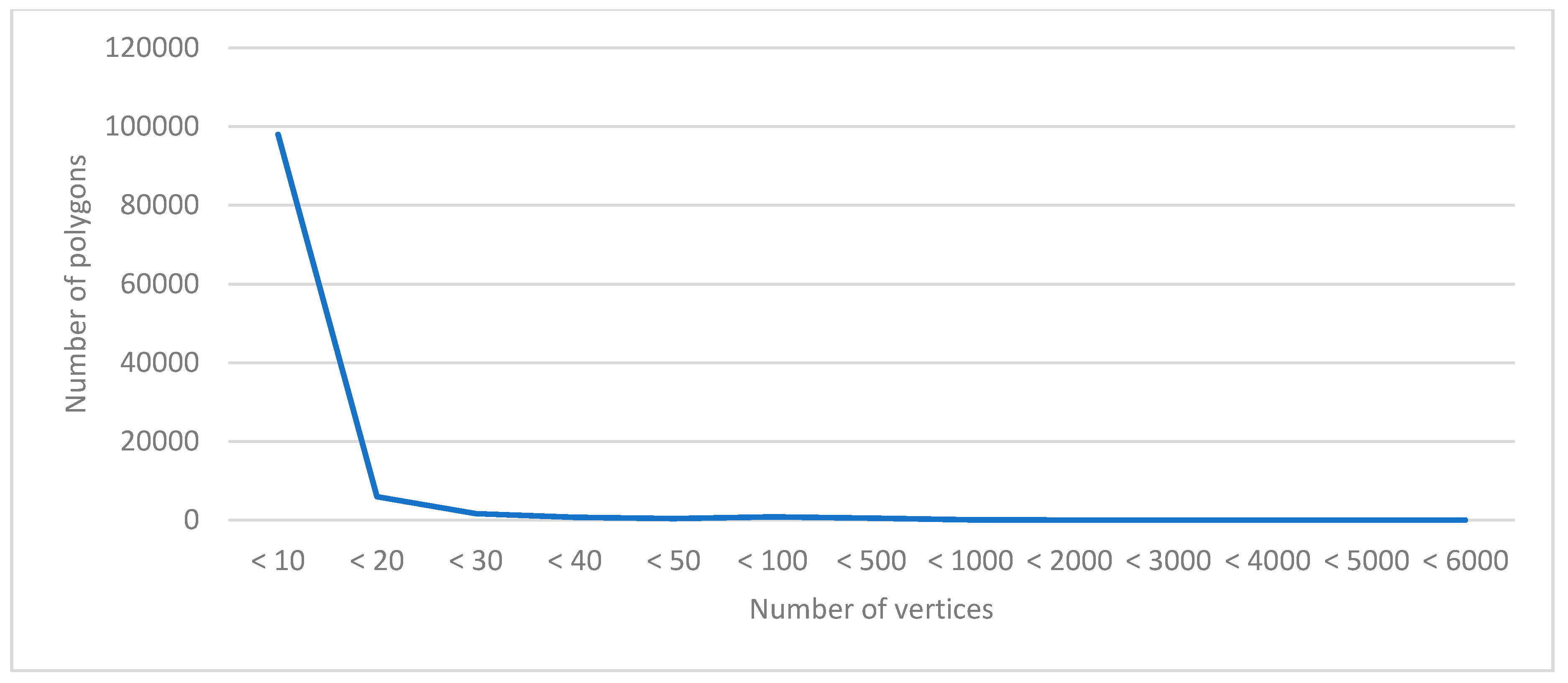
| Equipment | Num | Hardware Configuration | Operating System | Software | Remark |
|---|---|---|---|---|---|
| portable computer | 1 | Thinkpad T470p, 8 vcore, 16 G RAM, SSD (Solid State Drive) | Windows 10 | ArcMap 10.4.1 | Single computer experiment for desktop overlay analysis. |
| X86 Server | 6 | DELL R720, 24 core, 64 G RAM, HDD (Hard Disk Drive) | Centos7 | Hadoop 2.7, Spark 2.3.1 | Spark Computing Cluster |
| Mode Abbreviation | Equipment | Data Storage Mode | Notes |
|---|---|---|---|
| ArcMap | 1 portable computer with ArcMap | Local File System | Use the clip tool of Toolbox to perform overlay analysis on the portable computer |
| Spark_original | Multiple X86 servers with Spark | HDFS | Directly partition the data randomly and do parallel overlay analysis without any improvement. |
| Spark_improved | Multiple X86 servers with Spark | HDFS | Completely implement parallel overlay analysis according to the process of Section 3.3. Hilbert partitioning method considering graph complexity |
| Spark_NoComlexity | Multiple X86 servers with Spark | HDFS | Except that the complexity of polygon graphics is not considered, all of them are the same as the Spark_improved mode. |
| Spark_MBR | Multiple X86 servers with Spark | HDFS | Based on the Spark_original model, MBR filtering is performed first, and then parallel overlay analysis is performed. |
| Spark_MBR_Hilbert | Multiple X86 servers with Spark | HDFS | Based on the Spark_original model, MBR filtering and a Hilbert partitioning operation are added. |
| Spark_MBR_Hilbert_R-tree | Multiple X86 servers with Spark | HDFS | Based on the Spark_original model, MBR filtering, Hilbert partitioning and R-tree index creation operation are added. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Jin, B.; Fan, H.; Song, W.; Zhou, S.; Jiang, Y. High-Performance Overlay Analysis of Massive Geographic Polygons That Considers Shape Complexity in a Cloud Environment. ISPRS Int. J. Geo-Inf. 2019, 8, 290. https://doi.org/10.3390/ijgi8070290
Zhao K, Jin B, Fan H, Song W, Zhou S, Jiang Y. High-Performance Overlay Analysis of Massive Geographic Polygons That Considers Shape Complexity in a Cloud Environment. ISPRS International Journal of Geo-Information. 2019; 8(7):290. https://doi.org/10.3390/ijgi8070290
Chicago/Turabian StyleZhao, Kang, Baoxuan Jin, Hong Fan, Weiwei Song, Sunyu Zhou, and Yuanyi Jiang. 2019. "High-Performance Overlay Analysis of Massive Geographic Polygons That Considers Shape Complexity in a Cloud Environment" ISPRS International Journal of Geo-Information 8, no. 7: 290. https://doi.org/10.3390/ijgi8070290
APA StyleZhao, K., Jin, B., Fan, H., Song, W., Zhou, S., & Jiang, Y. (2019). High-Performance Overlay Analysis of Massive Geographic Polygons That Considers Shape Complexity in a Cloud Environment. ISPRS International Journal of Geo-Information, 8(7), 290. https://doi.org/10.3390/ijgi8070290




