GeoSOT-Based Spatiotemporal Index of Massive Trajectory Data
Abstract
:1. Introduction
2. Related Work
3. Materials and Methods
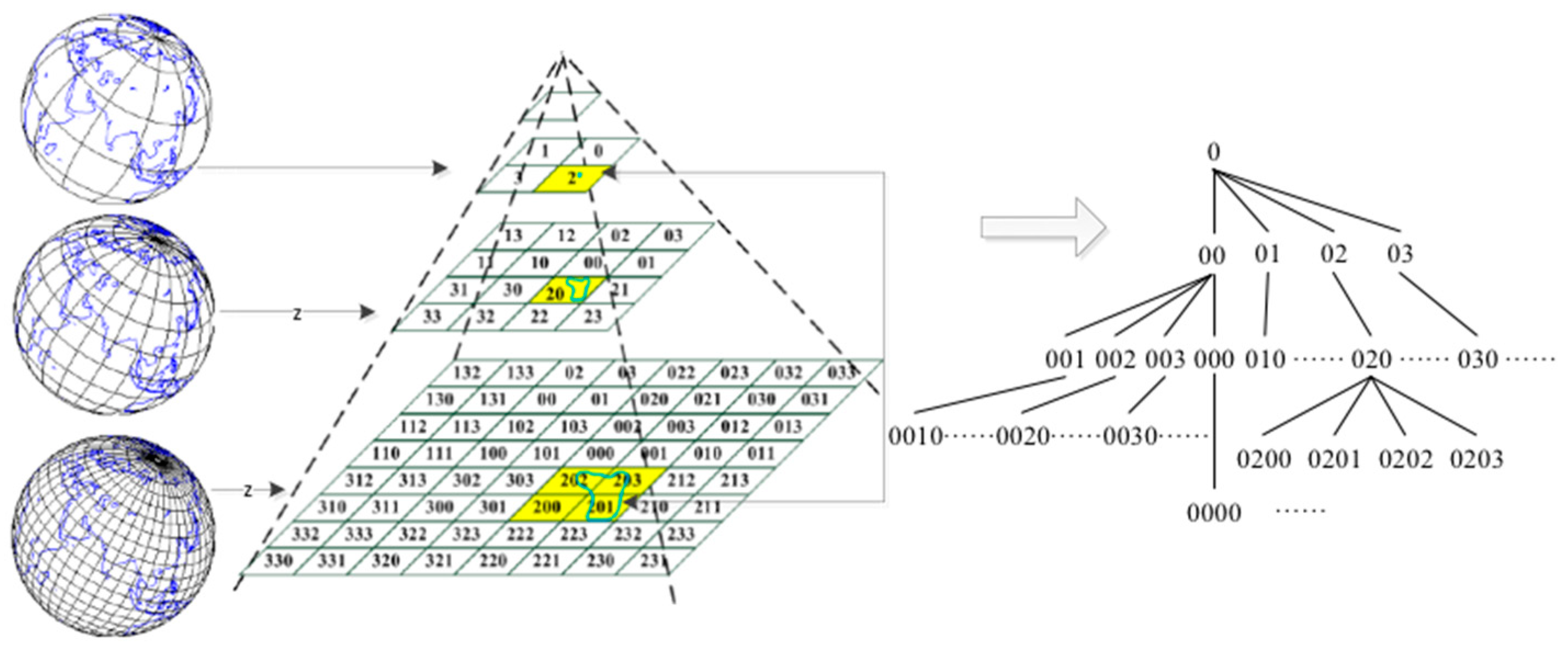
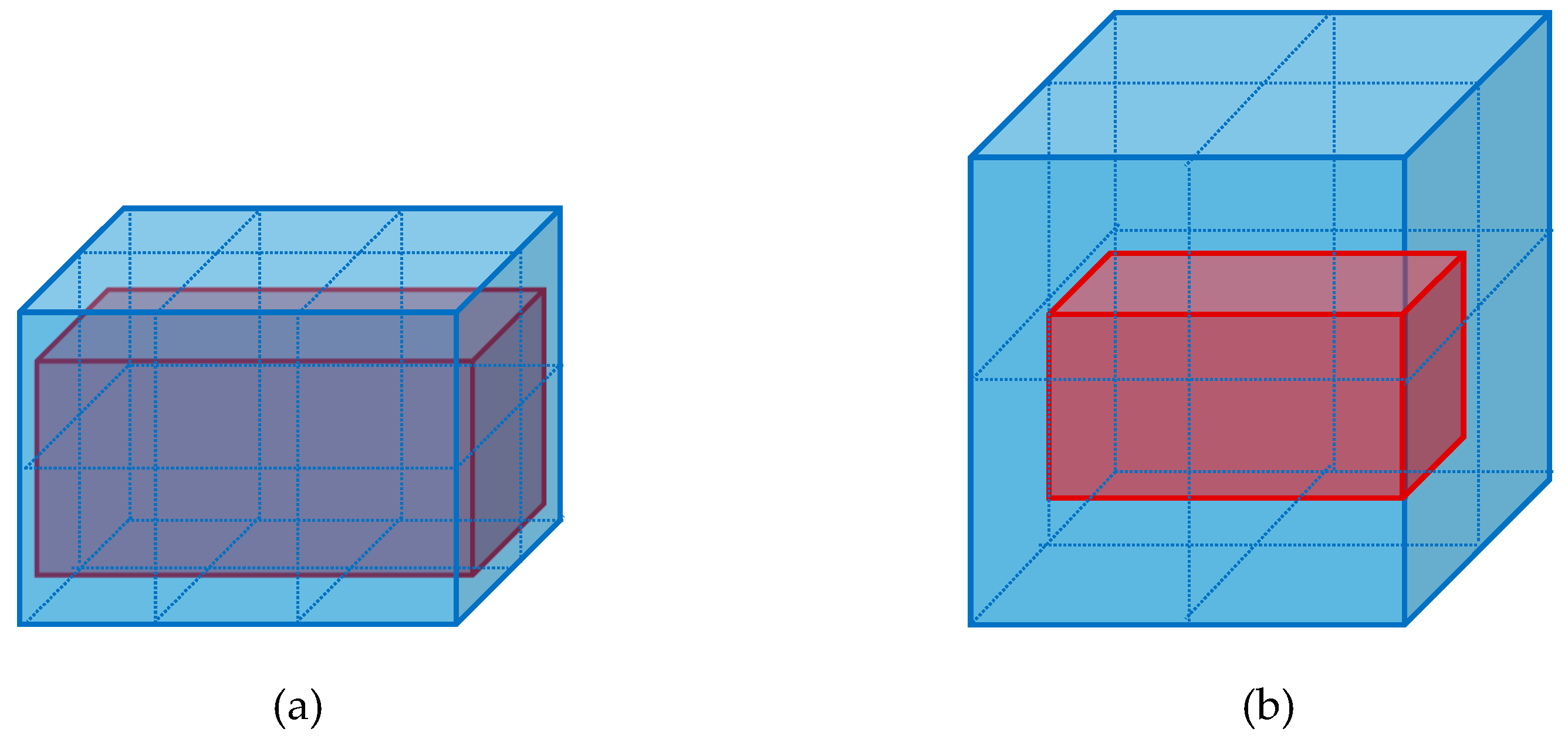
3.1. GeoSOT Global Subdivision Model
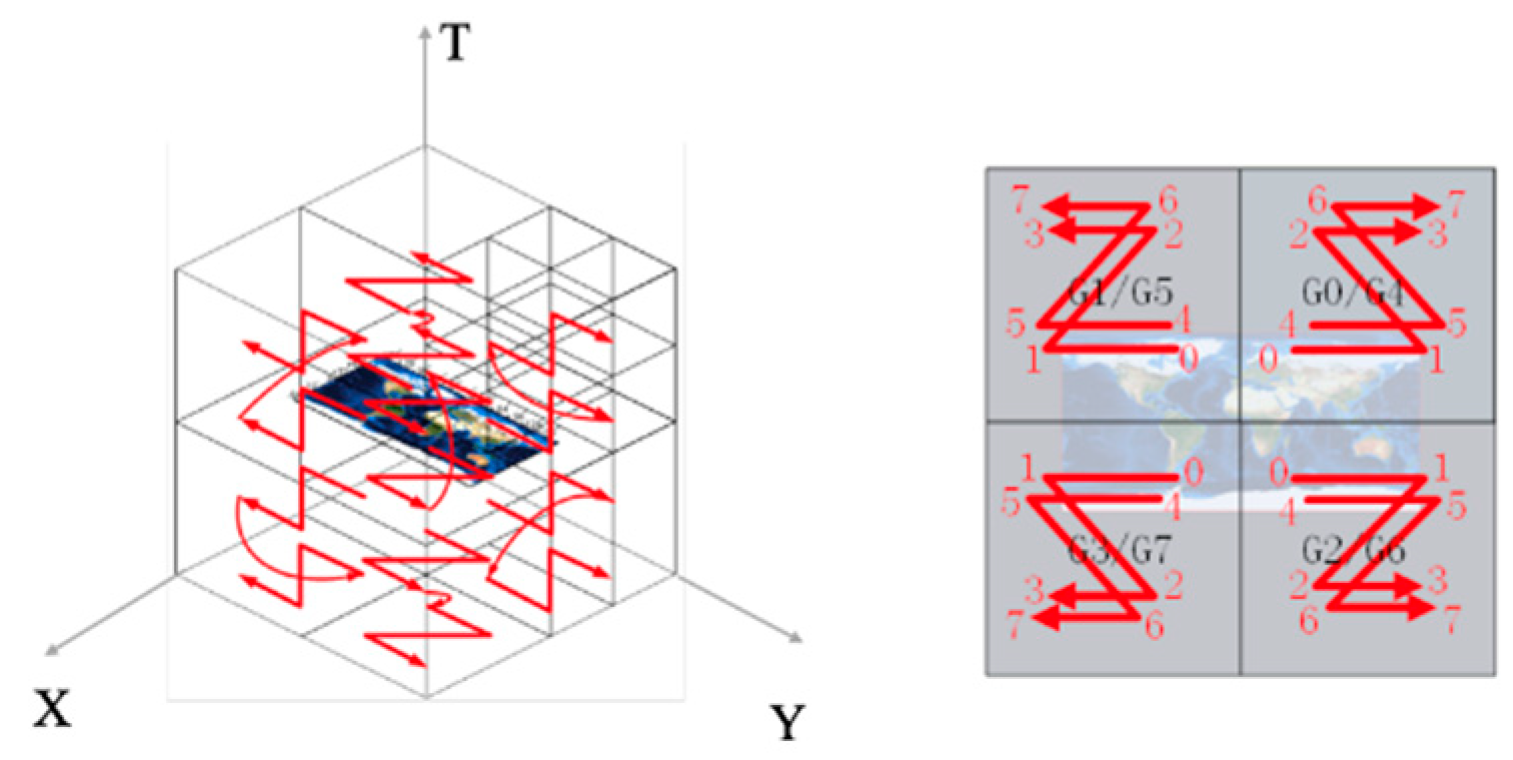
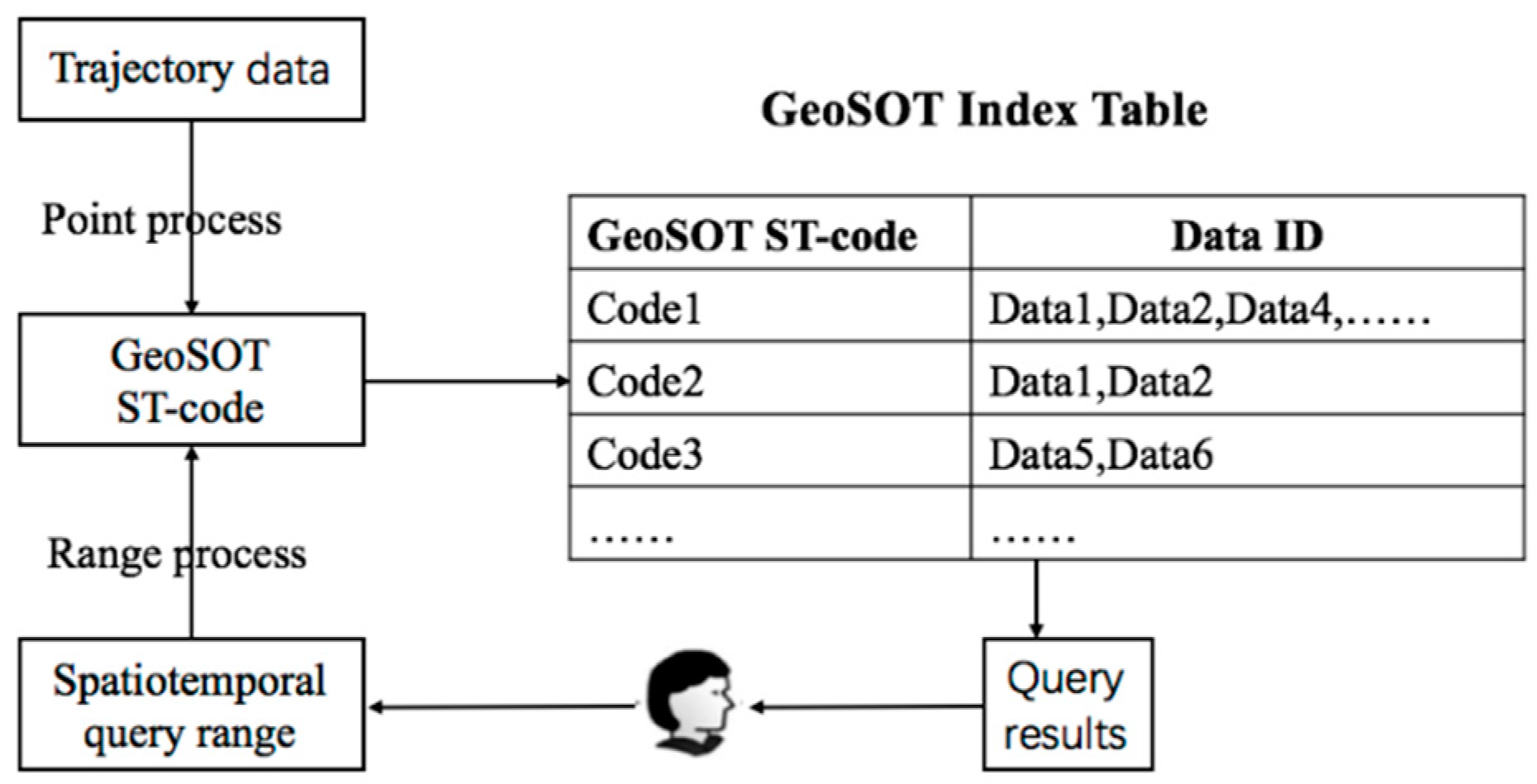
3.2. GeoSOT-Based Spatiotemporal Index Model
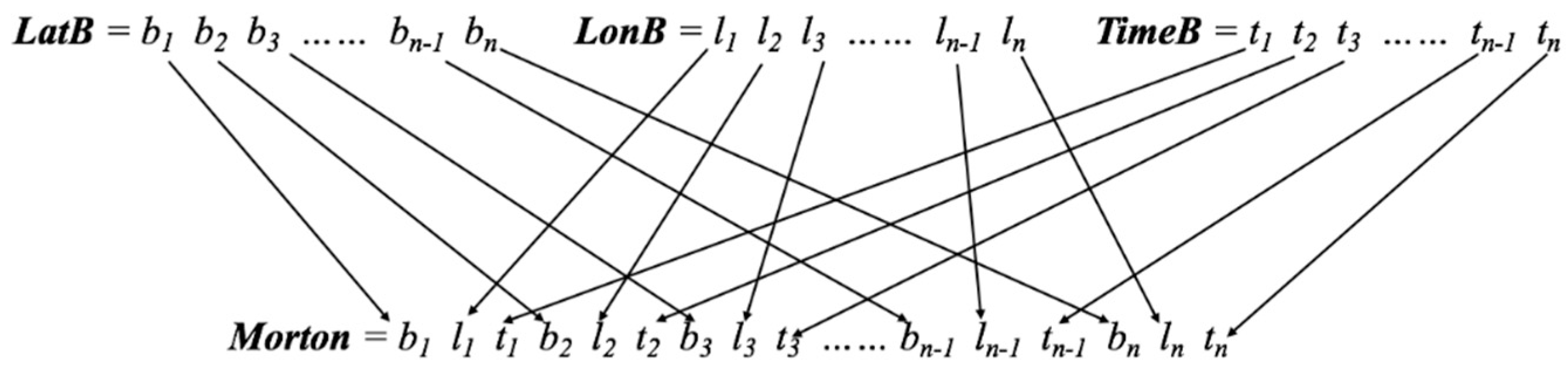
3.3. GeoSOT Space–Time Code for One Trajectory Point
4. Spatiotemporal Range Query Based on the GeoSOT ST-Index
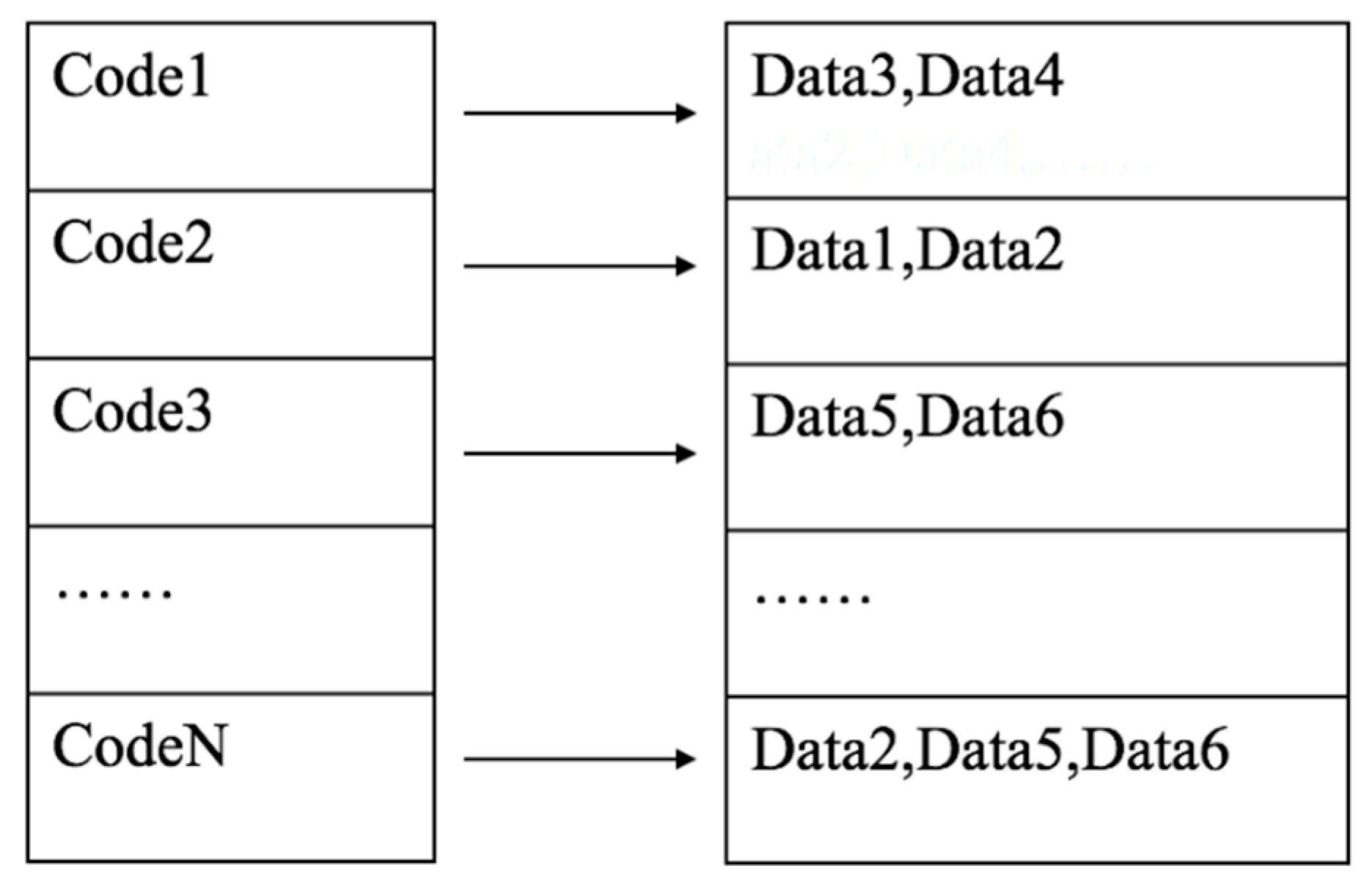
4.1. Spatiotemporal Retrieve Model for Trajectory Data
4.2. Query Processing
5. Performance Results and Discussion
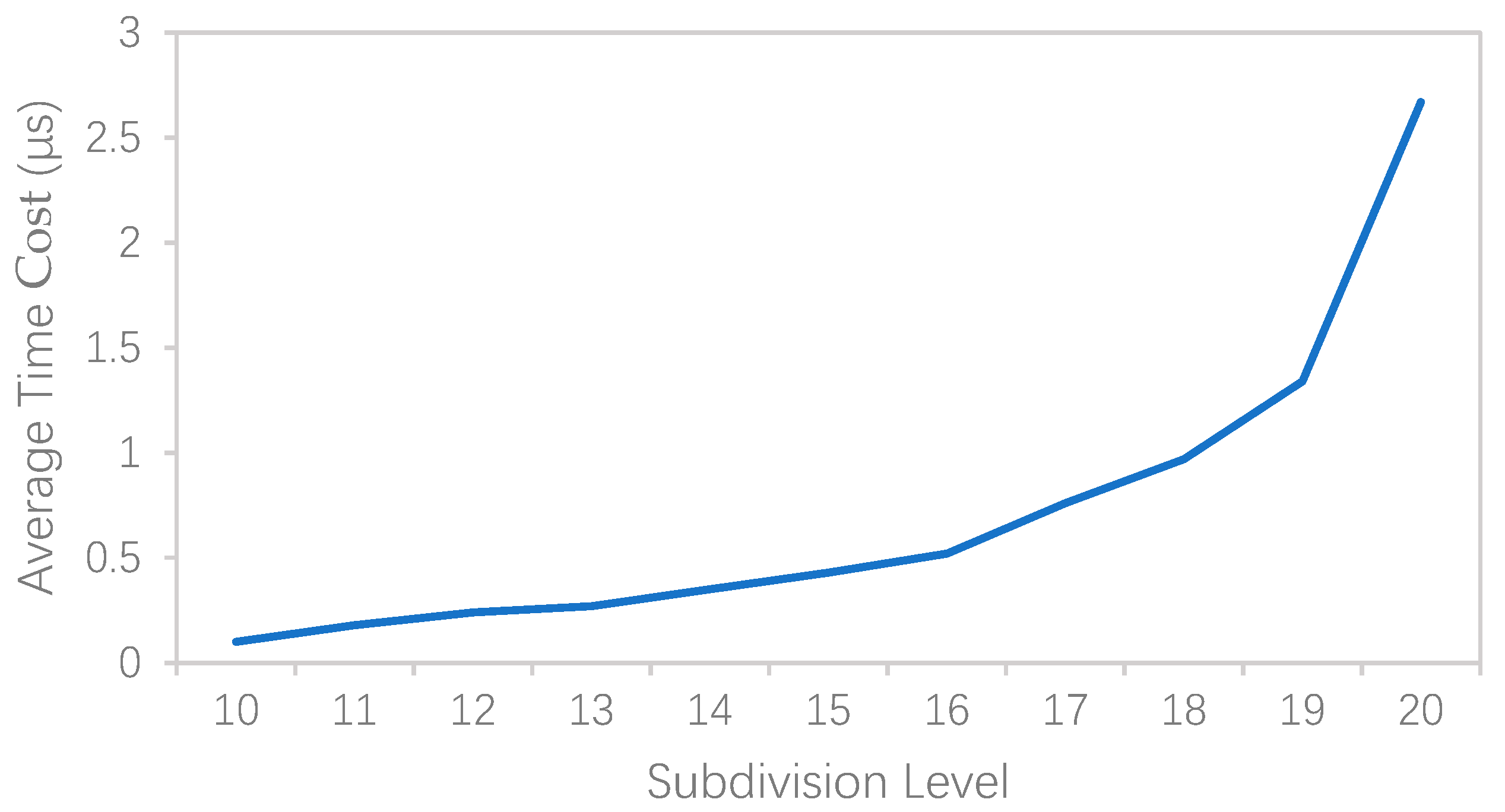
5.1. The Efficiency of GeoSOT ST-Code Generation
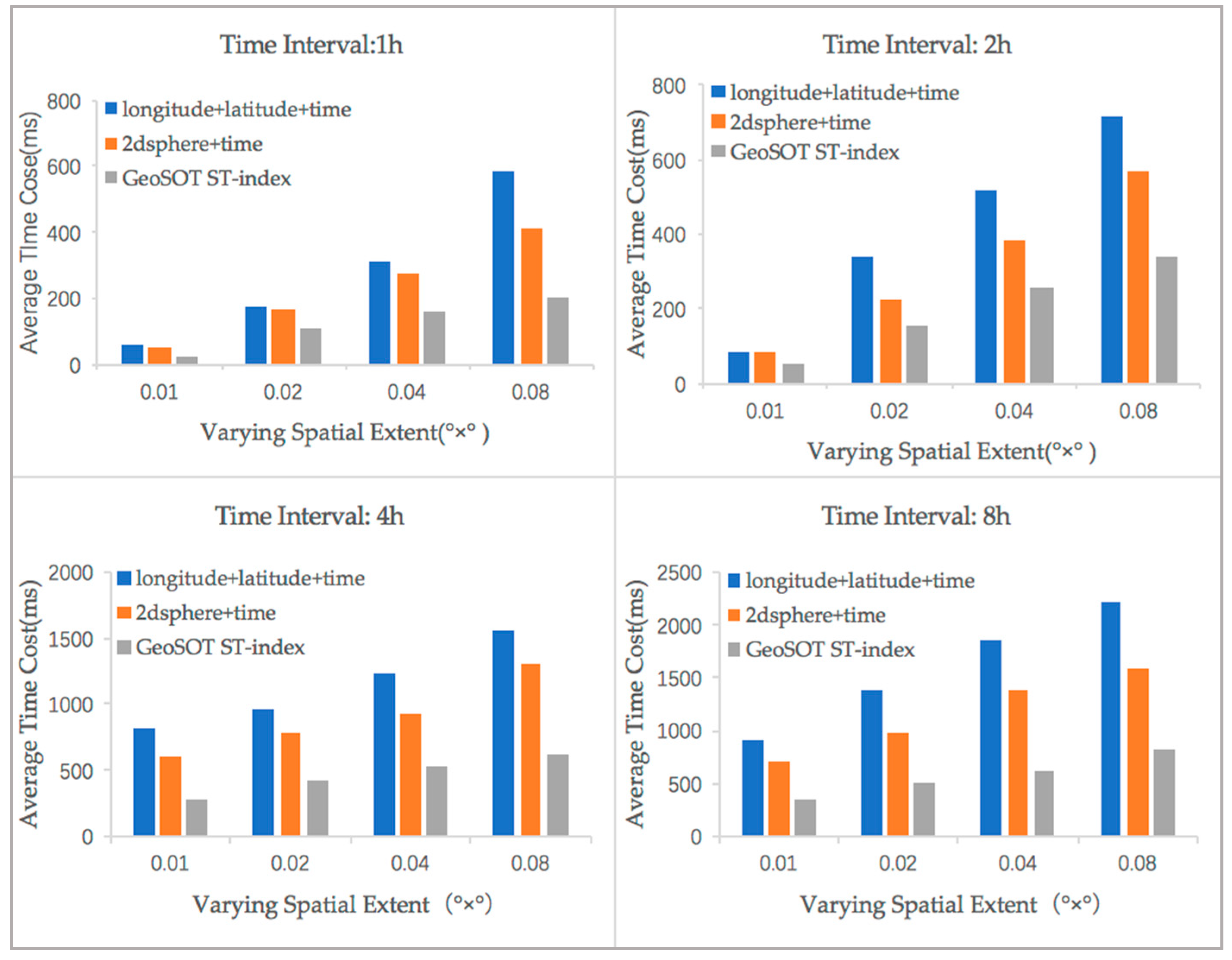
5.2. Comparisons of Spatiotemporal Range Query Efficiency Levels
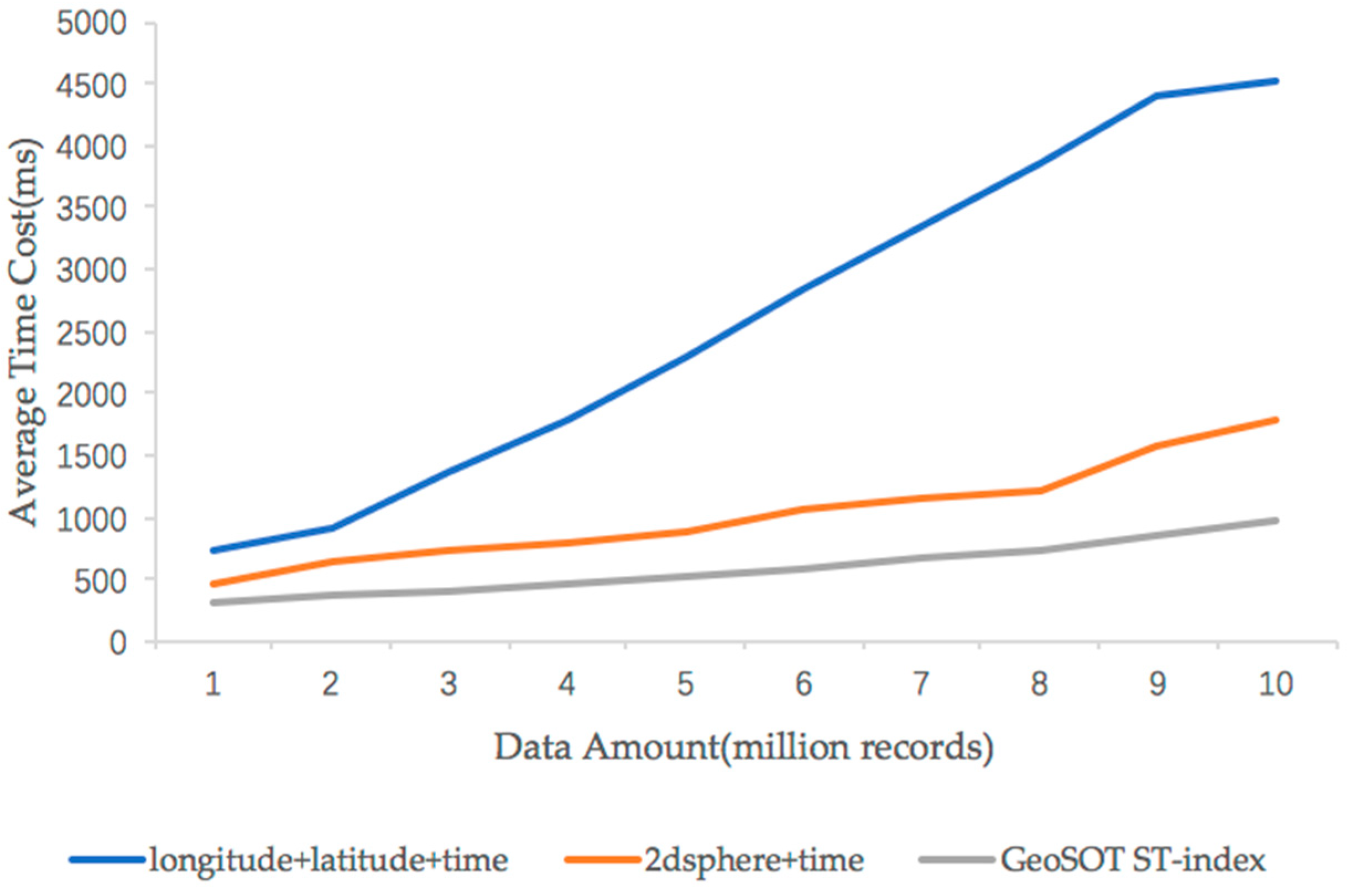
5.3. Comparisons of Scalability Performance
6. Conclusions and Directions for Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, Y. Trajectory Data Mining: An Overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 29. [Google Scholar] [CrossRef]
- Ding, Z.; Huang, G. Real-time traffic flow statistical analysis based on network-constrained moving object trajectories. In Proceedings of the International Conference Database & Expert Systems Applications (DEXA), Linz, Austria, 31 August–4 September 2009. [Google Scholar]
- Wang, X.; Liu, Z.; Jia, Y. A Rush-Hour Vehicles Scheduling Strategy in Online Car-Sharing System Based on Urban Trajectory Data Analysis. In International Conference on Internet of Vehicles; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Renso, C.; Baglioni, M.; de Macedo, J.A.F.; Trasarti, R.; Wachowicz, M. How you move reveals who you are: Understanding human behavior by analyzing trajectory data. Knowl. Inf. Syst. 2013, 37, 331–362. [Google Scholar] [CrossRef]
- Deng, K.; Xie, K.; Zheng, K.; Zhou, X. Trajectory Indexing and Retrieval. In Computing with Spatial Trajectories; Springer: New York, NY, USA, 2011. [Google Scholar]
- Parent, C.; Spaccapietra, S.; Renso, C.; Andrienko, G.; Andrienko, N.; Bogorny, V.; Theodoridis, Y. Semantic trajectories modeling and analysis. ACM Comput. Surv. 2013, 45, 1–32. [Google Scholar] [CrossRef]
- Xing, X.; Li, M.; Hu, W.; Huang, W.; Song, G.; Xie, K. A Spatial-temporal Topic Segmentation Model for Human Mobile Behavior. International Conference on Web-Age Information Management. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Jin, P.; Zhang, X.; Yue, L. NBR-tre: A Novel Spatio-Temporal Index for Urban Traffic Networks. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 147–151. [Google Scholar]
- Jun, G.; Shengnan, K.; Qing, Z. An Efficient Trajectory Data Index Integrating R-tree, Hash and B*-tree. Acta Geod. Cartogr. Sin. 2015, 44, 570–577. [Google Scholar]
- Zhu, Q.; Gong, J.; Zhang, Y. An efficient 3D R-tree spatial index method for virtual geographic environments. ISPRS J. Photogramm. Remote Sens. 2007, 62, 217–224. [Google Scholar] [CrossRef]
- Chakka, V.P.; Everspaugh, A.; Patel, J.M. Indexing large trajectory data sets with SETI. In Proceedings of the Conference on Innovative Data Systems Research, Asilomar, CA, USA, 5–8 January 2003. [Google Scholar]
- Song, Z.; Roussopoulos, N. SEB-tree: An Approach to Index Continuously Moving Objects. In Proceedings of the Mobile Data Management, International Conference, Melbourne, Australia, 21–24 January 2003. [Google Scholar]
- Pfoser, D.; Jensen, C.S.; Theodoridis, Y. Novel approaches in query processing for moving object trajectories. In Proceedings of the International Conference on Very Large Data Bases, Cairo, Egypt, 10–14 September 2000; pp. 395–406. [Google Scholar]
- Li, G.; Tang, J. A New R-tree Spatial Index Based on Space Grid Coordinate Division. In Proceedings of the 2011 International Conference on Informatics, Cybernetics, and Computer Engineering (ICCE2011), Melbourne, Australia, 19–21 November 2011. [Google Scholar]
- Kwon, D.; Lee, S.; Lee, S. Indexing the Current Positions of Moving Objects Using the Lazy Update R-Tree. In Proceedings of the Third International Conference on Mobile Data Management, Singapore, 8–11 January 2002. [Google Scholar]
- Xiong, X.; Aref, W.G. R-trees with Update Memos. In Proceedings of the International Conference on Data Engineering, Atlanta, Georgia, 3–7 April 2006. [Google Scholar]
- Ding, R.; Meng, X. A quadtree based dynamic attribute index structure and query process. In Proceedings of the International Conference on Computer Networks & Mobile Computing, Beijing, China, 6–19 October 2001. [Google Scholar]
- Huang, M.; Peng, H.; Xia, L. A grid based trajectory indexing method for moving objects on fixed network. In Proceedings of the International Conference on Geoinformatics, Beijing, China, 18–20 June 2010. [Google Scholar]
- Guan, X.; Bo, C.; Li, Z.; Yu, Y. ST-hash: An efficient spatiotemporal index for massive trajectory data in a NoSQL database. In Proceedings of the 2017 25th International Conference on Geoinformatics, Buffalo, NY, USA, 2–4 August 2017. [Google Scholar]
- Zheng, K.; Shang, S.; Yuan, N.J.; Yang, Y. Towards efficient search for activity trajectories. In Proceedings of the 2013 IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, Australia, 8–12 April 2013. [Google Scholar]
- Ilic, M.; Spalevic, P.; Veinovic, M. Inverted index search in data mining. In Proceedings of the 2014 22nd Telecommunications Forum Telfor (TELFOR), Belgrade, Serbia, 25–27 November 2014. [Google Scholar]
- Wang, K.; Chen, N.; Chen, Z. Spatio-Temporal Indexing Method of Big Trajectory Data Based on MongoDB. Comput. Syst. Appl. 2017. [Google Scholar] [CrossRef]
- Yang, S.; He, Z.; Chen, Y.P.P. GCOTraj: A storage approach for historical trajectory data sets using grid cells ordering. Inf. Sci. 2018, 459, 1–19. [Google Scholar] [CrossRef]
- Qi, K.; Cheng, C.; Hu, Y.N.; Fang, H.; Ji, Y.; Chen, B. An Improved Identification Code for City Components Based on Discrete Global Grid System. ISPRS Int. J. Geo-Inf. 2017, 6, 381. [Google Scholar] [CrossRef]
- Li, S.; Cheng, C.; Chen, B.; Meng, L. Integration and management of massive remote-sensing data based on GeoSOT subdivision model. J. Appl. Remote Sens. 2016, 10, 034003. [Google Scholar] [CrossRef]
- Lv, X.; Cheng, C.; Xi, F. Study on Geographic Network Address of Geospatial Big Data Storage Management. Geogr. Geo-Inf. Sci. 2015, 31, 1–5. [Google Scholar]
- Xi, F.; Cheng, C.; Chen, D.; Dong, F. An efficient hierarchical data placement algorithm for massive spatial data storage systems. In Proceedings of the Geoscience Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Zhai, W.; Zhe, Y.; Lin, W.; Wu, F.; Cheng, C. The nonsql spatial data management model in big data time. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 4506–4509. [Google Scholar]
- Tong, X.; Cheng, C.; Wang, R.; Ding, L.; Zhang, Y.; Lai, G.; Chen, B. An Efficient Integer Coding and Computing Method for Multiscale Time Segment. Data Knowl. Eng. 2019, 119, 123–138. [Google Scholar] [CrossRef]
- Cheng, C.; Tong, X.; Chen, B.; Zhai, W. A Subdivision Method to Unify the Existing Latitude and Longitude Grids. Int. J. Geo-Inf. 2016, 5, 161. [Google Scholar] [CrossRef]
- Cheng, C. An Introduction to Spatial Information Subdivision Organization; Science Press: Beijing, China, 2012. [Google Scholar]
- Kilimci, P.; Kalipsiz, O. Indexing of spatiotemporal Data: A comparison between sweep and z-order space filling curves. In Proceedings of the International Conference on Information Society, London, UK, 27–29 June 2011. [Google Scholar]
- Su, Y.T.; Bethel, J.; Hu, S. Octree-based segmentation for terrestrial LiDAR point cloud data in industrial applications. ISPRS J. Photogramm. Remote Sens. 2016, 113, 59–74. [Google Scholar] [CrossRef]
- Jiang, H.; Kang, J.; Du, Z.; Zhang, F.; Huang, X.; Liu, R.; Zhang, X. Vector Spatial Big Data Storage and Optimized Query Based on the Multi-Level Hilbert Grid Index in HBase. Information 2018, 9, 116. [Google Scholar] [CrossRef]
- Alis, C.; Boehm, J.; Liu, K. Parallel Processing of Big Point Clouds Using Z-Order Partitioning. In Proceedings of the International Archives of the Photogrammetry Remote Sensing, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Jin, A.; Cheng, C.Q.; Song, S.H.; Chen, B. Regional Query of Area Data Based on Geohash. Geogr. Geo-Inf. Sci. 2013, 29, 31–35. [Google Scholar]
- Yuan, J.; Zheng, Y.; Xie, X.; Sun, G. Driving with knowledge from the physical world. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011. [Google Scholar]
- Yuan, J.; Zheng, Y.; Zhang, C.; Xie, W.; Xie, X.; Sun, G.; Huang, Y. T-drive: Driving directions based on taxi trajectories. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 99–108. [Google Scholar]
| Year | Month | Day | Hour | |
|---|---|---|---|---|
| Original range | 1969–2096 | 1–12 | 1–31 | 1–24 |
| Extended range | 1969–2096 | 1–16 | 1–32 | 1–32 |
| Level | Scale | Level | Scale | Level | Scale |
|---|---|---|---|---|---|
| 1 | 64 years 256° | 8 | 8 months 2° | 15 | 2 days 1′ |
| 2 | 32 year 128° | 9 | 4 months 1° | 16 | 1 day 32″ |
| 3 | 16 years 64° | 10 | 2 months 32′ | 17 | 16 h 16″ |
| 4 | 8 years 32° | 11 | 1 month 16′ | 18 | 8 h 8″ |
| 5 | 4 years 16° | 12 | 16 days 8′ | 19 | 4 h 4″ |
| 6 | 2 years 8° | 13 | 8 days 4′ | 20 | 2 h 2″ |
| 7 | 1 year 4° | 14 | 4 days 2′ | 21 | 1 h 1″ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, C.; Yi, C.; Cheng, C.; Pu, G.; Wei, X.; Zhang, H. GeoSOT-Based Spatiotemporal Index of Massive Trajectory Data. ISPRS Int. J. Geo-Inf. 2019, 8, 284. https://doi.org/10.3390/ijgi8060284
Qian C, Yi C, Cheng C, Pu G, Wei X, Zhang H. GeoSOT-Based Spatiotemporal Index of Massive Trajectory Data. ISPRS International Journal of Geo-Information. 2019; 8(6):284. https://doi.org/10.3390/ijgi8060284
Chicago/Turabian StyleQian, Chunyao, Chao Yi, Chengqi Cheng, Guoliang Pu, Xiaofeng Wei, and Huangchuang Zhang. 2019. "GeoSOT-Based Spatiotemporal Index of Massive Trajectory Data" ISPRS International Journal of Geo-Information 8, no. 6: 284. https://doi.org/10.3390/ijgi8060284
APA StyleQian, C., Yi, C., Cheng, C., Pu, G., Wei, X., & Zhang, H. (2019). GeoSOT-Based Spatiotemporal Index of Massive Trajectory Data. ISPRS International Journal of Geo-Information, 8(6), 284. https://doi.org/10.3390/ijgi8060284





