Indoor Routing on Logical Network Using Space Semantics
Abstract
:1. Introduction
2. Background
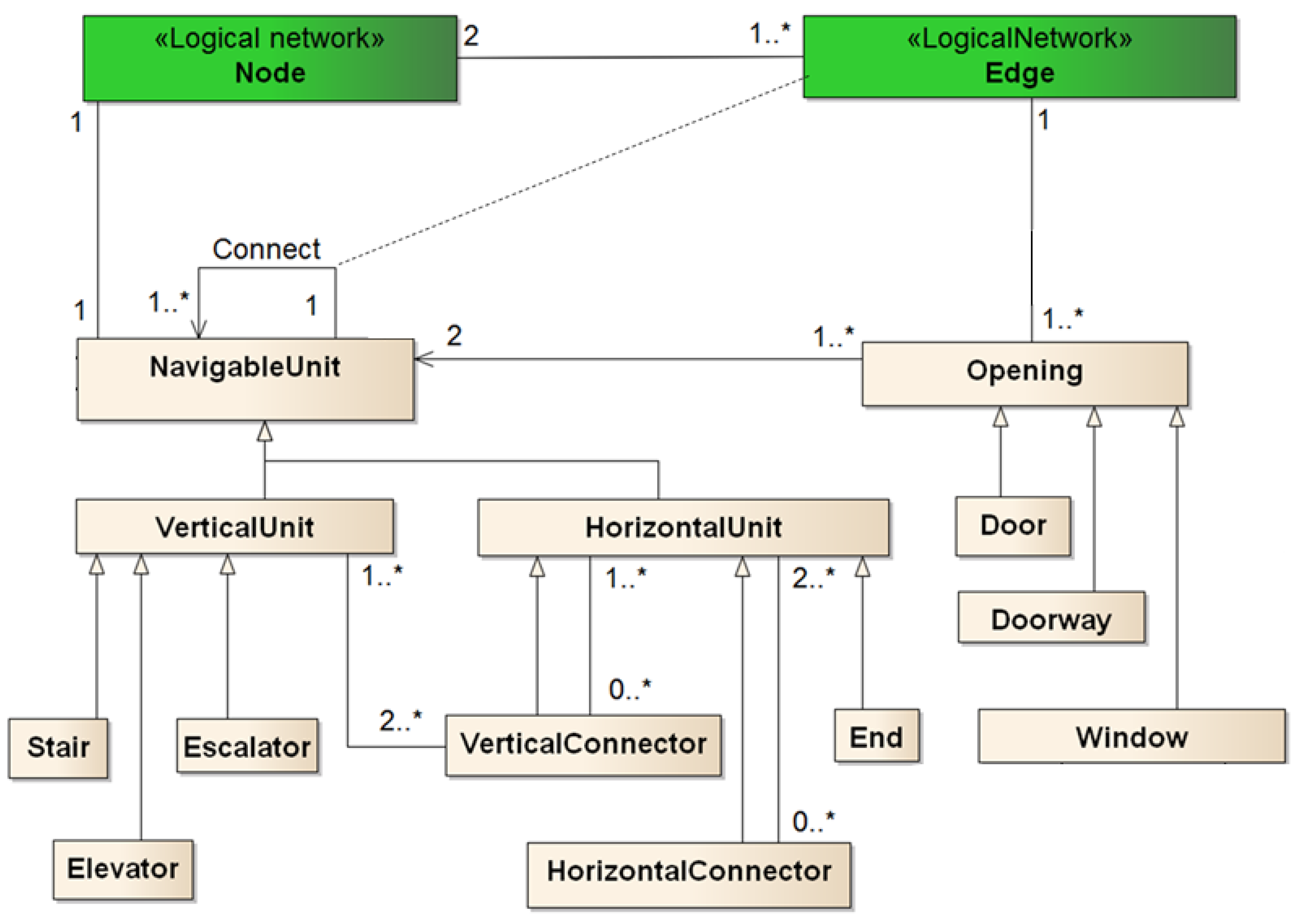
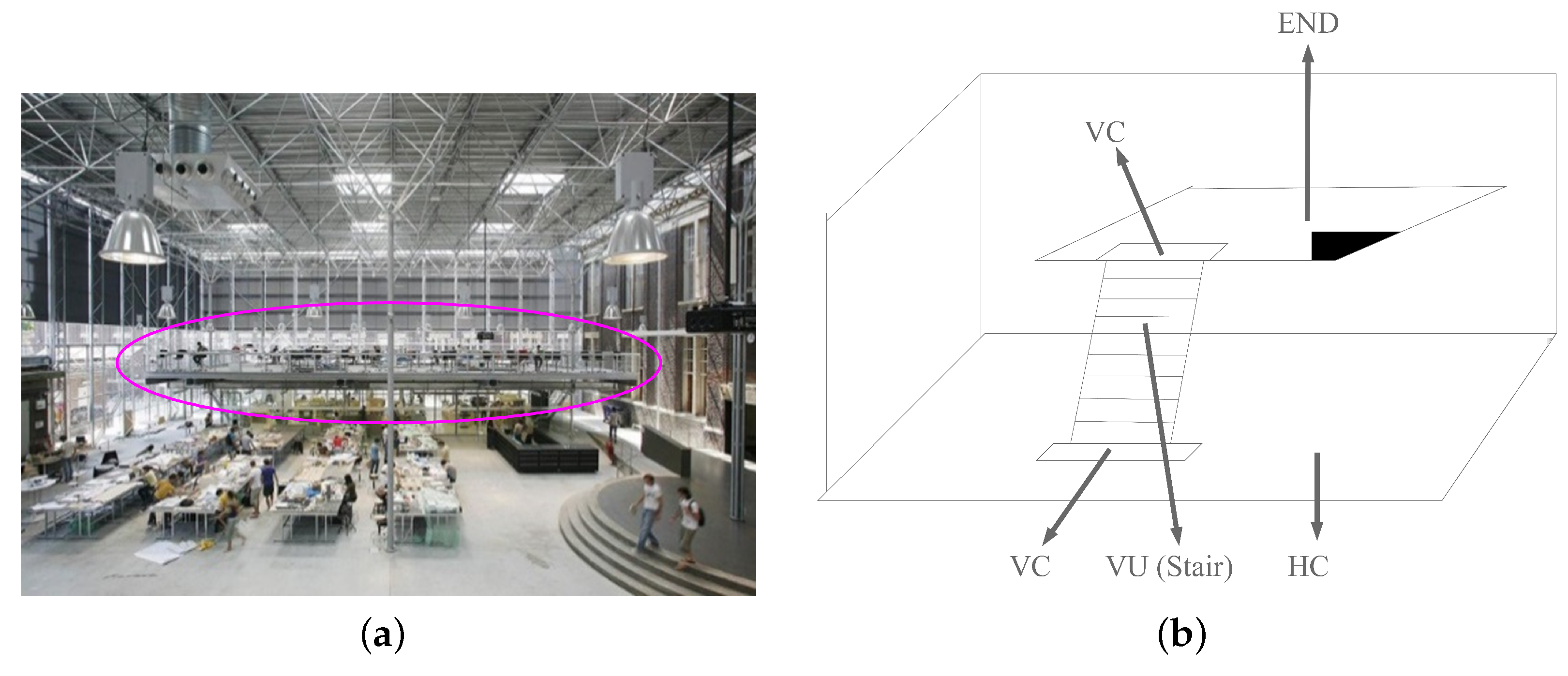
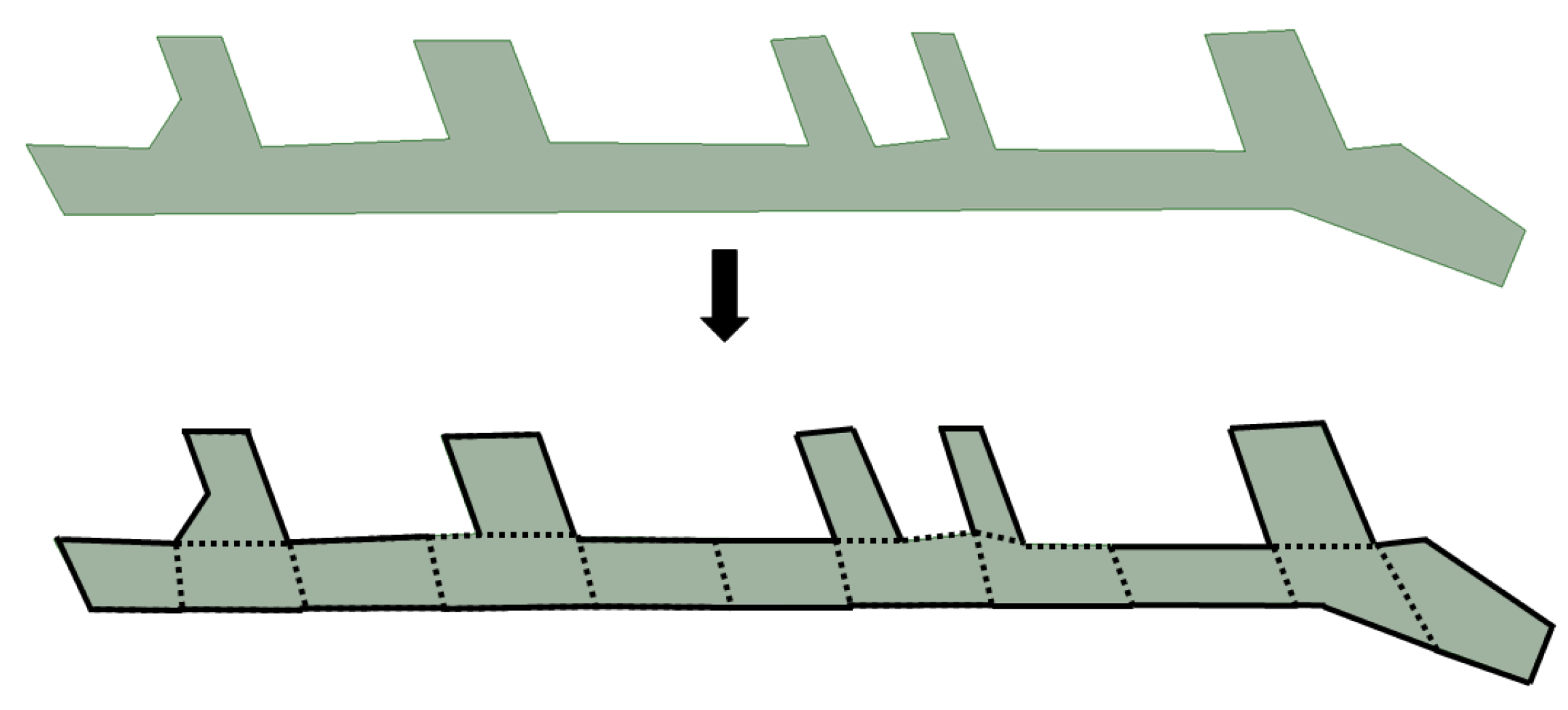
3. Generic Space Classification for Routing
- Opening. This is a transition space which connects one space with another. These spaces (e.g., an entrance) can connect the outdoor space as well.
- Navigable Unit (NU). This is a space in which users (e.g., pedestrians) can move freely (e.g., walk or drive) without crossing any opening.
- Vertical Unit (VU). VU is a subclass of NU in which pedestrians can move (or be transported) in vertical directions (i.e., up and down) along the same slope.
- Horizontal Unit (HU). This is a subclass of NU in which pedestrians can move in horizontal directions.
- Horizontal Connector (HC). An HC is an HU that connects with at least two other HUs.
- Vertical Connector (VC). A VC is an HU that connects at least two other different NUs, and at least one of them is a VU.
- End. End is a subtype of HU that is connected with one NU at most.
4. Routing Criteria Based on Space Semantics
- Fewest Navigable Unit (Fewest NU): .
- Fewest Horizontal Connector (Fewest HC): .
- Fewest Vertical Unit (Fewest VU): .
- Central Horizontal Connector (Central HC): .
- Horizontal Connector Prior (HC Prior): .
- Vertical Unit Prior (VU Prior): .
5. Routing Procedure
| Algorithm 1 Derive edge weights from node weights in a logical network. |
| Input: A logical network G, the values Ws of node weights. Output: The logical network G where the edges have been weighted in light of Ws.
|
| Algorithm 2 Compute logical paths with ordered criteria in a priority list on a logical network. |
| Input: A prioritized list of ordered routing criteria F, a logical network N. Output: The set of logical path(s) .
|
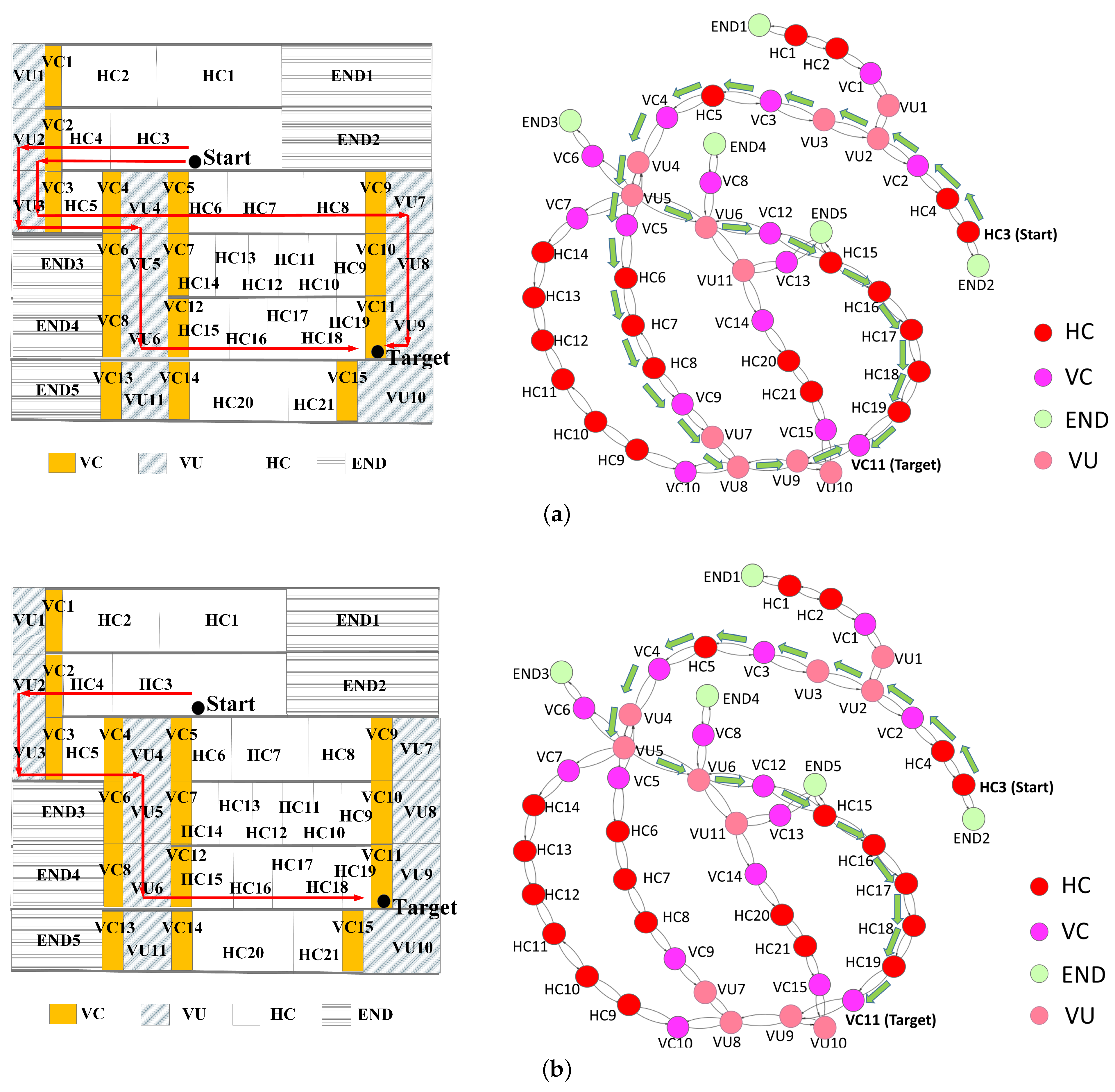
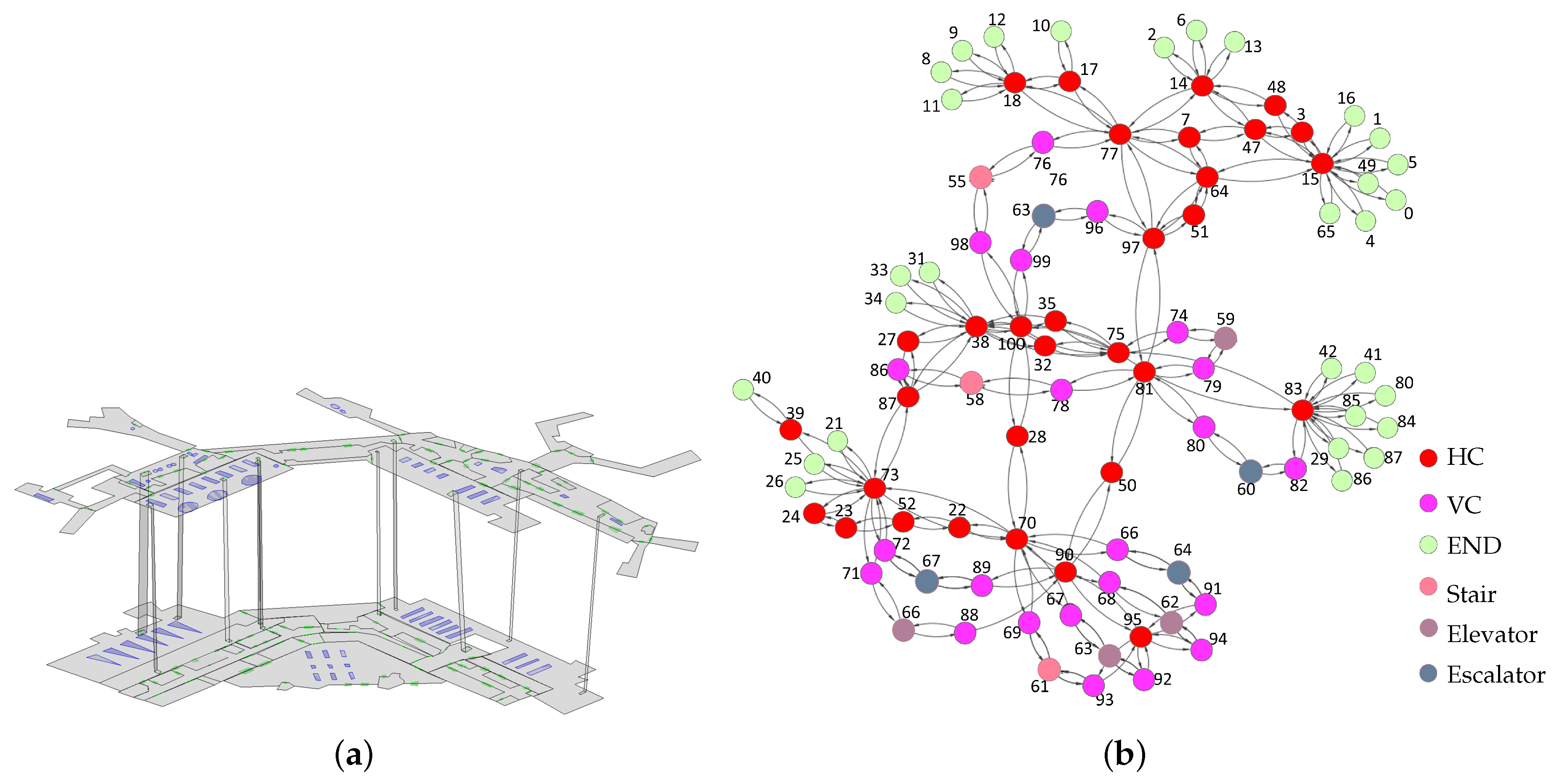
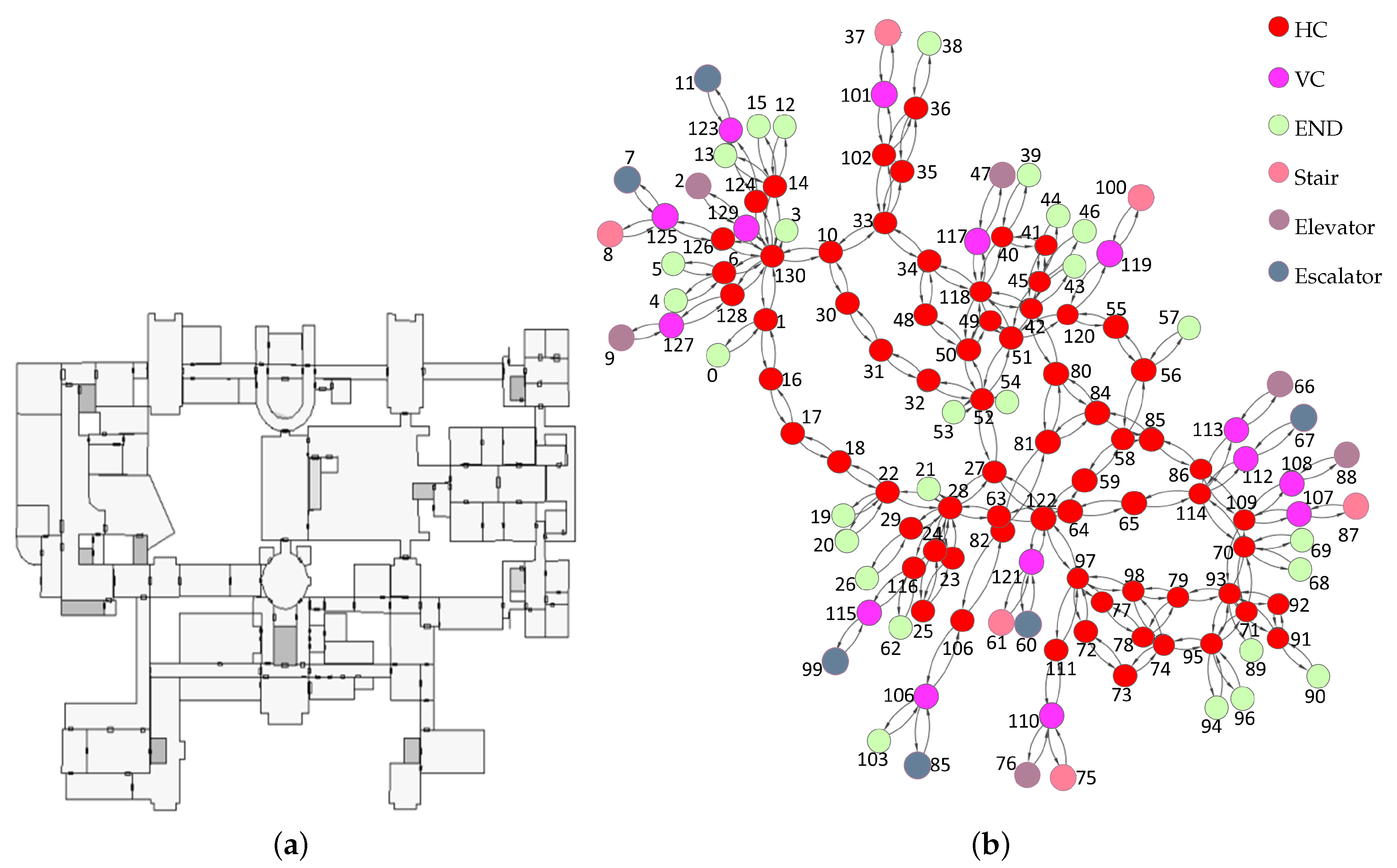
6. Experiments
- p1: 1END, 64HC, 62HC, 72HC, 71VC, 54Stair, 88VC, 90HC, 70HC, 42HC;
- p2: 1END, 64HC, 62HC, 87HC, 86VC, 61Ele, 89VC, 90HC, 70HC, 42HC;
- p3: 1END, 64HC, 62HC, 87HC, 76HC, 74VC, 58Ele, 69VC, 70HC, 42HC.
- The sequence of r1 is 130HC, 10HC, 30HC, 31HC, 32HC, 52HC, 27HC, 122HC, 97HC, 98HC, 79HC, 93HC.
- The sequence of r2 is 130HC, 10HC, 33HC, 34HC, 118HC, 42HC, 80HC, 84HC, 85HC, 86HC, 109HC, 93HC.
7. Discussions
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, J. A Spatial Access-Oriented Implementation of a 3-D GIS Topological Data Model for Urban Entities. GeoInformatica 2004, 8, 237–264. [Google Scholar] [CrossRef]
- Kwan, M.P.; Lee, J. Emergency response after 9/11: The potential of real-time 3D {GIS} for quick emergency response in micro-spatial environments. Comput. Environ. Urban Syst. 2005, 29, 93–113. [Google Scholar] [CrossRef]
- Pu, S.; Zlatanova, S. Evacuation Route Calculation of Inner Buildings. In Geo-Information for Disaster Management; Van Oosterom, P., Zlatanova, S., Fendel, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1143–1161. [Google Scholar]
- Boguslawski, P.; Gold, C. Euler operators and navigation of multi-shell building models. In Developments in 3D Geo-Information Sciences; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–16. [Google Scholar]
- Worboys, M. Modeling Indoor Space. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Chicago, IL, USA, 1 November 2011; ACM: New York, NY, USA, 2011; pp. 1–6. [Google Scholar]
- Stoffel, E.P.; Schoder, K.; Ohlbach, H.J. Applying Hierarchical Graphs to Pedestrian Indoor Navigation. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008; ACM: New York, NY, USA, 2008. [Google Scholar]
- Zheng, J.; Winstanley, A.C.; Pan, Z.; Coveney, S. Spatial Characteristics of Walking Areas for Pedestrian Navigation. In Proceedings of the Third International Conference on Multimedia & Ubiquitous Engineering, Qingdao, China, 4–6 June 2009. [Google Scholar]
- Liu, L.; Zlatanova, S. A two-level path-finding strategy for indoor navigation. In Intelligent Systems for Crisis Management; Springer: Berlin/Heidelberg, Germany, 2013; pp. 31–42. [Google Scholar]
- Lin, Z.; Xu, Z.; Hu, D.; Hu, Q.; Li, W. Hybrid Spatial Data Model for Indoor Space: Combined Topology and Grid. ISPRS Int. J. Geo-Inf. 2017, 6, 343. [Google Scholar] [CrossRef]
- Nagel, C.; Stadler, A.; Kolbe, T. Conceptual requirements for the automatic reconstruction of building information models from uninterpreted 3D models. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Vancouver, BC, Canada, 27–31 July 2009; Copernicus Publications: Göttingen, Germany, 2009; pp. 46–53. [Google Scholar]
- Afyouni, I.; Ray, C.; Claramunt, C. Spatial models for context-aware indoor navigation systems: A survey. J. Spat. Inf. Sci. 2012, 4, 85–123. [Google Scholar] [CrossRef]
- Vasardani, M.; Winter, S.; Richter, K.F. Locating place names from place descriptions. Int. J. Geogr. Inf. Sci. 2013, 27, 2509–2532. [Google Scholar] [CrossRef]
- Winter, S.; Hamzei, E.; Van de Weghe, N.; Ooms, K. A Graph Representation for Verbal Indoor Route Descriptions. In Proceedings of the German Conference on Spatial Cognition, Tuebingen, Germany, 5–8 September 2018; Springer: Cham, Switzerland, 2018; pp. 77–91. [Google Scholar]
- Goetz, M.; Zipf, A. Extending OpenStreetMap to indoor environments. In Urban and Regional Data Management; CRC Press: Leiden, The Netherlands, 2011; pp. 51–61. [Google Scholar]
- Yang, L.; Worboys, M. A Navigation Ontology for Outdoor-indoor Space: (Work-in-progress). In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Chicago, IL, USA, 1 November 2011; ACM: New York, NY, USA, 2011; pp. 31–34. [Google Scholar]
- Lee, J.; Li, K.; Zlatanova, S.; Kolbe, T.; Nagel, C.; Becker, T. IndoorGML. Standard, The Open Geospatial Consortium (OGC); IndoorGML: London, UK, 2014. [Google Scholar]
- Vanclooster, A.; De Maeyer, P.; Fack, V.; Van de Weghe, N. Calculating least risk paths in 3D indoor space. In Innovations in 3D Geo-Information Sciences; Springer: Cham, Switzerland, 2014; pp. 13–31. [Google Scholar]
- Vanclooster, A.; Ooms, K.; Viaene, P.; Fack, V.; Weghe, N.V.D.; Maeyer, P.D. Evaluating suitability of the least risk path algorithm to support cognitive wayfinding in indoor spaces: An empirical study. Appl. Geogr. 2014, 53, 128–140. [Google Scholar] [CrossRef]
- Stoffel, E.P. Hierarchical Graphs as Organisational Principle and Spatial Model Applied to Pedestrian Indoor Navigation. Ph.D. Thesis, Ludwig-Maximilians-Universität München, Munich, Germany, 2009. [Google Scholar]
- Belouaer, L.; Brosset, D.; Claramunt, C. From verbal route descriptions to sketch maps in natural environments. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Burlingame, CA, USA, 31 October–3 November 2016. [Google Scholar]
- Dijkstra, E. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Jones, D.; Tamiz, M. Practical Goal Programming; Springer: Boston, MA, USA, 2010; Volume 141. [Google Scholar]
- Lee, J.; Kwan, M.P. A combinatorial data model for representing topological relations among 3D geographical features in microspatial environments. Int. J. Geogr. Inf. Sci. 2005, 19, 1039–1056. [Google Scholar] [CrossRef]
- Ye, J.; Coyle, L.; Dobson, S.; Nixon, P. A Unified Semantics Space Model. In Location- and Context-Awareness; Hightower, J., Schiele, B., Strang, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4718, pp. 103–120. [Google Scholar]
- Lee, K.; Kang, H.Y.; Lee, J. Topological Analysis in Indoor Shopping Mall using Ontology. J. Korean Soc. Surv. Geod. Photogram. Cartogr. 2013, 31, 405–415. [Google Scholar] [CrossRef]
- Li, D.; Lee, D.L. A topology-based semantic location model for indoor applications. In Proceedings of the ACM Sigspatial International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 November 2008; pp. 1–10. [Google Scholar]
- Jiang, S.; Feng, Z.; Zhang, X.; Wang, X.; Rao, G. A Multi-dimension Weighted Graph-Based Path Planning with Avoiding Hotspots. In Knowledge Graph and Semantic Computing: Semantic, Knowledge, and Linked Big Data; Chen, H., Ji, H., Sun, L., Wang, H., Qian, T., Ruan, T., Eds.; Springer: Singapore, 2016; pp. 15–26. [Google Scholar]
- Ohlbach, H.J.; Rosner, M.; Lorenz, B.; Stoffel, E.P. NL Navigation Commands from Indoor WLAN Fingerprinting Position Data; Technical Report; University of Munich: Munich, Germany, 2006. [Google Scholar]
- Stoffel, E.P.; Lorenz, B.; Ohlbach, H.J. Towards a Semantic Spatial Model for Pedestrian Indoor Navigation. In Proceedings of the 2007 Conference on Advances in Conceptual Modeling: Foundations and Applications, Auckland, New Zealand, 5–9 November 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 328–337. [Google Scholar]
- Becker, T.; Nagel, C.; Kolbe, T. A Multilayered Space-Event Model for Navigation in Indoor Spaces. In 3D Geo-Information Sciences; Lee, J., Zlatanova, S., Eds.; Lecture Notes in Geoinformation and Cartography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 61–77. [Google Scholar]
- Zlatanova, S.; Liu, L.; Sithole, G. A conceptual framework of space subdivision for indoor navigation. In Proceedings of the Fifth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Orlando, FL, USA, 5–8 November 2013; pp. 37–41. [Google Scholar]
- Richter, K.F.; Winter, S.; Santosa, S. Hierarchical representations of indoor spaces. Environ. Plan. B Plan. Des. 2011, 38, 1052–1070. [Google Scholar] [CrossRef]
- Krūminaitė, M.; Zlatanova, S. Indoor space subdivision for indoor navigation. In Proceedings of the Sixth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Dallas, TX, USA, 4–7 November 2014; pp. 25–31. [Google Scholar]
- Tsetsos, V.; Anagnostopoulos, C.; Kikiras, P.; Hasiotis, P.; Hadjiefthymiades, S. A human-centered semantic navigation system for indoor environments. In Proceedings of the International Conference on Pervasive Services 2005, Santorini, Greece, 11–14 July 2005; pp. 146–155. [Google Scholar]
- Dudas, P.; Ghafourian, M.; Karimi, H. ONALIN: Ontology and algorithm for indoor routing. In Proceedings of the 2009 Tenth International Conference on Mobile Data Management: Systems, Services and Middleware, Washington, DC, USA, 18–20 May 2009; pp. 720–725. [Google Scholar]
- Karimi, H.; Ghafourian, M. Indoor Routing for Individuals with Special Needs and Preferences. Trans. GIS 2010, 14, 299–329. [Google Scholar] [CrossRef]
- Khan, A.; Kolbe, T. Constraints and their role in subspacing for the locomotion types in indoor navigation. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, NSW, Australia, 13–15 November 2012; p. 12. [Google Scholar]
- Alattas, A.; Zlatanova, S.; Van Oosterom, P.; Chatzinikolaou, E.; Lemmen, C.; Li, K.J. Supporting Indoor Navigation Using Access Rights to Spaces Based on Combined Use of IndoorGML and LADM Models. ISPRS Int. J. Geo-Inf. 2017, 6, 384. [Google Scholar] [CrossRef]
- Liu, L.; Zlatanova, S. A Semantic Data Model for Indoor Navigation. In Proceedings of the Fourth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, New York, NY, USA, 6 November 2012; ACM: New York, NY, USA, 2012; pp. 1–8. [Google Scholar]
- Brown, G.; Nagel, C.; Zlatanova, S.; Kolbe, T. Modelling 3D topographic space against indoor navigation requirements. In Progress and New Trends in 3D Geoinformation Sciences; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–22. [Google Scholar]
- Caramia, M.; Dell Olmo, P. Multi-objective optimization. In Multi-Objective Management in Freight Logistics: Increasing Capacity, Service Level and Safety with Optimization Algorithms; Springer: London, UK, 2008; pp. 11–36. [Google Scholar]
- Deb, K. Multi-objective Optimization. In Search Methodologies; Burke, E., Kendall, G., Eds.; Springer: Boston, MA, USA, 2014; pp. 403–449. [Google Scholar]
- Lyardet, F.; Szeto, D.; Aitenbichler, E. Context-aware indoor navigation. In Proceedings of the European Conference on Ambient Intelligence, Nuremberg, Germany, 19–22 November 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 290–307. [Google Scholar]
- Borgatti, S.P. Centrality and network flow. Soc. Netw. 2005, 27, 55–71. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef] [PubMed]
- Boldi, P.; Vigna, S. Axioms for Centrality. Internet Math. 2013, 10, 222–262. [Google Scholar] [CrossRef]
- Brandes, U. A Faster Algorithm for Betweenness Centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Systems, B. I-Models: Access and Share Information-Rich Models. 2016. Available online: https://www.bentley.com/en/i-models (accessed on 1 March 2019).
- Igraph Core Team. Igraph. 2016. Available online: https://pypi.org/project/python-igraph/ (accessed on 1 March 2019).
- Liu, L.; Zlatanova, S. Generating Navigation Models from Existing Building Data. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus Publications: Göttingen, Germany, 2013; pp. 19–25. [Google Scholar]





| Type | Constraint | HC | VC | VU | ||
|---|---|---|---|---|---|---|
| EL | ES | ST | ||||
| Minimizing specific types | Fewest NU | 1 | 1 | 1 | 1 | 1 |
| Fewest HC | 1 | 0 | 0 | 0 | 0 | |
| Fewest VU | 0 | 0 | 1 | 1 | 1 | |
| Fewest EL | 0 | 0 | 1 | 10,000 | 10,000 | |
| Fewest ES | 0 | 0 | 10,000 | 1 | 10,000 | |
| Fewest ST | 0 | 0 | 10,000 | 10,000 | 1 | |
| Fewest EL&ES | 0 | 0 | 1 | 1 | 10,000 | |
| Fewest EL&ST | 0 | 0 | 1 | 10,000 | 1 | |
| Fewest ES&ST | 0 | 0 | 10,000 | 1 | 1 | |
| Setting priority to specific types | Central HC | 10,000-Centrality | 10,000 | 10,000 | 10,000 | 10,000 |
| HC Prior | 1 | 10,000 | 10,000 | 10,000 | 10,000 | |
| VU Prior | 10,000 | 10,000 | 1 + | 1 + | 1 + | |
| EL Prior | 10,000 | 10,000 | 1 + | 10,000 | 10,000 | |
| ES Prior | 10,000 | 10,000 | 10,000 | 1 + | 10,000 | |
| ST Prior | 10,000 | 10,000 | 10,000 | 10,000 | 1 + | |
| EL&ES Prior | 10,000 | 10,000 | 1 + | 1 + | 10,000 | |
| EL&ST Prior | 10,000 | 10,000 | 1 + | 10,000 | 1 + | |
| ES&ST Prior | 10,000 | 10,000 | 10,000 | 1 + | 1 + | |
| Fewest NU | Fewest HC | Fewest VU | VU Prior | HC Prior | Central HC |
|---|---|---|---|---|---|
| p1, p2, p3 | p1, p2, p3 | p1, p2, p3 | p1, p2 | p3 | p1 |
| Fewest NU | Fewest HC | HC Prior | Central HC |
|---|---|---|---|
| r1, r2 | r1, r2 | r1, r2 | r1 |
| Start-Target | Path Set |
|---|---|
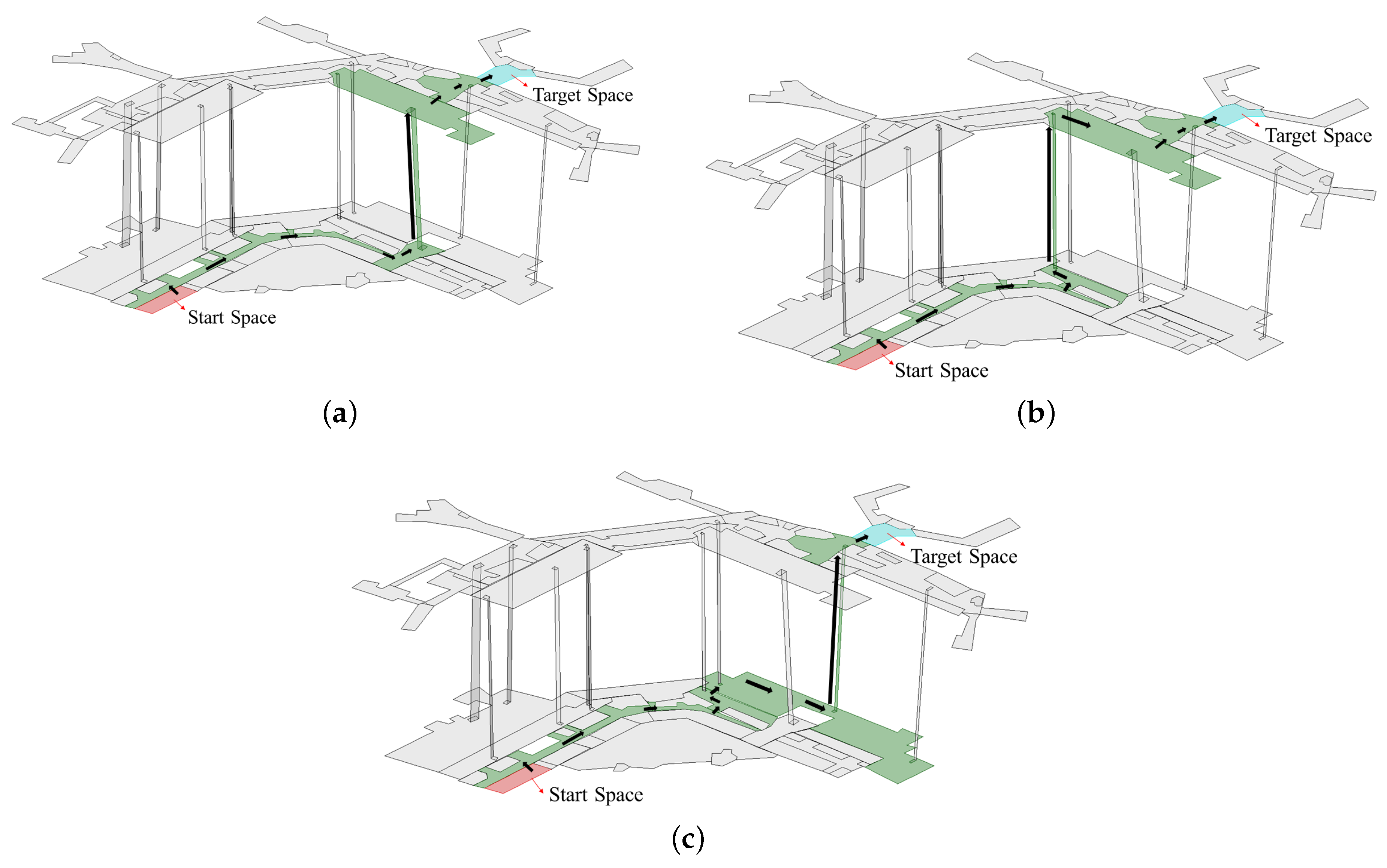
| 1–82 | A1: 1END, 64HC, 95HC, 91VC, 53Esc, 96VC, 100HC, 68HC, 82HC A2: 1END, 64HC, 95HC, 85HC, 84VC, 56Esc, 67VC, 68HC, 82HC A3: 1END, 64HC, 62HC, 87HC, 76HC, 73VC, 57Stair, 81VC, 82HC A4: 1END, 64HC, 95HC, 85HC, 83VC, 55Ele, 66VC, 68HC, 82HC A5: 1END, 64HC, 95HC, 94VC, 65Esc, 98VC, 100HC, 68HC, 82HC A6: 1END, 64HC, 95HC, 93VC, 60Stair, 99VC, 100HC, 68HC, 82HC A7: 1END, 64HC, 95HC, 92VC, 52Ele, 97VC, 100HC, 68HC, 82HC |
| 1–26 | B1: 1END, 64HC, 95HC, 91VC, 53Esc, 96VC, 100HC, 68HC, 82HC, 26HC B2: 1END, 64HC, 95HC, 85HC, 84VC, 56Esc, 67VC, 68HC, 82HC, 26HC B3: 1END, 64HC, 62HC, 87HC, 86VC, 61Ele, 89VC, 90HC, 37HC, 26HC B4: 1END, 64HC, 95HC, 93VC, 60Stair, 99VC, 100HC, 68HC, 82HC, 26HC B5: 1END, 64HC, 95HC, 85HC, 83VC, 55Ele, 66VC, 68HC, 82HC, 26HC B6: 1END, 64HC, 95HC, 92VC, 52Ele, 97VC, 100HC, 68HC, 82HC, 26HC B7: 1END, 64HC, 95HC, 94VC, 65Esc, 98VC, 100HC, 68HC, 82HC, 26HC B8: 1END, 64HC, 62HC, 87HC, 76HC, 73VC, 57Stair, 81VC, 82HC, 26HC B9: 1END, 64HC, 62HC, 72HC, 71VC, 54Stair, 88VC, 90HC, 37HC, 26HC |
| 10–25 | C1: 10END, 16HC, 72HC, 71VC, 54Stair, 88VC, 90HC, 27HC, 100HC, 68HC, 25END C2: 10END, 16HC, 72HC, 87HC, 76HC, 73VC, 57Stair, 81VC, 82HC, 68HC, 25END C3: 10END, 16HC, 72HC, 71VC, 54Stair, 88VC, 90HC, 37HC, 82HC, 68HC, 25END |
| 4–38 | D1: 4HC, 95HC, 85HC, 84VC, 56Esc, 67VC, 68HC, 38HC D2: 4HC, 95HC, 92VC, 52Ele, 97VC, 100HC, 68HC, 38HC D3: 4HC, 95HC, 94VC, 65Esc, 98VC, 100HC, 68HC, 38HC D4: 4HC, 95HC, 85HC, 83VC, 55Ele, 66VC, 68HC, 38HC D5: 4HC, 95HC, 91VC, 53Esc, 96VC, 100HC, 68HC, 38HC D6: 4HC, 95HC, 93VC, 60Stair, 99VC, 100HC, 68HC, 38HC |
| 15–95 | E1: 11END, 17HC, 72HC, 87HC, 76HC, 73VC, 57Stair, 81VC, 82HC, 68HC, 24END E2: 11END, 17HC, 72HC, 71VC, 54Stair, 88VC, 90HC, 27HC, 100HC, 68HC, 24END E3: 11END, 17HC, 72HC, 71VC, 54Stair, 88VC, 90HC, 37HC, 82HC, 68HC, 24END |
| Start and Target Space | 1–82 | 1–26 | 10–25 | 4–38 | 15–95 |
|---|---|---|---|---|---|
| Path Set | A1, A2, A3, A4, A5, A6, A7 | B1, B2, B3, B4, B5, B6, B7, B8, B9 | C1, C2, C3: | D1, D2, D3, D4, D5, D6 | E1, E2, E3 |
| Fewest NU | A1, A2,A3, A4, A5, A6, A7 | B1, B2, B3, B4, B5, B6, B7, B8, B9 | C1, C2, C3 | D1, D2, D3, D4, D5, D6 | E1, E2, E3 |
| Fewest | |||||
| HC | A1, A2, A3, A4, A5, A6, A7 | B1, B2, B3, B4, B5, B6, B7, B8, B9 | C1, C2, C3 | D1, D2, D3, D4, D5, D6 | E1, E2, E3 |
| Fewest | |||||
| VU | A1, A2, A3, A4, A5, A6, A7 | B1, B2, B3, B4, B5, B6, B7, B8, B9 | C1, C2, C3 | D1, D2, D3, D4, D5, D6 | E1, E2, E3 |
| HC Prior | A3 | B8 | C2 | D1, D4 | E1 |
| VU Prior | A1, A5, A6, A7 | B1, B4, B6, B7 | C1, C3 | D2, D3, D5, D6 | E2, E3 |
| Central HC | A1, A5, A6, A7 | B9 | C3 | D2, D3, D5, D6 | E3 |
| Building | Nodes More Than 4 Degrees | All Nodes | Connector Ratio (%) |
|---|---|---|---|
| Schiphol Airport | 34 | 95 | 35.79 |
| MFA | 45 | 131 | 34.35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zlatanova, S.; Li, B.; van Oosterom, P.; Liu, H.; Barton, J. Indoor Routing on Logical Network Using Space Semantics. ISPRS Int. J. Geo-Inf. 2019, 8, 126. https://doi.org/10.3390/ijgi8030126
Liu L, Zlatanova S, Li B, van Oosterom P, Liu H, Barton J. Indoor Routing on Logical Network Using Space Semantics. ISPRS International Journal of Geo-Information. 2019; 8(3):126. https://doi.org/10.3390/ijgi8030126
Chicago/Turabian StyleLiu, Liu, Sisi Zlatanova, Bofeng Li, Peter van Oosterom, Hua Liu, and Jack Barton. 2019. "Indoor Routing on Logical Network Using Space Semantics" ISPRS International Journal of Geo-Information 8, no. 3: 126. https://doi.org/10.3390/ijgi8030126
APA StyleLiu, L., Zlatanova, S., Li, B., van Oosterom, P., Liu, H., & Barton, J. (2019). Indoor Routing on Logical Network Using Space Semantics. ISPRS International Journal of Geo-Information, 8(3), 126. https://doi.org/10.3390/ijgi8030126







