Evacuation Planning Optimization Based on a Multi-Objective Artificial Bee Colony Algorithm
Abstract
1. Introduction
2. Theoretical Background
2.1. Multi-Objective Optimization Problem
2.2. Mathematical Model for Evacuation Planning
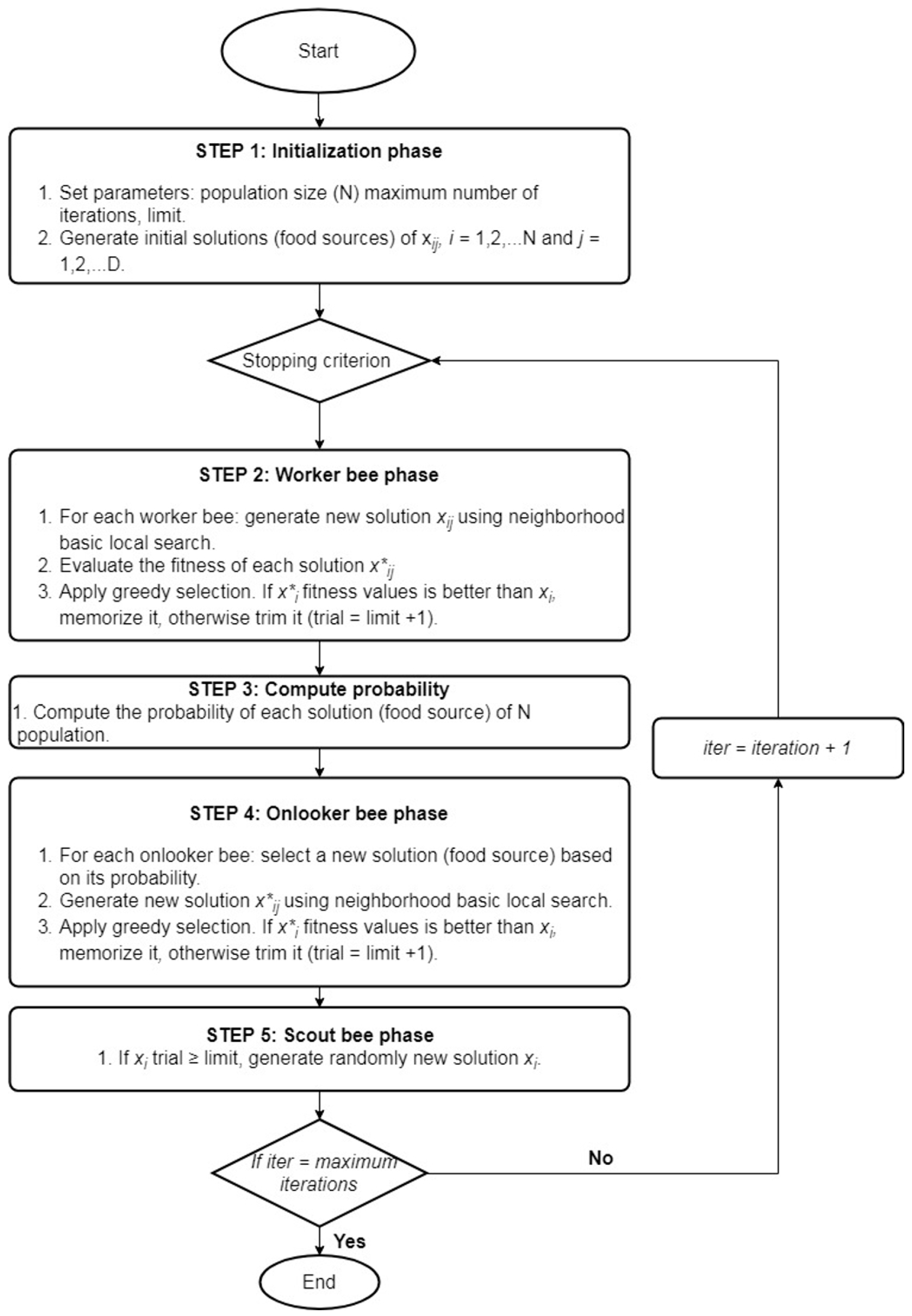
2.3. Introduction to Artificial Bee Colony Algorithm
3. Methodology
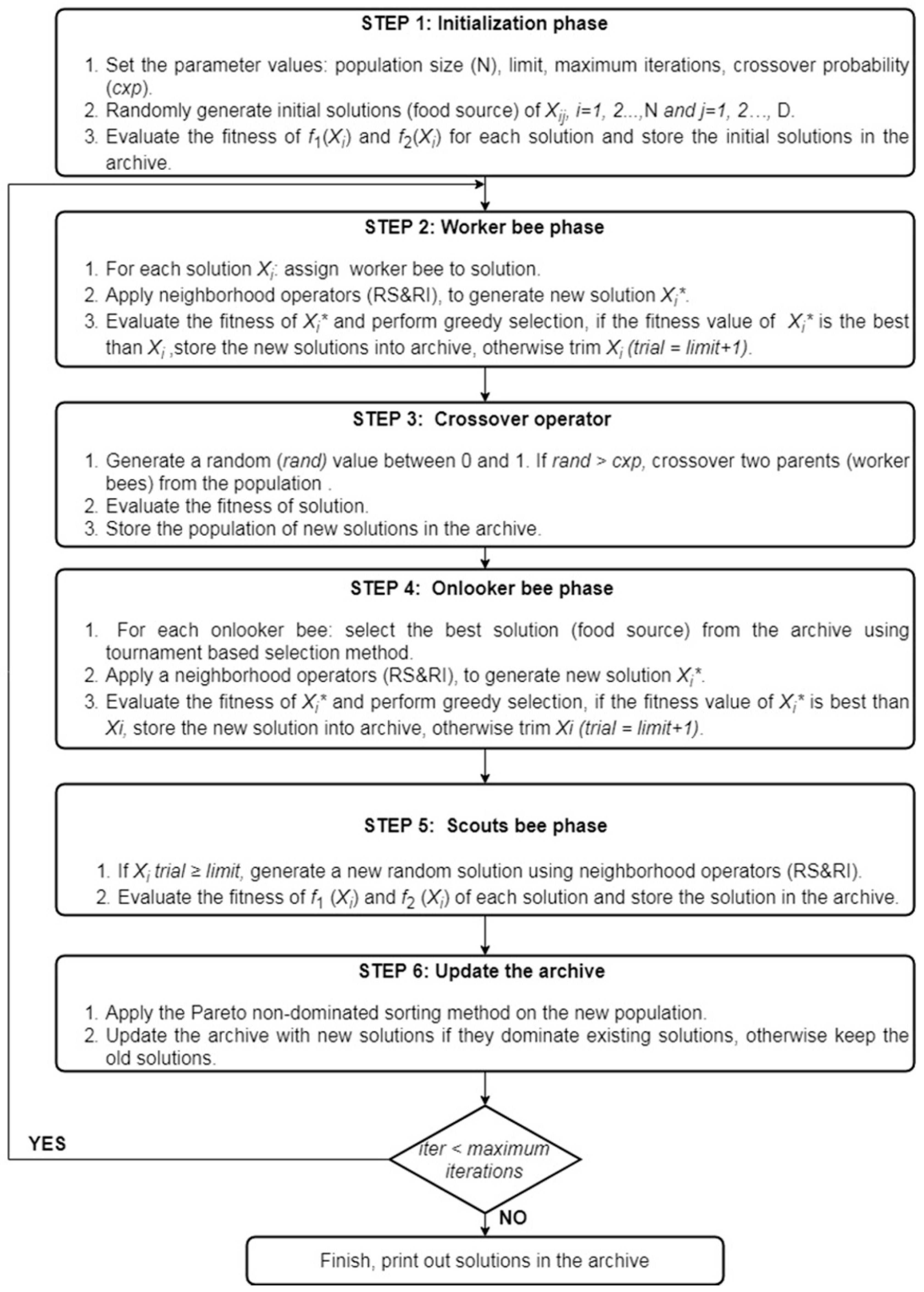
3.1. Modified ABC Algorithm for Multi-Objective Evacuation Problem
3.2. Encoding and Initialization of Solutions
3.3. Neighborhood Search Strategies
3.4. Crossover Operator
3.5. Selection of Onlooker Bees
3.6. Exploration of the Scout Bees
3.7. Pareto Optimization for Evaluation Fitness
4. Case Study
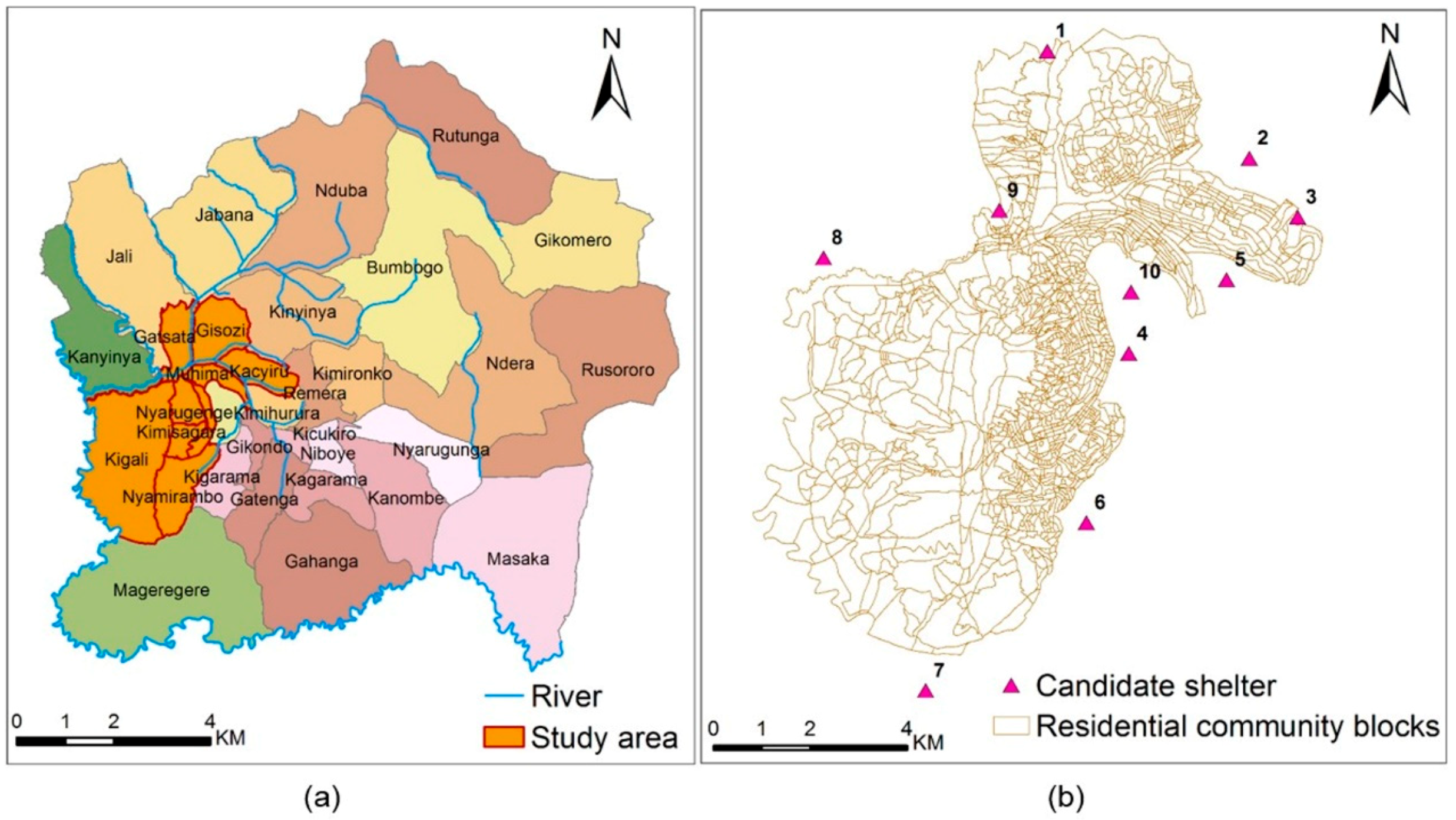
4.1. Input Data Preparation
4.1.1. Safe Area Selection and Capacity Computation
4.1.2. Distance Matrix
5. Results and Discussion
5.1. Parameter Setting
5.2. Effectiveness of Combining Neighborhood Search Random Swap and Random Insertion and Crossover Operator for MOABC
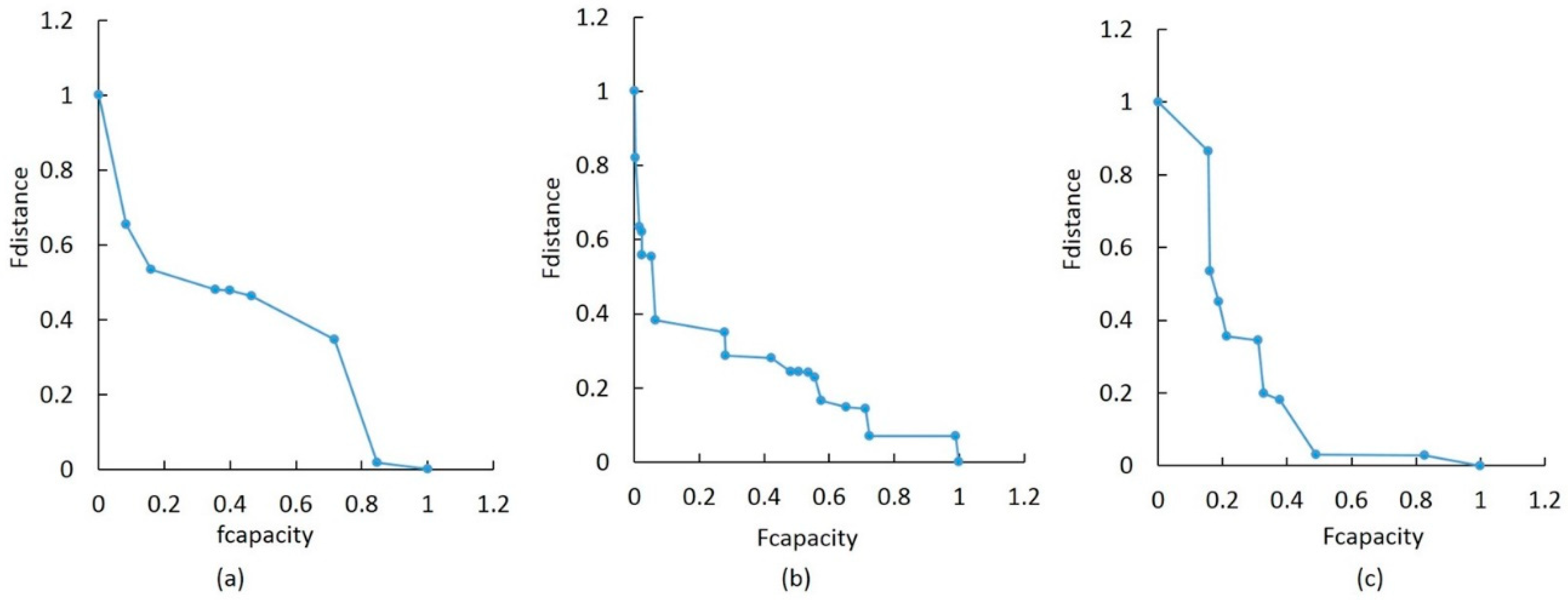
5.3. Pareto Optimal Front Analysis
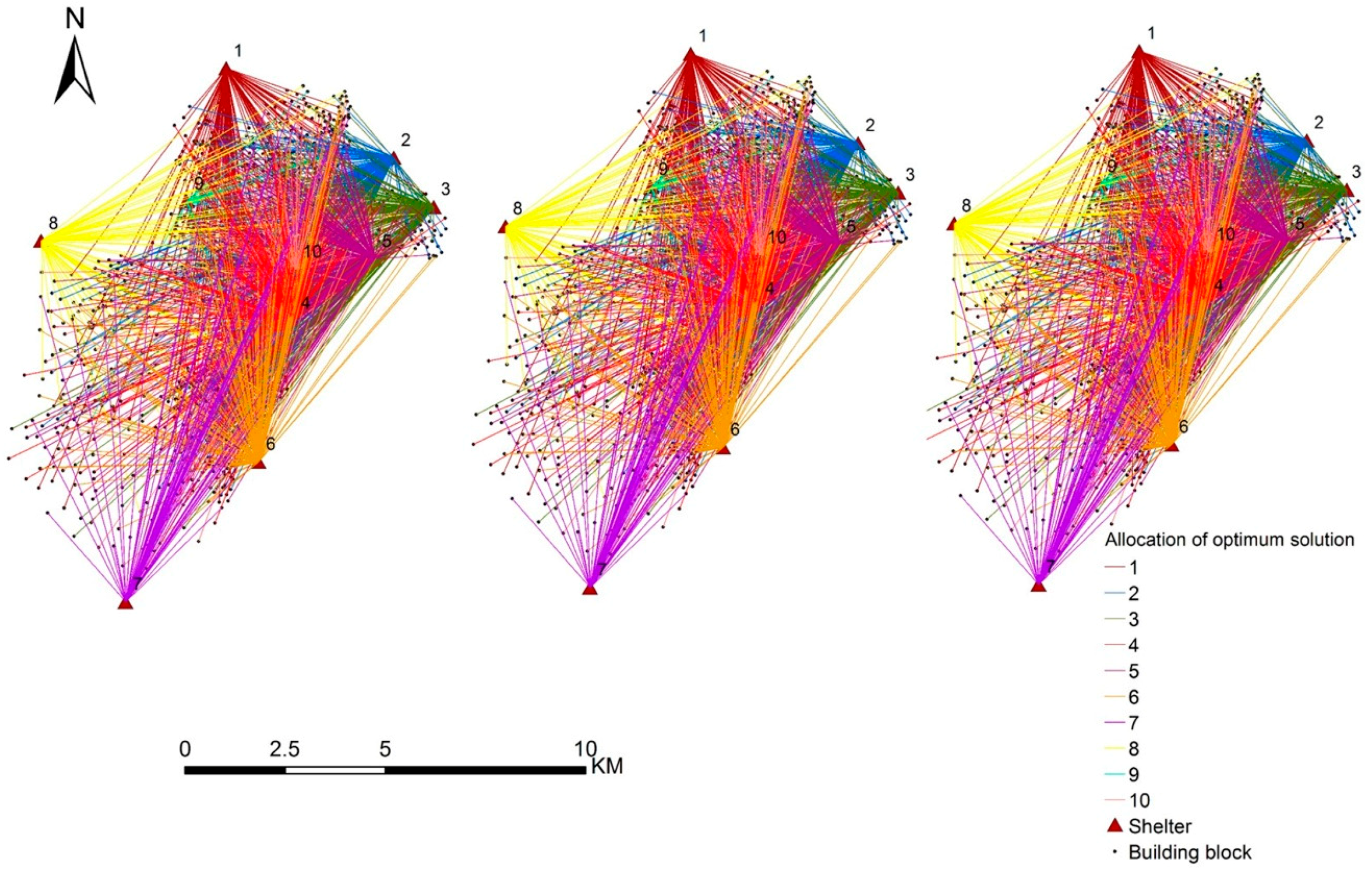
5.4. Optimization Results Analysis
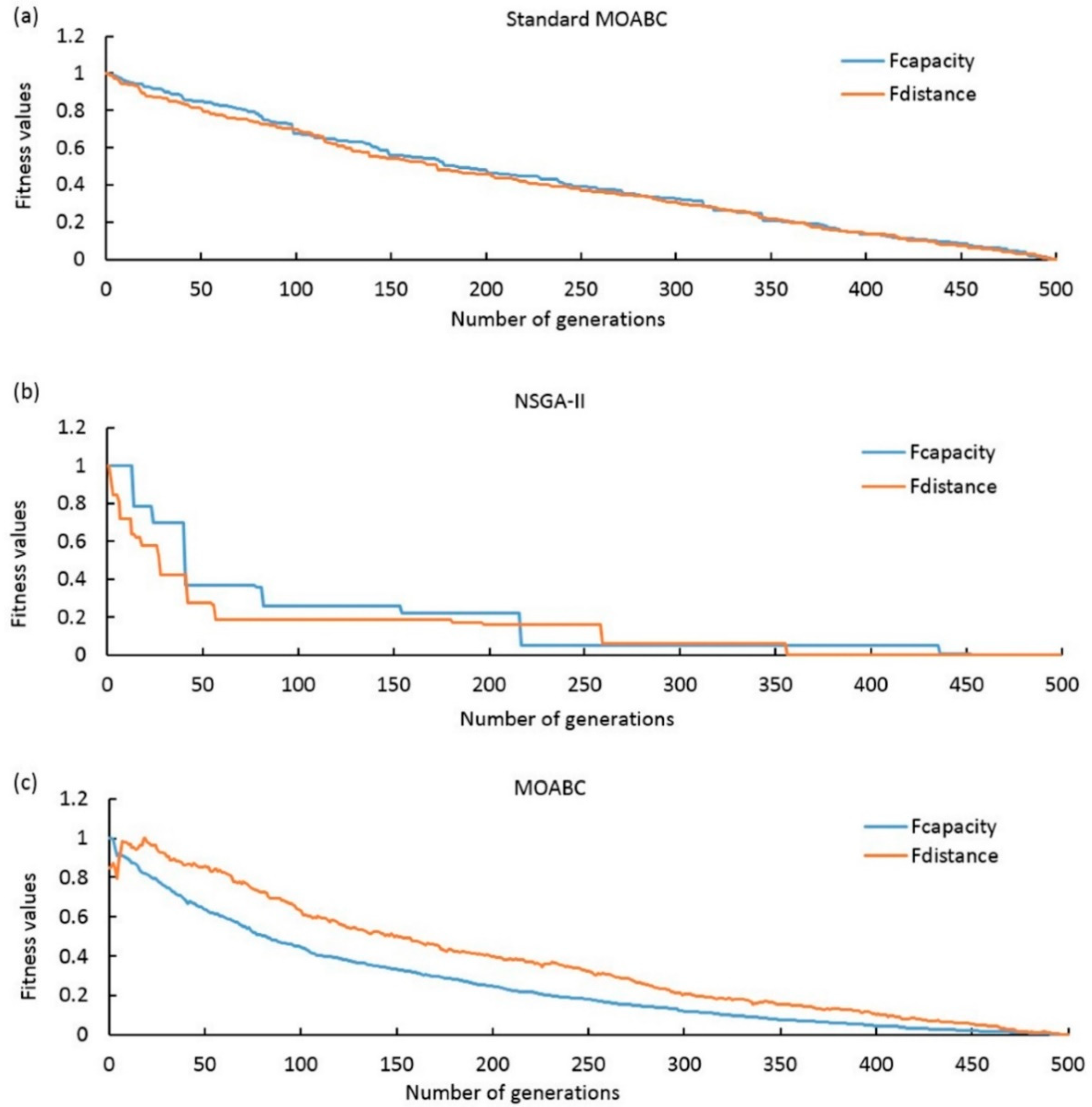
5.5. Comparison with Other Algorithms
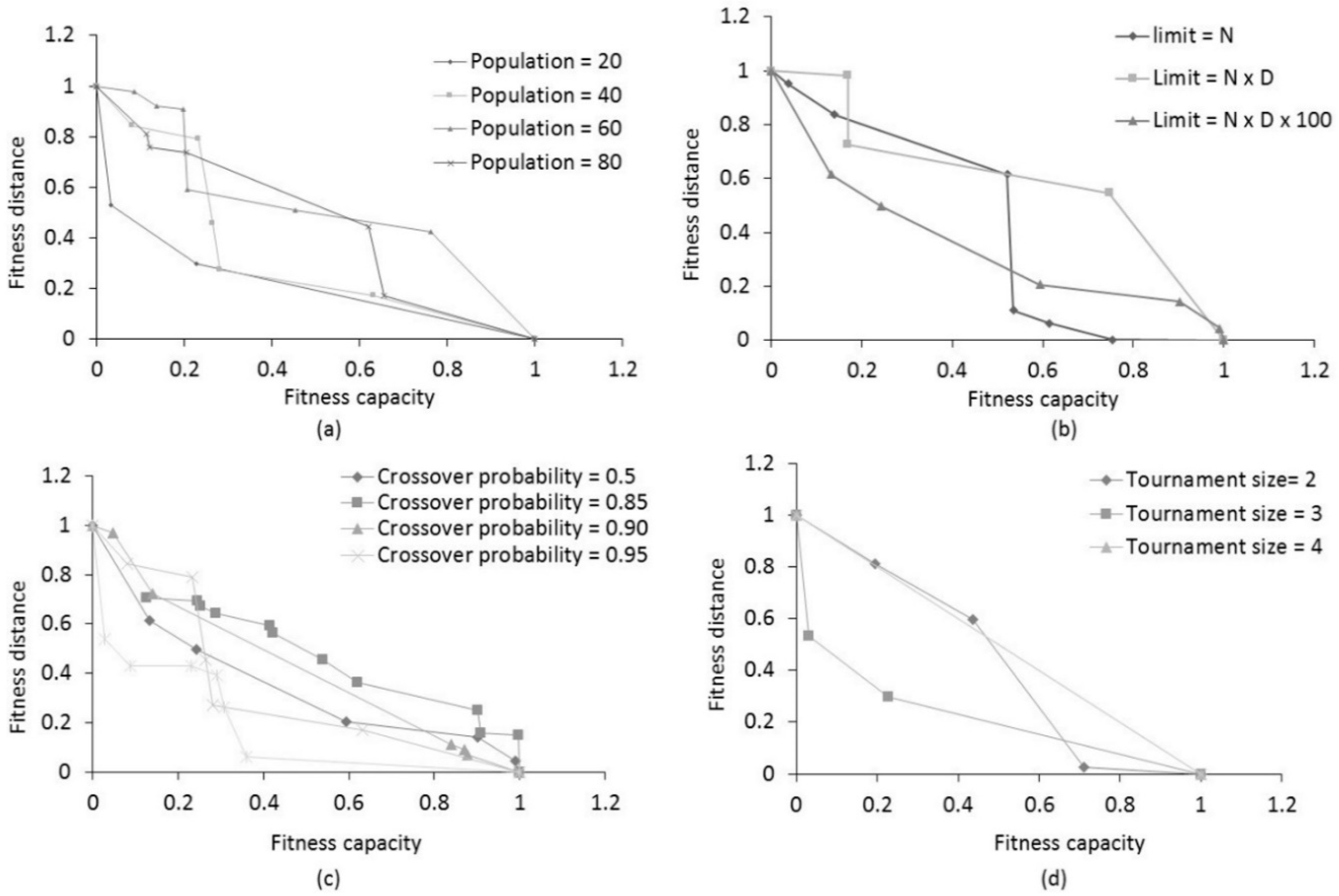
5.6. Sensitivity Analyses
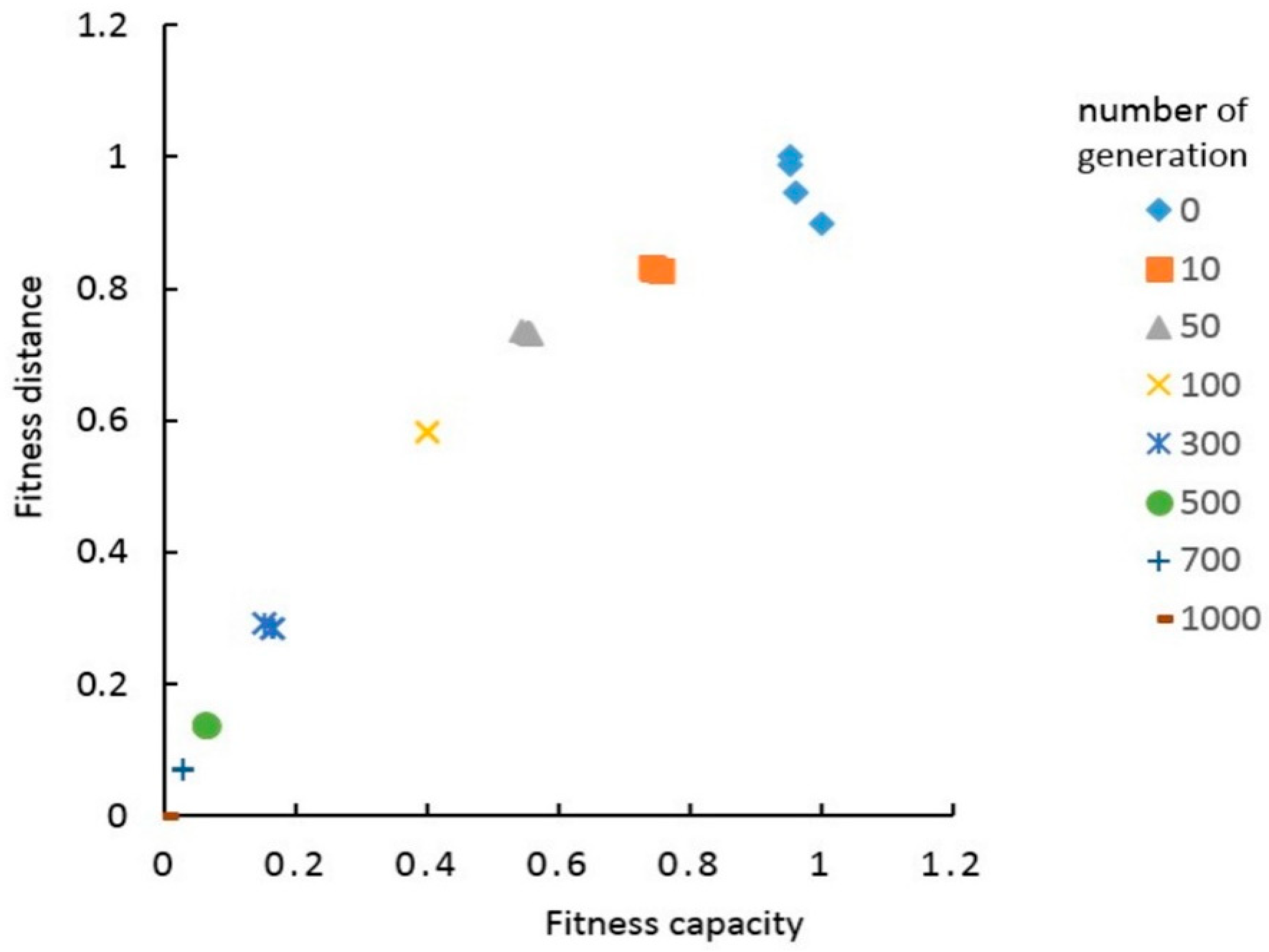
5.6.1. Impact of Parameters
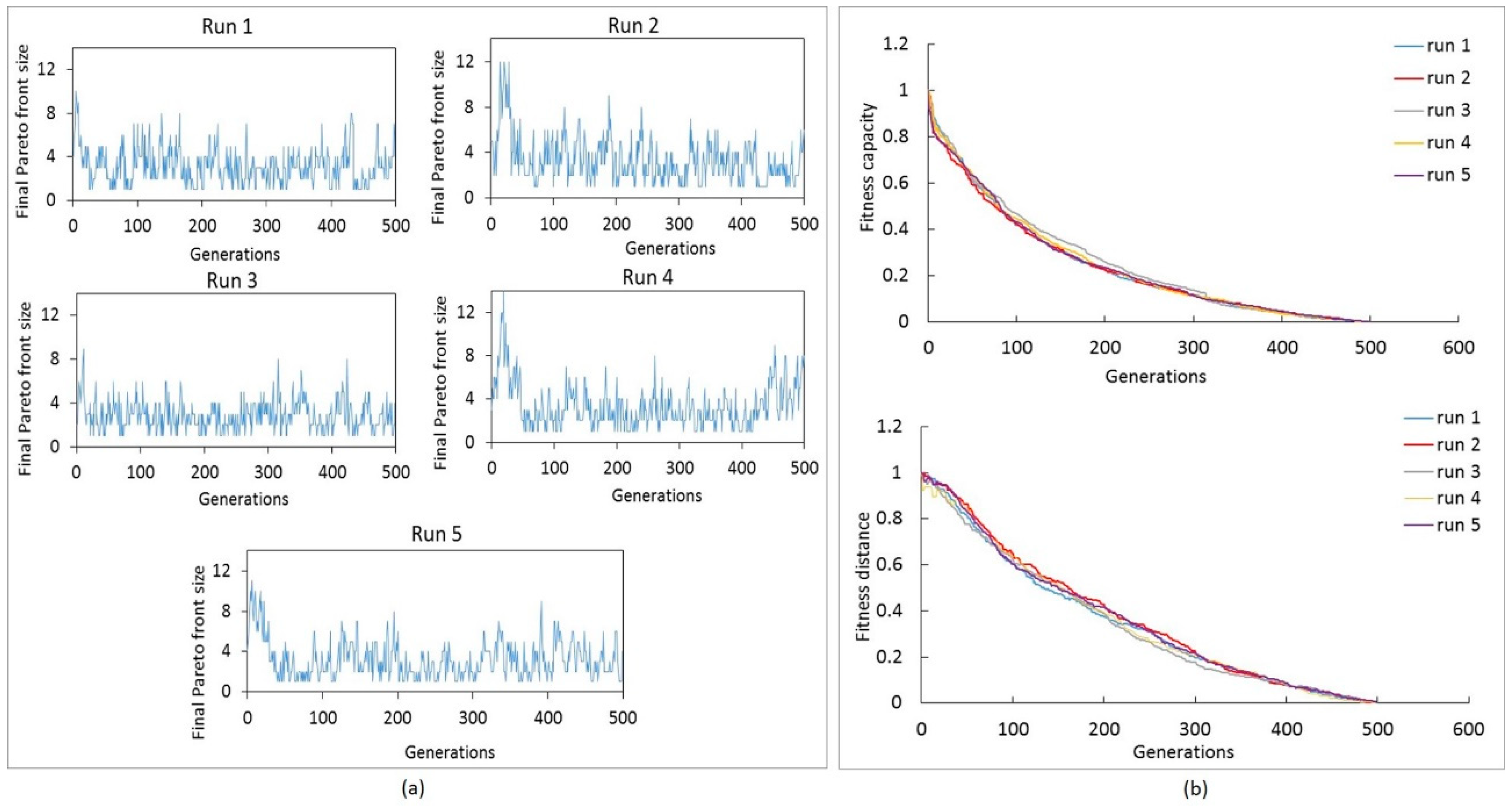
5.6.2. Repeatability Analysis
5.7. Potential Use of the Proposed MOABC
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dilley, M.; Chen, R.S.; Deichmann, U.; Lerner-Lam, A.L.; Arnold, M. Natural Disaster Hotspots: A Global Risk Analysis; The World Bank: Washington, DC, USA, 2005; ISBN 978-0-8213-5930-3. [Google Scholar]
- Guha-Sapir, D.; Hoyois, P.; Wallemacq, P.; Below, R. Annual Disaster Statistical Review 2016: The Numbers and Trends. Brussels: CRED; Centre for Research on the Epidemiology of Disasters (CRED), Institute of Health and Society (IRSS): Brussels, Belgium, 2016; p. 91. [Google Scholar]
- Yusoff, M.; Ariffin, J.; Mohamed, A. Optimization approaches for macroscopic emergency evacuation planning: A survey. In Proceedings of the 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–28 August 2008; Volume 3, pp. 1–7. [Google Scholar]
- Saadatseresht, M.; Mansourian, A.; Taleai, M. Evacuation planning using multiobjective evolutionary optimization approach. Eur. J. Oper. Res. 2009, 198, 305–314. [Google Scholar] [CrossRef]
- Horner, M.W.; Downs, J.A. Optimizing hurricane disaster relief goods distribution: Model development and application with respect to planning strategies. Disasters 2010, 34, 821–844. [Google Scholar] [CrossRef] [PubMed]
- Caunhye, A.M.; Nie, X.; Pokharel, S. Optimization models in emergency logistics: A literature review. Socio-Econ. Plan. Sci. 2012, 46, 4–13. [Google Scholar] [CrossRef]
- Kuligowski, E.D.; Peacock, R.D. A Review of Building Evacuation Models; National Bureau of Standards: Gaithersburg, MD, USA, 2005.
- Stepanov, A.; Smith, J.M. Multi-objective evacuation routing in transportation networks. Eur. J. Oper. Res. 2009, 198, 435–446. [Google Scholar] [CrossRef]
- Murray-Tuite, P.; Wolshon, B. Evacuation transportation modeling: An overview of research, development, and practice. Transp. Res. Part C Emerg. Technol. 2013, 27, 25–45. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Malczewski, J.; Rinner, C. Multicriteria Decision Analysis in Geographic Information Science; Advances in Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-540-74756-7. [Google Scholar]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-49690-9. [Google Scholar]
- Tong, D.; Murray, A.T. Spatial Optimization in Geography. Ann. Assoc. Am. Geogr. 2012, 102, 1290–1309. [Google Scholar] [CrossRef]
- Özdamar, L.; Ertem, M.A. Models, solutions and enabling technologies in humanitarian logistics. Eur. J. Oper. Res. 2015, 244, 55–65. [Google Scholar] [CrossRef]
- Alçada-Almeida, L.; Tralhão, L.; Santos, L.; Coutinho-Rodrigues, J. A Multiobjective Approach to Locate Emergency Shelters and Identify Evacuation Routes in Urban Areas. Geogr. Anal. 2009, 41, 9–29. [Google Scholar] [CrossRef]
- Coutinho-Rodrigues, J.; Tralhão, L.; Alçada-Almeida, L. Solving a location-routing problem with a multiobjective approach: The design of urban evacuation plans. J. Transp. Geogr. 2012, 22, 206–218. [Google Scholar] [CrossRef]
- Horner, M.W.; Ozguven, E.E.; Marcelin, J.M.; Kocatepe, A. Special needs hurricane shelters and the ageing population: Development of a methodology and a case study application. Disasters 2018, 42, 169–186. [Google Scholar] [CrossRef] [PubMed]
- Kocatepe, A.; Ozguven, E.E.; Horner, M.; Ozel, H. Pet- and special needs-friendly shelter planning in south Florida: A spatial capacitated p-median-based approach. Int. J. Disaster Risk Reduct. 2018, 31, 1207–1222. [Google Scholar] [CrossRef]
- Brownlee, J. Clever Algorithms: Nature-Inspired Programming Recipes; Revision 2; LuLu.com s.l.: Morrisville, NV, USA, 2012; ISBN 978-1-4467-8506-5. [Google Scholar]
- Zhou, A.; Qu, B.-Y.; Li, H.; Zhao, S.-Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Zhang, M.-X.; Zhang, B.; Zheng, Y.-J. Bio-Inspired Meta-Heuristics for Emergency Transportation Problems. Algorithms 2014, 7, 15–31. [Google Scholar] [CrossRef]
- Yanfang, L.; Dongping, M.; Jianyu, Y. Optimization of land use structure based on ecological GREEN equivalent. Geo-Spat. Inf. Sci. 2002, 5, 60–67. [Google Scholar] [CrossRef]
- Zhaobao, Z.; Hong, Z. The decision of the optimal parameters in Markov random fields of images by genetic algorithm. Geo-Spat. Inf. Sci. 2000, 3, 14–18. [Google Scholar] [CrossRef]
- Jiao, L.; Liu, Y. Model of land suitability evaluation based on computational intelligence. Geo-Spat. Inf. Sci. 2007, 10, 151–156. [Google Scholar] [CrossRef]
- Shaygan, M.; Alimohammadi, A.; Mansourian, A.; Govara, Z.S.; Kalami, S.M. Spatial Multi-Objective Optimization Approach for Land Use Allocation Using NSGA-II. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 906–916. [Google Scholar] [CrossRef]
- Song, M.; Chen, D. An improved knowledge-informed NSGA-II for multi-objective land allocation (MOLA). Geo-Spat. Inf. Sci. 2018, 21, 273–287. [Google Scholar] [CrossRef]
- Ma, S.; He, J.; Liu, F.; Yu, Y. Land-use spatial optimization based on PSO algorithm. Geo-Spat. Inf. Sci. 2011, 14, 54–61. [Google Scholar] [CrossRef]
- Ai, B.; Ma, S.; Wang, S. Land-use zoning in fast developing coastal area with ACO model for scenario decision-making. Geo-Spat. Inf. Sci. 2015, 18, 43–55. [Google Scholar] [CrossRef]
- Eldrandaly, K.A.; Abdallah, A.F. A novel GIS-based decision-making framework for the school bus routing problem. Geo-Spat. Inf. Sci. 2012, 15, 51–59. [Google Scholar] [CrossRef]
- Lei, T.L.; Church, R.L.; Lei, Z. A unified approach for location-allocation analysis: Integrating GIS, distributed computing and spatial optimization. Int. J. Geogr. Inf. Sci. 2016, 30, 515–534. [Google Scholar] [CrossRef]
- Yang, L.; Sun, X.; Peng, L.; Shao, J.; Chi, T. An improved artificial bee colony algorithm for optimal land-use allocation. Int. J. Geogr. Inf. Sci. 2015, 29, 1470–1489. [Google Scholar] [CrossRef]
- Goerigk, M.; Deghdak, K.; Heßler, P. A comprehensive evacuation planning model and genetic solution algorithm. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 82–97. [Google Scholar] [CrossRef]
- Zheng, Y.-J.; Chen, S.-Y.; Ling, H.-F. Evolutionary optimization for disaster relief operations: A survey. Appl. Soft Comput. 2015, 27, 553–566. [Google Scholar] [CrossRef]
- Garrett, A.; Carnahan, B.; Muhdi, R.; Davis, J.; Dozier, G.; SanSoucie, M.P.; Hull, P.V.; Tinker, M.L. Evacuation Planning via Evolutionary Computation. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 157–164. [Google Scholar]
- Georgiadou, P.S.; Papazoglou, I.A.; Kiranoudis, C.T.; Markatos, N.C. Multi-objective evolutionary emergency response optimization for major accidents. J. Hazard. Mater. 2010, 178, 792–803. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Xu, W.; Li, X. A modified particle swarm optimization algorithm for optimal allocation of earthquake emergency shelters. Int. J. Geogr. Inf. Sci. 2012, 26, 1643–1666. [Google Scholar] [CrossRef]
- Xu, W.; Ma, Y.; Zhao, X.; Li, Y.; Qin, L.; Du, J. A comparison of scenario-based hybrid bilevel and multi-objective location-allocation models for earthquake emergency shelters: A case study in the central area of Beijing, China. Int. J. Geogr. Inf. Sci. 2018, 32, 236–256. [Google Scholar] [CrossRef]
- Zong, X.; Xiong, S.; Fang, Z.; Li, Q. Multi-Objective Optimization for Massive Pedestrian Evacuation Using Ant Colony Algorithm. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Tan, K.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6145, pp. 636–642. ISBN 978-3-642-13494-4. [Google Scholar]
- Saeidian, B.; Mesgari, M.S.; Pradhan, B.; Ghodousi, M. Optimized Location-Allocation of Earthquake Relief Centers Using PSO and ACO, Complemented by GIS, Clustering, and TOPSIS. ISPRS Int. J. Geo-Inf. 2018, 7, 292. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005. [Google Scholar]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Fang, Z.; Li, L.; Li, B.; Zhu, J.; Li, Q.; Xiong, S. An artificial bee colony-based multi-objective route planning algorithm for use in pedestrian navigation at night. Int. J. Geogr. Inf. Sci. 2017, 31, 2020–2044. [Google Scholar] [CrossRef]
- Luo, J.; Liu, Q.; Yang, Y.; Li, X.; Chen, M.; Cao, W. An Artificial Bee Colony Algorithm for Multi-objective Optimisation. Appl. Soft Comput. 2017, 50, 235–251. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, A.; Shao, J.; Chi, T. A Knowledge-Informed and Pareto-Based Artificial Bee Colony Optimization Algorithm for Multi-Objective Land-Use Allocation. ISPRS Int. J. Geo-Inf. 2018, 7, 63. [Google Scholar] [CrossRef]
- Akbari, R.; Hedayatzadeh, R.; Ziarati, K.; Hassanizadeh, B. A multi-objective artificial bee colony algorithm. Swarm Evol. Comput. 2012, 2, 39–52. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lamont, G.B.; Veldhuizen, D.A.V. Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd ed.; Springer: New York, NY, USA, 2007; p. 810. [Google Scholar]
- Zhang, H.; Zhu, Y.; Zou, W.; Yan, X. A hybrid multi-objective artificial bee colony algorithm for burdening optimization of copper strip production. Appl. Math. Model. 2012, 36, 2578–2591. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Hassani, A.; Mousavi, S.M.; Baygi, M.B. A hybrid artificial bee colony for disruption in a hierarchical maximal covering location problem. Comput. Ind. Eng. 2014, 75, 129–141. [Google Scholar] [CrossRef]
- Huo, Y.; Zhuang, Y.; Gu, J.; Ni, S. Elite-guided multi-objective artificial bee colony algorithm. Appl. Soft Comput. 2015, 32, 199–210. [Google Scholar] [CrossRef]
- Roberts, S.A.; Hall, G.B.; Calamai, P.H. Evolutionary Multi-objective Optimization for landscape system design. J. Geogr. Syst. 2011, 13, 299–326. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- NISR Population and Housing Census of Rwanda, 2012—Rwanda Data Portal. Available online: http://rwanda.opendataforafrica.org//pkzmyhf/population-and-housing-census-of-rwanda-2012 (accessed on 22 November 2018).
- Bizimana, J.P.; Schilling, M. Geo-Information Technology for Infrastructural Flood Risk Analysis in Unplanned Settlements: A case study of informal settlement flood risk in the Nyabugogo flood plain, Kigali City, Rwanda. In Geospatial Techniques in Urban Hazard and Disaster Analysis; Springer: Berlin/Heidelberg, Germany, 2009; pp. 99–124. [Google Scholar]
- MIDIMAR. The National Risk Atlas of Rwanda; MIDIMAR: Kigali, Rwanda, 2015.
- Rolland, E.; Patterson, R.A.; Ward, K.; Dodin, B. Decision support for disaster management. Oper. Manag. Res. 2010, 3, 68–79. [Google Scholar] [CrossRef]
- The Sphere Project. Humanitarian Charter and Minimum Standards in Humanitarian Response: The Sphere Handbook; The Sphere Project: Rugby, Warwickshire, UK, 2011; ISBN 978-1-908176-00-4. [Google Scholar]
- Fortin, F.-A.; Rainville, F.M.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary Algorithms Made Easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]



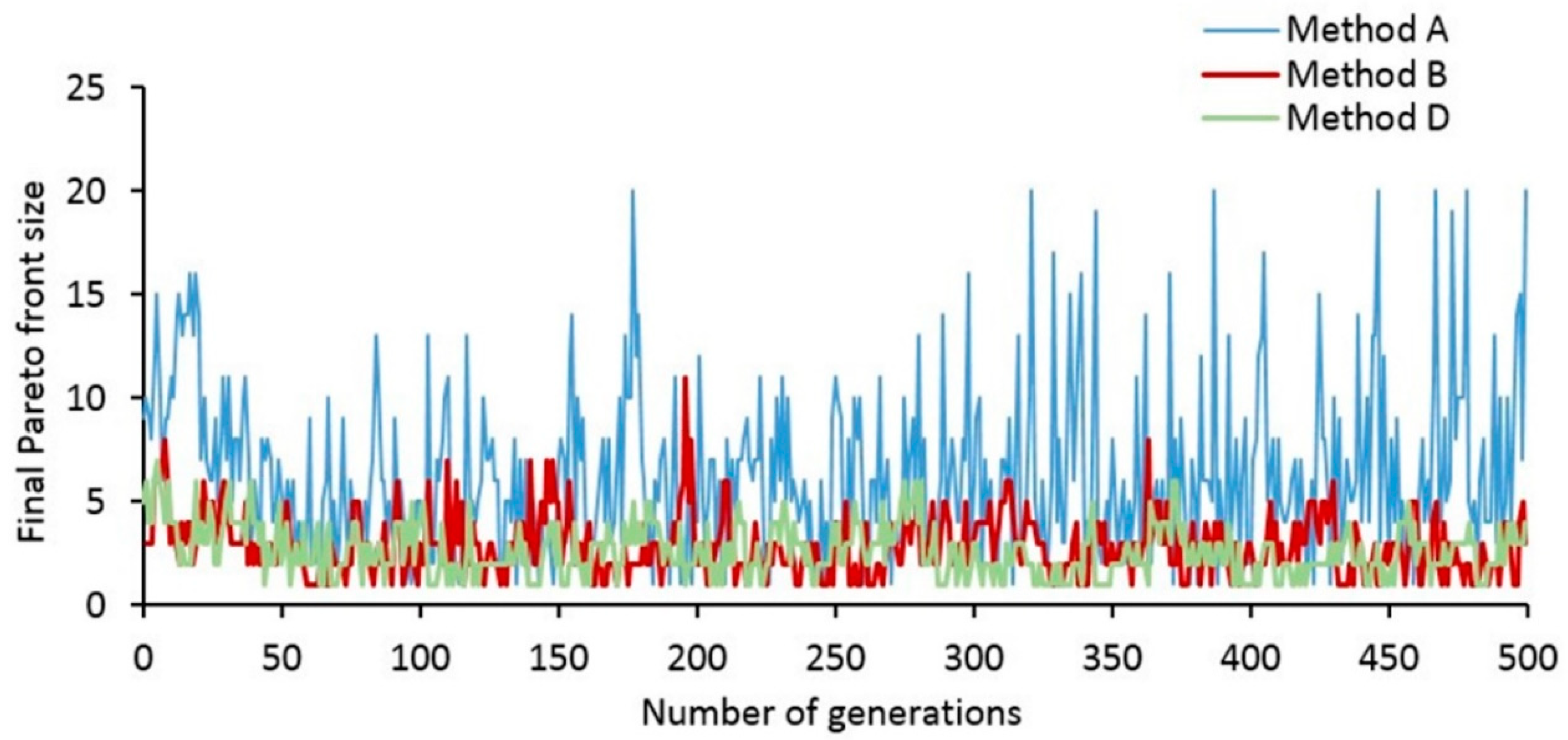
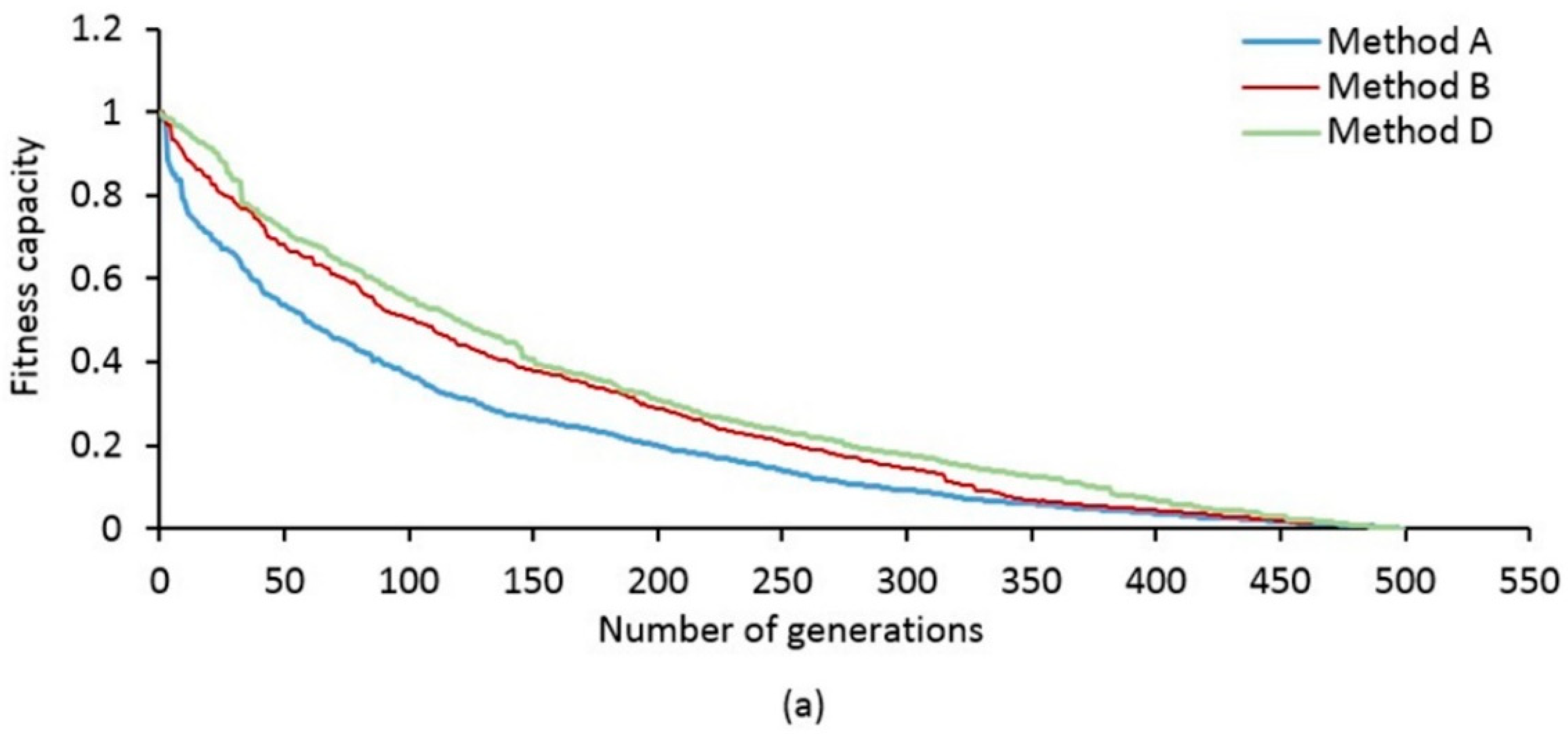
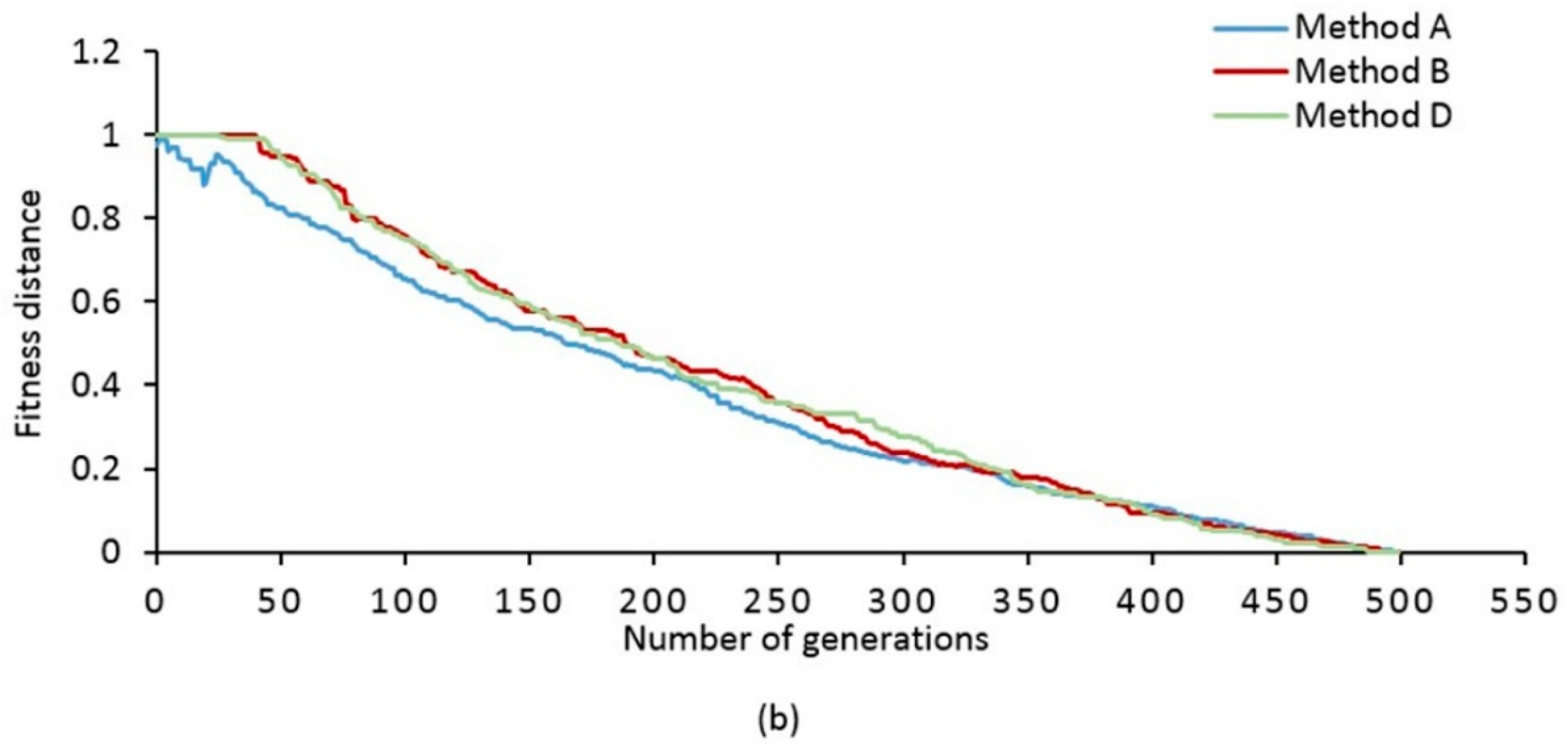
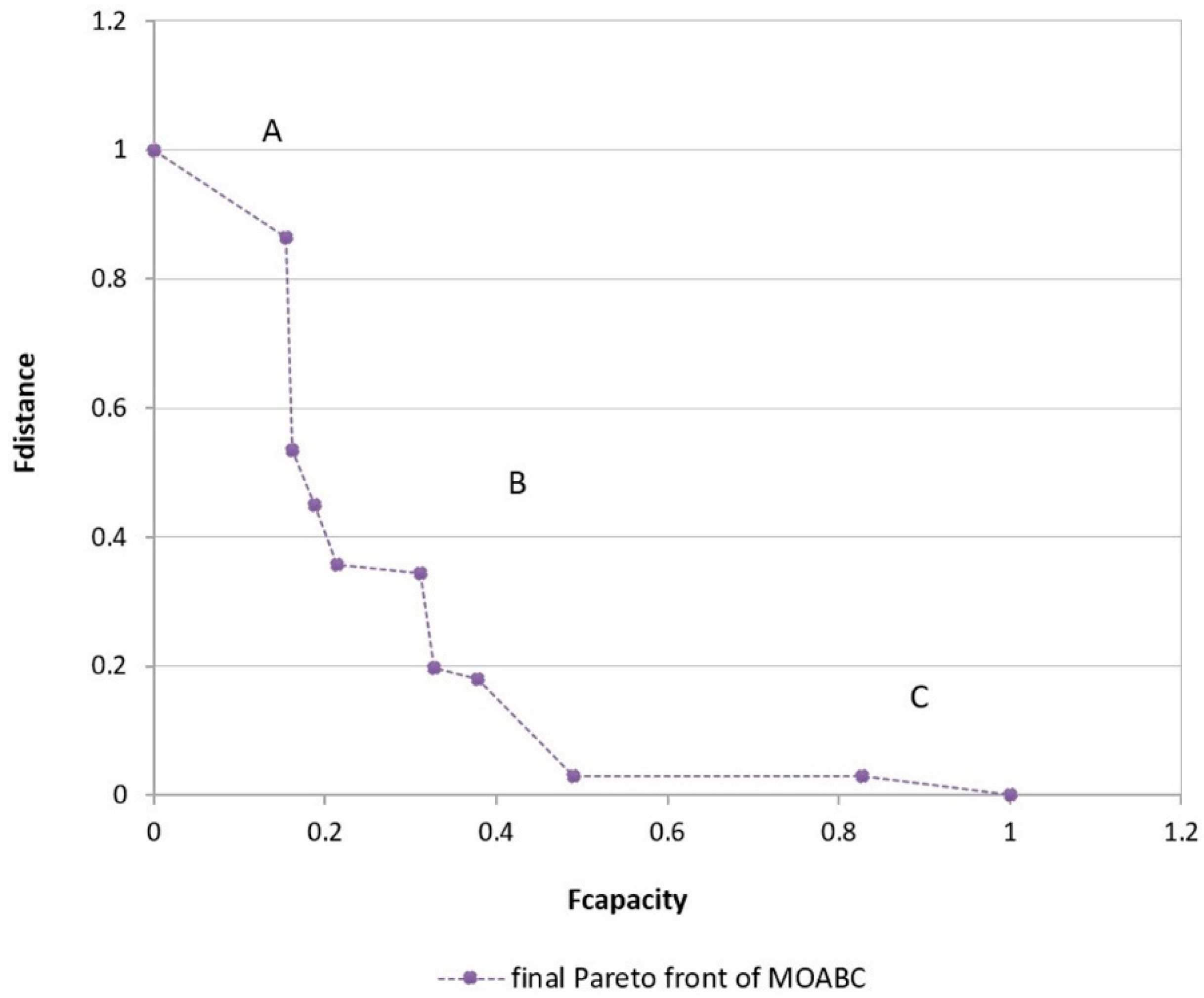

| Parameter | Value |
|---|---|
| Population size | 20 |
| Limit | N × D × 100 |
| Crossover probability rate | 0.5 |
| Tournament size | 3 |
| Maximum number of generations | 500 |
| Method | Algorithm | Population Size | Number of Generations | Final Pareto Front Size | Fcapacity | Fdistance | Execution Time (s) |
|---|---|---|---|---|---|---|---|
| A | MOABC with Combination of RS and RI | 20 | 500 | 8 | 3.44 | 9.29 × 108 | 199 |
| B | MOABC with the basic local search strategy | 20 | 500 | 3 | 3.96 | 8.61 × 108 | 274 |
| C | MOABC with crossover operator | 20 | 500 | 8 | 3.44 | 9.29 × 108 | 199 |
| D | MOABC without a crossover operator | 20 | 500 | 4 | 6.02 | 9.04 × 108 | 193 |
| Algorithm | Minimum Fitness Value of Fcapacity | Minimum Fitness Value of Fdistance | Execution Time (s) |
|---|---|---|---|
| Standard MOABC | 49.0 | 1.18 × 109 | 163 |
| NSGA-II | 38.9 | 1.08 × 109 | 1971 |
| Proposed MOABC | 5.8 | 8.72 × 108 | 161 |
| Run | Population Size | Number of Generations | Final Pareto Front Size | Fitness Value of Fcapacity | Fitness Value of Fdistance | Variance (Fcapacity) | Variance (Fdistance) |
|---|---|---|---|---|---|---|---|
| 1 | 20 | 500 | 4 | 4.73 | 8.84 × 108 | 0.056 | 0.080 |
| 2 | 20 | 500 | 6 | 5.85 | 8.89 × 108 | 0.051 | 0.086 |
| 3 | 20 | 500 | 4 | 5.62 | 8.83 × 108 | 0.058 | 0.080 |
| 4 | 20 | 500 | 8 | 5.1 | 8.87 × 108 | 0.057 | 0.082 |
| 5 | 20 | 500 | 4 | 6.29 | 8.91 × 108 | 0.053 | 0.082 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niyomubyeyi, O.; Pilesjö, P.; Mansourian, A. Evacuation Planning Optimization Based on a Multi-Objective Artificial Bee Colony Algorithm. ISPRS Int. J. Geo-Inf. 2019, 8, 110. https://doi.org/10.3390/ijgi8030110
Niyomubyeyi O, Pilesjö P, Mansourian A. Evacuation Planning Optimization Based on a Multi-Objective Artificial Bee Colony Algorithm. ISPRS International Journal of Geo-Information. 2019; 8(3):110. https://doi.org/10.3390/ijgi8030110
Chicago/Turabian StyleNiyomubyeyi, Olive, Petter Pilesjö, and Ali Mansourian. 2019. "Evacuation Planning Optimization Based on a Multi-Objective Artificial Bee Colony Algorithm" ISPRS International Journal of Geo-Information 8, no. 3: 110. https://doi.org/10.3390/ijgi8030110
APA StyleNiyomubyeyi, O., Pilesjö, P., & Mansourian, A. (2019). Evacuation Planning Optimization Based on a Multi-Objective Artificial Bee Colony Algorithm. ISPRS International Journal of Geo-Information, 8(3), 110. https://doi.org/10.3390/ijgi8030110






