Integrating Island Spatial Information and Integer Optimization for Locating Maritime Search and Rescue Bases: A Case Study in the South China Sea
Abstract
1. Introduction
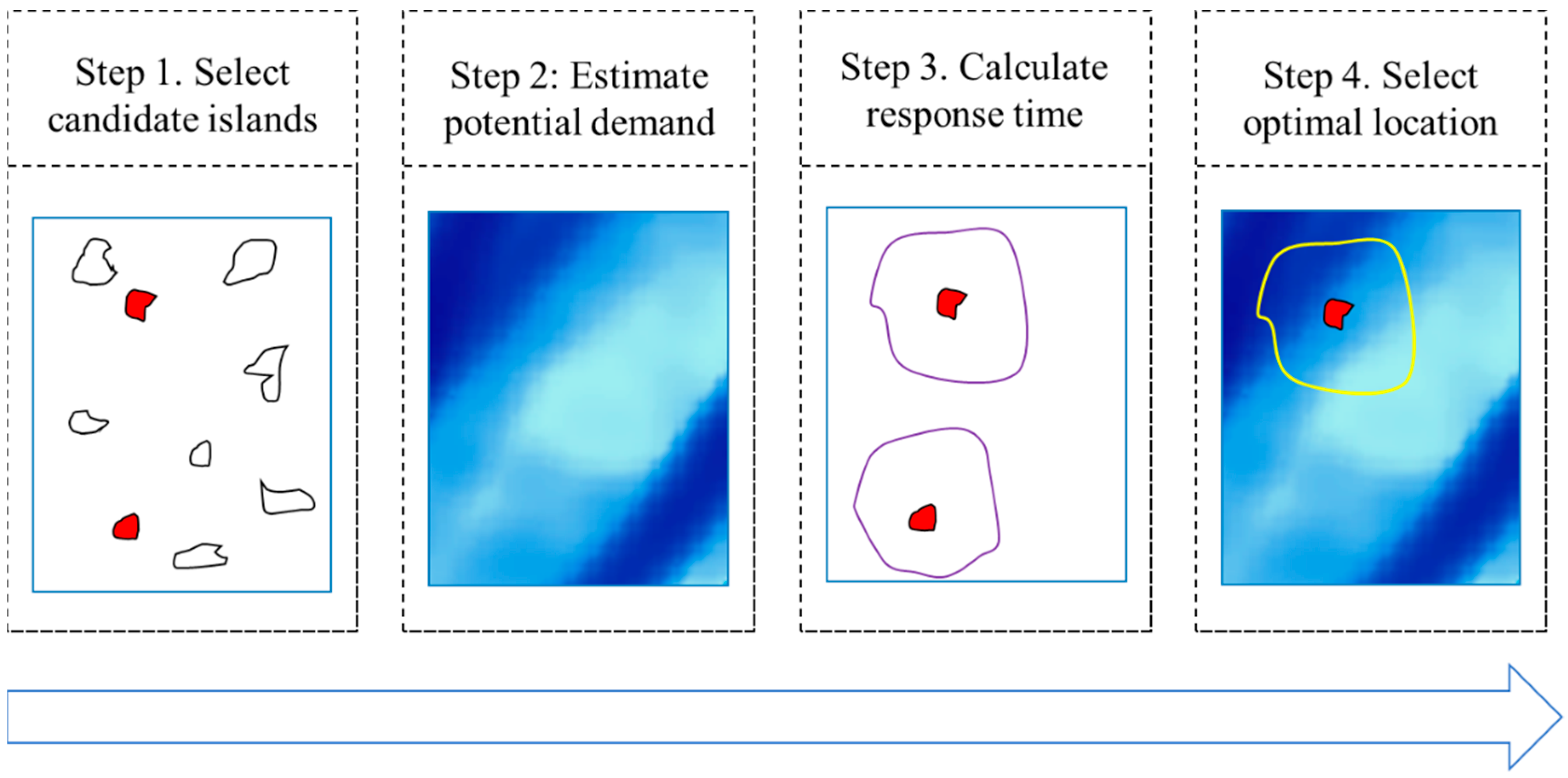
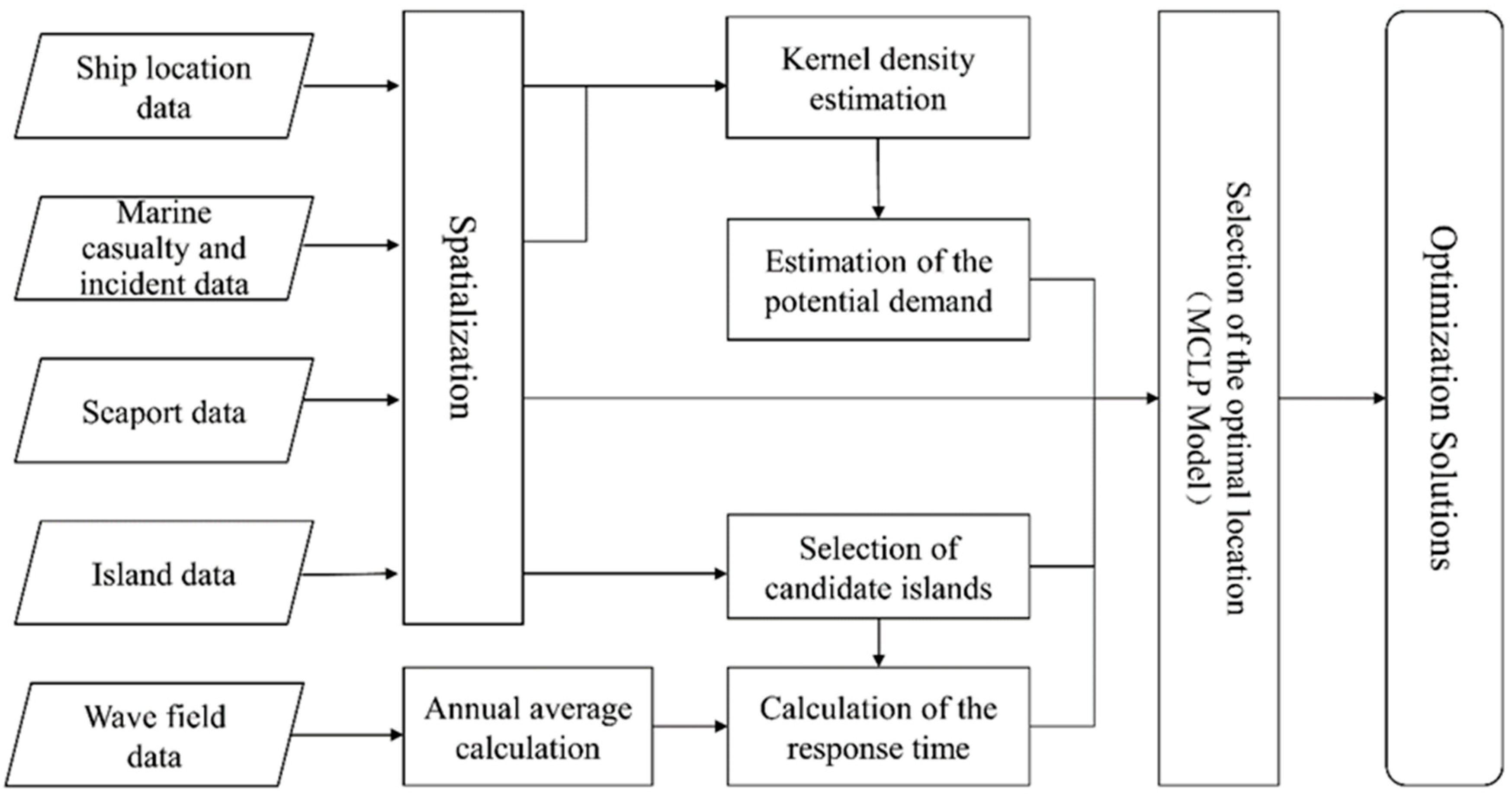
2. Methodology
2.1. Selection of Candidate Islands for a Maritime SAR Base
2.2. Estimation of the Potential Demand
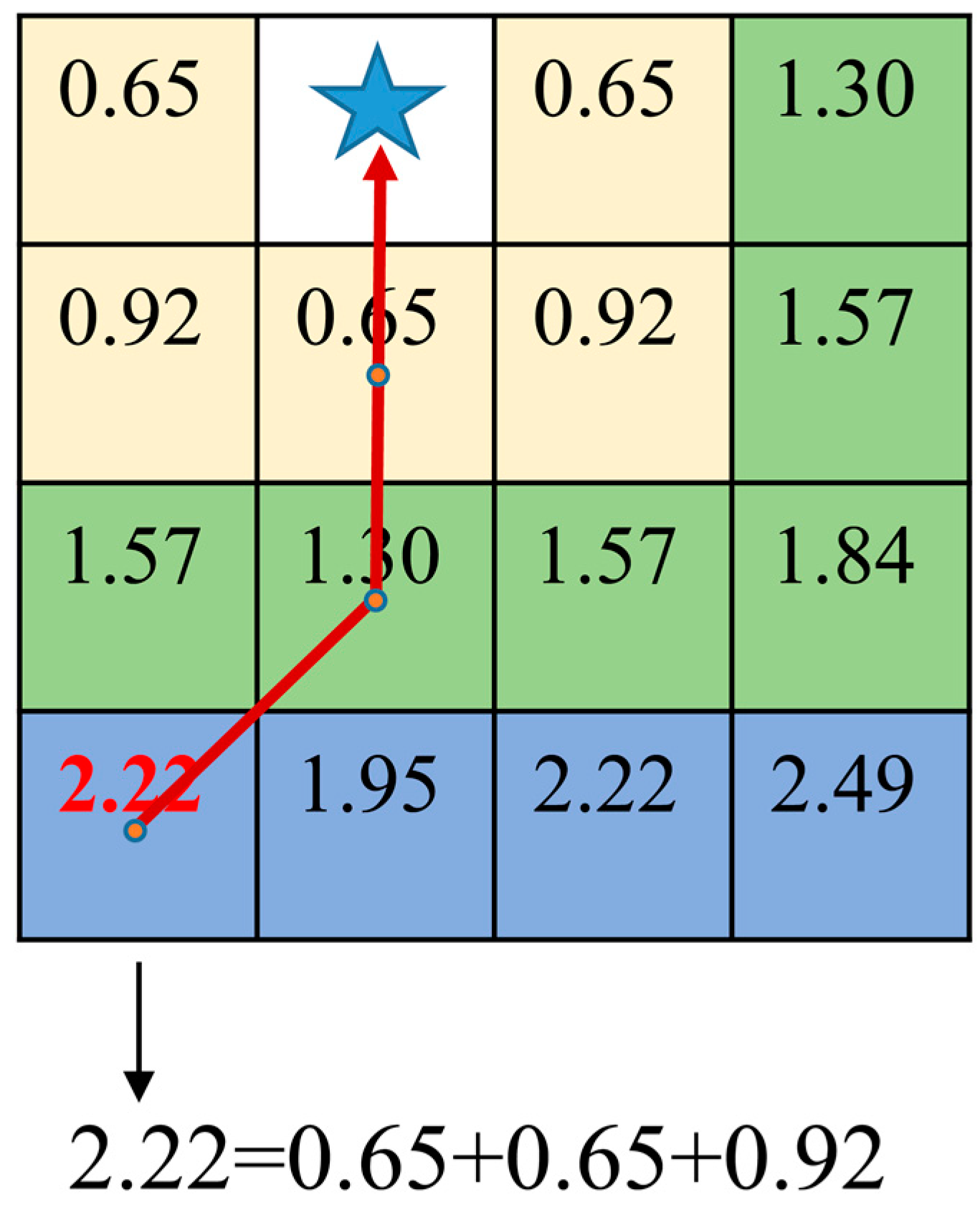
2.3. Calculation of the Response Time of the Rescue Vessel
2.4. Selection of the Optimal Location
3. An Illustrative Case Study
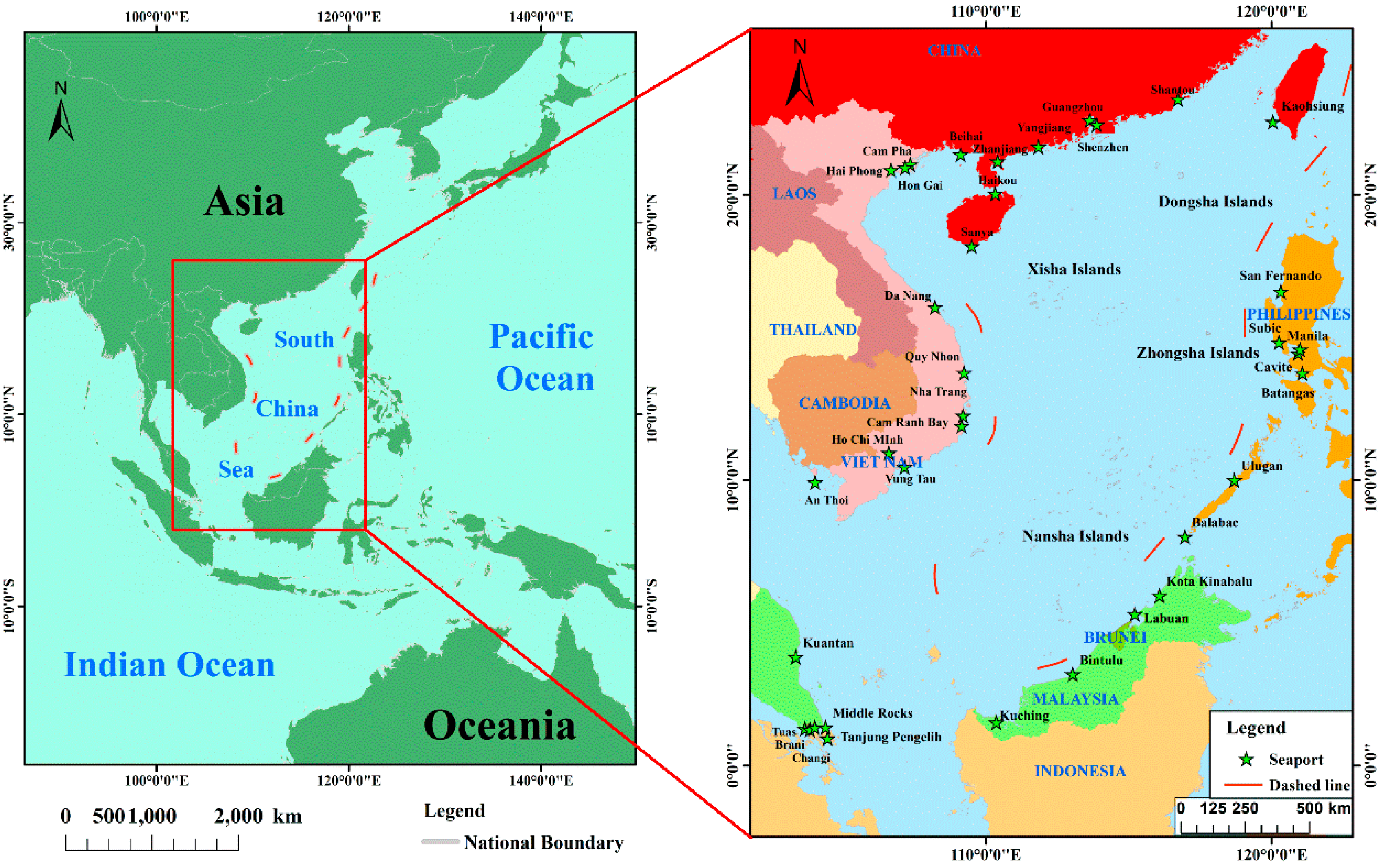
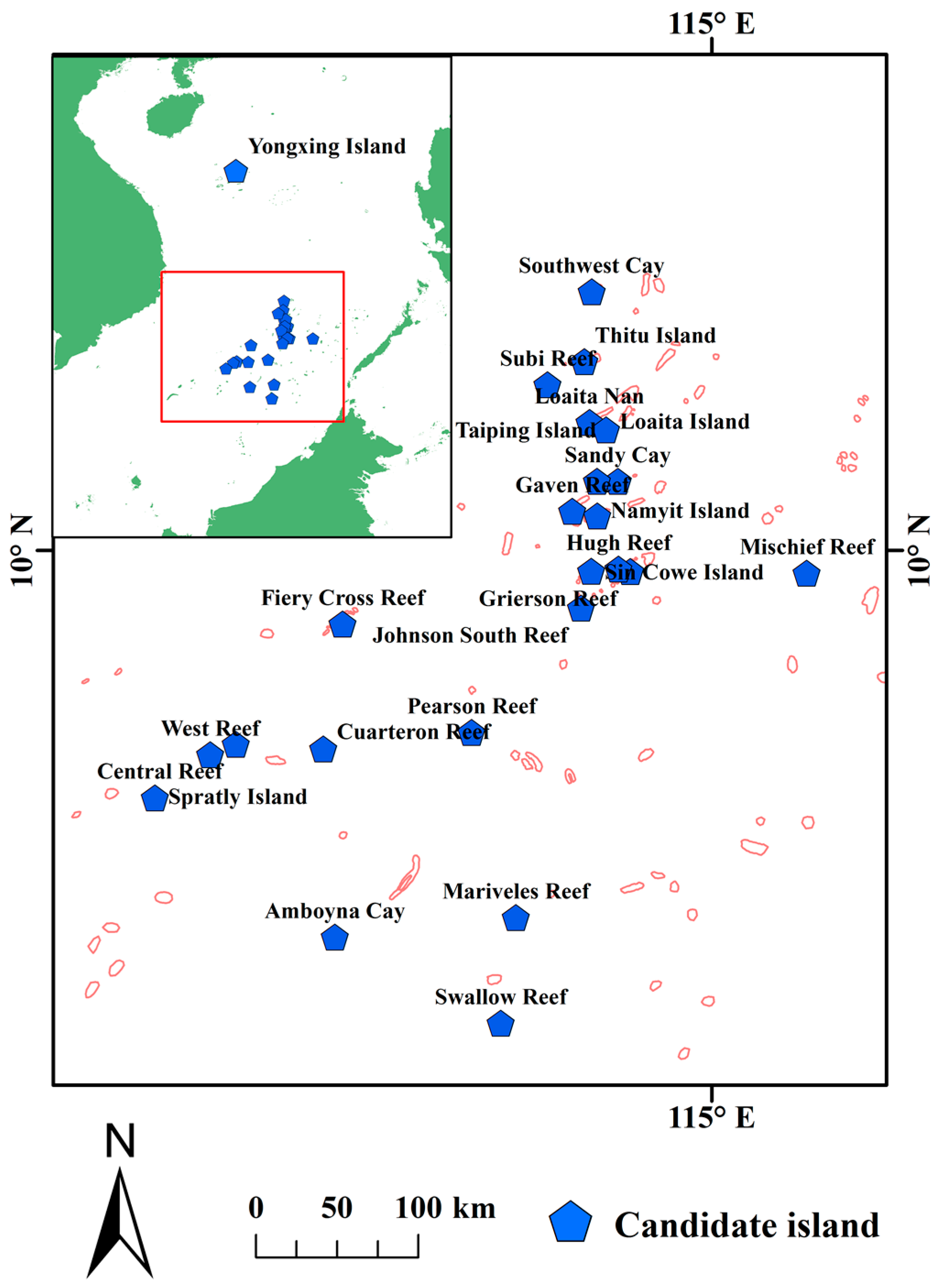
3.1. Study Area
3.2. Data and Preprocessing
4. Results
4.1. Candidate Islands for Maritime SAR Bases
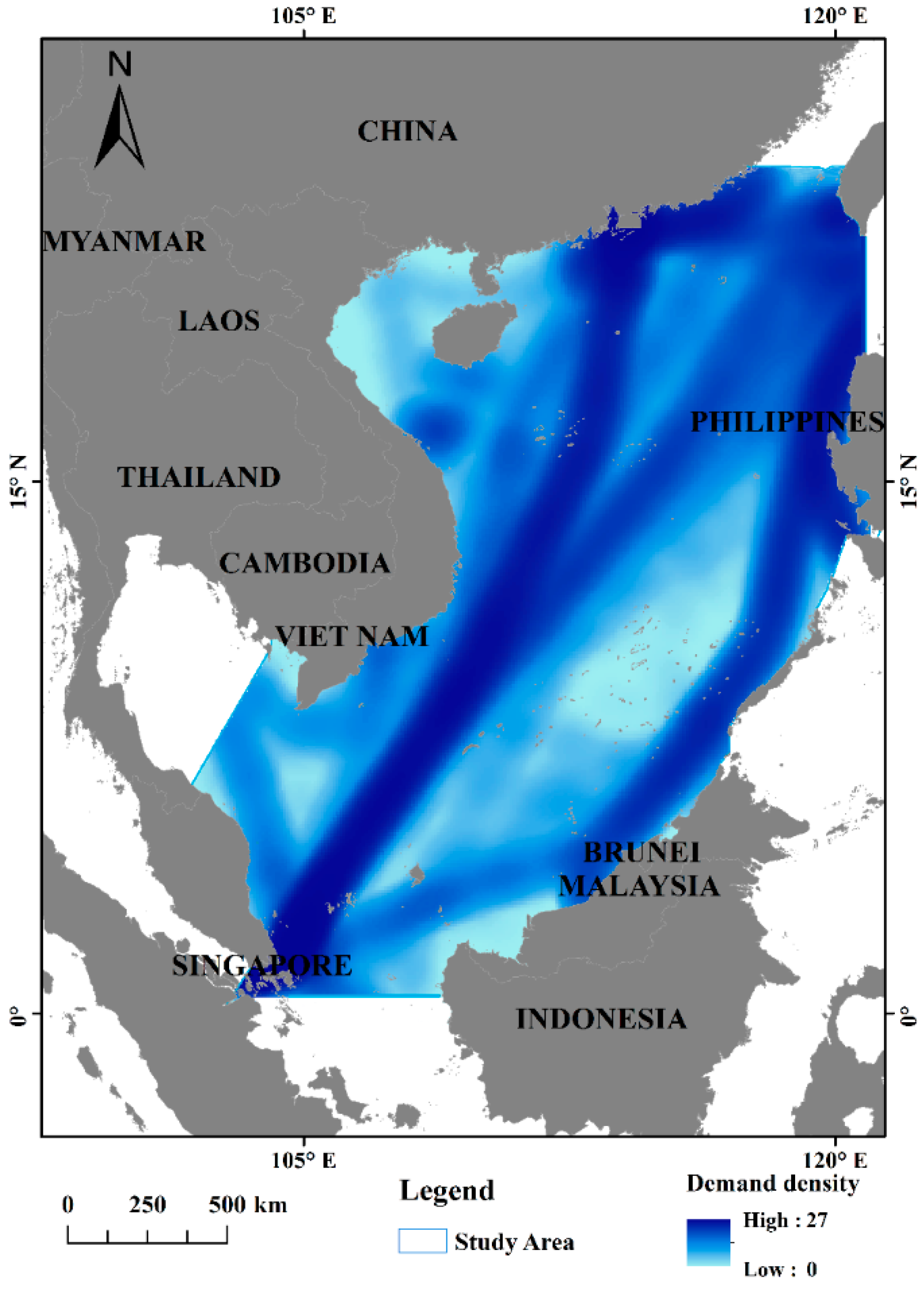
4.2. Potential Demand
4.3. Optimization Solutions
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, J.F.; Teixeira, A.P.; Soares, C.G.; Yan, X.P. Probabilistic modelling of the drifting trajectory of an object under the effect of wind and current for maritime search and rescue. Ocean Eng. 2017, 129, 253–264. [Google Scholar] [CrossRef]
- Breivik, O.; Allen, A.A. An operational search and rescue model for the Norwegian Sea and the North Sea. J. Mar. Syst. 2008, 69, 99–113. [Google Scholar] [CrossRef]
- Baldauf, M.; Benedict, K.; Fischer, S.; Gluch, M.; Kirchhoff, M.; Klaes, S.; Schröder-Hinrichs, J.-U.; Meißner, D.; Fielitz, U.; Wilske, E. e-Navigation and situation-dependent manoeuvring assistance to enhance maritime emergency response. WMU J. Marit. Aff. 2011, 10, 209. [Google Scholar] [CrossRef]
- Nordstrom, J.; Goerlandt, F.; Sarsama, J.; Leppanen, P.; Nissila, M.; Ruponen, P.; Lubcke, T.; Sonninen, S. Vessel TRIAGE: A method for assessing and communicating the safety status of vessels in maritime distress situations. Saf. Sci. 2016, 85, 117–129. [Google Scholar] [CrossRef]
- Karahalios, H. The severity of shipboard communication failures in maritime emergencies: A risk management approach. Int. J. Disaster Risk Reduct. 2018, 28, 1–9. [Google Scholar] [CrossRef]
- Shi, W.; Su, F.Z.; Zhou, C.H. A temporal accessibility model for assessing the ability of search and rescue in Nansha Islands, South China Sea. Ocean Coast. Manag. 2014, 95, 46–52. [Google Scholar] [CrossRef]
- Akbari, A.; Eiselt, H.A.; Pelot, R. A maritime search and rescue location analysis considering multiple criteria, with simulated demand. Infor 2018, 56, 92–114. [Google Scholar] [CrossRef]
- Azofra, M.; Perez-Labajos, C.A.; Blanco, B.; Achutegui, J.J. Optimum placement of sea rescue resources. Saf. Sci. 2007, 45, 941–951. [Google Scholar] [CrossRef]
- Dolven, B.; Elsea, J.; Lawrence, S.V.; O’Rourke, R.; Rinehart, I.E. Chinese Land Reclamation in the South China Sea: Implications and Policy Options; R44072 CRS Report Prepared for Members and Congressional Committees; Congressional Research Service: Washington, DC, USA, 2015. [Google Scholar]
- Liu, Y.; Li, Z.Z.; Liu, J.X.; Patel, H. A double standard model for allocating limited emergency medical service vehicle resources ensuring service reliability. Transp. Res. C Emerg. 2016, 69, 120–133. [Google Scholar] [CrossRef]
- Siljander, M.; Venalainen, E.; Goerlandt, F.; Pellikka, P. GIS-based cost distance modelling to support strategic maritime search and rescue planning: A feasibility study. Appl. Geogr. 2015, 57, 54–70. [Google Scholar] [CrossRef]
- De Dominicis, M.; Leuzzi, G.; Monti, P.; Pinardi, N.; Poulain, P.M. Eddy diffusivity derived from drifter data for dispersion model applications. Ocean Dyn. 2012, 62, 1381–1398. [Google Scholar] [CrossRef]
- Cho, K.H.; Li, Y.; Wang, H.; Park, K.S.; Choi, J.Y.; Shin, K.I.; Kwon, J.I. Development and Validation of an Operational Search and Rescue Modeling System for the Yellow Sea and the East and South China Seas. J. Atmos. Ocean. Technol. 2014, 31, 197–215. [Google Scholar] [CrossRef]
- Shchekinova, E.Y.; Kumkar, Y.; Coppini, G. Numerical reconstruction of trajectory of small-size surface drifter in the Mediterranean sea. Ocean Dyn. 2016, 66, 153–161. [Google Scholar] [CrossRef]
- Brushett, B.A.; Allen, A.A.; King, B.A.; Lemckert, C.J. Application of leeway drift data to predict the drift of panga skiffs: Case study of maritime search and rescue in the tropical pacific. Appl. Ocean Res. 2017, 67, 109–124. [Google Scholar] [CrossRef]
- Park, K.S.; Heo, K.Y.; Jun, K.; Kwon, J.I.; Kim, J.; Choi, J.Y.; Cho, K.H.; Choi, B.J.; Seo, S.N.; Kim, Y.H.; et al. Development of the Operational Oceanographic System of Korea. Ocean Sci. J. 2015, 50, 353–369. [Google Scholar] [CrossRef]
- Razi, N.; Karatas, M. A multi-objective model for locating search and rescue boats. Eur. J. Oper. Res. 2016, 254, 279–293. [Google Scholar] [CrossRef]
- Tong, S.Q.; Wang, N.; Song, N.Q. Emergency evacuation capability evaluation and optimization for an offshore airport: The case of Dalian Offshore Airport, Dalian, China. Saf. Sci. 2017, 92, 128–137. [Google Scholar] [CrossRef]
- Norrington, L.; Quigley, J.; Russell, A.; Van der Meer, R. Modelling the reliability of search and rescue operations with Bayesian Belief Networks. Reliab. Eng. Syst. Saf. 2008, 93, 940–949. [Google Scholar] [CrossRef]
- Goerlandt, F.; Torabihaghighi, F.; Kujala, P. A model for evaluating the performance and reliability of the voluntary rescue system in the Gulf of Finland. In Safety, Reliability and Risk Analysis: Beyond the Horizon; Steenbergen, R.D.J.M., van Gelder, P.H.A.J.M., Miraglia, S., Vrouwenvelder, A.C.W.M., Eds.; CRC Press: London, UK, 2014; pp. 1351–1356. [Google Scholar]
- Ai, Y.F.; Lu, J.; Zhang, L.L. The optimization model for the location of maritime emergency supplies reserve bases and the configuration of salvage vessels. Transp. Res. E Logist. 2015, 83, 170–188. [Google Scholar] [CrossRef]
- Pelot, R.; Akbari, A.; Li, L. Vessel location modeling for maritime search and rescue. In Applications of Location Analysis; Springer: Cham, Switzerland, 2015; pp. 369–402. [Google Scholar]
- Akbari, A.; Pelot, R.P.; Eiselt, H.A.; MacMackin, W.D. Determining the optimal mix and location of search and rescue vessels for the Canadian Coast Guard. Int. J. Oper. Quant. Manag. 2017, 23, 131–146. [Google Scholar]
- Akbari, A.; Pelot, R.; Eiselt, H.A. A modular capacitated multi-objective model for locating maritime search and rescue vessels. Ann. Oper. Res. 2018, 267, 3–28. [Google Scholar] [CrossRef]
- Wang, K.; Chen, N.C.; Tong, D.Q.; Wang, K.; Gong, J.Y. Optimizing the configuration of streamflow stations based on coverage maximization: A case study of the Jinsha River Basin. J. Hydrol. 2015, 527, 172–183. [Google Scholar] [CrossRef]
- Matisziw, T.C.; Murray, A.T. Siting a facility in continuous space to maximize coverage of a region. Socioecon. Plan. Sci. 2009, 43, 131–139. [Google Scholar] [CrossRef]
- Murray, A.T.; Matisziw, T.C.; Wei, H.; Tong, D. A geocomputational heuristic for coverage maximization in service facility siting. Trans. GIS 2008, 12, 757–773. [Google Scholar] [CrossRef]
- Gwak, J.H.; Lee, B.K.; Lee, W.K.; Sohn, S.Y. Optimal location selection for the installation of urban green roofs considering honeybee habitats along with socio-economic and environmental effects. J. Environ. Manag. 2017, 189, 125–133. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Liu, Y.; Li, M.; Zhou, M.; Yang, Y. Survey of reefs based on Landsat 8 operational land imager (OLI) images in the Nansha Islands, South China Sea. Acta Oceanol. Sin. 2016, 35, 11–19. [Google Scholar] [CrossRef]
- Park, C.; Sohn, S.Y. An optimization approach for the placement of bicycle-sharing stations to reduce short car trips: An application to the city of Seoul. Transp. Res. A Policy Pract. 2017, 105, 154–166. [Google Scholar] [CrossRef]
- Li, L.B.; Lu, W.Y.; Niu, J.W.; Liu, J.P.; Liu, D.X. AIS Data-based Decision Model for Navigation Risk in Sea Areas. J. Navig. 2018, 71, 664–678. [Google Scholar] [CrossRef]
- Mannarini, G.; Coppini, G.; Oddo, P.; Pinardi, N. A prototype of ship routing decision support system for an operational oceanographic service. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2013, 7, 53–59. [Google Scholar] [CrossRef]
- Fang, M.C.; Lin, Y.H. The optimization of ship weather-routing algorithm based on the composite influence of multi-dynamic elements (II): Optimized routings. Appl. Ocean Res. 2015, 50, 130–140. [Google Scholar] [CrossRef]
- Shao, W. Development of a novel forward dynamic programming method for weather routing. J. Mar. Sci. Technol. 2012, 17, 239–251. [Google Scholar] [CrossRef]
- Veneti, A.; Makrygiorgos, A.; Konstantopoulos, C.; Pantziou, G.; Vetsikas, I.A. Minimizing the fuel consumption and the risk in maritime transportation: A bi-objective weather routing approach. Comput. Oper. Res. 2017, 88, 220–236. [Google Scholar] [CrossRef]
- Başar, A.; Çatay, B.; Ünlüyurt, T. A taxonomy for emergency service station location problem. Optim. Lett. 2012, 6, 1147–1160. [Google Scholar] [CrossRef]
- Zhu, Y.S.; Du, Q.Y.; Tian, F.; Ren, F.; Liang, S.; Chen, Y. Location Optimization Using a Hierarchical Location-Allocation Model for Trauma Centers in Shenzhen, China. ISPRS Int. J. Geo-Inf. 2016, 5, 190. [Google Scholar] [CrossRef]
- Yin, P.; Mu, L. Modular capacitated maximal covering location problem for the optimal siting of emergency vehicles. Appl. Geogr. 2012, 34, 247–254. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Asgari, N.; Heidari, N.; Hosseininia, M.; Goh, M. Covering problems in facility location: A review. Comput. Ind. Eng. 2012, 62, 368–407. [Google Scholar] [CrossRef]
- Zhang, B.; Peng, J.; Li, S.G. Covering location problem of emergency service facilities in an uncertain environment. Appl. Math. Model. 2017, 51, 429–447. [Google Scholar] [CrossRef]
- Garner, A.A.; van den Berg, P.L. Locating helicopter emergency medical service bases to optimise population coverage versus average response time. BMC Emerg. Med. 2017, 17, 31. [Google Scholar] [CrossRef]
- Wang, K.; Guan, Q.F.; Chen, N.C.; Tong, D.Q.; Hu, C.L.; Peng, Y.L.; Dong, X.Y.; Yang, C. Optimizing the configuration of precipitation stations in a space-ground integrated sensor network based on spatial-temporal coverage maximization. J. Hydrol. 2017, 548, 625–640. [Google Scholar] [CrossRef]
- Asamer, J.; Reinthaler, M.; Ruthmair, M.; Straub, M.; Puchinger, J. Optimizing charging station locations for urban taxi providers. Transp. Res. A Policy Pract. 2016, 85, 233–246. [Google Scholar] [CrossRef]
- Church, R.; Revelle, C. The maximal covering location problem. Pap. Reg. Sci. Assoc. 1974, 32, 101–118. [Google Scholar] [CrossRef]
- Wang, J.S.; Li, M.C.; Liu, Y.X.; Zhang, H.X.; Zou, W.; Chen, L. Safety assessment of shipping routes in the South China Sea based on the fuzzy analytic hierarchy process. Saf. Sci. 2014, 62, 46–57. [Google Scholar] [CrossRef]
- Haghroosta, T.; Ismail, W.R. Typhoon activity and some important parameters in the South China Sea. Weather Clim. Extremes 2017, 17, 29–35. [Google Scholar] [CrossRef]
- Pan, X.J.; Wong, G.T.F.; Ho, T.Y.; Shiah, F.K.; Liu, H.B. Remote sensing of picophytoplankton distribution in the northern South China Sea. Remote Sens. Environ. 2013, 128, 162–175. [Google Scholar] [CrossRef]
- Zhao, M.X.; Yu, K.F.; Shi, Q.; Yang, H.Q.; Riegl, B.; Zhang, Q.M.; Yan, H.Q.; Chen, T.R.; Liu, G.H.; Lin, Z.Y. Comparison of coral diversity between big and small atolls: A case study of Yongle atoll and Lingyang reef, Xisha Islands, central of South China Sea. Biodivers. Conserv. 2017, 26, 1143–1159. [Google Scholar] [CrossRef]
- Rosenberg, D.; Chung, C. Maritime security in the South China Sea: Coordinating coastal and user state priorities. Ocean Dev. Int. Law 2008, 39, 51–68. [Google Scholar] [CrossRef]
- Weng, J.X.; Yang, D.; Du, G. Generalized F distribution model with random parameters for estimating property damage cost in maritime accidents. Marit. Policy Manag. 2018, 45, 963–978. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.K.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- McCauley, D.J.; Woods, P.; Sullivan, B.; Bergman, B.; Jablonicky, C.; Roan, A.; Hirshfield, M.; Boerder, K.; Worm, B. Ending hide and seek at sea. Science 2016, 351, 1148–1150. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.S.; Zhao, Y.H.; Nelson, P.; Li, Y.; Wang, X.T.; Zhou, Y.; Lang, J.L.; Guo, X.R. Estimating ship emissions based on AIS data for port of Tianjin, China. Atmos. Environ. 2016, 145, 10–18. [Google Scholar] [CrossRef]
- Edgard. Navy Renames Bases and Stations After Predecessors. Available online: http://navyspeak.blogspot.com/2009/08/navy-renames-bases-and-stations-after.html (accessed on 14 November 2018).
- Holmes, J.R. Strategic features of the South China Sea: A tough neighborhood for hegemons. Nav. War Coll. Rev. 2014, 67, 5. [Google Scholar]
- Rosenberg, D. The political economy of piracy in the South China Sea. Nav. War Coll. Rev. 2009, 62, 43. [Google Scholar]
- Weng, J.X.; Ge, Y.E.; Han, H. Evaluation of Shipping Accident Casualties using Zero-inflated Negative Binomial Regression Technique. J. Navig. 2016, 69, 433–448. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, X.; Murray, A.T. Location optimization of urban fire stations: Access and service coverage. Comput. Environ. Urban 2019, 73, 181–190. [Google Scholar] [CrossRef]
- Enayati, S.; Mayorga, M.E.; Toro-Diaz, H.; Albert, L.A. Identifying trade-offs in equity and efficiency for simultaneously optimizing location and multipriority dispatch of ambulances. Int. Trans. Oper. Res. 2019, 26, 415–438. [Google Scholar] [CrossRef]
- Mehdi, R.A.; Schröder-Hinrichs, J.U.; Ölçer, A.I.; Baldauf, M. A Framework to Improve the Coexistence of Maritime Activities & Offshore Wind Farms. In Trends and Challenges in Maritime Energy Management; Springer: Cham, Switzerland, 2018; pp. 513–525. [Google Scholar]
- Patraiko, D.; Holthus, P. The Shipping Industry and Marine Spatial Planning-A Professional Approach; The Nautical Institute, World Ocean Council: London, UK, 2013; pp. 1–14. [Google Scholar]
- IALA. IALA Guideline Navigational Safety within Marine Spatial Planning. Available online: https://www.iala-aism.org/product/g1121-navigational-safety-within-marine-spatial-planning/ (accessed on 14 February 2019).
- Liaropoulos, A.; Sapountzaki, K.; Nivolianitou, Z. Risk governance gap analysis in search and rescue at offshore platforms in the Greek territory. Saf. Sci. 2016, 86, 132–141. [Google Scholar] [CrossRef]
- Simon, S.W. Conflict and Diplomacy in the South China Sea The View from Washington. Asian Surv. 2012, 52, 995–1018. [Google Scholar] [CrossRef]
- Bateman, S. Building Cooperation for Managing the South China Sea Without Strategic Trust. Asia Pac. Policy Stud. 2017, 4, 251–259. [Google Scholar] [CrossRef]
- Nguyen, B.U.; Ng, K.Y.K. Modeling Canadian search and rescue operations. Mil. Oper. Res. 2000, 5, 5–16. [Google Scholar] [CrossRef]
- Yeong, S.P.; King, L.M.; Dol, S.S. A review on marine search and rescue operations using unmanned aerial vehicles. Int. J. Mech. Aerosp. Ind. Mech. Manuf. Eng. 2015, 9, 396–399. [Google Scholar]
- Al-Quhali, M.A.; Baldauf, M.; Fiorini, M. Enhanced Maritime Spatial Planning through VTS. In Proceedings of the 2018 16th International Conference on Intelligent Transportation Systems Telecommunications (ITST), Lisboa, Portugal, 15–17 October 2018; pp. 1–5. [Google Scholar]
- Li, Y.; Brimicombe, A.J.; Ralphs, M.P. Spatial data quality and sensitivity analysis in GIS and environmental modelling: The case of coastal oil spills. Comput. Environ. Urban 2000, 24, 95–108. [Google Scholar] [CrossRef]
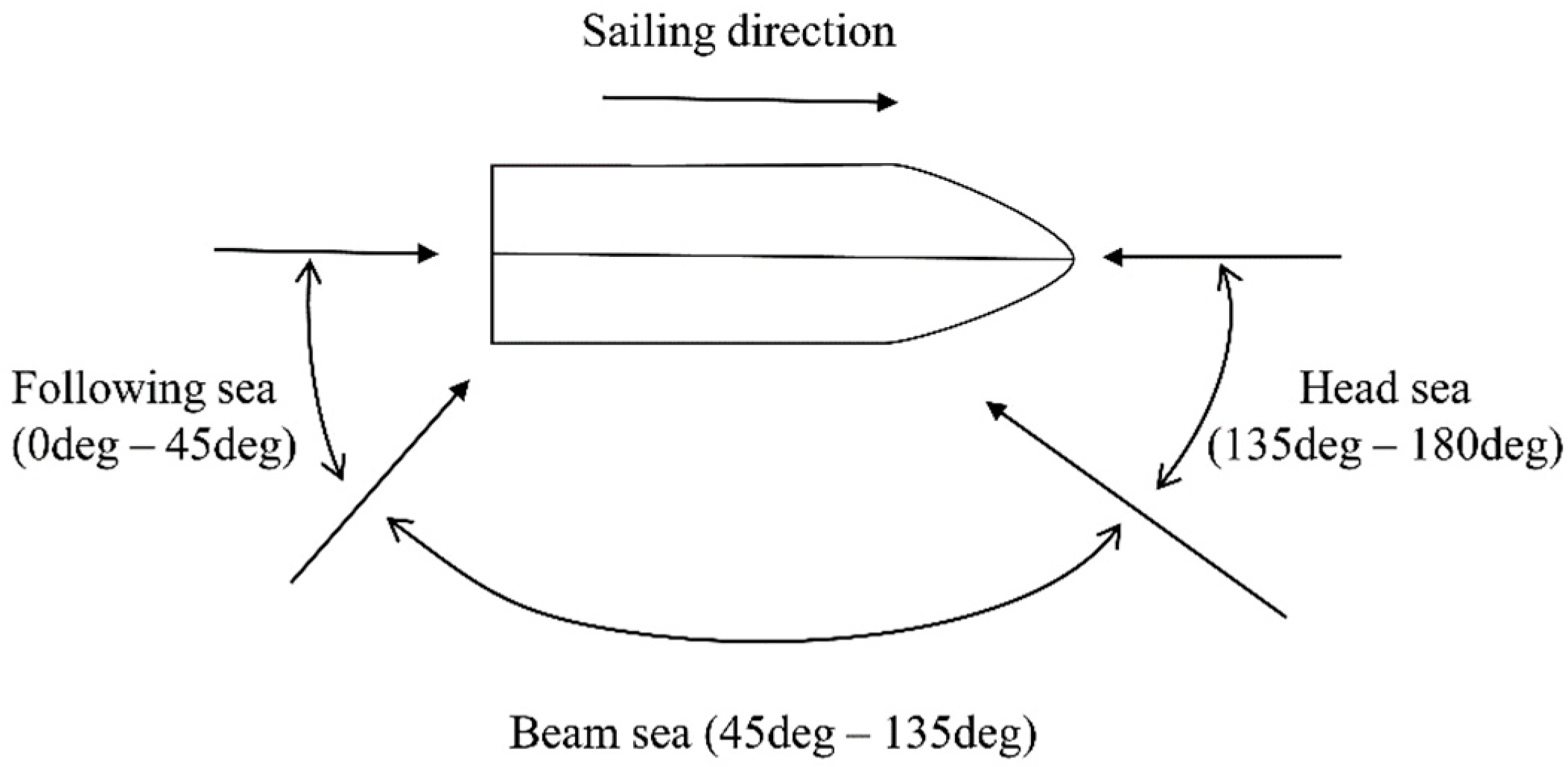
| Configuration Name | f [kn/ft2] | |
|---|---|---|
| Following seas | 0.0083 | |
| Beam seas | 0.0165 | |
| Head seas | 0.0248 |
| Number (P) | Island Name | Rate of Change of Coverable Demands, |
|---|---|---|
| 1 | Yongxing Island | - |
| 2 | Yongxing Island; Swallow Reef | 50.47 |
| 3 | Yongxing Island; Spratly Island; Mischief Island | 26.41 |
| 4 | Yongxing Island; Spratly Island; Mischief Island; Southwest Cay | 19.10 |
| 5 | Yongxing Island; Spratly Island; Mischief Island; Southwest Cay; Swallow Reef | 14.28 |
| 6 | Yongxing Island; Spratly Island; Mischief Island; Southwest Cay; Swallow Reef; Fiery Cross Island | 1.98 |
| 7–24 | - | 0 |
| Number of Islands | Primary Coverage (%) 1 | Mean Access Time (hour) |
|---|---|---|
| 0 | 62.63 | 5.15 |
| 1 | 66.57 | 4.79 |
| 2 | 70.23 | 4.57 |
| 3 | 74.11 | 4.32 |
| 4 | 77.33 | 4.15 |
| 5 | 78.19 | 4.09 |
| 6 | 80.02 | 4.06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Cheng, L.; Zhang, F.; Yan, Z.; Ruan, X.; Min, K.; Li, M. Integrating Island Spatial Information and Integer Optimization for Locating Maritime Search and Rescue Bases: A Case Study in the South China Sea. ISPRS Int. J. Geo-Inf. 2019, 8, 88. https://doi.org/10.3390/ijgi8020088
Zhou X, Cheng L, Zhang F, Yan Z, Ruan X, Min K, Li M. Integrating Island Spatial Information and Integer Optimization for Locating Maritime Search and Rescue Bases: A Case Study in the South China Sea. ISPRS International Journal of Geo-Information. 2019; 8(2):88. https://doi.org/10.3390/ijgi8020088
Chicago/Turabian StyleZhou, Xiao, Liang Cheng, Fangli Zhang, Zhaojin Yan, Xiaoguang Ruan, Kaifu Min, and Manchun Li. 2019. "Integrating Island Spatial Information and Integer Optimization for Locating Maritime Search and Rescue Bases: A Case Study in the South China Sea" ISPRS International Journal of Geo-Information 8, no. 2: 88. https://doi.org/10.3390/ijgi8020088
APA StyleZhou, X., Cheng, L., Zhang, F., Yan, Z., Ruan, X., Min, K., & Li, M. (2019). Integrating Island Spatial Information and Integer Optimization for Locating Maritime Search and Rescue Bases: A Case Study in the South China Sea. ISPRS International Journal of Geo-Information, 8(2), 88. https://doi.org/10.3390/ijgi8020088






