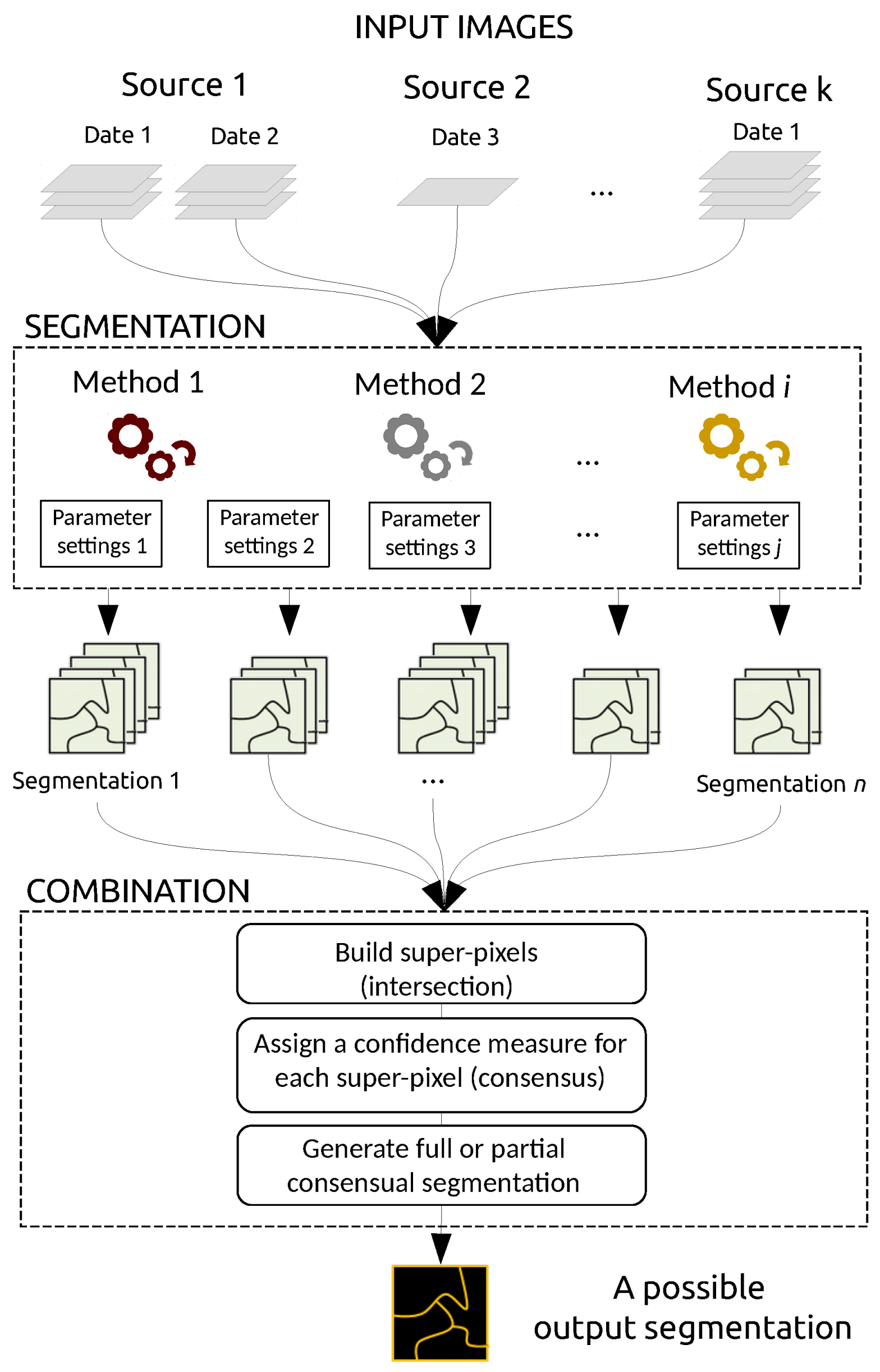
As mentioned in the introduction, our goal is to build an optimal segmentation map from a set of inputs. Our method is not a segmentation technique per se, but rather aims to merge existing segmentation maps. Such maps can be derived from various data sources (e.g., optical images and DSM), various dates, various segmentation techniques (e.g., thresholding, edge-based and region-based techniques), and defined from various parameter settings, as shown in
Figure 1. In the following subsections, we describe the general framework and discuss the confidence measure, the integration of prior knowledge, and the possible use of the confidence map that is the output of our combination framework.
3.2. Confidence Measure
Super-pixels are generated by intersecting all the segmentations that are fed to the framework. To illustrate this process,
Figure 2a–f shows some sample segmentations built from an input satellite image (Pleiades multispectral image,
Figure 2g).
Figure 2h illustrates the resulting oversegmentation built by intersecting the input maps. The combination framework proposed here makes it possible to derive a confidence value for each super-pixel, as shown in
Figure 2i.
The confidence measure is a core element of our framework. We rely on the measures proposed by Martin [
26] that were used to evaluate results in the well-known Berkeley Segmentation Dataset. Such measures have recently been used in an optimization scheme for segmentation fusion [
17]. First we recall the definitions provided in [
26], before defining the confidence measure used in this paper.
Let us first consider two input segmentations
and
. Writing
the set of pixels in segmentation
S that are in the same segment as pixel
p, we can measure the local refinement error
in each pixel
p of the image space through the following equation:
where
denotes cardinality and
set difference. Since this measure is not symmetric, Martin proposed several global symmetric measures: the Local Consistency Error (LCE), the Global Consistency Error (GCE), the Bidirectional Consistency Error (BCE) respectively computed as
and
The latter has been further extended considering a leave-one-out strategy, leading to
and we rely on this idea in our proposal, as described further on in this section. Let us recall that these measures were not used to merge segmentations, as a variant using an average operator is proposed in [
17] to achieve this goal:
In contrast to previous metrics, we consider the scale of super-pixels. Consequently, we assign a score to each super-pixel that measures the degree of consensus between the different input segmentations in the same super-pixel.
denotes the set of
m input segmentations, from which we derive a single set of
n super-pixels defined as
. Each super-pixel is obtained by intersecting the input segmentations, i.e., two pixels
p and
q are in the same super-pixel
if and only if
. In order to counter the directional effect of the local refinement error at the pixel scale, we propose the following measure:
In other words, we measure the ratio of the smaller region that does not intersect (or is not included in) the larger region. It differs considerably from the bidirectional definitions given in [
17,
26] that do not distinguish between each pair or regions.
Since our goal is not to aggregate this error at the global scale of an image like with
(or a pair of images with
,
,
,
), but rather to measure a consistency error for each super-pixel, we define the Super-pixel Consistency Error as:
that is by definition equal for all
, so we simply write
instead of
. Since our revised local refinement error is bidirectional in (
7), we can add the constraint
in (
8) to reduce computation time. Finally we define the confidence value of each super-pixel
with
. Furthermore, the computation is limited to super-pixels instead of to the original pixels, leading to an efficient algorithm. For the sake of comparison, we recall that the maximum operator in (
8) was replaced by an average operator at the image scale in [
17].
Our framework assigns a high confidence value when the regions that make up a super-pixel resemble each other, and a low confidence value in the case of locally conflicting segmentations, as shown in
Figure 2i. The figure shows that such conflicts appear mostly at the edges of the super-pixels, since these parts of the image are more likely to change between different segmentations. A more comprehensive close-up is provided in
Figure 3, in which three different scenarios to combine six segmentations
Figure 3a are compared. For the sake of visibility, a single object is considered and the overlapping segments in the input segmentations are provided. In the first case
Figure 3b, all the regions share a very similar spatial support and the confidence in the intersecting super-pixel is consequently high. Conversely, there is a notable mismatch between overlapping regions in
Figure 3c, leading to a low confidence score. Finally, we avoid penalizing nested segmentations such as those observed in
Figure 3d, thanks to our definition of the local refinement error (
7) that focuses on the ratio of the smaller region that does not belong to the larger one.
By relying on the consensus between the different input segmentation maps, our combination framework provides a single feature when dealing with multiple dates as inputs. Indeed, in a change detection context, high confidence will be assigned to stable regions (i.e., regions that are not affected by changes) since they correspond to agreements between the different inputs. Conversely, areas of change will lead to conflicts between the input segmentations and thus will be characterized by a low confidence score. The (inverted) confidence map could then be used as an indicator of change, but this possibility is left for future work.
3.3. Prior Knowledge
In the GEOBIA framework, expert knowledge is often defined through rulesets, selection of relevant attributes or input data. Here, we consider that while the framework might be fed with many input segmentations, some prior knowledge about the quality of such segmentations may be available and is worth using.
More precisely, it is possible to assess the quality of the segmentation at two different levels. On the one hand, a user can assign a confidence score to a full segmentation map. This happens in some cases where specific input data (or a set of parameters) do not provide accurate segmentation (e.g., a satellite image acquired at a date when different land cover cannot be clearly distinguished or the image has a high cloud cover). Conversely, there are situations in which we can assume that a given segmentation will produce better results than others, e.g., due to a higher spatial resolution (i.e., a level of detail that fit the targeted objects) or a more relevant source (e.g., height from nDSM is known to be better than spectral information to distinguish between buildings and roads). In both cases, the weight remains constant for all the regions of a segmentation.
On the other hand, such confidence can be determined locally. Indeed, it is possible that a segmentation is accurate for some regions and inaccurate for others. In this case, the user is able to weight specific regions of each input, either to express confidence in the region considered or to identify regions of low quality. Note that the quality assessment could originate either from the geographical area (e.g., the presence of relief) or from the image segments themselves.
In order to embed such priors in the combination framework, we simply update our local refinement error defined in (
7):
with
denoting the weight given to
, i.e., the segment of
S containing
p. If the prior is defined locally, then two pixels
belonging to the same region in
S will have the same weight, i.e.,
. If it is defined globally, then it is shared among all pixels of the image
. By default, we set
, and only expert priors change the standard behavior of the framework. If one region or one image is given high confidence, then its contribution to local refinement error will be higher, and it will thus have a strong effect on the super-pixel consistency error (the region lacks consensus with other regions). Conversely, if one region or image is given low confidence, then the local refinement error will be low, and the region/image will not drive the computation of the super-pixel consistency error. Since the local refinement error compares two individual regions, we include both related weights in the computation (while still keeping a symmetric measure). Finally, note that while all measures discussed in
Section 3.2 are defined in
, the weighting by
leads to confidence measures also defined on
. A normalization step is required before computation of the confidence map to insure it remains in
. When illustrating the confidence map in this paper, we consider only the unweighted version and rescale it into gray levels.
From a practical point of view, assigning weights to prioritize some segmentation maps or some regions in a segmentation is an empirical task that relies on heuristics (knowledge of data and metadata, knowledge of the study site, expertise on segmentation algorithms). The pairwise comparison matrix inspired by the Analytical Hierarchy Process [
27] is one way to rank criteria related to segmentations (data source, date, method, parameters) and to define quantitative weights.
3.4. Using the Confidence Map
We have presented a generic framework that is able to combine different segmentations and derive a confidence score for each super-pixel. Here we discuss how the confidence score can be further used to perform image segmentation, and we distinguish between partial and full segmentation.
3.4.1. Partial Segmentation
Let us recall that in each super-pixel, the confidence map measures the level of consensus between the different input segmentations. Super-pixels with a high confidence level most likely represent robust elements in the segmentation map, and thus need to be preserved. Conversely, super-pixels with a low confidence level denote areas of the image where the input segmentations do not match. Such regions could be reasonably filtered out by applying a threshold (
in Equation (
10)) on the confidence map.
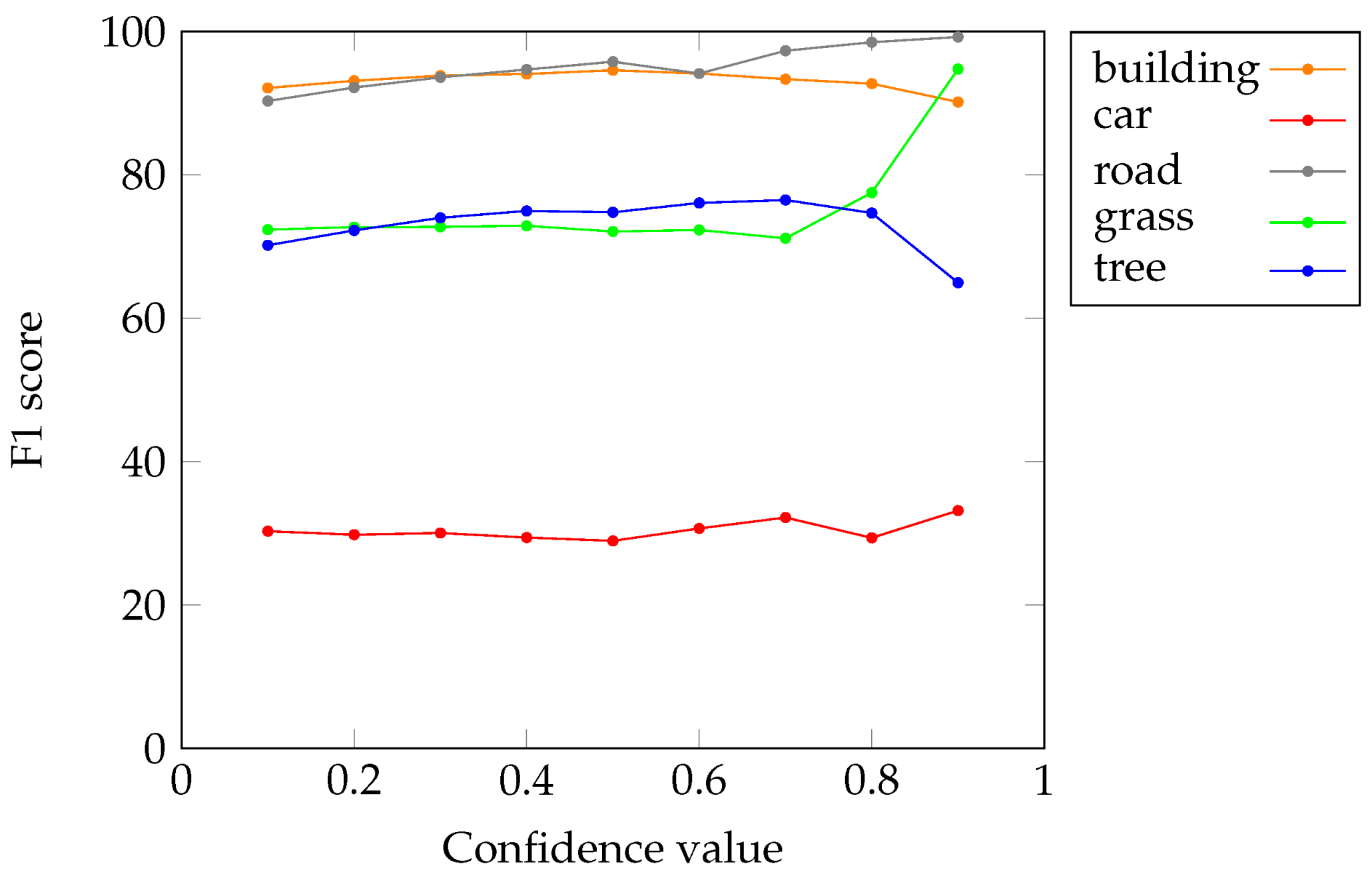
Figure 4 illustrates the effect of confidence thresholding with various thresholds, as follows:
where super-pixels with confidence lower levels than
are discarded (shown in black).
This process leads to partial segmentation, which provides only super-pixels for which the consensus was high. All the regions in the image that correspond to some mismatch between the input segmentations are removed and assigned to the background. This strategy is useful when the subsequent steps of the GEOBIA process have to be conducted on the significant objects only (here defined as those leading to a consensus between the input segmentations).
3.4.2. Full Segmentation
In order to obtain a full segmentation from the partial segmentation discussed above, background pixels have to be assigned to some of the preserved super-pixels. Several strategies can be used.
For instance, it is possible to merge each low-confidence super-pixel with its most similar neighbor. However this requires defining an appropriate criterion to measure the so-called similarity. While the similarity might rely on the analysis of the input data, it can also remain independent of the original data by assigning each low-confidence super-pixel to the neighbor with the highest confidence, or with which it shares the most border. Note that if a discarded super-pixel is surrounded by other super-pixels whose confidence levels are also below the threshold, the neighborhood has to be extended.
More advanced filtering and merging methods are reported in the literature [
28], such as region growing on a region adjacency graph of super-pixels (called quasi-flat zones in [
28]). Filtering is then based on the confidence of super-pixels rather than on their size. The growing process in [
28] requires describing each super-pixel by its average color. Any of the available data sources can be used, leading to a process that is not fully independent of the input data (note that such input data are only used to reassign the areas of the image where the consensus is low, not to process the complete image). Otherwise, geometric or confidence criteria can be used.
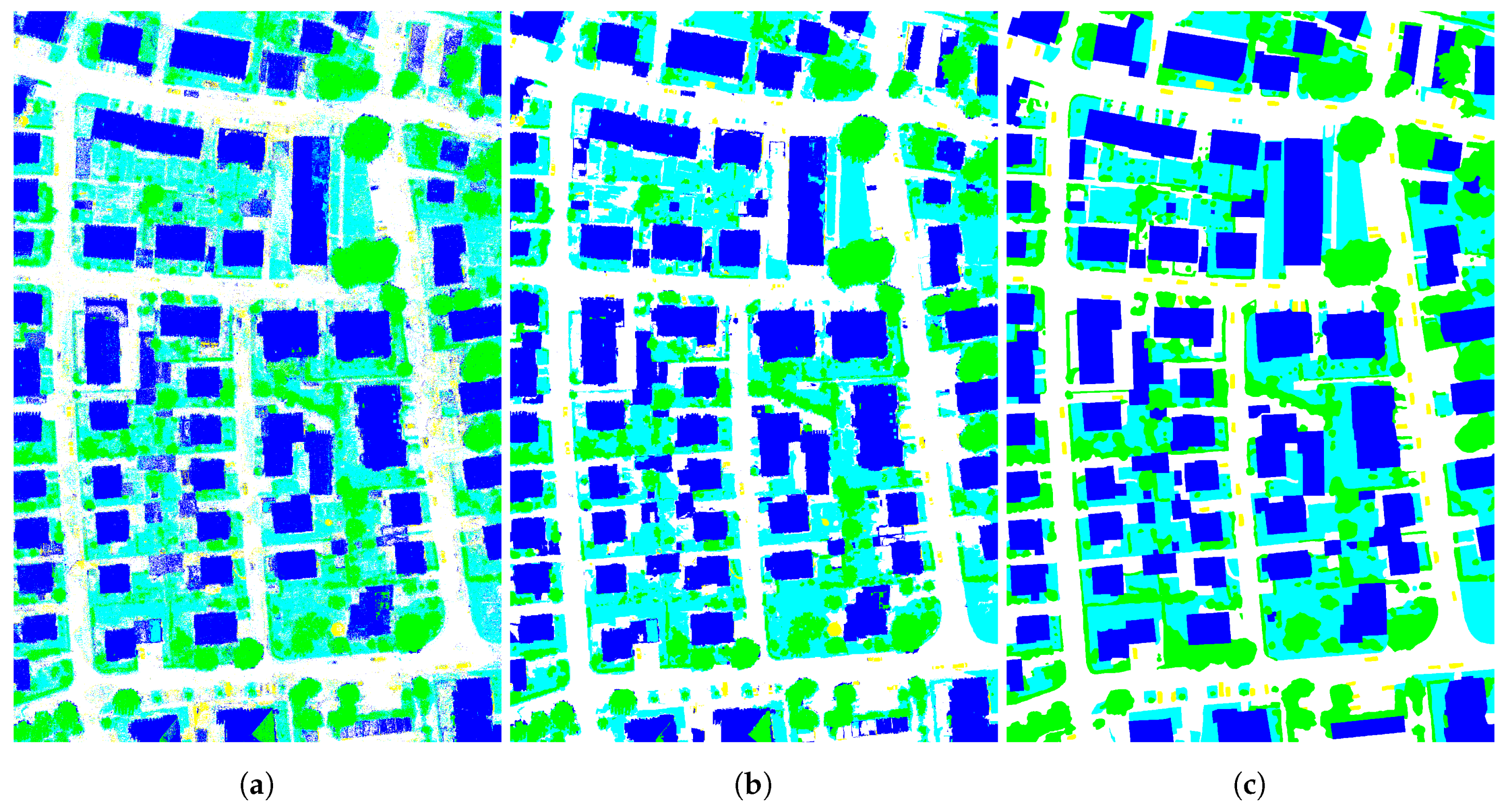
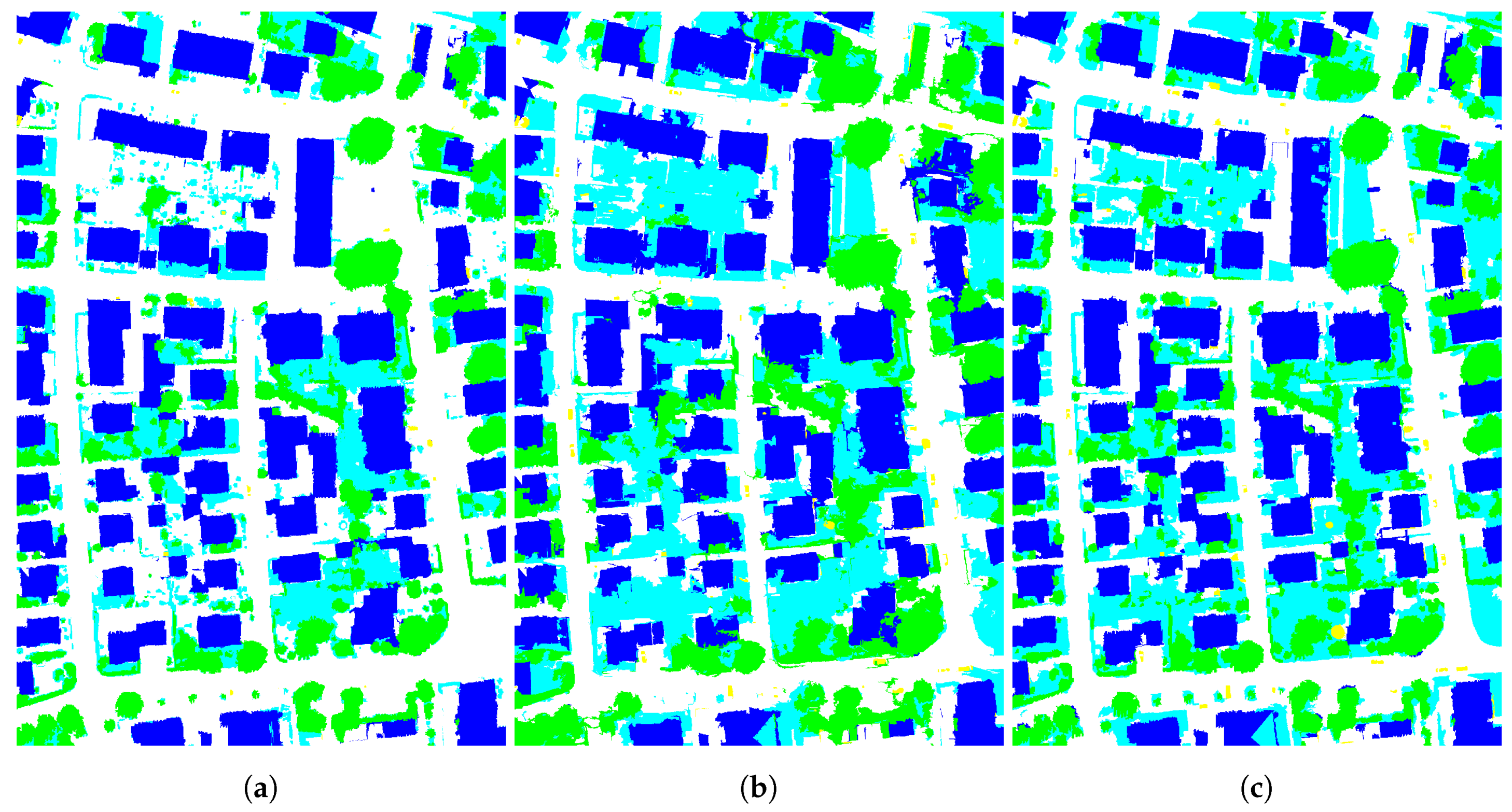
Figure 5c highlights the super-pixels with low confidence levels (shown in white) that have to be removed and merged with the remaining ones (shown in black). As might have been expected, super-pixels in which input segmentations disagree actually correspond to object borders
Figure 5b. Such areas are known to be difficult to process. Indeed, most of the publicly available contests in remote sensing apply specific evaluation measures to tackle this issue, e.g., eroding the ground truth by a few pixels to prevent penalizing the submitted semantic segmentation or classification map with inaccurate borders.
Finally, it is also possible to retain all super-pixels but to use their confidence score in a subsequent process. In the context of geographic object-based image analysis, such a process might consist of a fuzzy classification scheme, in which the contribution of the super-pixel samples in the training of a prediction model will be weighted by their confidence. Since the focus of this paper is on the combination of segmentations and not their subsequent use, we do not explore this strategy further here, but we do include some preliminary assessments in the following section.