Abstract
Knowledge graphs (KGs) are crucial resources for supporting geographical knowledge services. Given the vast geographical knowledge in web text, extraction of geo-entity relations from web text has become the core technology for construction of geographical KGs; furthermore, it directly affects the quality of geographical knowledge services. However, web text inevitably contains noise and geographical knowledge can be sparsely distributed, both of which greatly restrict the quality of geo-entity relationship extraction. We propose a method for filtering geo-entity relations based on existing knowledge bases (KBs). Accordingly, ontology knowledge, fact knowledge, and synonym knowledge are integrated to generate geo-related knowledge. Then, the extracted geo-entity relationships and the geo-related knowledge are transferred into vectors, and the maximum similarity between vectors is the confidence value of one extracted geo-entity relationship triple. Our method takes full advantage of existing KBs to assess the quality of geographical information in web text, which is helpful to improve the richness and freshness of geographical KGs. Compared with the Stanford OpenIE method, our method decreased the mean square error (MSE) from 0.62 to 0.06 in the confidence interval [0.7, 1], and improved the area under the receiver operating characteristic (ROC) curve (AUC) from 0.51 to 0.89.
1. Introduction
Web text contains huge volumes of geographical knowledge that can help to improve the richness and freshness of geographical information. However, knowledge represented by natural language is difficult for computers to understand. Knowledge graphs (KGs) [1] are introduced to organize the knowledge of natural language descriptions in a way that can be processed by computers. KGs link the semantic content of entities into a network, namely Semantic Web [2], that facilitates knowledge interoperability. This semantic content describes the entity’s attributes in the form of the object–attribute–value triple [3], commonly written as A (O, V). That is, an object O has an attribute A with the value V. The attribute can express a relationship when the value is also an object.
Relation extraction (RE) is a primary work of KG construction. With breakthroughs in natural language processing technologies, many RE systems have been developed and are publicly available, for example: Reverb [4], ClausIE [5], OLLIE [6], Stanford OpenIE [7], OpenIE4 [8], and OpenIE5 [9]. These RE systems make it easier to identify relations between geo-entities from web text. However, web text is noisy and geographical knowledge in web text is often relatively sparse, leading to low-quality geo-entity relations extracted by RE systems. Hence, quality assessment of geo-entity relations extracted from web text must be performed before they can be used. In fact, many of the relations extracted from web text are unknown or have changed, and a gold standard may be unavailable or may not even exist, which poses a significant challenge for the quality assessment of geo-entity relations.
We propose a knowledge-based method to filter geo-entity relations extracted from web text. Geo-related knowledge (the semantic links between geo-entity classes) is introduced to assess the extracted relations. To generate the geo-related knowledge, we take full advantage of ontology knowledge, fact knowledge, and synonym knowledge from common knowledge bases (KBs) [10]. Moreover, we transfer the extracted geo-entity relations and geo-related knowledge into low-dimensional dense vectors, so as to calculate the maximum semantic similarity as the confidence value. Finally, credible geo-entity relations are filtered out if their confidence values are bigger than a given threshold. Experimental results show that the proposed method is effective for assessing the confidence level of geo-entity relations extracted from web text. To summarize, our main contributions are as follows:
- (1)
- Propose a novel framework to automatically filter geo-entity relations. This framework provides a new way of identifying credible geographic information from web text according to human knowledge.
- (2)
- Establish a credible KB of geo-entity relations (confidence value ≥ 0.7), which can be used to construct and complement a geographic knowledge graph.
2. Related Works
2.1. Quality Assessment of Structured Geographical Information
The International Standard ISO 19157 [11] accepts two perspectives on data quality: data producer and data user. This means that the quality criteria of geographic datasets vary according to their product specification or user requirements.
Structured geographical information is stored as a table, tree, or graph with multiple attribute items. Senaratne et al. [12] summarized the quality indicators of structured geographical information into position (geometric) accuracy, topological consistency, temporal accuracy, thematic accuracy, and completeness. Position (geometric) accuracy is assessed by matching with reference data or manual inspection. Usually, reference datasets are gathered from the authorities. Topological consistency is checked by geometrical analysis or heuristic metrics. Temporal accuracy is the update date, which is closely related to the number of contributors. Thematic accuracy focuses on the category error caused by manual annotation; it is assessed by clustering or semantic similarity matching methods. Completeness aims to track omissions and is assessed by matching with reference data.
The geo-entity relations extracted from web text may involve positional, topological, and thematic information. However, they are described in natural language that is difficult to match with reference data. Besides, the extracted information can reach a “web-scale” level, for which manual inspection is unattainable. In addition to evaluating entity categories, many complex and flexible relations in web text have not been assessed.
2.2. Quality Assessment of Unstructured Geographical Information
Unstructured geographical information focuses on natural language text. Provenance credibility and content specification are two core indicators to assess text-based geographical information by supervised classification methods. Features used include expertise, reputation, recognition of contributor; and typos, punctuation, morphology of text. Recently, unstructured geographical information evaluation has mainly been aimed at social media data and does not involve content credibility.
More generally, unstructured information is transformed into triples using information extraction techniques, and the content credibility of triples is assessed. A large-scale annotated corpus is the reference dataset for assessing pre-defined relations. Some authorities build reference datasets using a unified evaluation system. The TAC 2013 English Regular Slot Filling Corpus is the most commonly used empirical data [13]. It is built based on Wikipedia articles, and contains 50 organization entities with 16 official named attributes, and 50 person entities with 25 official named attributes. All instances of an attribute for every entity in the text are annotated manually (a total of 27,655 instances). However, the building process is tedious, including five steps: (1) Design a guideline; (2) query all instances of an attribute in the text and adjudicate them by senior annotators; (3) automatically annotate and manually edit; (4) assess every instance with an assessor and ensure 90% or higher accuracy for all annotated instances; and (5) review the work of their peers. Although TAC 2013 English Regular Slot Filling Corpus is highly credible, it lacks fine-grained categories of organization and other types of geo-entities. Therefore, it is not applicable for assessment of geo-entity relations extracted from web text.
It is almost impossible to create a reference dataset that covers all relations in web text. The main evaluation method is manual inspection of randomly selected samples. First, triples randomly sampled from the results are added to the evaluation set. Then, the evaluation set is manually assessed by domain experts. To guarantee the assessment consistency among different experts, each triple is assessed by two independent experts, and their agreement is measured using Cohen’s kappa coefficient [14]. Finally, the evaluation results are accepted only if they pass the consistency check.
Automatic evaluation methods fall into two categories: evidence collection and link prediction. The evidence collection methods filter out reliable triples by using KBs, web co-occurrences, or query logs as evidence [15]. Link prediction is known as the completion or reasoning of knowledge graphs. The main methods of link prediction are: (1) The rule-based method [16]; (2) the probabilistic graphical model (PGM), which conforms to the idea of deductive inference [17]; (3) the knowledge graph embedding method, which transforms the symbolic representation of triples into vectors [18] and calculates the reliability by vector operations.
3. Methodology
There are many open access KBs, such as Yago, DBpedia, and WordNet, that have been widely used for place name disambiguation [19], semantic search [20], knowledge discovery [21], and so on. A well-known application of KBs is Watson [22], a question-answering computer system that uses multiple information sources (including ontologies, encyclopedias, dictionaries, and other material) to build knowledge.
We use common KBs as the reference data to assess the credibility of geo-entity relations extracted from web text. These relations are described in natural language, and express position, topology, direction, distance, and other semantic information between two geo-entities. According to the formalisms used in the Semantic Web, we defined the relevant concepts as follows.
Geo-entity relation triple: <subjectgeo, relation, objectgeo>, abbreviated as <subgeo, rel, objgeo>. Similar to the triple A(O, V), rel expresses a relationship between its subject and object that are geo-entities.
Class pair of geo-entities: <class_subgeo, class_objgeo>; this describes the geographical categories to which the subject and object belong.
Relational indicator: Abbreviated as rel_ind. Similar to the object property defined by ontology, the relational indicator is a property whose subjects and objects must belong to the extension of pointed geographical categories. Each class pair of geo-entities corresponds to a set of relational indicators, written as <(class_subgeo, class_objgeo), set(rel_ind)>.
If the relation in the extracted triple is more semantically similar to one relational indicator, the extracted triple will probably be correct. The proposed method is divided into two steps, described as follows.
3.1. Acquiring Geo-Related Knowledge from KBs
This step aims to establish the mapping <(class_subgeo, class_objgeo), set(rel_ind)>, namely geo-related knowledge. Figure 1 shows the process of integrating three types of knowledge to generate geo-related knowledge.
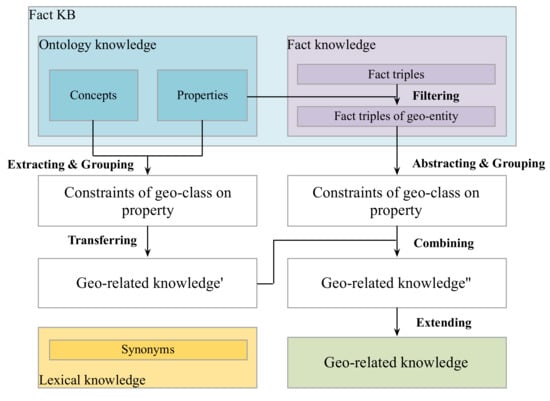
Figure 1.
Flowchart for acquiring geo-related knowledge.
Firstly, ontology well defines concepts and relationships in some communities [3]. Properties represent relationships in ontology. If the subjects and objects of one property belong to geographical categories, this property is saved as the relational indicator. For instance, the class pair of geo-entities (road, city) has the relational indicator “beltway city” in DBpedia Ontology.
Secondly, fact triples of KBs characterize object attributes in the real world. The attributes in fact triples can complement relational indicators. For example, the relational indicators of (road, city) are extended to (beltway city, route junction) by using the fact triples of DBpedia. Besides, fact triples of KBs can supply additional class pairs of geo-entities that are missing in ontology. So, the attributes and categories in fact triples of KBs are added into the mapping <(class_subgeo, class_objgeo), set(rel_ind)>.
Thirdly, synonym KBs group words together based on their semantic similarities. In natural language text, there are limited vocabularies to describe direction and distance relationships; their relational indicators can be acquired by enumeration. However, the expressions of topological relations are much more complex and the used vocabularies are very different from domain definitions. By using the synonyms in WordNet (http://wordnet.princeton.edu), we generate the relational indicators for eight topological relations (defined by Egenhofer [23]: disjoint, meet, overlap, inside, contain, cover, coveredBy, equal). According to the topological constraints between different shapes of geo-entities, the relational indicators of (road, city) are finally updated as (beltway city, route junction, pass through, cross, enter, connect, in).
3.2. Predicting Confidence for Geo-Entity Relations
The confidence value of geo-entity relations can be predicted based on the similarities between the extracted relation and its relational indicators. Considering that a relation has different expressions in natural language text, which may not precisely match its relational indicators, we firstly project the relation and its relational indicators into a dense, low-dimensional vector space by a machine learning model, namely doc2vec [24]. In this vector space, the semantic similarity of any two objects can be calculated based on the cosine distance or the Euclidean distance.
The flowchart of confidence prediction is shown in Figure 2. First, for all of the relation triples extracted by the RE system, we only save the geo-related triples whose subjects and objects belong to geographical categories. Besides, we obtain the relational indicators according to the mapping <(class_subgeo, class_objgeo), set(rel_ind)>. Second, we train the machine learning model ‘doc2vec’ (https://github.com/inejc/paragraph-vectors) to transfer the extracted relations and the relational indicators into vectors. Third, for each geo-related triple, we calculate the similarity between the extracted relation and each of its relational indicators, and take the maximal similarity as the confidence value. Finally, the triple is considered a credible extraction if its confidence value is bigger than a given threshold, which is introduced in Section 5.4.
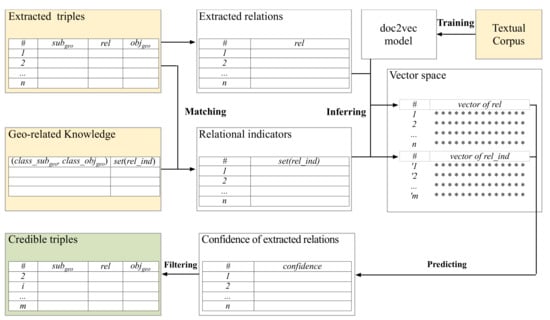
Figure 2.
Flowchart of confidence prediction of geo-entity relations.
The confidence function is defined as Formula (1). Here, Ct(subgeo, rel, objgeo) denotes the confidence value of the geo-entity relation triple, I is the set of the relational indicators for the class pair (class_subgeo, class_objgeo), i is a relational indicator in the set, erel is the vector representation of the relation rel, and ei is the vector representation of the relational indicator i.
4. Experiments
4.1. Data
In the experiment, DBpedia and WordNet were selected as the KBs, and Wikipedia articles were used as the corpus for extracting geo-entity relation triples and training the doc2vec model. The details are as follows:
- (1)
- Fine-grained categories of geo-entities were extracted from DBpedia Ontology (261 in total). These contain organization (i.e., company, school, government agency, bank, etc.) and place (i.e., island, country, ocean, mountain, road, factory, hotel, etc.).
- (2)
- Class pairs of geo-entities were extracted from the ontology and fact triples of DBpedia (1,159 in total).
- (3)
- Relational indicators were acquired from the ontology and fact triples of DBpedia and WordNet (177 in total).
- (4)
- English Wikipedia articles of geographical entries were used to extract geo-entity relation triples (2.8 GB in total). We generated 517,805 triples by inputting these articles into an RE system (Stanford OpenIE system, https://nlp.stanford.edu/software/openie.html).
- (5)
- All articles from English Wikipedia were used as a corpus to train the doc2vec model; the corpus size is 14.2 GB. Each vector has 100 dimensions.
As there is no gold standard for extracted triples, the correctness (right is 1 and wrong is 0) and the relational type (spatial or semantic) of partial triples were manually annotated in order to verify the effectiveness of the proposed method. First, we randomly arranged 517,805 triples by their confidence values and divided them into 10 equal sections, ensuring that each section had approximately the same number of triples. Second, 100 triples were randomly selected from each section, and in all, 1000 triples were annotated by two researchers in GIS major. Third, we re-divided the sampled triples according to their confidence values into the ranges of [0, 0.1), [0.1, 0.2), …, [0.8, 0.9), [0.9, 1]. Then, we computed the accuracy of each interval as the real probability of triple confidence.
4.2. Experimental Design
The extraction results of the three methods are compared (Table 1). (1) StanOIE: The original Stanford OpenIE system, which outputs confidence for each extracted triple. (2) KNOWfact: The presented method whose geo-related knowledge is only obtained from ontology and fact triples of KBs. (3) KNOWfact+lex: The presented method extends the indicators of topological relations using synonym KBs. Moreover, we separate all samples into semantic relations (e.g., “sisterCollege”, “largestSettlement”) and spatial relations (e.g., “closeTo”, “riverBranchOf”), to test how relational indicators affect different relation types.

Table 1.
Experiment design schema.
4.3. Metrics
Since the accuracy of confidence prediction decides the effect of geo-entity relation filtration, the introduced metrics focus on verifying the rationality of confidence prediction results. The mean square error (MSE), the curve of receiver operating characteristic (ROC), and the area under the ROC curve (AUC) are calculated.
- (1)
- MSE: We measure MSE between the predicted confidence value and the real probability; the lower the better. As given in Formula (2), n is the triple number of each interval, is the predicted confidence value, and is the real probability of each interval.
- (2)
- ROC and AUC: We order triples according to their confidence values, compute the true positive rate (TPR) and the false positive rate (FPR) according to Formulas (3) and (4) and the confusion matrix (Table 2), and then plot the ROC curve, where the x-axis represents the FPR and the y-axis represents the TPR. If a method’s ROC is closer to the point (0,1), its performance is better. AUC computes the area under the ROC curve; the higher the better.
 Table 2. Confusion matrix of classification results.
Table 2. Confusion matrix of classification results.
5. Results and Discussion
5.1. MSE
Figure 3 shows the MSE for all samples (Figure 3a), for semantic relation samples (Figure 3b), and for spatial relation samples (Figure 3c), where the x-axis represents the confidence interval and the y-axis represents the MSE (note that the line of Sp-StanOIE is discontinuous in Figure 3c, because no confidence predicted by Sp-StanOIE falls into some intervals).
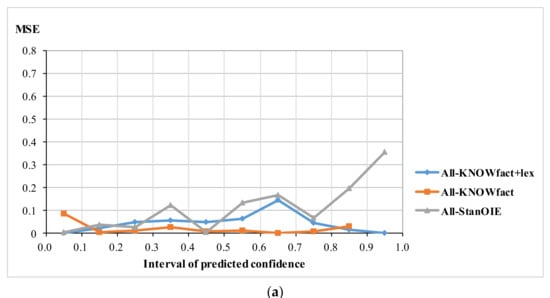
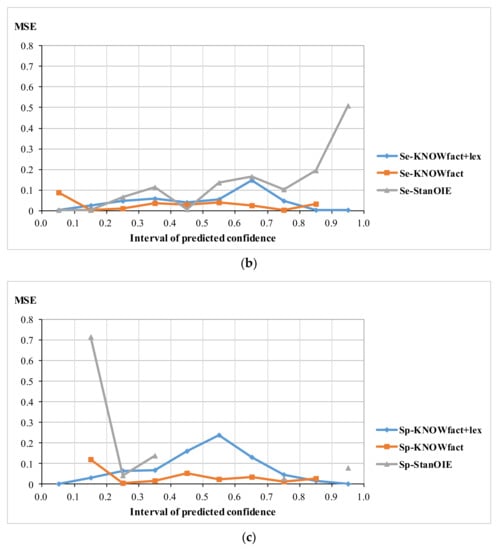
Figure 3.
(a) MSE for all samples; (b) MSE for semantic relation samples; (c) MSE for spatial relation samples.
For the three types of sample, KNOWfact+lex has a significant advantage with the lowest MSE in the range of [0, 0.2] and [0.8, 1]. This means that if the confidence value predicted by KNOWfact+lex falls in [0, 0.2], the triple is most likely a negative sample. Likewise, if the confidence value predicted by KNOWfact+lex falls in [0.8, 1], the triple is probably positive. This implies that fact and synonym knowledge are effective for distinguishing between right and wrong geo-related triples.
Stanford OpenIE (StanOIE) performs the worst for the three different types of sample. As shown Figure 3a,b , it has a very high MSE for positive samples. This is because StanOIE assigns the confidence value 1.0 to 94.14% of samples (in fact, only 39.78% of samples in Figure 3a and 28.52% of samples in Figure 3b are positive samples), which leads to several false positive triples. For spatial relation samples (Figure 3c), StanOIE performs well for positive samples but poorly for negative samples. This is because the number of the confidence value of 1.0 predicted by StanOIE is almost the total number of real positive samples, but a confidence value of 0.0 is only assigned to 1% of negative samples, leading to a low true negative rate.
5.2. ROC and AUC
Figure 4a–c shows the ROC curves for all samples, semantic relation samples, and spatial relation samples, respectively. In each group of samples, the ROC curve of KNOWfact+lex completely envelops the ROC curves of KNOWfact and StanOIE. Besides, the AUC value intuitively reflects the superiority of adding the topological words, which reaches a high level (AUC(Sp-KNOWfact+lex) = 0.96) for spatial relation triples. This indicates that synonym knowledge plays a pivotal role in estimating spatial relations.
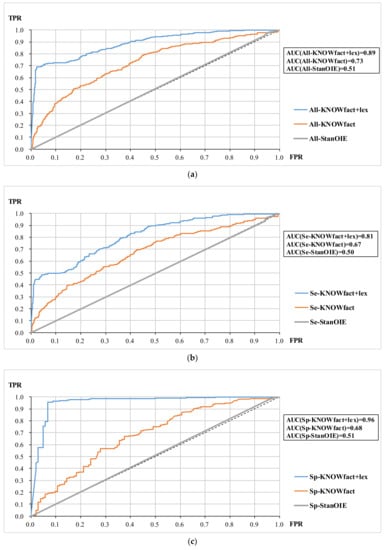
Figure 4.
(a) ROC and AUC for all samples; (b) ROC and AUC for semantic relation samples; (c) ROC and AUC for spatial relation samples.
The ROC curves of StanOIE are close to the 0-1 diagonal, meaning that the confidences predicted by StanOIE are similar to random results. Thus, StanOIE cannot be directly used for extracting geo-entity relation triples.
5.3. Determine the Threshold
We analyze the relationship between precision and recall, to determine an appropriate threshold for generating credible triples.
Figure 5a shows the precision curve and the recall curve changing with different thresholds. When the threshold is 0.7, the precision is 0.96 and the recall is 0.67. When the threshold is greater than 0.7, the precision remains steady but the recall drops sharply. Figure 5b shows a curve in which recall varies with precision. It implies that the precision and recall maintain a good balance when the threshold is less than 0.7. When the recall is greater than 0.7, the precision drops severely, although the recall continues to improve. Therefore, we set 0.7 as the confidence threshold to filter out credible triples of geo-entity relations.
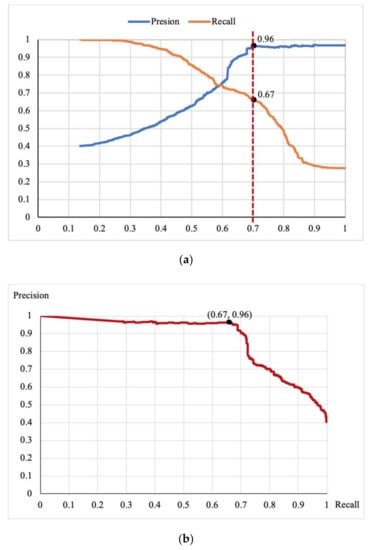
Figure 5.
(a) Precision curve and recall curve changing with different thresholds; (b) curve in which recall varies with precision.
5.4. Effect of Credible Triple Filtering
Ideally, we wish to predict lower confidence for negative samples (manual annotation is 0) and higher confidence for positive samples (manual annotation is 1). Table 3 shows the percentages of the predictions on negative and positive samples in the range of [0,0.3) and [0.7, 1], respectively, so as to analyze the consistency between the predicted confidence values and the manual annotations.

Table 3.
(a) Percentages of the predictions for all samples; (b) percentages of the predictions for semantic relation samples; (c) percentages of the predictions for spatial relation samples.
For the negative samples in three groups, KNOWfact+lex always accounts for the highest percentage below a probability of 0.3 and the lowest percentage above a probability of 0.7. Similarly, for the positive samples in three groups, KNOWfact+lex accounts for a higher percentage above a probability of 0.7 and a lower percentage below a probability of 0.3 than KNOWfact. In particular, for positive samples of spatial relations, none of the KNOWfact+lex output is for the confidence interval [0,0.3), but 95.75% is for the confidence interval [0.7, 1], as shown in Table 3c. This confirms that the geographical knowledge extended by synonym KBs can effectively distinguish the correct spatial relations.
Although StanOIE filters out almost all positive samples, it judges most of the negative samples to be correct. This indicates that StanOIE always predicts high confidence for its extracted triples irrespective of whether they are correct.
5.5. Discussion
From the experimental results, it can be inferred that the extraction results of Stanford OpenIE should be filtered because it prefers to assign a confidence value of 1.0. The reason for this phenomenon is that current RE tools focus on general relation extraction and mostly use syntactic information to predict confidence. These RE methods are based on dependency parsing, and the improvements are also related to syntax, including natural logic [7], coordination analyzer [8], linguistic constraints [9], and syntax patterns. Consequently, if triples accord with certain syntactic features (whether obtained by manual or machine learning), they will be outputted with high confidence by these tools. Unfortunately, the complexity of natural language causes a large number of extracted triples to be wrong, even if these triples conform to syntactic features. For example, <Summer Palace, covers expanse by, WanHill> with a confidence value of 1.0 is extracted from the sentence “Dominated by WanHill, Summer Palace covers an expanse of 2.9 square kilometers” by StanOIE, but this triple is obviously not correct. Therefore, information extracted by RE tools cannot directly support domain applications such as geographical KG construction. Our method solves this program by exploring the semantic connection between geo-classes. With this approach, we are able to achieve the desired filtering effect and have confirmed that external knowledge is critical to domain relation extraction.
Although the presented method successfully filters credible geo-entity relations, its effect is still inhibited by a number of factors. Firstly, our method is based on the results of a current RE tool. If the RE tool outputs a triple whose subject and object have no relationship in the textual description, but its class pair simply conforms to our geo-related knowledge, we still identify this triple as correct. Take the sentence “In the upper area of the Weilburg Lahntal (the Lhnberg Basin) are mineral springs, such as the famous Selters mineral spring in the municipality of Lhnberg” as an illustration. Stanford OpenIE extracts the triple <Weilburg, of area be, Lhnberg> from this sentence, and our method assigns confidence of 0.73 to this triple, which conforms to the geo-related knowledge <Settlement, geolocDepartment, PopulatedPlace>. Secondly, the geo-related knowledge acquired in this paper is not enough to cover all relational expressions in natural language. Many extracted triples describe events, such as (Apple Inc., receive state aid from, Republic of Ireland), which consists of multiple phrases to explain the relation and is not similar to any obtained knowledge. A solution is the integration of multiple similar types of knowledge from collective KBs. At the data level, the triple accuracy can be enhanced by votes of multiple RE tools. Besides, using Semantic Web alignment techniques [25] to fuse multiple fact KBs (e.g., Freebase, Yago, Wikidata) will increase the coverage of relational knowledge. At the algorithm level, algorithms such as expectation–maximization [26] can be invoked to further improve our method’s capacity for estimating unknown geo-entity relations.
6. Conclusions
We have proposed a knowledge-based filtering method for automatic identification of credible geo-entity relations extracted from web text. Multiple knowledge sources were utilized to predict the confidence value of geo-entity relations, which consider the semantic restrictions and diverse expressions of geo-entity relations in natural language. The proposed method decreased the MSE from 0.62 to 0.06 in the confidence interval [0.7, 1], and improved the AUC from 0.51 to 0.89, as compared with the Stanford OpenIE method. Analysis and identification of the best confidence threshold aided in establishing a credible geographical KB. This credible KB, which will serve to geographical KG construction, geo-entity relation corpus annotation, and geographical question answering, can be a good dataset for follow-up research. Future studies will aim to fuse the extracted results of multiple RE tools and integrate the geo-related knowledge of multiple KBs, so as to overcome the limitations of a single KB or extractor. Besides, multiple web texts (such as newswire, social media, and domain literature) can become the corpus to obtain more relations in various language scenes. Meanwhile, this corpus can also be used to train a vector model to improve the performance of semantic similarity methods.
Author Contributions
Li Yu and Feng Lu came up with the original research idea, conceived and designed the experiments; Peiyuan Qiu prepared the experimental data; Jialiang Gao supplemented the related works; Li Yu analyzed the data and performed the experiments; Li Yu wrote the paper; Feng Lu, Peiyuan Qiu, and Jialiang Gao revised the paper.
Funding
This research was supported by the National Natural Science Foundation of China (Grant No.41631177, No.41801320), the National Key Research and Development Program (Grant No. 2016YFB0502104), and a grant from State Key Laboratory of Resources and Environmental Information System. Their supports are gratefully acknowledged. We also thank the anonymous referees for their helpful comments and suggestions.
Acknowledgments
We also thank the anonymous referees for their helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ehrlinger, L.; Wöß, W. Towards a definition of knowledge graphs. In Proceedings of the SEMANTiCS 2016, Leipzig, Germany, 13–14 September 2016. [Google Scholar]
- Martinez-Rodriguez, J.L.; Hogan, A.; Lopez-Arevalo, I. Information extraction meets the Semantic Web: A survey. Semant. Web Interoperability Usability Appl. 2018, 1–81. [Google Scholar] [CrossRef]
- Synak, M.; Dabrowski, M.; Kruk, S.R. Semantic Web and Ontologies. In Semantic Digital Libraries; Springer: Berlin/Heidelberg, Germany, 2009; pp. 41–54. [Google Scholar]
- Fader, A.; Soderland, S.; Etzioni, O. Identifying relations for open information extraction. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP’11), Edinburgh, UK, 27–31 July 2011; pp. 1535–1545. [Google Scholar]
- Corro, L.D.; Gemulla, R. Clauseie: Clause-based open information extraction. In Proceedings of the 22nd International Conference on World Wide Web (WWW ’13), Rio de Janeiro, Brazil, 13–17 May 2013; pp. 355–366. [Google Scholar]
- Mausam, M.; Schmitz, R.; Bart, S.; Soderland, O. Etzioni, Open language learning for information extraction. In Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, Jeju Island, Korea, 12–14 July 2012; pp. 523–534. [Google Scholar]
- Angeli, G.; Premkumar, M.J.; Manning, C.D. Leveraging linguistic structure for open domain information extraction. In Proceedings of the 54th Annual Meeting of the Association for Computer Linguistics, Beijing, China, 26–31 July 2015; pp. 344–354. [Google Scholar]
- Pal, H. Demonyms and compound relational nouns in nominal open IE. In Proceedings of the 5th Workshop on Automated Knowledge Base Construction (AKBC 2016), Diego, CA, USA, 17 June 2016; pp. 35–39. [Google Scholar]
- Saha, S. Open information extraction from conjunctive sentences. In Proceedings of the 27th International Conference on Computational Linguistics (COLING 2018), Santa Fe, NM, USA, 20–26 August 2018; pp. 2288–2299. [Google Scholar]
- Lehmann, J.; Isele, R.; Jakob, M. DBpedia—A large-scale, multilingual knowledge base extracted from Wikipedia. Semantic Web 2015, 6, 1–5. [Google Scholar]
- ISO 19157:2013(en), Geographical information—Data quality. Available online: https://www.iso.org/obp/ui/#iso:std:iso:19157:ed-1:v1:en (accessed on 25 January 2019).
- Senaratne, H.; Mobasheri, A.; Ali, A.L. A review of volunteered geographic information quality assessment methods. Int. J. Geogr. Inf. Sci. 2017, 31, 139–167. [Google Scholar] [CrossRef]
- Li, X.; Ellis, J.; Griffitt, K.; Strassel, S.M.; Parker, R.; Wright, J. Linguistic resources for 2011 knowledge base population evaluation. In Proceedings of the Text Analysis Conference 2011, Gaithersburg, MD, USA, 14–15 November 2011; pp. 1–8. [Google Scholar]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Li, F.; Dong, X.; Langen, A.; Li, Y. Knowledge verification for long-tail verticals. Proc. VLDB Endow. 2017, 10, 1370–1381. [Google Scholar] [CrossRef]
- Galarraga, L.A.; Teflioudi, C.; Hose, K.; Suchanek, F. Amie: Association rule mining under incomplete evidence in ontological knowledge bases. In Proceedings of the 22nd International Conference on World Wide Web (WWW ’13), Rio de Janeiro, Brazil, 13–17 May 2013; pp. 413–422. [Google Scholar]
- Huang, B.; Kimmig, A.; Getoor, L.; Golbeck, J. Probabilistic soft logic for trust analysis in social networks. In Proceedings of the 3rd International Workshop on Statistical Relational AI (StaRAI-13), Rio de Janeiro, Brazil, 28–30 August 2013; pp. 1–8. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence (AAAI-14), Québec City, QC, Canada, 27–31 July 2014; pp. 1112–1119. [Google Scholar]
- Hu, Y.; Janowicz, K.; Prasad, S. Improving Wikipedia-based place name disambiguation in short texts using structured data from DBpedia. In Proceedings of the Geographic Information Retrieval Workshop (GIR 2014), Dallas, TX, USA, 4–7 November 2014. [Google Scholar]
- Hu, Y.; Janowicz, K.; Prasad, S.; Gao, S. Metadata topic harmonization and semantic search for linked-data-driven geoportals: A case study using ArcGIS online. Trans. GIS 2015, 19, 398–416. [Google Scholar] [CrossRef]
- Keßler, C.; Janowicz, K.; Kauppinen, T. Exploring the research field of GIScience with linked data. In Proceedings of the Seventh International Conference on Geographic Information Science (GIScience 2012), Columbus, OH, USA, 18–21 September 2012. [Google Scholar]
- Ferrucci, D.; Levas, A.; Bagchi, S.; Gondek, D.; Mueller, E.T. Watson: Beyond Jeopardy! Artif. Intell. 2013, 199–200, 93–105. [Google Scholar] [CrossRef]
- Egenhofer, M.J. A formal definition of binary topological relationships. In Proceedings of the 3rd International Conference on Foundations of Data Organization and Algorithms (FODO 1989), Paris, France, 21–23 June 1989; pp. 457–472. [Google Scholar]
- Le, Q.; Mikolov, T. Distributed representations of sentences and documents. In Proceedings of the 31st International Conference on Machine Learning (ICML’14), Beijing, China, 21–26 June 2014; pp. 1188–1196. [Google Scholar]
- Yu, L.; Qiu, P.; Liu, X.; Lu, F.; Wan, B. A holistic approach to aligning geospatial data with multidimensional similarity measuring. Int. J. Digit. Earth 2018, 11, 845–862. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Ma, F.; Gao, J.; Su, L. Texttruth: An unsupervised approach to discover trustworthy information from multi-sourced text data. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery Data Mining (KDD 18), London, UK, 19–23 August 2018; pp. 2729–2737. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).