Exploring Housing Rent by Mixed Geographically Weighted Regression: A Case Study in Nanjing
Abstract
1. Introduction
2. Materials and Methods
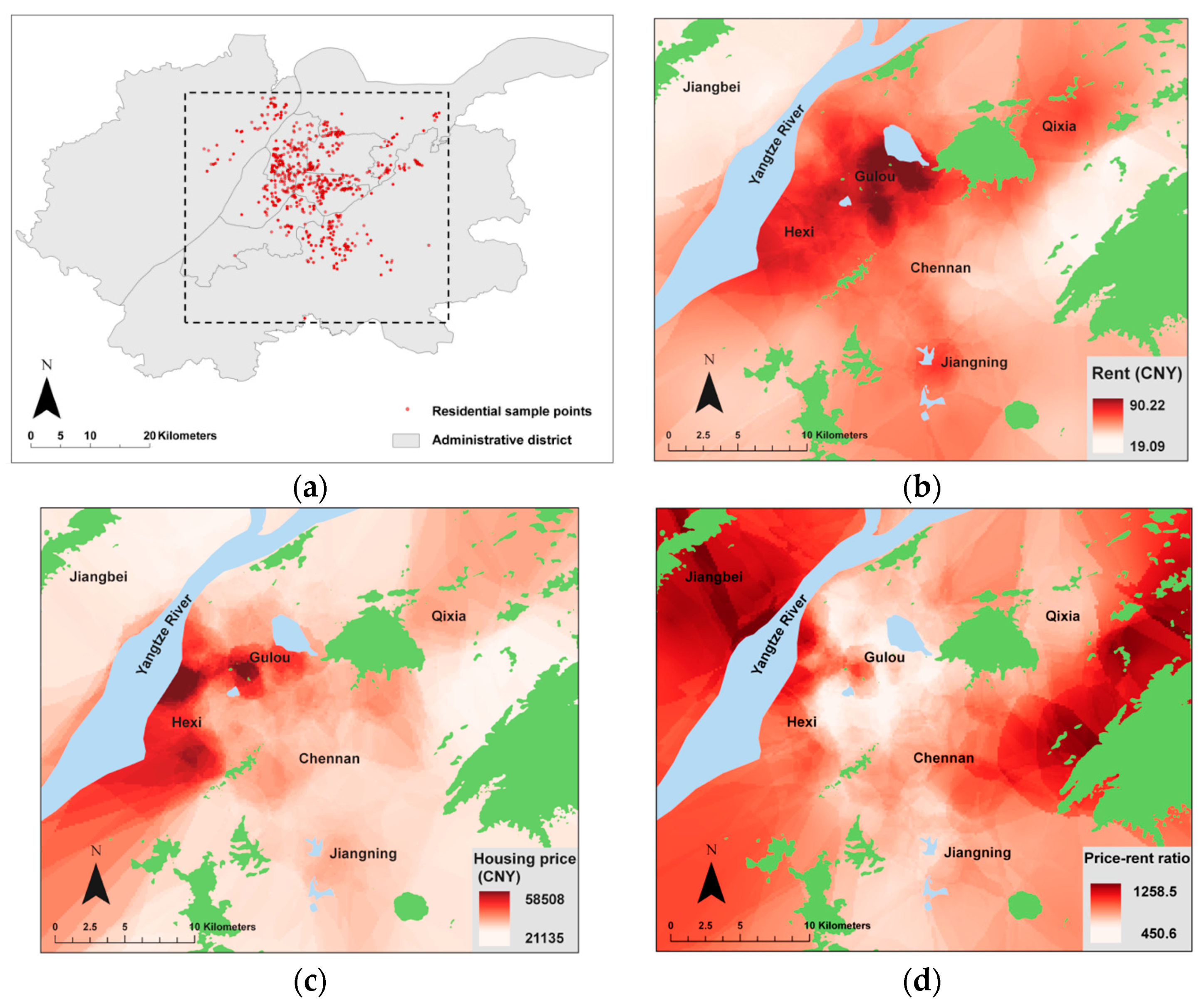
2.1. Study Area
2.2. Housing Data Collection and Processing
2.3. Process and Models
2.3.1. Spatial Autocorrelation Analysis
2.3.2. Mixed Geographically Weighted Regression
2.4. Spatial Distribution of Housing Rent, Price, and the Price–Rent Ratio
2.5. Selection of Explanatory Variables
2.6. OLS Estimation of Explanatory Variables
3. Results
3.1. Estimation of MGWR Model
3.2. Local Variables Result
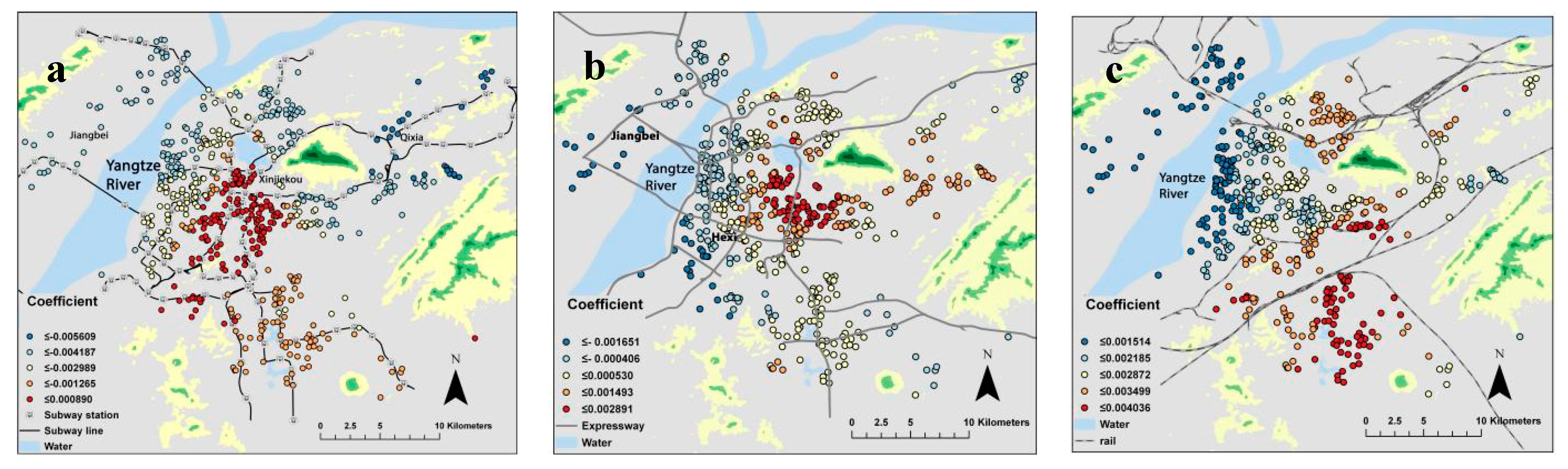
3.2.1. Traffic Conditions
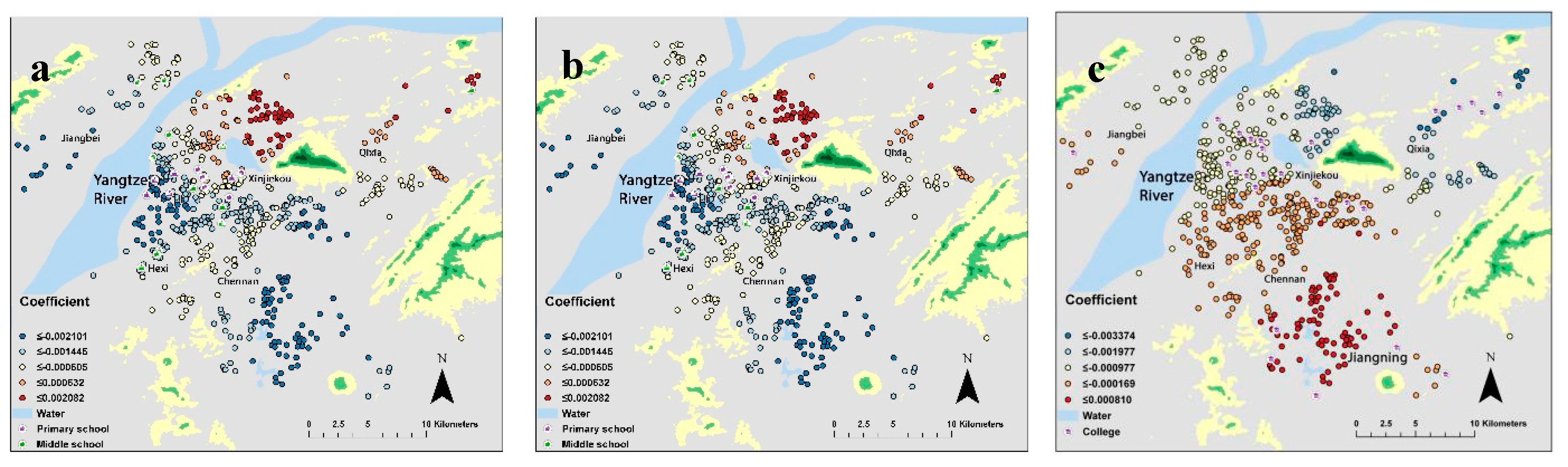
3.2.2. Neighborhood Environment
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Niu, F.; Li, J. China Real Estate Development Market Report 2006; Social sciences academic press(CHINA): Beijing, China, 2007. [Google Scholar]
- Niu, F.; Li, J. China real Estate Development Market Report 2018; Social sciences academic press(CHINA): Beijing, China, 2019. [Google Scholar]
- China PBC & CCDC: Treasury Bond and Other Bond Yield: Daily. Available online: https://www.ceicdata.com/en/china/pbc--ccdc-treasury-bond-and-other-bond-yield-daily (accessed on 22 August 2019).
- De Mare, G.; Manganelli, B.; Nesticò, A. Dynamic Analysis of the Property Market in the City of Avellino (Italy)—The Wheaton-Di Pasquale Model Applied to the Residential Segment; Murgante, B., Misra, S., Carlini, M., Torre, C., Nguyen, H.Q., Taniar, D., Apduhan, B.O., Gervasi, O., Eds.; Lecture Notes in Computer Science LNCS; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7973, pp. 509–523. [Google Scholar]
- Qing, T.; Wei, X.; Fu, A. A GWR-Based Study on Spatial Patter and Structurals Housing Price Deter minants of Shanghai. Econ. Geogr. 2012, 32, 52–58. [Google Scholar]
- Geniaux, G.; Martinetti, D. A new method for dealing simultaneously with spatial autocorrelation and spatial heterogeneity in regression models. Reg. Sci. Urban Econ. 2016, 72, 74–85. [Google Scholar] [CrossRef]
- Zou, Y. Analysis of spatial autocorrelation in higher-priced mortgages: Evidence from Philadelphia and Chicago. Cities 2014, 40, 1–10. [Google Scholar] [CrossRef]
- Li, H.; Wei, Y.D.; Wu, Y.; Tian, G. Analyzing housing prices in Shanghai with open data: Amenity, accessibility and urban structure. Cities 2019, 91, 165–179. [Google Scholar] [CrossRef]
- Lu, J. The value of a south-facing orientation: A hedonic pricing analysis of the Shanghai housing market. Habitat Int. 2018, 81, 24–32. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, R.; Xu, D.; Zhou, W. Spatial and hedonic analysis of housing prices in Shanghai. Habitat Int. 2017, 67, 69–78. [Google Scholar] [CrossRef]
- Rosen, S.; Journal, T.; Feb, N.J.; Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Gao, J.; Li, S. Detecting spatially non-stationary and scale-dependent relationships between urban landscape fragmentation and related factors using Geographically Weighted Regression. Appl. Geogr. 2011, 31, 292–302. [Google Scholar] [CrossRef]
- O’Sullivan, D. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships (review). Geogr. Anal. 2003, 35, 272–275. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Geographically weighted summary statistics—A framework for localised exploratory data analysis. Comput. Environ. Urban Syst. 2002, 26, 501–524. [Google Scholar] [CrossRef]
- Helbich, M.; Brunauer, W. Mixed Geographically Weighted Regression for Hedonic House Price Modelling in Austria; Univerity of Heidelberg: Heidelberg, Germany, 2010; Available online: https://www.geog.uni-heidelberg.de/md/chemgeo/geog/gis/helbich_brunauer_giforum2010.pdf (accessed on 29 September 2019).
- Liang, X.; Liu, Y.; Qiu, T.; Jing, Y.; Fang, F. The effects of locational factors on the housing prices of residential communities: The case of Ningbo China. Habitat Int. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Qin, Z.; Yu, Y.; Liu, D. The Effect of HOPSCA on Residential Property Values: Exploratory Findings from Wuhan, China. Sustainability 2019, 11, 471. [Google Scholar] [CrossRef]
- Liebelt, V.; Bartke, S.; Schwarz, N. Urban Green Spaces and Housing Prices: An Alternative Perspective. Sustainability 2019, 11, 3707. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Xu, S.; Zhao, Y. An Extended Semi-Supervised Regression Approach with Co-Training and Geographical Weighted Regression: A Case Study of Housing Prices in Beijing. ISPRS Int. J. Geo-Inf. 2016, 5, 4. [Google Scholar] [CrossRef]
- Development Planning of Urban Agglomeration in Yangtze River Delta. Available online: http://www.ndrc.gov.cn/zcfb/zcfbghwb/201606/t20160603_806390.html (accessed on 22 August 2019).
- Baumont, C.; Ertur, C.; Le Gallo, J. Spatial Analysis of Employment and Population Density: The Case of the Agglomeration of Dijon 1999. Geogr. Anal. 2003, 36, 146–176. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.; Charlton, M. Some Notes on Parametric Significance Test for Geographically Weighted Regression. J. Reg. Sci. 1999, 39, 497–524. [Google Scholar] [CrossRef]
- Waltert, F.; Schläpfer, F. Landscape amenities and local development: A review of migration, regional economic and hedonic pricing studies. Ecol. Econ. 2010, 70, 141–152. [Google Scholar] [CrossRef]
- Farber, S.; Páez, A. A systematic investigation of cross-validation in GWR model estimation: Empirical analysis and Monte Carlo simulations. J. Geogr. Syst. 2007, 9, 371–396. [Google Scholar] [CrossRef]
- Chen, A. China’s Urban Housing Reform: Price-rent ratio and Market Equilibrium. Urban Stud. 1996, 33, 1077–1092. [Google Scholar] [CrossRef]
- Ozanne, L.; Thibodeau, T. Explaining metropolitan housing price differences. J. Urban Econ. 1983, 13, 51–66. [Google Scholar] [CrossRef]
- Shiller, R.; Case, K. Forecasting Prices and Excess Returns in the Housing Market. Real Estate Econ. 1990, 18, 253–273. [Google Scholar]
- Potepan, M.J. Explaining Intermetropolitan Variation in Housing Prices, Rents and Land Prices. Real Estate Econ. 1996, 24, 219–245. [Google Scholar] [CrossRef]
- Wheaton, W. Real Estate “Cycles”: Some Fundamentals. Real Estate Econ. 1999, 27, 209–230. [Google Scholar] [CrossRef]
- Quigley, J. Real Estate Prices and Economic Cycles. Int. Real Estate Rev. 1999, 2, 1–20. [Google Scholar]
- Aoki, K.; Proudman, J.; Vlieghe, G. House Prices, Consumption, and Monetary Policy: A Financial Accelerator Approach. J. Financ. Intermed. 2002, 13, 414–435. [Google Scholar] [CrossRef]
- Bernanke, B.; Gertler, M. Monetary Policy and Asset Price Volatility. Econ. Rev. 1999, 84, 17–51. [Google Scholar]
- Bencardino, M.; Nesticò, A. Demographic changes and real estate values. A quantitative model for analyzing theur ban-rurallinkages. Sustainability 2017, 9, 536. [Google Scholar] [CrossRef]
- Marks, D. The Effect of Rent Control on the Price of Rental Housing: An Hedonic Approach. Land Econ. 1984, 60, 61–94. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Hang, J.; Yao, D.; Shi, G. Do urban rail transit facilities affect housing prices? Evidence from China. Sustainability 2016, 8, 380. [Google Scholar] [CrossRef]
- Guang, T.; Wei, Y.H.D.; Li, H. Effects of accessibility and environmental health risk on housing prices: A case of Salt Lake County, Utah. Appl. Geogr. 2017, 89, 12–21. [Google Scholar]
- Blanco, J.C.; Flindell, I.H. Property Prices in Urban Areas Affected by Road Traffic Noise. Appl. Acoust. 2011, 72, 133–141. [Google Scholar] [CrossRef]
- Wang, A.; Lin, L.; Bao, S.J. Spatially Non-stationary Analysis Between Commercial Land Price and Driving Factors in Hefei City. Sci. Geogr. Sin. 2017, 37, 1535–1545. [Google Scholar]
- Xu, Y.; Song, W.; Liu, C. Social-spatial accessibility to urban educational resources under the school district system: A case study of public primary schools in Nanjing, China. Sustainability 2018, 10, 2305. [Google Scholar] [CrossRef]
- Won, J.; Lee, J.S. Investigating how the rents of small urban houses are determined: Using spatial hedonic modeling for Urban Residential Housing in Seoul. Sustainability 2018, 10, 31. [Google Scholar] [CrossRef]
| Category | Variable | Variable Type | Definition |
|---|---|---|---|
| Dependent Variable | Rent | continuous | Monthly rent per square meters |
| Neighborhood environment | Commercial Center | continuous | Network distance to the nearest commercial center 1 (meters) |
| Supermarket | continuous | Network distance to the nearest supermarket (meters) | |
| School | continuous | Network distance to the nearest key public primary and middle school 2 (meters) | |
| College | continuous | Network distance to the nearest key university and college 3 (meters) | |
| Open Space | continuous | Network distance to the nearest urban park, green space, or square (meters) | |
| Hospital | continuous | Network distance to the nearest large hospital 4 (meters) | |
| Traffic conditions | Subway | continuous | Network distance to the nearest subway station (meters) |
| Expressway | continuous | Network distance to the nearest Expressway (meters) | |
| Railway | continuous | Network distance to the nearest Railway (meters) | |
| Building structure | Area | continuous | Living Area (m2) |
| Age | continuous | The age of the building: 2018 minus the actual built years | |
| Orientation | dummy | Orientation of the house (south = 2; Southeast, east, southwest = 1; others = 0) | |
| Decoration | dummy | Decoration of the house (furnished = 1; not furnished = 0) |
| Variable | Std-Coefficient | T-Statistic | Sig. | VIF |
|---|---|---|---|---|
| Area | −0.199 | 0.000 | 0.000 * | 1.237 |
| Direction | −0.102 | 0.000 | 0.000 * | 1.151 |
| Decoration | 0.181 | 0.000 | 0.000 * | 1.071 |
| Expressway | 0.074 | 0.002 | 0.002 * | 1.924 |
| Railway | 0.139 | 0.000 | 0.000 * | 1.349 |
| Subway | −0.191 | 0.000 | 0.000 * | 1.508 |
| Commercial Center | −0.413 | 0.000 | 0.000 * | 4.215 |
| School | −0.235 | 0.000 | 0.000 * | 2.567 |
| Supermarket | 0.165 | 0.000 | 0.000 * | 1.888 |
| Age | −0.024 | 0.190 | 0.190 | 1.041 |
| Open Space | −0.006 | 0.799 | 0.799 | 1.550 |
| College | −0.284 | 0.000 | 0.000 * | 1.600 |
| Hospital | 0.039 | 0.342 | 0.342 | 5.392 |
| R2 | 0.512 |
| Variable | Moran Index | Spatial Non-Stationarity |
|---|---|---|
| Area | 0.272 | |
| Campus * | 0.901 | √ |
| Commercial Center * | 0.978 | √ |
| Decoration | 0.086 | |
| Expressway * | 0.835 | √ |
| Orientation | 0.132 | |
| School * | 0.967 | √ |
| Railway * | 0.916 | √ |
| Subway * | 0.739 | √ |
| Supermarket * | 0.767 | √ |
| Models | AICc | R2 | Adjusted R2 | RMSE |
|---|---|---|---|---|
| OLS | 13,102 | 0.512 | 0.508 | 302,889 |
| GWR | 12,682 | 0.634 | 0.619 | 224,667 |
| MGWR | 5331 | 0.724 | 0.689 | 78,943 |
| Variable | Min | Quartile 1 | Mean | Quartile 3 | MAX |
|---|---|---|---|---|---|
| supermarket | −0.00233 | −0.00059 | 0.00012 | 0.00074 | 0.00291 |
| School * | −0.00278 | −0.00198 | −0.00124 | −0.00087 | 0.00173 |
| Commercial Center * | −0.00402 | −0.00359 | −0.00231 | −0.00097 | 0.00102 |
| Subway * | −0.00660 | −0.00503 | −0.00355 | −0.00192 | −0.00026 |
| Expressway * | −0.00349 | −0.00114 | −0.00035 | 0.00044 | 0.00241 |
| Railway * | 0.00063 | 0.00141 | 0.00233 | 0.00328 | 0.00396 |
| Campus * | −0.00436 | −0.00157 | −0.00110 | −0.00040 | 0.00087 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wang, L.; Lu, F. Exploring Housing Rent by Mixed Geographically Weighted Regression: A Case Study in Nanjing. ISPRS Int. J. Geo-Inf. 2019, 8, 431. https://doi.org/10.3390/ijgi8100431
Zhang S, Wang L, Lu F. Exploring Housing Rent by Mixed Geographically Weighted Regression: A Case Study in Nanjing. ISPRS International Journal of Geo-Information. 2019; 8(10):431. https://doi.org/10.3390/ijgi8100431
Chicago/Turabian StyleZhang, Shiwei, Lin Wang, and Feng Lu. 2019. "Exploring Housing Rent by Mixed Geographically Weighted Regression: A Case Study in Nanjing" ISPRS International Journal of Geo-Information 8, no. 10: 431. https://doi.org/10.3390/ijgi8100431
APA StyleZhang, S., Wang, L., & Lu, F. (2019). Exploring Housing Rent by Mixed Geographically Weighted Regression: A Case Study in Nanjing. ISPRS International Journal of Geo-Information, 8(10), 431. https://doi.org/10.3390/ijgi8100431




