A Reconstruction Method for Broken Contour Lines Based on Similar Contours
Abstract
:1. Introduction
2. Relevant Works
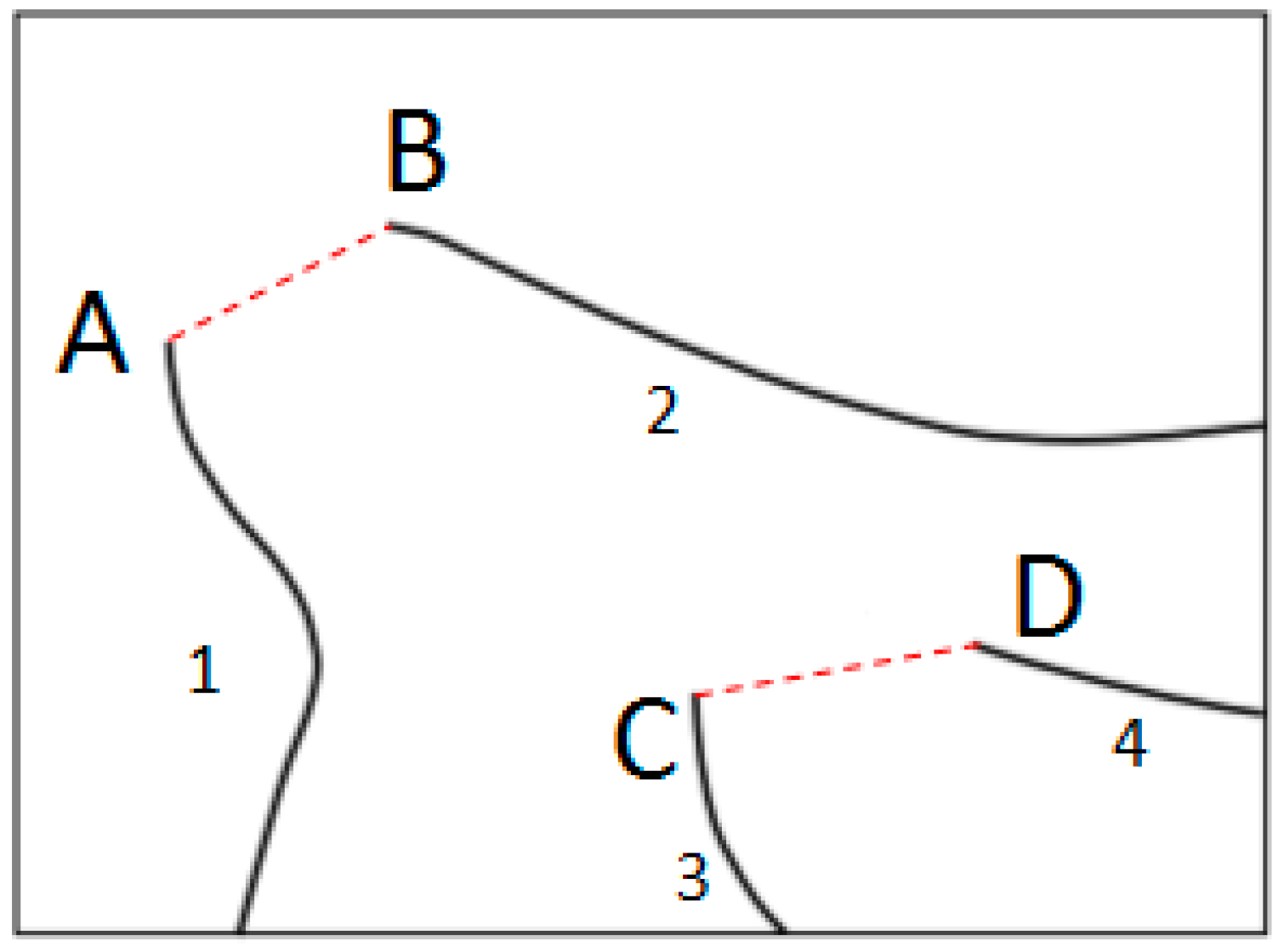
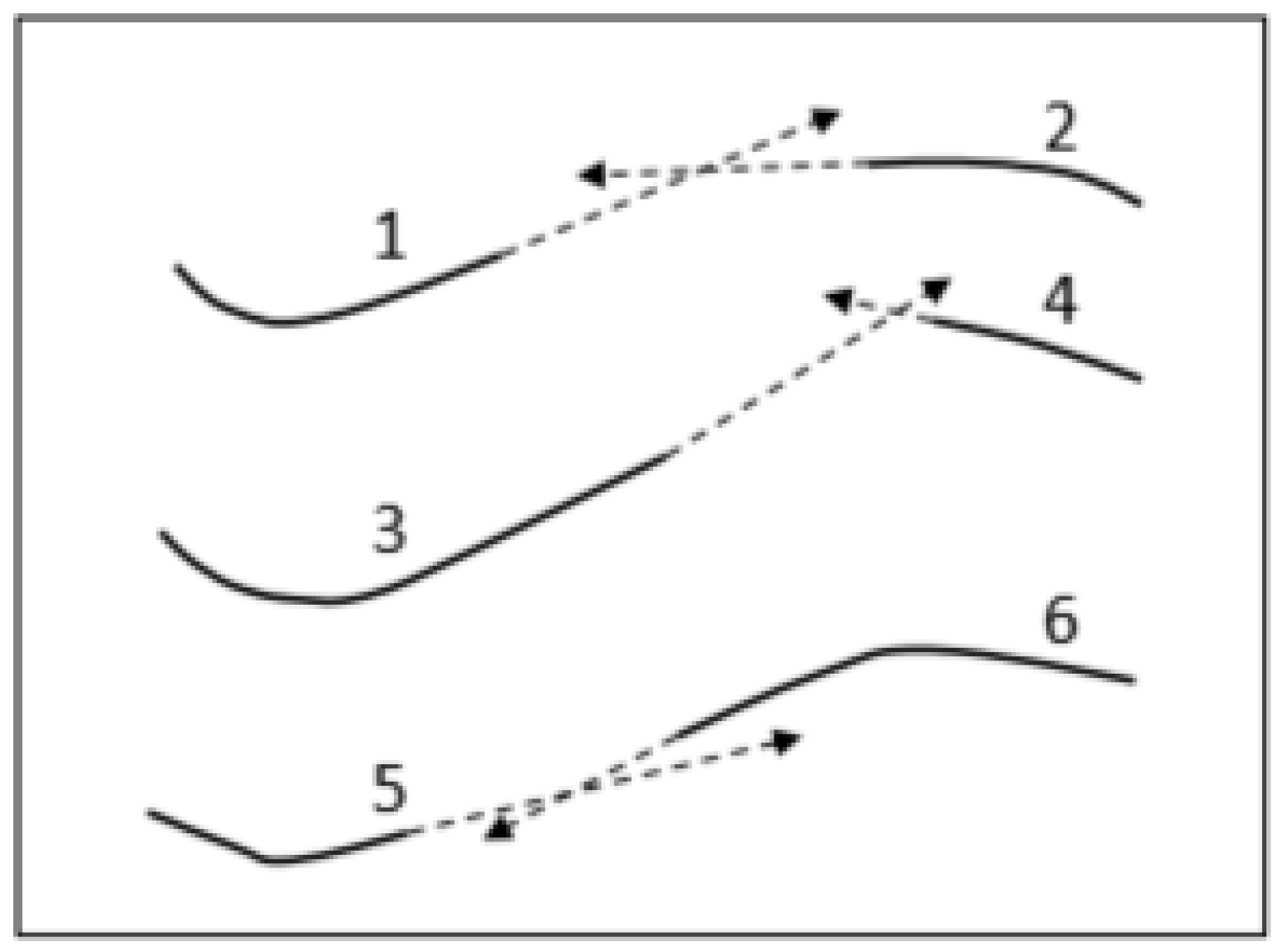
2.1. Continuity-Based Reconstruction Method of Contour Lines
2.2. Limitations in Existing Methods
2.3. Improved Idea via the Introduction of Fréchet Distance
3. The Reconstruction of Broken Contour Lines Based on a Reference Line
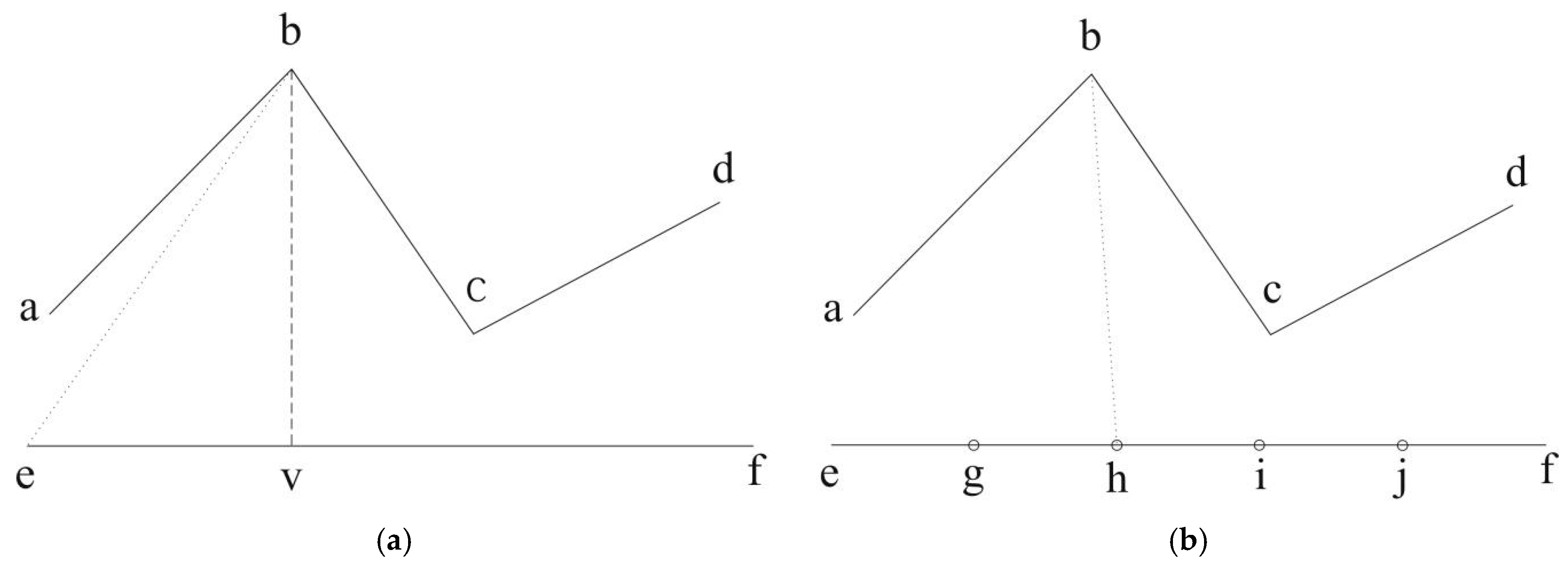
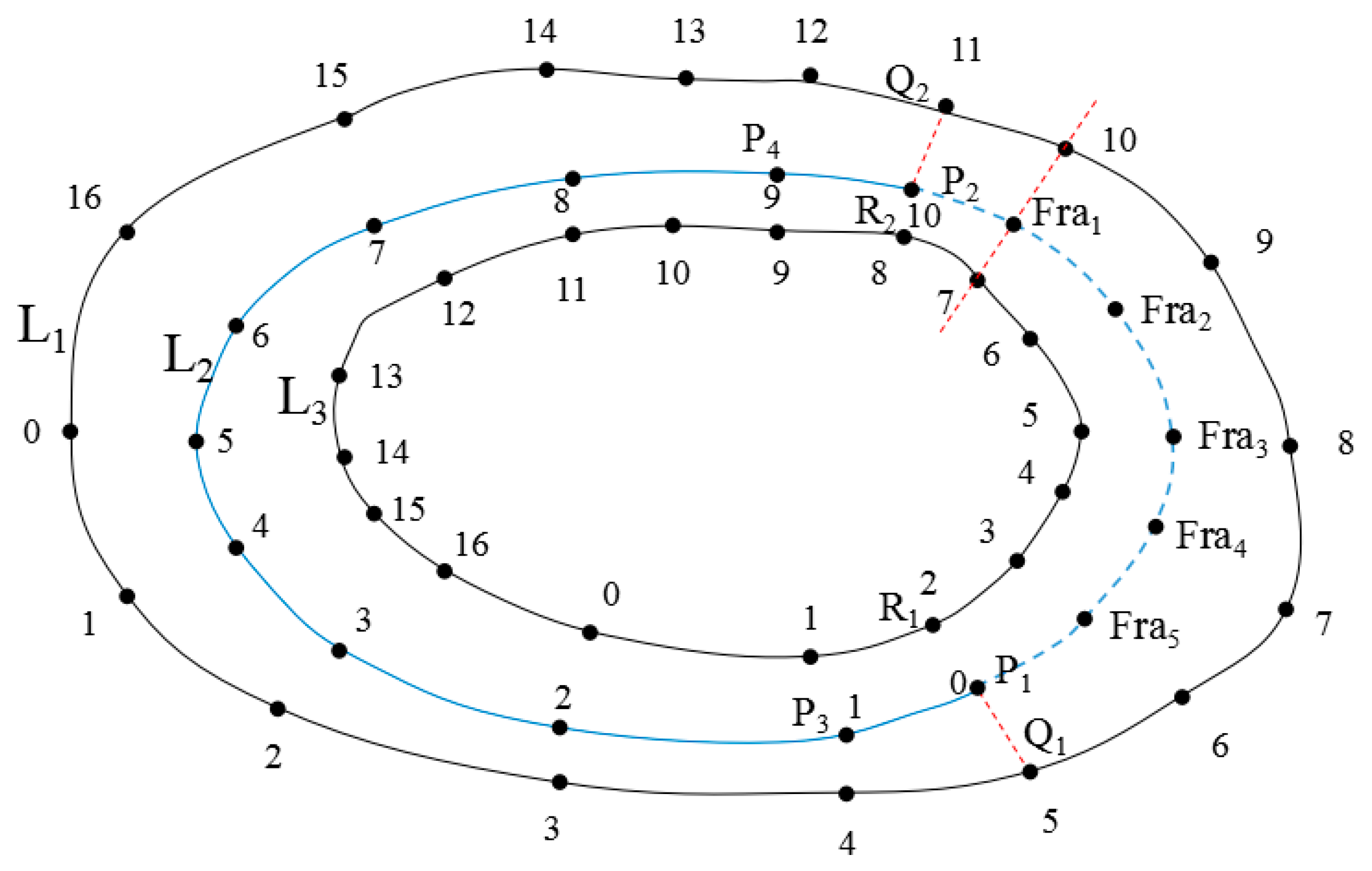
3.1. Contour Line Node Densification
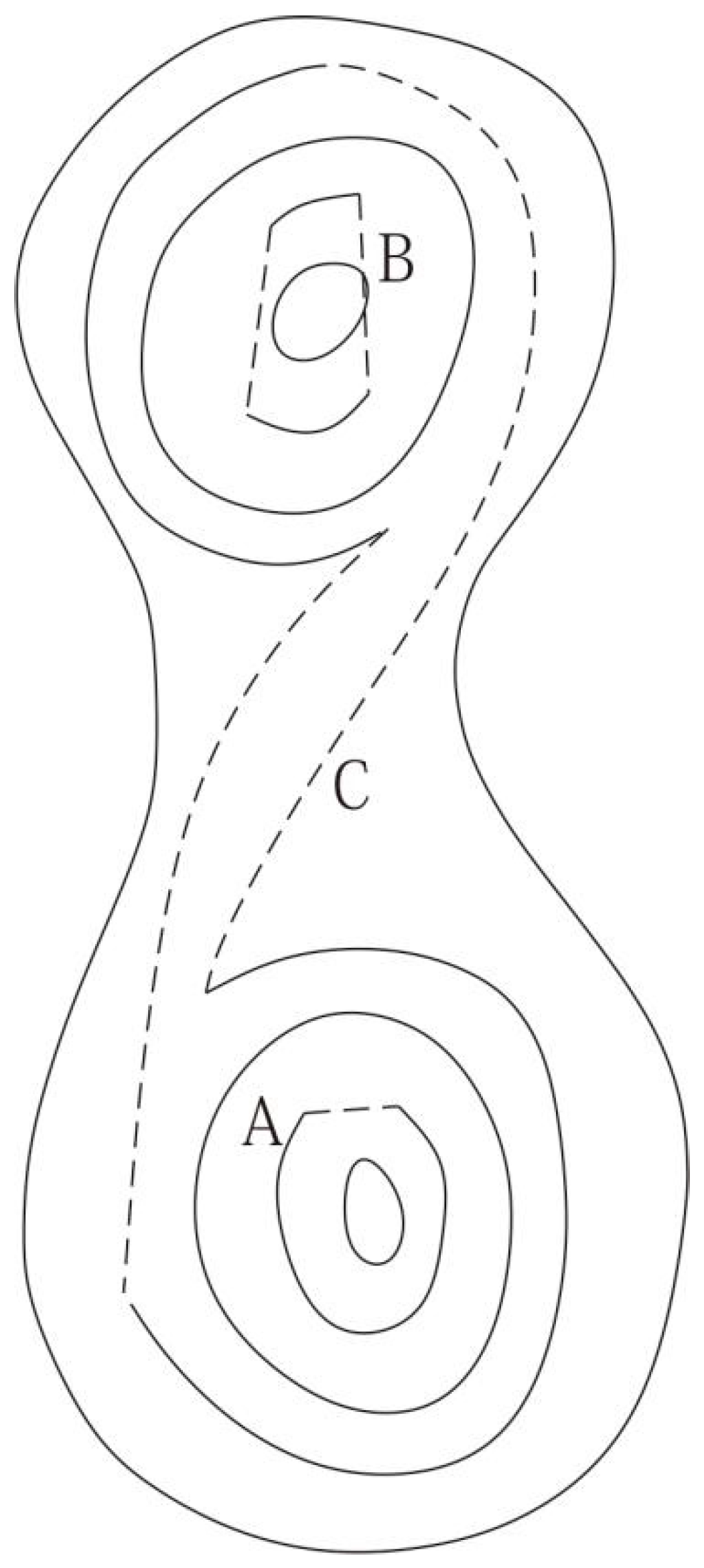
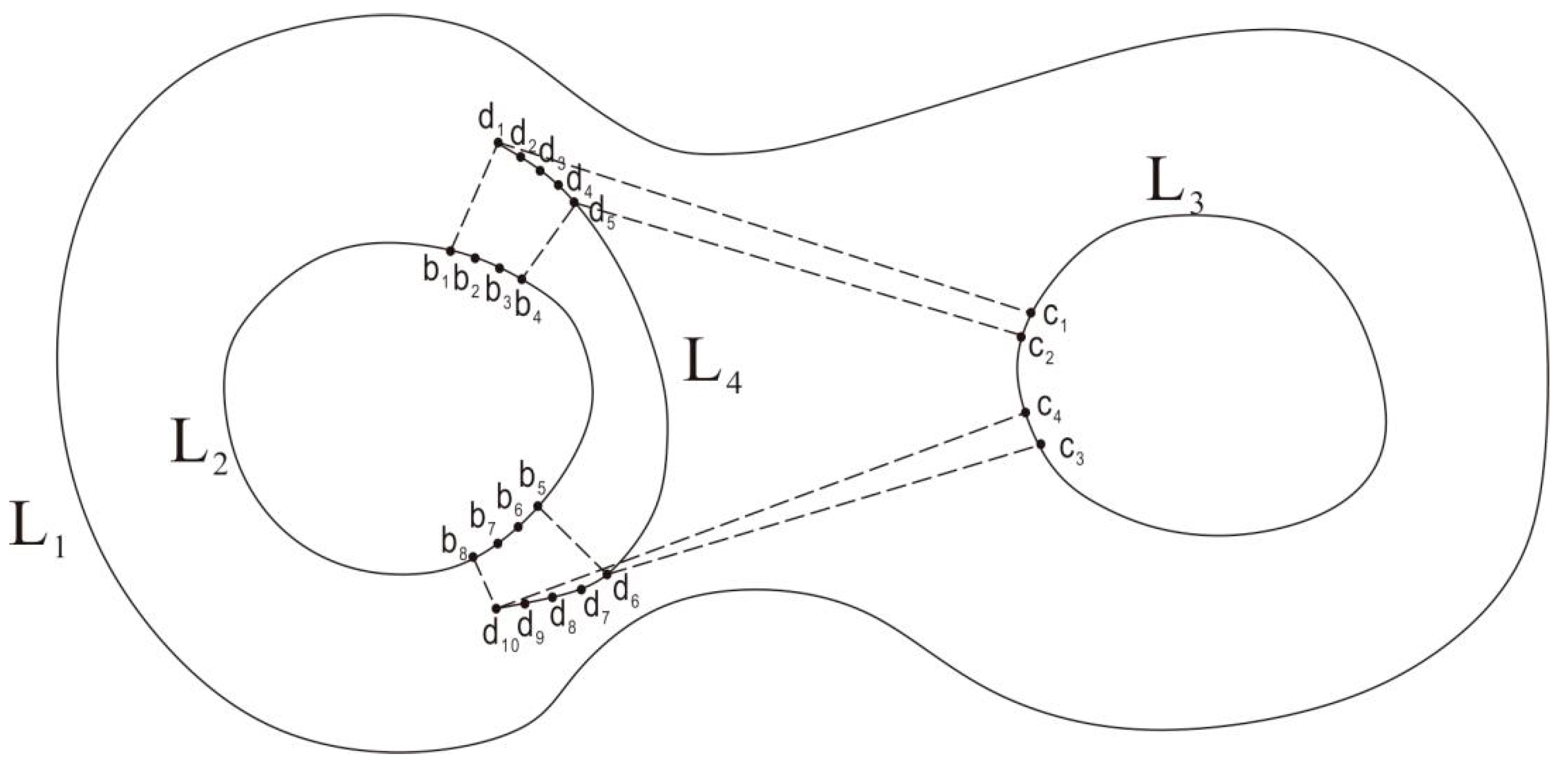
3.2. Reference Line Selection Based on the Fréchet Distance
3.3. Broken Contour Line Interpolation and Connection Based on the Reference Line
4. Experiment and Results
4.1. Experimental Data and Environment
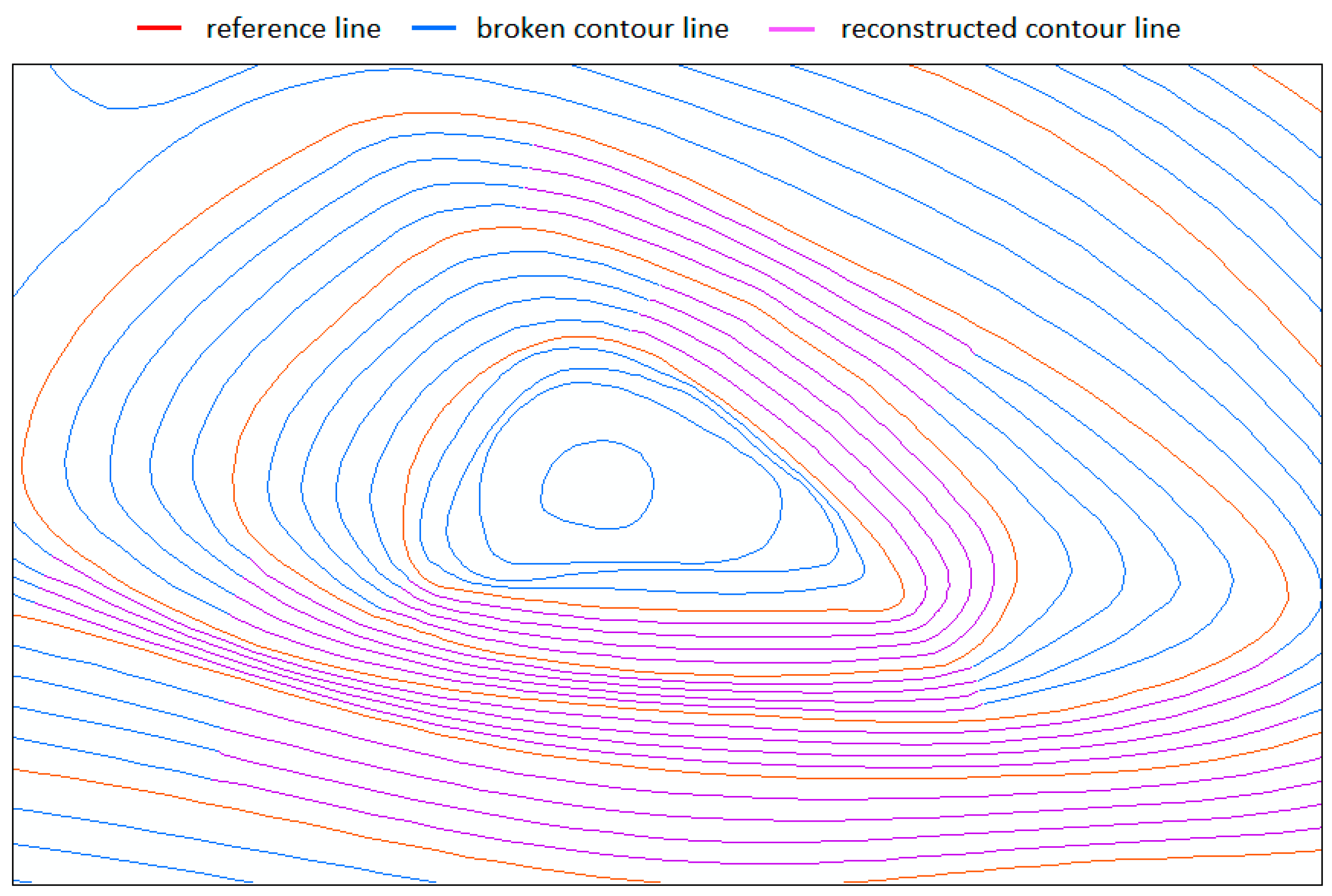
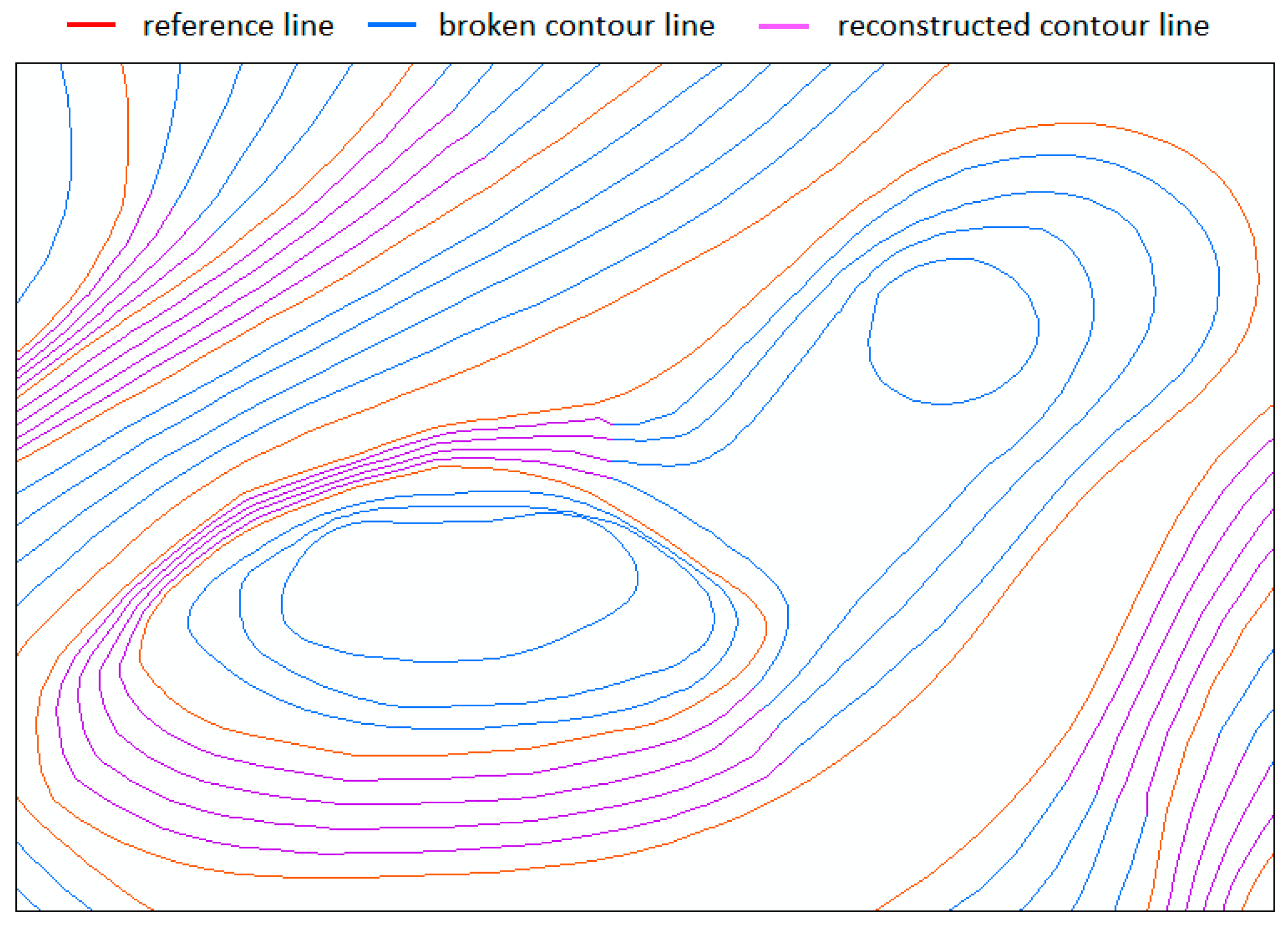
4.2. Universality Analysis
4.2.1. Reference Line Selection
4.2.2. Contour Line Reconstruction
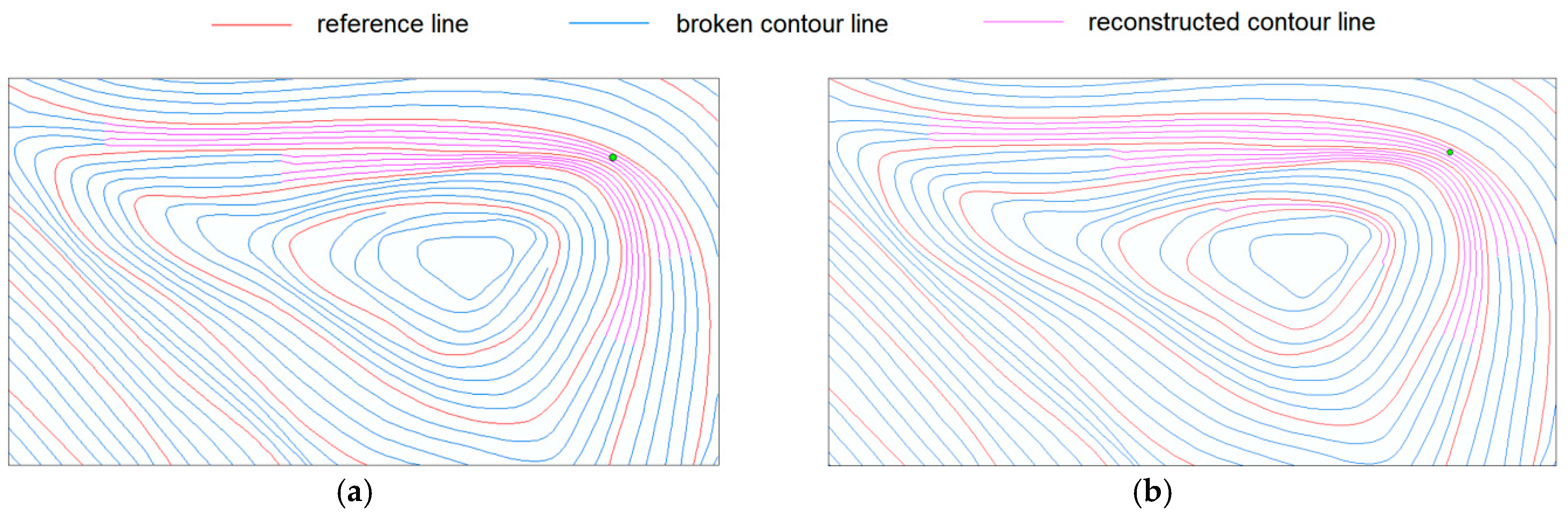
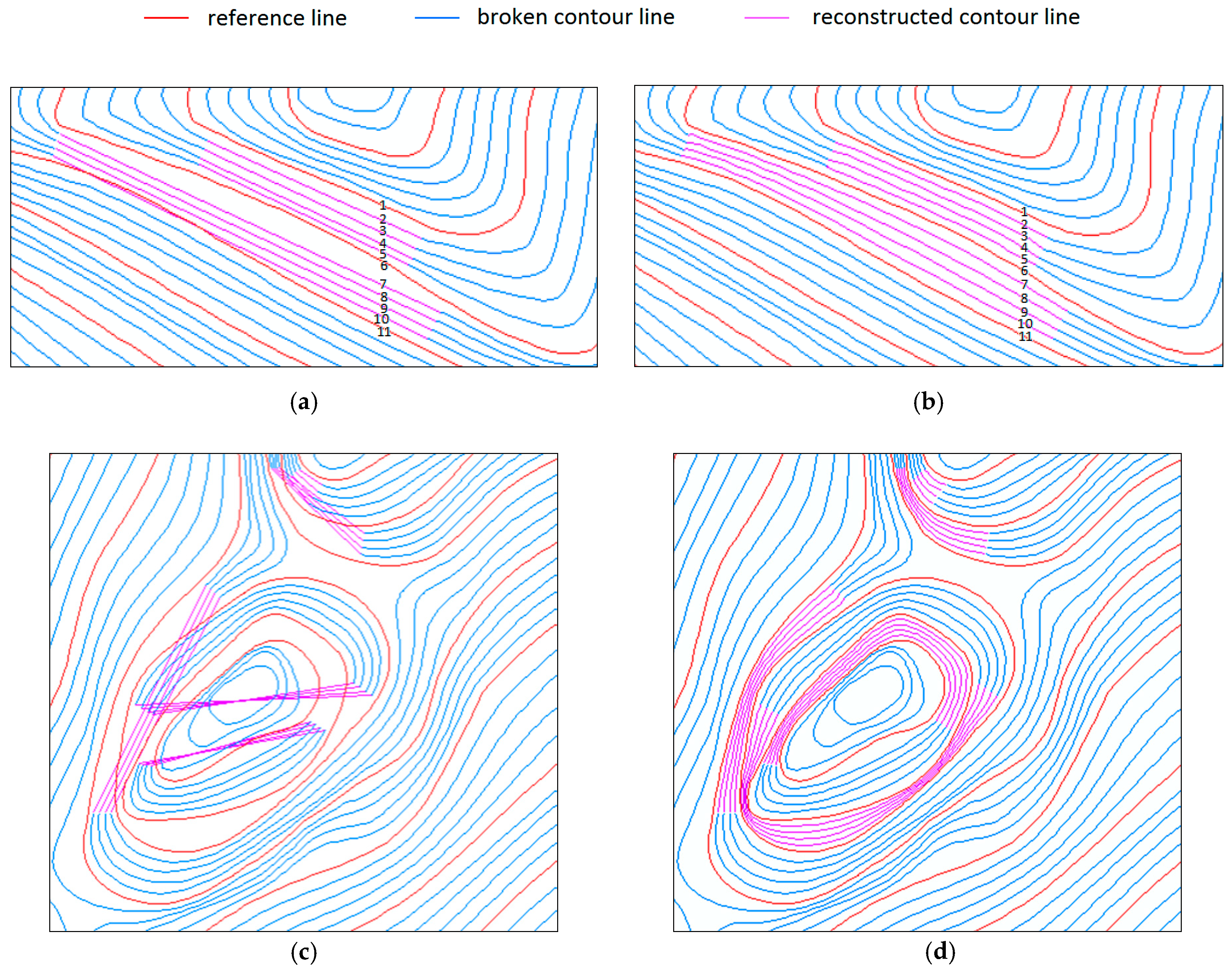
4.3. Superiority Analysis
5. Discussion and Conclusions
- (1)
- In terms of general analysis, the experimental results show that the proposed method is applicable for the reconstruction of both complex broken contours and general broken contours, with good universality.
- (2)
- In terms of reconstruction accuracy, the reconstruction results were compared with results from the minimum point pair method under the same conditions. The method in this paper had better results for connection and reconstruction in a simple broken contour zone, and the reconstruction accuracy in a complex broken contour zone was significantly improved.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Samet, R.; Hancer, E. A new approach to the reconstruction of contour lines extracted from topographic maps. J. Vis. Commun. Image Represent. 2012, 23, 642–664. [Google Scholar] [CrossRef]
- Spinello, S.; Guitton, P. Contour Line Recognition from Scanned Topographic Maps. Winter Sch. Comput. Graph. 2004, 12, 419–426. [Google Scholar]
- Du, J.; Zhang, Y. Automatic extraction of contour lines from scanned topographic map. IEEE Int. Geosci. Remote. Sens. Symp. 2004, 5, 2886–2888. [Google Scholar]
- Gul, S.; Khan, M.F. Automatic Extraction of Contour Lines from Topographic Maps. In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications, Sydney, NSW, Australia, 1–3 December 2010; pp. 593–598. [Google Scholar]
- Hancer, E.; Samet, R. Advanced contour reconnection in scanned topographic maps. In Proceedings of the International Conference on Application of Information and Communication Technologies, Baku, Azerbaijan, 12–14 October 2011; pp. 1–5. [Google Scholar]
- Pouderoux, J.; Spinello, S. Global Contour Lines Reconstruction in Topographic Maps. In Proceedings of the International Conference on Document Analysis and Recognition. IEEE Comput. Soc. 2007, 2, 779–783. [Google Scholar]
- Xin, D.; Zhou, X.; Zheng, H. Contour Line Extraction from Paper-based Topographic Maps. J. Infrom. Comput. Sci. 2006, 1, 275–283. [Google Scholar]
- Ghircoias, T.; Brad, R. Contour Lines Extraction and Reconstruction from Topographic Maps. Ubiquitous Comput. Commun. J. 2011, 6, 681–691. [Google Scholar]
- Arrighi, P.; Soille, P. From scanned topographic maps to digital elevation models. In Proceedings of the International Symposium on Imaging Applications in Geology, Liege, Belgium, 6–7 May 1999. [Google Scholar]
- Min, F.U.; Xiao-Ning, L.I. Iteration approach for contour lines reconstruction based on breakpoint classification and orientation difference. J. Sichuan Univ. 2013, 50, 737–742. [Google Scholar]
- Cheng, J.; Liu, P.; Wang, F. Comparison of Reconstruction Methods for Broken contour Lines on Raster Topographic Maps. Geomat. Sci. Eng. 2015, 35, 36–42. (In Chinese) [Google Scholar]
- Xiaoya, A.N.; Liu, P.; Yun, Y.; Hou, S. A geometric similarity measurement method and applications to linear feature. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1225–1229. (In Chinese) [Google Scholar]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Fréchet, M.M. A few points on the functional design. Rendiconti del Circolo Matematico di Palermo (1884–1940) 1906, 22, 1–72. (In French) [Google Scholar] [CrossRef]
- Alt, H.; Knauer, C.; Wenk, C. Matching Polygonal Curves with Respect to the Fréchet Distance. Comput. Geom. 2005, 30, 113–127. [Google Scholar]
- Zhu, J.; Huang, Z.; Peng, X. Curve Similarity Judgment Based on the Discrete Fréchet Distance. J. Wuhan Univ. 2009, 55, 227–232. (In Chinese) [Google Scholar]
- Schlesinger, M.I.; Vodolazskiy, E.V.; Yakovenko, V.M. Fréchet Similarity of Closed Polygonal Curves. Int. J. Comput. Geom. Appl. 2016, 26, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Eiter, T.; Mannila, H. Computing discrete Fréchet distance. See Also 1994, 64, 636–637. [Google Scholar]
- Li, C.; Yin, Y.; Liu, X.; Wu, P. An Automated Processing Method for Agglomeration Areas. ISPRS Int. J. Geo-Inf. 2018, 7, 204. [Google Scholar] [CrossRef]
| No | Statistical Item | Statistical Result |
|---|---|---|
| 1 | Total number of contour lines | 5948 |
| 2 | Total number of broken contour lines | 3277 |
| 3 | Proportion of breaks | 55% |
| 4 | The number of general broken contour lines | 1246 |
| 5 | The number of complex broken contour lines | 2031 |
| 6 | Correct reconstruction of broken contour lines | 3064 |
| 7 | Correct reconstruction of general broken contour lines | 1225 |
| 8 | Correct reconstruction of complex broken contour lines | 1839 |
| 9 | Reconstruction accuracy rate of the broken contour lines | 93.5% |
| Method | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | SD | 6–7 | 7–8 | 8–9 | 9–10 | 10–11 | SD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Minimum point pair method | 3.3 | 3.1 | 3.2 | 1.8 | 1.3 | 0.82 | 5.1 | 2.8 | 2.9 | 2.6 | 1.0 | 1.31 |
| Our method | 2.9 | 3.0 | 3.0 | 2.9 | 2.8 | 0.07 | 3.4 | 3.5 | 3.3 | 3.4 | 3.3 | 0.07 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Liu, X.; Wu, W.; Hao, Z. A Reconstruction Method for Broken Contour Lines Based on Similar Contours. ISPRS Int. J. Geo-Inf. 2019, 8, 8. https://doi.org/10.3390/ijgi8010008
Li C, Liu X, Wu W, Hao Z. A Reconstruction Method for Broken Contour Lines Based on Similar Contours. ISPRS International Journal of Geo-Information. 2019; 8(1):8. https://doi.org/10.3390/ijgi8010008
Chicago/Turabian StyleLi, Chengming, Xiaoli Liu, Wei Wu, and Zhiwei Hao. 2019. "A Reconstruction Method for Broken Contour Lines Based on Similar Contours" ISPRS International Journal of Geo-Information 8, no. 1: 8. https://doi.org/10.3390/ijgi8010008
APA StyleLi, C., Liu, X., Wu, W., & Hao, Z. (2019). A Reconstruction Method for Broken Contour Lines Based on Similar Contours. ISPRS International Journal of Geo-Information, 8(1), 8. https://doi.org/10.3390/ijgi8010008




