Method for the Analysis and Visualization of Similar Flow Hotspot Patterns between Different Regional Groups
Abstract
1. Introduction
2. Literature Review
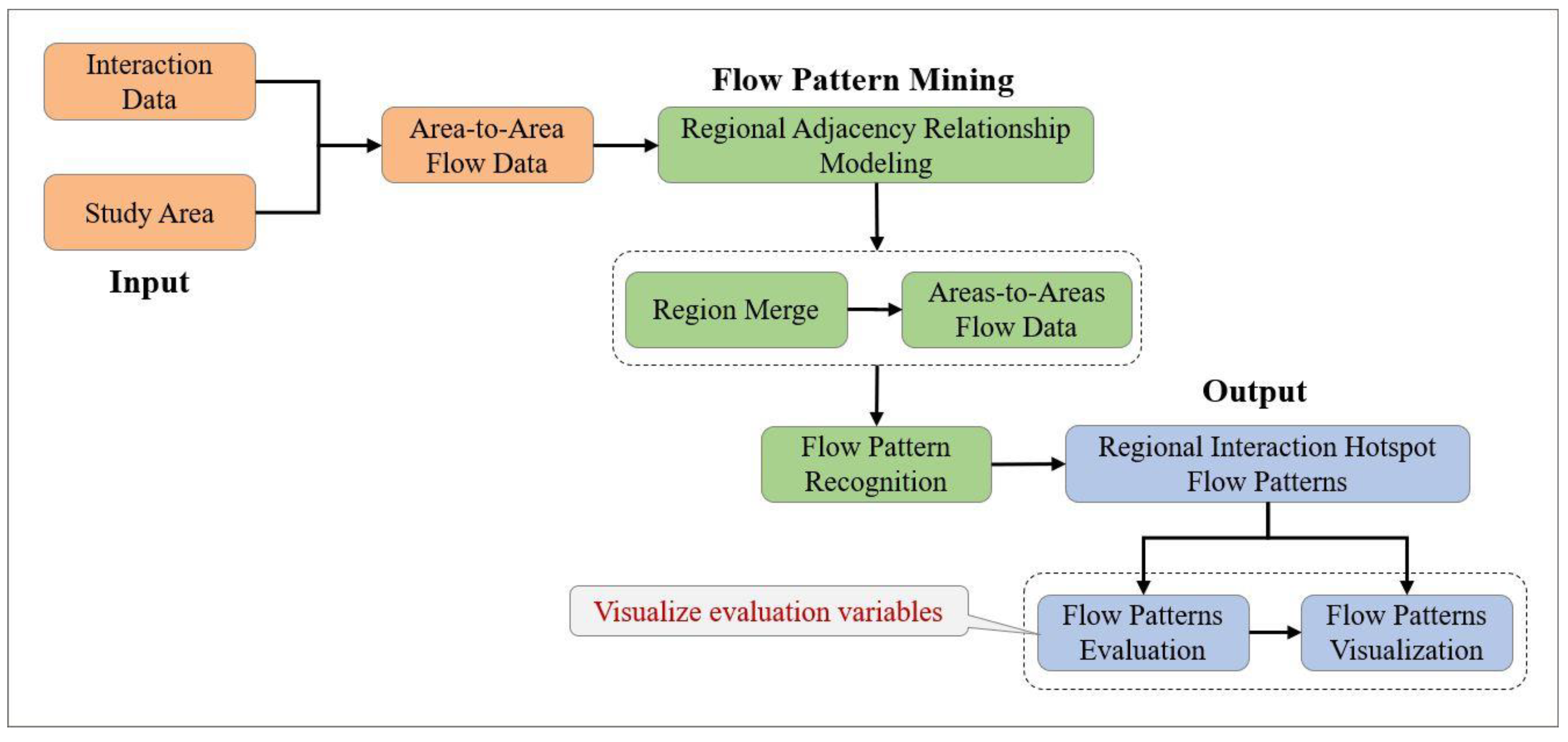
3. Methodology
3.1. Algorithm for Similar Hotspot Patterns between Regional Groups
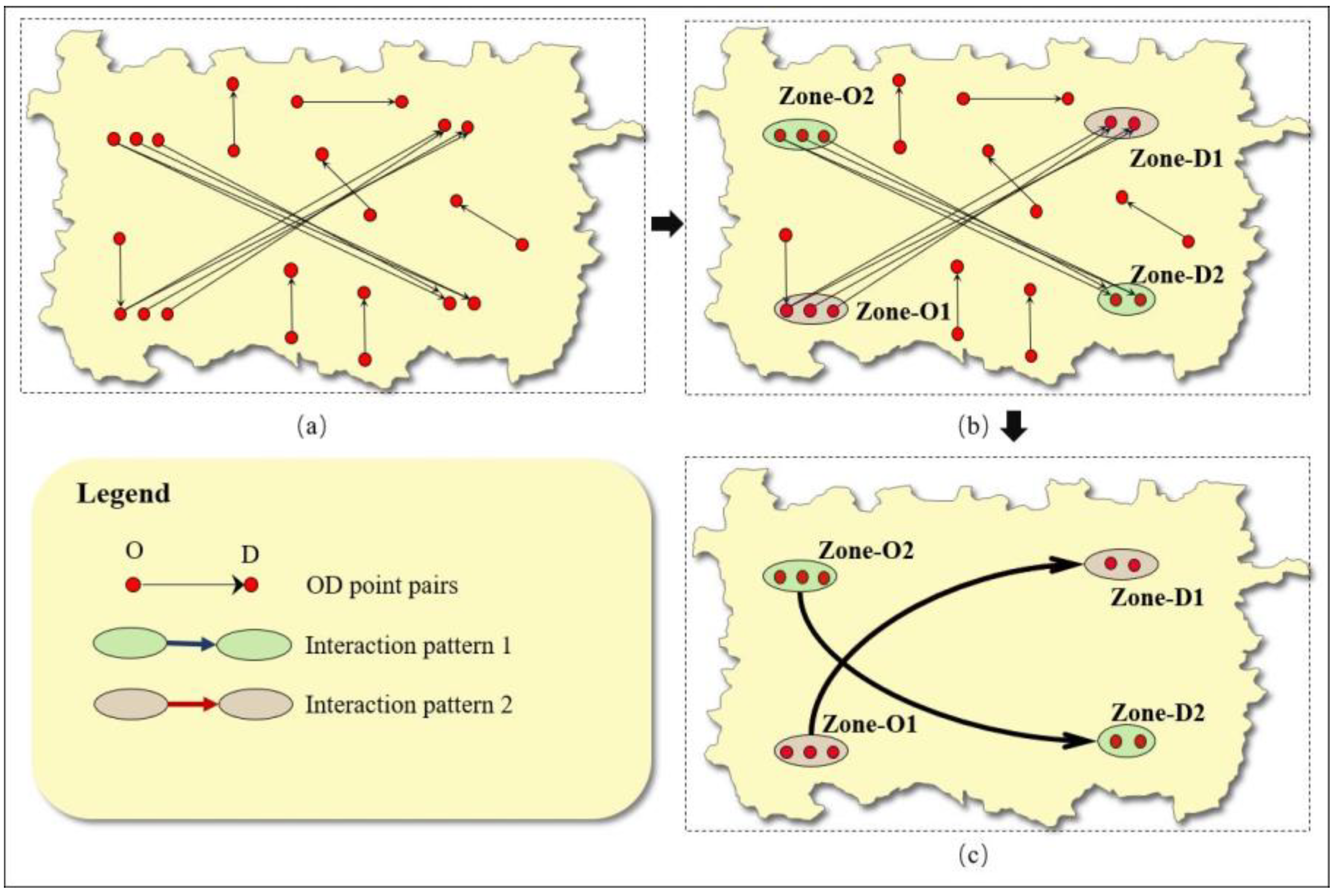
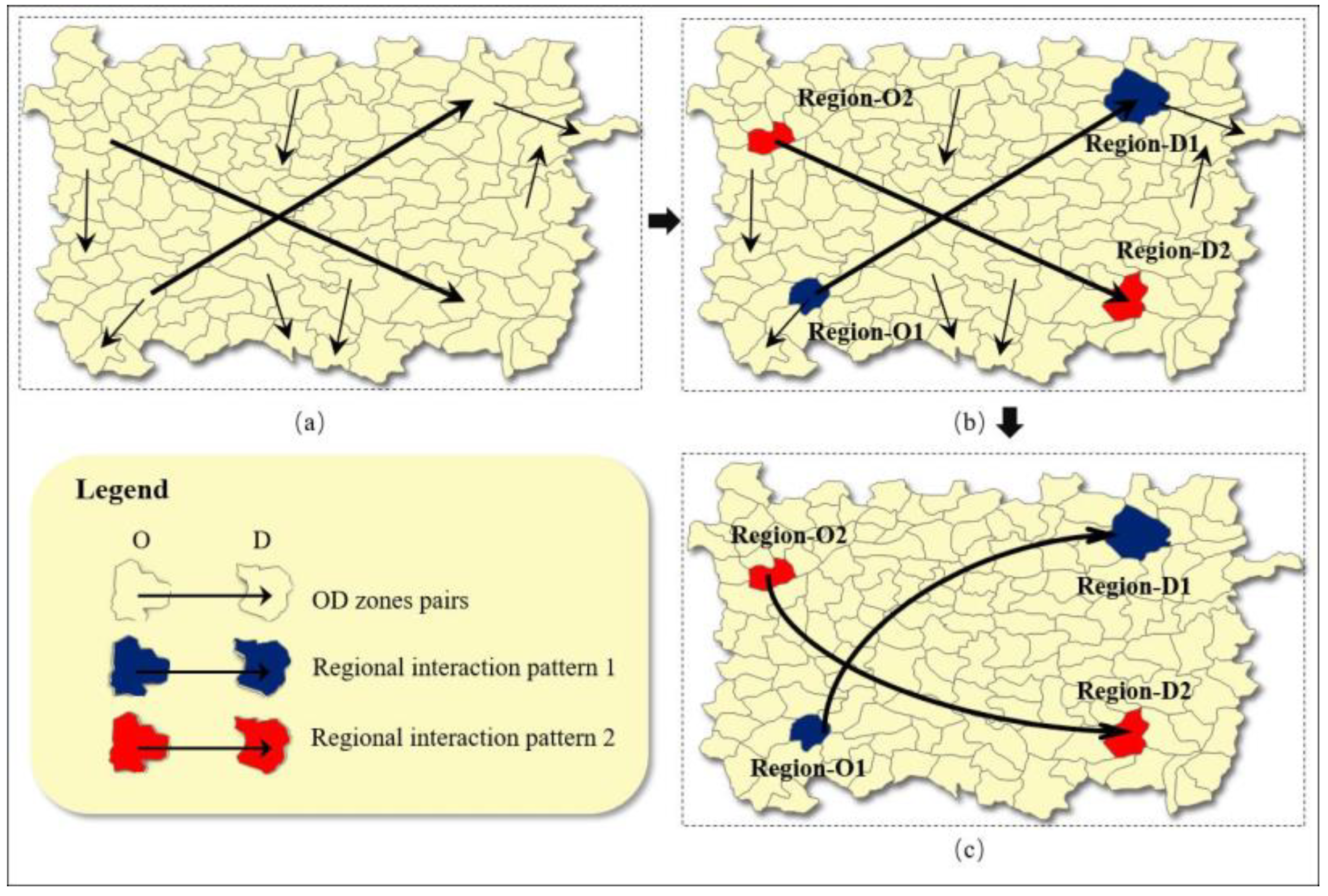
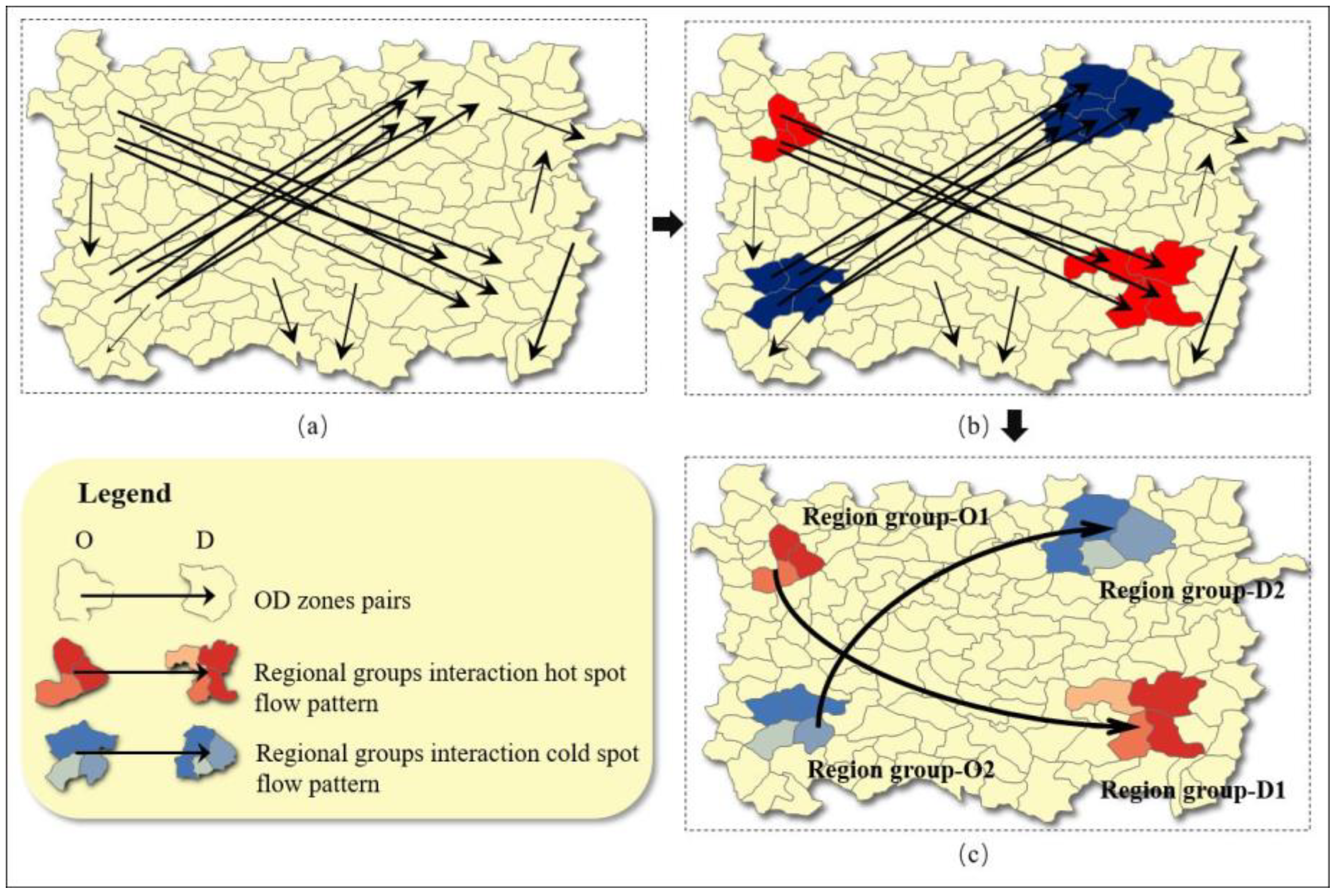
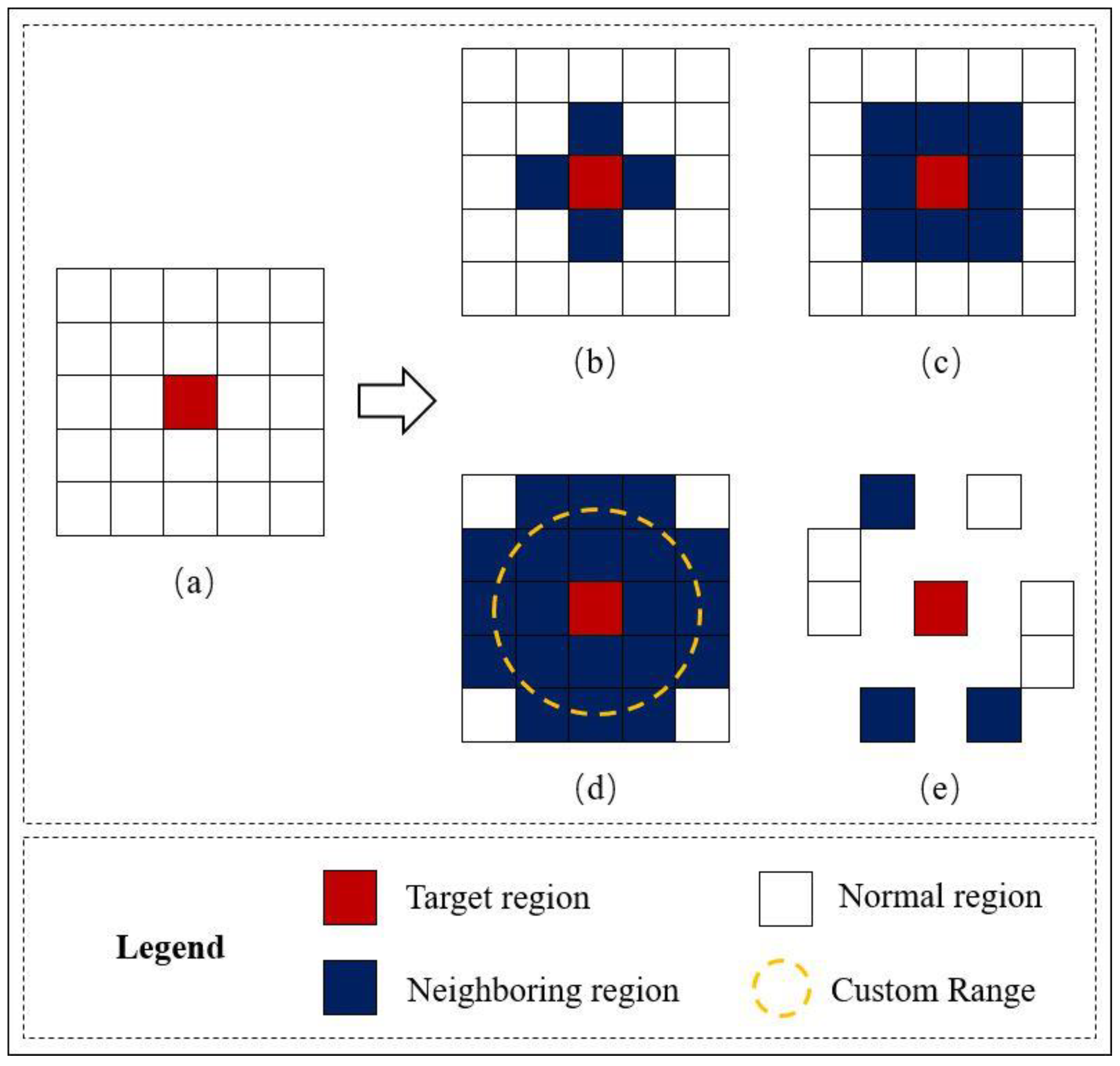
3.1.1. Regional Adjacency Relationship Modeling
3.1.2. Region Merging and Recognition of Similar Hotspot Flow Patterns
3.2. SHFP-RG Visualization Method Based on Geo-Information Tupo Theory
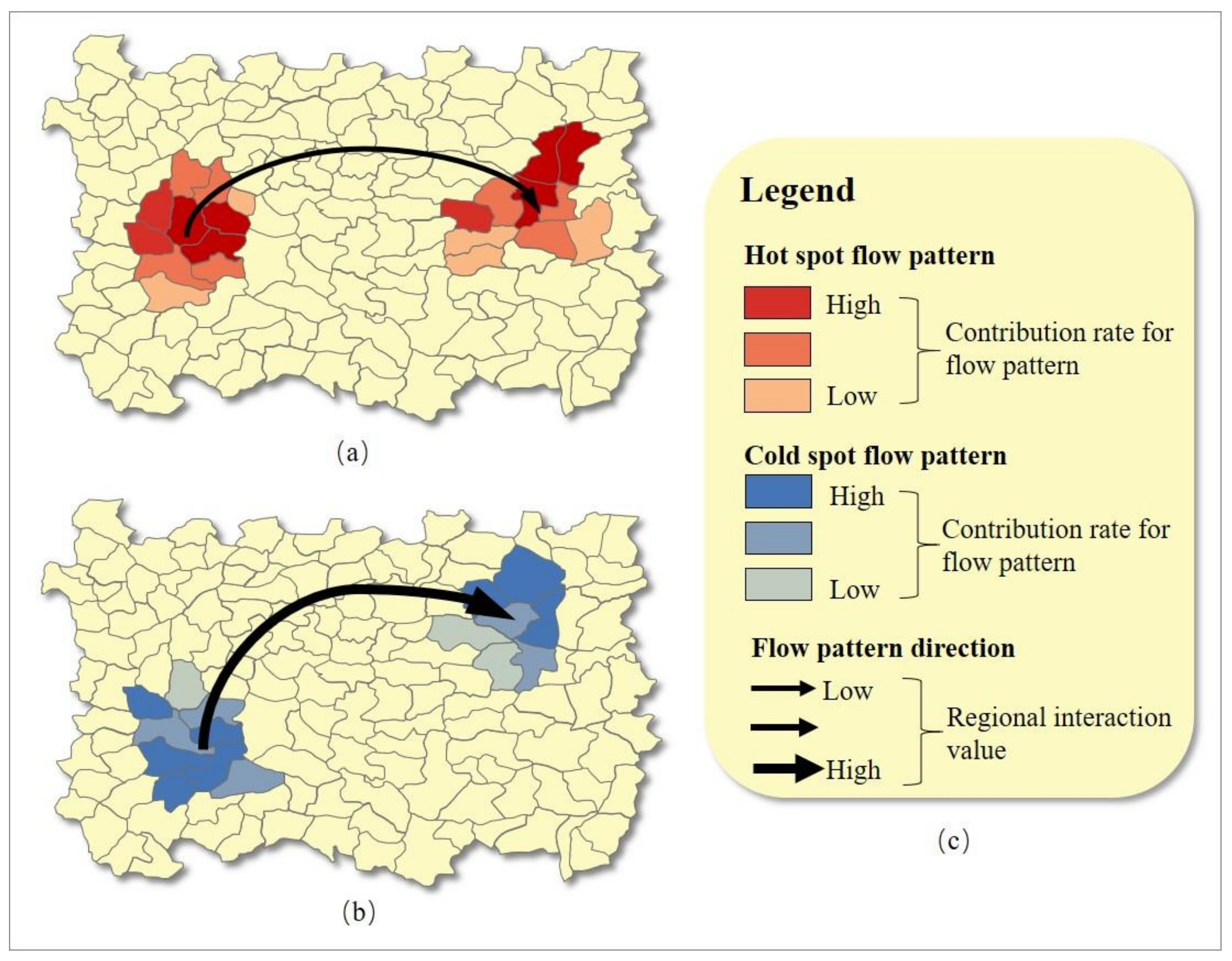
3.2.1. Visualization of a Single RG-Flow-Pattern
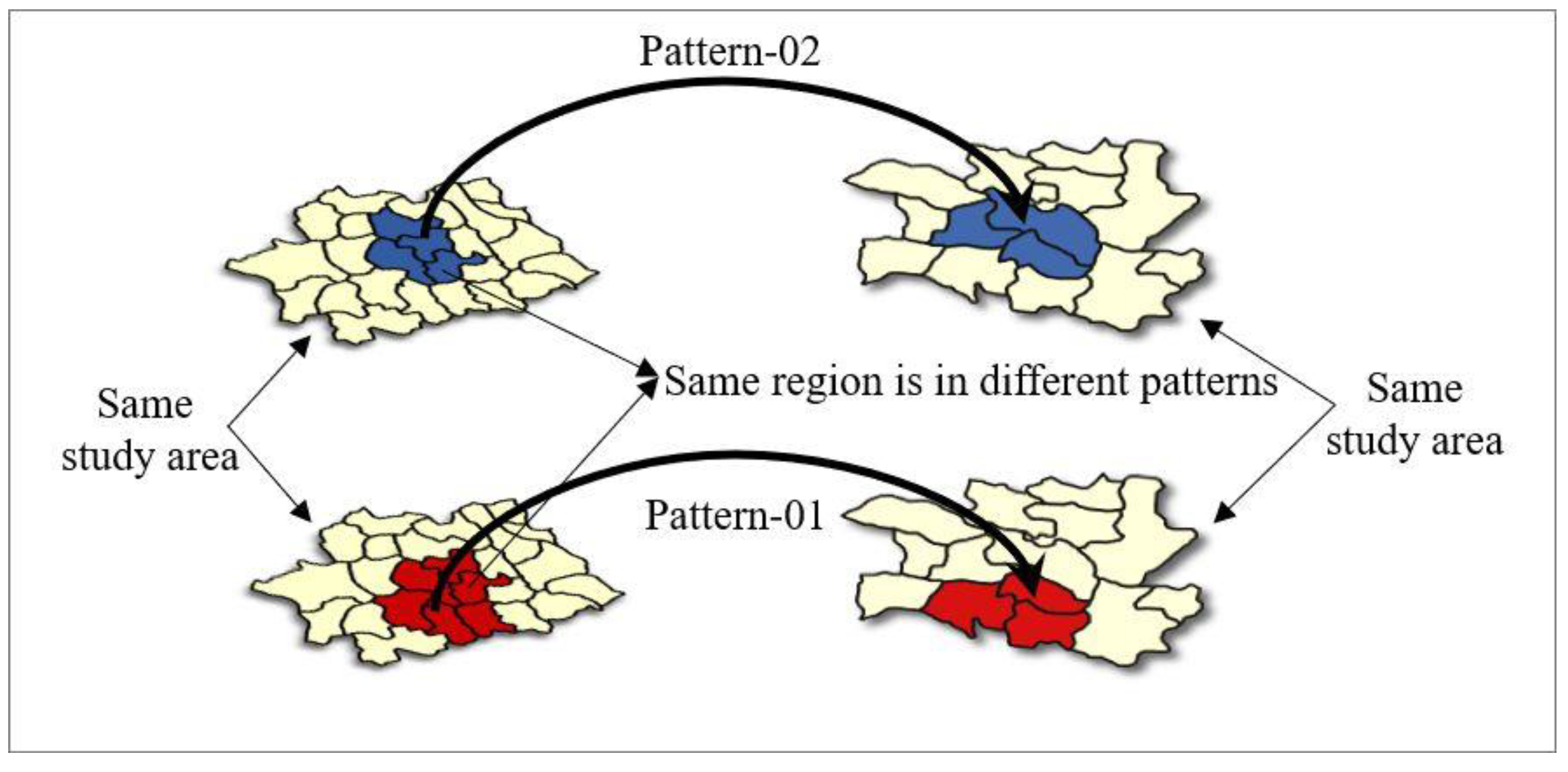
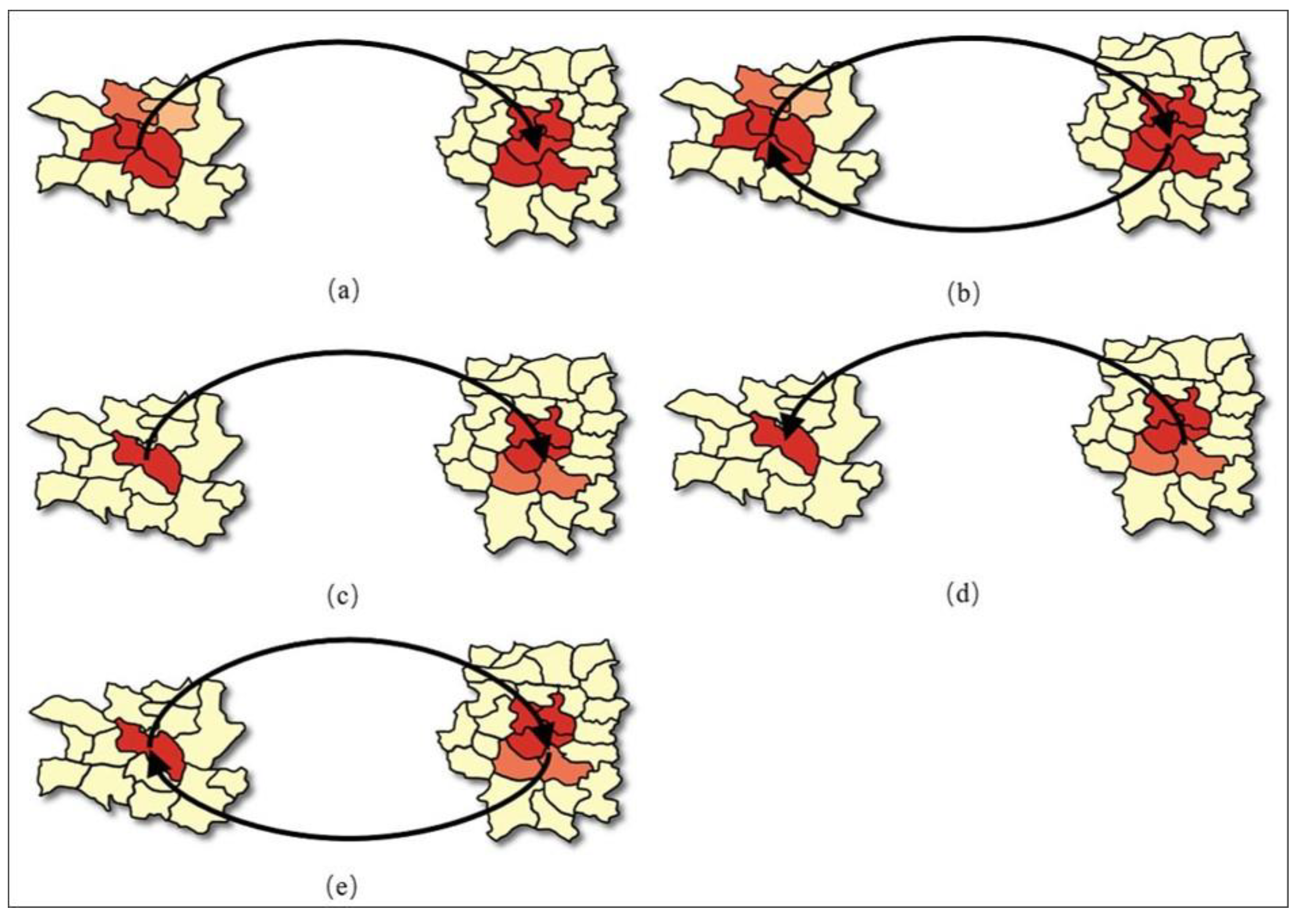
3.2.2. Visualization and Classification of Multiple RG-Flow-Patterns Based on Geo-information Tupu
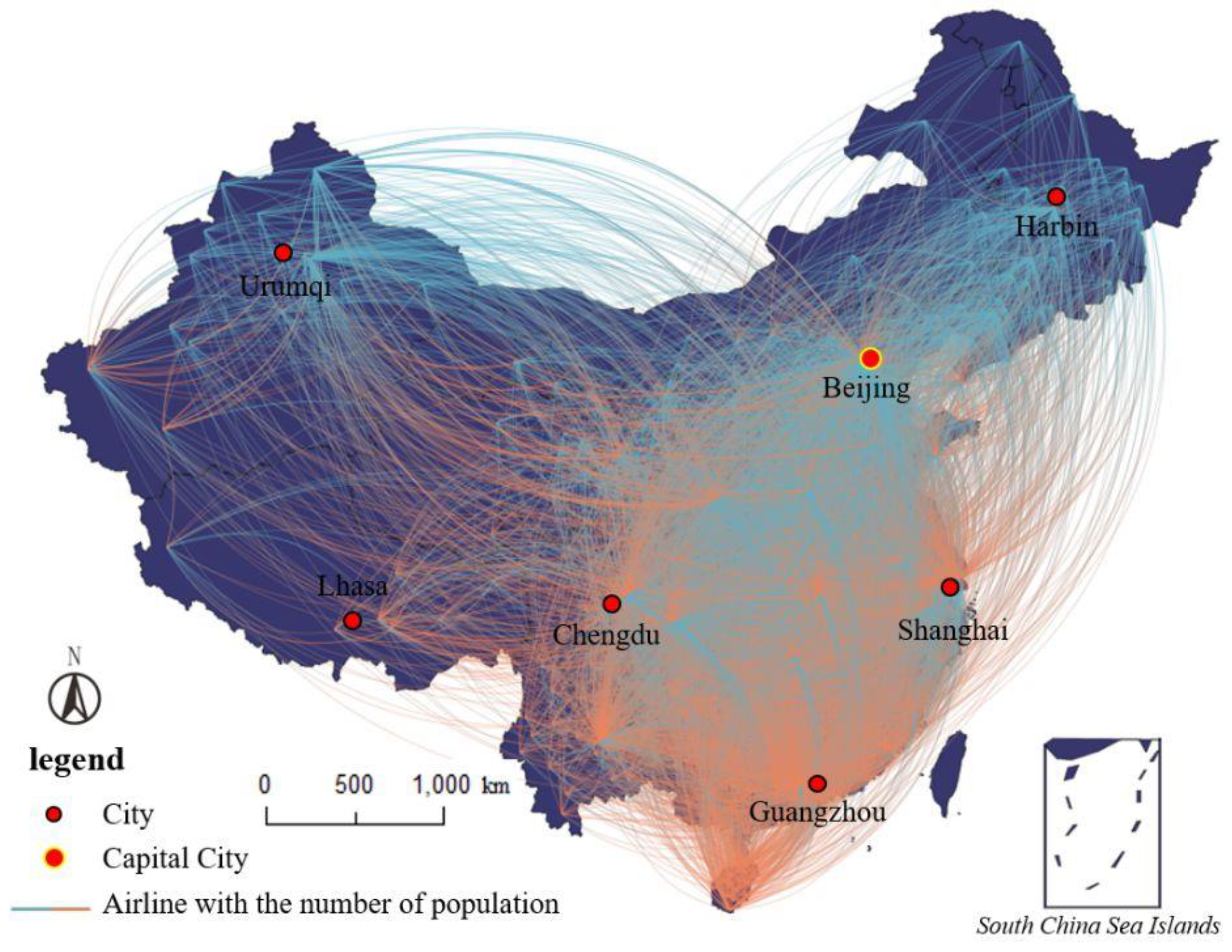
4. Case Study: National Migration Flow Data of China
4.1. Study Area and Data Descriptions
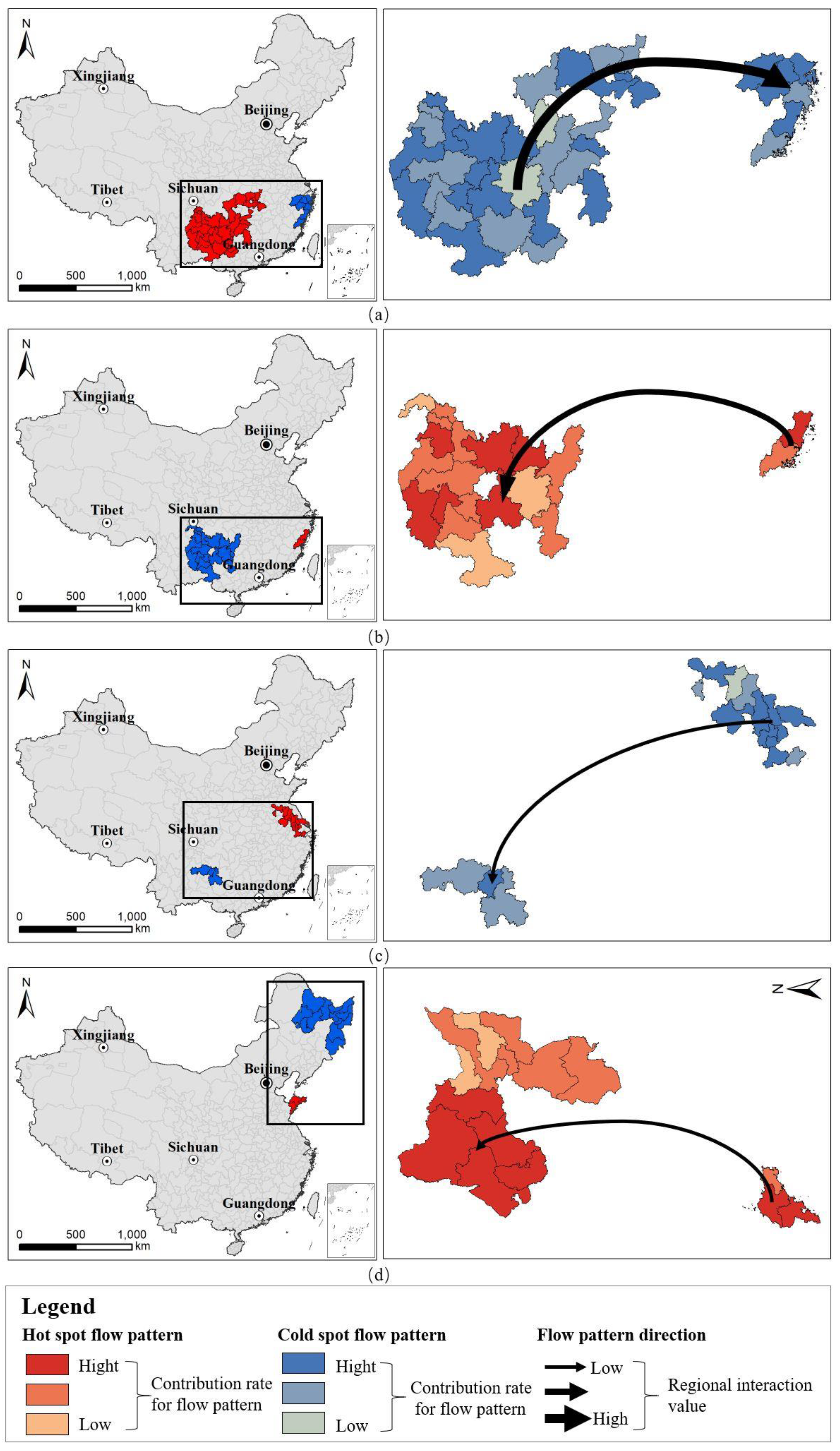
4.2. Result
5. Discussion and Conclusions
5.1. Discussion
5.1.1. Principle underlying the Selection of the Regional Adjacency Relationship and Regional Merge Threshold
5.1.2. Evaluation of Results
5.1.3. Shortcomings and Future Improvements
5.2. Conclusions
Abbreviations
| Point-to-point | From one point to another point |
| Area-to-area | From one area to another area |
| Areas-to-areas | From a group of areas to another group of areas |
| RG-Flow-Pattern | Regional Group Flow Patterns |
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marty, P.F. An introduction to digital convergence: Libraries, archives, and museums in the information age. Libr. Quart. 2010, 80, 1–5. [Google Scholar] [CrossRef]
- Andris, C.; Liu, X.; Ferreira, J. Challenges for social flows. Comput. Environ. Urban Syst. 2018, 70, 197–207. [Google Scholar] [CrossRef]
- Andris, C. Integrating social network data into GISystems. Int. J. Geogr. Inf. Sci. 2016, 30, 2009–2031. [Google Scholar] [CrossRef]
- Midler, J.C. Non-euclidean geographic spaces: Mapping functional distances. Geogr. Anal. 2010, 14, 189–203. [Google Scholar] [CrossRef]
- Alamri, S.; Taniar, D.; Safar, M.; Al-Khalidi, H. A connectivity index for moving objects in an indoor cellular space. Pers. Ubiquit. Comput. 2014, 18, 287–301. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the heshun region, china. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Limtanakool, N.; Schwanen, T.; Dijst, M. Developments in the dutch urban system on the basis of flows. Reg. Stud. 2009, 43, 179–196. [Google Scholar] [CrossRef]
- McKenzie, G.; Janowicz, K.; Gao, S.; Gong, L. How where is when? On the regional variability and resolution of geosocial temporal signatures for points of interest. Comput. Environ. Urban. 2015, 54, 336–346. [Google Scholar] [CrossRef]
- Tao, R.; Thill, J.C. Spatial cluster detection in spatial flow data. Geogr. Anal. 2016, 48, 355–372. [Google Scholar] [CrossRef]
- Seto, K.C.; Reenberg, A.; Boone, C.G.; Fragkias, M.; Haase, D.; Langanke, T.; Marcotullio, P.; Munroe, D.K.; Olah, B.; Simon, D. Urban land teleconnections and sustainability. Proc. Natl. Acad. Sci. USA 2012, 109, 7687–7692. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Guo, D.S. Mapping large spatial flow data with hierarchical clustering. Trans. GIS 2014, 18, 421–435. [Google Scholar] [CrossRef]
- Adams, P.C. A taxonomy for communication geography. Prog. Hum. Geogr. 2011, 35, 37–57. [Google Scholar] [CrossRef]
- Mesbah, M.; Currie, G.; Lennon, C.; Northcott, T. Spatial and temporal visualization of transit operations performance data at a network level. J. Transp. Geogr. 2012, 25, 15–26. [Google Scholar] [CrossRef]
- Fonte, C.C.; Fontes, D.; Cardoso, A. A web GIS-based platform to harvest georeferenced data from social networks: Examples of data collection regarding disaster events. Int. J. Online Eng. 2018, 14, 165–172. [Google Scholar] [CrossRef]
- Hale, M.L.; Ellis, D.; Gamble, R.; Walter, C.; Lin, J. Secuwear: An open source, multi-component hardware/software platform for exploring wearable security. In Proceedings of the IEEE International Conference on Mobile Services, Combra, Portugal, 27 June–2 July 2015. [Google Scholar]
- Li, M.; Sun, Y.R.; Fan, H.C. Contextualized relevance evaluation of geographic information for mobile users in location-based social networks. ISPRS Int. J. Geo.-Inf. 2015, 4, 799–814. [Google Scholar] [CrossRef]
- Li, J.W.; Ye, Q.Q.; Deng, X.K.; Liu, Y.L.; Liu, Y.F. Spatial-temporal analysis on spring festival travel rush in china based on multisource big data. Sustaina.-Basel. 2016, 8, 1184. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Esquivel, A.V.; Rosvall, M. Compression of flow can reveal overlapping-module organization in networks. Phys. Rev. X 2011, 1, 1668–1678. [Google Scholar]
- Zhou, M.; Yue, Y.; Li, Q.Q.; Wang, D.G. Portraying temporal dynamics of urban spatial divisions with mobile phone positioning data: A complex network approach. ISPRS Int. J. Geo.-Inf. 2016, 5, 240. [Google Scholar] [CrossRef]
- Kempinska, K.; Longley, P.; Shawe-Taylor, J. Interactional regions in cities: Making sense of flows across networked systems. Int. J. Geogr. Inf. Sci. 2018, 32, 1348–1367. [Google Scholar] [CrossRef]
- Kim, K.; Oh, K.; Lee, Y.K.; Kim, S.; Jung, J.Y. An analysis on movement patterns between zones using smart card data in subway networks. Int. J. Geogr. Inf. Sci. 2014, 28, 1781–1801. [Google Scholar] [CrossRef]
- Chen, Z.L.; Gong, X.; Xie, Z. An analysis of movement patterns between zones using taxi GPS data. Trans. GIS 2017, 21, 1341–1363. [Google Scholar] [CrossRef]
- Liu, L.A.; Hou, A.Y.; Biderman, A.; Ratti, C.; Chen, J. Understanding individual and collective mobility patterns from smart card records: A case study in Shenzhen. Intell. Transp. Syst. 2009, 1–6. [Google Scholar] [CrossRef]
- Munizaga, M.A.; Palma, C. Estimation of a disaggregate multimodal public transport origin-destination matrix from passive smartcard data from Santiago, Chile. Transp. Res. C-Emer. 2012, 24, 9–18. [Google Scholar] [CrossRef]
- Ghasemzadeh, M.; Fung, B.C.M.; Chen, R.; Awasthi, A. Anonymizing trajectory data for passenger flow analysis. Transp. Res. C-Emer. 2014, 39, 63–79. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Martens, K.; Long, Y. Revealing group travel behavior patterns with public transit smart card data. Travel Behav. Soc. 2018, 10, 42–52. [Google Scholar] [CrossRef]
- Chu, K.K.A.; Chapleau, R. Enriching archived smart card transaction data for transit demand modeling. Transp. Res. Rec. 2008, 2063, 63–72. [Google Scholar] [CrossRef]
- Higuchi, T.; Shimamoto, H.; Uno, N.; Shiomi, Y. A trip-chain based combined mode and route choice network equilibrium model considering common lines problem in transit assignment model. Procedia-Soc. Behav. Sci. 2011, 20, 354–363. [Google Scholar] [CrossRef]
- Concas, S.; DeSalvo, J.S. The effect of density and trip-chaining on the interaction between urban form and transit demand. J. Public Transp. 2014, 17, 16–38. [Google Scholar] [CrossRef]
- Zhou, L.; Ji, Y.X.; Wang, Y.Z. Analysis of public transit trip chain of commuters based on mobile phone data and GPS data. In Proceedings of the International Conference on Transportation Information Safety, Edmonton, AB, Canada, 8–10 August 2017. [Google Scholar]
- Blythe, P.T. Improving public transport ticketing through smart cards. In Proceedings of Institution of Civil Engineers-Municipal Engineer; Thomas, Telford, Ltd.: London, UK, 2004; Volume 157. [Google Scholar]
- Pelletier, M.P.; Trepanier, M.; Morency, C. Smart card data use in public transit: A literature review. Transp. Res. C-Emer. 2011, 19, 557–568. [Google Scholar] [CrossRef]
- Wang, Y.; Lim, E.P.; Hwang, S.Y. Efficient algorithms for mining maximal valid groups. Vldb. J. 2008, 17, 515–535. [Google Scholar] [CrossRef]
- Aung, H.H.; Tan, K.L. Discovery of evolving convoys. Sci. Stat. Database Manag. 2010, 6187, 196–213. [Google Scholar]
- Li, Y.X.; Bailey, J.; Kulik, L. Efficient mining of platoon patterns in trajectory databases. Data & Knowl. Eng. 2015, 100, 167–187. [Google Scholar]
- Williams, H.J.; Holton, M.D.; Shepard, E.L.C.; Largey, N.; Norman, B.; Ryan, P.G.; Duriez, O.; Scantlebury, M.; Quintana, F.; Magowan, E.A.; et al. Identification of animal movement patterns using tri-axial magnetometry. Mov. Ecol. 2017, 5, 6. [Google Scholar] [CrossRef] [PubMed]
- Bunting, R.J.; Chang, O.Y.; Cowen, C.; Hankins, R.; Langston, S.; Warner, A.; Yang, X.X.; Louderback, E.R.; Sen Roy, S. Spatial patterns of larceny and aggravated assault in Miami-Dade County, 2007–2015. Prof. Geogr. 2018, 70, 34–46. [Google Scholar] [CrossRef]
- Grieve, J. A regional analysis of contraction rate in written standard American English. Int. J. Corpus Linguis. 2011, 16, 514–546. [Google Scholar] [CrossRef]
- Zhang, S.L.; Zhang, K. Comparison between general moran’s index and getis-ord general g of spatial autocorrelation. Acta Sci. Nat. Univ. Sunyatseni 2007, 46, 93–97. [Google Scholar]
- Ye, Q.; Tian, G.; Liu, G.; Ye, J.; Yao, X.; Liu, Q.; Lou, W.; Wu, S. Tupu methods of spatial-temporal pattern on land use change. J. Geogr. Sci. 2004, 14, 131–142. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
| Data Type | Attribute | Meaning | Attribute Type |
|---|---|---|---|
| Administrative polygons | city_name | Name of each city | String |
| Population flow data of flights | origin_city_name | Name of origin city | String |
| destination_city_name | Name of destination city | String | |
| hot_value | Hot value between cities | Double |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhou, X.; Gu, X.; Zhou, L.; Ji, G.; Tang, G. Method for the Analysis and Visualization of Similar Flow Hotspot Patterns between Different Regional Groups. ISPRS Int. J. Geo-Inf. 2018, 7, 328. https://doi.org/10.3390/ijgi7080328
Zhang H, Zhou X, Gu X, Zhou L, Ji G, Tang G. Method for the Analysis and Visualization of Similar Flow Hotspot Patterns between Different Regional Groups. ISPRS International Journal of Geo-Information. 2018; 7(8):328. https://doi.org/10.3390/ijgi7080328
Chicago/Turabian StyleZhang, Haiping, Xingxing Zhou, Xin Gu, Lei Zhou, Genlin Ji, and Guoan Tang. 2018. "Method for the Analysis and Visualization of Similar Flow Hotspot Patterns between Different Regional Groups" ISPRS International Journal of Geo-Information 7, no. 8: 328. https://doi.org/10.3390/ijgi7080328
APA StyleZhang, H., Zhou, X., Gu, X., Zhou, L., Ji, G., & Tang, G. (2018). Method for the Analysis and Visualization of Similar Flow Hotspot Patterns between Different Regional Groups. ISPRS International Journal of Geo-Information, 7(8), 328. https://doi.org/10.3390/ijgi7080328





