Hexagon-Based Adaptive Crystal Growth Voronoi Diagrams Based on Weighted Planes for Service Area Delimitation
Abstract
:1. Introduction
2. Adaptive Crystal Growth Voronoi Diagrams
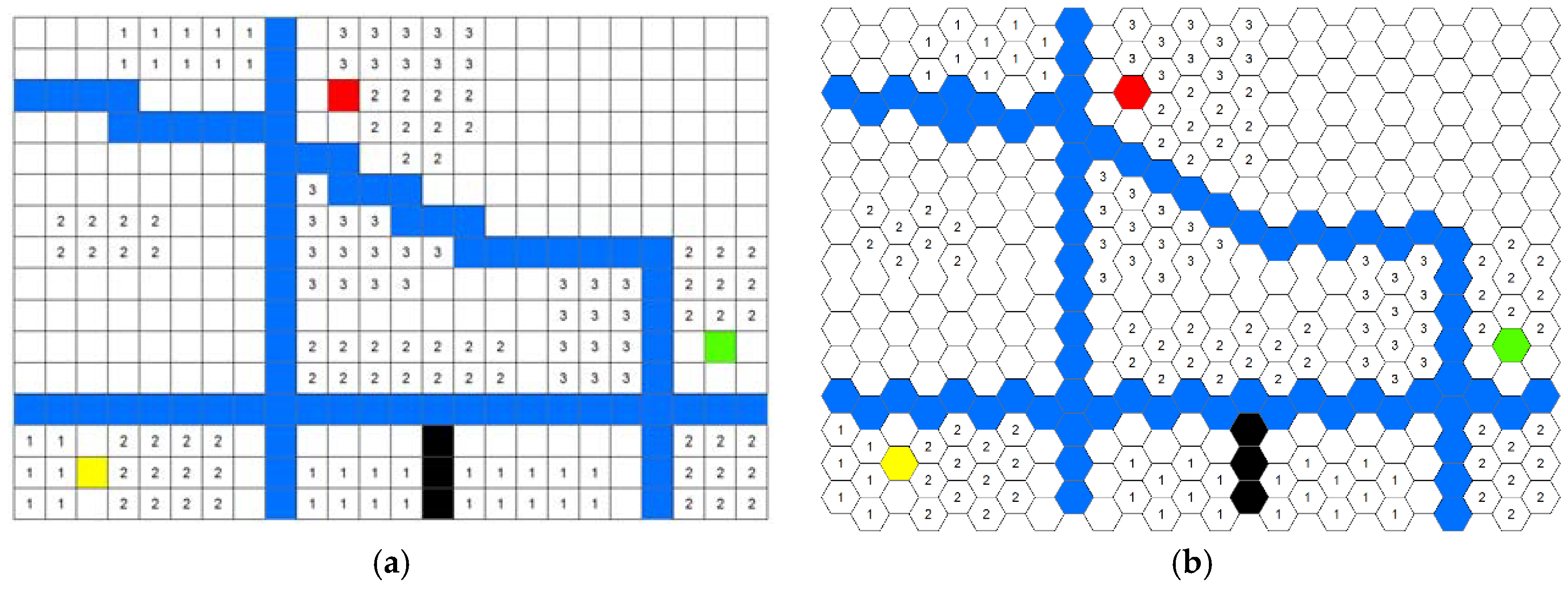
2.1. Raster-Based Adaptive Crystal Growth Voronoi Diagrams
2.2. Hexagon-Based Adaptive Crystal Growth Voronoi Diagrams
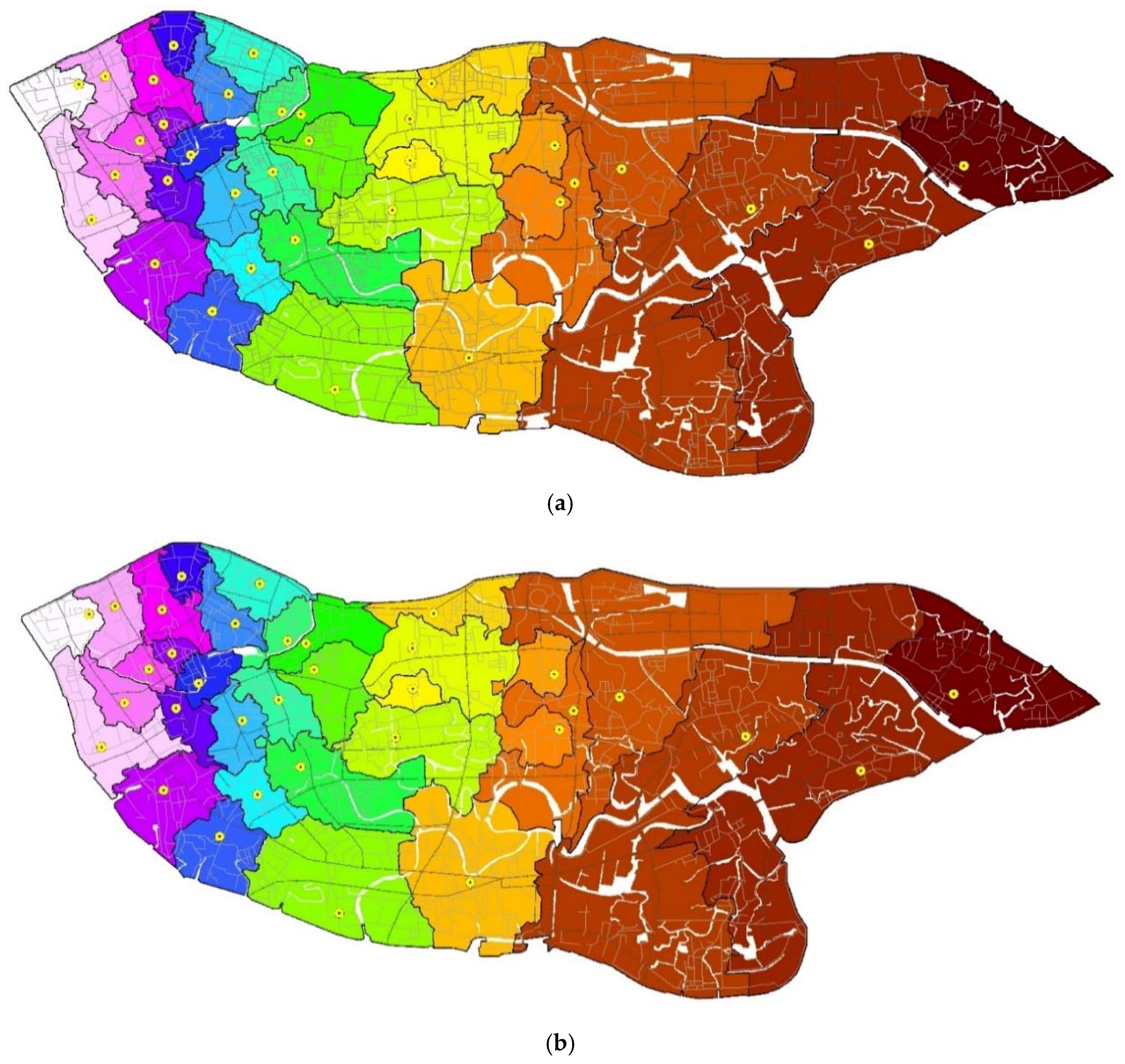
3. Middle School Service Area Delimitation
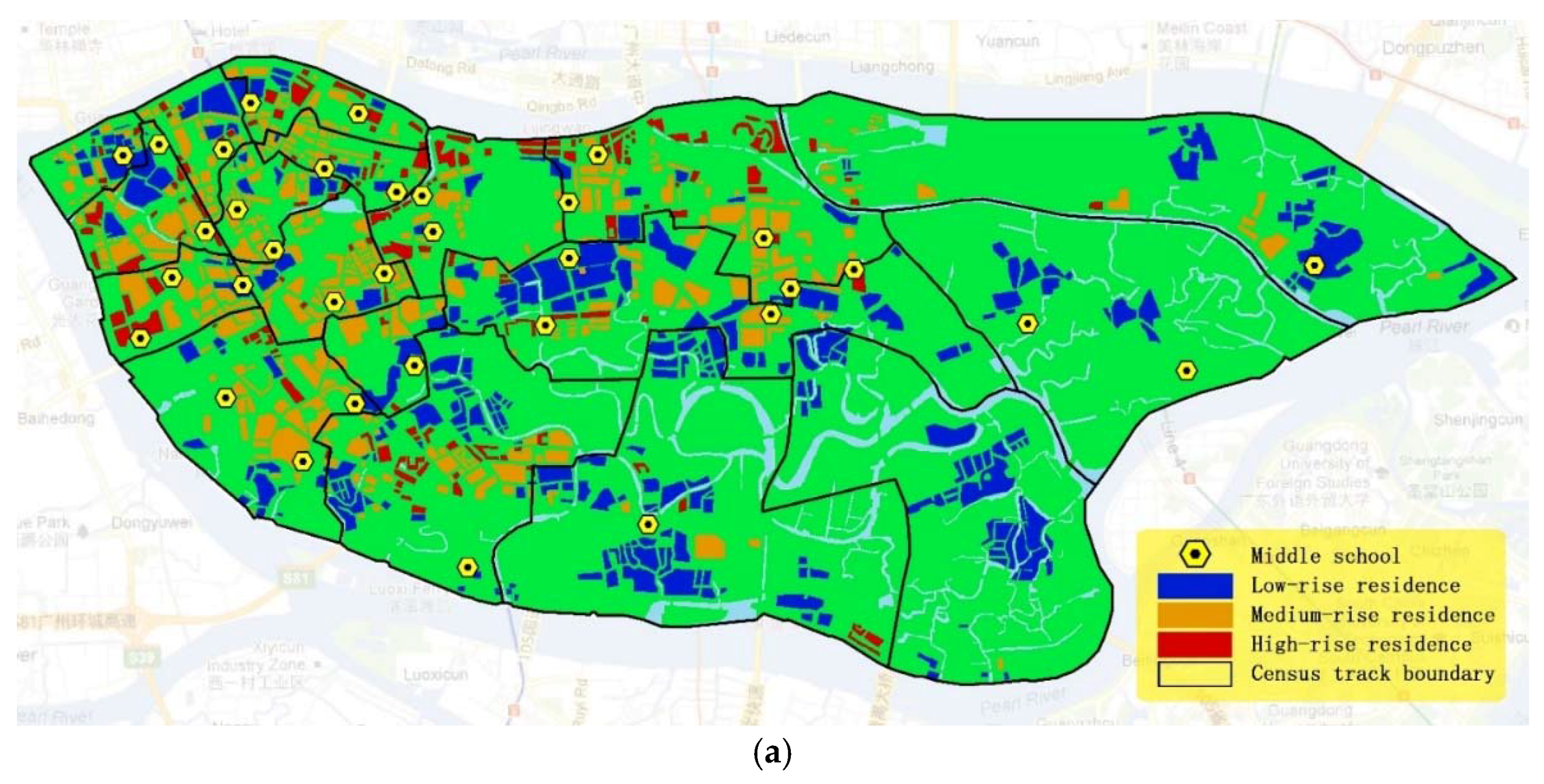
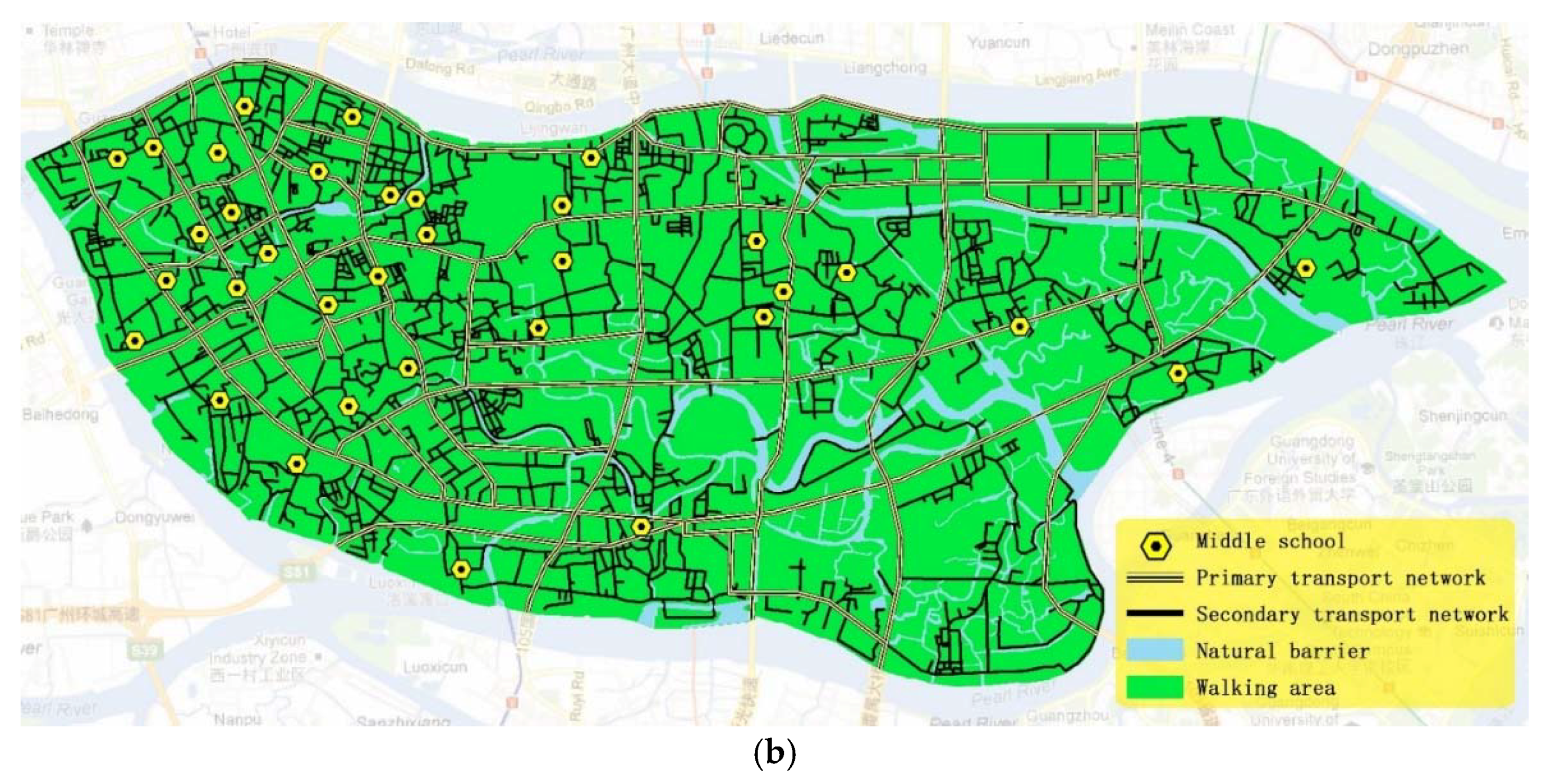
3.1. Study Area
3.2. Weighted Planes
3.3. Crystal Growth Configuration
- (1)
- The seed cells for the raster-based method are the raster cells that intersect with the locations of the 34 middle schools, while the seed point cells for the hexagon-based method are the hexagon cells that intersect with the locations of the 34 middle schools. In the crystal growth process, the service area of each facility grows from the seed point simultaneously.
- (2)
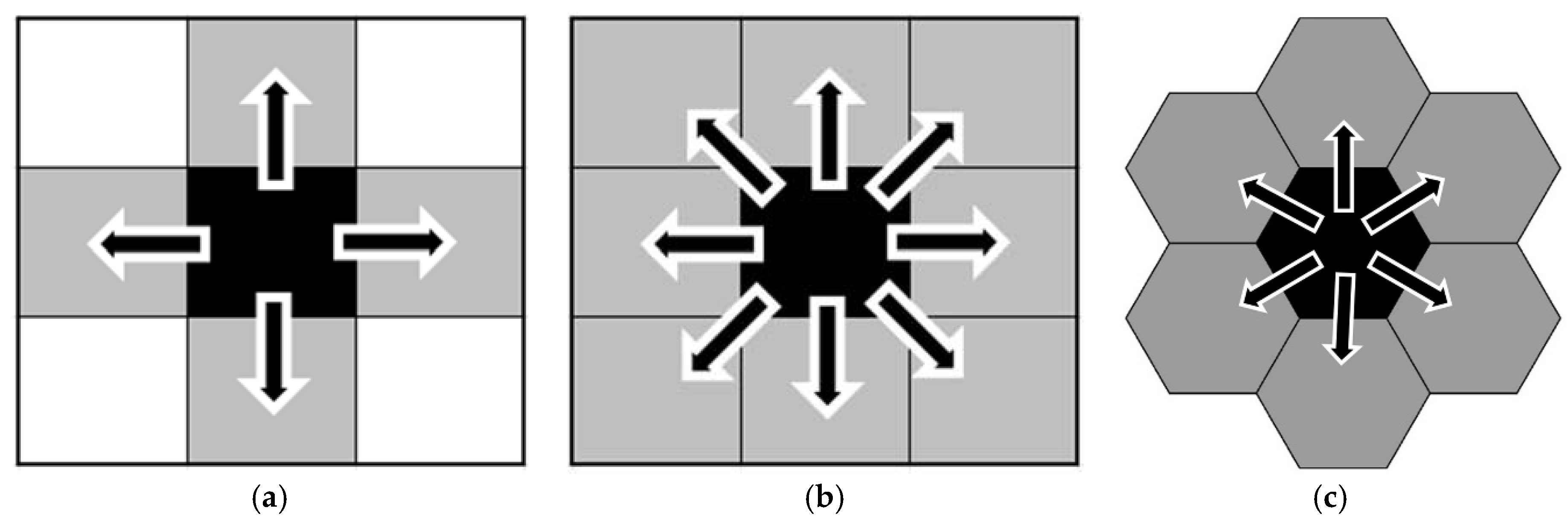
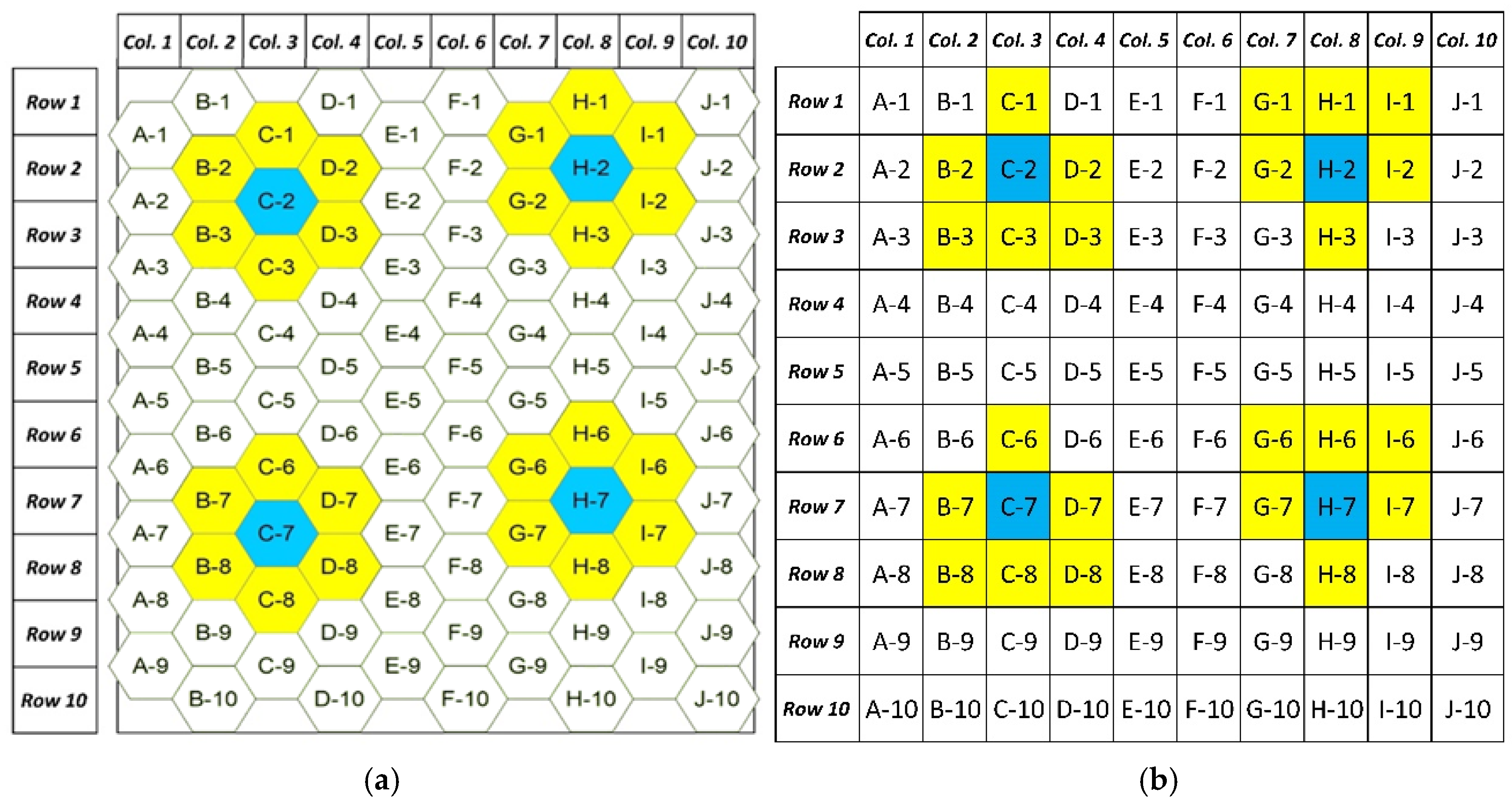
- In each crystal growth cycle of the raster-based method, the 8-domain region-growing algorithm was used for the crystal growth of road network cells due to their high accessibility, while the 4-domain region-growing algorithm was utilized for the crystal growth of other cells. Regarding the hexagon-based method, the 6-domain region-growing algorithm was used.
- (3)
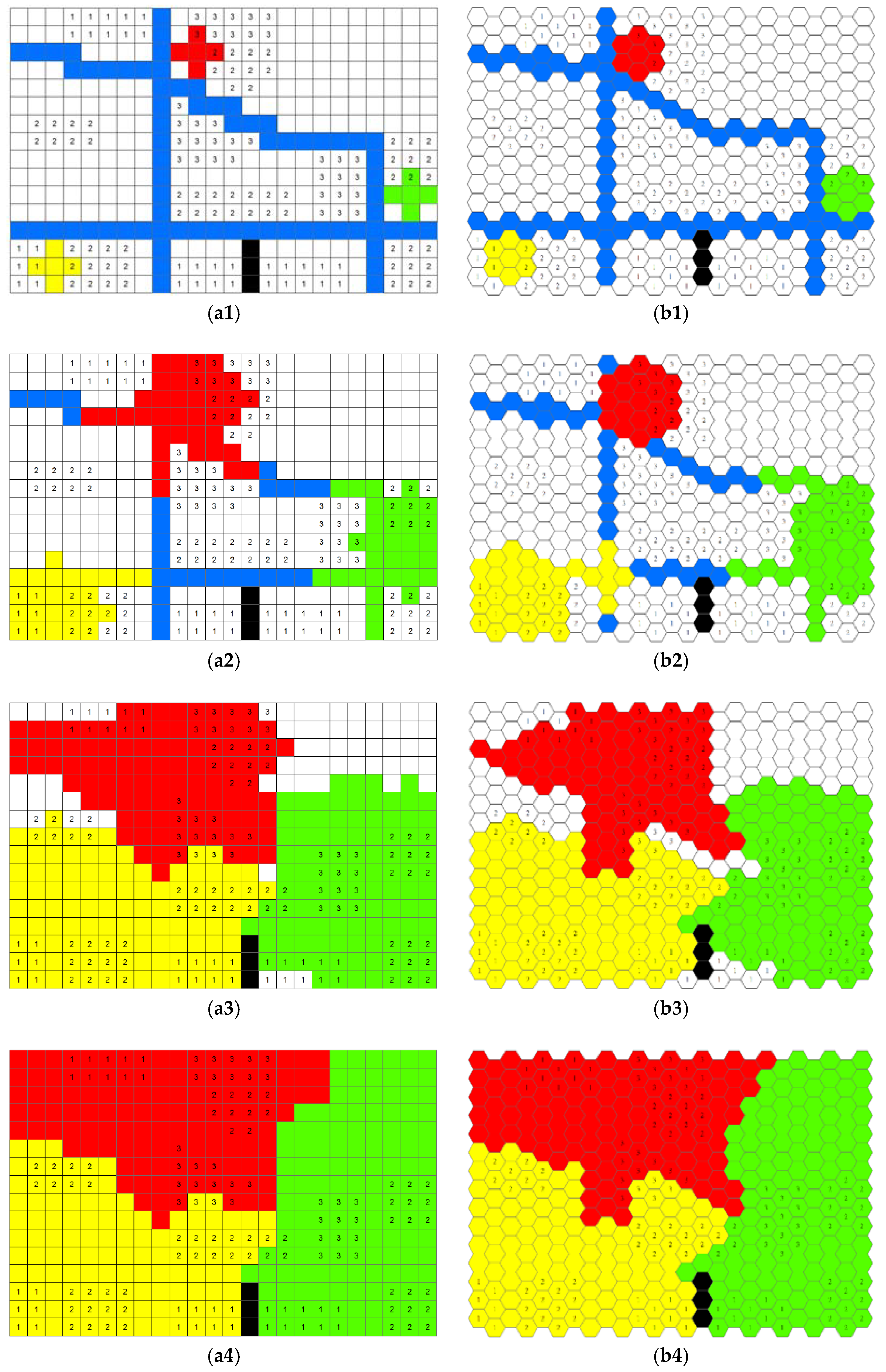
- If a neighbor cell has already been labeled as a grown area or it is a barrier cell, it will be skipped. Otherwise, the neighbor cell will be labeled as a grown area of the specific middle school. Whenever a particular cell is incorporated into the grown service area of a particular seed, it becomes part of that service area. In other words, the calculation is based on the rules of “first come, first served.” If the growth patterns of two service areas come into contact with each other at one place, the growth at that border location will stop for both service areas because the cells beyond that point are already incorporated into either of the service areas. If a cell is claimed by two or more different service areas at the same cycle during the crystal growth process, this cell will be randomly assigned to one of the service areas.
- (4)
- The speed of crystal growth for each cell is determined by the cell value and its growth speed, which was defined on the accessibility-weighted plane. Therefore, the speed is 1 cell per crystal growth cycle for seed point cells, walkable area cells, and residential area cells, while the speed is 4 cells per cycle for secondary transport network cells (the average travel speed on secondary transport network is about 4 times the speed of walking) and 6 cells per cycle for primary transport network cells (the average travel speed on primary transport network is about 6 times the speed of walking).
- (5)
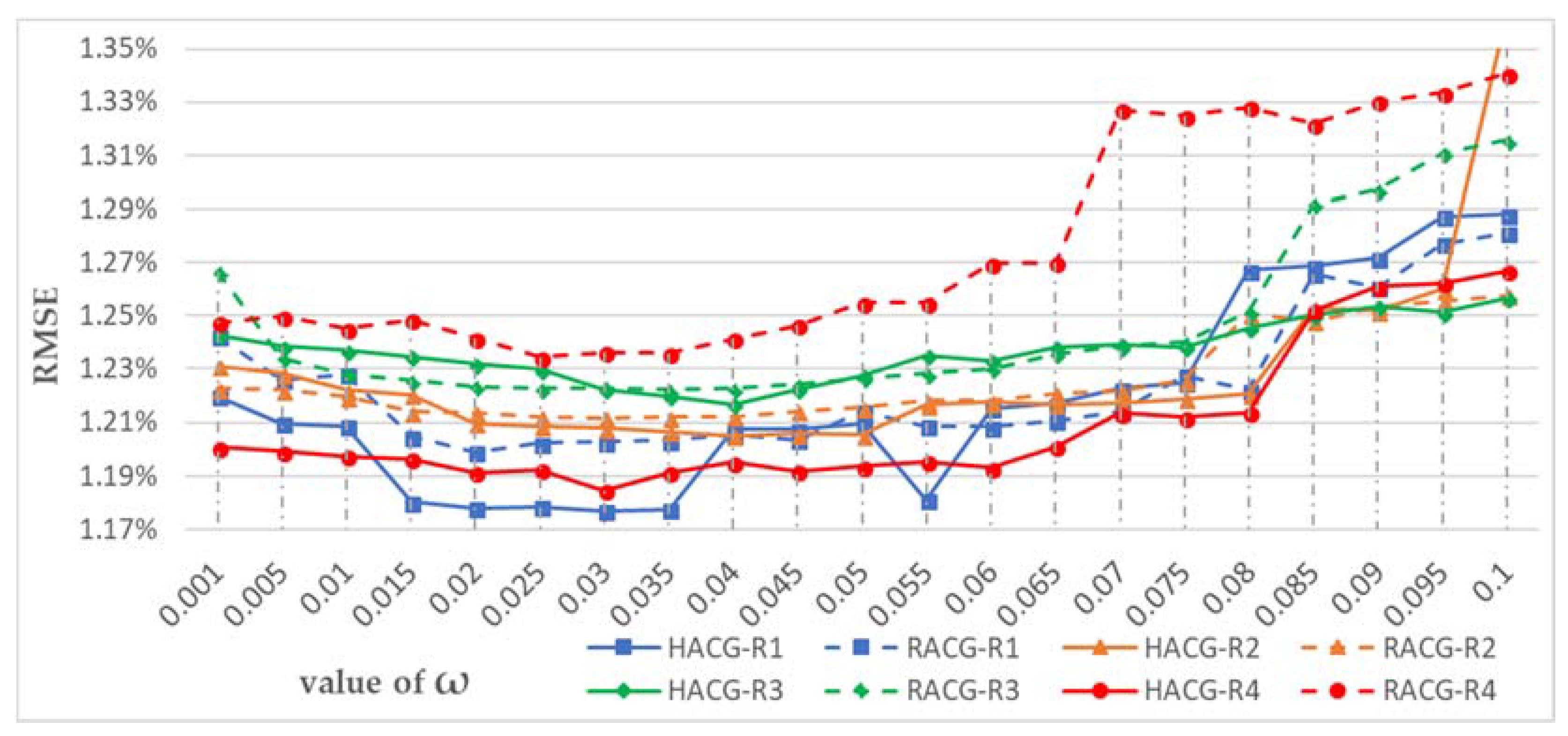
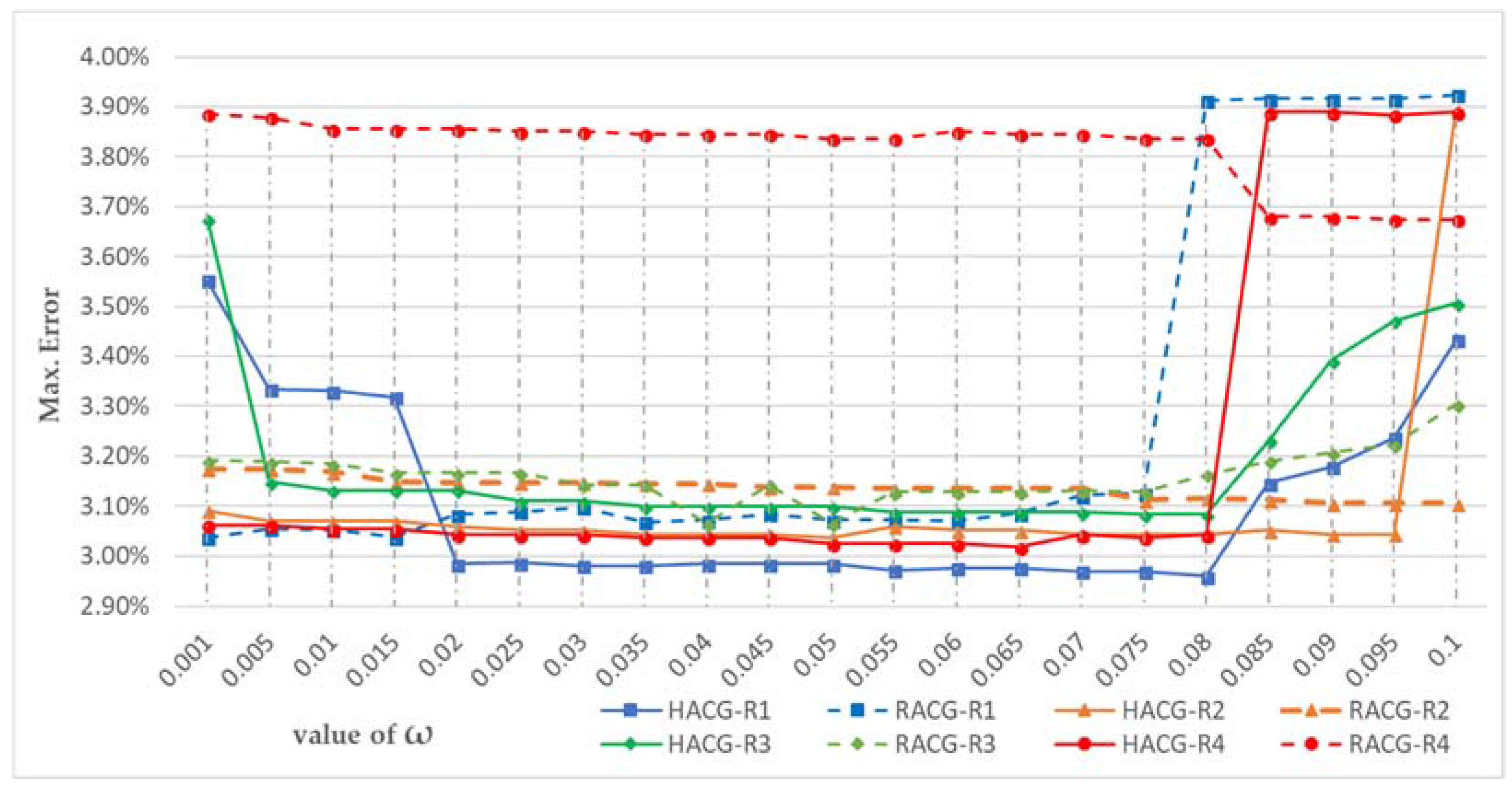
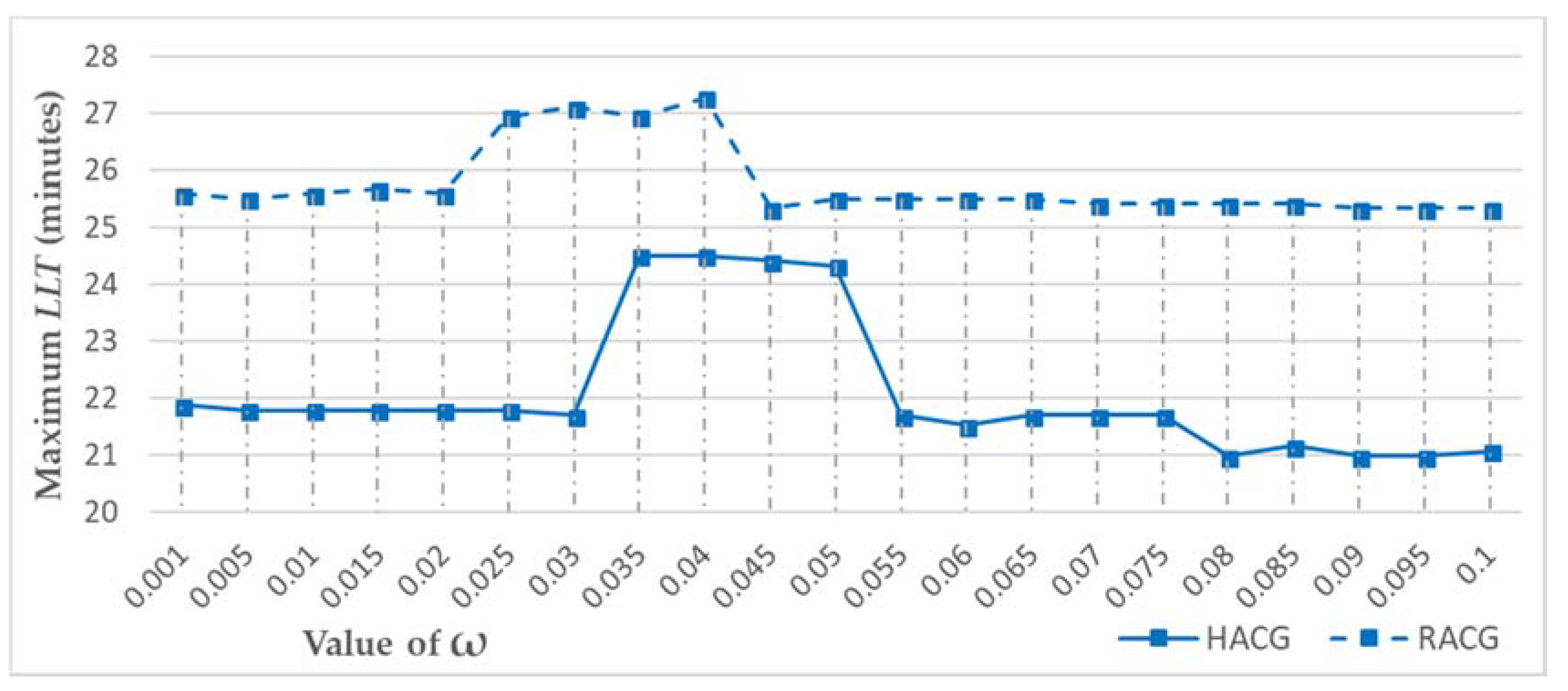
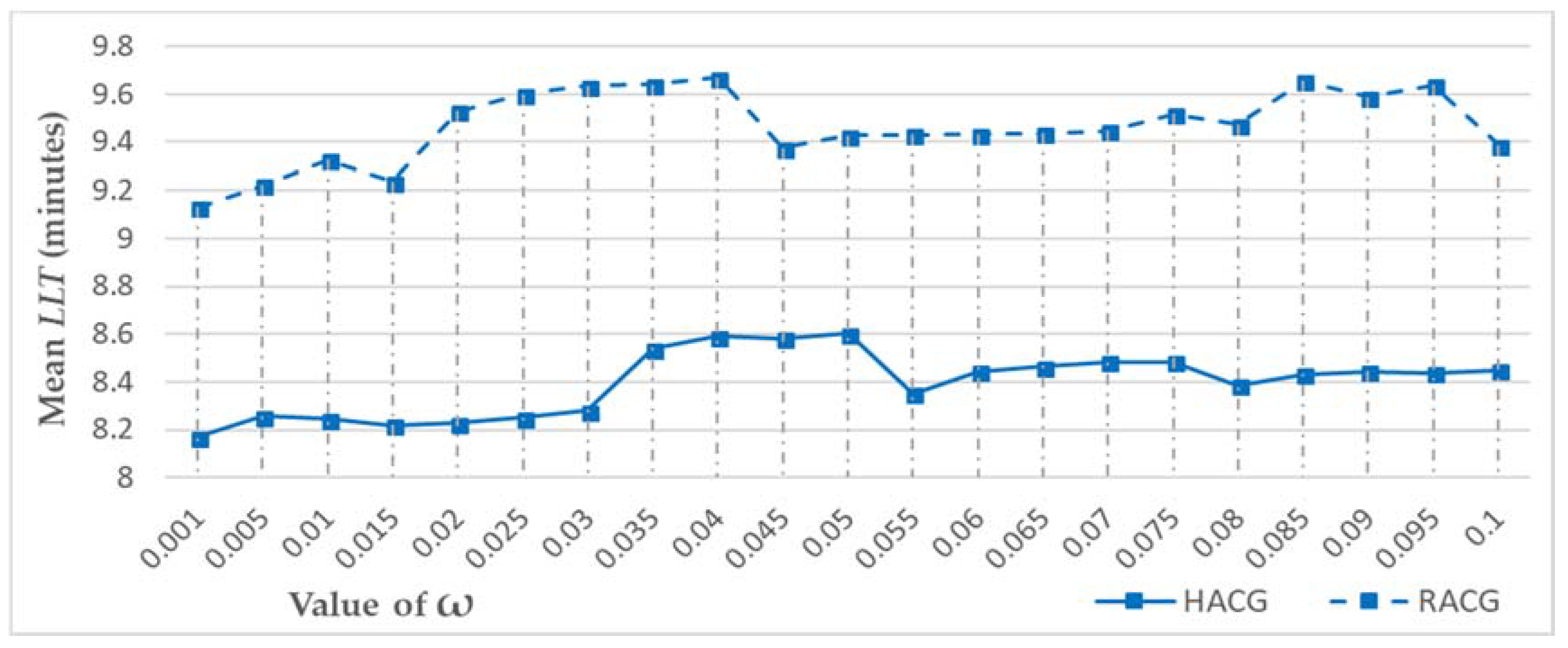
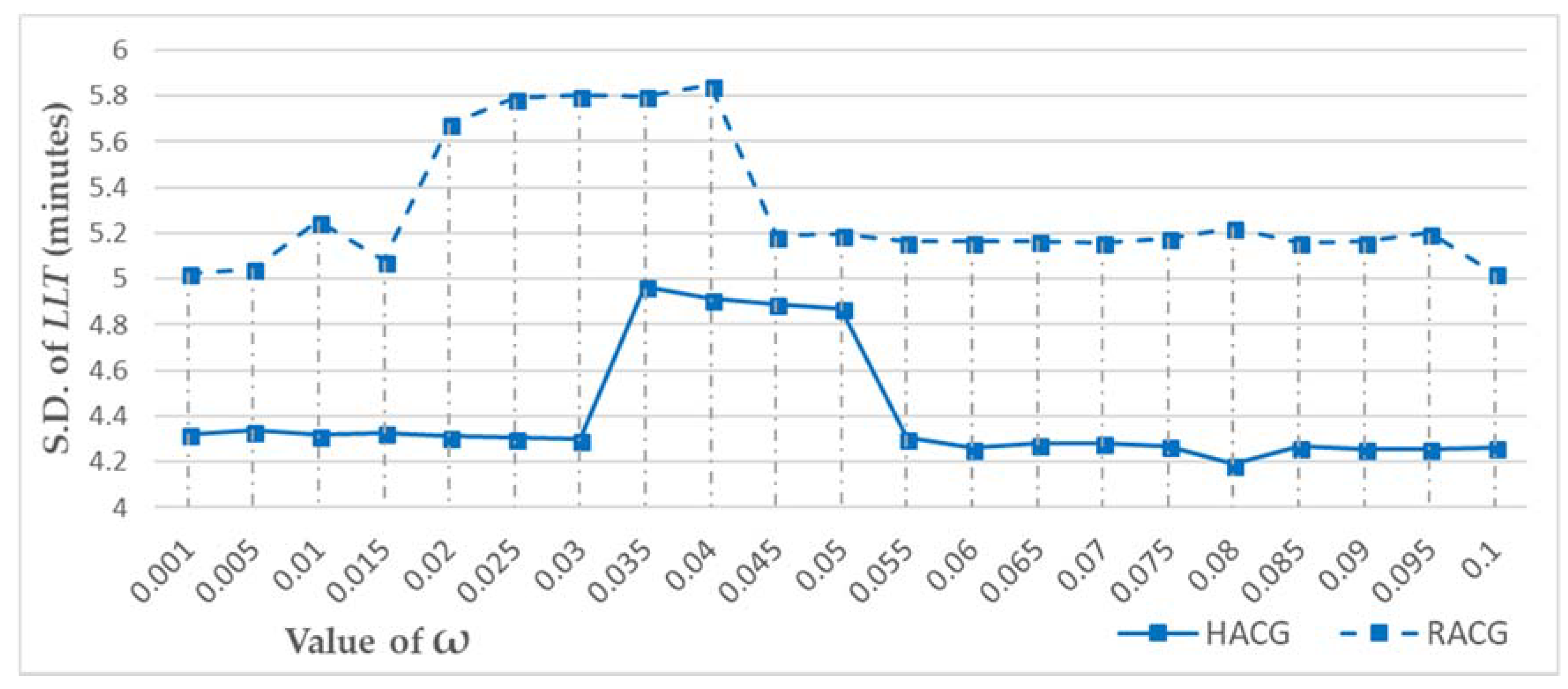
- The growth speed of each grown area is adaptively adjusted in real time to optimize the population in each service area because the population in each service area should be commensurate with the enrollment capacity of each middle school. Therefore, the enrollment capacity of middle schools and the corresponding proportions of enrollment capacity out of the total enrollment capacity in the study area are considered as benchmarks for adjusting the crystal growth speed of each service area. The population of each grown area is calculated based on the population-weighted plane in real time. If the proportion of the population of a grown area () is larger than the proportion of its enrollment capacity () by a defined value (e.g., = 10%), the growth of the corresponding middle school will be restricted:where N is the number of middle schools, is the enrollment capacity of middle schools, is the proportion of enrollment capacity of each middle school out of the total enrollment capacity in the study area, is the population in each grown area, and is the proportion of the population of each grown area out of the total population in all the grown areas.If , then the growth of middle school will be restricted until . is the parameter that defines the strictness of the crystal growth constraint, and it is calibrated to achieve the best result. Generally speaking, the lower the value, the stricter the growth control; the higher the value, the less restrictive the crystal growth. For the specific case study of middle school service areas, the capacity of the service area of each middle school is controlled in the following manner. Equations (1)–(3) are used to calculate the proportion of the population of a grown area () and the proportion of its enrollment capacity () among all middle schools in the study area. Both values are calculated for each grown area after each growth cycle. For any grown service area, if the is larger the by a defined value (e.g., = 10%), the growth of the corresponding middle school will be restricted. In the calculation, the value will iterate from 0.001 to 0.1 in steps of 0.005 to find the best setting for the delineation considering the supply/demand ratio of the results.
- (6)
- The crystal growth will finish if all the accessible cells are grown and assigned to the grown area of one seed point (middle school).
3.4. Hexagon Data Structure
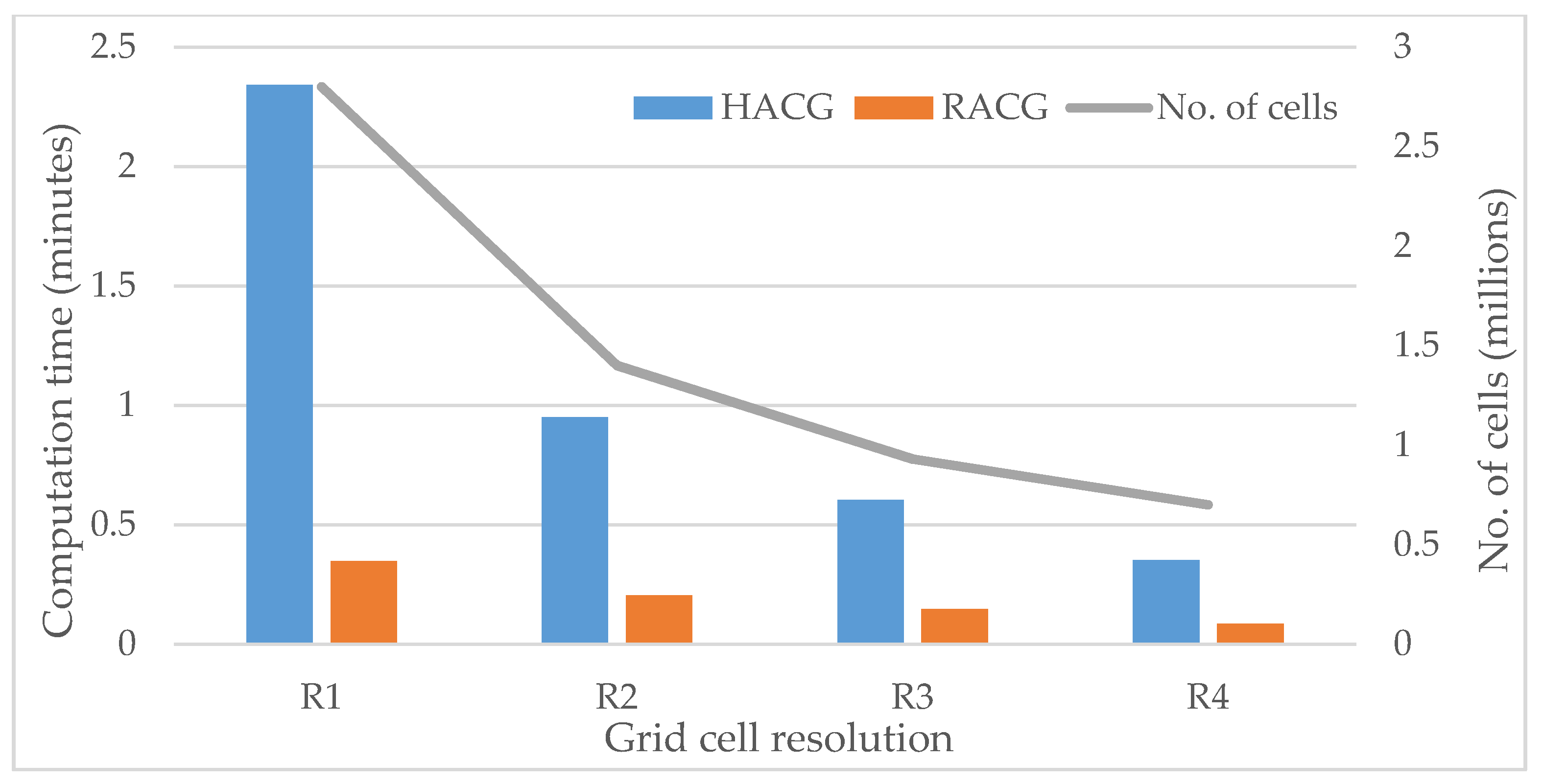
3.5. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hess, S.W.; Samuels, S.A. Experiences with a Sales Districting Model: Criteria and Implementation. Manag. Sci. 1971, 18, P-41–P-54. [Google Scholar] [CrossRef]
- Shanker, R.J.; Turner, R.E.; Zoltners, A.A. Sales Territory Design: An Integrated Approach. Manag. Sci. 1975, 22, 309–320. [Google Scholar] [CrossRef]
- Marlin, P.G. Application of the transportation model to a large-scale “Districting” problem. Comput. Oper. Res. 1981, 8, 83–96. [Google Scholar] [CrossRef]
- Fleischmann, B.; Paraschis, J.N. Solving a large scale districting problem: A case report. Comput. Oper. Res. 1988, 15, 521–533. [Google Scholar] [CrossRef]
- Sinha, P.; Zoltners, A.A. Sales-Force Decision Models: Insights from 25 Years of Implementation. Interfaces 2001, 31, S8–S44. [Google Scholar] [CrossRef]
- Ríos-Mercado, R.Z.; Fernández, E. A reactive GRASP for a commercial territory design problem with multiple balancing requirements. Comput. Oper. Res. 2009, 36, 755–776. [Google Scholar] [CrossRef]
- Ferland, J.A.; Guénette, G. Decision Support System for the School Districting Problem. Oper. Res. 1990, 38, 15–21. [Google Scholar] [CrossRef] [Green Version]
- Caro, F.; Shirabe, T.; Guignard, M.; Weintraub, A. School Redistricting: Embedding GIS Tools with Integer Programming. J. Oper. Res. Soc. 2004, 55, 836–849. [Google Scholar] [CrossRef]
- Yeates, M. Hinterland delimitation: A distance minimizing approach. Prof. Geogr. 1963, 15, 7–10. [Google Scholar] [CrossRef]
- Franklin, A.D.; Koenigsberg, E. Computed School Assignments in a Large District. Oper. Res. 1973, 21, 413–426. [Google Scholar] [CrossRef]
- Holloway, C.A.; Wehrung, D.A.; Zeitlin, M.P.; Nelson, R.T. An Interactive Procedure for the School Boundary Problem with Declining Enrollment. Oper. Res. 1975, 23, 191–206. [Google Scholar] [CrossRef]
- Steiner, M.T.A.; Datta, D.; Steiner Neto, P.J.; Scarpin, C.T.; Rui Figueira, J. Multi-objective optimization in partitioning the healthcare system of parana state in brazil. Omega 2015, 52, 53–64. [Google Scholar] [CrossRef]
- Benzarti, E.; Sahin, E.; Dallery, Y. Modeling Approaches for the home health care districting problem. In Proceedings of the 8th International Conference of Modeling and Simulation-MOSIM, Hammamet, Tunisia, 10–12 May 2010; pp. 1–10. [Google Scholar]
- Ma, H.; Carlin, B.P.; Banerjee, S. Hierarchical and Joint Site-Edge Methods for Medicare Hospice Service Region Boundary Analysis. Biometrics 2010, 66, 355–364. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.Y.; Yu, T.-Y.; Lu, T.-Y.; Chuang, W.-L.; Lai, J.-S.; Yeh, C.-H.; Oyang, Y.-J.; Heui-Ming Ma, M.; Sun, W.-Z. Ambulance Service Area Considering Disaster-Induced Disturbance on the Transportation Infrastructure. J. Test. Eval. 2015, 43, 20140084. [Google Scholar] [CrossRef]
- Ricca, F.; Scozzari, A.; Simeone, B. Political districting: From classical models to recent approaches. Ann. Oper. Res. 2013, 204, 271–299. [Google Scholar] [CrossRef]
- Bozkaya, B.; Erkut, E.; Laporte, G. A tabu search heuristic and adaptive memory procedure for political districting. Eur. J. Oper. Res. 2003, 144, 12–26. [Google Scholar] [CrossRef]
- Hess, S.W.; Weaver, J.B.; Siegfeldt, H.J.; Whelan, J.N.; Zitlau, P.A. Nonpartisan Political Redistricting by Computer. Oper. Res. 1965, 13, 998–1006. [Google Scholar] [CrossRef]
- George, J.A.; Lamar, B.W.; Wallace, C.A. Political district determination using large-scale network optimization. Socioecon. Plan. Sci. 1997, 31, 11–28. [Google Scholar] [CrossRef]
- Zoltners, A.A.; Sinha, P. Sales Territory Alignment: A Review and Model. Manag. Sci. 1983, 29, 1237–1256. [Google Scholar] [CrossRef]
- Williams, J.C. A Zero-One Programming Model for Contiguous Land Acquisition. Geogr. Anal. 2002, 34, 330–349. [Google Scholar] [CrossRef] [Green Version]
- Shirabe, T. A Model of Contiguity for Spatial Unit Allocation. Geogr. Anal. 2005, 37, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Hakimi, S.L. Optimum Locations of Switching Centers and the Absolute Centers and Medians of a Graph. Oper. Res. 1964, 12, 450–459. [Google Scholar] [CrossRef]
- Hakimi, S.L. Optimum Distribution of Switching Centers in a Communication Network and Some Related Graph Theoretic Problems. Oper. Res. 1965, 13, 462–475. [Google Scholar] [CrossRef]
- Pearce, J. Techniques for defining school catchment areas for comparison with census data. Comput. Environ. Urban Syst. 2000, 24, 283–303. [Google Scholar] [CrossRef]
- Fraley, G.; Jankowska, M.; Jankowski, P. Towards Memetic Algorithms in GIScience: An Adaptive Multi-Objective Algorithm for Optimized Delineation of Neighborhood Boundaries. In Proceedings of the GIScience Conference, Zurich, Switzerland, 9 September 2010; Volume 184. Available online: https://pdfs.semanticscholar.org/21da/8d0d071957c0a4d0fa1a07fa4291f1f2396d.pdf (accessed on 1 May 2018).
- Openshaw, S.; Rao, L. Algorithms for Reengineering 1991 Census Geography. Environ. Plan. A 1995, 27, 425–446. [Google Scholar] [CrossRef] [PubMed]
- Macmillan, W. Redistricting in a GIS environment: An optimisation algorithm using switching-points. J. Geogr. Syst. 2001, 3, 167–180. [Google Scholar] [CrossRef]
- Aerts, J.C.J.H.; Heuvelink, G.B.M. Using simulated annealing for resource allocation. Int. J. Geogr. Inf. Sci. 2002, 16, 571–587. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, S.J.; Wang, S.-J.; Batta, R.; Rump, C.M. A simulated annealing approach to police district design. Comput. Oper. Res. 2002, 29, 667–684. [Google Scholar] [CrossRef]
- Voronoï, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar]
- Boyle, P.J.; Dunn, C.E. Redefinition of Enumeration District Centroids: A Test of Their Accuracy by Using Thiessen Polygons. Environ. Plan. A 1991, 23, 1111–1119. [Google Scholar] [CrossRef]
- Boots, B.; South, R. Modeling retail trade areas using higher-order, multiplicatively weighted voronoi diagrams. J. Retail. 1997, 73, 519–536. [Google Scholar] [CrossRef]
- Okabe, A.; Suzuki, A. Locational optimization problems solved through Voronoi diagrams. Eur. J. Oper. Res. 1997, 98, 445–456. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.Y. Research on public establishment location selection based on the voronoi diagram in GIS. Comput. Eng. Appl. 2004, 9, e227. [Google Scholar]
- Zhu, H.; Yan, H.; Li, Y. An optimization method for the layout of public service facilities based on Voronoi diagrams. Sci. Surv. Mapp. 2008, 2, 29. [Google Scholar]
- Schaudt, B.F.; Drysdale, R.L.S. Multiplicatively weighted crystal growth Voronoi diagrams (extended abstract). In Proceedings of the Seventh Annual Symposium on Computational Geometry, North Conway, NH, USA, 10–12 June 1991; ACM Press: New York, NY, USA, 1991; pp. 214–223. [Google Scholar]
- Moreno-Regidor, P.; García López de Lacalle, J.; Manso-Callejo, M.-Á. Zone design of specific sizes using adaptive additively weighted Voronoi diagrams. Int. J. Geogr. Inf. Sci. 2012, 26, 1811–1829. [Google Scholar] [CrossRef] [Green Version]
- Ricca, F.; Scozzari, A.; Simeone, B. Weighted Voronoi region algorithms for political districting. Math. Comput. Model. 2008, 48, 1468–1477. [Google Scholar] [CrossRef]
- Aichholzer, O.; Aurenhammer, F.; Palop, B. Quickest Paths, Straight Skeletons, and the City Voronoi Diagram. Discret. Comput. Geom. 2004, 31, 17–35. [Google Scholar] [CrossRef]
- Wang, J.; Kwan, M.-P.; Ma, L. Delimiting service area using adaptive crystal-growth Voronoi diagrams based on weighted planes: A case study in Haizhu District of Guangzhou in China. Appl. Geogr. 2014, 50, 108–119. [Google Scholar] [CrossRef]
- Murray, A.T. Geography in coverage modelling: Exploiting spatial strucutre to address complementray partial service of areas. Ann. Assoc. Am. Geogr. 2008, 95, 761–772. [Google Scholar] [CrossRef]
- Murray, A.T. Site placement uncertainty in location analysis. Comput. Environ. Urban Syst. 2003, 27, 205–221. [Google Scholar] [CrossRef]
- Church, R.L. Location modelling and GIS. In Geographical Information Systems; Longley, P., Goodchild, M.F., Maguire, D.J., Rhind, D.W., Eds.; John Wiley: Chichester, UK ; Sussex, NJ, USA; New York, NY, USA, 1999; Volume 1, pp. 293–303. [Google Scholar]
- Miller, H.J. GIS and geometric representation in facility location problems. Int. J. Geogr. Inf. Syst. 1996, 10, 791–816. [Google Scholar] [CrossRef]
- Murray, A.T.; O’Kelly, M.E.; Church, R.L. Regional service coverage modeling. Comput. Oper. Res. 2008, 35, 339–355. [Google Scholar] [CrossRef]
- Suzuki, A.; Drezner, Z. The p-center location problem in an area. Locat. Sci. 1996, 4, 69–82. [Google Scholar] [CrossRef]
- Bennett, C.D.; Mirakhor, A. Optimal facility location with respect to several regions. J. Reg. Sci. 1974, 14, 131–136. [Google Scholar] [CrossRef]
- Aly, A.A.; Marucheck, A.S. Generalized Weber problem with rectangular regions. J. Oper. Res. Soc. 1982, 33, 983–989. [Google Scholar] [CrossRef]
- Love, R.F. A computational procedure for optimally locating a facility with respect to several rectangular regions. J. Reg. Sci. 1972, 12, 233–242. [Google Scholar] [CrossRef]
- Carr, D.B.; Olsen, A.R.; White, D. Hexagon Mosaic Maps for Display of Univariate and Bivariate Geographical Data. Cartogr. Geogr. Inf. Sci. 1992, 19, 228–236. [Google Scholar] [CrossRef]
- Birch, C.P.D.; Oom, S.P.; Beecham, J.A. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology. Ecol. Modell. 2007, 206, 347–359. [Google Scholar] [CrossRef]
- Feick, R.; Robertson, C. A multi-scale approach to exploring urban places in geotagged photographs. Comput. Environ. Urban Syst. 2015, 53, 96–109. [Google Scholar] [CrossRef]
- Sahr, K.; White, D.; Kimerling, A.J. Geodesic Discrete Global Grid Systems. Cartogr. Geogr. Inf. Sci. 2003, 30, 121–134. [Google Scholar] [CrossRef]
- Zook, M. Small Stories in Big Data: Gaining Insights from Large Spatial Point Pattern Datasets. Cityscape J. Policy Dev. Res. 2015, 17, 151–160. [Google Scholar]
- GDAL—Geospatial Data Abstraction Library. Available online: http://gdal.org (accessed on 1 May 2018).
| Cell Type | Cell Value | Growth Speed | |
|---|---|---|---|
| Accessibility-weighted plane | Natural Barrier Cells | 0 | 0 |
| Primary Transport Network Cells | 1 | 6 pixels/cycle | |
| Secondary Transport Network Cells | 2 | 4 pixels/cycle | |
| Walkable Area Cells | 3 | 1 pixel/cycle | |
| Population-weighted plane | Low-Rise Residential Cells | 4 | 1 pixel/cycle |
| Medium-Rise Residential Cells | 5 | 1 pixel/cycle | |
| High-Rise Residential Cells | 6 | 1 pixel/cycle | |
| Seed Point Cells (Middle Schools) | 10 | 1 pixel/cycle |
| RMSE | Max. Error | Max. LTT | Mean LTT | S.D. LTT | |
|---|---|---|---|---|---|
| RACG | 1.2048% | 3.0379% | 25.6759 | 9.2379 | 5.0803 |
| HACG | 1.1779% | 2.9833% | 21.7985 | 8.2283 | 4.3100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Kwan, M.-P. Hexagon-Based Adaptive Crystal Growth Voronoi Diagrams Based on Weighted Planes for Service Area Delimitation. ISPRS Int. J. Geo-Inf. 2018, 7, 257. https://doi.org/10.3390/ijgi7070257
Wang J, Kwan M-P. Hexagon-Based Adaptive Crystal Growth Voronoi Diagrams Based on Weighted Planes for Service Area Delimitation. ISPRS International Journal of Geo-Information. 2018; 7(7):257. https://doi.org/10.3390/ijgi7070257
Chicago/Turabian StyleWang, Jue, and Mei-Po Kwan. 2018. "Hexagon-Based Adaptive Crystal Growth Voronoi Diagrams Based on Weighted Planes for Service Area Delimitation" ISPRS International Journal of Geo-Information 7, no. 7: 257. https://doi.org/10.3390/ijgi7070257
APA StyleWang, J., & Kwan, M.-P. (2018). Hexagon-Based Adaptive Crystal Growth Voronoi Diagrams Based on Weighted Planes for Service Area Delimitation. ISPRS International Journal of Geo-Information, 7(7), 257. https://doi.org/10.3390/ijgi7070257






