Multi-Objective Optimisation Based Planning of Power-Line Grid Expansions
Abstract
:1. Introduction
- development and implementation of a client-server based Pareto-optimisation system for power-line routing,
- design and implementation of an interactive visualisation system for intuitive navigation of Pareto-optimal solutions and support of decision-making.
2. Background
2.1. Common Planning Workflow
2.2. State of the Art in Multi-Criteria Spatial Analysis
2.3. State of the Art in Multi-Objective Shortest Path Methods
3. Methods
3.1. Overview
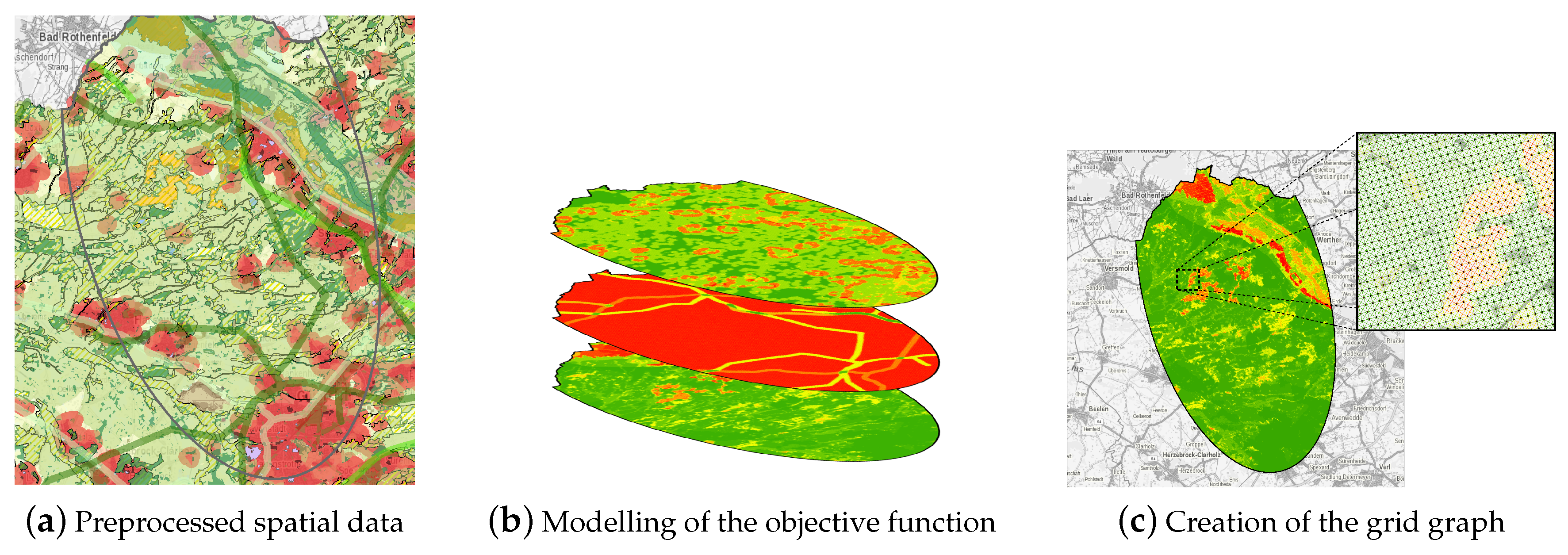
3.2. Modelling of Optimisation Criteria
3.3. Building the Grid Graph
3.4. Multi-Objective Optimisation
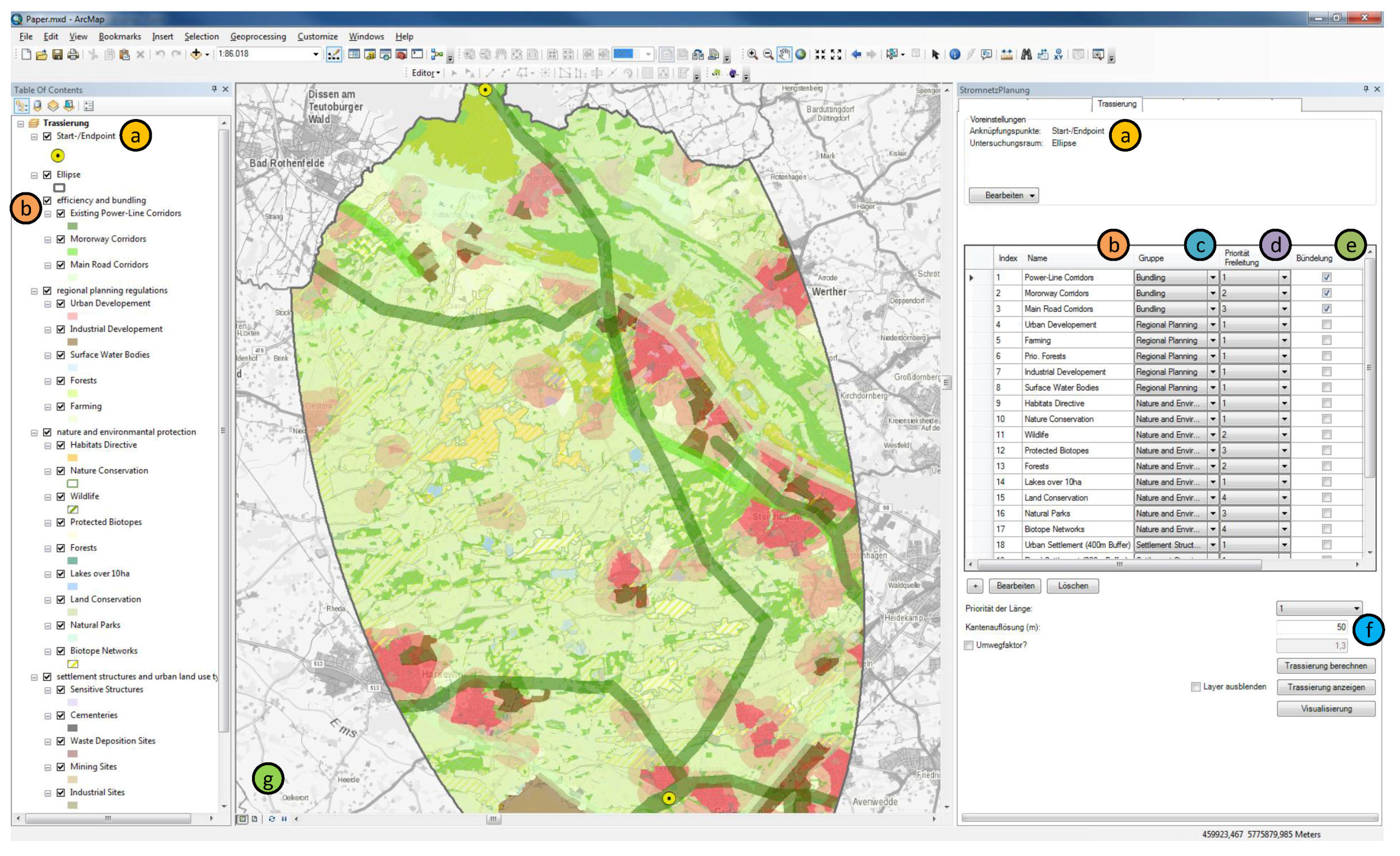
3.5. Designing an Interactive Visualisation System
4. Data
4.1. Study Area
4.2. Criteria
5. Results
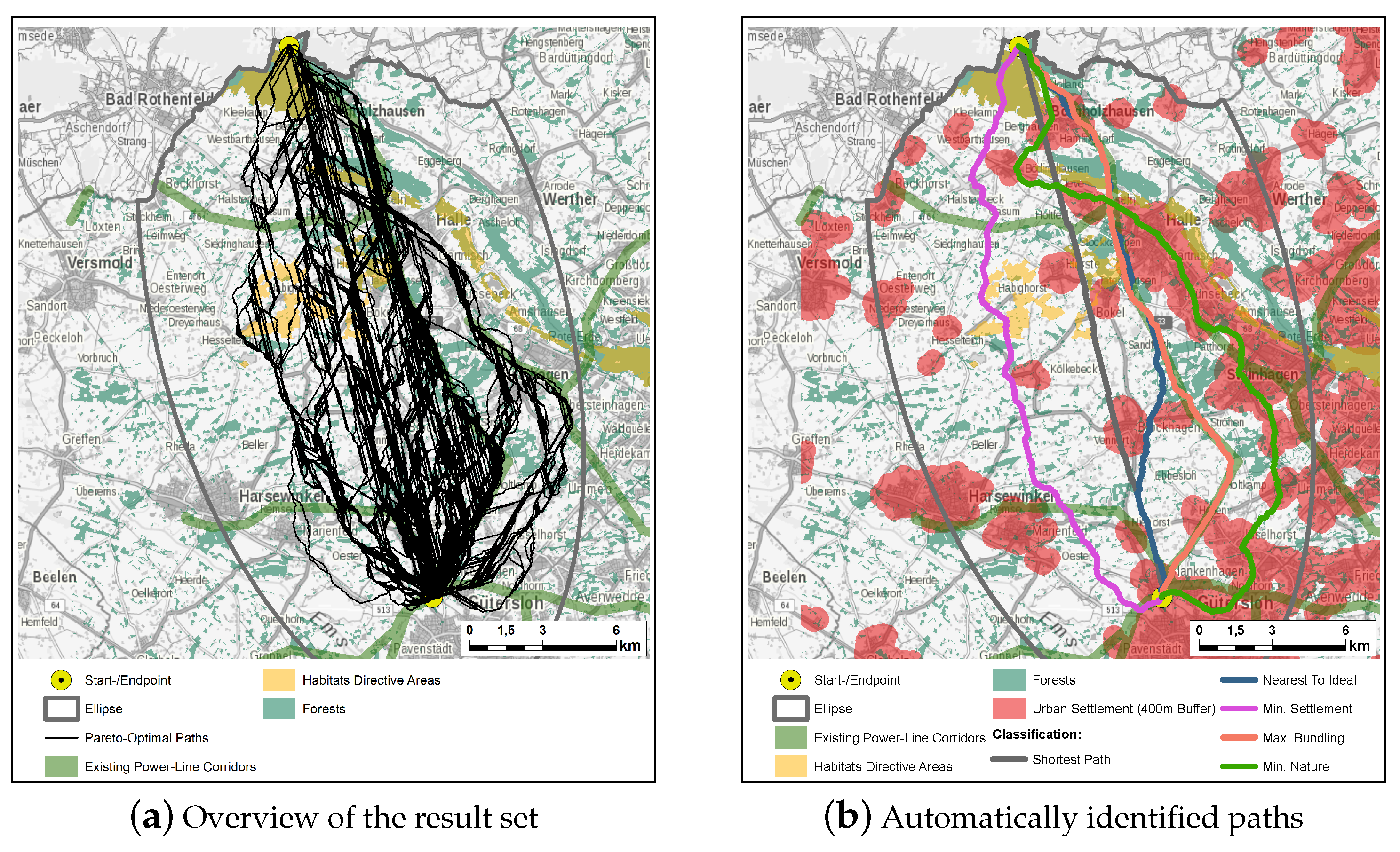
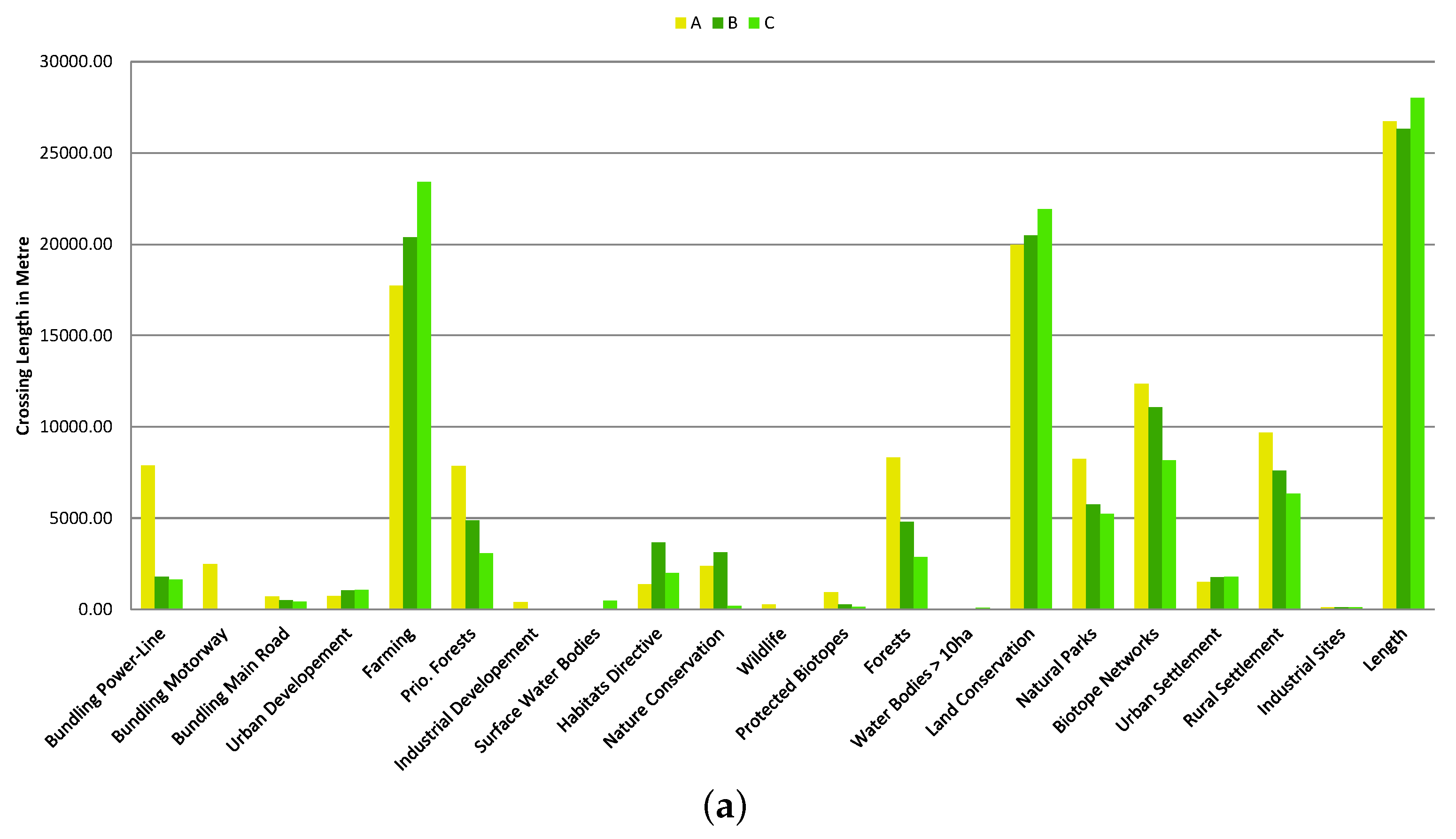
5.1. Automated Identification of Power-Line Routes
5.2. Interactive Identification of Power-Line Routes
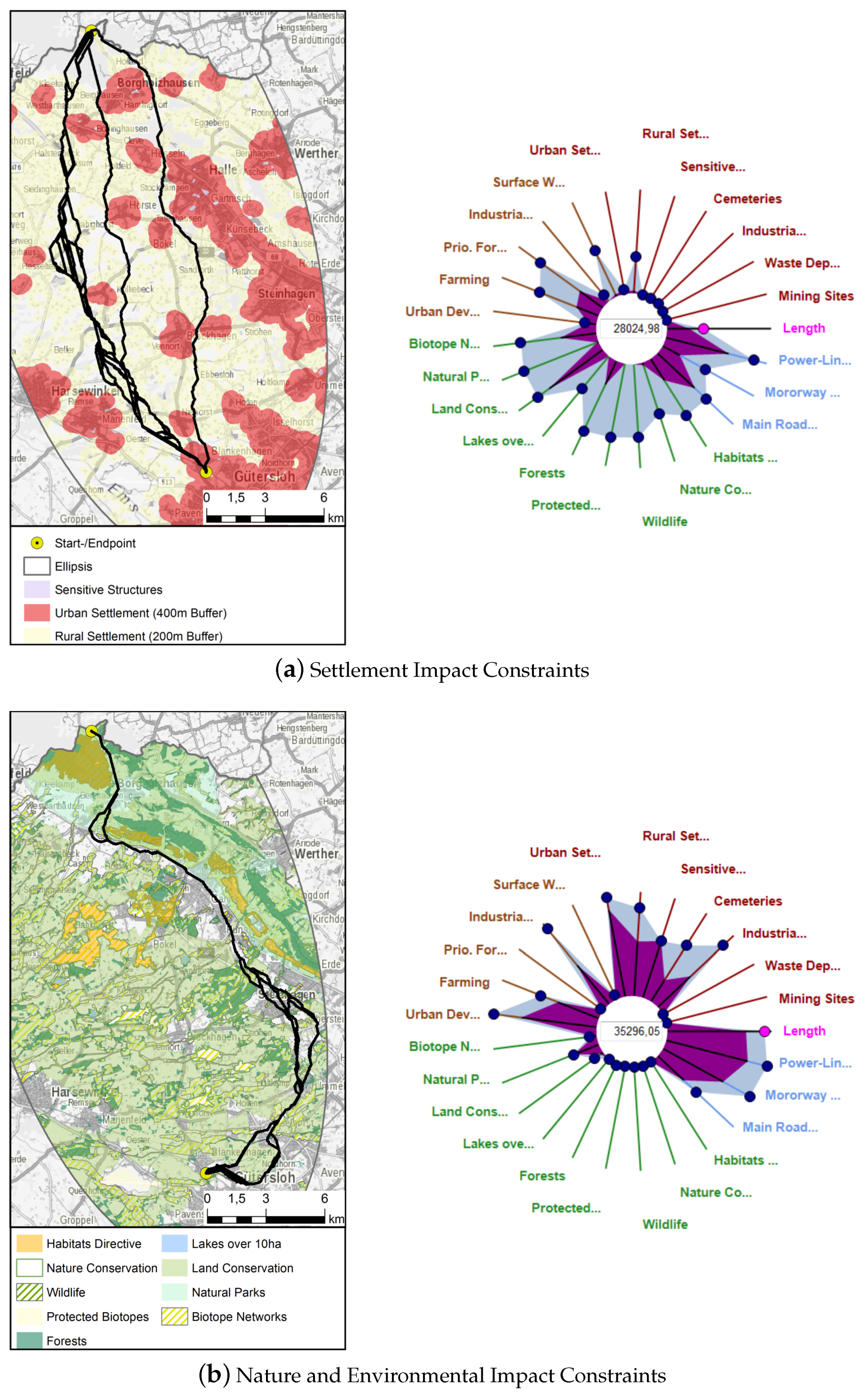
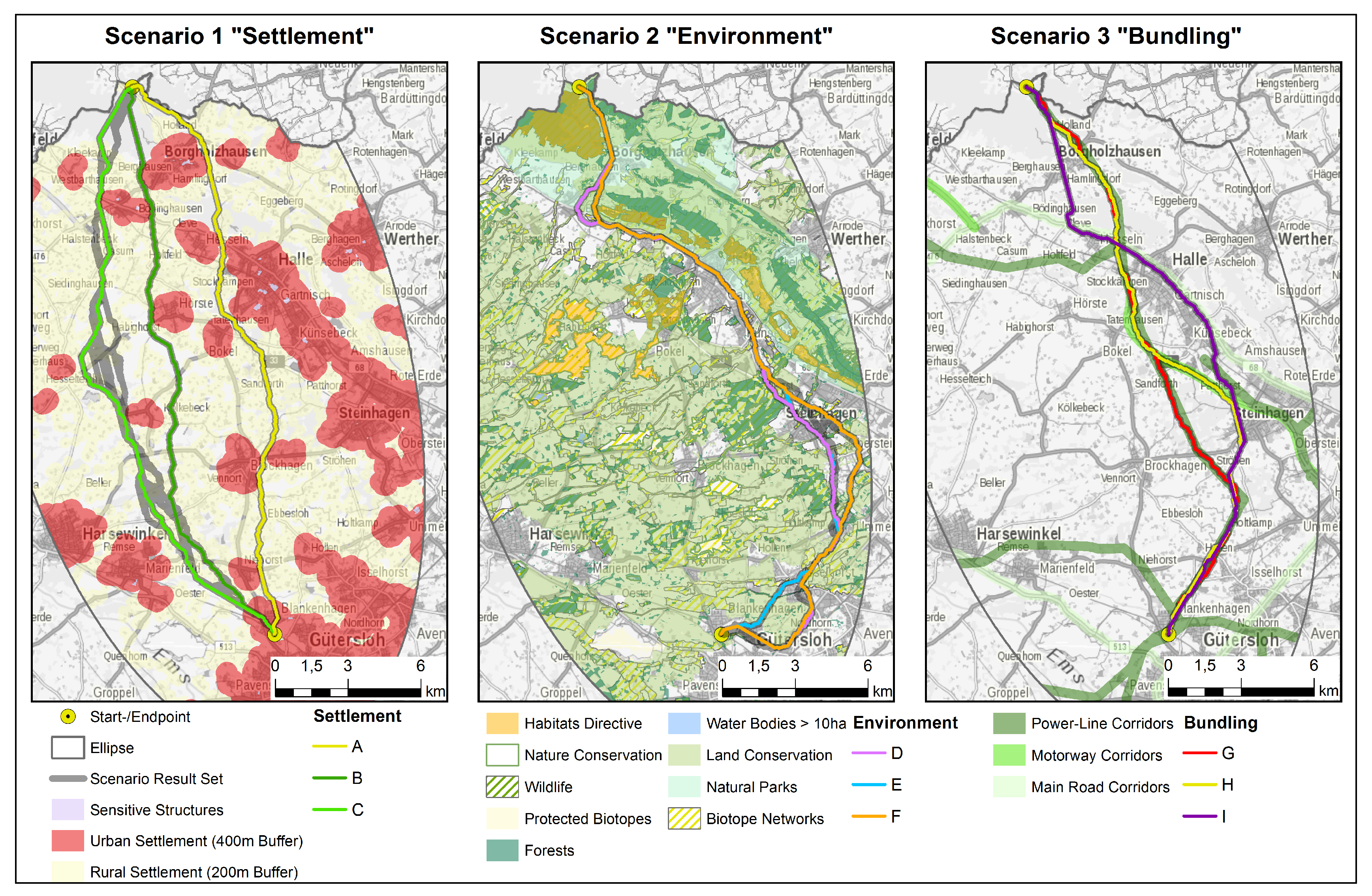
5.2.1. Scenario 1 “Settlement”
5.2.2. Scenario 2 “Environment”
5.2.3. Scenario 3 “Bundling”
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Federal Ministry for Economic Affairs and Energy. Fifth “Energy Transition” Monitoring Report; Federal Ministry for Economic Affairs and Energy: Berlin, Germany, 2016.
- Federal Ministry for Economic Affairs and Energy; Silber Druck oHG. Germany’s New Energy Policy—Heading Towards 2050 with Secure, Affordable and Environmentally Sound Energy; Federal Ministry for Economic Affairs and Energy: Berlin, Germany, 2012.
- German Energy Agency (Dena). Dena Grid Study II. Integration of Renewable Energy Sources in the German Power Supply System from 2015–2020 with an Outlook to 2025; German Energy Agency: Berlin, Germany, 2011.
- Federal Network Agency. Grid Expansion in Germany. What You Need to Know; Federal Network Agency: Bonn, Germany, 2016.
- 50Hertz Transmission GmbH; Amprion GmbH; TenneT TSO GmbH; TransnetBW GmbH. [Application for Federal Sectoral Planning. Sample Application according to § 6 NABEG. Part 1: Coarse and Route Corridors] Antrag auf Bundesfachplanung. Musterantrag nach § 6 NABEG. Teil 1: Grob- und Trassenkorridore; 50Hertz Transmission GmbH; Amprion GmbH; TenneT TSO GmbH; TransnetBW GmbH: Berlin/Dortmund/Bayreuth/Stuttgart, Germany, 2015. [Google Scholar]
- Monteiro, C.; Ramirez-Rosado, I.J.; Miranda, V.; Zorzano-Santamaria, P.J.; Garcia-Garrido, E.; Fernandez-Jimenez, L.A. GIS Spatial Analysis Applied to Electric Line Routing Optimization. IEEE Trans. Power Deliv. 2005, 20, 934–942. [Google Scholar] [CrossRef]
- Eroğlu, H.; Aydın, M. Genetic Algorithm in Electrical Transmission Lines Path Finding Problems. In Proceedings of the 2013 8th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2013; pp. 112–116. [Google Scholar]
- Douglas, D.H. Least-cost Path in GIS Using an Accumulated Cost Surface and Slopelines. Cartogr. Int. J. Geogr. Inf. Geovis. 1994, 31, 37–51. [Google Scholar] [CrossRef]
- Saaty, T.L. A Scaling Method for Priorities in Hierarchical Structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Saaty, T.L. Multicriteria Decision Making: The Analytic Hierarchy Process: Planning, Priority Setting Resource Allocation; RWS: Chalfont St Peter, UK, 1990. [Google Scholar]
- Ho, W.; Ma, X. The State-of-the-Art Integrations and Applications of the Analytic Hierarchy Process. Eur. J. Oper. Res. 2018, 267, 399–414. [Google Scholar] [CrossRef]
- Jeong, J.S.; García-Moruno, L.; Hernández-Blanco, J. A Site Planning Approach for Rural Buildings into a Landscape using a Spatial Multi-criteria Decision Analysis Methodology. Land Use Policy 2013, 32, 108–118. [Google Scholar] [CrossRef]
- Abudeif, A.; Moneim, A.A.; Farrag, A. Multicriteria Decision Analysis based on Analytic Hierarchy Process in GIS Environment for Siting Nuclear Power Plant in Egypt. Ann. Nucl. Energy 2015, 75, 682–692. [Google Scholar] [CrossRef]
- Terh, S.H.; Cao, K. GIS-MCDA Based Cycling Paths Planning: A Case Study in Singapore. Appl. Geogr. 2018, 94, 107–118. [Google Scholar] [CrossRef]
- Mileu, N.; Queirós, M. Integrating Risk Assessment into Spatial Planning: RiskOTe Decision Support System. ISPRS Int. J. Geo-Inf. 2018, 7, 184. [Google Scholar] [CrossRef]
- Hu, H.; Lin, T.; Wang, S.; Rodriguez, L.F. A cyberGIS Approach to Uncertainty and Sensitivity Analysis in Biomass Supply Chain Optimization. Appl. Energy 2017, 203, 26–40. [Google Scholar] [CrossRef]
- Houston, G.; Johnson, C. EPRI-GTC Overhead Electric Transmission Line Siting Methodology; Georgia Transmission Corporation: Georgia, CA, USA, 2006. [Google Scholar]
- Linstone, H.A.; Turoff, M. The Delphi Method: Techniques and Applications; Addison-Wesley: Reading, MA, USA, 1975. [Google Scholar]
- Schmidt, A.J. Implementing a GIS Methodology for Siting High Voltage Electric Transmission Lines. Pap. Resour. Anal. 2009, 11, 17. [Google Scholar]
- ArcMap Model Builder. Available online: http://desktop.arcgis.com/de/arcmap/latest/analyze/modelbuilder/what-is-modelbuilder.htm (accessed on 4 May 2018).
- Bagli, S.; Geneletti, D.; Orsi, F. Routeing of Power Lines through Least-Cost Path Analysis and Multicriteria Evaluation to Minimise Environmental Impacts. Environ. Impact Assess. Rev. 2011, 31, 234–239. [Google Scholar] [CrossRef]
- Janssen, R.; Herwijnen, M.V.; Beinat, E. Definite-Case Studies and User Manual; Vrije Universiteit Amsterdam/IVM: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Grassi, S.; Friedli, R.; Grangier, M.; Raubal, M. A GIS-Based Process for Calculating Visibility Impact from Buildings During Transmission Line Routing. In Connecting a Digital Europe Through Location and Place; Huerta, J., Schade, S., Granell, C., Eds.; Springer: Cham, Switzerland, 2014; pp. 383–402. [Google Scholar]
- Beryozkina, S.; Sauhats, A.; Neimane, V. Designing a Transmission Line Using Pareto Approach. In Proceedings of the IEEE Grenoble PowerTech (POWERTECH) Conference, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Aissi, H.; Chakhar, S.; Mousseau, V. GIS-Based Multicriteria Evaluation Approach for Corridor Siting. Environ. Plan. B Plan. Des. 2012, 39, 287–307. [Google Scholar] [CrossRef]
- Medrano, F.A.; Church, R.L. Corridor Location for Infrastructure Development A Fast Bi-objective Shortest Path Method for Approximating the Pareto Frontier. Int. Reg. Sci. Rev. 2014, 37, 129–148. [Google Scholar] [CrossRef]
- Hansen, P. Bicriterion Path Problems. In Multiple Criteria Decision Making Theory and Application; Fandel, G., Gal, T., Eds.; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/ Heidelberg, Germay; New York, NY, USA, 1979; Volume 177, pp. 109–127. [Google Scholar]
- Bökler, F.; Ehrgott, M.; Morris, C.; Mutzel, P. Output-sensitive Complexity of Multiobjective Combinatorial Optimization. J. Multi-Criteria Decis. Anal. 2017, 24, 25–36. [Google Scholar] [CrossRef]
- Paixao, J.; Santos, J. Labelling Methods for the General Case of the Multiobjective Shortest Path Problem: A Computational Study. In Computational Intelligence and Decision Making; Intelligent Systems, Control and Automation: Science and Engineering; Springer: Dordrecht, The Netherlands, 2009; pp. 489–502. [Google Scholar]
- Guerriero, F.; Musmanno, R. Label Correcting Methods to Solve Multicriteria Shortest Path Problems. J. Optim. Theory Appl. 2001, 111, 589–613. [Google Scholar] [CrossRef]
- Bökler, F.; Mutzel, P. Tree-Deletion Pruning in Label-Correcting Algorithms for the Multiobjective Shortest Path Problem. In WALCOM: Algorithms and Computation. WALCOM 2017; Poon, S.H., Rahman, M., Yen, H.C., Eds.; Lecture Notes in Computer Science 10167; Springer: Cham, The Netherlands, 2017; pp. 190–203. [Google Scholar]
- Erb, S.; Kobitzsch, M.; Sanders, P. Parallel Bi-objective Shortest Paths Using Weight-Balanced B-trees with Bulk Updates. In Experimental Algorithms. SEA 2014; Lecture Notes in Computer Science 8504; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Warburton, A. Approximation of Pareto Optima in Multiple-Objective Shortest-Path Problems. Oper. Res. 1987, 35, 70–79. [Google Scholar] [CrossRef]
- Tsaggouris, G.; Zaroliagis, C.D. Multiobjective Optimization: Improved FPTAS for Shortest Paths and Non-Linear Objectives with Applications. Algorithms Comput. 2006, 4288, 389–398. [Google Scholar]
- ESRI (Environmental Systems Research Institute) ArcGIS Desktop. Available online: http://desktop.arcgis.com/en/arcmap/ (accessed on 20 March 2018).
- Adamczyk, P.; Smith, P.H.; Johnson, R.; Hafiz, M. REST and Web Services: In Theory and in Practice. In REST: From Research to Practice; Springer: New York, NY, USA, 2011. [Google Scholar]
- Bökler, F. Output-Sensitive Complexity of Multiobjective Combinatorial Optimization with an Application to the Multiobjective Shortest Path Problem. Ph.D. Thesis, Department of Computer Science, TU Dortmund University, Dortmund, Germany, 2018. [Google Scholar]
- Chambers, J.; Cleveland, W.; Kleiner, B.; Tukey, P. Graphical Methods for Data Analysis; The Wadsworth Statistics/Probability Series; Duxury: Boston, MA, USA, 1983. [Google Scholar]
- Amprion GmbH. Available online: https://www.amprion.net/index-2.html (accessed on 6 April 2018).
- European Habitats Directive. Available online: http://ec.europa.eu/environment/nature/legislation/habitatsdirective/index_en.htm (accessed on 10 April 2018).
- Federal Agency for Cartography and Geodesy. Digitalc Basic Landscape Model (AAA Modelling); Geodaten der Deutschen Landesvermessung; Federal Agency for Cartography and Geodesy: Frankfurt am Main, Germany, 2016. [Google Scholar]
- GDI-DE: German Data Infrastructure. Available online: http://www.geoportal.de/EN/GDI-DE/INSPIRE/Legal_Implementation/legal_implementation.html?lang=en (accessed on 6 June 2018).
- Flaxman, M. Fundamentals of Geodesign. In Peer Reviewed Proceedings of Digital Landscape Architecture 2010 at Anhalt University of Applied Sciences; Wichmann Herbert: Berlin, Germany, 2010; Volume 2, pp. 28–41. [Google Scholar]
- Steinitz, C. A Framework for Geodesign: Changing Geography by Design; Esri: Redlands, CA, USA, 2012. [Google Scholar]




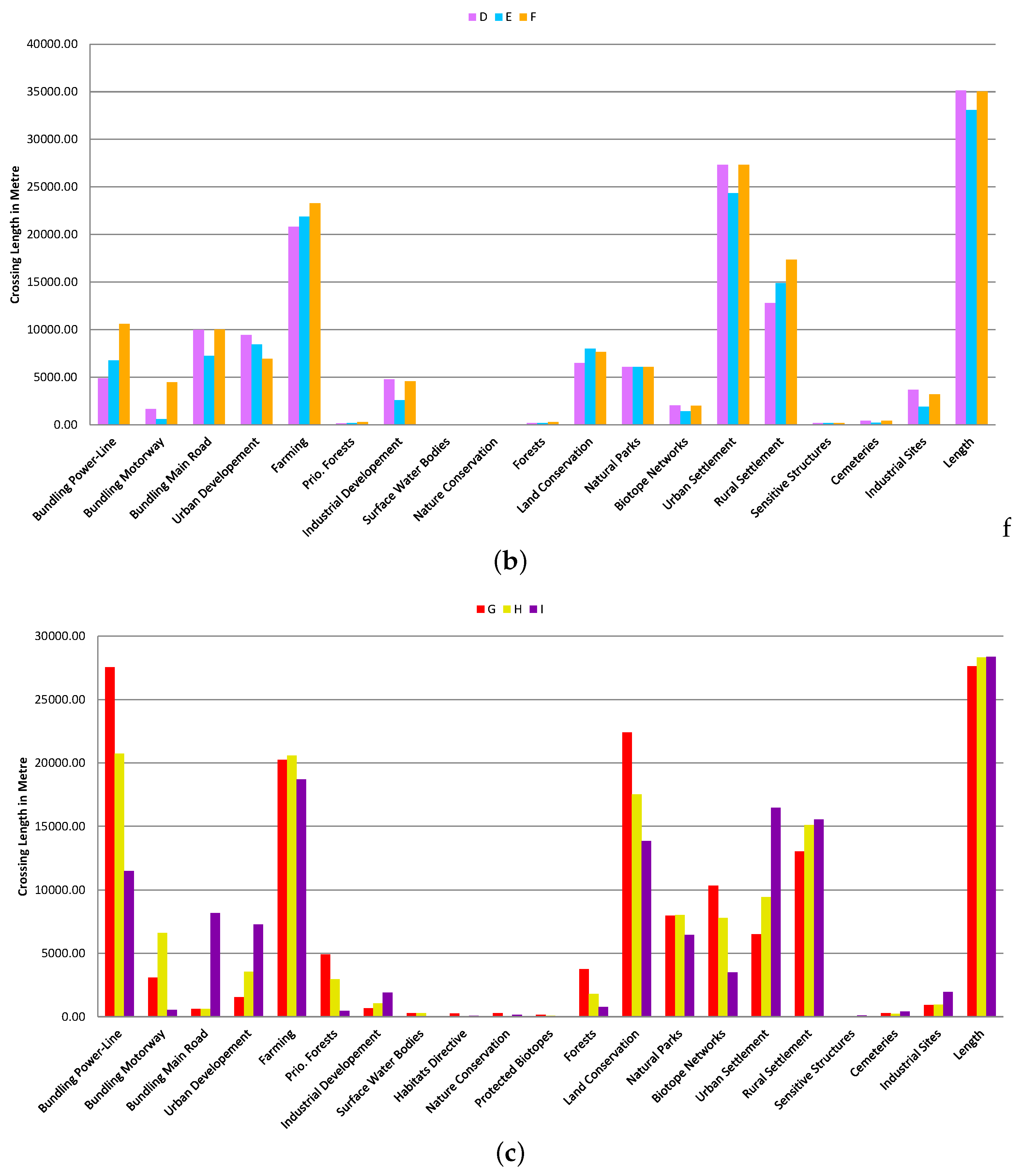
| Category | ID | Description | Impact Class |
|---|---|---|---|
| bundling with linear infrastructure (+ 200 buffer) | concentration along existing power-lines concentration along motorways concentration along main roads | high moderate low | |
| regional planning regulations | priority areas for urban development priority areas for farming priority areas for forestry priority areas for industrial development priority areas for surface water bodies | lowest lowest lowest lowest lowest | |
| nature and environmental protection | habitats directive areas nature conservation areas protected wildlife areas protected biotopes forests water bodies > 10 landscape conservation areas natural parks biotope networks | high moderate moderate low low low lowest lowest lowest | |
| settlement structures and urban land use | urban settlement areas + 400 buffer rural settlement areas + 200 buffer sensitive structures (e.g., hospitals) cemeteries industrial sites waste deposition sites mining sites | high high moderate moderate moderate moderate moderate | |
| length | length | high |
| mean | 262,215.54 | 135,263.14 | 94,531.76 | 94,083.08 | 27,052.36 |
| std | 40,486.08 | 8393.63 | 27,074.91 | 38,241.67 | 1678.49 |
| min | 176,490.00 | 118,364.00 | 34,113.70 | 25,723.70 | 23,672.79 |
| 25% | 232,537.00 | 129,646.00 | 74,141.05 | 64,968.20 | 25,929.22 |
| 50% | 265,687.00 | 133,836.00 | 94,012.90 | 87,675.10 | 26,767.26 |
| 75% | 289,193.50 | 139,407.00 | 112,216.50 | 115,919.00 | 27,881.48 |
| max | 367,991.00 | 180,637.00 | 192,218.00 | 247,791.00 | 36,127.42 |
| mean | 16,400.10 | 650.24 | 814.71 | 259.98 | 2861.54 | 19,135.67 | 7663.80 | 6760.39 | 11,519.39 | 35.15 | 670.53 | 27,052.36 |
| std | 6928.15 | 934.87 | 867.86 | 230.42 | 2288.32 | 3369.19 | 3384.64 | 5043.95 | 3071.71 | 58.76 | 471.50 | 1678.49 |
| min | 77.25 | 0.00 | 0.00 | 0.00 | 91.75 | 5920.21 | 1068.14 | 736.38 | 4180.24 | 0.00 | 67.17 | 23,672.79 |
| 25% | 11,851.90 | 0.00 | 243.48 | 75.00 | 1011.57 | 17,226.39 | 4858.99 | 3311.09 | 9263.85 | 0.00 | 244.71 | 25,929.22 |
| 50% | 17,725.41 | 250.00 | 565.56 | 187.07 | 2348.32 | 19,533.72 | 7667.46 | 5398.64 | 11,302.53 | 14.14 | 723.30 | 26,767.26 |
| 75% | 21,447.03 | 730.42 | 1058.01 | 396.75 | 3932.75 | 21,431.00 | 10,167.91 | 8057.41 | 13,985.11 | 28.28 | 883.42 | 27,881.48 |
| max | 30,281.46 | 5652.94 | 6022.24 | 1279.33 | 11,141.00 | 27,013.01 | 16,518.35 | 28,585.28 | 19,947.25 | 316.92 | 4283.53 | 36,127.42 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bachmann, D.; Bökler, F.; Kopec, J.; Popp, K.; Schwarze, B.; Weichert, F. Multi-Objective Optimisation Based Planning of Power-Line Grid Expansions. ISPRS Int. J. Geo-Inf. 2018, 7, 258. https://doi.org/10.3390/ijgi7070258
Bachmann D, Bökler F, Kopec J, Popp K, Schwarze B, Weichert F. Multi-Objective Optimisation Based Planning of Power-Line Grid Expansions. ISPRS International Journal of Geo-Information. 2018; 7(7):258. https://doi.org/10.3390/ijgi7070258
Chicago/Turabian StyleBachmann, Daniel, Fritz Bökler, Jakob Kopec, Kira Popp, Björn Schwarze, and Frank Weichert. 2018. "Multi-Objective Optimisation Based Planning of Power-Line Grid Expansions" ISPRS International Journal of Geo-Information 7, no. 7: 258. https://doi.org/10.3390/ijgi7070258
APA StyleBachmann, D., Bökler, F., Kopec, J., Popp, K., Schwarze, B., & Weichert, F. (2018). Multi-Objective Optimisation Based Planning of Power-Line Grid Expansions. ISPRS International Journal of Geo-Information, 7(7), 258. https://doi.org/10.3390/ijgi7070258





