An Automated Processing Method for Agglomeration Areas
Abstract
1. Introduction
2. Related Works
3. Methodology for the Automated Processing of Agglomeration Areas
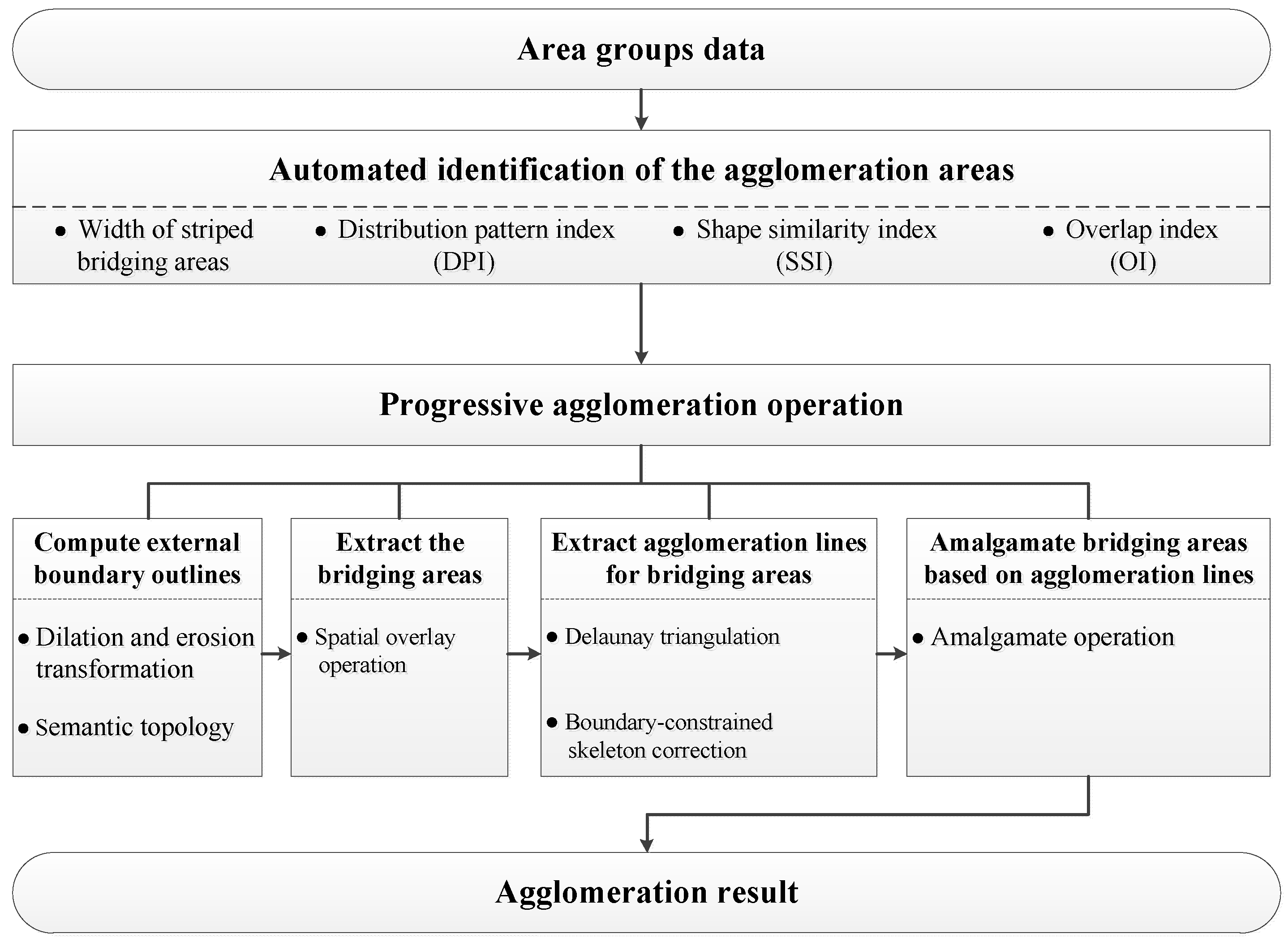
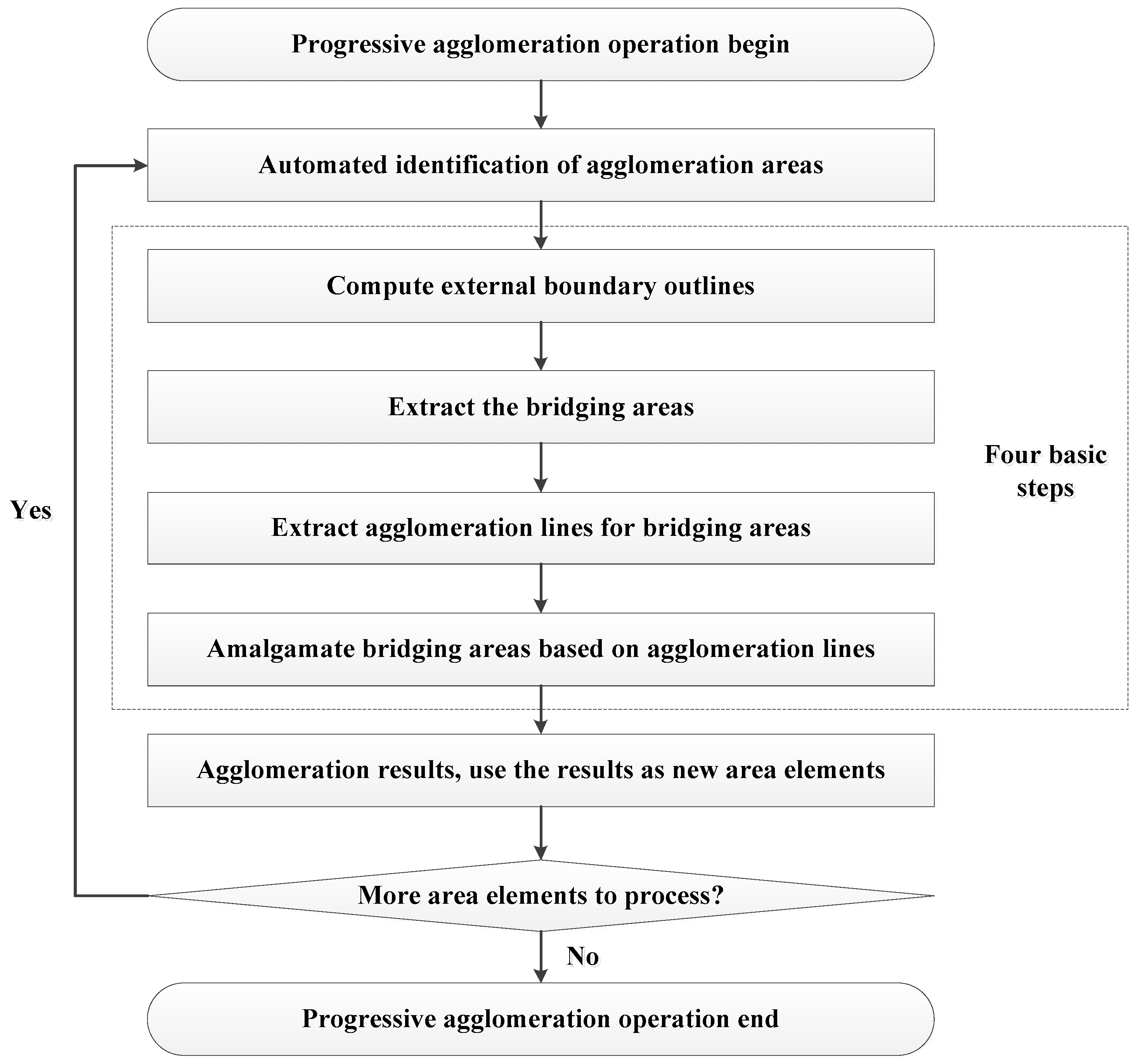
3.1. Framework for the Proposed Method
- (1)
- Computing the external boundary outlines for each agglomeration area;
- (2)
- Extracting bridging areas through the spatial overlay operation;
- (3)
- Extracting skeletons for bridging areas on the basis of the Delaunay triangulation and using the boundaries as constraints to correct the skeletons and form agglomeration lines; and
- (4)
- Amalgamating bridging areas based on agglomeration lines to obtain the agglomeration result.
3.2. Automated Identification of Agglomeration Areas
3.2.1. Typical Characteristics of Agglomeration Areas
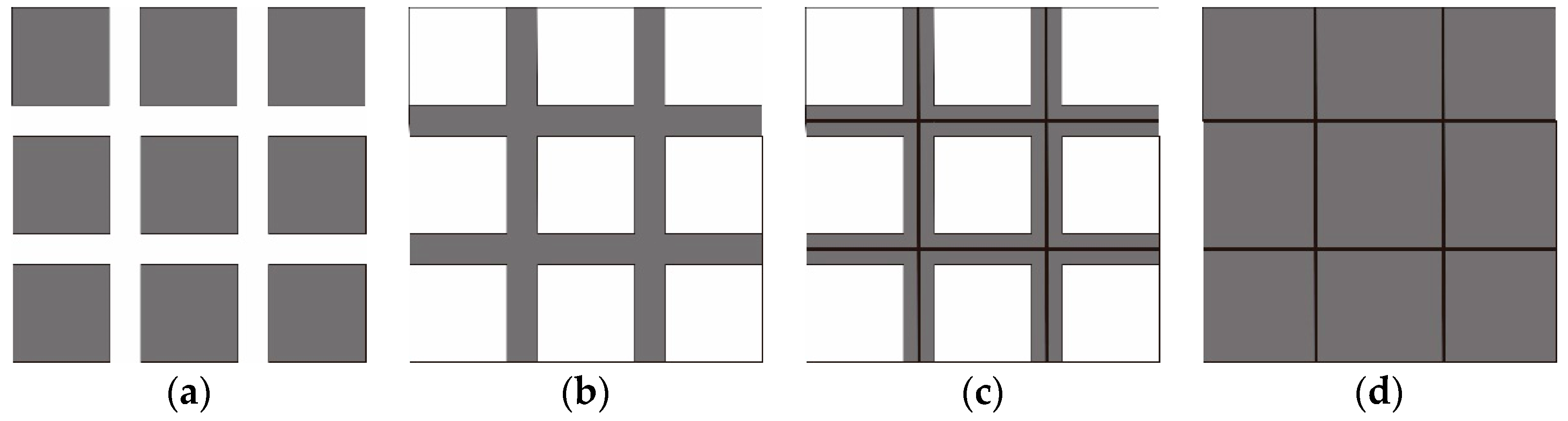
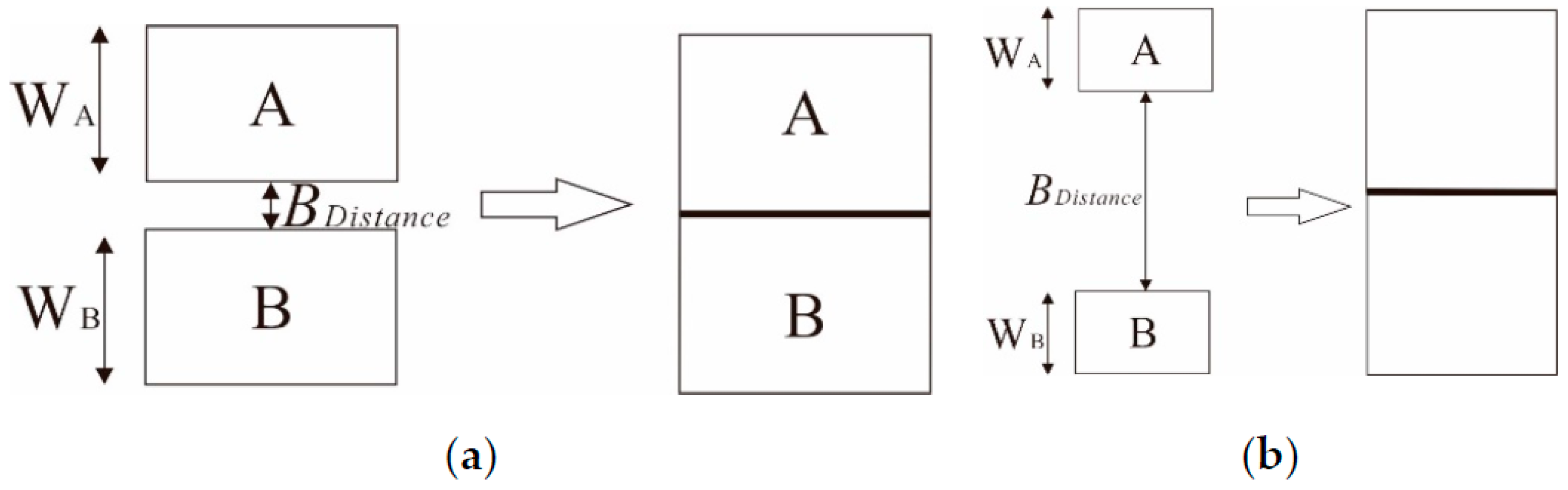
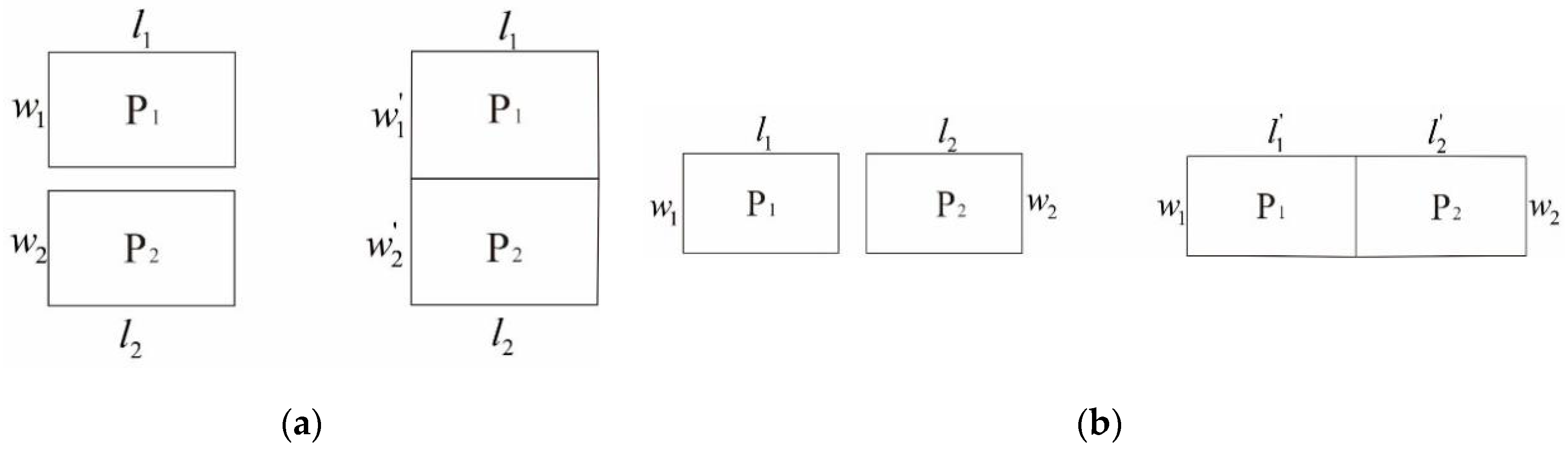
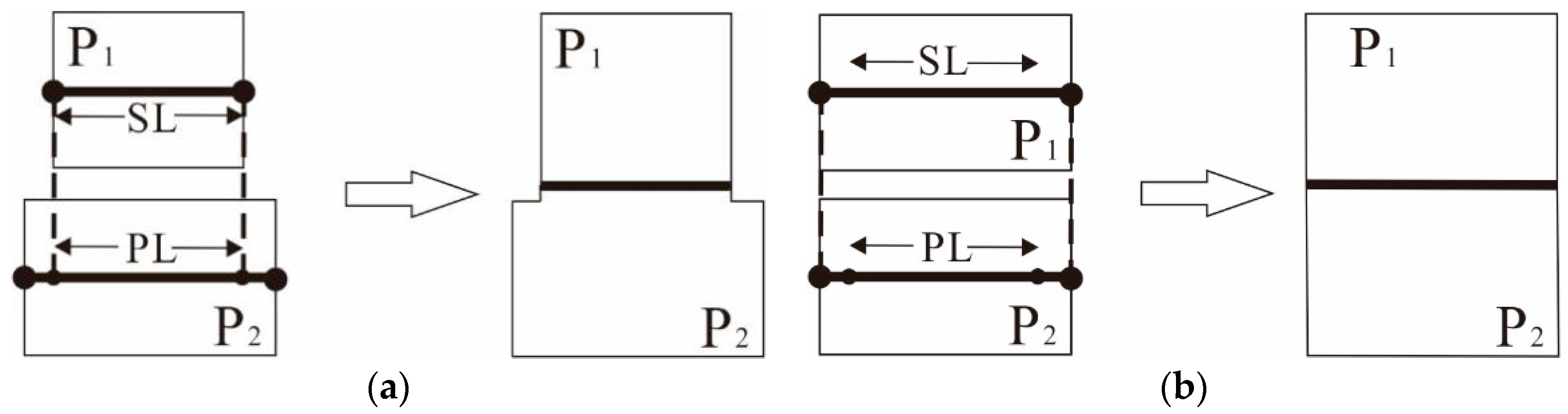
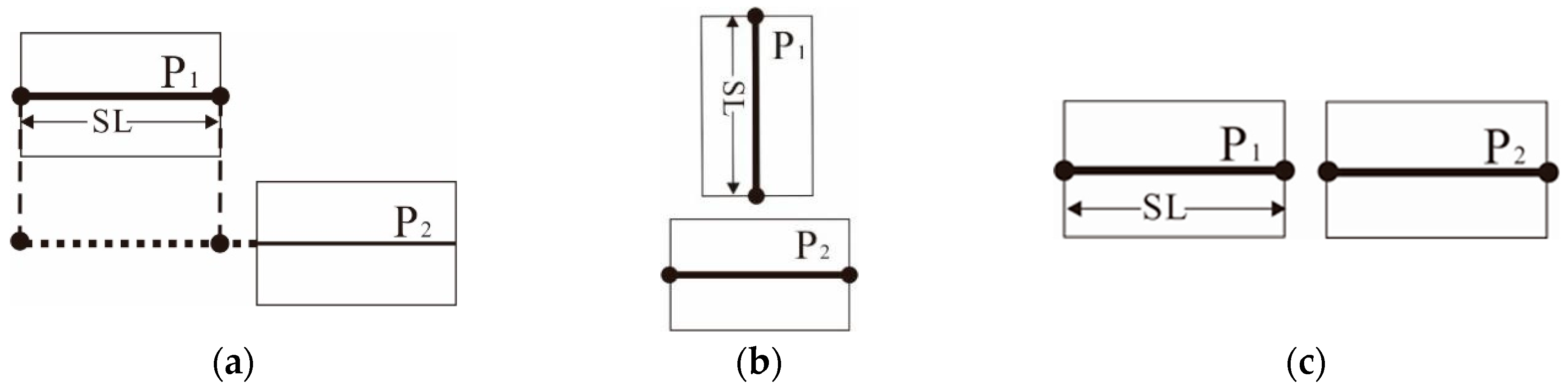
Width of Striped Bridging Area
Distribution Pattern Index (DPI) of Area Elements
Shape Similarity Index (SSI) of Area Elements
Overlap Index (OI) of the Area Elements
3.2.2. Identification
3.3. Progressive Agglomeration Operation
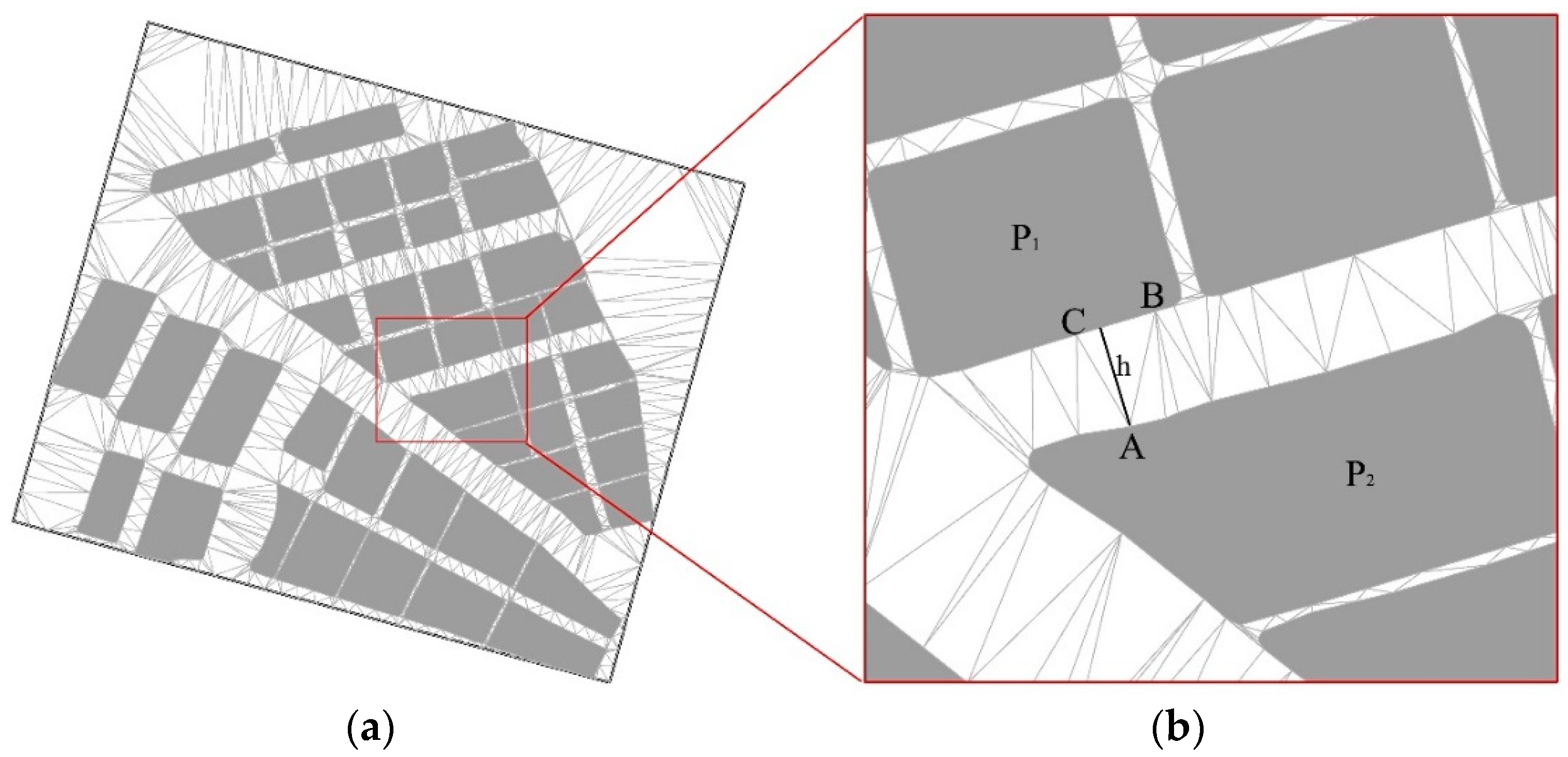
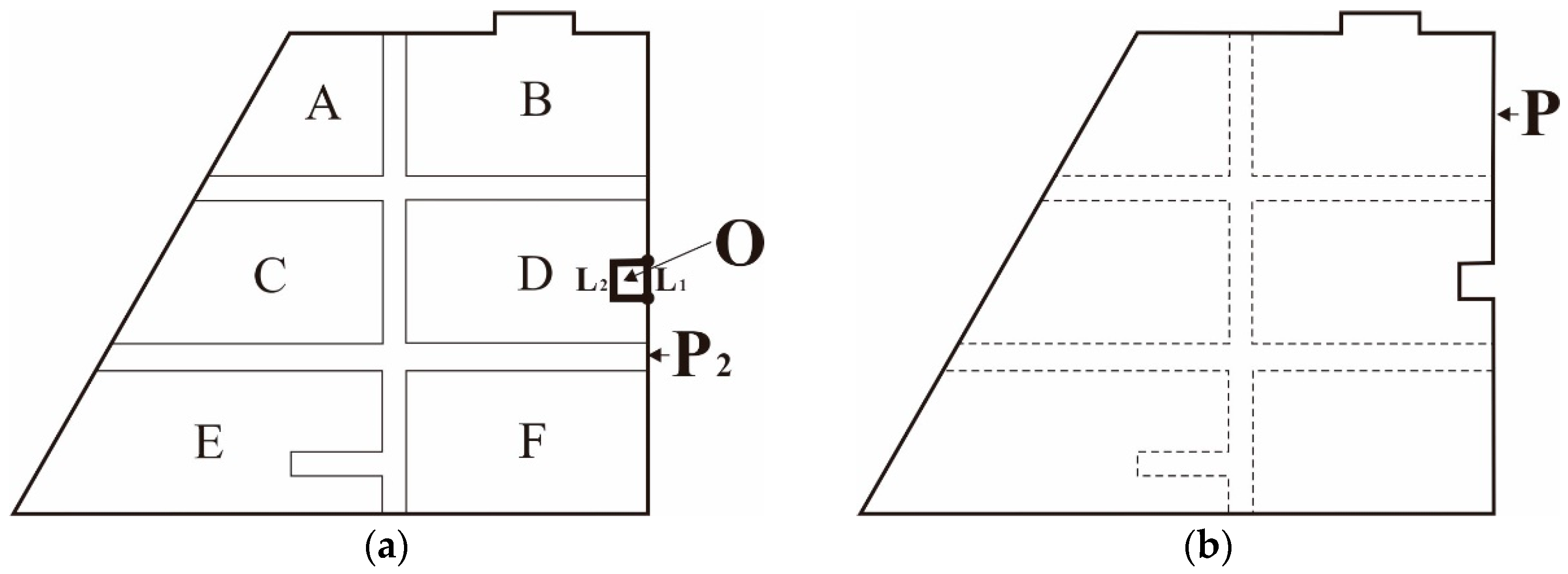
3.3.1. Computation of External Boundary Outlines
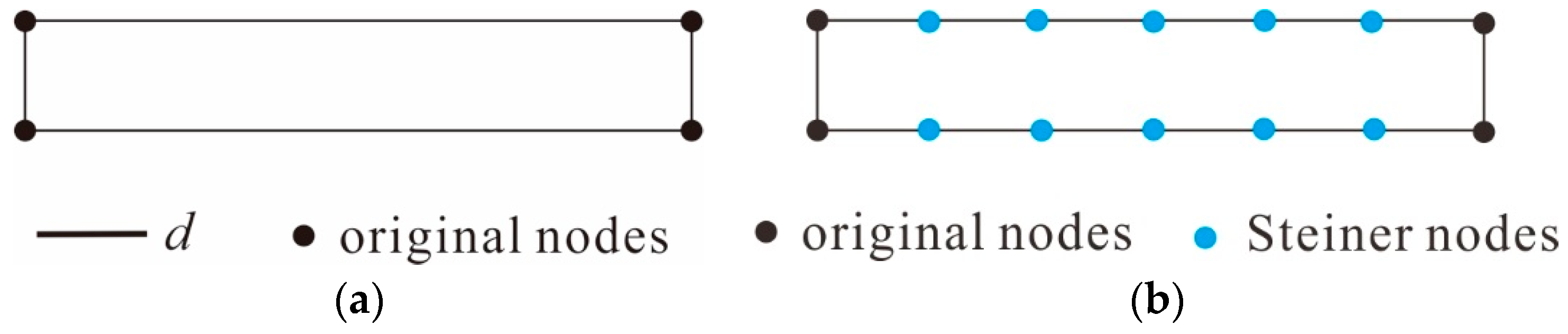
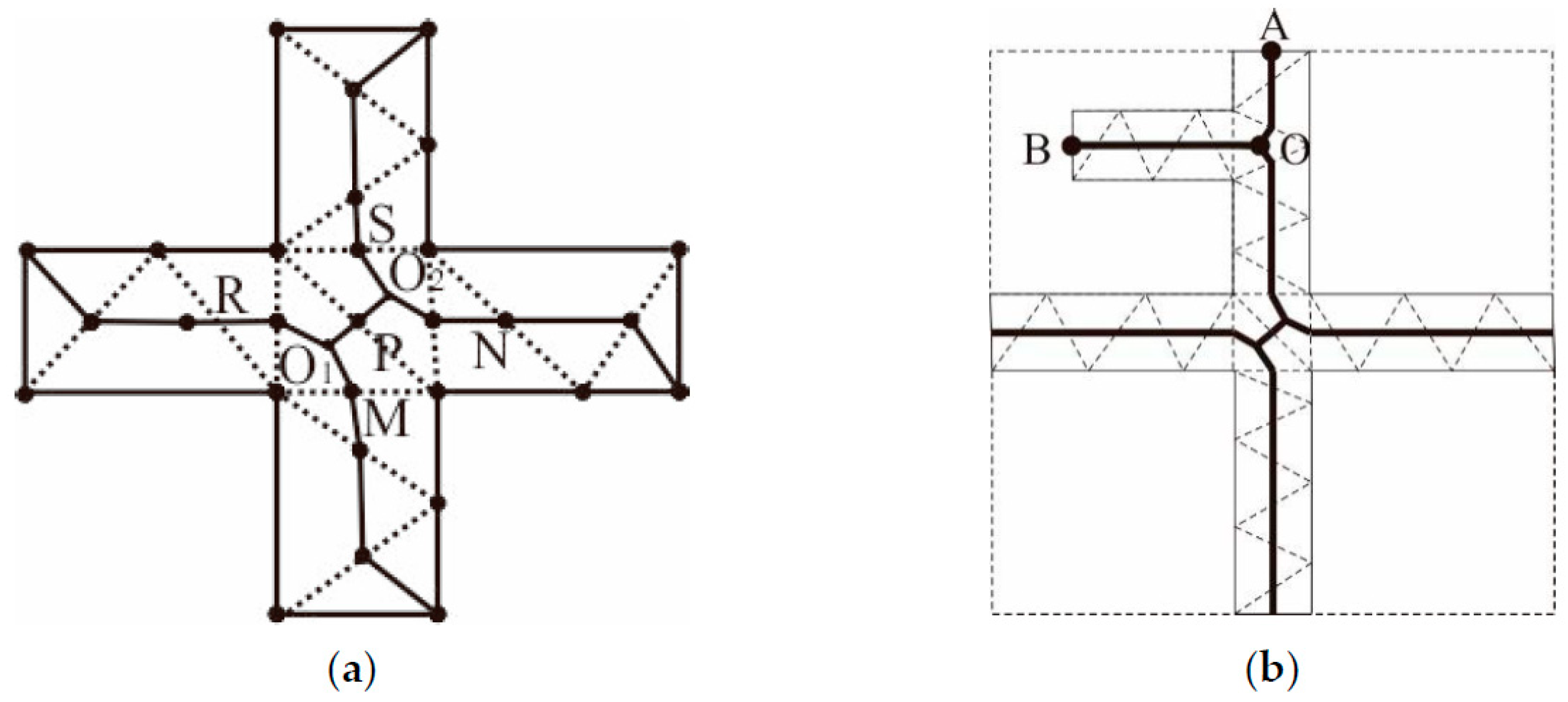
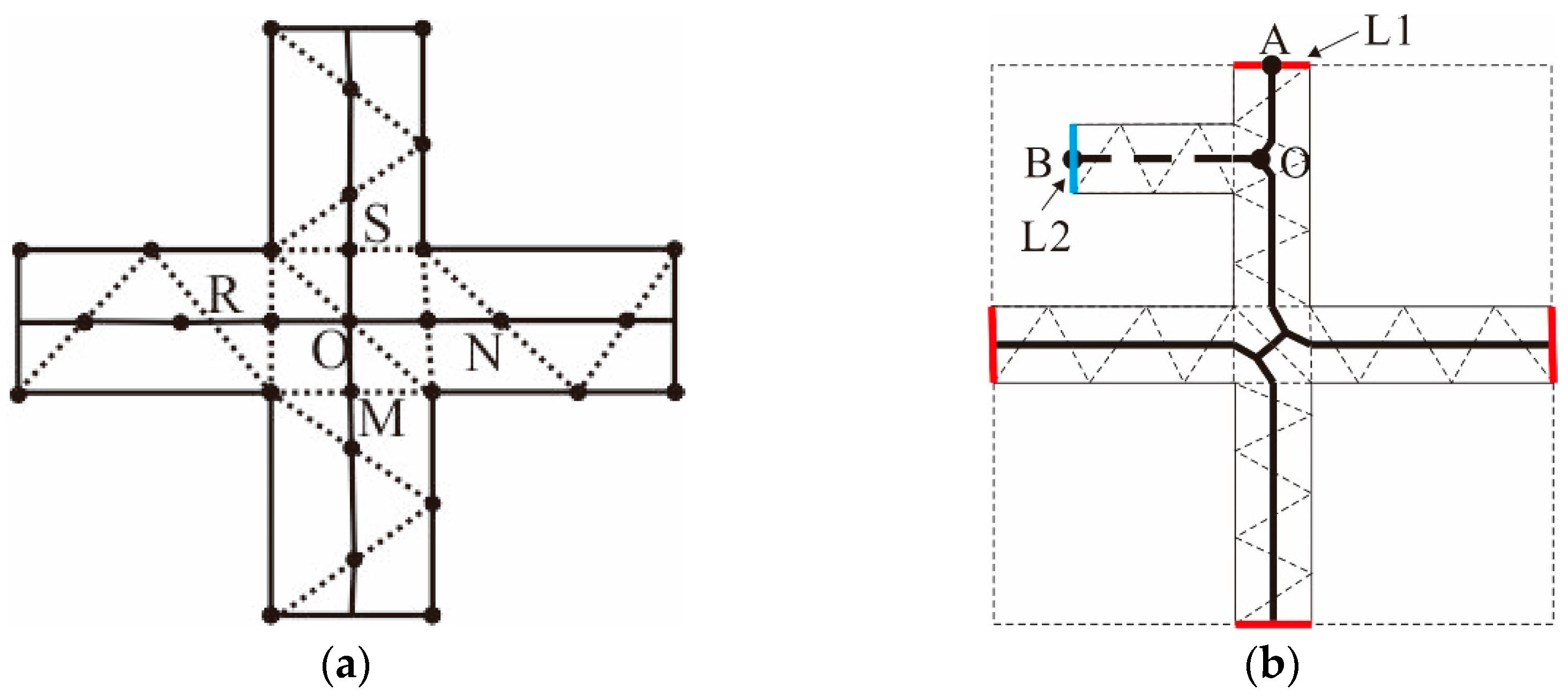
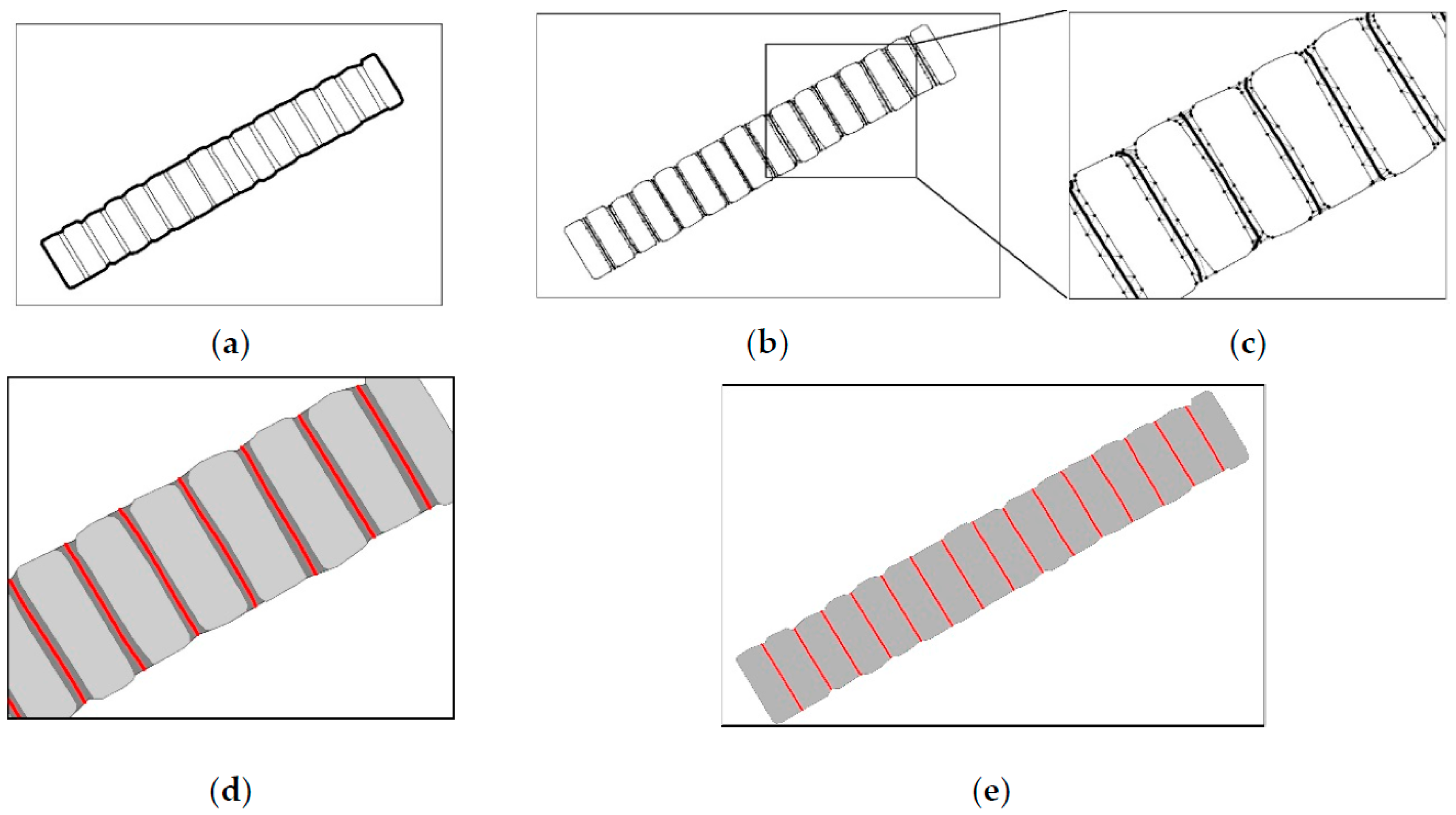
3.3.2. Extraction of Agglomeration Lines
- (1)
- Bridging areas are usually regular in shape, similar in width, and straight. However, most of their branches intersect with one another to form “+”-shaped junctions, leading to Y-shaped jitter that are very likely to occur in these areas due to the aggregation of type III triangles, as depicted in Figure 15a.
- (2)
- The concave and convex structures of bridging areas tends to induce errors during the extraction of agglomeration lines. In Figure 15b, it is shown that, if the main skeleton is extracted based on the SL or triangular area occupied by a skeleton, the OB skeleton, which corresponds to a concave structure, replaces the OA skeleton and becomes the main agglomeration line. Obviously, the extracted agglomeration line is not reasonable because the terminal node is not located on the boundary due to the influence of the concave area.
3.3.3. Progressive Process for the Agglomeration Operation
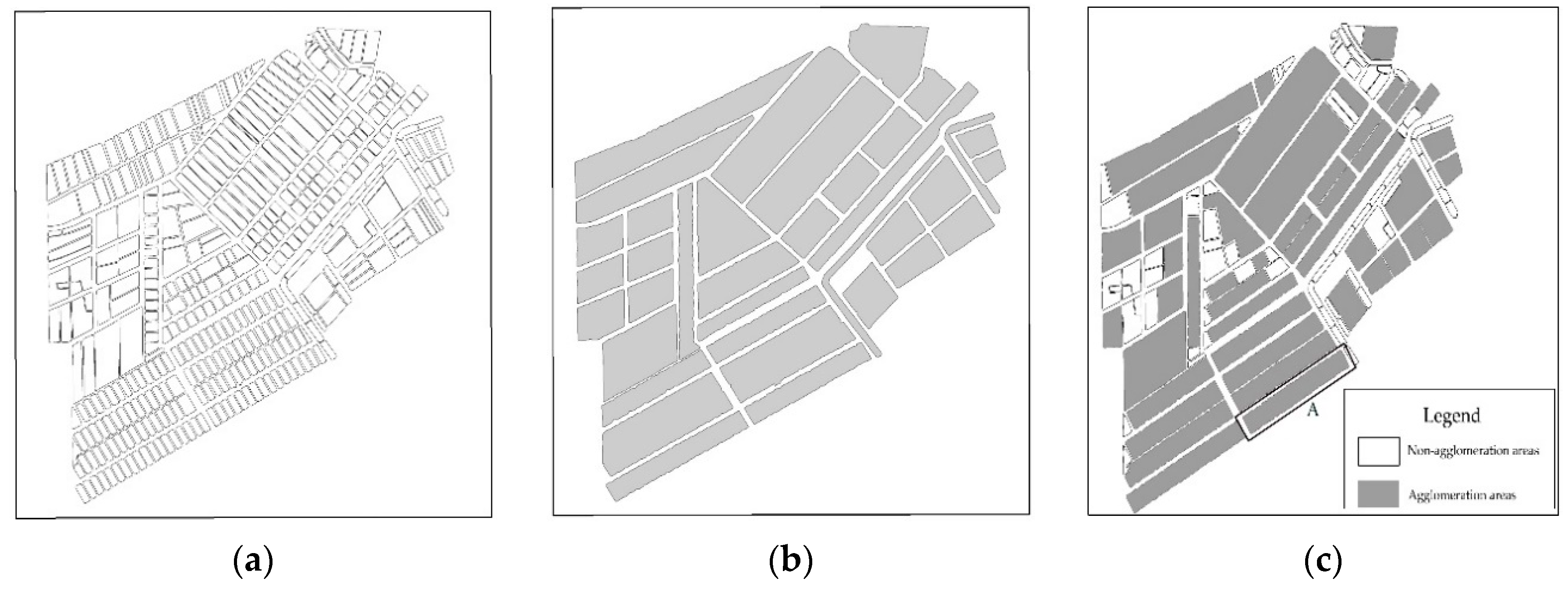
4. Experiment and Results
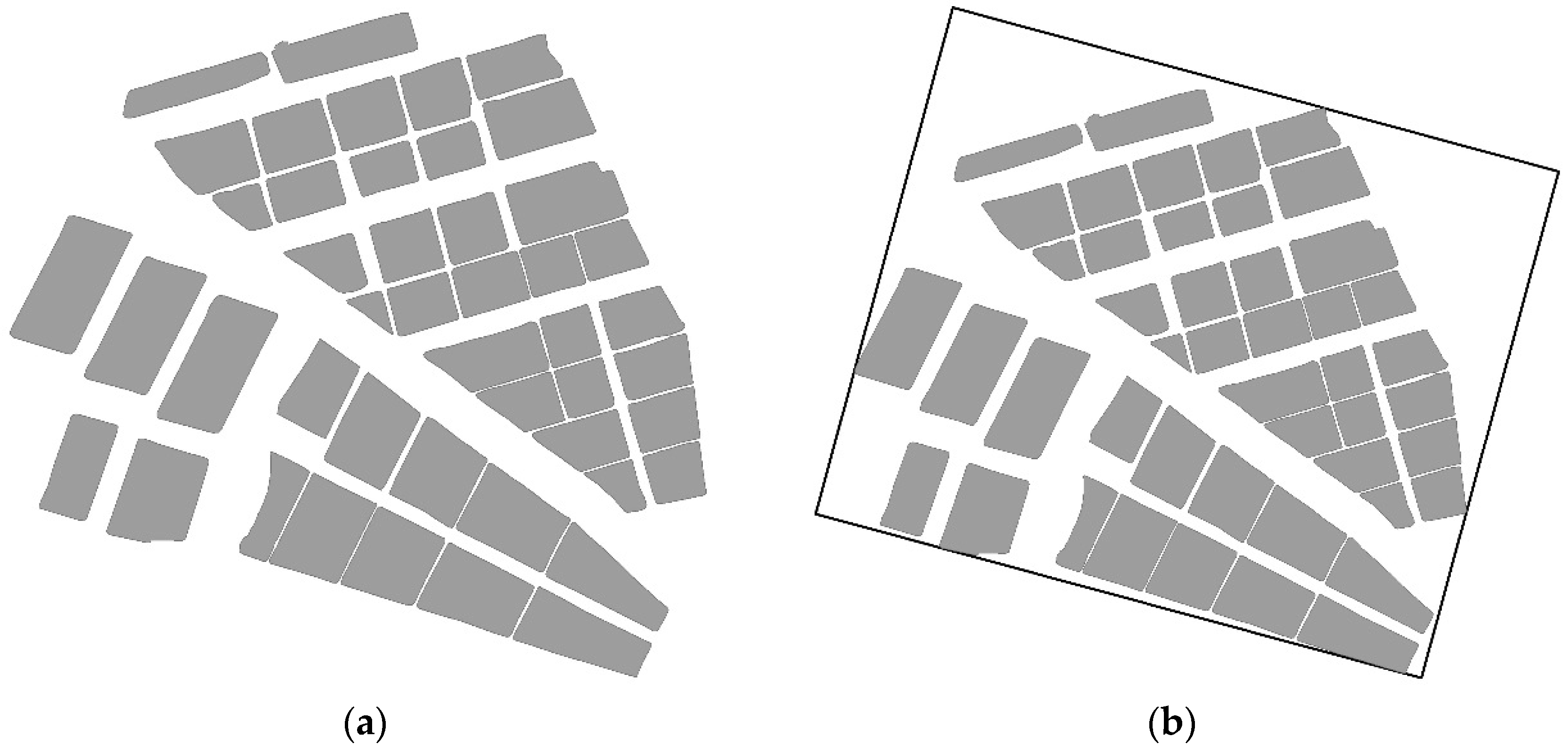
4.1. Experimental Data and Environment
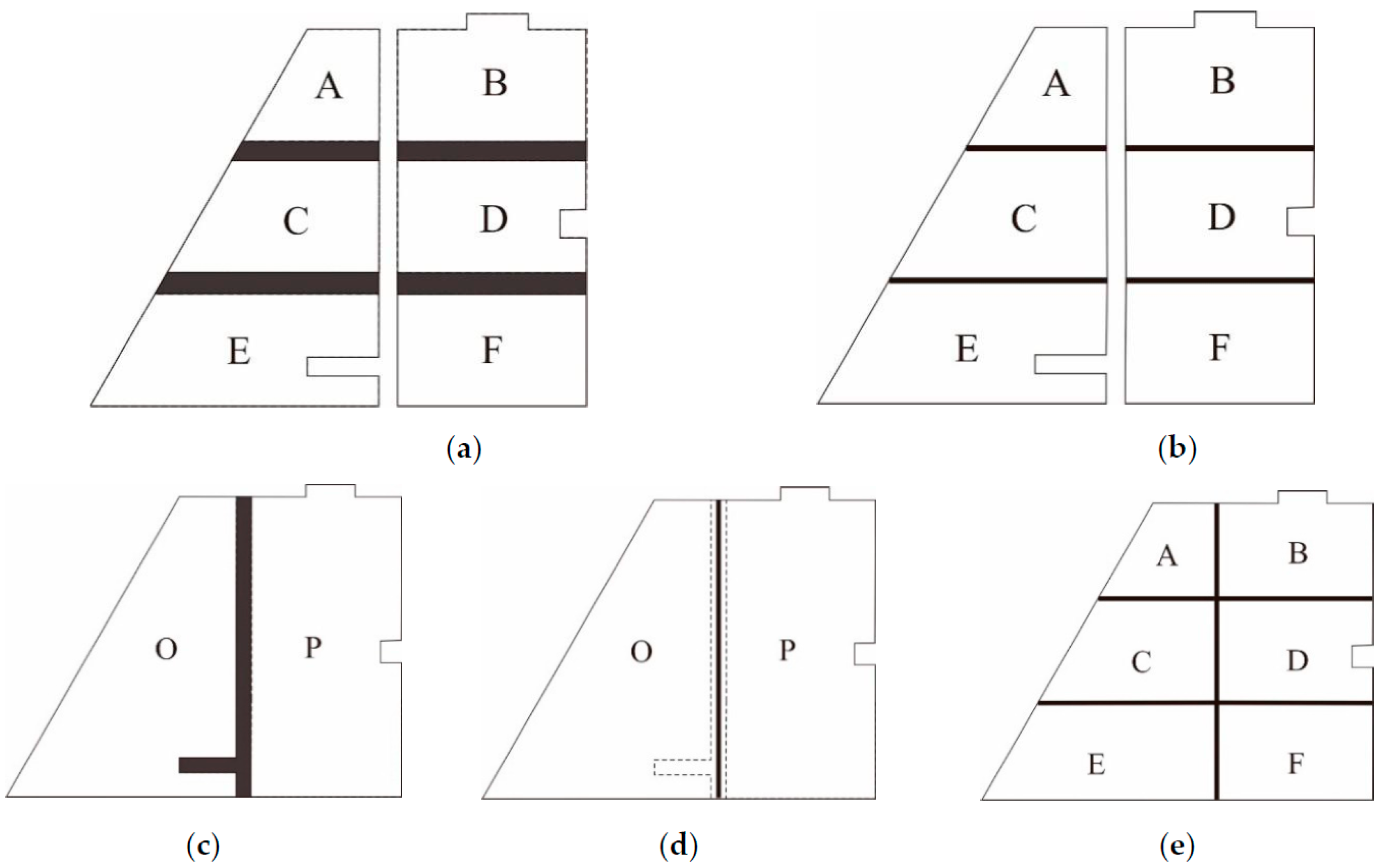
4.2. Results of the Agglomeration Operation
- (1)
- A dilation-erosion transformation was first performed on the original agglomeration area group and its external boundary outline was identified, as shown in Figure 19a.
- (2)
- The original data and boundary contours were overlaid to obtain the bridging areas, followed by node densification along the bridging area boundaries and boundary-constrained Delaunay triangulation to extract the main skeleton of the bridging areas, as shown in Figure 19b.
- (3)
- The terminal nodes of the main skeleton were then adjusted, while the boundaries were used as constraints for skeleton corrections to obtain the agglomeration lines, as shown by the red line in Figure 19c.
- (4)
- Based on these agglomeration lines, the bridging areas were amalgamated to obtain the agglomeration result shown in Figure 19d.
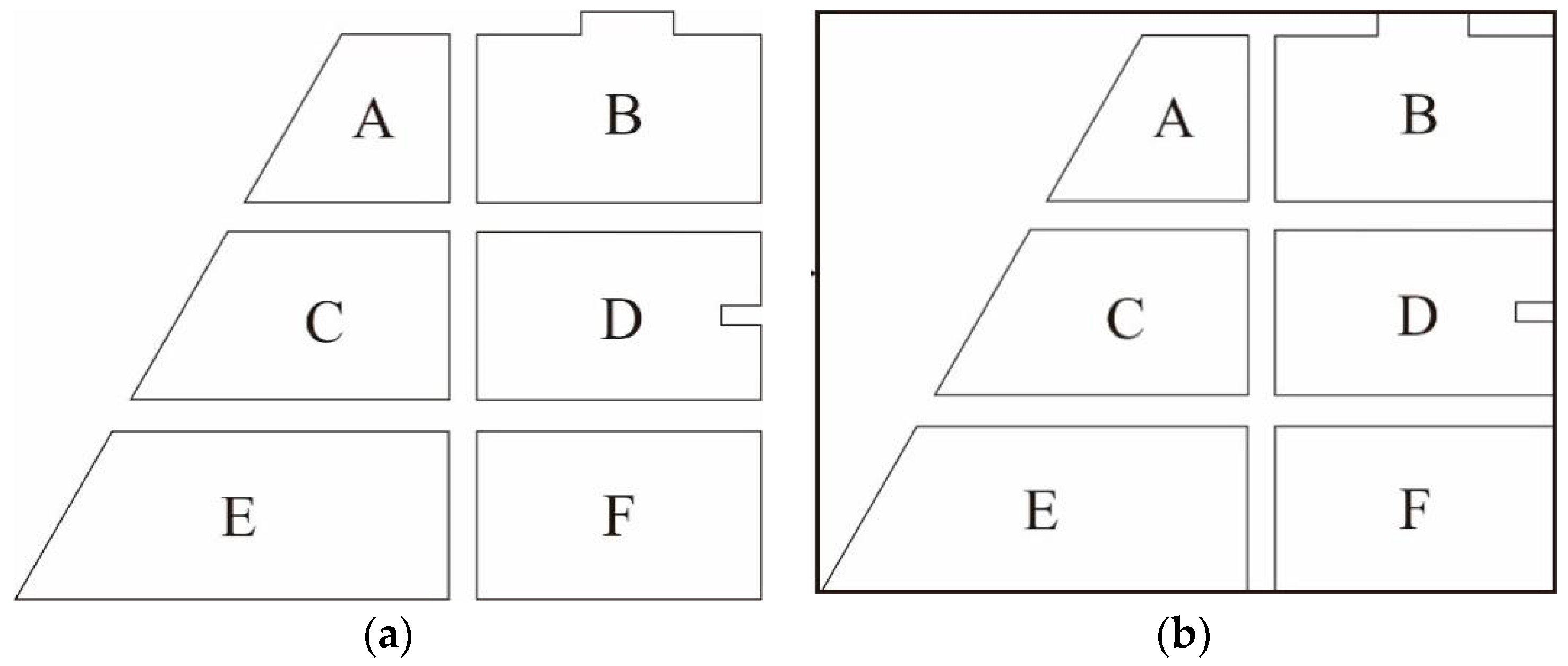
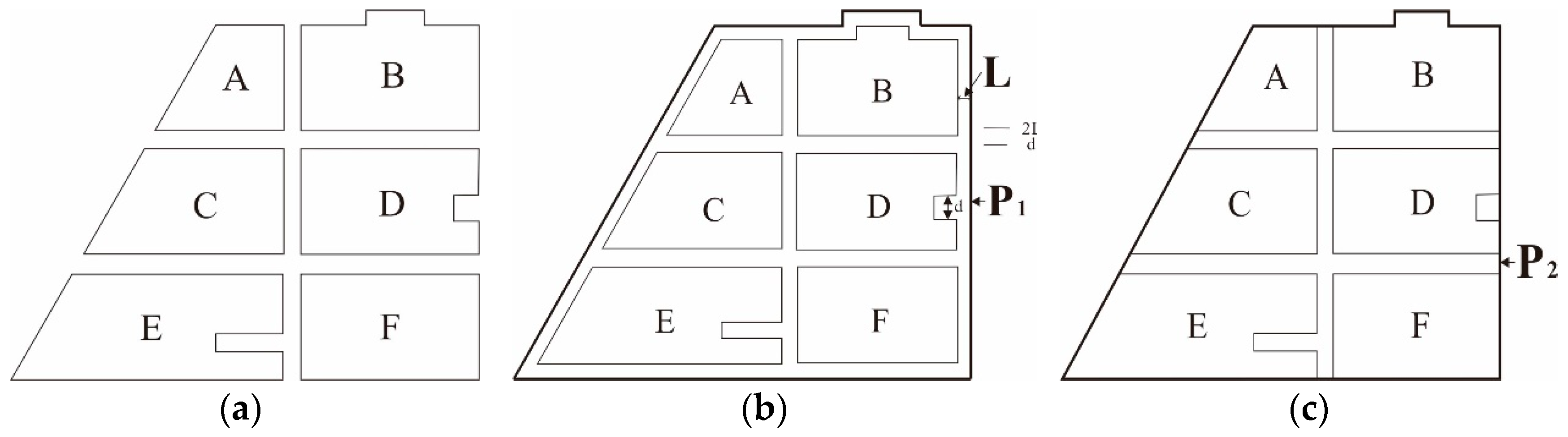
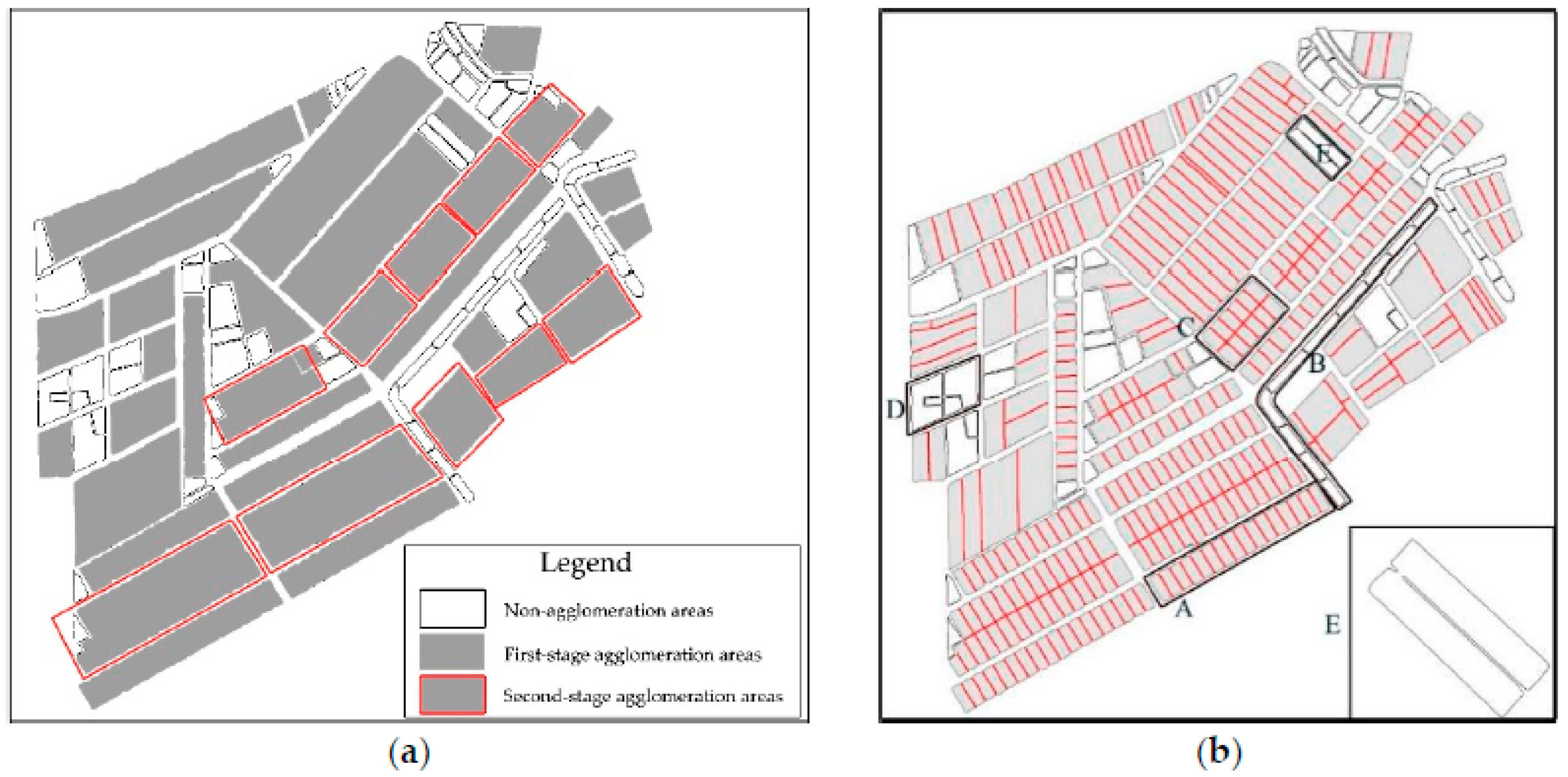
- (1)
- Noncompliance with side-adjacency criteria (OI): By using candidate area B as an example, the elements within this area are highly similar in shape and are linearly ordered. However, these elements are side-adjacent along their shorter edge; thus, they were deemed unsuitable for agglomeration.
- (2)
- Noncompliance with shape similarity criteria (SSI): For example, although the elements in candidate area D superficially appeared to have the same overall shape, they were different based on their internal structure details. Area D was, therefore, deemed unsuitable for agglomeration due to the low shape similarity of its elements.
- (3)
- Element E was not agglomerated despite the overall shape of E being similar to that of its adjacent element because the identification of this element (for agglomeration suitability) was affected by the presence of a deep concave area inside the element. This result is a special case in the agglomeration process, and its treatment will require further study.
5. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Haunert, J.H.; Wolff, A. Area aggregation in map generalisation by mixed-integer programming. Int. J. Geogr. Inf. Sci. 2010, 24, 1871–1897. [Google Scholar] [CrossRef]
- Cheng, T.; Li, Z. Toward quantitative measures for the semantic quality of polygon generalization. Cartogr. Int. J. Geogr. Inf. Geovis. 2006, 41, 135–148. [Google Scholar] [CrossRef]
- Zhou, X.; Truffet, D.; Han, J. Efficient polygon amalgamation methods for spatial OLAP and spatial data mining. In International Symposium on Spatial Databases; Springer: Berlin/Heidelberg, German, 1999; pp. 167–187. [Google Scholar]
- Regnauld, N. Algorithms for the amalgamation of topographic data. In Proceedings of the 21st International Cartographic Conference, Durban, South Africa, 10–16 August 2003; p. 1016. [Google Scholar]
- Delucia, A.A.; Black, R.B. A comprehensive approach to automatic feature generalisation. In Proceedings of the 13th International Cartographic Conference, Morelia, Mexico, 12–22 October 1987; pp. 169–192. [Google Scholar]
- Li, Z. Algorithmic Foundation of Multi-Scale Spatial Representation; CRC Press: Bacon Raton, FL, USA, 2006. [Google Scholar]
- Cheng, P.; Yan, H.; Han, Z. An algorithm for computing the minimum area bounding rectangle of an arbitrary polygon. J. Eng. Graph. 2008, 1, 122–126. [Google Scholar]
- Ruas, A. Multiple paradigms for automating map generalisation: Geometry, topology, hierarchical partitioning and local triangulation. In Proceedings of the ACSM/ASPRS Annual Convention and Exposition, Charlotte, North Carolina, 27 February–2 March 1995; pp. 69–78. [Google Scholar]
- Ware, J.M.; Jones, C.B.; Bundy, G.L. A triangulated spatial model for cartographic generalisation of areal objects. In Advances in GIS Research II (the 7th Int. Symposium on Spatial Data Handling); Kraak, M.J., Molenaar, M., Eds.; Taylor & Francis: London, UK, 1997; pp. 173–192. [Google Scholar]
- Cao, T.; Edelsbrunner, H.; Tan, T. Proof of correctness of the digital Delaunay triangulation algorithm. Comput. Geom. Theory Appl. 2015, 48, 507–519. [Google Scholar] [CrossRef]
- Yu, W. Assessing the implications of the recent community opening policy on the street centrality in China: A GIS-Based method and case study. Appl. Geogr. 2017, 89, 61–76. [Google Scholar] [CrossRef]
- Technical Specification for Resulting Map of National Census Geography; GDPJ 17-2016; Leading Group Office of the First National Census Geography of the State Council: Beijing, China, 2016.
- Penninga, F.; Verbree, E.; Quak, W.; van Oosterom, P. Construction of the planar partition postal code map based on cadastral registration. GeoInformatica 2005, 9, 181–204. [Google Scholar] [CrossRef]
- Mitropoulos, V.; Xydia, A.; Nakos, B.; Vescoukis, V. The use of epsilonconvex area for attributing bends along a cartographic line. In Proceedings of the International Cartographic Conference, A Coruňa, Spain, 9–16 July 2005. [Google Scholar]
- Gabay, Y.; Doytsher, Y. Automatic adjustment of line maps. In Proceedings of the GIS/LIS, Phoenix, Arizona, 25–27 October 1994; Volume 94, pp. 332–340. [Google Scholar]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or caricature. Can. Cartogr. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Zou, J.J.; Yan, H. Skeletonization of ribbon-like shapes based on regularity and singularity analyses. IEEE Trans. Syst. Man Cybern. B Cybern. 2001, 31, 401–407. [Google Scholar] [PubMed]
- Morrison, P.; Zou, J.J. Triangle refinement in a constrained Delaunay triangulation skeleton. Pattern Recognit. 2007, 40, 2754–2765. [Google Scholar] [CrossRef]
- Serna, A.; Marcotegui, B. Detection, segmentation and classification of 3D urban objects using mathematical morphology and supervised learning. ISPRS J. Photogramm. Remote Sens. 2014, 93, 243–255. [Google Scholar] [CrossRef]
- Haunert, J.H.; Sester, M. Area collapse and road centerlines based on straight skeletons. GeoInformatica 2008, 12, 169–191. [Google Scholar] [CrossRef]

| Type | Map Width (mm) (1:500,000 > Scale > 1:10,000) |
|---|---|
| Roads | 0.4 |
| Rivers, canals and drains | 0.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Yin, Y.; Liu, X.; Wu, P. An Automated Processing Method for Agglomeration Areas. ISPRS Int. J. Geo-Inf. 2018, 7, 204. https://doi.org/10.3390/ijgi7060204
Li C, Yin Y, Liu X, Wu P. An Automated Processing Method for Agglomeration Areas. ISPRS International Journal of Geo-Information. 2018; 7(6):204. https://doi.org/10.3390/ijgi7060204
Chicago/Turabian StyleLi, Chengming, Yong Yin, Xiaoli Liu, and Pengda Wu. 2018. "An Automated Processing Method for Agglomeration Areas" ISPRS International Journal of Geo-Information 7, no. 6: 204. https://doi.org/10.3390/ijgi7060204
APA StyleLi, C., Yin, Y., Liu, X., & Wu, P. (2018). An Automated Processing Method for Agglomeration Areas. ISPRS International Journal of Geo-Information, 7(6), 204. https://doi.org/10.3390/ijgi7060204




