Comprehensive Analysis of System Calibration between Optical Camera and Range Finder
Abstract
1. Introduction
2. Related Work
3. Sensor Geometric Functional Models and Calibration Testbed
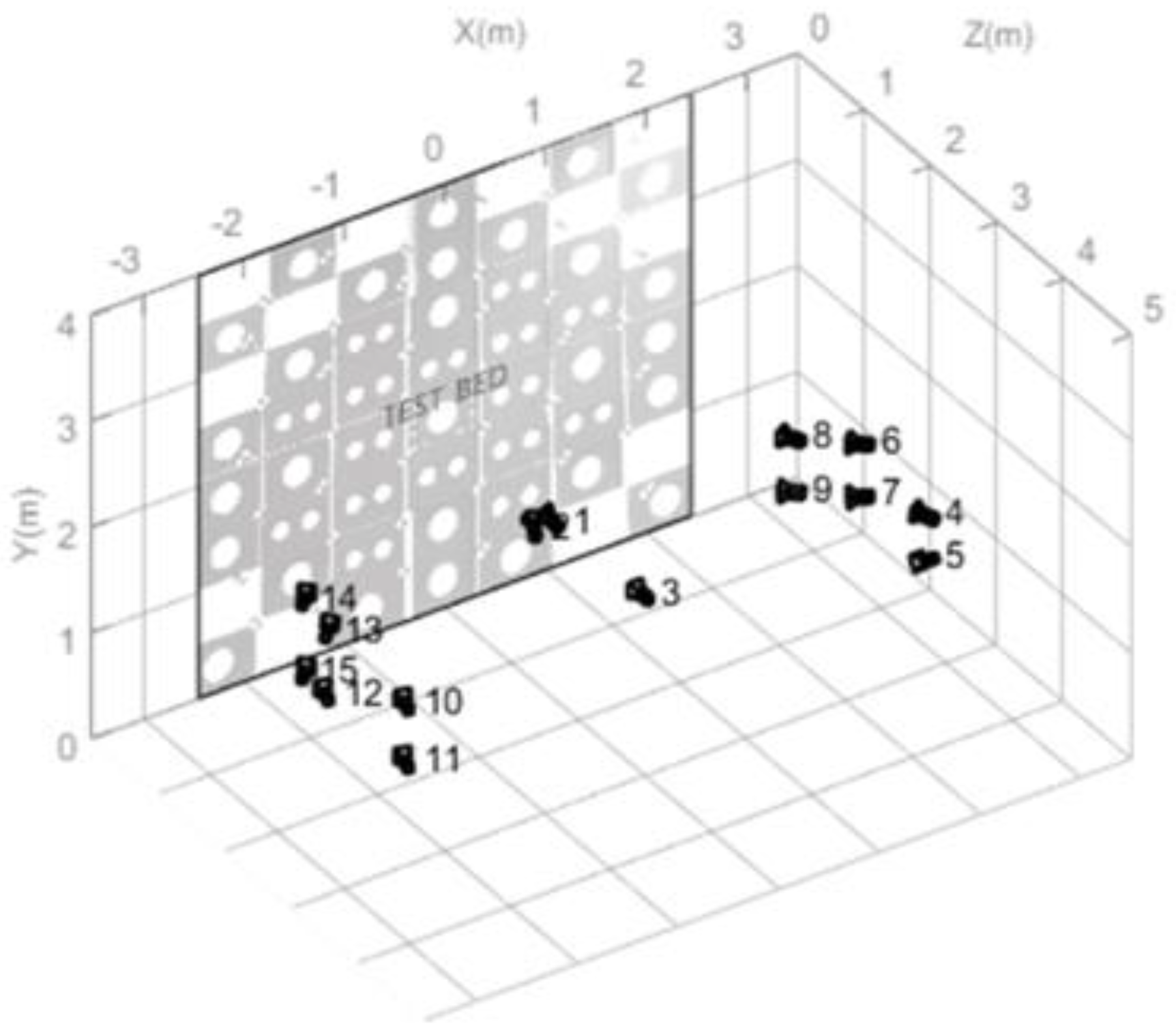
3.1. Testbed Designed for Calibration Procedure
3.2. Sensors and Mathematical Models
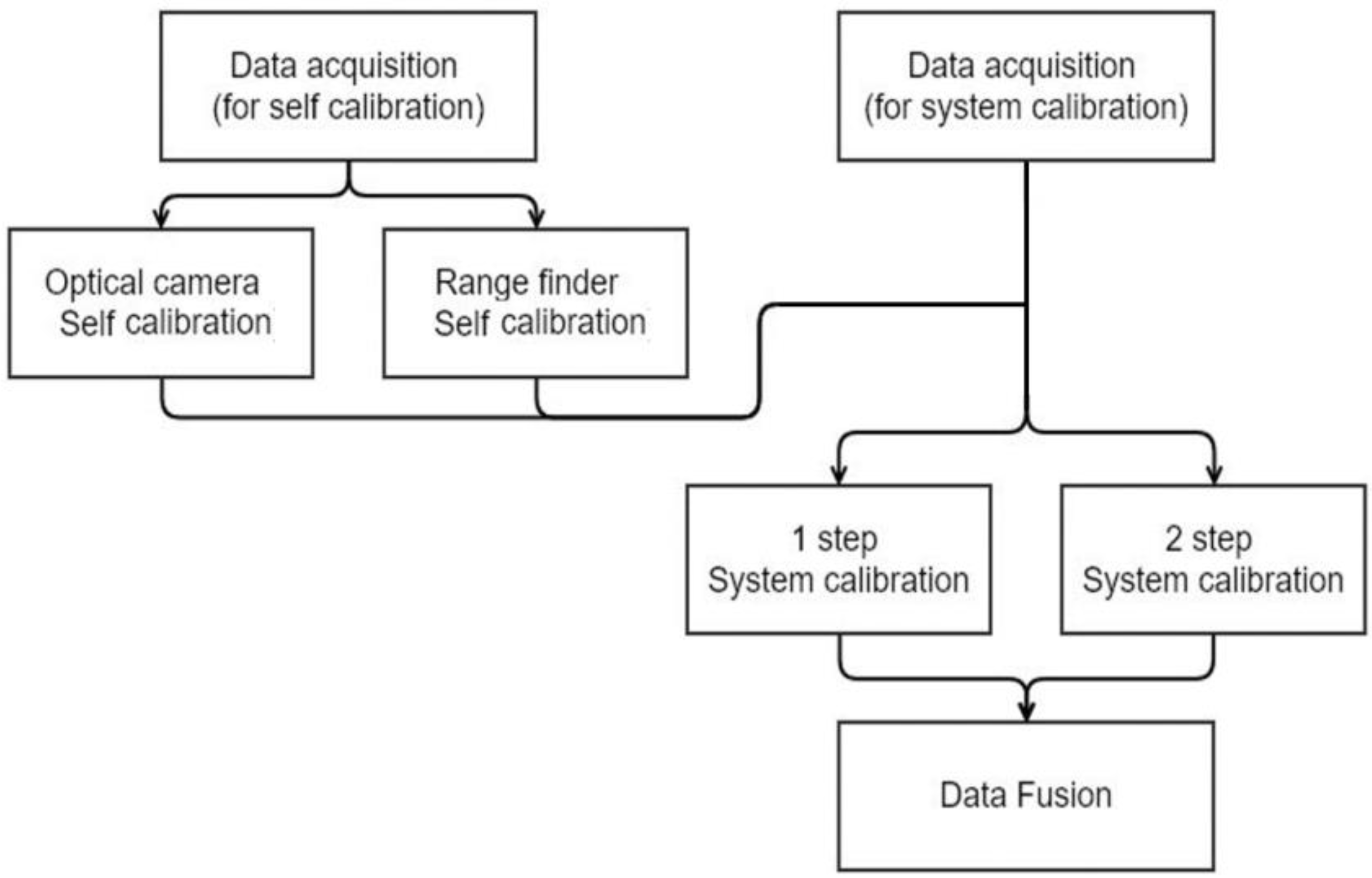
4. Calibrations and Comparative Evaluation Strategy
4.1. Self-Calibration
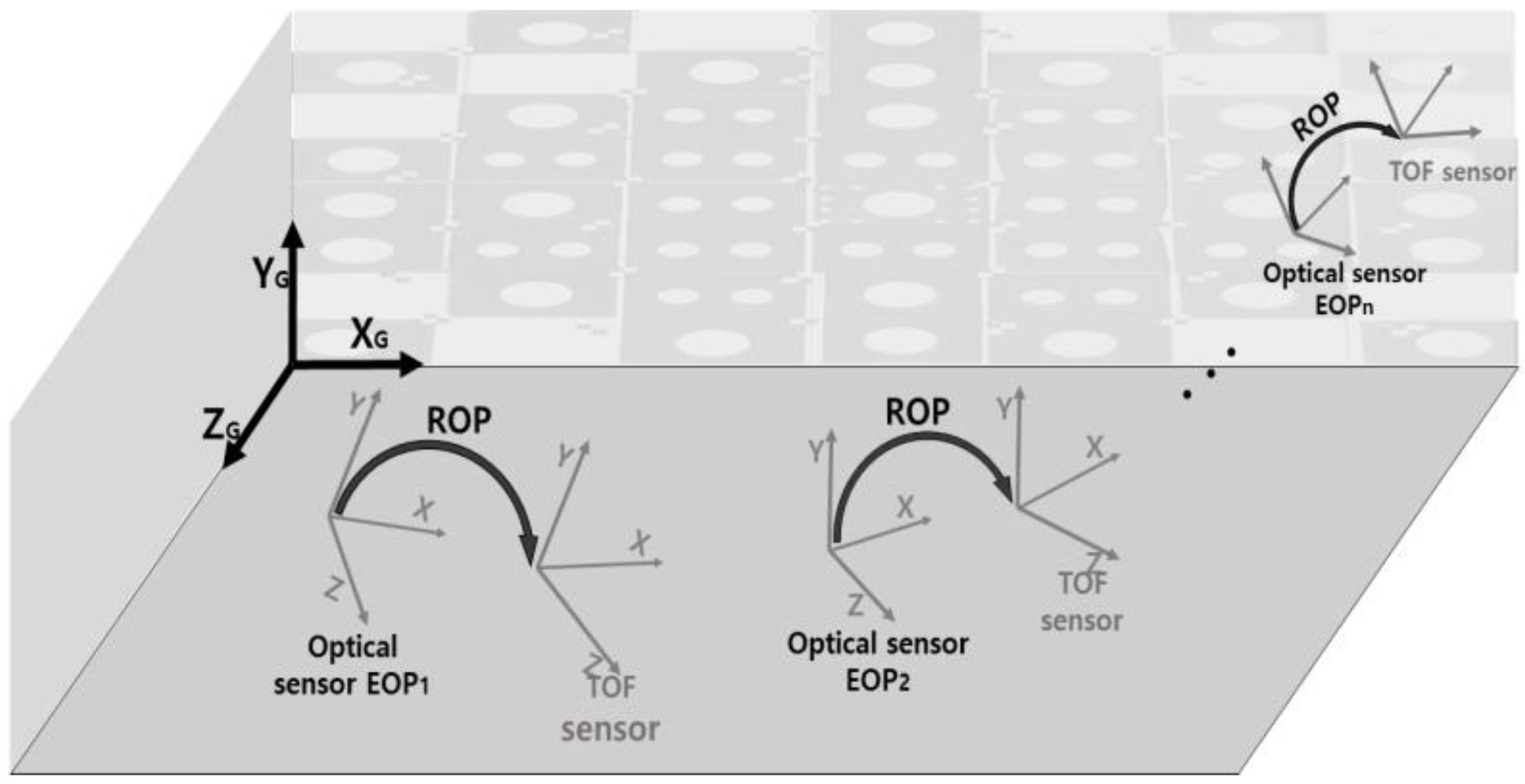
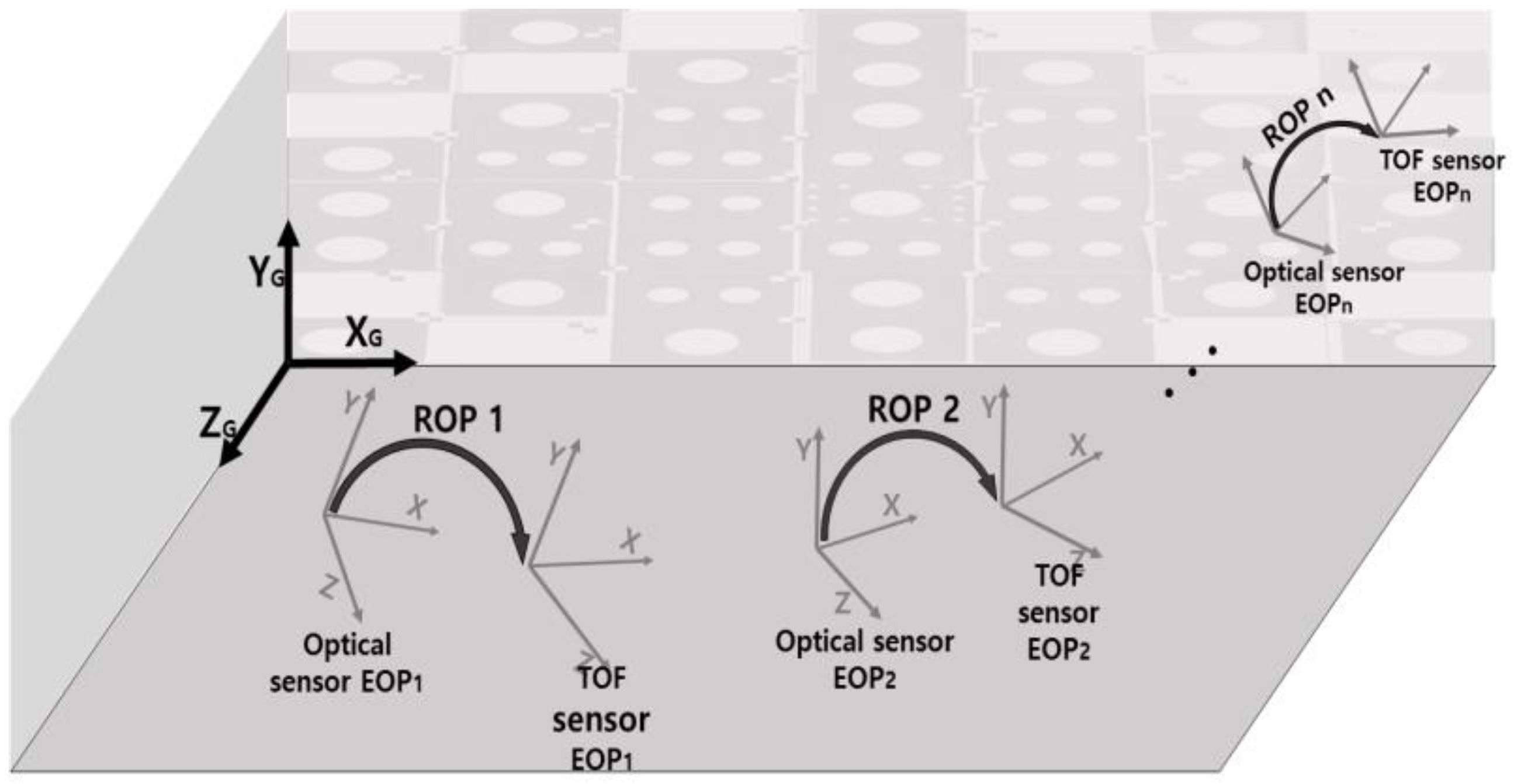
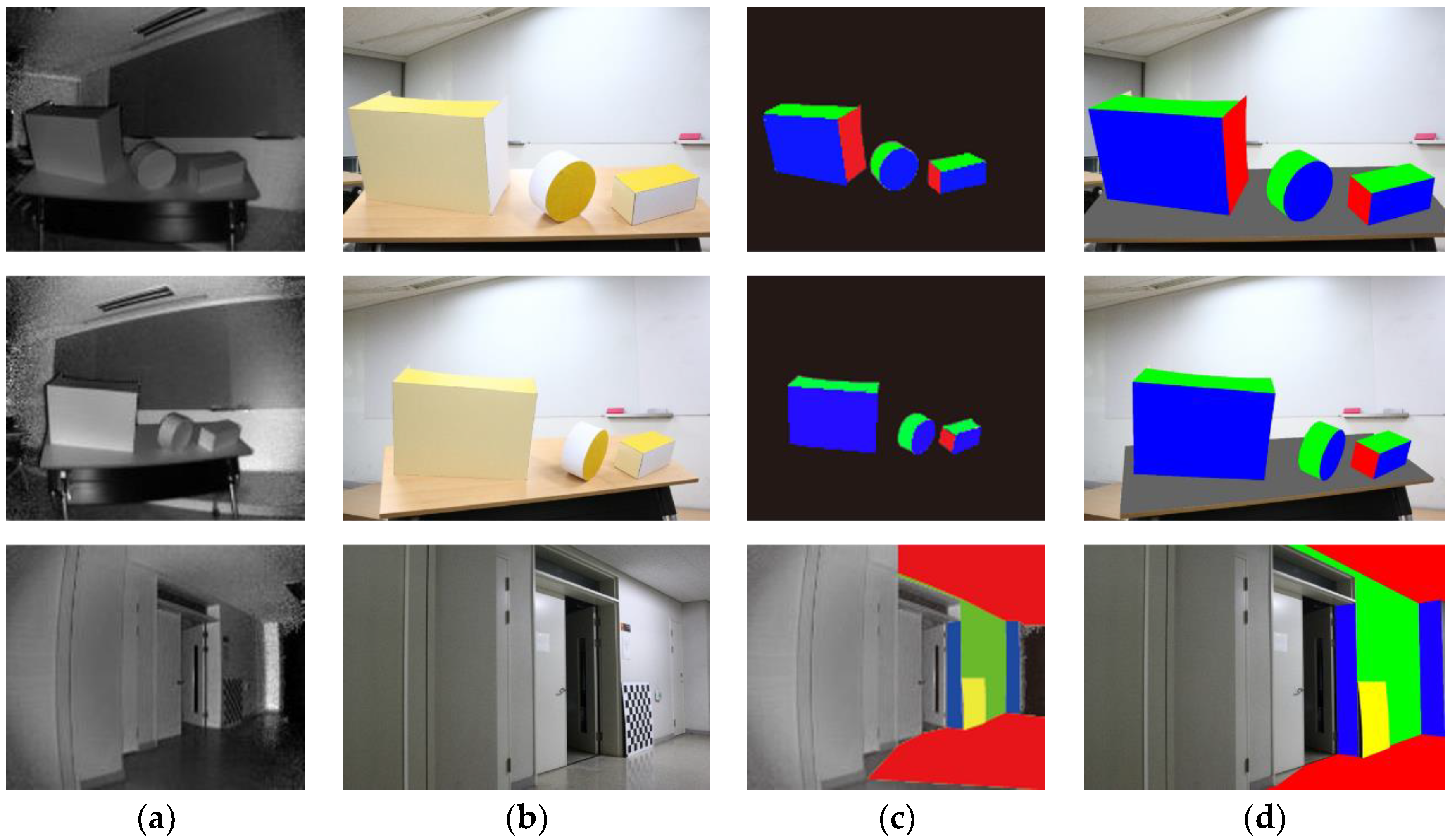
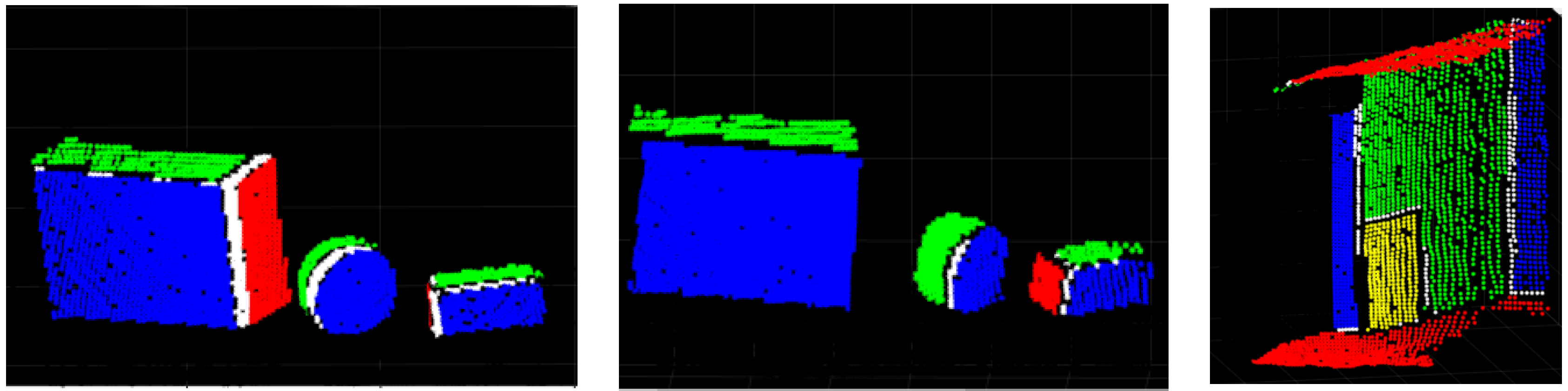
4.2. System Calibration
4.3. Optical and Range-Finder Data Fusion
4.4. Proposed Evaluation Strategies
5. Experimental Results and Discussion
5.1. Self-Calibration Results
5.2. System Calibration Results
6. Conclusions and Recommendations
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Chow, J.C.; Lichti, D.D.; Hol, J.D.; Bellusci, G.; Luinge, H. Imu and multiple RGB-D camera fusion for assisting indoor stop-and-go 3D terrestrial laser scanning. Robotics 2014, 3, 247–280. [Google Scholar] [CrossRef]
- Salinas, C.; Fernández, R.; Montes, H.; Armada, M. A New Approach for Combining Time-of-Flight and RGB Cameras Based on Depth-Dependent Planar Projective Transformations. Sensors 2015, 15, 24615–24643. [Google Scholar] [CrossRef] [PubMed]
- Shim, H.; Adelsberger, R.; Kim, J.D.; Rhee, S.-M.; Rhee, T.; Sim, J.-Y.; Gross, M.; Kim, C. Time-of-flight sensor and color camera calibration for multi-view acquisition. Visual Comput. 2012, 28, 1139–1151. [Google Scholar] [CrossRef]
- Nair, R.; Ruhl, K.; Lenzen, F.; Meister, S.; Schäfer, H.; Garbe, C.S.; Eisemann, M.; Magnor, M.; Kondermann, D. A survey on time-of-flight stereo fusion. In Time-of-Flight and Depth Imaging. Sensors, Algorithms, and Applications; Springer: Berlin/Heidelberg, Germany, 2013; pp. 105–127. [Google Scholar]
- Zhang, L.; Dong, H.; Saddik, A.E. From 3D sensing to printing: A survey. ACM Trans. Multimed. Comput. Commun. Appl. (TOMM) 2016, 12, 27. [Google Scholar] [CrossRef]
- Beyer, H.A. Geometric and Radiometric Analysis of a CCD-Camera Based Photogrammetric Close-Range System; ETH Zurich: Zurich, Germany, 1992. [Google Scholar]
- Brown, D.C. Decentering distortion of lenses. Photogramm. Eng. Remote Sens. 1966, 3, 444–462. [Google Scholar]
- Fraser, C.S. Digital camera self-calibration. ISPRS J. Photogramm. Remote sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]
- Remondino, F.; Fraser, C. Digital camera calibration methods: considerations and comparisons. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 266–272. [Google Scholar]
- Lichti, D.D.; Kim, C.; Jamtsho, S. An integrated bundle adjustment approach to range camera geometric self-calibration. ISPRS J. Photogramm. Remote Sens. 2010, 65, 360–368. [Google Scholar] [CrossRef]
- Lichti, D.D.; Kim, C. A comparison of three geometric self-calibration methods for range cameras. Remote Sens. 2011, 3, 1014–1028. [Google Scholar] [CrossRef]
- Lichti, D.D.; Qi, X. Range camera self-calibration with independent object space scale observations. J. Spat. Sci. 2012, 57, 247–257. [Google Scholar] [CrossRef]
- Jamtsho, S. Geometric Modelling of 3D Range Cameras and Their Application for Structural Deformation Measurement. Master’s Thesis, University of Calgary, Calgary, AB, Canada, 2010. [Google Scholar]
- Westfeld, P.; Mulsow, C.; Schulze, M. Photogrammetric calibration of range imaging sensors using intensity and range information simultaneously. Proc. Opt. 3-D Meas. Tech. IX 2009, 2, 1–10. [Google Scholar]
- Lindner, M.; Kolb, A. Lateral and depth calibration of PMD-distance sensors. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 14–16 December 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 524–533. [Google Scholar]
- Zhu, J.; Wang, L.; Yang, R.; Davis, J.E. Reliability fusion of time-of-flight depth and stereo geometry for high quality depth maps. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1400–1414. [Google Scholar] [PubMed]
- Mikhelson, I.V.; Lee, P.G.; Sahakian, A.V.; Wu, Y.; Katsaggelos, A.K. Automatic, fast, online calibration between depth and color cameras. J. Vis. Commun. Image Represent. 2014, 25, 218–226. [Google Scholar] [CrossRef]
- Van den Bergh, M.; Van Gool, L. Combining RGB and ToF cameras for real-time 3D hand gesture interaction. In Proceedings of the 2011 IEEE Workshop on Applications of Computer Vision (WACV), Kona, HI, USA, 5–7 January 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 66–72. [Google Scholar]
- Hansard, M.; Evangelidis, G.; Pelorson, Q.; Horaud, R. Cross-calibration of time-of-flight and colour cameras. Comput. Vis. Image Underst. 2015, 134, 105–115. [Google Scholar] [CrossRef]
- Herrera, D.; Kannala, J.; Heikkilä, J. Joint depth and color camera calibration with distortion correction. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2058–2064. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhou, Y.; Yu, H.; Zhang, Z. Improved 3D depth image estimation algorithm for visual camera. In Proceedings of the 2nd International Congress on Image and Signal Processing, CISP′09, Tianjin, China, 17–19 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–4. [Google Scholar]
- Jung, J.; Lee, J.-Y.; Jeong, Y.; Kweon, I.S. Time-of-flight sensor calibration for a color and depth camera pair. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1501–1513. [Google Scholar] [CrossRef] [PubMed]
- Vidas, S.; Moghadam, P.; Bosse, M. 3D thermal mapping of building interiors using an RGB-D and thermal camera. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2311–2318. [Google Scholar]
- Lindner, M.; Kolb, A.; Hartmann, K. Data-fusion of PMD-based distance-information and high-resolution RGB-images. In Proceedings of the International Symposium on Signals, Circuits and Systems, ISSCS 2007, Iasi, Romania, 13–14 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–4. [Google Scholar]
- Borrmann, D.; Afzal, H.; Elseberg, J.; Nüchter, A. Mutual calibration for 3D thermal mapping. IFAC Proc. Vol. 2012, 45, 605–610. [Google Scholar] [CrossRef]
- Munaro, M.; Basso, F.; Menegatti, E. OpenPTrack: Open source multi-camera calibration and people tracking for RGB-D camera networks. Robot. Autonomous Syst. 2016, 75, 525–538. [Google Scholar] [CrossRef]
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; John Wiley and Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Owens, J.L.; Osteen, P.R.; Daniilidis, K. MSG-cal: Multi-sensor graph-based calibration. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3660–3667. [Google Scholar]
- Shin, Y.-D.; Park, J.-H.; Bae, J.-H.; Baeg, M.-H. A study on reliability enhancement for laser and camera calibration. Int. J. Control Autom. Syst. 2012, 10, 109–116. [Google Scholar] [CrossRef]
- Wang, W.; Yamakawa, K.; Hiroi, K.; Kaji, K.; Kawaguchi, N. A Mobile System for 3D Indoor Mapping Using LiDAR and Panoramic Camera. Spec. Interest Group Tech. Rep. IPSJ 2015, 1, 1–7. [Google Scholar]


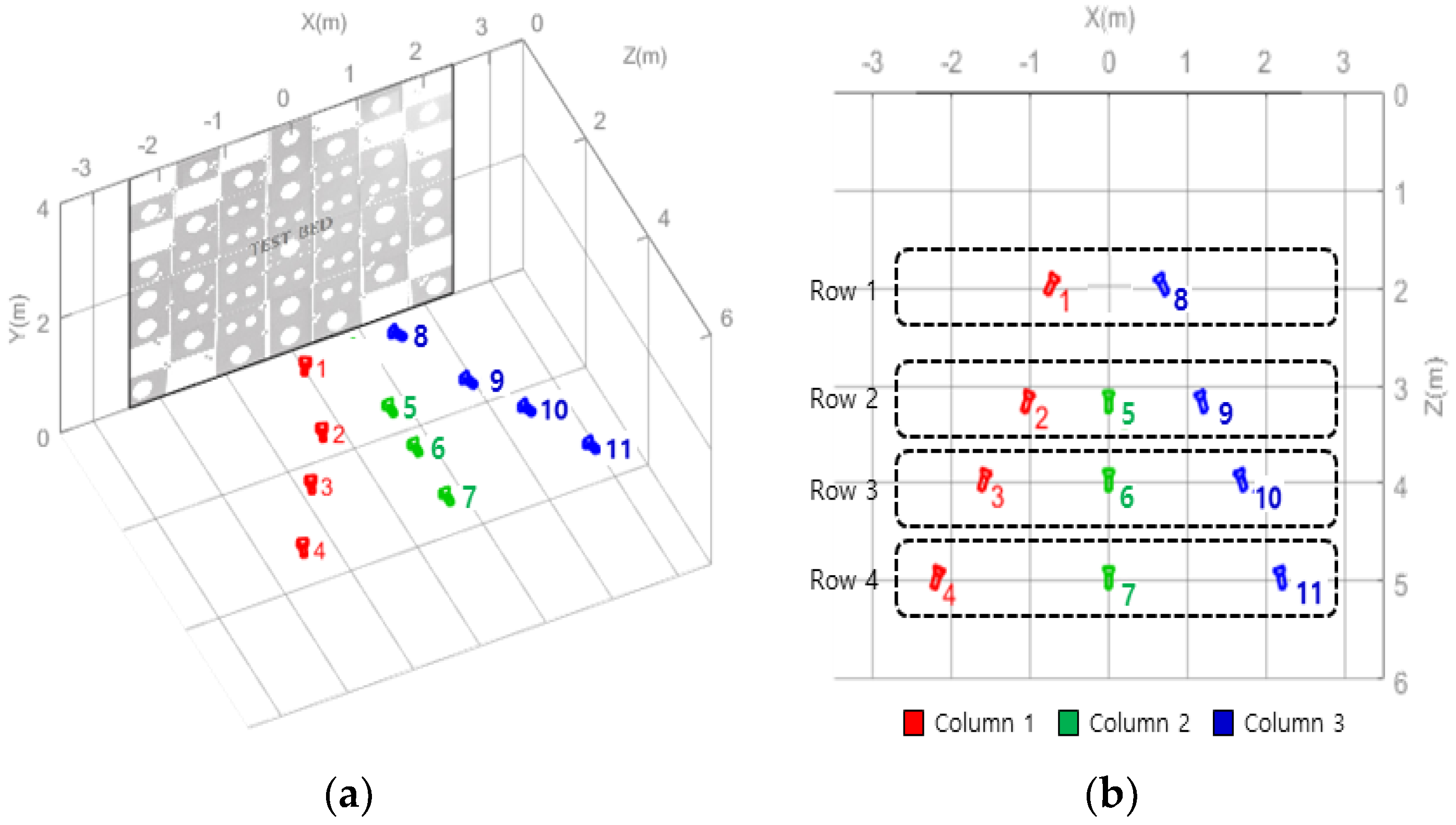

| Sensor Type | Model Name | Image Size (Pixels) | Pixel Size (mm) | Focal Length (Nominal/mm) | Field of View |
|---|---|---|---|---|---|
| Optical camera | Canon 6D | 5472 × 3648 | 0.00655 | 35 | 63° |
| Range finder | SR4000 (Mesa imaging) | 176 × 144 | 0.04 | 5.8 | 69° (h) × 56° (v) |
| Number of Datasets | Location of Selected Datasets | |
|---|---|---|
| One Column | Two or More Columns | |
| 2 | 8 cases (e.g., dataset 5, and 6) | 4 cases (e.g., dataset 2, and 9) |
| 3 | 5 cases (e.g., dataset 5, 6, and 7) | 3 cases (e.g., dataset 2, 5, and 9) |
| 4 | 2 cases (e.g., dataset 1, 2, 3, and 4) | 7 cases (e.g., dataset 2, 3, 9, and 10) |
| 5 | - | 6 cases (e.g., dataset 2, 3, 5, 9, and 10) |
| 6 | - | 5 cases (e.g., dataset 2, 3, 5, 6, 9, and 10) |
| 8 | - | 3 cases (e.g., dataset 2, 3, 4, 5, 6, 9, 10, and 11) |
| 9 | - | 2 cases (e.g., dataset 2, 3, 4, 5, 6, 7, 9, 10, and 11) |
| 11 | - | 1 case (all dataset) |
| total | 15 cases | 31 cases |
| Sensors | Estimated IOPs | ||||||
|---|---|---|---|---|---|---|---|
| Optical camera | xp (mm) | yp (mm) | focal length (mm) | ||||
| −0.02850 | 0.01401 | 34.190 | |||||
| K1 | K2 | K3 | P1 | P2 | A1 | A2 | |
| −6.3×10−5 | 2.94×10−8 | 3.82×10−11 | −2.1×10−5 | 1.5×10−5 | −1.4×10−5 | 5.47×10−5 | |
| Range finder | xp (mm) | yp (mm) | focal length (mm) | ||||
| 0.04607 | −0.00513 | 5.7647 | |||||
| K1 | K2 | K3 | P1 | P2 | A1 | A2 | |
| 0.001093 | −0.00255 | 0.000145 | 0.000841 | −0.0003 | −0.00236 | 0.001952 | |
| d0 | d1 | e1 | e2 | ||||
| −48.9753 | 0.022105 | 2.827089 | 3.428659 | ||||
| Sensors | RMS of Residuals | Standard Deviations of the Estimated IOPs | ||||||
|---|---|---|---|---|---|---|---|---|
| Optical camera | 0.0025 mm (0.38 pixels) | xp (mm) | yp (mm) | focal length (mm) | ||||
| 0.0007 | 0.0006 | 0.0021 | ||||||
| K1 | K2 | K3 | P1 | P2 | A1 | A2 | ||
| 2.61×10−7 | 1.23×10−9 | 1.73×10−12 | 3.40×10−7 | 2.69×10−7 | 6.10×10−6 | 7.07×10−6 | ||
| Range finder | 0.0305 mm (0.76 pixels) | xp (mm) | yp (mm) | focal length (mm) | ||||
| 0.0044 | 0.0039 | 0.0644 | ||||||
| K1 | K2 | K3 | P1 | P2 | A1 | A2 | ||
| 6.56×10−5 | 1.20×10−5 | 6.72×10−7 | 4.70e×10−6 | 5.15×10−6 | 3.21×10−5 | 3.19×10−5 | ||
| 6.84 mm (range) | d0 | d1 | e1 | e2 | ||||
| 2.37 | 0.0021 | 0.1823 | 0.1659 | |||||
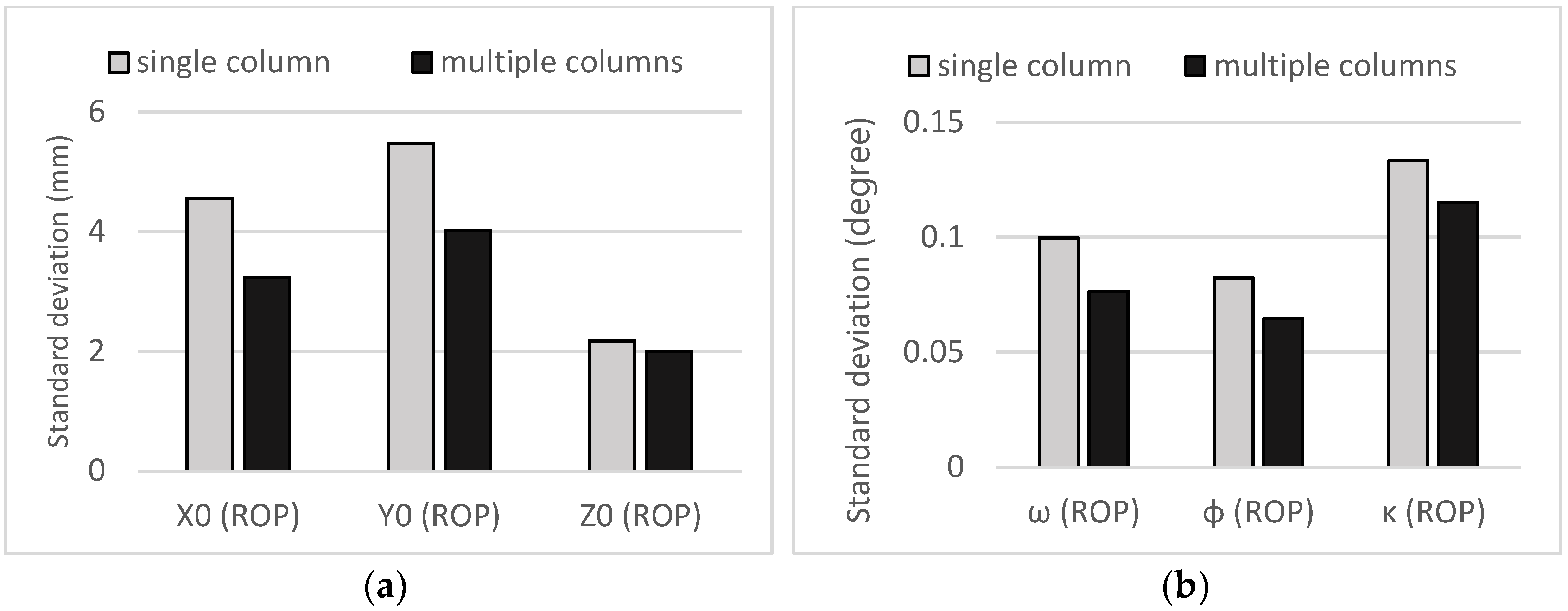
| Matching Rate (%) | Standard Deviations of ROPs | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| X0 (mm) | Y0 (mm) | Z0 (mm) | ω (Degree) | ϕ (Degree) | κ (Degree) | ||||
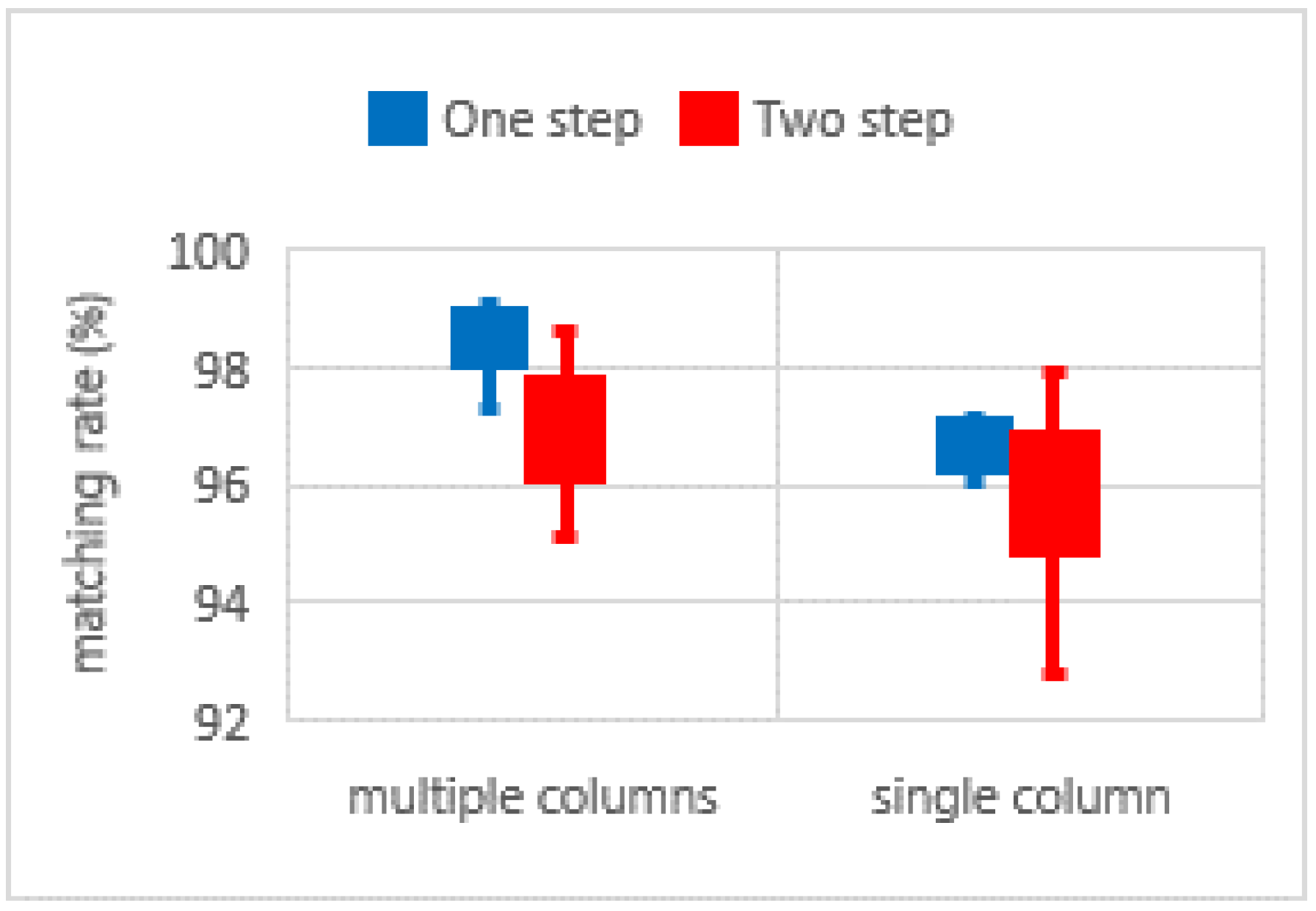
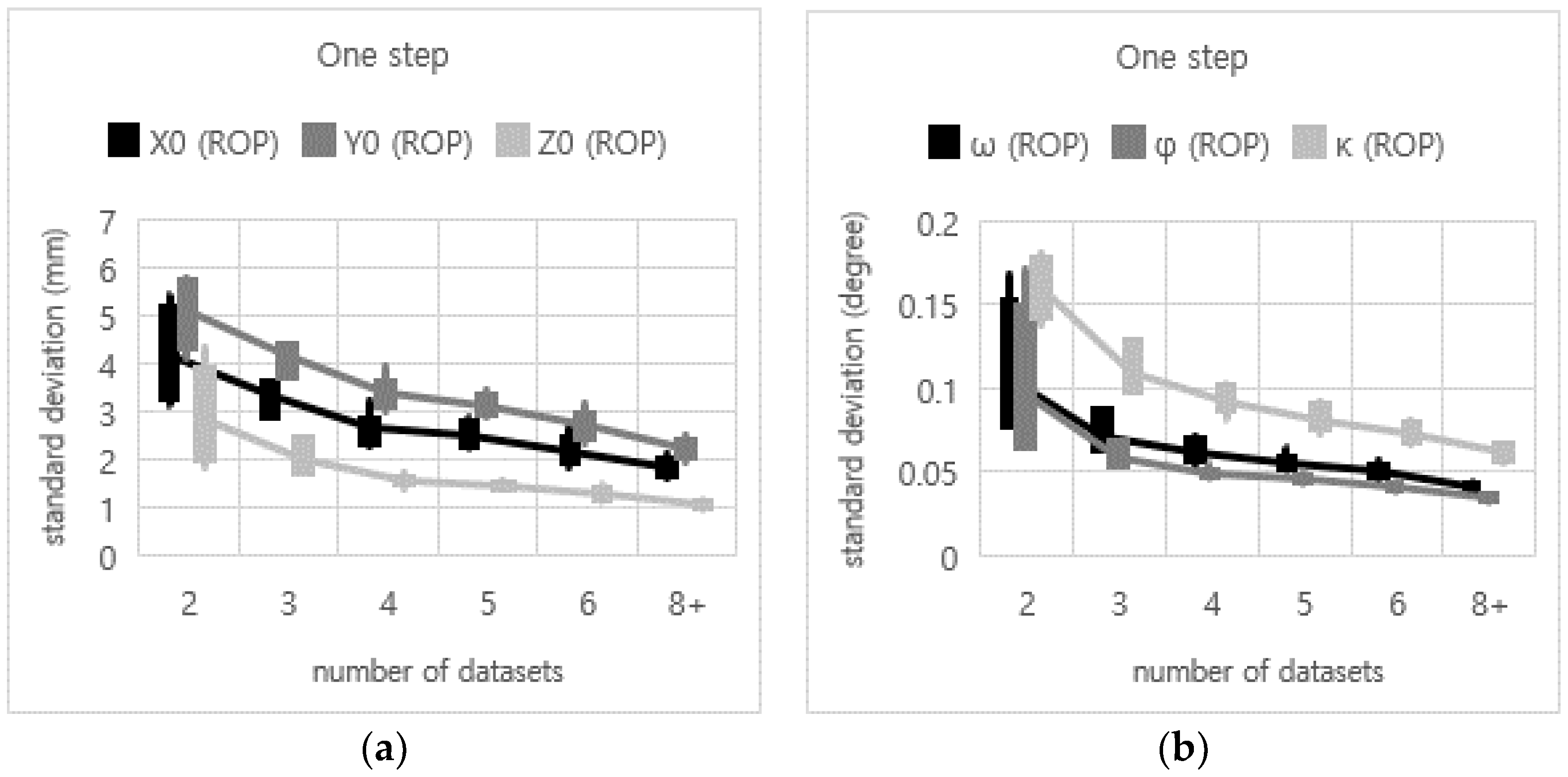
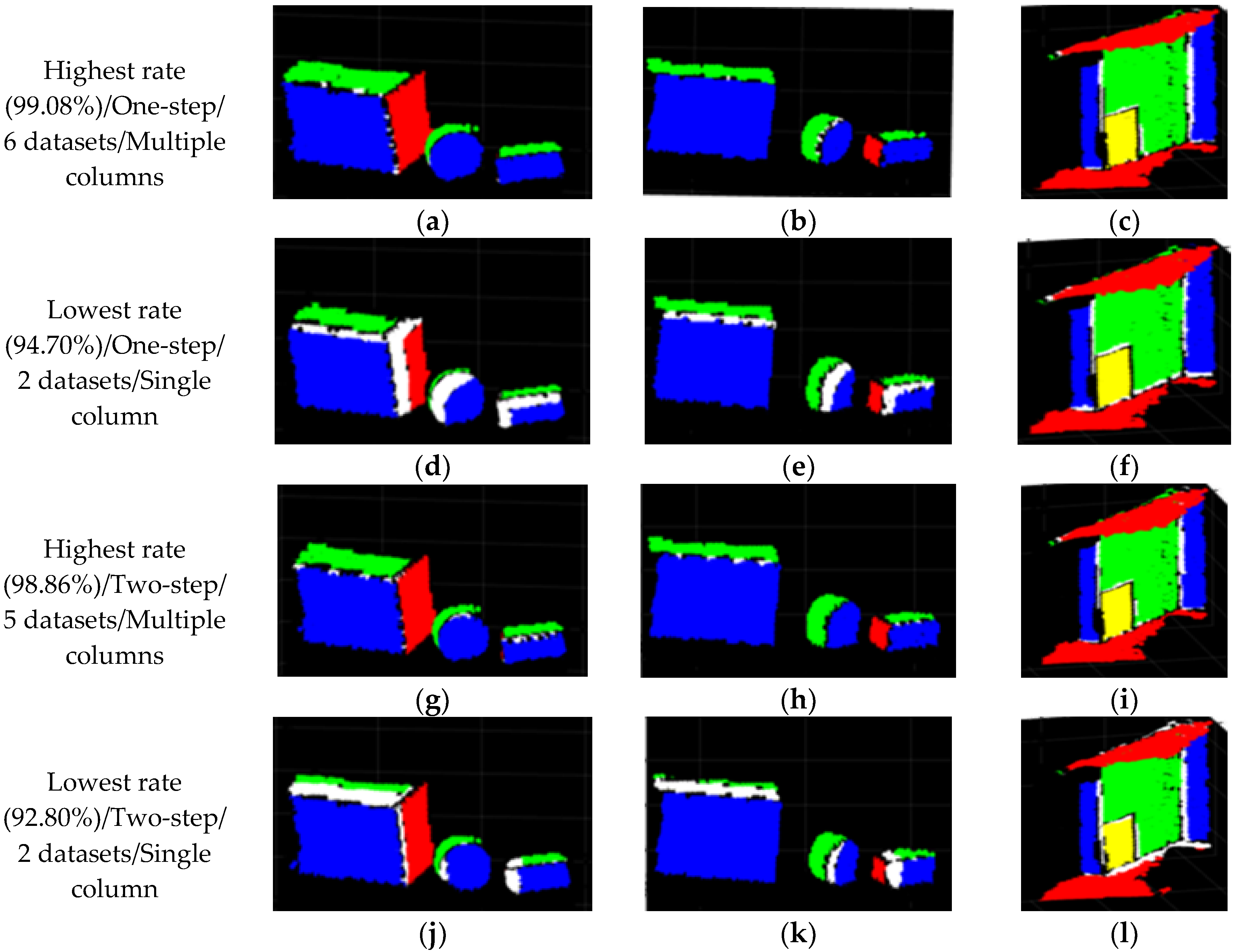
| One Step | Mean | 97.85 | 3.27 | 4.00 | 1.78 | 0.07 | 0.06 | 0.10 | From all 46 cases |
| Highest rate | 99.08 | 2.67 | 3.18 | 1.49 | 0.04 | 0.04 | 0.08 | 6 datasets used (from multiple columns) | |
| Lowest rate | 94.7 | 7.22 | 8.03 | 2.86 | 0.14 | 0.13 | 0.15 | 2 datasets used (from single column) | |
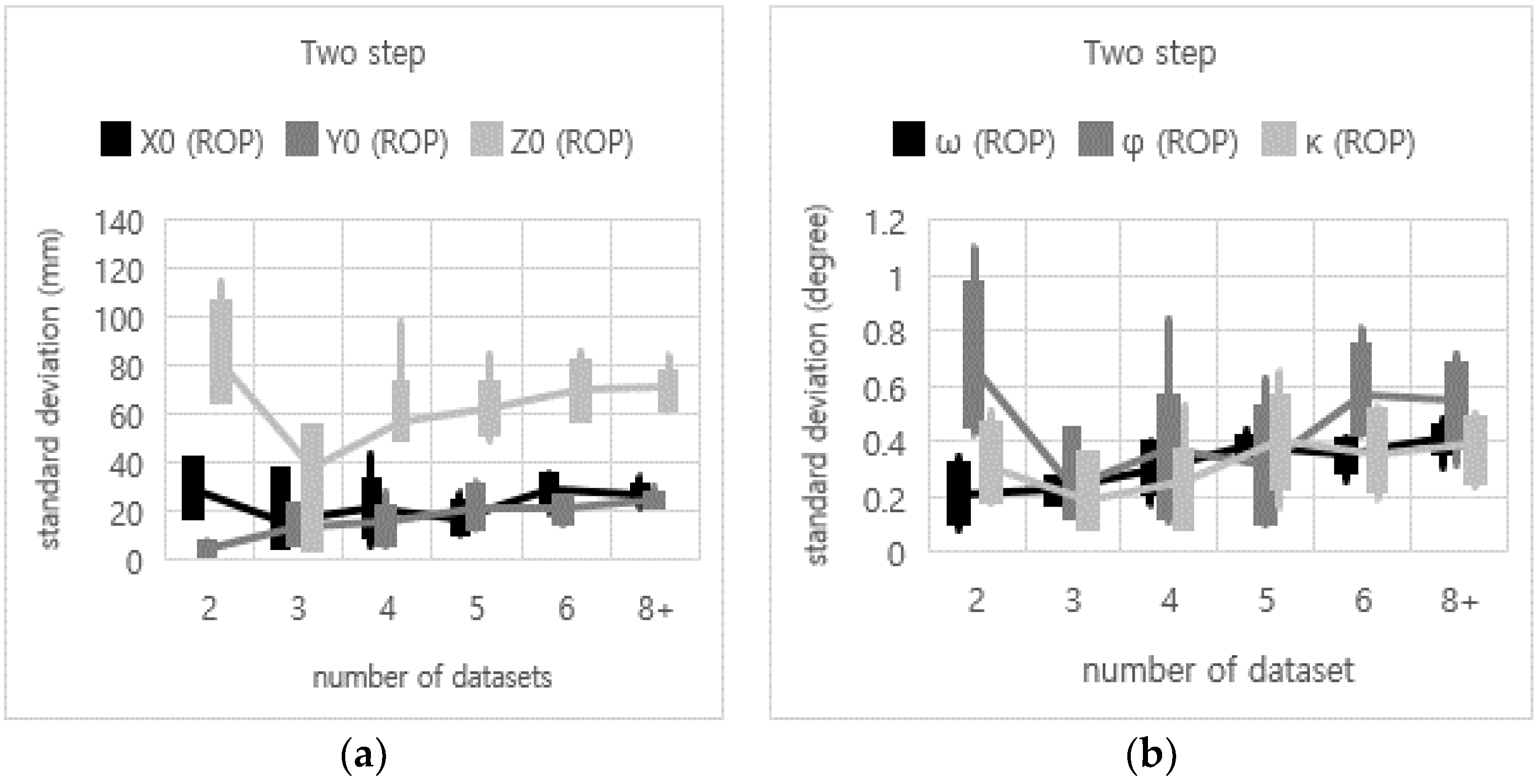
| Two step | Mean | 97 | 22.1 | 19.93 | 49.33 | 0.31 | 0.40 | 0.26 | From all 46 cases |
| Highest rate | 98.86 | 11.55 | 20.28 | 53.47 | 0.40 | 0.3 | 0.16 | 5 datasets used (from multiple columns) | |
| Lowest rate | 92.8 | 20.00 | 51.21 | 0.76 | 0.53 | 0.23 | 0.09 | 2 datasets used (from single column) | |
| Dataset Location | Matching Rate (%) | ||
|---|---|---|---|
| Mean | Standard Deviation | ||
| One-step | single | 96.72 | 0.83 |
| multiple | 98.36 | 0.58 | |
| Two-step | single | 95.69 | 1.35 |
| multiple | 97.00 | 1.02 | |
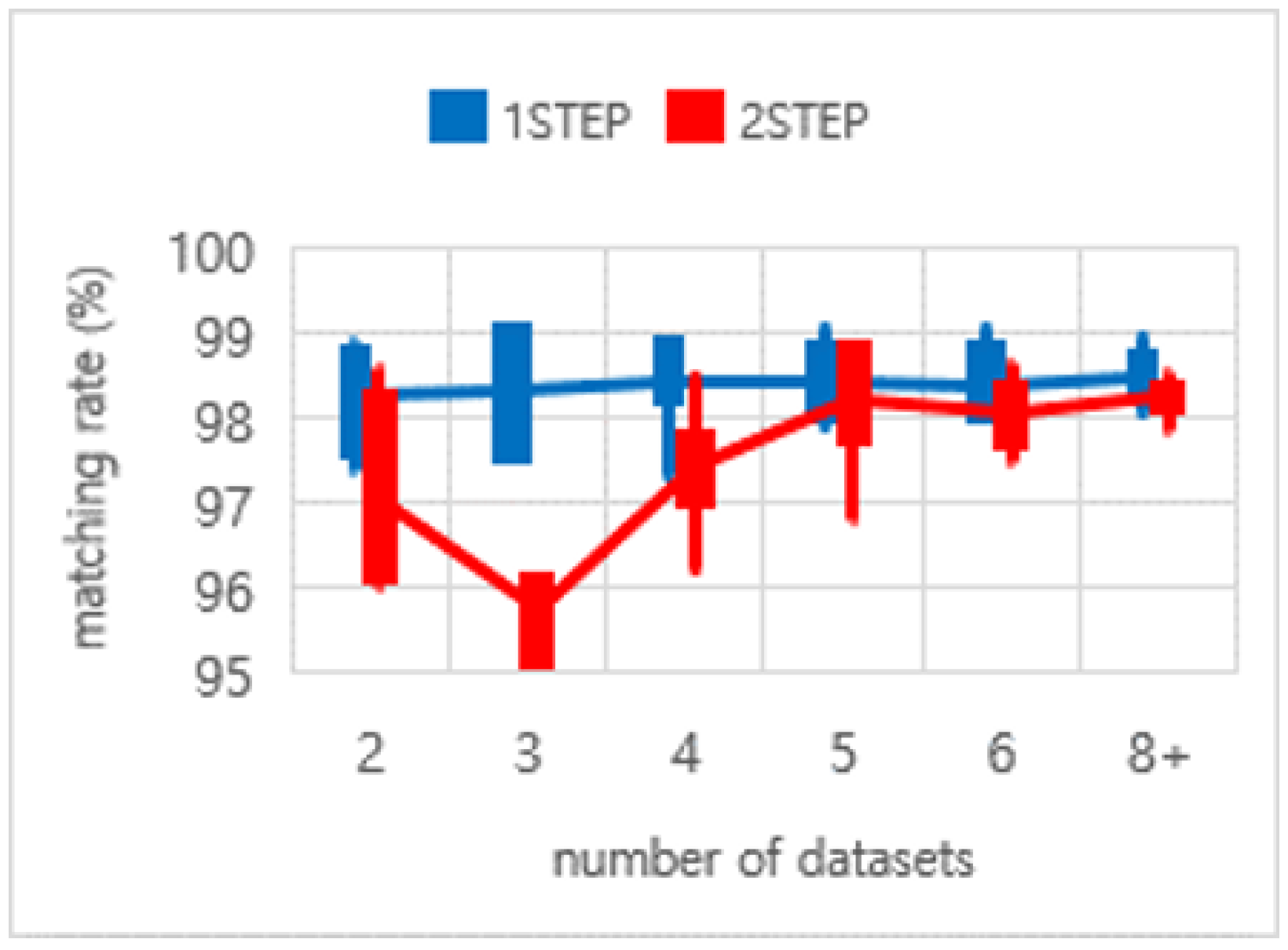
| Number of Datasets (Only from Multiple Columns) | 2 | 3 | 4 | 5 | 6 | 8+ (8~11) | |
|---|---|---|---|---|---|---|---|
| Mean of matching rates (%) | one-step | 98.25 | 98.31 | 98.45 | 98.41 | 98.38 | 98.48 |
| two-step | 97.07 | 95.76 | 97.44 | 98.2 | 98.04 | 98.25 | |
| Standard deviation of matching rates (%) | one-step | 0.64 | 0.76 | 0.55 | 0.45 | 0.48 | 0.30 |
| two-step | 1.14 | 0.58 | 0.72 | 0.77 | 0.43 | 0.23 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, K.H.; Kim, C.; Kim, Y. Comprehensive Analysis of System Calibration between Optical Camera and Range Finder. ISPRS Int. J. Geo-Inf. 2018, 7, 188. https://doi.org/10.3390/ijgi7050188
Choi KH, Kim C, Kim Y. Comprehensive Analysis of System Calibration between Optical Camera and Range Finder. ISPRS International Journal of Geo-Information. 2018; 7(5):188. https://doi.org/10.3390/ijgi7050188
Chicago/Turabian StyleChoi, Kang Hyeok, Changjae Kim, and Yongil Kim. 2018. "Comprehensive Analysis of System Calibration between Optical Camera and Range Finder" ISPRS International Journal of Geo-Information 7, no. 5: 188. https://doi.org/10.3390/ijgi7050188
APA StyleChoi, K. H., Kim, C., & Kim, Y. (2018). Comprehensive Analysis of System Calibration between Optical Camera and Range Finder. ISPRS International Journal of Geo-Information, 7(5), 188. https://doi.org/10.3390/ijgi7050188






