Multilevel Cloud Detection for High-Resolution Remote Sensing Imagery Using Multiple Convolutional Neural Networks
Abstract
:1. Introduction
- (1)
- In order to reduce the loss of image features during the process of pooling, we propose self-adaptive pooling (SAP).
- (2)
- A novel MCNNs architecture is designed for multilevel cloud detection.
- (3)
- Adaptive simple linear iterative clustering (A-SLIC) algorithm is proposed through affinity propagation clustering and expanding the searching space. The A-SLIC algorithm was applied to obtain segmentation of the image into good-quality superpixels.
2. Datasets
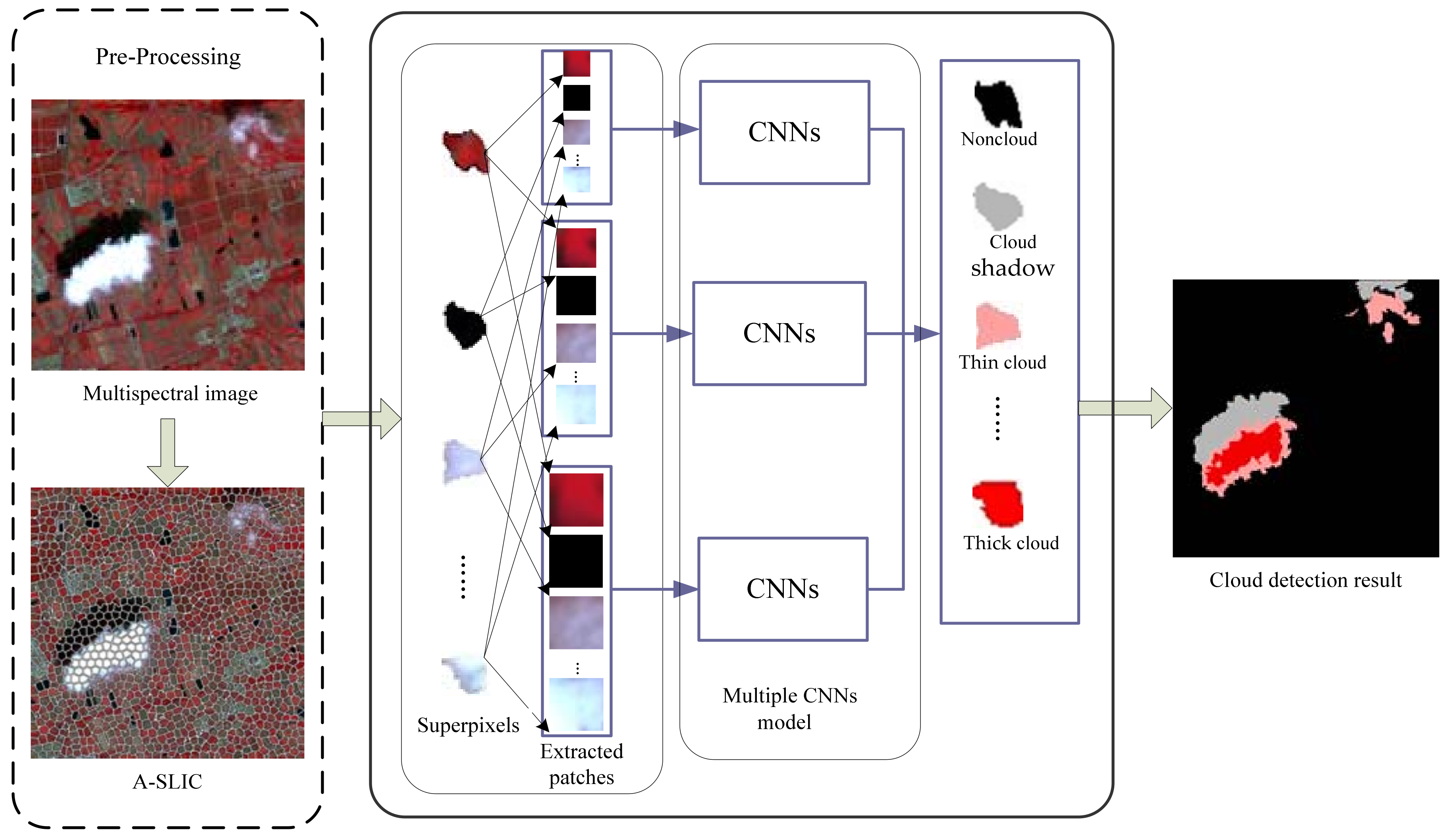
3. Methods
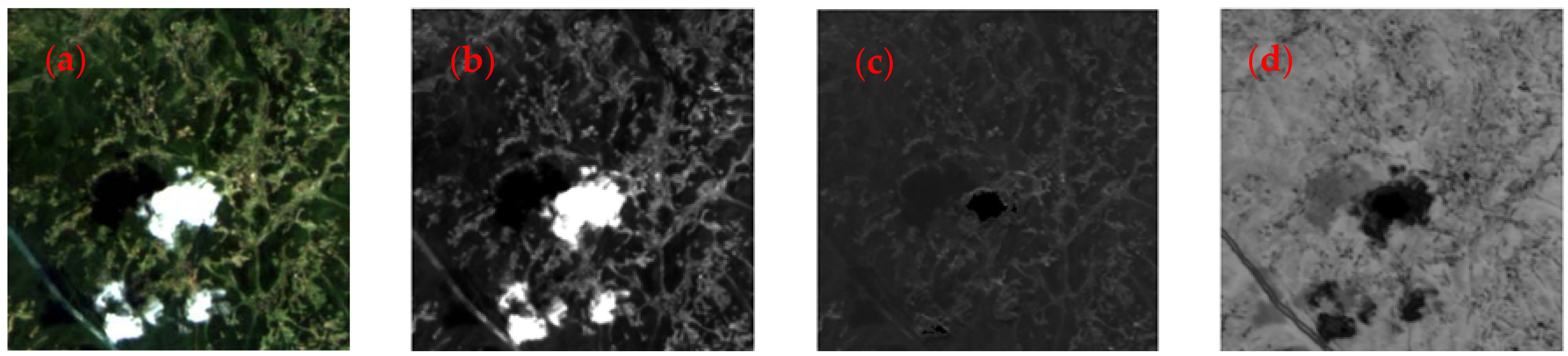
3.1. Preprocessing
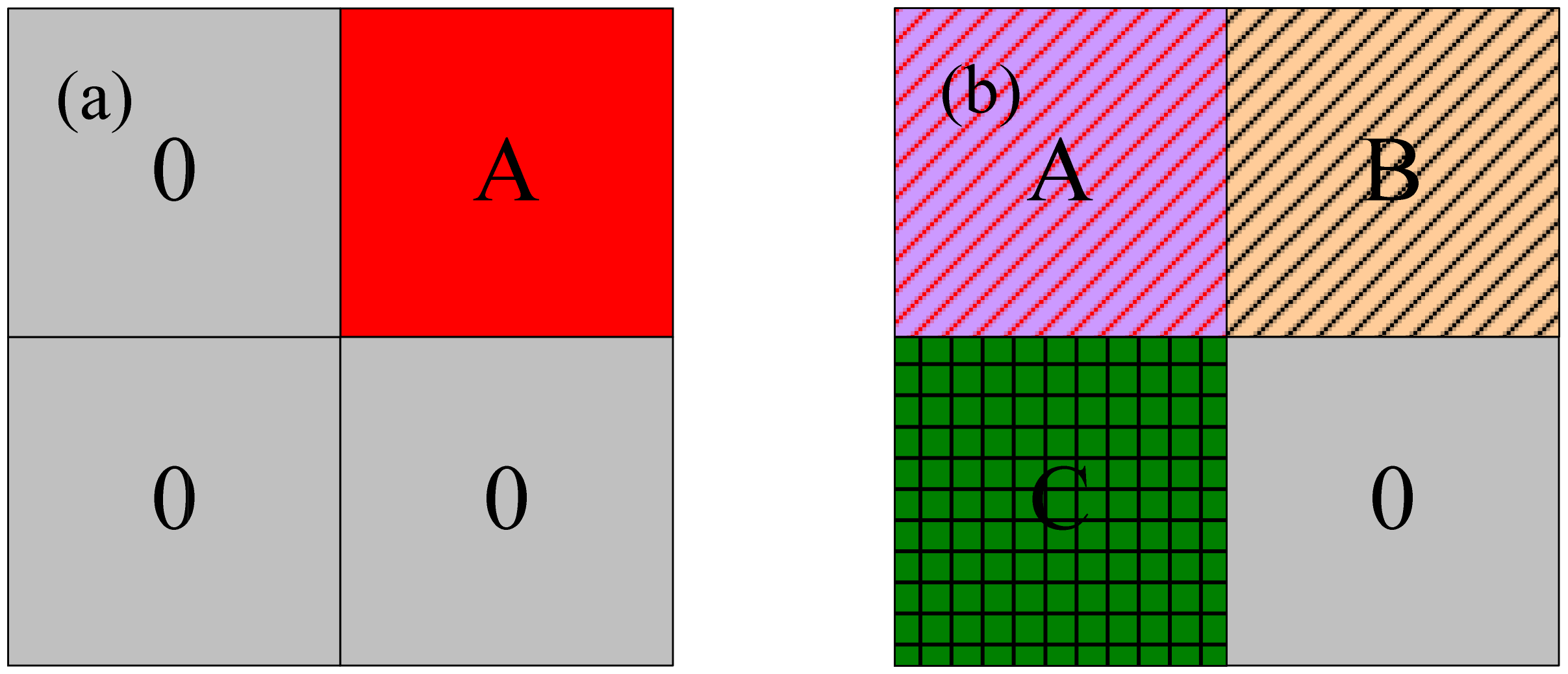
- Step 1. For an image containing pixels, the size of the predivided region in this algorithm is , and the number of regions is . Each predivided area is labeled as . and is defined as zero, and is defined as one.
- Step 2. HIS transformation is performed on the image of the marked area. In the th region, according to Equation (5), the similarity between two pixels is calculated in turn.
- Step 3. According to Equations (9) and (11), the sum of and is calculated and the iteration begins.
- Step 4. If and no longer change or reach the maximum number of iterations, the iteration is terminated. The point where the sum of and is maximum is regarded as the cluster center .
- Step 5. Repeat steps 3 to 4 until the entire image is traversed, and adaptively determine the number of superpixels (). Finally, complete the superpixel segmentation.
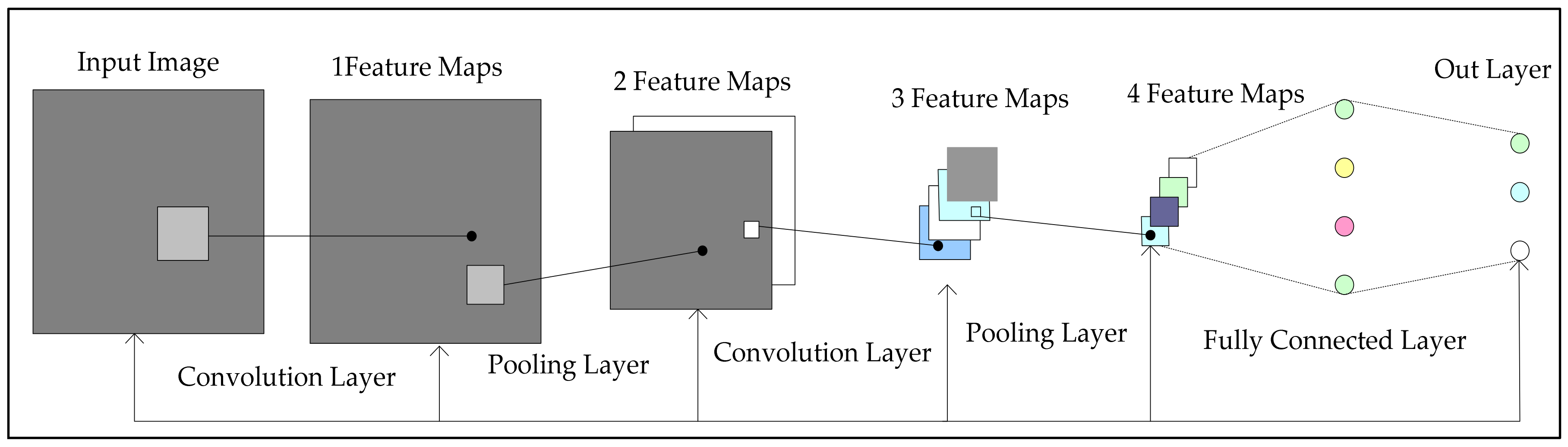
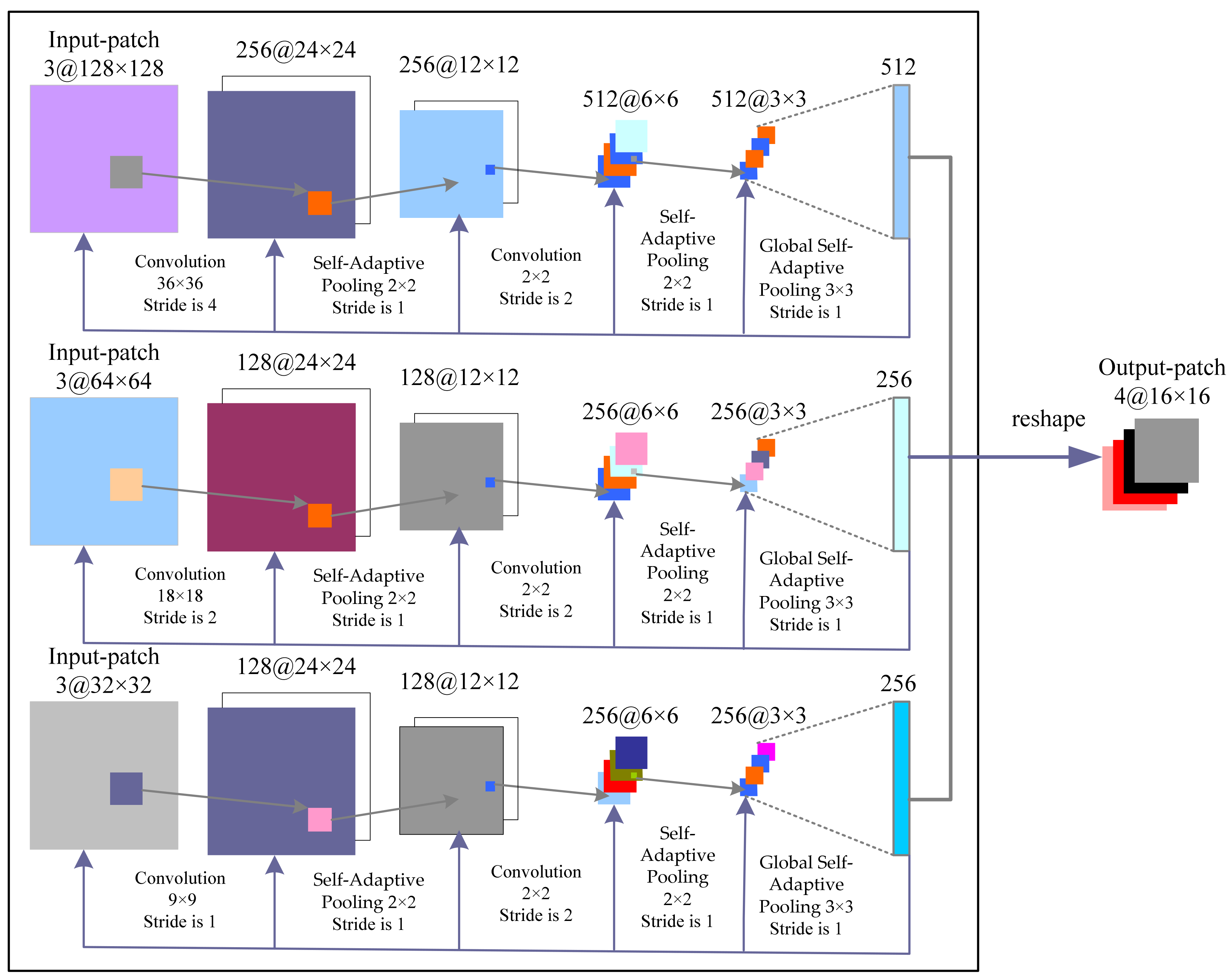
3.2. Proposed Convolutional Neural Network Architecture
3.3. Accuracy Assessment Method
- : true positives, i.e., the number of correct extractions;
- : false negatives, i.e., the number of cloud pixels not detected;
- : false positives, i.e., the number of incorrect extractions;
- : true negatives, i.e., the number of non-cloud pixels that were correctly rejected.
4. Experiments and Discussion
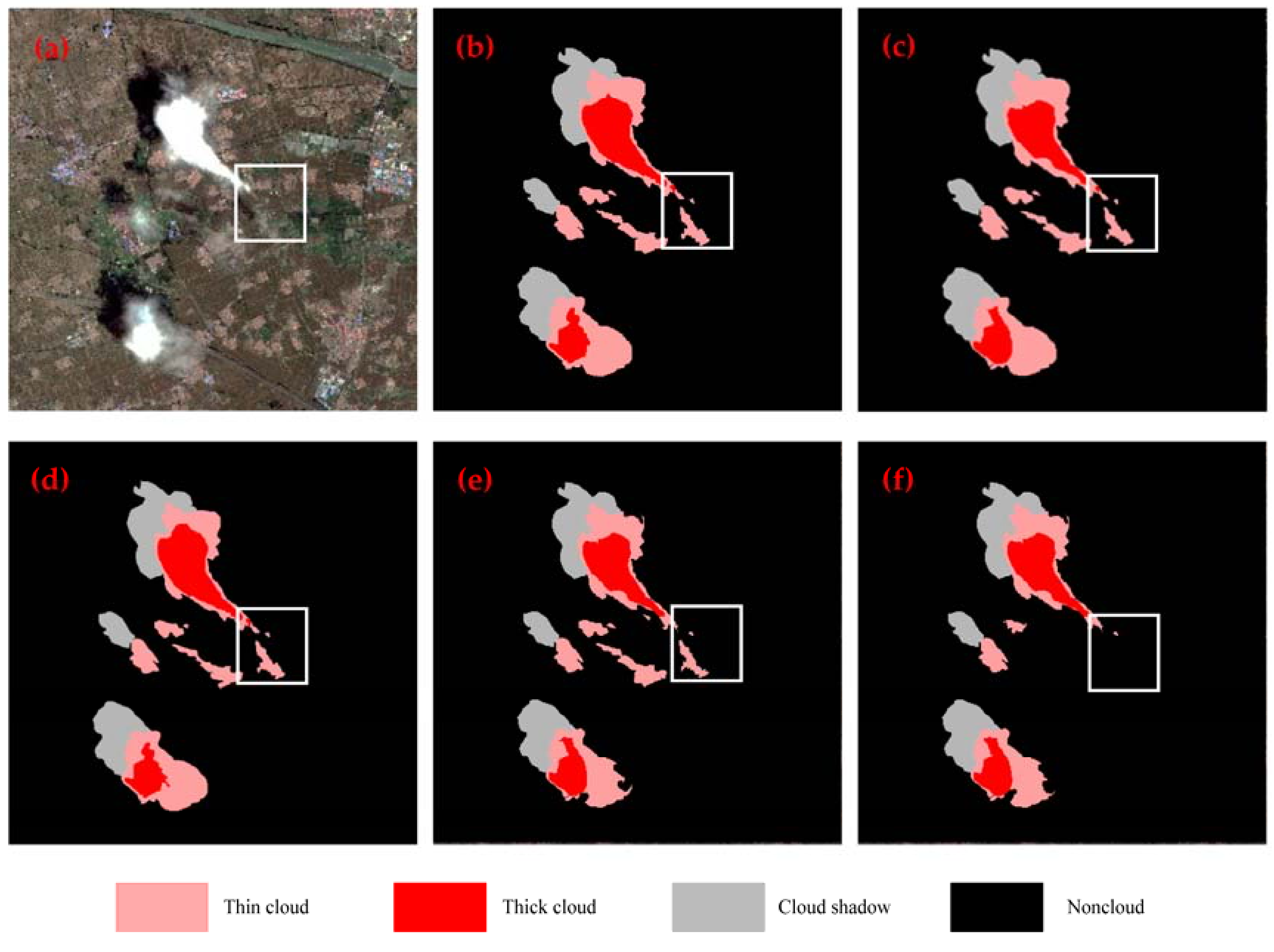
4.1. Impact of the Superpixel Segmentation on the Performance of Multilevel Cloud Detection
4.2. Comparison Between Different CNN Architectures
4.3. Comparison with Other Methods
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zortea, M.; De Martino, M.; Serpico, S. A SVM Ensemble Approach for Spectral-Contextual Classification of Optical High Spatial Resolution Imagery. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1489–1492. [Google Scholar]
- Zhang, Y.; Rossow, W.B.; Lacis, A.A. Calculation of radiative fluxes from the surface to top of atmosphere based on ISCCP and other global data sets. J. Geophys. Res. 2004, 109, 1121–1125. [Google Scholar] [CrossRef]
- Xu, X.; Guo, Y.; Wang, Z. Cloud image detection based on Markov Random Field. Chin. J. Electron. 2012, 29, 262–270. [Google Scholar] [CrossRef]
- Qing, Z.; Chunxia, X. Cloud detection of rgb color aerial photographs by progressive refinement scheme. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7264–7275. [Google Scholar] [CrossRef]
- Lee, K.-Y.; Lin, C.-H. Cloud detection of optical satellite images using support vector machine. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 289–293. [Google Scholar]
- Marais, I.V.; Du Preez, J.A.; Steyn, W.H. An optimal image transform for threshold-based cloud detection using heteroscedastic discriminant analysis. Int. J. Remote Sens. 2011, 32, 1713–1729. [Google Scholar] [CrossRef]
- Li, Q.; Lu, W.; Yang, J.; Wang, J.Z. Thin cloud detection of all-sky images using markov random fields. IEEE Geosci Remote Sens. Lett. 2012, 9, 417–421. [Google Scholar] [CrossRef]
- Shao, Z.; Hou, J.; Jiang, M.; Zhou, X. Cloud detection in landsat imagery for antarctic region using multispectral thresholds. SPIE Asia-Pac. Remote Sens. Int. Soc. Opt. Photonics 2014. [Google Scholar] [CrossRef]
- Wu, W.; Luo, J.; Hu, X.; Yang, H.; Yang, Y. A Thin-Cloud Mask Method for Remote Sensing Images Based on Sparse Dark Pixel Region Detection. Remote Sens. 2018, 10, 617. [Google Scholar] [CrossRef]
- Bai, T.; Li, D.R.; Sun, K.M.; Chen, Y.P.; Li, W.Z. Cloud detection for high-resolution satellite imagery using machine learning and multi-feature fusion. Remote Sens. 2016, 8, 715. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.; Guan, H. Application support vector machines in cloud detection using EOS/MODIS. In Proceedings of the Remote Sensing Applications for Aviation Weather Hazard Detection and Decision Support, San Diego, CA, USA, 25 August 2008. [Google Scholar]
- Base ski, E.; Cenaras, C. Texture color based cloud detection. In Proceedings of the 2015 7th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 16–19 June 2015. [Google Scholar]
- Alireza, T.; Fabio, D.F.; Cristina, C.; Stefania, V. Neural networks and support vector machine algorithms for automatic cloud classification of whole-sky ground-based images. IEEE Trans. Geosci. Remote Sens. 2015, 12, 666–670. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; MacEachren, A.M.; Mitra, P.; Onorati, T. Visually-Enabled Active Deep Learning for (Geo) Text and Image Classification: A Review. ISPRS Int. J. Geo-Inf. 2018, 7, 65. [Google Scholar] [CrossRef]
- Sherrah, J. Fully Convolutional Networks for Dense Semantic Labelling of High-Resolution Aerial Imagery. arXiv, 2016; arXiv:1606.02585. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Csillik, O. Fast Segmentation and Classification of Very High Resolution Remote Sensing Data Using SLIC Superpixels. Remote Sens. 2017, 9, 243. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. An SVM ensemble approach combining spectral, structural, and semantic features for the classification of high-resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
- Guangyun, Z.; Xiuping, J.; Jiankun, H. Superpixel-based graphical model for remote sensing image mapping. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5861–5871. [Google Scholar]
- Li, H.; Shi, Y.; Zhang, B.; Wang, Y. Superpixel-Based Feature for Aerial Image Scene Recognition. Sensors 2018, 18, 156. [Google Scholar] [CrossRef] [PubMed]
- Hagos, Y.B.; Minh, V.H.; Khawaldeh, S.; Pervaiz, U.; Aleef, T.A. Fast PET Scan Tumor Segmentation Using Superpixels, Principal Component Analysis and K-Means Clustering. Methods Protoc. 2018, 1, 7. [Google Scholar] [CrossRef]
- Zollhöfer, M.; Izadi, S.; Rehmann, C.; Zach, C.; Fisher, M.; Wu, C.; Fitzgibbon, A.; Loop, C.; Theobalt, C.; Stamminger, M. Real-time non-rigid reconstruction using an RGB-D camera. ACM Trans. Graph. 2014, 33, 156. [Google Scholar] [CrossRef]
- Fouad, S.; Randell, D.; Galton, A.; Mehanna, H.; Landini, G. Epithelium and Stroma Identification in Histopathological Images Using Unsupervised and Semi-Supervised Superpixel-Based Segmentation. J. Imaging 2017, 3, 61. [Google Scholar] [CrossRef]
- Yang, J.; Yang, G. Modified Convolutional Neural Network Based on Dropout and the Stochastic Gradient Descent Optimizer. Algorithms 2018, 11, 28. [Google Scholar] [CrossRef]
- Chen, F.; Ren, R.; Van de Voorde, T.; Xu, W.; Zhou, G.; Zhou, Y. Fast Automatic Airport Detection in Remote Sensing Images Using Convolutional Neural Networks. Remote Sens. 2018, 10, 443. [Google Scholar] [CrossRef]
- Pouliot, D.; Latifovic, R.; Pasher, J.; Duffe, J. Landsat Super-Resolution Enhancement Using Convolution Neural Networks and Sentinel-2 for Training. Remote Sens. 2018, 10, 394. [Google Scholar] [CrossRef]
- Scarpa, G.; Gargiulo, M.; Mazza, A.; Gaetano, R. A CNN-Based Fusion Method for Feature Extraction from Sentinel Data. Remote Sens. 2018, 10, 236. [Google Scholar] [CrossRef]
- Cai, Z.; Fan, Q.; Feris, R.; Vasconcelos, N. A Unified Multi-scale Deep Convolutional Neural Network for Fast Object Detection. In Proceedings of the IEEE European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 354–370. [Google Scholar]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, R.; Yang, X.; Wang, J.; Latif, A. Extraction of Urban Water Bodies from High-Resolution Remote-Sensing Imagery Using Deep Learning. Water 2018, 10, 585. [Google Scholar] [CrossRef]
- Weatherill, G.; Burton, P.W. Delineation of shallow seismic source zones using K-means cluster analysis, with application to the Aegean region. Geophys. J. Int. 2009, 176, 565–588. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Stein, A.; Aryal, J.; Gort, G. Use of the Bradley-Terry model to quantify association in remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 852–856. [Google Scholar] [CrossRef]




| Image Name | Image Size (Pixels) | Spatial Resolution (m) | Cloud Types | Surface Types | True Color Multispectral Image |
|---|---|---|---|---|---|
| ZY-3 | 2900 × 3000 | 5.8 | medium thin cloud; medium thick cloud; cloud shadow | water; mountain; bare rock |  |
| ZY-3 | 3000 × 3000 | 5.8 | small thin cloud; medium thick cloud; cloud shadow | building; river; city road |  |
| GF-1 | 2100 × 2399 | 8 | non-cloud | lake; mountain; bare rock; ice; snow |  |
| GF-2 | 3000 × 3000 | 4 | medium thick cloud; small thin cloud; cloud shadow | vegetation; building; road; lake |  |
| Parameter | A-SLIC + MCNNs | SLIC + MCNNs | Pixel + MCNNs |
|---|---|---|---|
| OA (%) | 98.27 | 94.34 | 92.14 |
| Kappa (%) | 92.34 | 88.31 | 87.31 |
| EOA (%) | 97.36 | 93.13 | 90.38 |
| EOE (%) | 0.94 | 2.61 | 4.24 |
| ECE (%) | 1.70 | 4.26 | 5.38 |
| Superpixel segmentation (s) | 6.81 | 5.63 | 0 |
| MCNNs prediction (s) | 2.37 | 5.91 | 481 |
| Total time (s) | 9.18 | 11.54 | 481 |
| Parameter | Proposed Approach | SAP + MCNNs | MP + MCNNs | AP + MCNNs |
|---|---|---|---|---|
| OA (%) | 98.64 | 96.17 | 89.07 | 84.13 |
| Kappa (%) | 95.27 | 88.34 | 89.34 | 87.81 |
| EOA (%) | 97.37 | 94.01 | 87.34 | 82.41 |
| EOE (%) | 1.02 | 2.28 | 4.81 | 8.17 |
| ECE (%) | 1.61 | 3.71 | 7.85 | 9.42 |
| Parameter | Proposed Approach | SVM | Neural Network | K-Means |
|---|---|---|---|---|
| OA (%) | 98.53 | 81.34 | 78.07 | 65.27 |
| Kappa (%) | 94.37 | 78.34 | 70.34 | 60.74 |
| EOA (%) | 96.17 | 79.51 | 76.39 | 62.37 |
| EOE (%) | 1.14 | 8.12 | 10.39 | 16.18 |
| ECE (%) | 2.69 | 12.37 | 13.22 | 21.45 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Fan, R.; Bilal, M.; Yang, X.; Wang, J.; Li, W. Multilevel Cloud Detection for High-Resolution Remote Sensing Imagery Using Multiple Convolutional Neural Networks. ISPRS Int. J. Geo-Inf. 2018, 7, 181. https://doi.org/10.3390/ijgi7050181
Chen Y, Fan R, Bilal M, Yang X, Wang J, Li W. Multilevel Cloud Detection for High-Resolution Remote Sensing Imagery Using Multiple Convolutional Neural Networks. ISPRS International Journal of Geo-Information. 2018; 7(5):181. https://doi.org/10.3390/ijgi7050181
Chicago/Turabian StyleChen, Yang, Rongshuang Fan, Muhammad Bilal, Xiucheng Yang, Jingxue Wang, and Wei Li. 2018. "Multilevel Cloud Detection for High-Resolution Remote Sensing Imagery Using Multiple Convolutional Neural Networks" ISPRS International Journal of Geo-Information 7, no. 5: 181. https://doi.org/10.3390/ijgi7050181
APA StyleChen, Y., Fan, R., Bilal, M., Yang, X., Wang, J., & Li, W. (2018). Multilevel Cloud Detection for High-Resolution Remote Sensing Imagery Using Multiple Convolutional Neural Networks. ISPRS International Journal of Geo-Information, 7(5), 181. https://doi.org/10.3390/ijgi7050181







