A Low-Cost Collaborative Location Scheme with GNSS and RFID for the Internet of Things

1. Introduction

The Internet of Things (IoT) equipped with pervasive computing and ubiquitous intelligence is emerging as a novel computing paradigm [1]. The novel technologies characterizing the IoT have advanced real smart environments, enabling livable sensing, real-time monitoring, and powerful intelligence. Relating to intelligence concerns, one key feature is to employ the systems as autonomously as possible [2]. The current trend is to configure these services as location-aware services, called location-based services (LBS), i.e., applications driven by location information, for example, public infrastructure inspection by location in smart cities initiatives. This paper aims to contribute to the localization and tracking capacities of the IoT.

The effort to automatically collect location information from public infrastructure has been receiving increased attention in the academic environment and industry, especially in the smart cities era. The exact location of public infrastructure is essential for active monitoring and a rapid information update of the infrastructure, which is helpful for government administrators and urban planning authorities. Existing public infrastructure inspection and inventory methods in smart cities include image recognition [3], field survey [4,5] and light detection and ranging (LiDAR) information extraction [6], which has been widely used in traffic-sign detection [3], street-light pole location [6], tree extraction [7], and so on. For these methods, complex urban environments limit the practice owing to the heavy occupation of the target object and huge workload. Sensing-based radio frequency identification (RFID) technology has the potential ability to overcome this constraint upon location. However, IoT-based location in the large urban area is subject to issues of enormous investment and difficulties in deployment in a complex environment. With some specific application areas, for example, in an emergency scenario, rapid and easy implementation is crucial to rescue services. Therefore, it is essential to deploy devices and collect the location information of objects rapidly and economically.

In general, most of the existing RFID-based location methods used on a large-scale and that are emerging have the following drawbacks. First, the deployment cost is expensive, because either every target object has to be mounted in one Global Navigation Satellite System (GNSS) receiver in a GNSS locating system or a number of reference tags in the RFID-based scheme. When applying such systems in public infrastructure asset management, the investment increases linearly with the number of objects. Second, prior knowledge of the target sites is required. For example, a pre-measured fingerprint database for signal matching in a fingerprint solution and the pre-measurement of reference tags’ locations deployed at fix places are required. Finally, deployment has been limited mainly by the environment. For example, in an emergency scenario, timely rescue requires a rapid and easy deployment of a locating system. The position of reference tags needs to be carefully chosen for achieving high-level accuracy. Unfortunately, in some situations, such as museums, hardware infrastructure installation is not usually permitted.

Therefore, in this paper, taking the aspects described above into consideration, we proposed a new low-cost collaborating location system, supporting the rapid and easy deployment of location tags. In our scheme, one mobile RFID reader mounted on one GNSS receiver simulates reference tags with a known location in the traditional scheme, which dramatically decreases the cost. A weighting algorithm is proposed to achieve high-level accuracy. This low-cost localization scheme has potential applications in infrastructure inspection and inventory on a large scale in smart cities.

The rest of our paper is organized as follows. Section 2 presents related works. In Section 3, an overview of our proposed locating system is demonstrated. Optimization for signal and location estimation algorithms is also introduced in this section. In Section 4, we design an experiment to validate the effectiveness and accuracy of the proposed system. Section 5 discusses the results and proposed solution. We conclude our work and provide paths for future work in Section 6.

2. Related Works

Location information is fundamental to IoT applications such as infrastructure asset management [8] and infrastructure health [9,10]. LBS has become increasingly important with the development of IoT. In the face of large and variable business requirements, the design of an ecosystem and easy deployment location method for LBS is challenging [11]. Compared with various localization technologies, such as Bluetooth, computer vision and ultrasonic and infrared, the features of the RFID-based method are non-line of sight (NLOS), low-cost and automatic tracking.

2.1. Radio Frequency Identification (RFID)-Based Location

In general, existing RFID-based location schema can be classified into three categories: range-based, fingerprinting, and proximity [8,12]. In the range-based RFID location scheme, many distance measurement technologies are proposed for calculating location. Those classical technologies include the angle of arrival (AOA) [13], the time of arrival (TOA) [14], the time difference of arrival (TDOA) [15], the received signal strength indicator (RSSI) [16], and the received signal phase (RSP) [17]. Although it can usually achieve sufficient location accuracy, there are a couple of drawbacks. First, the time must be precisely aligned between the RFID tags and the readers, which is challenging depending on the methods and the hardware. More sophisticated hardware results in greater cost. Second, for RSSI measurement, it suffers from multipath fading and shadowing such as with indoor environments. For high-level accuracy, sophisticated hardware is used, which means some extra cost. In the fingerprinting scheme, the location is calculated by comparing the similarity between the real-time RSSI fingerprinting and the pre-measured prior RSSI fingerprinting. The probability of the match determines their location. However, the fingerprinting should be collected as a prior, making it more complicated and impractical in some emergency applications [18]. In the proximity scheme, the tag location is determined by the position of the RFID reader that detects the target tag. The reader can only detect the tags’ proximity but not their exact locations. Therefore, denser RFID readers achieve a higher location accuracy. To reduce the cost, reference tags deployed at a fixed position in an area of interest are used to replace RFID reader. For both RFID readers and reference tags, denser RFID readers are necessary for higher location accuracy, which creates higher cost and more work to position site the reference tag. Unfortunately, some scenarios such as a museum do not allow the installation of reference tags. Therefore, this scheme also faces environmental and hardware challenges in deployment [18,19].

In smart cities initiatives, the exact coordinates of the infrastructure are necessary for inspection and management. However, proximity within a radio range information is not sufficient for LBS-based services. Another method—a fingerprinting method with pre-measured variables—may be impractical owing to the dynamic urban environment. Therefore, devising a scheme with rapid deployment and immune to the environment is a crucial challenge, especially, in large-scale and emergency scenarios.

2.2. Low-Cost Location Scheme

To propel the location application on a large scale, research on the low-cost RFID-based scheme has been one of the hot topics. Although GNSS and the ultra-wide band (UWB) can obtain a higher accuracy for indoor and outdoor scenarios, the primary disadvantage is the high cost [20,21]. The most famous low-cost solution is reference tags deployed at fixed positions to replacement the expensive RFID reader [22,23]. Target tag location uses three or more signals between the target tag and the readers or reference tags, while dense reference tags and a good connectivity RFID network is necessary [8,24,25], which requires more investment for a larger number of RFID readers or tags. Two methods have been developed to reduce the investment cost. The first is the tag matrix schema with a number of RFID readers, in which the column and row indexes of tags denotes the tags’ locations [26]. However, proximity coordinates are not suitable for infrastructure management. The second approach is to design virtual references replacing the physical reference tags. For example, with a specified number of virtual reference tags between two real adjacent reference tags every 30 cm, an interpolated RSSI reading sequence was generated [8]. Depending on the communication among adjacent tags and virtually dense deployment, higher location accuracy is achieved. However, the position of the neighboring physical reference tags and the number of virtual reference tags need to be carefully designed [27].

Because the deployment of readers and reference tags and the location accuracy are fixed, the conventional RFID-based location is widely used in small areas or closed spaces such as museums [2], and digital manufacturing workshops [28]. For application in a large area, an easily deployable and low-cost scheme is needed.

2.3. Deployment Method and Pattern

In smart cities, all kinds of sensor devices will promote the intelligent level of a city; however, this poses a significant challenge to deployment [29], especially the deployment position and pattern. This challenge is the same as the RFID location scheme.

The current range-based RFID localization system is mostly based on the vast deployment of reference tags [30,31]. Reference tags and matrix deployment are the mainstream deployment pattern. In the reference tags model, the position of reference tags needs to be carefully designed [27]; their coordinates need to be pre-measured. Virtual reference tags, as the variant method, need a dynamically and robustly coordinate generation algorithm for the virtual tags [8]. In the matrix deployment pattern [26,32], reference tags or readers are not necessary, but the two-dimensional matrix tags’ or readers’ deployment are introduced to determine the relative position of the targets. While it is a satisfactory solution for RFID localization with acceptable accuracy, it is not very appropriate nor always feasible on a large scale in a smart city context because of the large sensor deployment.

For a large-scale application and emergency scenario, the aforementioned deployment methods and patterns are not practical to deploy [30]. Despite the large investment for many tags, some areas do not usually allow the installation of hardware infrastructure, for example, in museums and emergency situations. Another drawback is the pre-measurement of referenced tags location. In an emergent situation, the time is rarely for rescue.

3. Collaborative Scheme with Global Navigation Satellite System (GNSS) and RFID Location

In this section, we propose a collaborative location scheme using GNSS and RFID. It is a low-cost and easily deployable system in which only one RFID reader and one GNSS device are used without any reference tags. This system can achieve sufficient location accuracy for urban public infrastructure asset management in the era of smart cities.

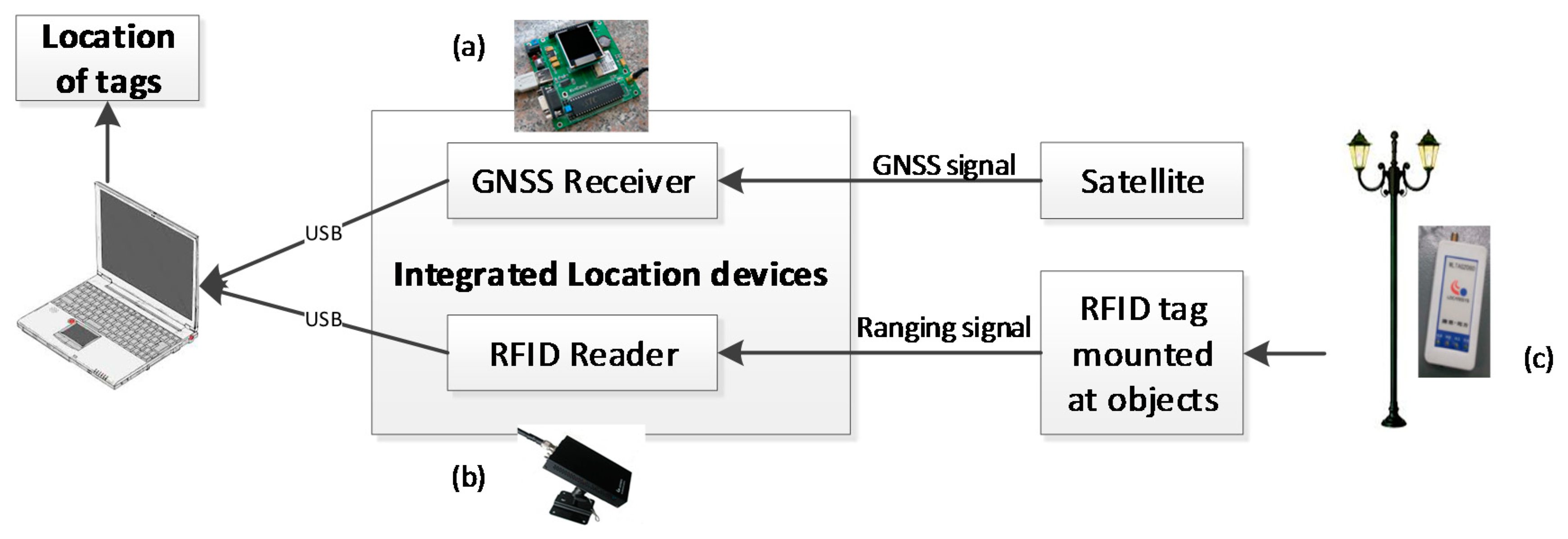
3.1. System Overview

This scheme employs one mobile RFID reader and one GNSS receiver to determine the RFID tag location. The target object (such as the light pole shown in Figure 1) is equipped with one RFID tag to obtain the position. The hardware is shown in Figure 1. Figure 1a is the GNSS receiver that measures the position of the RFID reader. Figure 1b denotes the range-based RFID reader. Figure 1c is the RFID tag.

One of the requirements in public infrastructure asset inspection and management is to obtain the exact coordinates of objects, and then its location is projected on a street view or map for inspection. In our system, we achieve such a goal through the following steps.

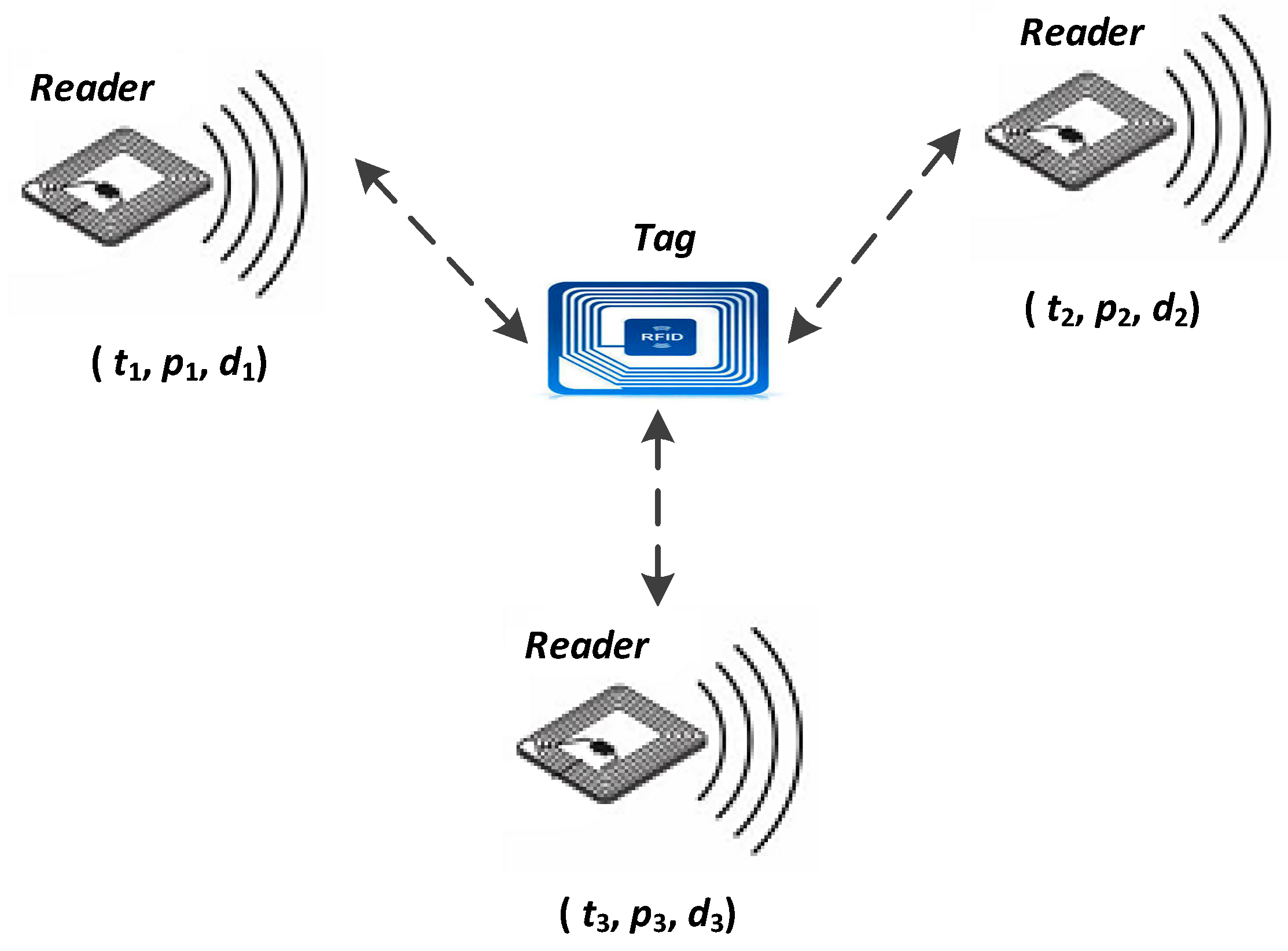
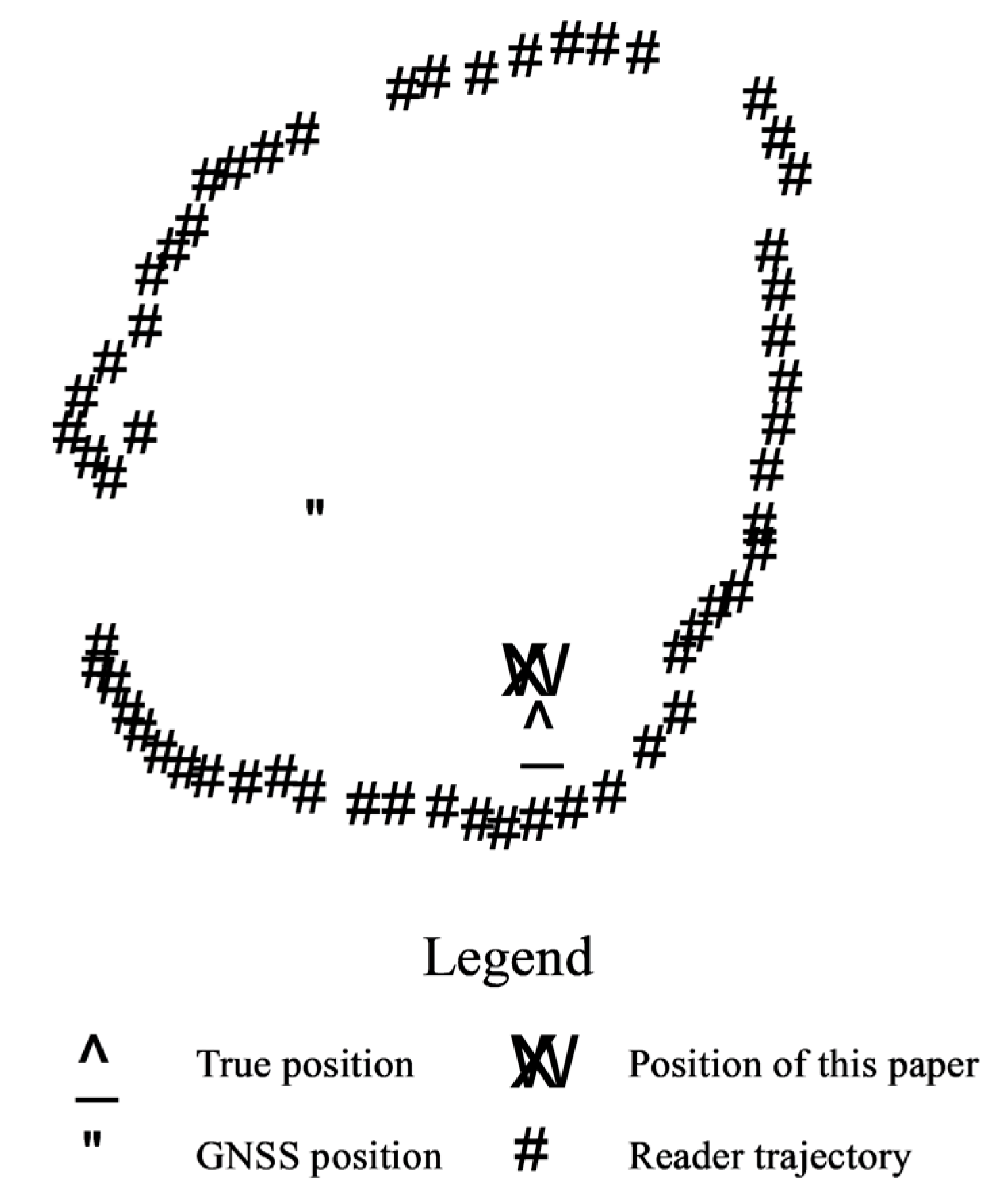
• The RFID reader measures the distance (d_i) between the reader and the RFID tag attached to the target object when the RFID reader is moving, where i denotes the i-th location in RFID reader trajectory.
• The RFID reader position (p_i) is measured by the GNSS receiver, which is expressed as (x_i, y_i) for the coordinate values.
• When the RFID reader is moving, two tuples (p_i, d_i) are ready. When three or more tuples are prepared, the exact location of the target tag can be estimated according to the method shown in the following section.

Figure 2 illustrates the snapshot of the RFID tag location process. At time t₁, the RFID reader gets the distance d₁ and its position p₁, then the tuple is (t₁, p₁, d₁). When the reader is moving, the other tuples are obtained, such as (t₂, p₂, d₂) and (t₃, p₃, d₃). Finally, the coordinates of the tag are calculated based on these tuples.

There are two phases to locate the target object: the reader location and the tag position computation. In our scheme, the reader location is achieved by the GNSS receiver mounted on the reader. Although the GNSS receiver is of low accuracy and the GNSS signal is weak in high building-density areas, the GNSS error is a systematic error, which can be computed with many methods or mitigated by some augmented methods such as ground enhancement signal networks or satellite enhancement networks [33,34]. Therefore, in our scheme, GNSS devices are adopted as the reader locations, which largely reduces the total cost. Tag position computation is introduced in the following section.

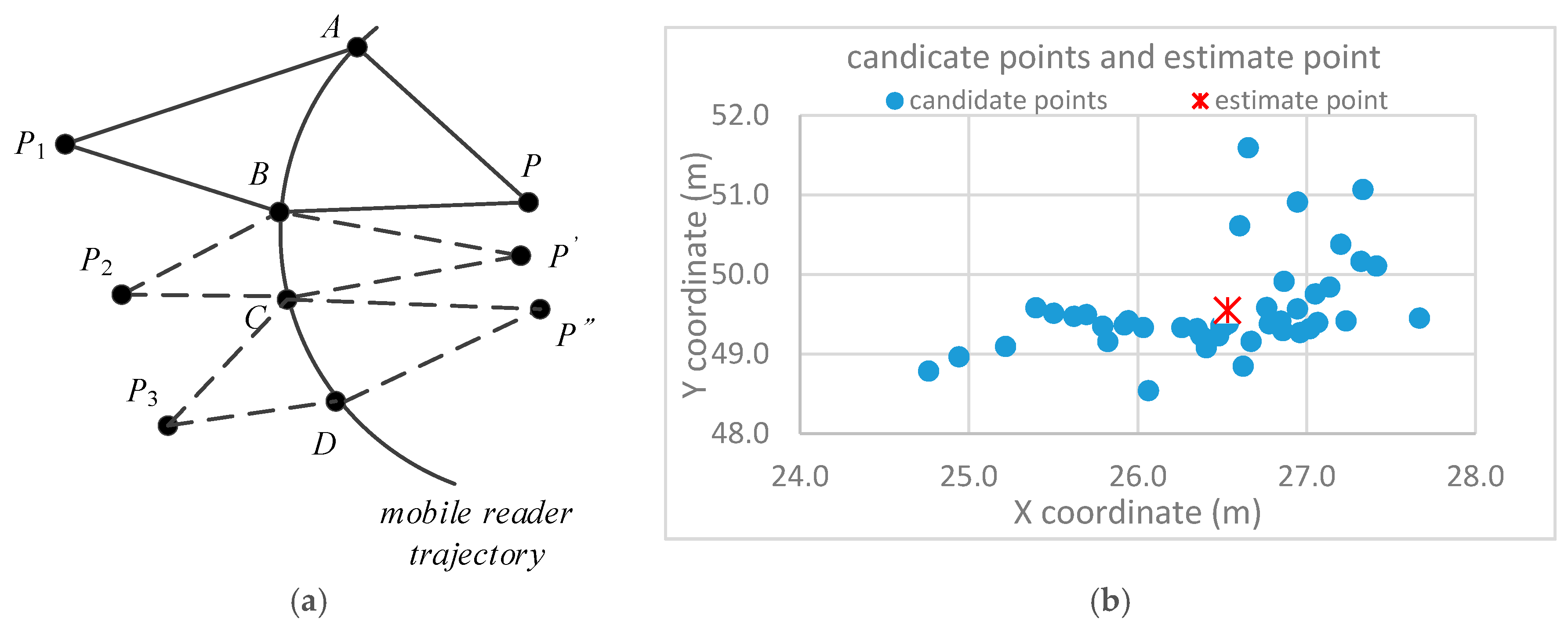
3.2. Tag-Location Principle

According to the description of the system overview, assuming n tuples have been achieved, for the i-th location, we get the value (t_i, p_i, d_i), where t_i represents the locating time; p_i is the position of the mobile RFID reader, using (x_i, y_i) denotes the coordinates value of the position p_i at time t_i. d_i is measured by the RFID reader under the RFID ranging principle, which records the distance between the reader and the tag. The effective ranging distance is about 160 m, which may change with the surrounding conditions. Given the coordinates of the target tag as (x_p, y_p), this satisfies the following equation, where n denotes the n-th location:

$${\left(x_{\mathrm{i}}-x_{\mathrm{p}}\right)}^2+{(y_{\mathrm{i}}-y_{\mathrm{p}})}^2={d_{\mathrm{i}}}^2 \mathrm{i}=1,2,3\dots n$$

(1)

With two points of mobile moving trajectory and the target tag point, such as triangle (∆ABP), is constructed as shown in Figure 3a. According to Equation (1), this triangle can be transformed to an algebraic equation in Equation (2). The solution of Equation (2) is the coordinates of the target tag. Unfortunately, in an algebraic sense, this algebraic equation has two solutions, namely p and p₁ shown in Figure 3a, which is a conflict of the reality that it has only one target tag at point p.

$$\{\begin{array}{c}{\left(x_{\mathrm{i}}-x_{\mathrm{p}}\right)}^2+{(y_{\mathrm{i}}-y_{\mathrm{p}})}^2={d_{\mathrm{i}}}^2 i=1,2,3\dots n\\ {\left(x_{\mathrm{j}}-x_{\mathrm{p}}\right)}^2+{(y_{\mathrm{j}}-y_{\mathrm{p}})}^2={d_{\mathrm{j}}}^2 j=1,2,3\dots n\end{array}$$

(2)

Inspired by the redundant observation methodology in the geomatics domain, in addition to a necessary number of measurements, we took redundant observations and measures to strengthen the measurement accuracy in the survey process [35]. In our location scheme, every triangle has two solutions, namely p and p_i (i = 1, 2, 3,…), in which point P is ideally in the same position while the p_i is different mainly for all triangles (as shown in Figure 3a). Therefore, p is the unique value of the target tag. As the mobile reader moves, we will obtain more numbers of the triangles, along with the coordinates of the target tag. However, due to measurement error, we will get a suite of possible positions of point p, as P, P’, and P’’ in Figure 3a. A simple arithmetic mean value is then taken to achieve the estimated position of p with Equation (3), wherein (x_p, y_p) denotes the coordinates of point p. The pseudo code of the tag localization algorithm is shown in Algorithm 1.

$$(x_{\mathrm{p}},y_{\mathrm{p}})= \frac{1}{n}{\displaystyle \sum }_{\mathrm{i}=1}^n\left(x_{\mathrm{i}, } y_{\mathrm{i}}\right)$$

(3)

The algorithm implementation for computing the tag location is as below:

Algorithm 1. Tag localization algorithm
Input: reader location, distance Output: coordinate of target tag
1	For each point in saved reader location points set do
2	set pi = point coordinate of points set
3	set pi+1 = reader location
4	set d1 = distance between pi and tag
5	set d2 = distance between pi and pi+1
6	set d3 = distance between pi+1 and tag
7	if (pi, pi+1, d1, d2, d3) can build a triangle then
8	calculate the coordinate of target tag
9	add the coordinate to a candidate points set
10	else
11	continuous the next loop
12	end if
13	End for
14	Add (pi+1, d3) to reader location points set for next reader location calculate
15	For each coordinate of candidate points set do
16	Calculate the mean value of all points
17	End for

3.3. Optimization

As mentioned in Algorithm 1, the RFID ranging signal and RFID reader location are the input parameters of our location scheme. The two signals are ideally time-synchronized for higher-level location accuracy. However, the time-synchronous signals are limited, which reduces the effectiveness of the redundant observations method. In our scheme, the GNSS receiver has a lower signal frequency than the RFID reader, which means there are fewer reader positions compared to the reader distance points. To overcome the time-synchronous problem, we developed a linear interpolation algorithm of GNSS signal point according to the RFID ranging signal receiving time. The detailed implementation of the algorithm is shown as follow (Algorithm 2). With the interpolation of points, many synchronized signal points are generated, which ensures a higher location accuracy with enough redundant observations.

Algorithm 2. Linear interpolation algorithm for reader location
Input: reader location, time, distance detection times array Output: synchronous reader location array
1	Set ps = reader location started, ts = start time
2	Set pd = reader location ended, td = end time
3	# find the closest time from the distance points
4	Set deltaTstart = t0 − ts, iIndexStart = 0
5	Set deltaTend = td − t0, iIndexEnd = 0
6	For each time ti of distance detection times array do
7	if ti − ts < deltaTstart then
8	set deltaTstart = ti − ts
9	set iIndexStart = i
10	end if
11	if td − ti < deltaTend then
12	set deltaTend = td − ti
13	set iIndexEnd = i
14	end if
15	End for
16	# Calculate the synchronous points
17	For each time ti of distance detection times array do
18	pi = ps + (ti − ts)/(td − ts) × (pd − ps)
19	add pi to synchronous reader location array
20	End for

Additionally, the uncertainty of candidate points is another concern. As mentioned in Figure 3, candidate points (p’, p” …) may have different locations due to the measurement error. The arithmetic mean approach can often achieve a relatively good result; however, it does not consider the influence of every candidate point on the final result as the signal path loss propagation is distance-dependent [36,37]. Therefore, we proposed a distance-based proportionality function to weight individual candidate points. The inverse distance (1/d) is used to compute the weight. As a longer distance has a higher probability of importing noise, it has a smaller weight on the true value. Inspired by the weighted centroid localization (WCL) algorithm [36], we introduced a power-law based weight to emphasize the importance of the transmitting distance (Equation (4)), where λ is used as the power of distance, w denotes the weight.

$$w_{\mathrm{i}}=\frac{1}{{\left(d_{\mathrm{i}}\right)}^{\lambda }}$$

(4)

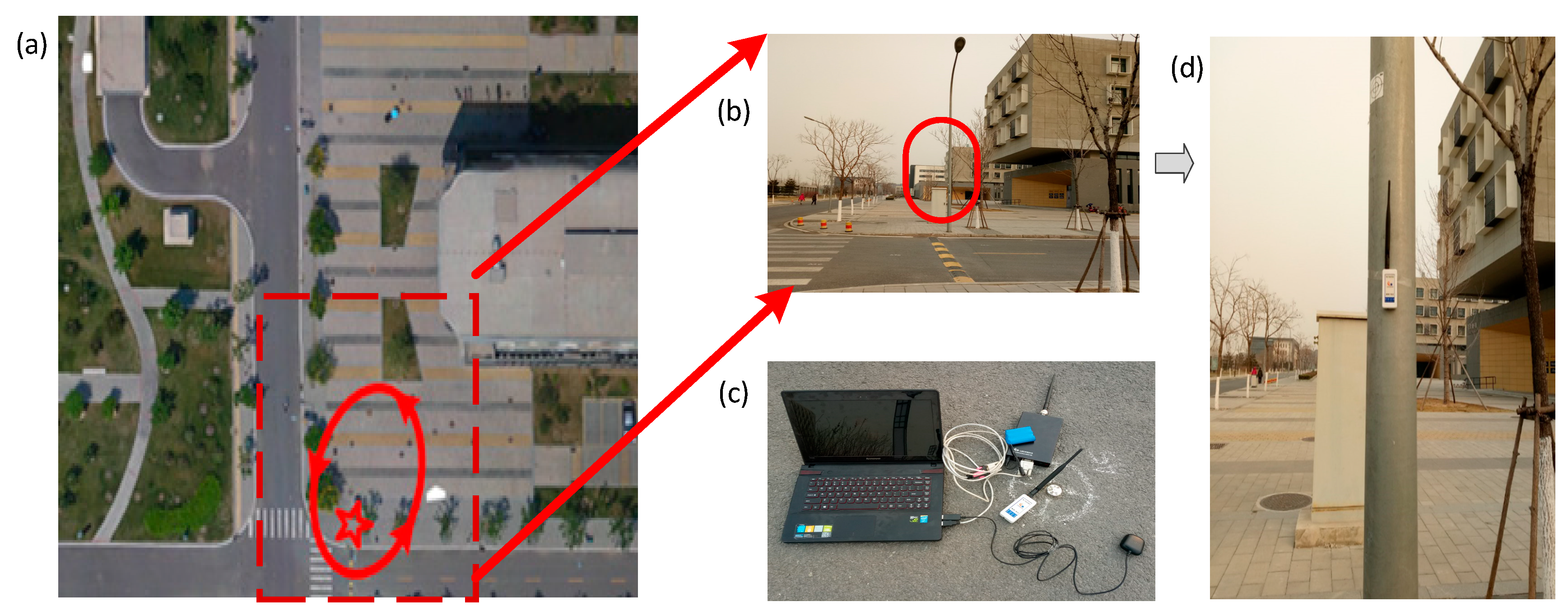
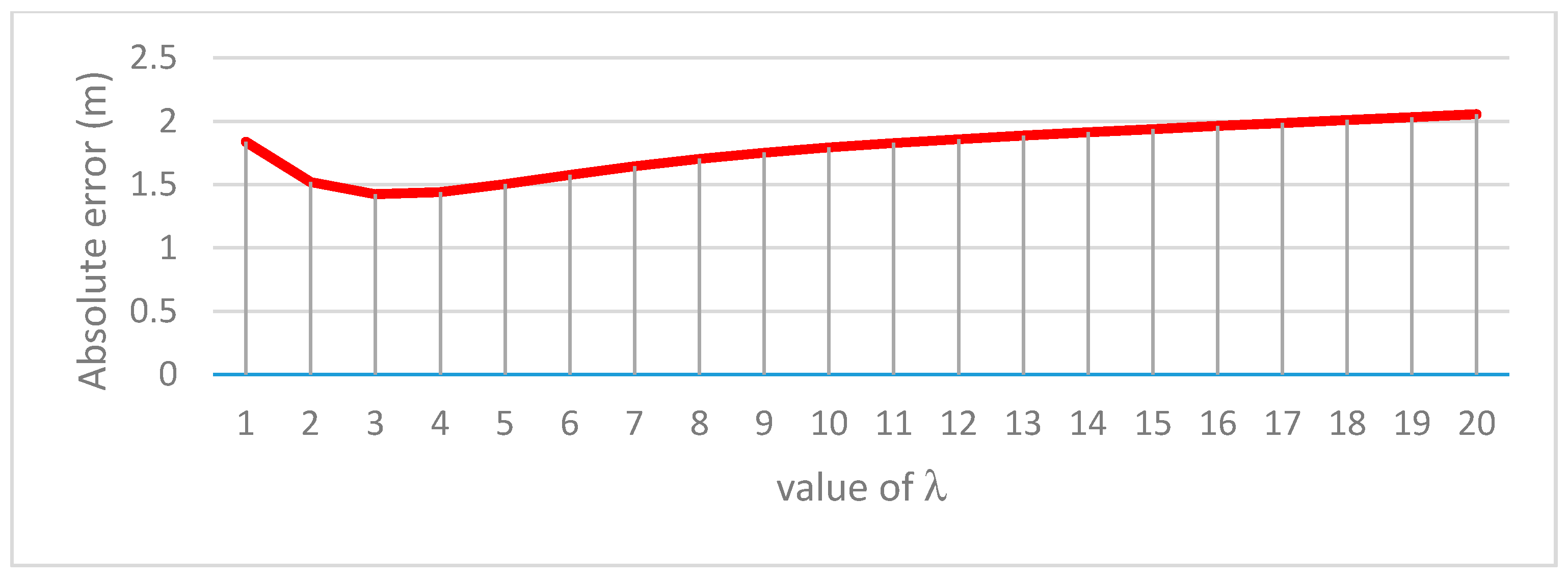
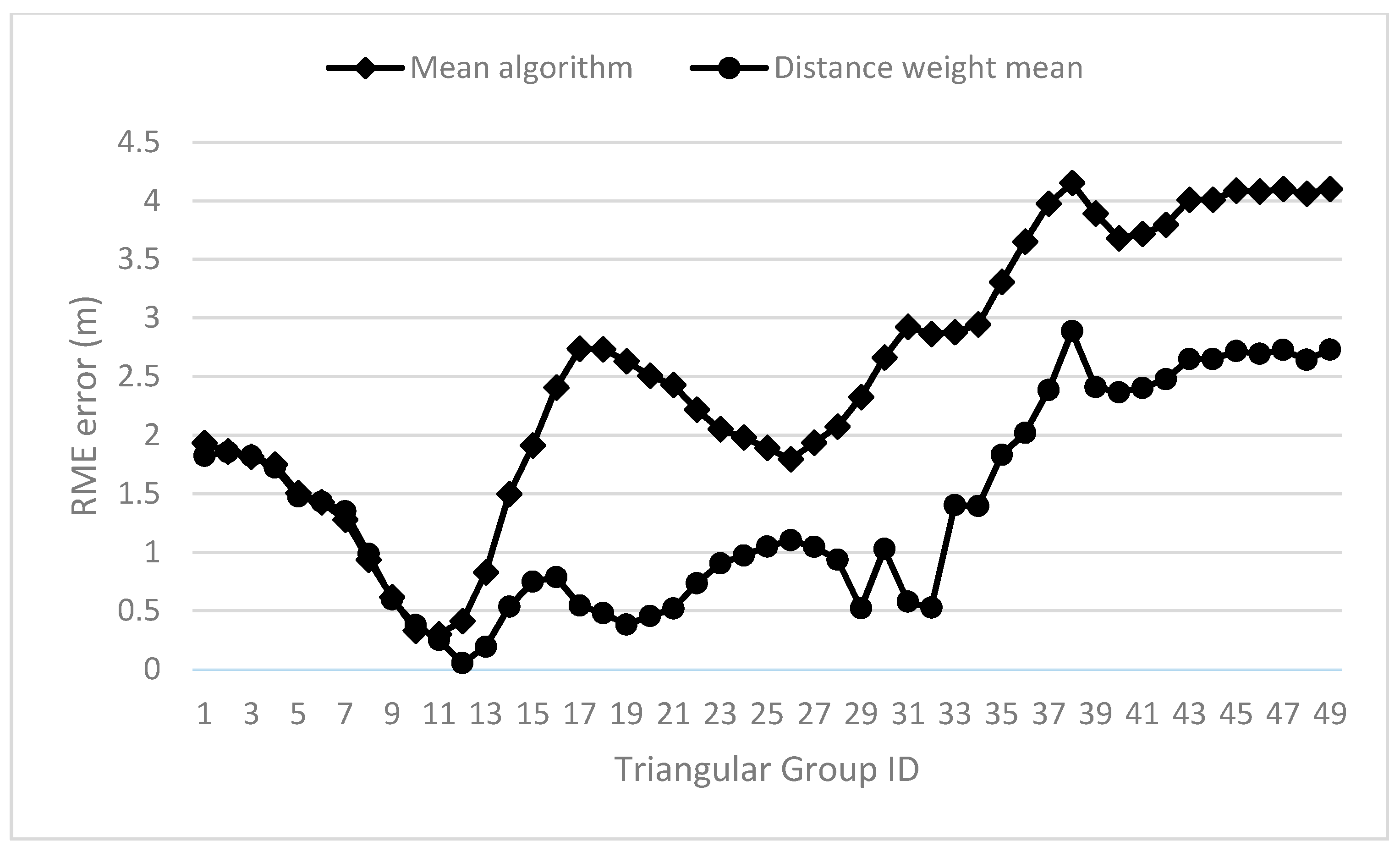
4. Experiment and Result

In this section, we conducted a suite of experiments to evaluate the efficiency and effectiveness of our proposed scheme. This experiment was run on the university campus of Beijing University of Civil Engineering and Architecture, China. The experimental scenario is shown in Figure 4. The devices are composed of a mobile RFID reader, an RFID tag, and a portable GNSS receiver with the RS232 protocol. As shown in Figure 4c, the RFID reader and GNSS receiver were connected to a notebook to get the reader position and the distance between the reader and the tags. We moved the RFID readers to simulate multiple RFID readers. A tag was deployed at the target object as shown in Figure 4d. The coordinates were measured as ground truth by the Leica TS06 Total Station. The observed coordinates were estimated based on our algorithms in Section 3. The root mean error (RME) was opted to measure the absolute difference between the true coordinates and the computed coordinates (Equation (5)), where (x_r, y_r) is the ground truth coordinates of the target object; (x_i, y_i) is the estimated coordinates; n is the triangle number; and ε represents the RME error. The smaller the ε is, the better the performance of the location scheme:

$$\mathsf{\epsilon }=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\sqrt{{\left(x_{\mathrm{r}}-x_{\mathrm{i}}\right)}^2+{\left(y_{\mathrm{r}}-y_{\mathrm{i}}\right)}^2}.$$

(5)

Figure 5 shows one of the experiments, where the triangle markers indicate the RFID reader trajectory, and the star is the true position of the RFID tag. The largest distance between the reader and the tag is 24.89 m, and the shortest distance between them is 3.23 m. In this experiment, 49 groups of triangles are generated with a different number of triangles in each group. The coordinates are calculated based on Equations (3)–(5). The detailed coordinate information is shown in

Table 1. The result of the experiment (where x_c and y_c denote the coordinates of this paper, for the concise description of the table, the digital prefix number is shown in the table headline).

Triangle Group ID	Triangle Number	xc (m)	yc (m)	Root Mean Error (m)	Triangle Group ID	Triangle Number	xc (m)	yc (m)	Root Mean Error (m)
b1	15	494,125.50	286,449.52	1.8215	b26	184	494,126.21	286,449.35	1.1016
b2	24	494,125.47	286,449.52	1.8545	b27	258	494,126.27	286,449.40	1.0447
b3	24	494,125.51	286,449.51	1.8205	b28	192	494,126.39	286,449.44	0.9349
b4	42	494,125.60	286,449.49	1.7216	b29	259	494,126.96	286,449.68	0.5216
b5	78	494,125.84	286,449.37	1.4762	b30	174	494,127.61	286,450.28	1.0269
b6	67	494,125.88	286,449.32	1.4303	b31	112	494,127.03	286,449.79	0.5772
b7	93	494,125.96	286,449.29	1.3482	b32	200	494,126.97	286,449.69	0.5259
b8	96	494,126.33	286,449.20	0.9850	b33	246	494,127.70	286,450.64	1.4010
b9	28	494,126.72	286,449.26	0.5963	b34	203	494,127.63	286,450.65	1.3932
b10	84	494,126.93	286,449.27	0.3788	b35	173	494,127.74	286,451.07	1.8299
b11	140	494,127.06	286,449.28	0.2500	b36	268	494,127.60	286,451.29	2.0181
b12	144	494,127.27	286,449.32	0.0532	b37	205	494,127.66	286,451.65	2.3832
b13	108	494,127.48	286,449.38	0.1929	b38	73	494,127.99	286,452.10	2.8866
b14	129	494,127.80	286,449.52	0.5338	b39	293	494,127.84	286,451.64	2.4099
b15	37	494,127.98	286,449.62	0.7472	b40	184	494,128.07	286,451.53	2.3650
b16	72	494,127.97	286,449.73	0.7879	b41	482	494,128.07	286,451.57	2.4019
b17	74	494,127.58	286,449.77	0.5453	b42	93	494,128.05	286,451.66	2.4760
b18	156	494,127.48	286,449.74	0.4792	b43	188	494,127.86	286,451.88	2.6478
b19	86	494,127.22	286,449.66	0.3827	b44	258	494,127.86	286,451.88	2.6478
b20	40	494,126.96	286,449.58	0.4542	b45	196	494,127.60	286,451.99	2.7157
b21	86	494,126.86	286,449.54	0.5181	b46	450	494,127.59	286,451.97	2.6938
b22	86	494,126.60	286,449.46	0.7336	b47	294	494,127.48	286,452.01	2.7256
b23	92	494,126.41	286,449.41	0.9043	b48	188	494,127.28	286,451.93	2.6417
b24	123	494,126.35	286,449.39	0.9713	b49	564	494,127.12	286,452.01	2.7276
b25	46	494,126.27	286,449.37	1.0478	-	-	-	-	-
Group number = 49; Average = 1.3904 m; maximum = 2.8866 m; minimum = 0.0532 m

. The result show that the average error is 1.3904 m, the max error is 2.8866 m, and the minimum error is 0.0532 m. Compared to the error of 14.1497 m that is tested outdoors when only the GNSS receiver is used (the solid rectangle in Figure 5), the location accuracy is largely improved in our proposed location system. This accuracy can support infrastructure asset management in smart cities. Also, this scheme only requires one RFID reader and one portable GNSS receiver. Therefore, it is practical for infrastructure asset management in large areas.

5. Discussion

More than six billion people (about 70% of the world’s population) will live in cities by 2050 [38], resulting in a pressing need for urban public infrastructure [39]. IoT increasingly plays an essential role in meeting this fundamental requirement. Gartner indicates the market for IoT will explode and the number of connected devices will reach 21 billion by 2020 [40]. In the era of IoT and smart cities initiatives, a low-cost and easily deployed location scheme is crucial to LBS. In this section, we discuss the effectiveness of the proposed location method by combining GNSS with RFID. We will discuss the cost and deployment aspects of our scheme, compared to existing techniques first. Then, the accuracy of our scheme is evaluated.

5.1. Low-Cost and Easy Deployment

It is clear that the IoT plays a predominant role in localization and tracking capabilities for smart cities. As mentioned in the review of related work, existing location schemes have drawbacks in cost and deployment.

Existing RFID-based location schemes incur high costs for smart cities. RFID, GNSS, and GSM have been used in a variety of projects to provide the location of the target, but GNSS as the popular outdoor location method is limited in high-rise buildings, indoor and underground environments due to the weak signal. Methods combining GNSS, GSM and RFID to track vehicles were proposed [33], in which RFID was used in complex environments to overcome the poor signal drawback of GNSS [41]. Reference tags have been proved as a low-cost solution, but the vast number of reference tags means high investment [42]. Virtual reference elimination (VIRE) based on LocAtioN iDentification through the dynaMic Active Rfid Calibration (LANDMARC) system is proposed to replace the physical reference tags with virtual ones, which dramatically decreases the installation cost while keeping similar accuracy [43]. But for smart cities applications in a large area, a large amount of physical reference tags is necessary to generate these virtual reference tags.

The deployment pattern has different uncertainties for location accuracy. Many deployment patterns such as cell tag and hexagon deployment [44], triangular deployment [45] and key reference tag [46] have been validated in locations, which show that the layout pattern and number of reference tags influence positioning accuracy [47]. Therefore, research conducted spatiotemporal accuracy analysis with different deployment patterns and reader numbers [27]. This increased the deployment time and technological difficulty, especially in an emergency scenario in which time is crucial for decision-making processes.

In research on combining RFID and GNSS for location and tracking, complementary location and location-sensing are the two main categories. For the collaborative location, RFID is a complementary method where the GNSS signal is weak or lower, such as indoor or underground environments [41,48]. In a construction site, the four or more mobile RFID reader-mounted Global Positioning System (GPS) is used to locate the static construction material [49]. However, the topology of readers must be maintained during movement, which is a critical constraint in practice. For the location-sensing model, GNSS responses the location and tracking, while the RFID senses the target object, such as solid waste monitoring [50], logistics management [51], and vehicle location within connected vehicle networks [52].

According to the above analysis, low-cost, easy deployment and immunity to dynamic environment location schemes are necessary for smart cities. In our proposed method, one moving RFID reader-mounted GNSS receiver simulates the reference tags, which massively reduced the cost and project investment. Although the GNSS location error can propagate to tag location accuracy, it should be noted that the location accuracy could be further improved by implementing methods such as dead-reckoning and Kalman filtering [53]. With the wide application of ground-based augmentation systems (GBAS) at a city scale, GNSS location accuracy can be enhanced [54]. Also, the redundant observations method as a difference calculation model can reduce the GNSS error partly. From our experiment results, we can see a single GNSS receiver error is 14.1497 m, while it is only 1.3904 m in our location scheme. Therefore, our method with one mobile RFID reader and one GNSS receiver has ensured the low-cost and easy deployment features with sufficient location accuracy. However, synchronicity between the RFID signal and the GNSS signal relies on a computer, which makes it challenging to achieve higher accuracy, but this can be improved by the hardware signal synchronously.

5.2. Location Determination Methods

Estimating a target coordinate from candidate points must consider the influence factors and computation complexity. The algebraic mean algorithm is a simple and effective method to calculate the right position from candidate points with the same weight for all factors. It has been used in position recognition from the image [55], and spatial co-location analysis [56]. However, for RFID-based location, a signal propagation error still exists in the averaged result. Some literature shows that the relationship between the spatial transmission distance and RFID signal is a power function [57]. Cui used a specified number of readers, the nearest number of reference tags and the distance between reader and tag as the synthetic weight for the location calculation [58]. Although better accuracy is achieved, such a method adds more computation complexity.

Inspired by the WCL algorithm [36], we applied a power-law based weight (Equation (4)) to increase the location accuracy. A sensibility analysis is conducted for the optimized parameter of λ in Equation (4). We set the λ value from 1 to 20 respectively, comparing the absolute error. Figure 6 shows the results, in which the best result was achieved when λ = 3. Figure 7 shows the absolute errors of the mean algorithm and the distance-weighted mean algorithm. Average accuracy is improved from 2.5095 m to 1.3904 m. For the maximum error group ID (b38), the accuracy has been increased from 4.1518 m to 2.8866 m.

6. Conclusions

In this paper, we proposed a novel low-cost and easy deployment locating system scheme, where RFID is combined with GNSS. In our proposed scheme, one mobile RFID reader is equipped with a GNSS receiver to calculate the target tags’ locations. To reduce the system’s cost, it takes advantage of the GNSS receiver to replace a large number of reference tags used in current RFID-based location systems. Another advantage of our scheme is its rapid and easy deployment, especially in an emergency scenario. To achieve fine-grained localization accuracy, we put forth a distance-based weight algorithm, rather than a simple average algorithm, in this system. The experimental results demonstrate the effectiveness and efficiency of our scheme, which has potential applications for public infrastructure inspection and management in smart cities.

Nevertheless, this location scheme has room for further improvement. For example, the hardware signal synchronicity and outlier detection algorithms will optimize the RFID signal and GNSS signal, which will help to improve the location accuracy further. We also plan to expand our location systems to location-based business applications and services in smart cities initiatives.