1. Introduction
Texture is an important image spatial feature [
1,
2,
3]. Many texture descriptors have been developed in the past, such as frequency domain analysis based on the Fourier transform, the wavelet transform approach, the hidden Markov approach, the local binary pattern (LBP), the local multiple patterns (LMP), the geostatistical-based approach, the watershed-based approach, the gray-level co-occurrence matrix (GLCM)-based approach, and other statistical approaches [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. Most of these approaches are mainly designed for a simple and clear classification system or a specific object, similar to in the fields of medicine, industry, the military, etc. [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. However, when using high-resolution optical remote sensing (RS) images for geographical classification, the classification system will change with the needs of different geo-scenes, even in the same image, so the phenomena of “same object different spectrum”, “same spectrum different object”, and “mixed pixels” will become more prevalent, and the textures will be more complex and changeable [
1,
2,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30]. Scholars have emphasized that such image analysis can be improved by employing geo-domain knowledge (especially various general statistical characteristics such as topology, location, spatial relationship, etc.) [
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30]. Thus, in this paper, a GLCM-based approach that can be easily associated with geo-knowledge is chosen to build texture features for geo applications. This is because the GLCM obtains statistics by using a certain scale window, where one can intuitively observe the actual objects and reflect the domain knowledge (mainly spatial shape attributes). Moreover, it provides information in image gray direction, interval and change amplitude, so that 14 kinds of texture features can be effectively defined based on it [
3], and it meets the requirement for the classification of complex and variable geo-scenes [
31].
Since 1990, scientists have created studies on the impact of various parameters on the validity of GLCM-based texture, and they found that it is very sensitive to the scale parameter, and the classification accuracy can even decrease if the parameter is unreasonable [
31,
32,
33,
34,
35,
36]. Marceau D.J. (1990) first used SOPT data to conduct a quantified study [
31]. He used the factor analysis method to measure the impact on window size, quantization level, and four texture statistics (Energy, Contrast, Homogeneity, Entropy) for land cover types. The impacts are as follows: the scale of the window has the greatest effect on the classification, followed by the texture statistics, and the least significant is the level of quantization [
31]. Later, other researchers also successively obtained similar study results [
32,
33,
34,
35,
36,
37]. In Cui L.’s Ph.D. dissertation (2005), this issue was described in depth [
32]. She measured the impact on window scale, direction and level of quantization, and found that different directions had little effect on the classification reliability of most types, and the best solution was to use the average value of the omni direction. Different bands play a crucial role in the extraction of texture features for multispectral TM data, so the use of combined band information is important. In addition, she took the scale parameters from 3 to 50 separately for the TM image analysis and found the variation rule of 8 GLCM texture features of 14 types of geo-objects by using the enumerated window scale. She found that there was a correspondence between the different texture features and the different windows. When the window was small, the feature space composed of a combination of 2 texture features achieved good results. When the window was gradually increased, the combination dimension of the texture feature space was also increased, and the combination of 5 texture features achieved best results. Moreover, she found that the overall classification accuracy gradually increased with scale, reaching the highest value when the scale reached 35. Therefore, she concluded that the optimal identification windows of different objects were different, although only an optimal scale of 35 was used in the subsequent classification [
32]. That is, multi-scale is an essential and necessary feature of spatial data, and it has a significant impact on GLCM-based texture features [
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43].
In many practical applications, the choice of scale parameters is still very arbitrary when using empirical method, and a small scale value is commonly chosen, either 3, 5, 7 or 9. It is easy to operate, but also extremely unreliable [
32,
33,
34]. In addition, researchers have also developed various statistical methods for analyzing texture scales, including a histogram algorithm, a variogram algorithm, a Markov algorithm, a mean shift algorithm, and a fractal network evolutionary algorithm of Ecognition, etc. [
1,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18]. Additionally, Binaghi, E. et al. (2003) set the scale parameters by taking the statistics of the spatial characteristics of sampled data [
43]. These methods can sometimes obtain multi-scale parameters. Therefore, they are able to achieve adaptive estimation to some extent and can improve the validity of texture features. However, the number of scales was random and few, and the values of the scales were usually low. In terms of the algorithms themselves, local optima or independent of actual categories will appear easily if they rely too much on the sample selection or the local image gray level variability analysis, or the errors will accumulate if they adopt an iterative calculation model. It can be seen that there are still many uncertainties in current studies for the selection of texture scale [
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44]. Some are only aimed at a certain application, some are only able to obtain a single scale parameter, and some are able to obtain multi-scales, but each time the results are commonly inconsistent and small for the number and value of scales. Therefore, it is necessary to find a quick and reliable setting method for multi-scale image texture in geo-analysis.
To solve the problems above, this paper proposes a new method for determining multi-scale windows of image GLCM texture descriptors by means of the integrated use of a geographic information system (GIS) and geo-spatial domain knowledge. First, we explain the rules for the changes in texture scales under different geo-scenes and classification systems and construct a framework for texture scale recognition and extraction by simulating human visual attention and interpretation characteristics [
1,
2,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29]. Second, a body of effective geo-spatial domain knowledge is mined from an existing GIS database. Then, the link between domain knowledge and texture scale is established, so that multi-scale windows can be quickly determined for each category. The approach uses geo domain knowledge that is extracted from different GIS informative layers (which is likely to be cheap to source from historical databases) to define the characteristic size and shape of the geo-scene categories of interest. These informative layers can be topographic maps, digital elevation models (DEM), land-use maps, etc. It must be noted that there is a possibility that these maps could cover a wide temporal range, and due to this potential temporal variability of the landscape, the accuracy of the domain knowledge should be taken into account. Finally, the Fisher function analysis based on the enumeration method is used to evaluate the validity of the above multi-scale parameters [
44,
45,
46,
47]. In this paper, experiments were designed to distinguish the categories of a certain geo-scene based on GLCM texture features with multi-scales by using high-resolution optical RS images and existing GIS data in the study area. The results show that the scale parameters of geo-textures can be quantified with a one-to-one model, making them easier to understand and express, and the proposed method shows a significant improvement in efficiency with similarly good performance when compared with the traditional enumeration method. Furthermore, GLCM texture descriptors under multi-scale windows can evidently represent different thematic categories; thereby, they will increase the total number of categories in the classification system, reduce the classification uncertainty, and better meet the requirements of large-scale image geo-analysis. Therefore, the integrated use of GIS and domain knowledge is proved feasible in image geo-texture analysis, and able avoid the disadvantages of local optimization, sample dependence, and initial error accumulation of iterative calculations.
2. Overall Framework
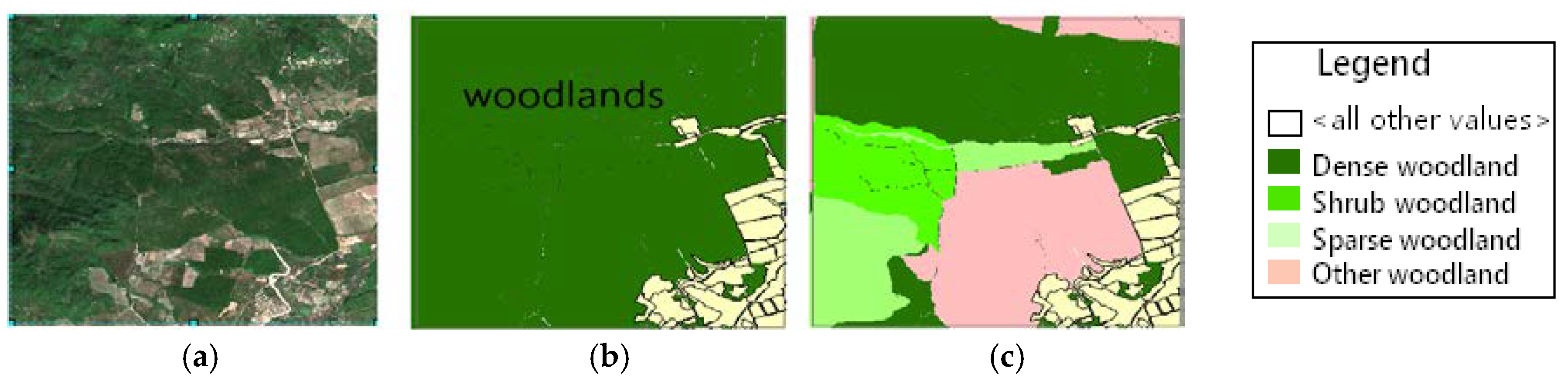
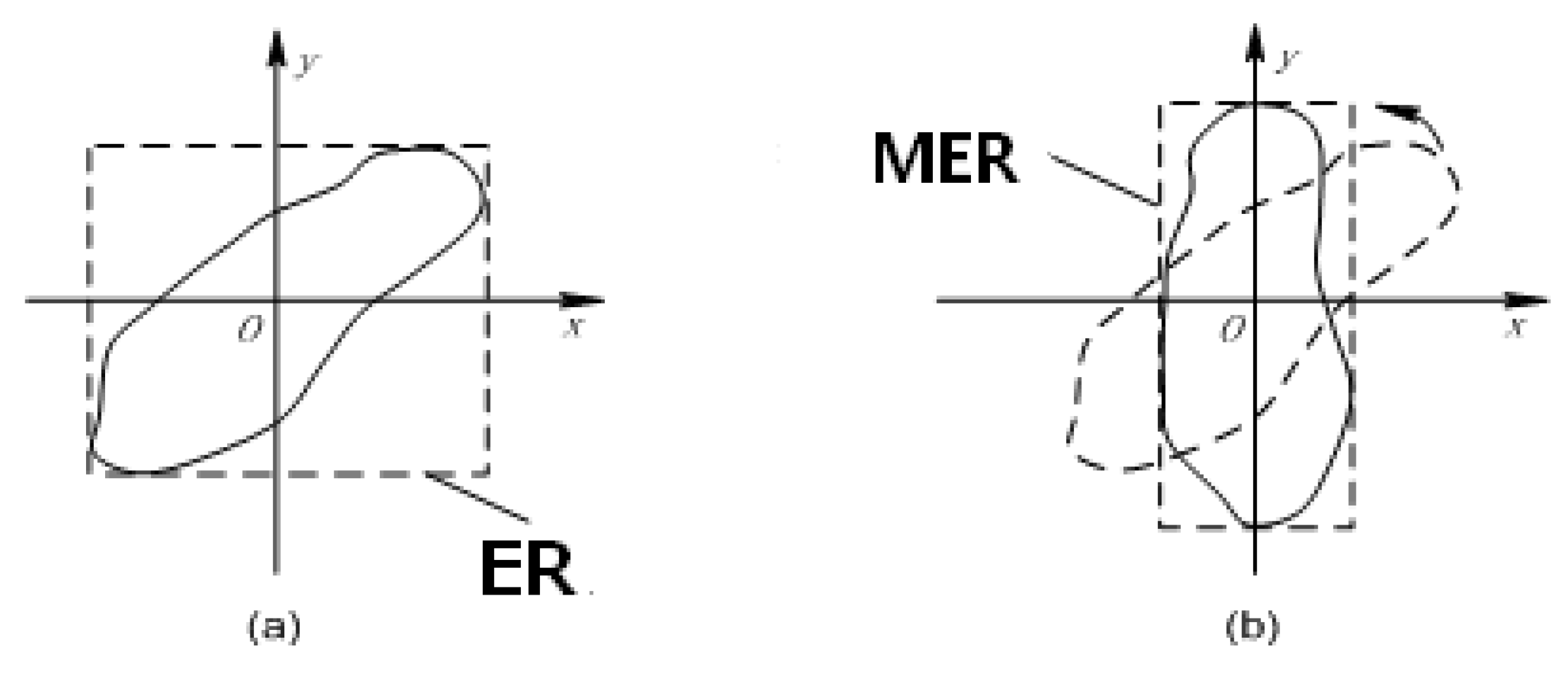
GLCM is actually a statistical matrix of joint conditional probability distribution between the gray levels of image pixel pairs with some distance and direction within a certain window, and is used for texture descriptors [
1,
2,
3]. Each geo-texture observation window based on GLCM must reflect the real spatial characteristics of the corresponding category. For example, in the classification system of land cover of I level, “woodlands” are taken as a single classified object. Thus, its texture unit is expanded, and a larger observation window and complex spatial structures are formed. In a classification system of land cover of II level, woodlands are subdivided into four sub-types: Dense woodland, Shrub woodland, Sparse land and other woodlands [
31,
32,
33,
48,
49]. Obviously, for a texture unit of sub-types, its corresponding observation window should be relatively microscopic in the same place, and the spatial structure relatively simple. A case in which the classified geo-objects vary with the change of geo-classification system in an image can be seen in
Figure 1.
In the geo-analysis of an image, each category should have its own texture observation window, which is strongly correlated with the actual definition and shape of the classified objects [
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39]. In addition, the scale selection algorithm is essentially equivalent to setting the image pixel number as the optimal scale according to the size of the object shape and the image resolution. Therefore, this paper uses GIS data and technology to mine domain knowledge (mainly the statistical characteristics of objects’ shapes), in order to determine the multi-scale of GLCM texture observation windows. The overall framework is designed as shown in
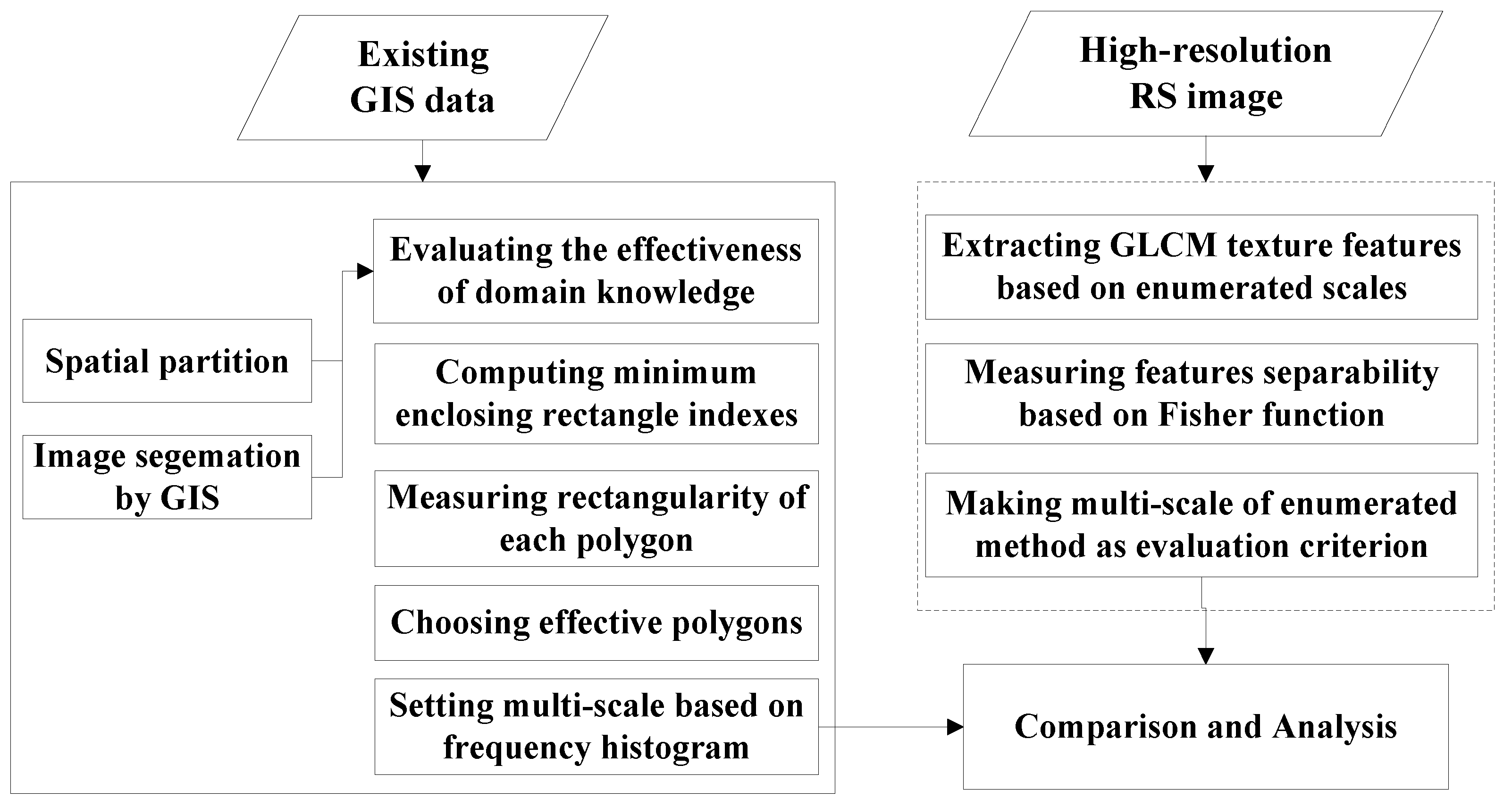
Figure 2; the steps will be described below.
• Evaluating the validity of domain knowledge by spatial partitioning and image segmentation
The validity of the domain knowledge must be taken into account when using it to analyze texture windows. Because domain knowledge is mined from an existing GIS database, there is potential knowledge variability in the two time-phases, i.e., from GIS data to RS data. To obtain more effective domain knowledge and reduce the impact of such changes on the analysis results, some spatial data mining algorithms are employed, including spatial partitioning and image segmentation by GIS. The spatial partitioning can ensure the overall spatial consistency of a geo-scene, and the GIS-based image segmentation can further measure the stability of domain knowledge by analyzing the change rule of categories in segmentation blocks.
• Domain knowledge mining by GIS
In a stable time-space system, a set of effective polygons with representative shapes can be obtained from an existing GIS database, and the general shape characteristics of each category can be mined by employing GIS shape indices.
• Determination of multi-scale GLCM texture windows
According to the principle of determination, we set up a one-to-one model of the correlation between domain shape knowledge and texture scale to extract the appropriate multi-scale window for GLCM texture features.
• Evaluation of multi-scale parameters
To quantitatively evaluate the validity of texture scales extracted by GIS and domain knowledge, we employ the Fisher distance method, which can measure the separability of GLCM texture features under different scales; and the higher the separability, the better the setting of the corresponding scale parameters. First, a set of criteria for multi-scale parameters is obtained by measuring the separability of texture features based on enumerated scales. Then, the results deduced by the proposed method can be evaluated by means of a comparison analysis.
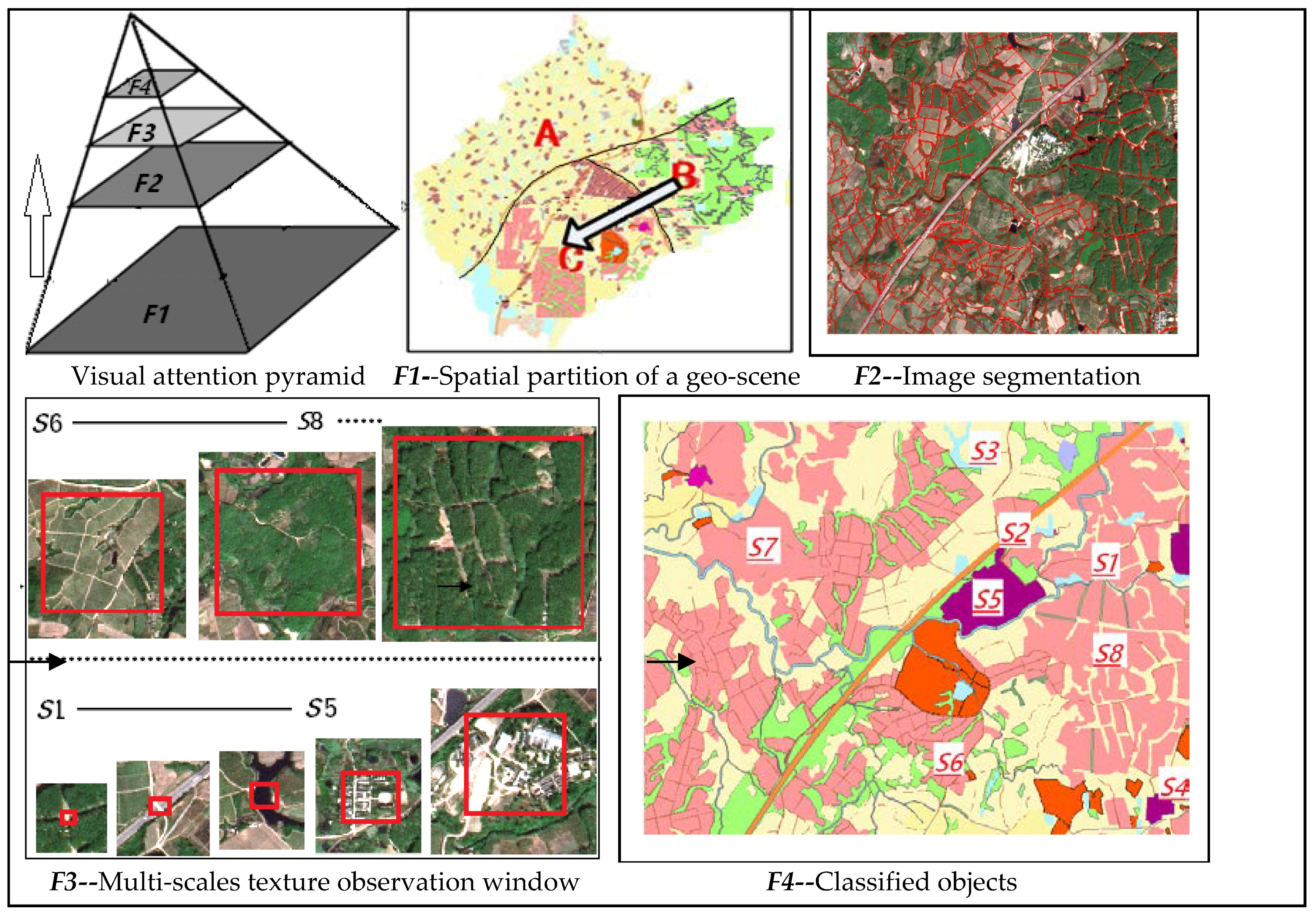
Overall, the progressive visual attention and cognitive process for the geo-texture scale in a geo-scene can be seen as “from the whole to the local, and from the window to the details” [
21,
45,
46,
47,
48,
49,
50,
51]. The process is illustrated in
Figure 3:
4. Experiment and Discussion
4.1. Study Data
In this paper, Changjiang County, Hainan Province was chosen as the study area. We aimed to obtain effective scale parameters for multi-scale GLCM texture features in distinguishing the land-use categories. Land-use classification is a common geo-scene in practical work, with a complex system and specific meaning. The collected study data include the following. (1) The 2008 SPOT5 RS image, which has a high spatial resolution of 2.5 m and a true color space (Red, Green, Blue). It is intended for land-use classification cartography of 1:10,000. (2) The existing GIS database in vector format, including 2005 and 2008 GIS land-use maps at the scale of 1:10,000, where the 2005 GIS data can be used to extract domain knowledge, and the 2008 GIS data can be taken as the current real geo-objects to verify the classification accuracy. The other auxiliary GIS data, which are mainly used for spatial partitioning, include the 2006–2020 land-use planning map and DEM graded map, etc.
4.2. Spatial Partition and Classification System of Land-Use
First, by using the 2006–2020 GIS and land-use planning data, we extract the following partitioning factors: important resource distributions, administrative boundaries, and the functional division map. Meanwhile, the 2005 land-use polygon boundary is taken as the basic unit. Their cartographic priority is set according to the visual size in the local region as follows: DEM graded map > railway distribution map > provincial and municipal highway distribution map > important river distribution map > functional division map > village administrative boundary map. According to this order, each factor map should be superimposed on the basic land-use polygon. Finally, the study area is divided into five homogeneous regions, which have to maintain the integrity and continuity of land-use polygons and administrative boundary, as shown in
Figure 7.
According to land-use planning, the land-use pattern of the Zones 2–4 will not be extensively adjusted in 2005–2008, so the domain knowledge mined from the 2005 land-use map in these regions is seen to be usable. To better illustrate the adaptability of the proposed method, the 4′ Zone has been chosen for the experiments because it has a more complex land-use pattern.
According to the latest land-use classification system used in practical work, there should be 12 land-use classification categories (see in
Table 1).
4.3. Evaluation of Domain Knowledge
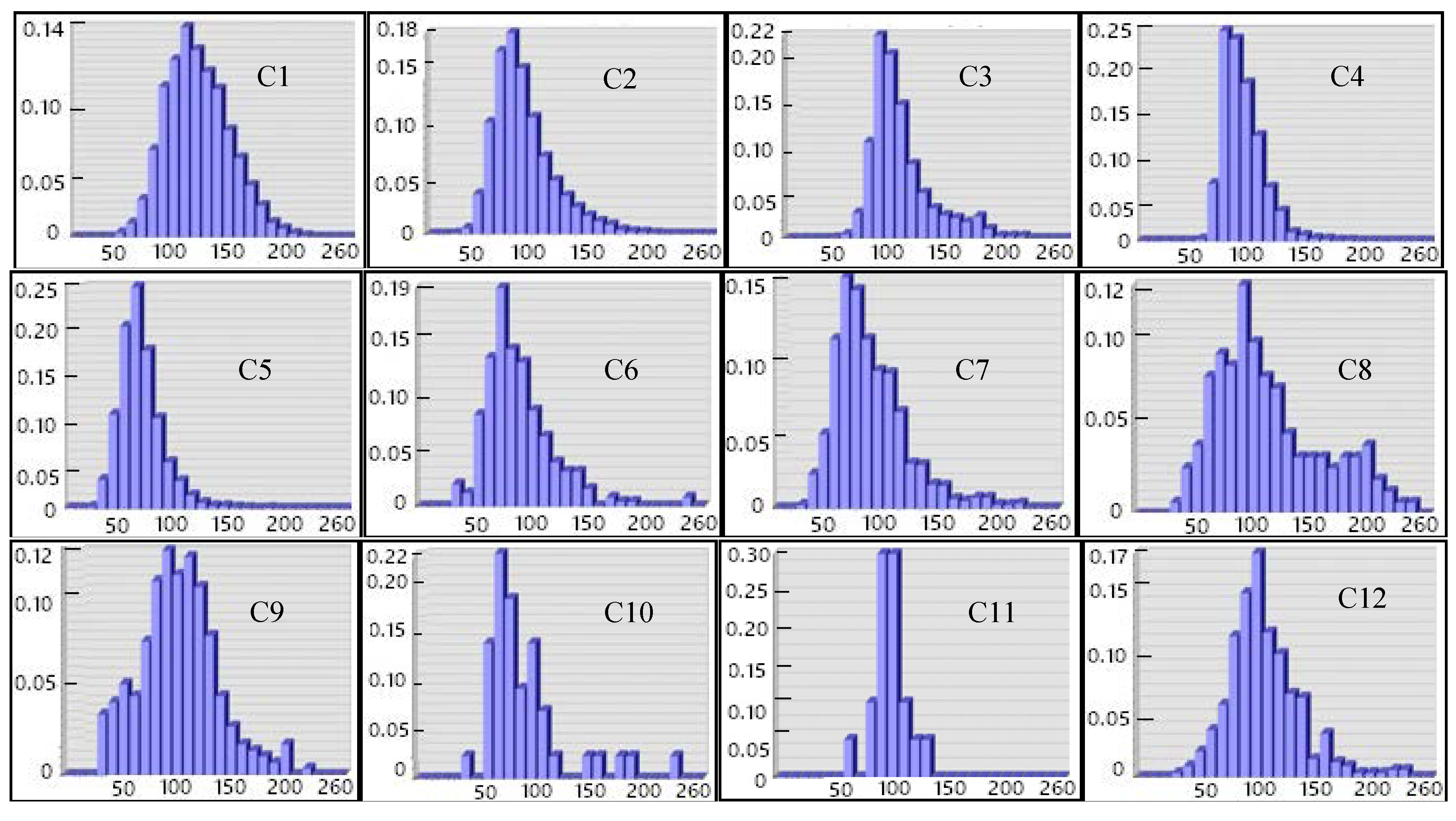
In the ArcGIS software, we first split up the RS raster image using the GIS vector polygon boundary and calculate the mean gray value of each segmentation block. For this RS image with 3 bands, its gray image can be obtained by converting color space from RGB (red, green, blue) to HSI (hue, saturation, and luminance) and eliminating the hue and saturation information while retaining the luminance values. When we plot the frequency histograms of the blocks under the corresponding gray levels of each category, the gray level is set as 26, which means that there are 26 breaks/bars in the histogram, i.e.,
rk = 1, 2, …, 26, and each level is 10. Since the category number is 12, we get 12 groups of statistical graphs of the gray level of segmentation blocks, as shown in
Figure 8:
Thus, we can easily obtain the peak zone of a histogram above because of its approximate normal distribution. Then, Equation (2) will be used to count the changed-rate
V of the number of polygons for each category. The statistics are shown in
Table 2, where the total number of polygons of each category in the historical GIS data is denoted as
totNum, and the number of polygons for which the category has not been changed between the two-time phases is denoted as
tipNum. Following related previous works (especially by Yang C., Zhou C. 2001), in the classical statistical theories of the “golden section” and “five-grade marking”, the changed rate of polygons’ number of a category should be lower than the threshold
η as 40%; that is, at least 60% of the polygons’ categories should not have been changed. In this case, the domain knowledge system can be characterized as stable and qualified [
25,
48,
49].
In the table above, a smaller polygon category’s changed-rate results in higher stability. Because most categories meet the pre-defined judgment of Equation (2), they are relatively stable and unified under the selected spatial-time scale in which the corresponding domain knowledge is reliable. Meanwhile, the changed-rate of categories 8 and 10 are near 40%. Therefore, that corresponding domain knowledge may be relatively ineffective in the subsequent analysis.
4.4. Scales Determined by GIS and Domain Knowledge
Based on the secondary development program function of the ArcGIS platform, the following operators have been obtained.
- (1)
There are a total of 17,991 land-use polygons in the partition region, of which 3893 patches were selected according to their regularity as effective polygon shapes for morphological knowledge statistics.
- (2)
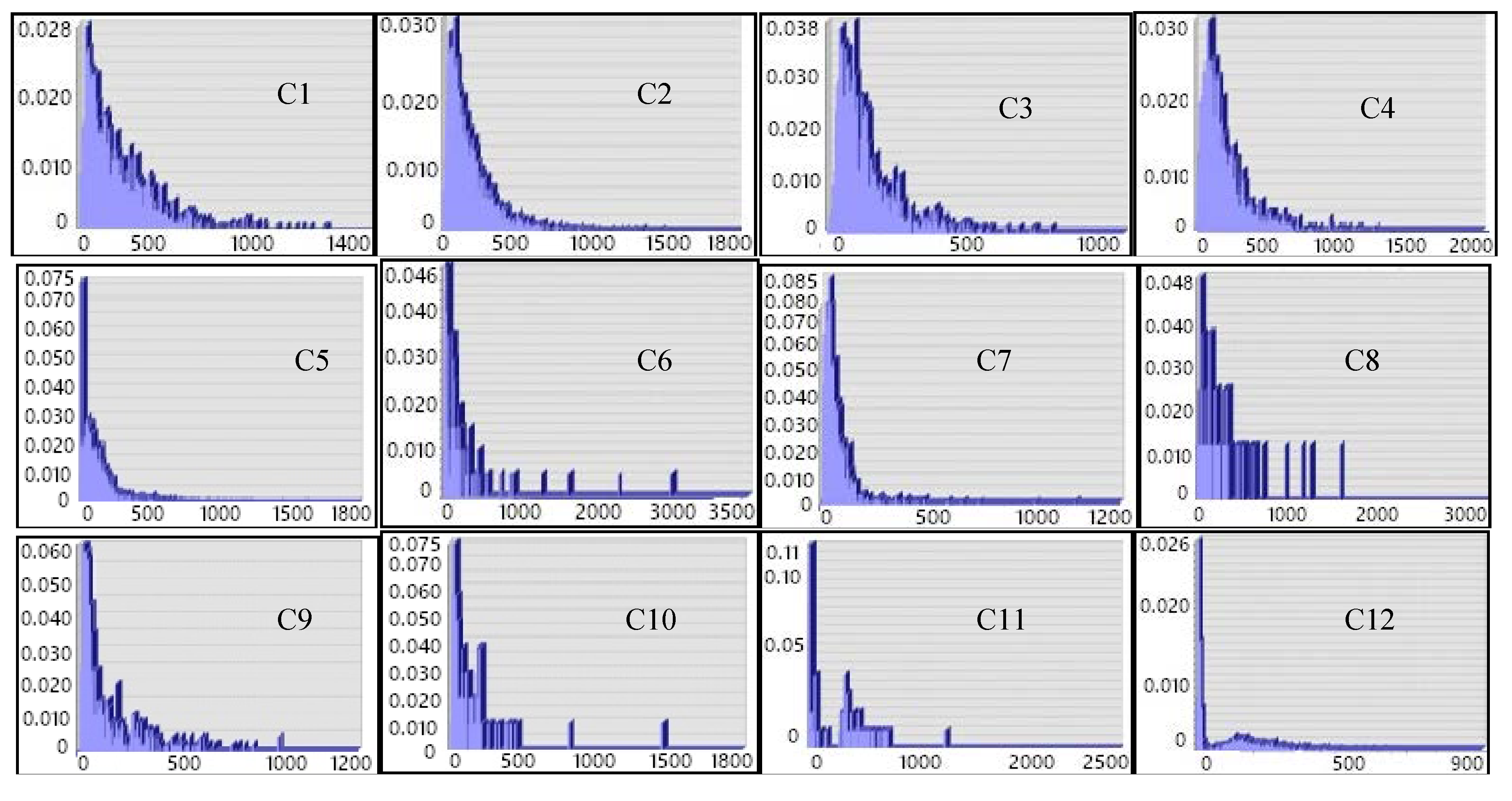
According to the effective polygon sets, we plot out the frequency histograms of the length and width of the MER for each category. Because we are interested only in the shorter side of the rectangle, as described in the discussion and Equation (6) above, frequency histograms of the widths of MER should be plotted for each category, as shown in
Figure 9.
These figures show the following rules. (1) There are obvious peaks in most categories, which shows that a strong regularity lies in their morphology. Moreover, a more concentrated frequency distribution indicates a more obvious morphological regularity with its category. (2) There is no obvious peak or peaks in a few categories. This includes category 8, which contains several morphological characteristics. Therefore, the validity of their domain knowledge has been further constrained.
- (3)
The texture scale parameter
Scalei of each category is set by selecting the smaller value of the statistical width and length of MER, in accordance with Equation (6). Meanwhile, we indicate the variance of the length and width as
STD_
Width and
STD_
Length to measure the representativeness of the selected texture scale. Then, the scale value should be the nearest odd number obtained by the window size in geo-space divided by pixel resolution × 2 (2.5 × 2 = 5 m in this study). The results are shown in
Table 3.
According to the analysis in
Table 3, some conclusions can be obtained. (1) The minimum texture scale corresponds to category 12 (rural road). It is a linear feature that takes the line width as a basis for analysis. The maximum texture scale corresponds to category 8 (river), which has the largest area and an irregular shape. At the same time, however, we should also note that there are still some short and small rivers in the study area. The texture features observed on this large a scale are not conducive to the extraction of these objects. For categories 1–6 (a series of cultivated lands), the selected texture scales are also larger, which indicates that there is a massive stretched distribution in the polygons. This conclusion can also be directly observed from the GIS historical database. Moreover, category 9 represents a rural residence, and its texture scale is much smaller than the urban residence in category 10. This result is also in accordance with the actual case. (2) The variances in the length and width of the enclosing rectangles for most categories are generally less than 50, except for category 8, which has a variance greater than 70. This result further illustrates that the differences in the morphological characteristics of category 8 will lead to a consequence of there beingno representative scale that can be selected.
In conclusion, the texture scale sets that are selected with the aid of GIS historical knowledge are in accordance with the local actual situation and people’s general cognition.
4.5. Scales Determined by the Enumeration Method
In this paper, the Fisher distance algorithm is employed to quantitatively measure the validity of the selected texture scales. The determinant ratio of the between-class scatter matrix and the within-class scatter matrix has been taken as the criterion of category separability in this index.
- (1)
First, the enumeration method is used to calculate texture features under a series of scales. On the basis of relevant research results [
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42], we select an enumeration scale of
L = 3:101.
As for setting the other parameters of GLCM-based texture features, some conventional and efficient methods were used (as shown in
Table 4), with the single-band image value also being obtained by converting the color space from RGB to HSI and retaining the luminance values of HSI, thereby obtaining the distance value that is most commonly set to 1, and obtaining the direction value by computing the average texture statistics in its four directions. Additionally, the dimension of GLCM is determined by the image gray level. Considering the calculation efficiency and the storage need of the matrix in practical applications, the gray level of the original image should be compressed, i.e., an 8-bit image with a gray level of 0–255 is compressed into a 3-bit image with a gray level of 0–8, which can effectively avoid the sparse matrices in GLCM.
In this way, we can calculate 8 classic GLCM-based texture features as described in
Section 3.3.1; meanwhile, we employ a principal component analysis algorithm to deduce 3 principal features, so as to reduce feature dimensions and ensure their independence. These two groups of texture features with number of 8 and 3 are denoted as I and II.
- (2)
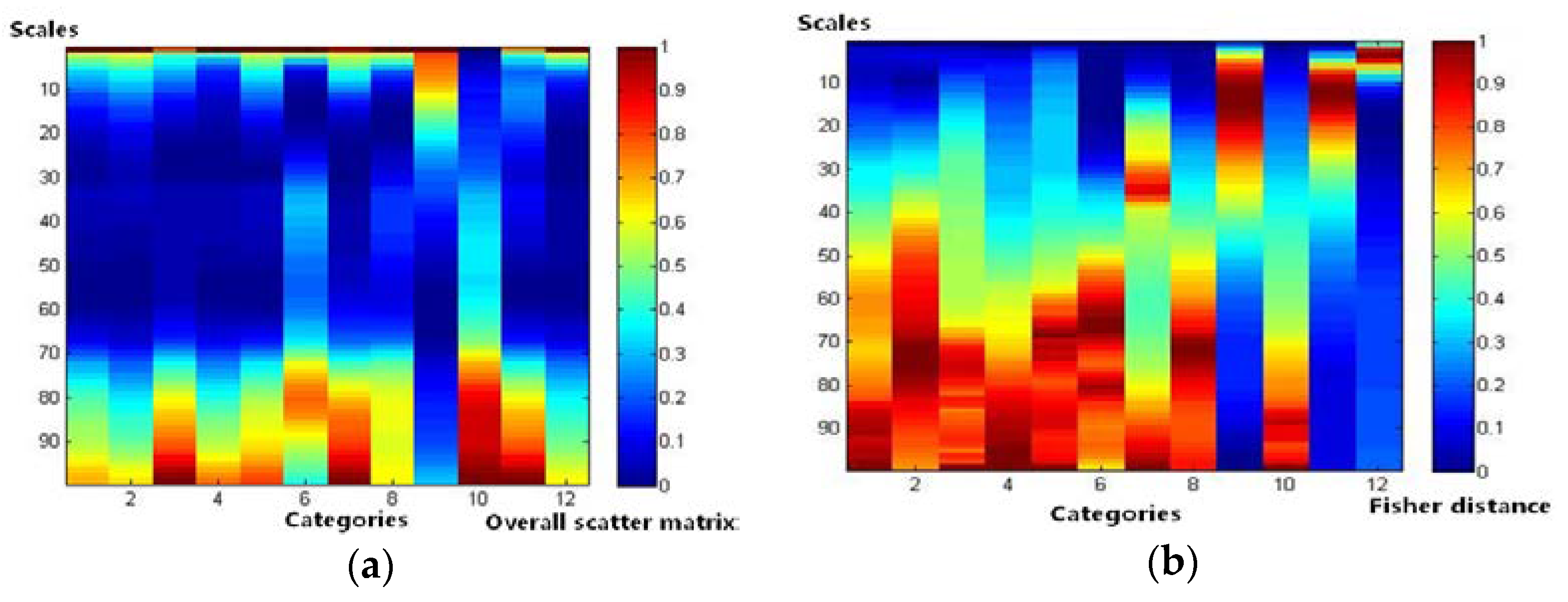
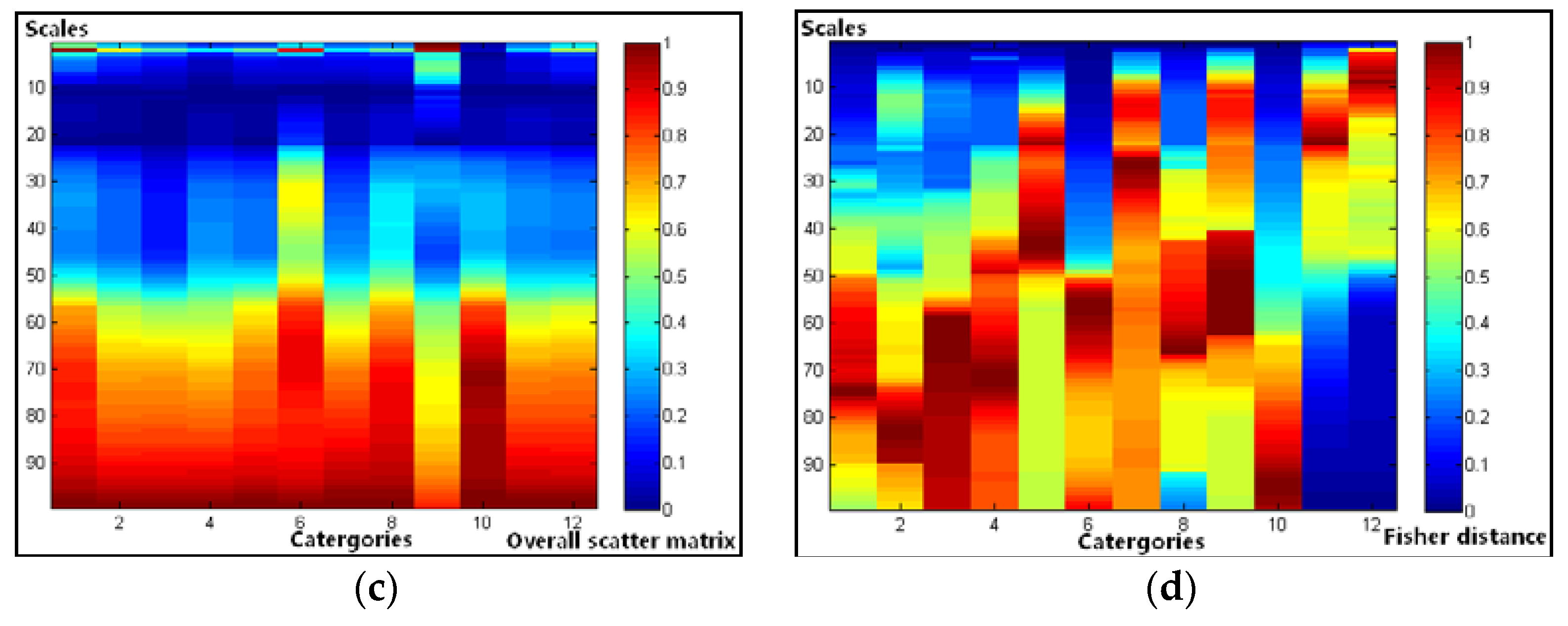
Second, the Fisher distances of the two groups of texture features based on the enumeration method are computed. In the following relational diagram, we define the category number as the x-axis and the texture scale as the y-axis. We also describe the value of the overall scatter matrix and the Fisher distance using different color blocks. Blue represents the smallest separability, and red represents the largest separability. Therefore, the relationship between the category separability and the texture scales can be clearly expressed.
The results are shown in
Figure 10. Group I of the overall scatter matrix and Fisher distance is derived under 8 texture features, while the group II of the overall scatter matrix and Fisher distance is derived under 3 independent texture features. It can be observed from these graphs that: (1) For the overall scatter matrix, the peak value is distributed in a more concentrated way and is more inconsistent in all categories in group I than in group II. In addition, most categories reach high separability on some slightly smaller scale values in group II than in group I. This illustrates that, when the texture features are more independent, the separability of all categories is more consistent and can be obtained on a smaller scale value. (2) For the Fisher distance, in any category (column), there is always a peak zone in the separability bar chart, and the separability of such zone changes mostly scales according to the normal distribution, and it fluctuates. The peak values of each category in group I and group II are close. However, fluctuations and noise occur occasionally in group I, such as in category 6, while the peak region has a more obvious and concentrated distribution in group II. This illustrates that the separability is more prominent and clear when the texture features are more independent, and vice versa.
In addition, it should be noted that most categories with complex texture features or mixed pixels can be separated under a bigger texture scale value; that is to say, if only one scale parameter can be used to calculate the texture features in a particular case, its value should be as large as possible.
As a result, the scales corresponding to the highest separability of each category were computed. The texture scale sets determined by the different methods can be seen in
Table 5.
4.6. Comparison of the Different Scale Sets
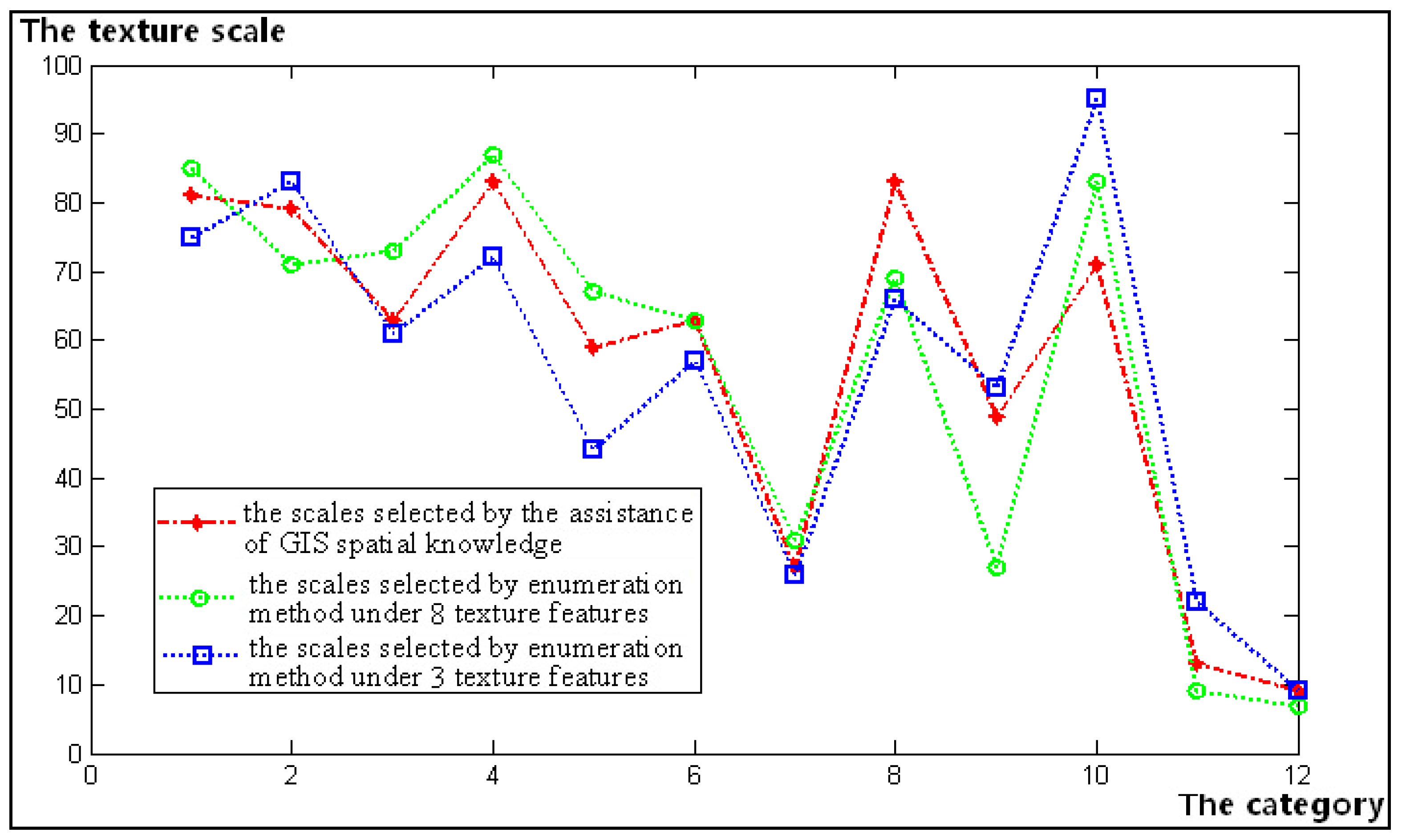
For the three groups of texture scale sets shown in
Table 5, the relationship among them can be summarized as shown in
Figure 11.
Some conclusions can be reached.
- (1)
Intuitively, the scales that are selected by the different methods are very close and even have the same values in some categories. However, there is also a larger difference between categories 8 and 10. By analyzing the cause of the divergence, we find that category 8 represents river water, whose shape is larger in the GIS historical database. Therefore, the texture scale that is determined by its domain knowledge has a larger value of 83. However, significant changes have occurred in this category within two time-phases (see
Table 1, with the change rate of 41.1%), because many rivers continue to diminish, and the standard scale parameter that is determined by the enumeration method has a smaller value of 69 or 66. Moreover, similar to category 10 (urban settlement), the scale that is determined with the aid of the GIS historical data is 71, but the standard texture scale that is determined by the enumeration method has increased to 83 or 95 with the continuous expansion of the town over several years. Therefore, under this unstable cognitive spatial-temporal system, the reliability of its domain knowledge is greatly reduced. In the scale sets 2 and 3, which are selected by the enumeration method, we can generally gain a smaller value in set 3 for most categories under 3 independent texture features. This shows that, under the same distinguishing performance, the independent texture features can slightly reduce the window scale value for texture observation in most instances.
- (2)
The correlation of the different texture scale sets was computed, as seen in
Table 6.
The calculation results show that the relativity Re reaches 0.93, and the significance p reaches 0.00075 in the first group of scale sets, while the relativity Re reaches 0.91, and the significance p reaches 0.00039 in the second group of scale sets. The closer the Re value is to 1, the higher the relativity between the two sets of data is; and the further the p value is below 0.05, the more significant the correlation is. Although the relativity value in the second group is slightly worse than that of the first group, its significance value is better. It is reaffirmed that the increase in the independence of the texture features enables a more significant and clear value of the scale sets derived, while the scale sets also maintain a strong performance.
4.7. Classification Results Analysis
To further evaluate the proposed method for setting texture scale sets, we carried out an experiment comparing classification ability. The SVM algorithm was employed. As a classic method, it has performed well in image analysis in many studies [
1]. Specifically, we achieved image classification by using GLCM-based texture features under a series of typical single- or multi-scale sets.
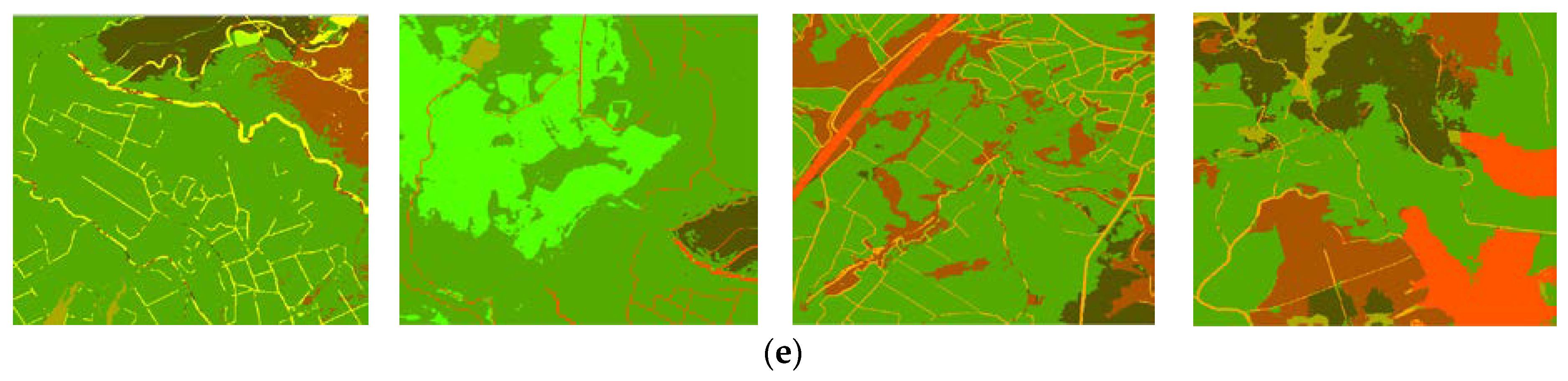
First, we choose any images cut from the RS data in the study area (as shown in
Figure 7) for testing. The size of each cut image is 500 × 500 pixels, and its classification system is as shown in
Table 7 and
Figure 12.
Then, the sample ratio parameter is set as 0.3, 0.6, or 0.8, while the other parameters remain unchanged from the SVM algorithm. Since the variation in classification accuracy is within 1%, its influence on the algorithm can be regarded as negligible. Therefore, we use the sample ratio of 0.3, in consideration of algorithm efficiency. The experiments results are as shown in
Figure 13.
The overall accuracy and kappa coefficient are calculated in
Table 7.
As shown in the results above, the classification abilities of different feature spaces are as follows: the classification accuracy is lowest when only spectral features are used, followed by the integrated usage of texture features under a single scale, and the highest accuracy, especially the highest kappa coefficient, is from the integrated usage of texture features under multi-scale sets.
When the single-scale value is gradually increased from 1, the overall classification accuracy significantly increases and reaches the highest level when the scale value, respectively, is 89, 81, 79, 73 in image 1–4. When the multi-scale is respectively given as sets 1, sets 2, and sets 3, the classification accuracy are all high value and very close in images 1–4. However, the optimal scale sets is different for these different classification systems, that is to say, no a kind of scale sets has absolute classification advantage. Overall, there are strong and significant correlations between the 3 groups of scale sets, which further proves the rationality and validity of the proposed method that extracts the texture scale based on domain knowledge and GIS.
4.8. Algorithm Efficiency Analysis
- (1)
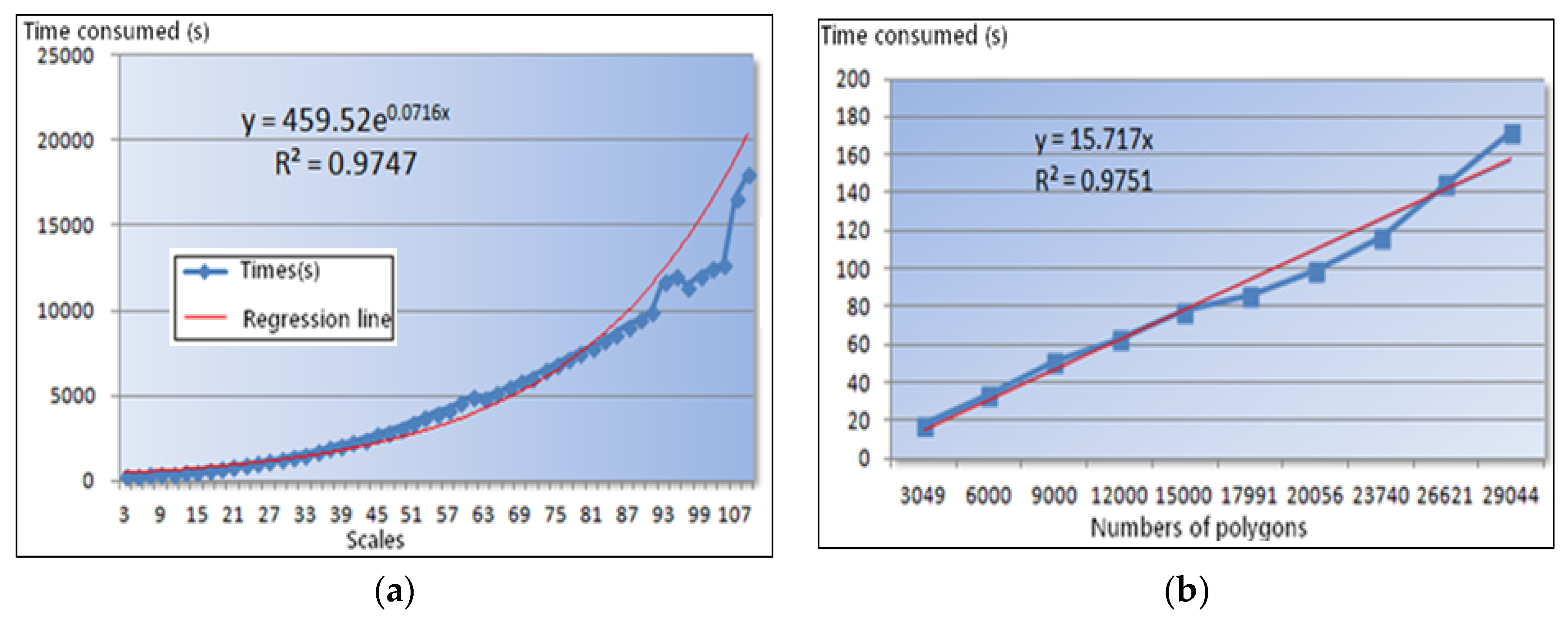
With the enumeration method, the best scale parameters can be gained by comparing texture features under numerous scales. When the range of the enumerated scale was set from 3 to 111 in this experiment, the algorithm’s time consumption changed, as shown in
Figure 14a.
Clearly, this algorithm is extremely time-consuming. As the texture scale increases, the time consumption for calculating texture features increases exponentially. When the scale is larger than 15, the time consumption exceeds 10 min, with the maximum even reaching 5 h (i.e., when scale = 111). If the enumeration method is used to determine texture scale parameters, as the image data continues to increase, the accumulated time will reach an unbearable degree, such as in Equation (16):
The equation above is derived from the exponential regression line in this study, where k1 and a are the variables determined by the computer’s performance, and maxEN represents the maximum value of the enumeration number. It shows that algorithm complexity is a relationship of cumulative exponential regression.
- (2)
Based on the GIS and the domain knowledge-assisted method, the texture scale features can also be effectively extracted. This is realized through traversal, statistics, and the analysis of patches from the existing GIS database using the ArcGIS platform. When the proposed method is widely used, and GIS data can be managed in a standardized way, then its algorithmic complexity will be largely proportional to the number of patches. The corresponding time consumption can be reflected in the following statistical curve in
Figure 14b.
It can be seen that this algorithm has superior performance, especially in terms of efficiency. It only takes 180 s to perform the operation on the entire experimental area (region 4 of size 581 km
2). Therefore, compared with the enumeration method, it substantially increases efficiency and is therefore more suitable for high-resolution remote sensing image analysis of larger geo-data. We summarize the relationship between polygon numbers and time consumption in Equation (17):
The equation shows a simple linear relationship, where b is the time of data management and data cleansing of GIS, and k2 is the variable determined by the computer’s performance. The algorithm has very low complexity; moreover, the calculation results are reasonable and valid, which is consistent with the scales selected by the enumeration method. It can be said that the texture scale extraction method based on the spatial knowledge of land-use proposed in this paper is scientific and reasonable and can meet the efficiency and precision requirements of classification.