A Novel Approach for Identifying Urban Built-Up Area Boundaries Using High-Resolution Remote-Sensing Data Based on the Scale Effect
Abstract
:1. Introduction
2. Materials and Methods
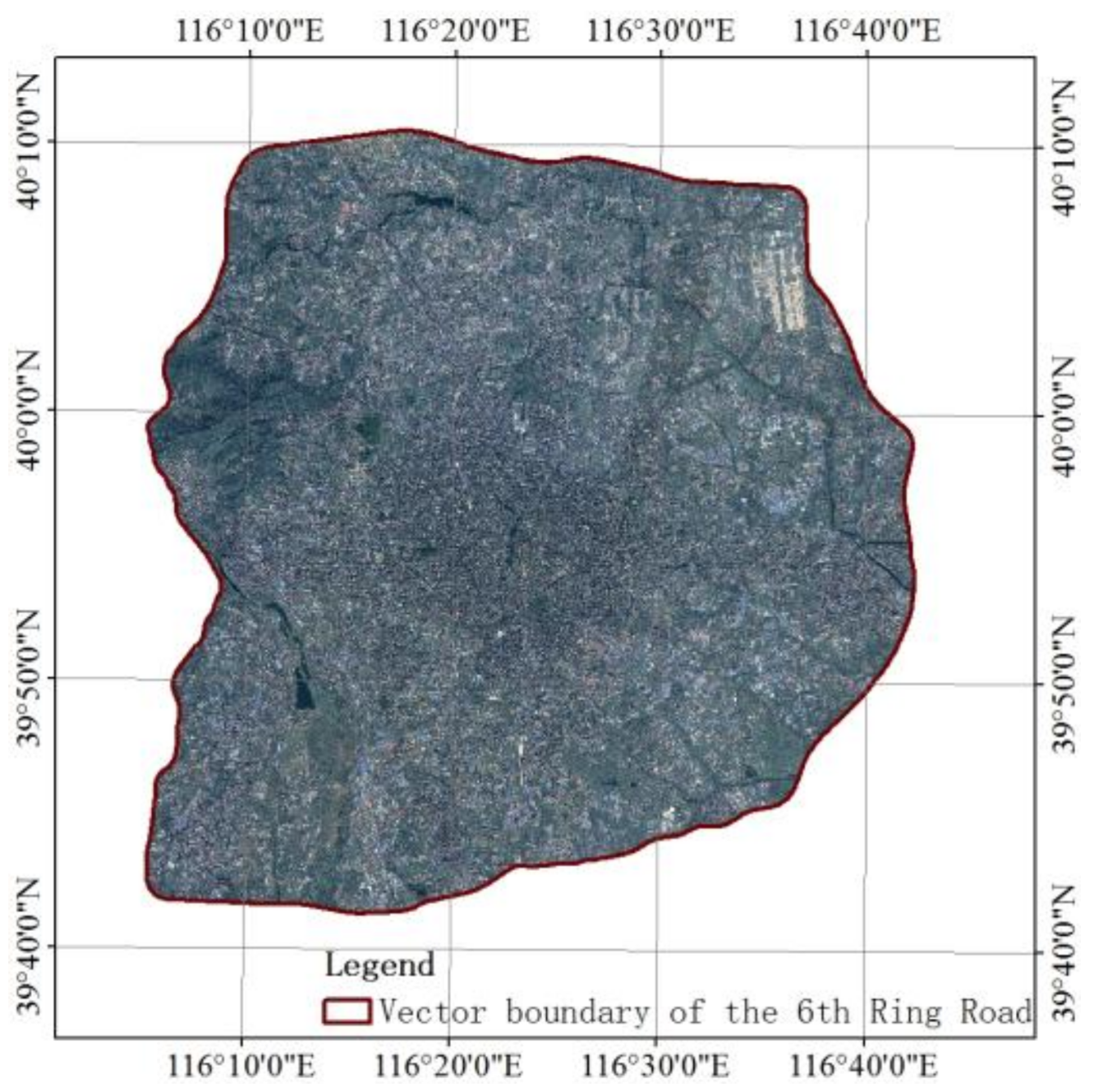
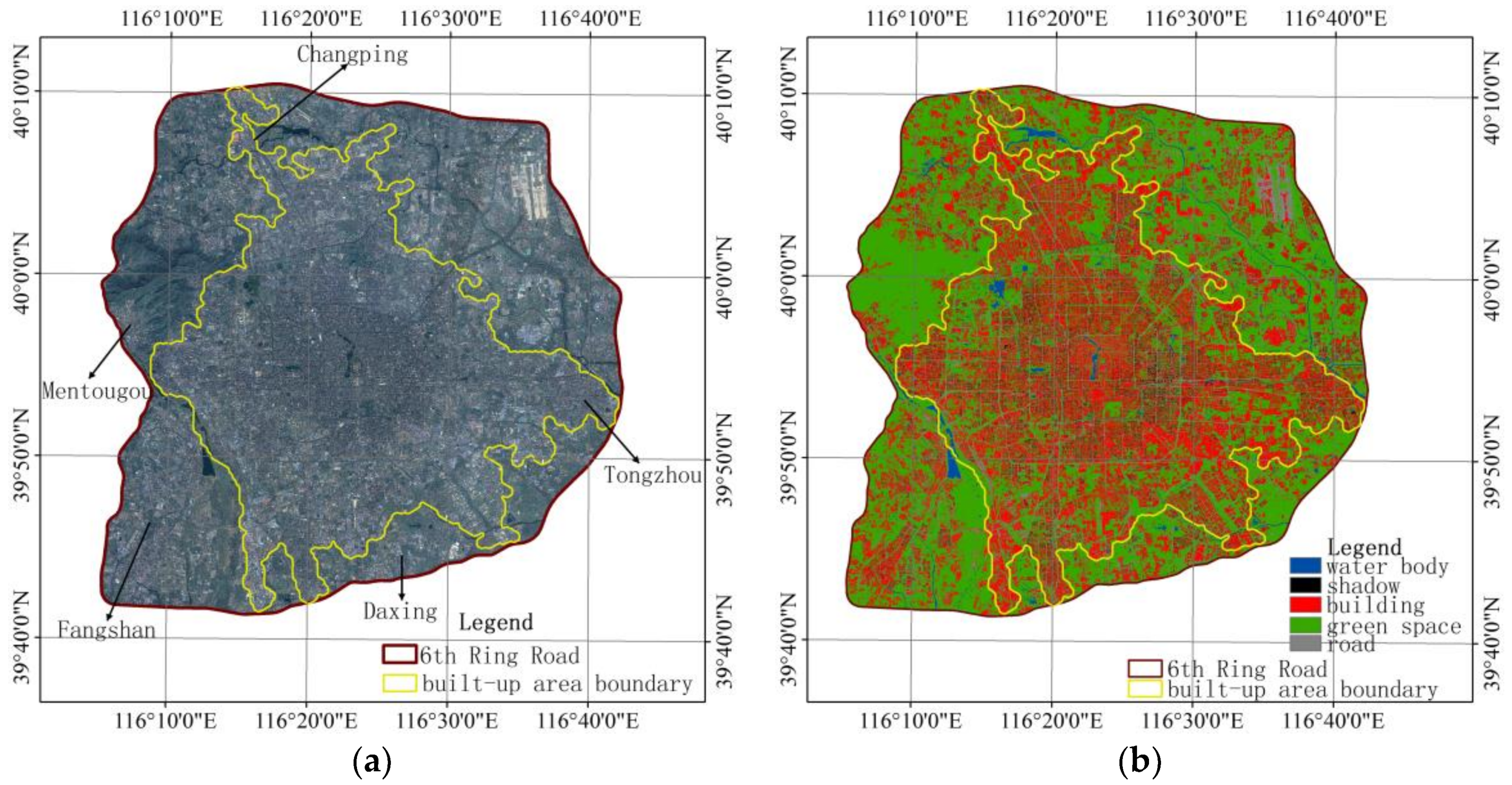
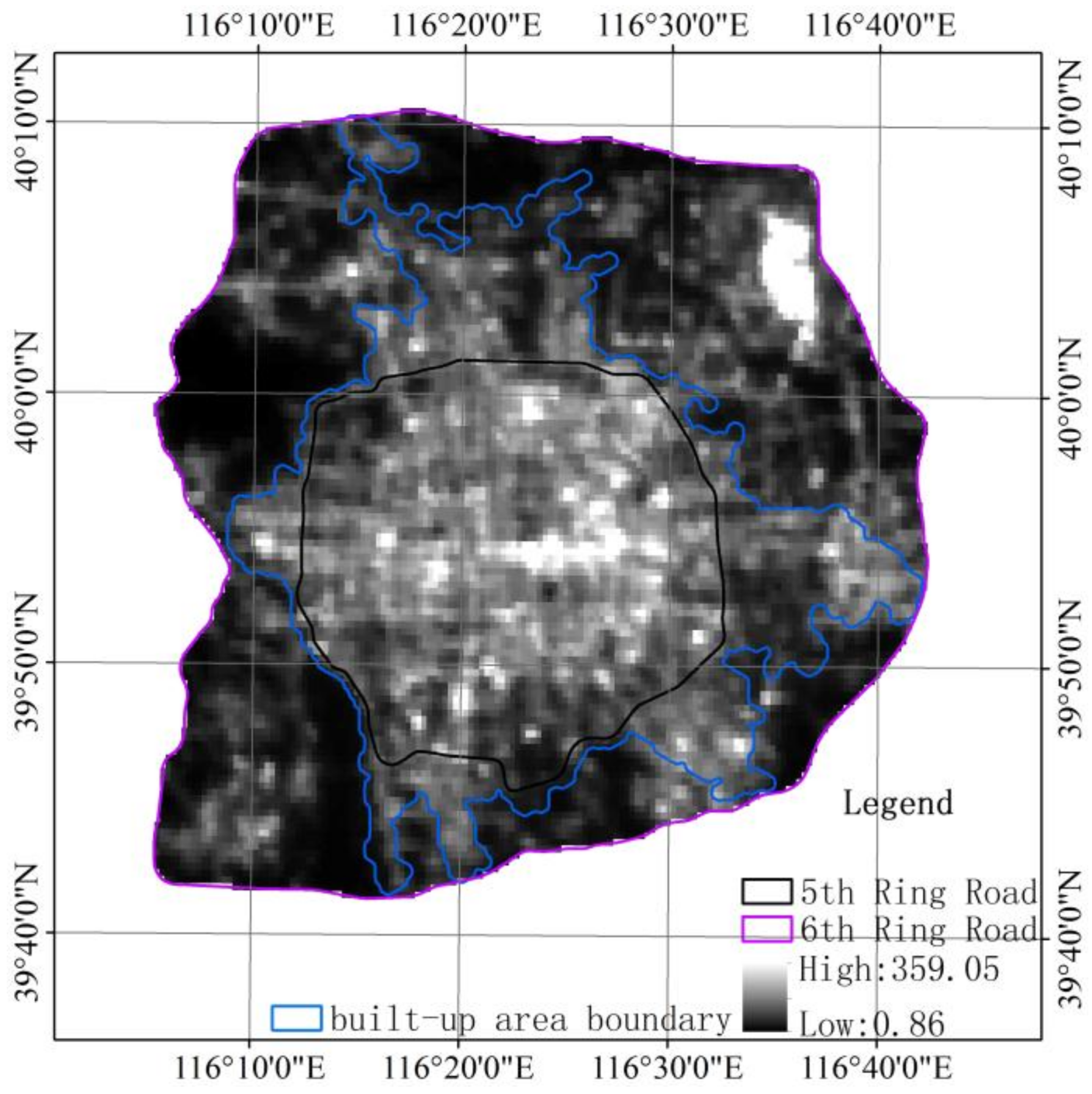
2.1. Study Area and Data
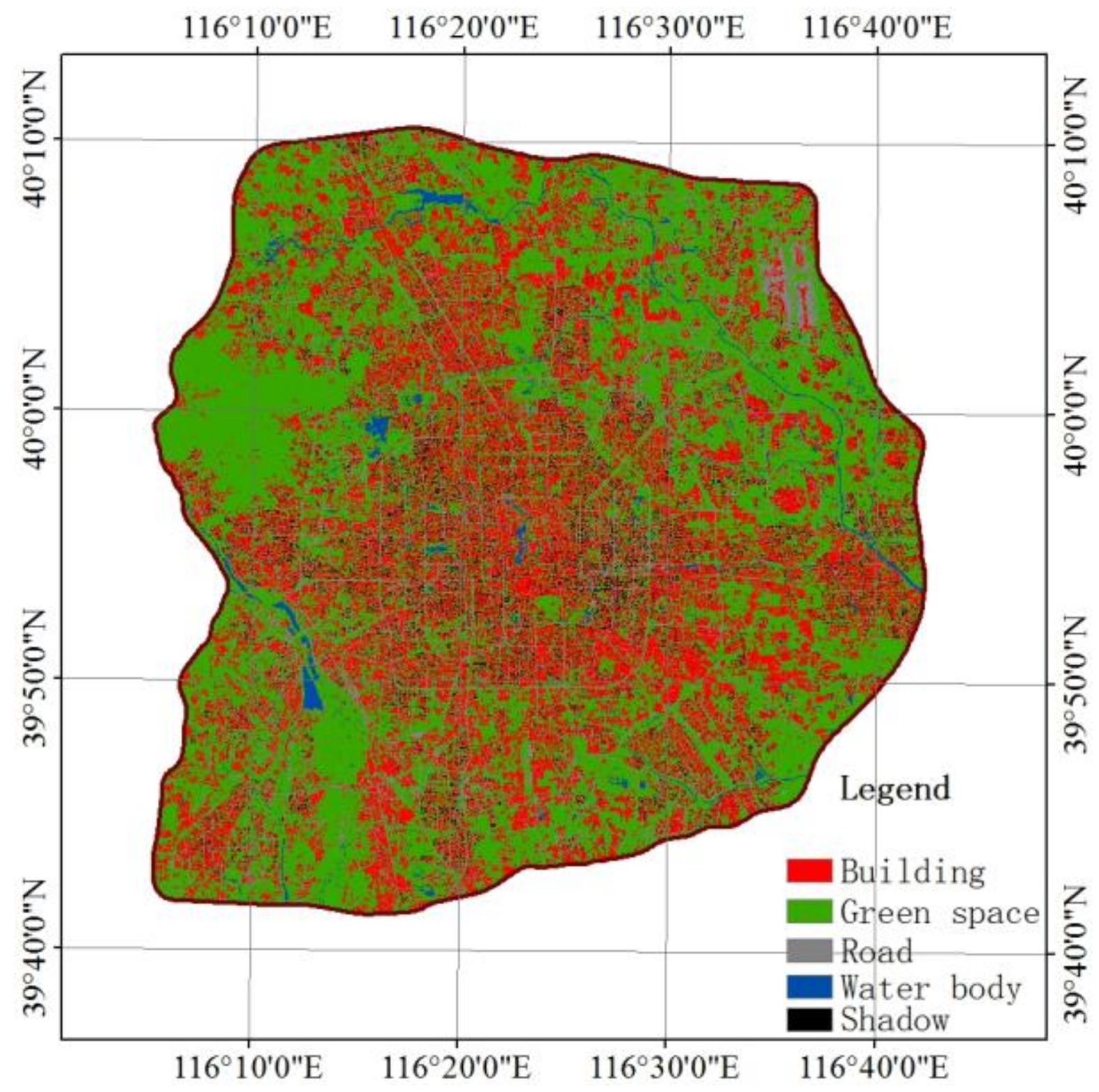
2.2. Data Pre-Processing and Analysis
2.3. Methods
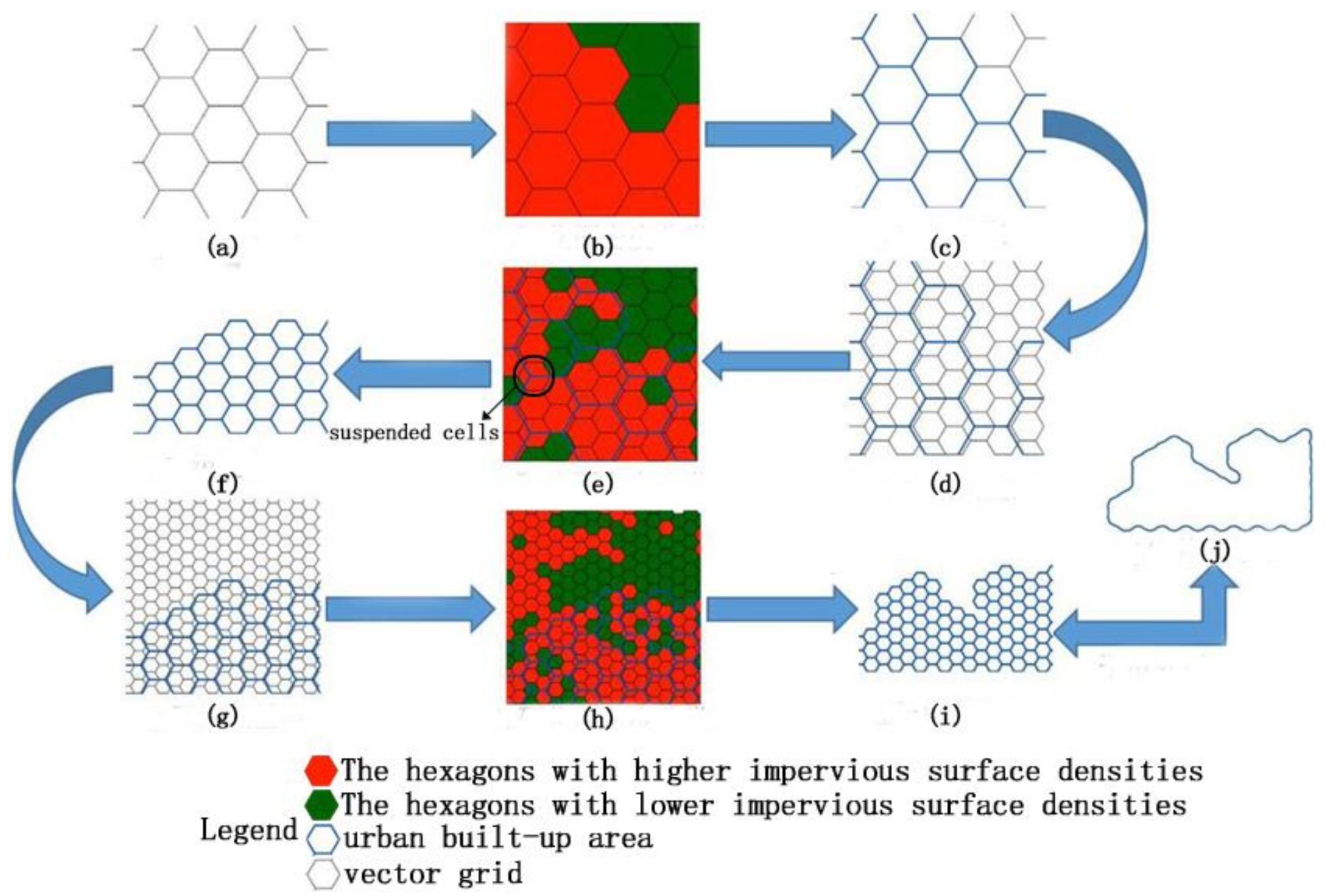
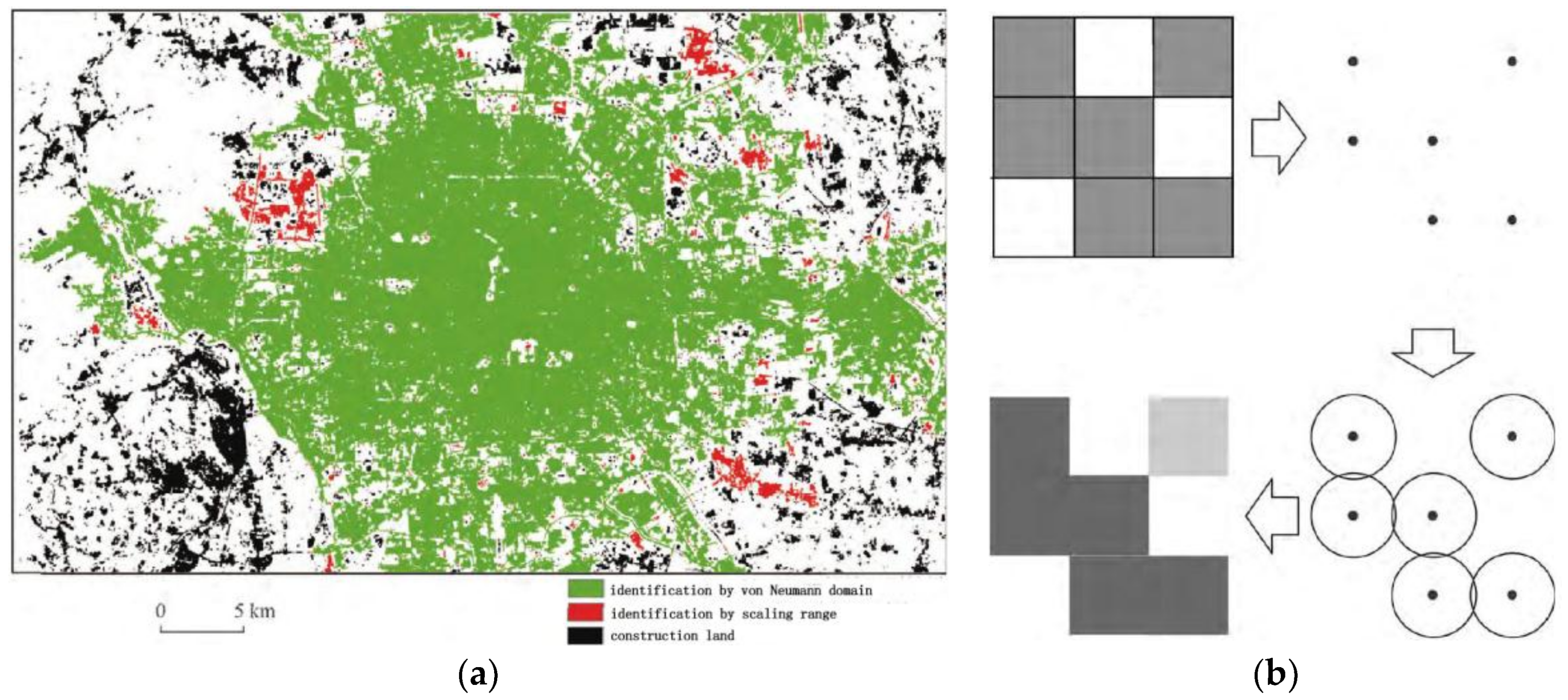
2.3.1. Defining a New Measurement Unit
2.3.2. Algorithm for Classifying Impervious Surface Densities
2.3.3. Steps for Extracting Continuous Impervious Surfaces of High Density
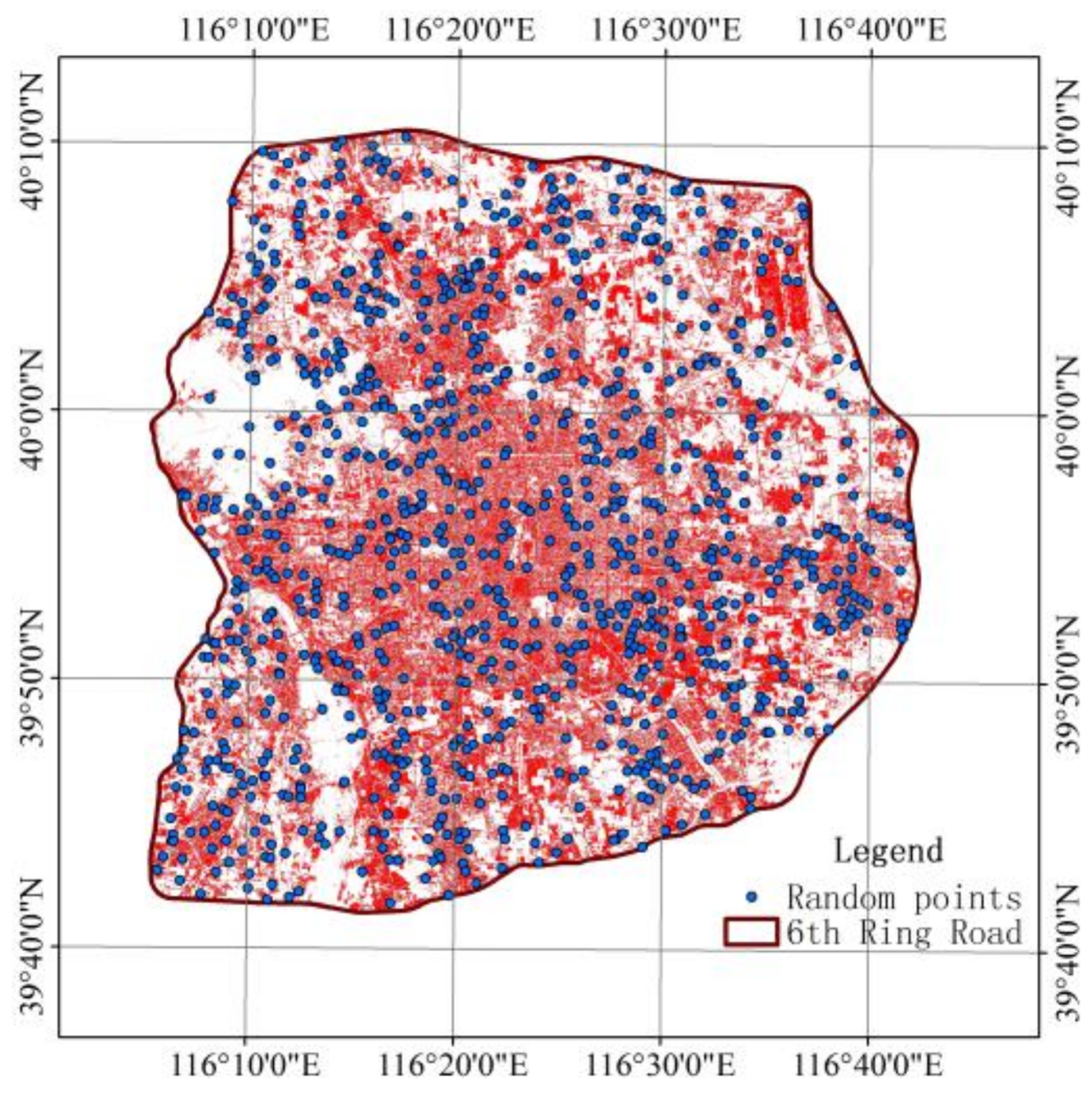
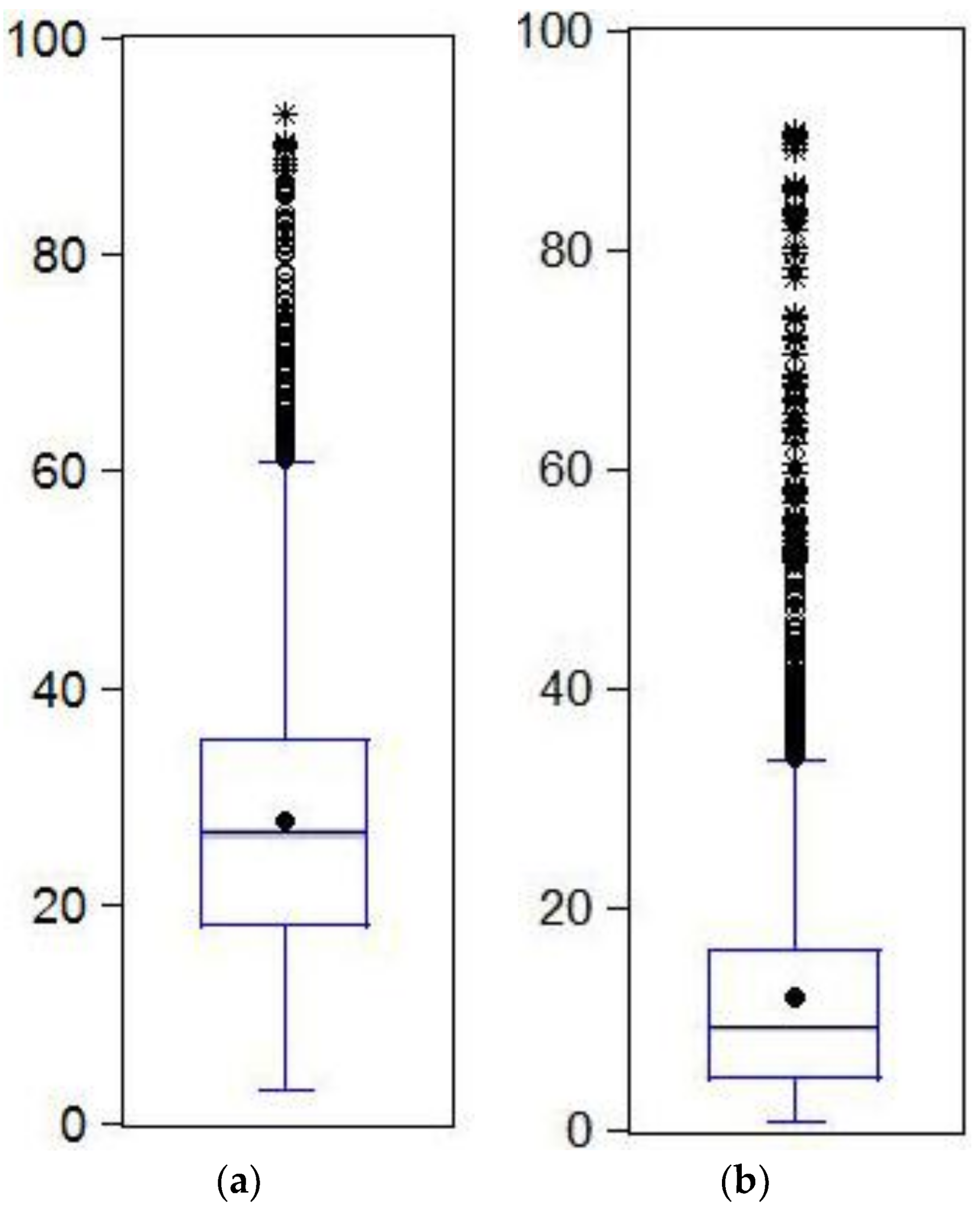
2.3.4. Plausibility Check and Accuracy Assessment
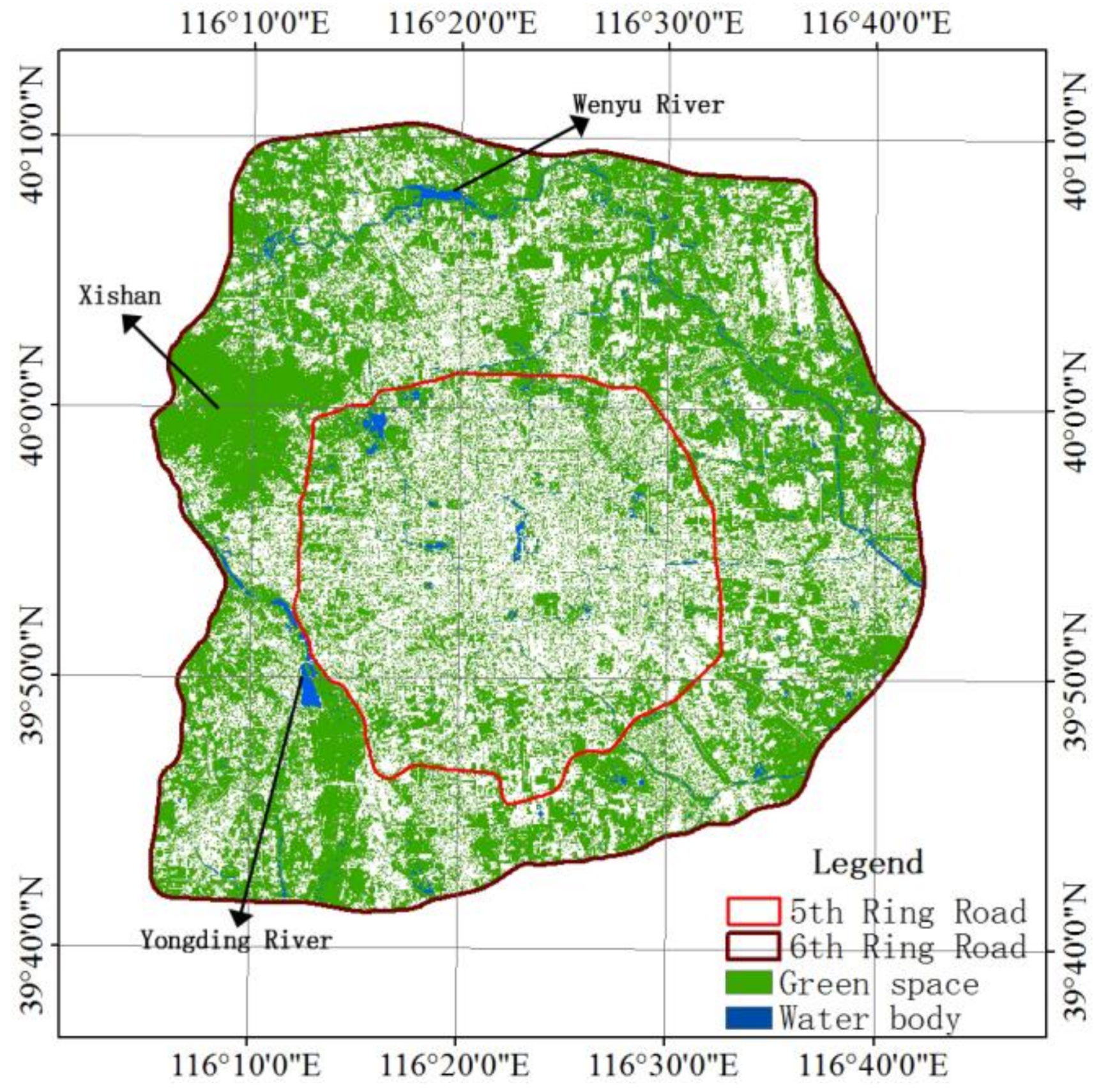
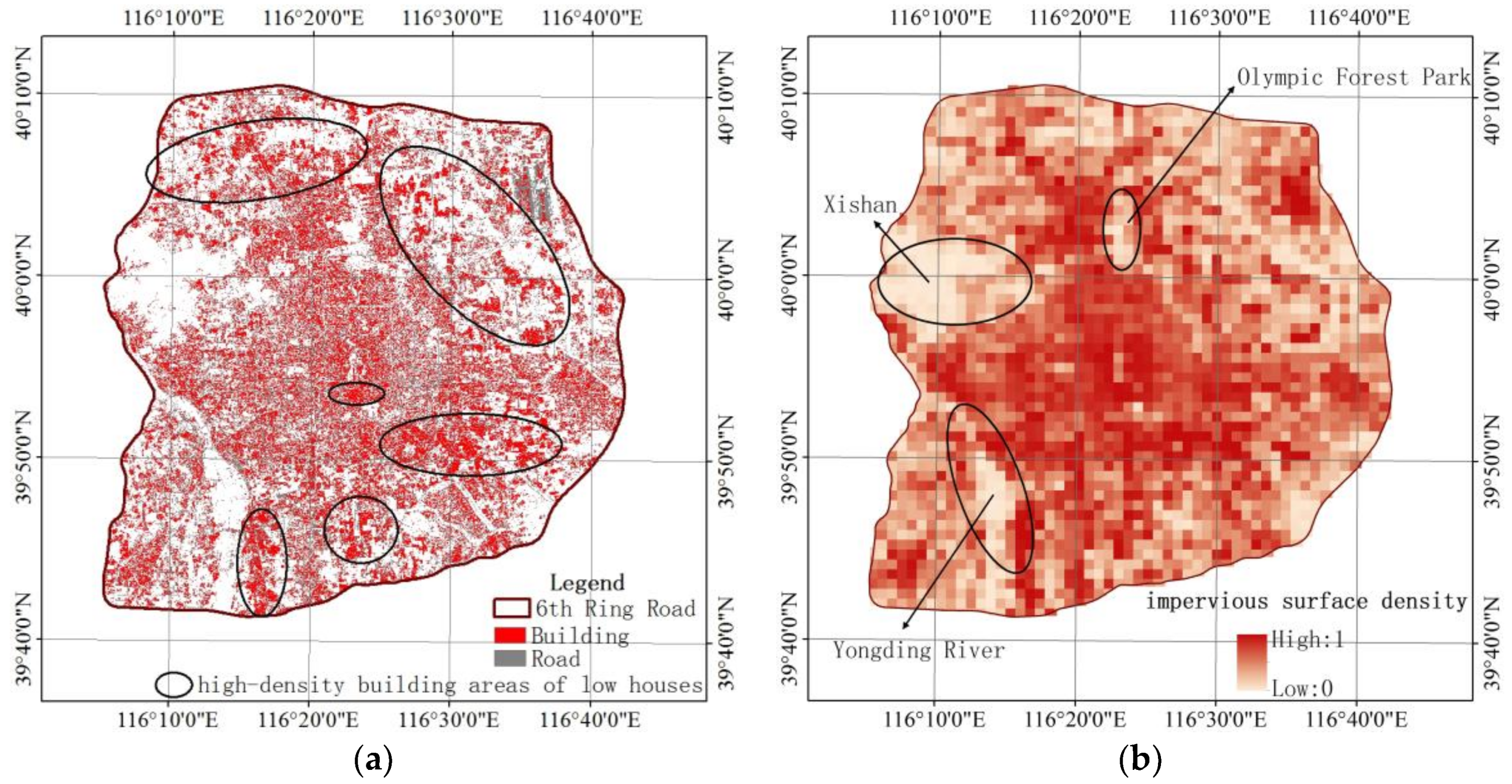
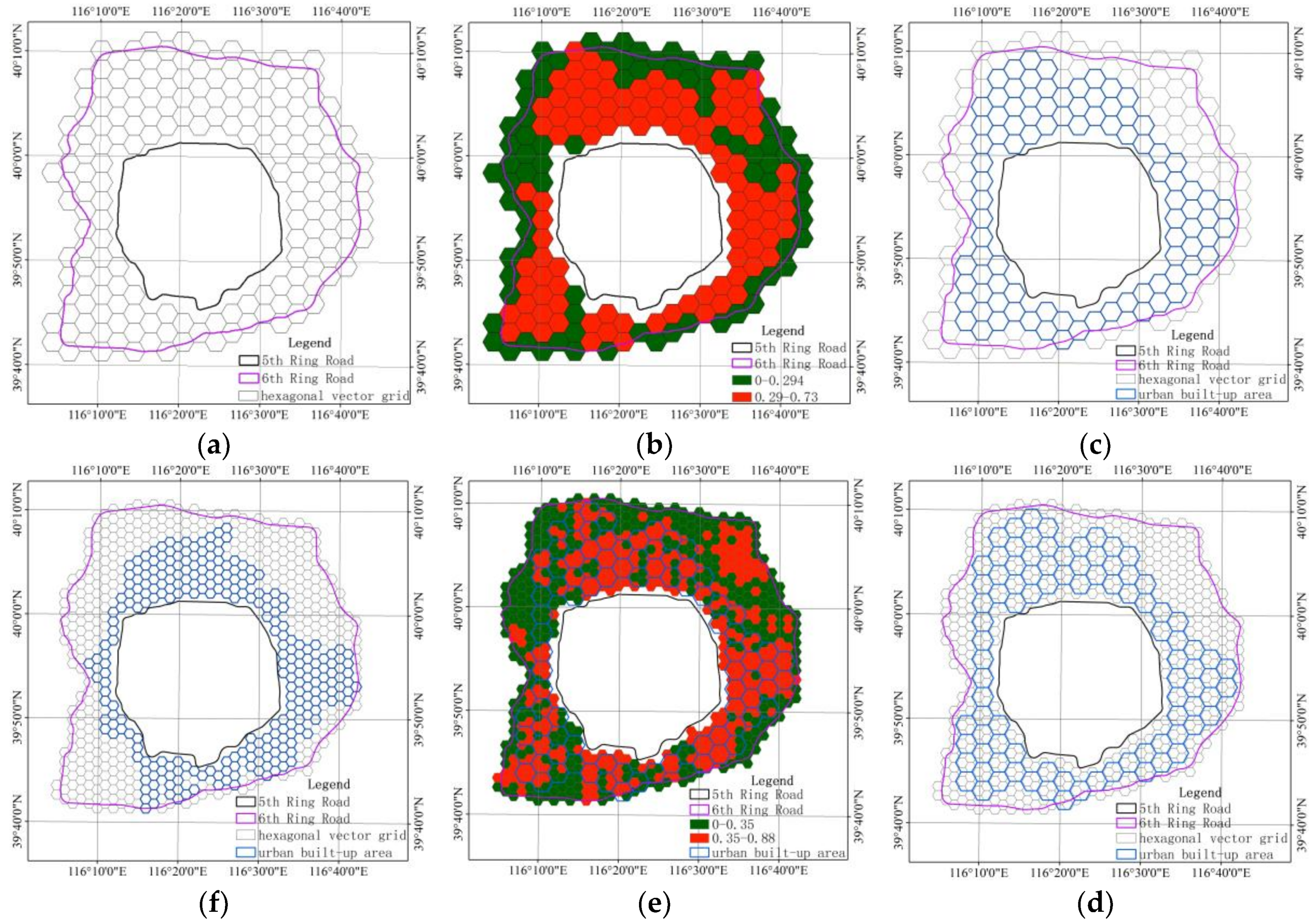
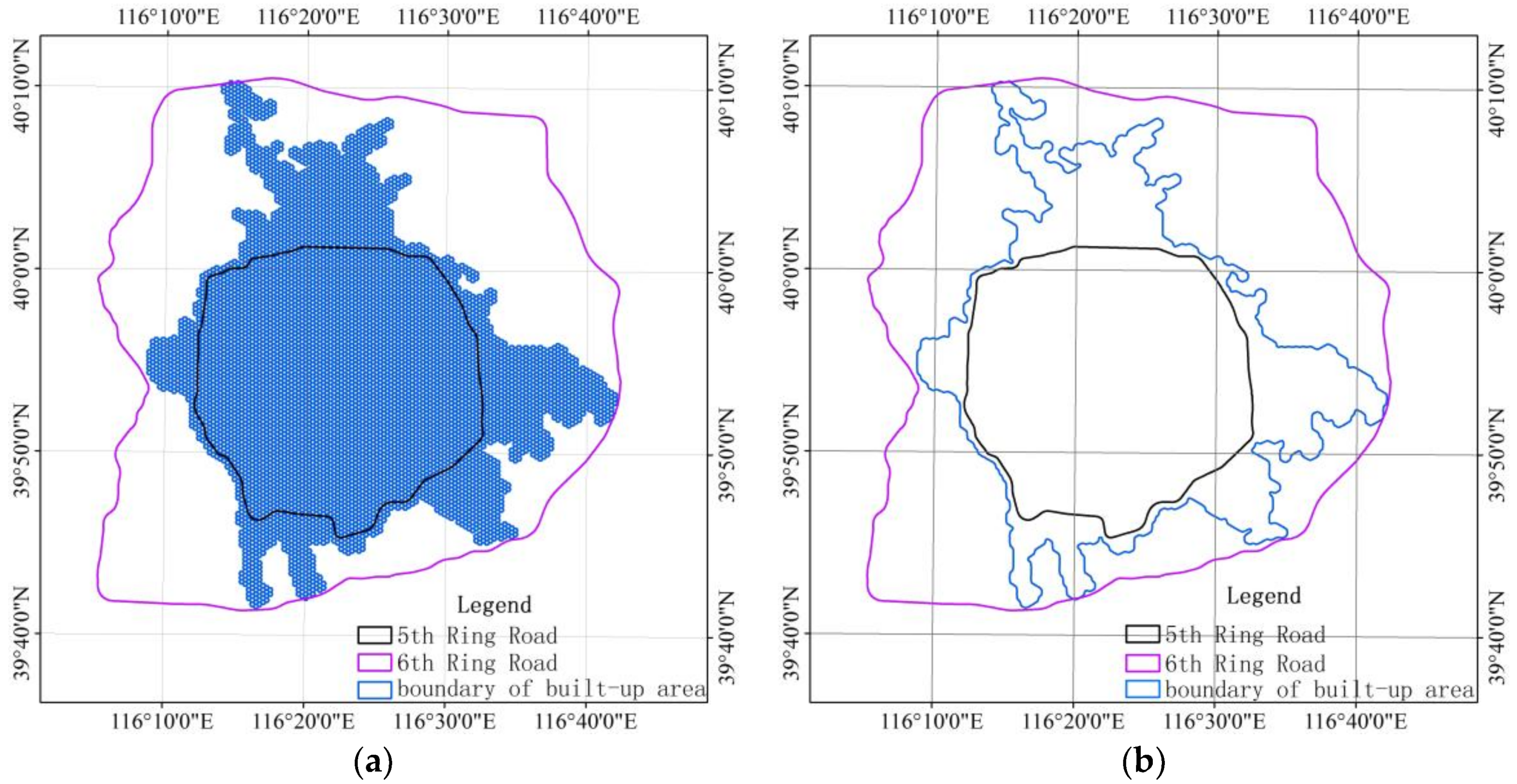
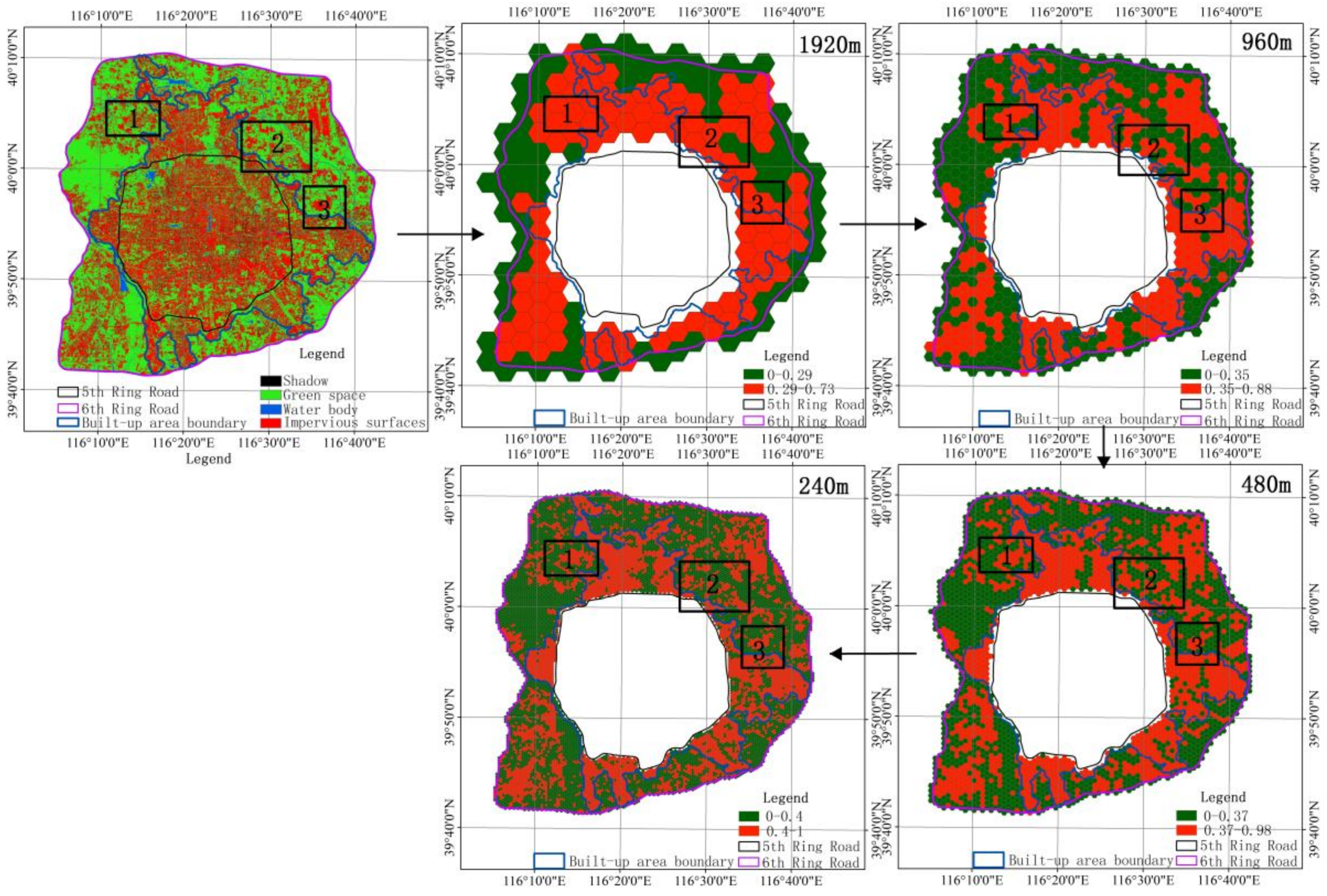
3. Results
4. Discussion and Conclusions
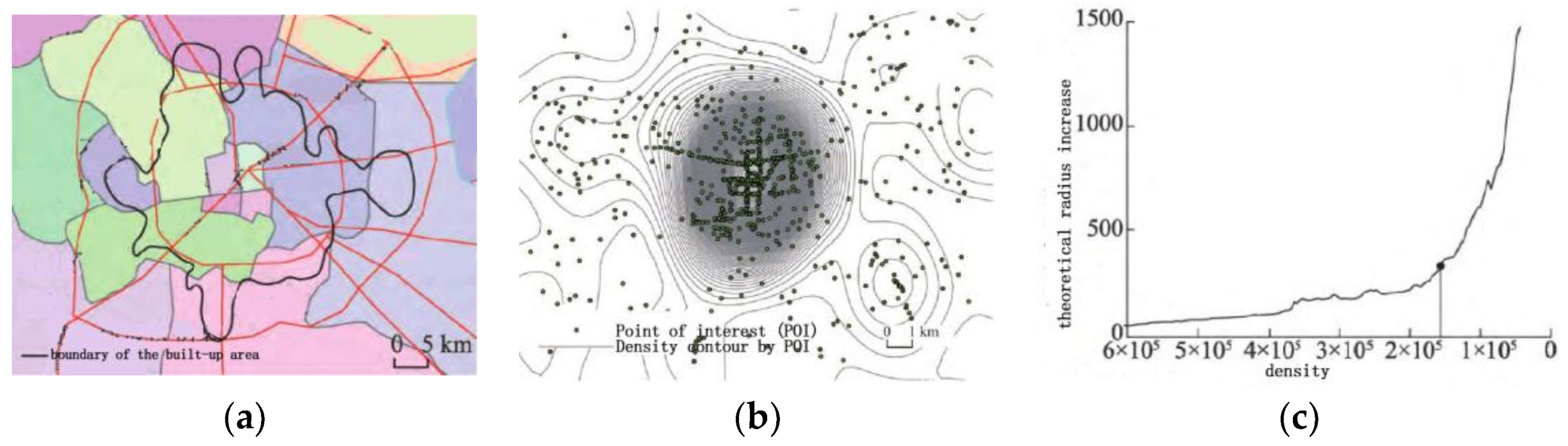
4.1. Comparison with Previous Studies
4.2. Plausibility Check and Accuracy Assesement
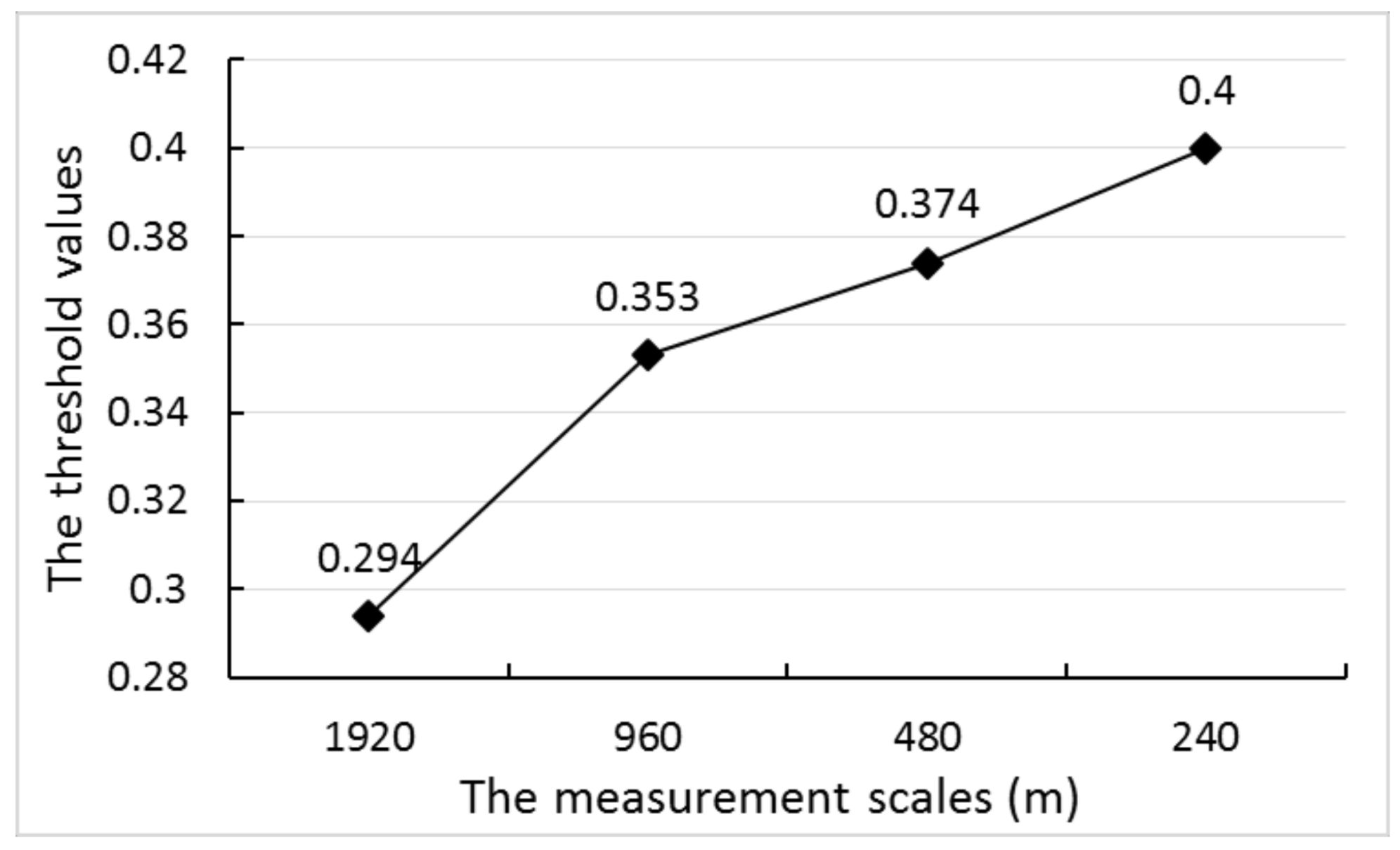
4.3. The Measurement Scale Effects on the Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, Z.; Gao, X. A novel method for identifying the boundary of urban built-up areas with poi data. Acta Geogr. Sin. 2016, 71, 928–939. [Google Scholar]
- Tannier, C.; Thomas, I.; Vuidel, G.; Frankhauser, P. A fractal approach to identifying urban boundaries. Geogr. Anal. 2011, 43, 211–227. [Google Scholar] [CrossRef]
- Forstall, R.L.; Chan, K.W. Urban places: Statistical definitions. Int. Encycl. Soc. Behav. Sci. 2015, 24, 854–861. [Google Scholar]
- Taubenböck, H.; Wiesner, M.; Felbier, A.; Marconcini, M.; Esch, T.; Dech, S. New dimensions of urban landscapes: The spatio-temporal evolution from a polynuclei area to a mega-region based on remote sensing data. Appl. Geogr. 2014, 47, 137–153. [Google Scholar] [CrossRef]
- Florida, R. Megaregions: The importance of place. Harv. Bus. Rev. 2008, 33, 18–19. [Google Scholar]
- Pryor, R.J. Defining the rural-urban fringe. Soc. Forces 1968, 47, 202–215. [Google Scholar] [CrossRef]
- Fesenmaier, D.R.; Goodchild, M.F.; Morrison, S. The spatial structure of the rural-urban fringe: A multivariate approach. Can. Geogr. 1979, 23, 255–265. [Google Scholar] [CrossRef]
- Sullivan, W.C.; Lovell, S.T. Improving the visual quality of commercial development at the rural-urban fringe. Landsc. Urban Plan. 2006, 77, 152–166. [Google Scholar] [CrossRef]
- Laurence, J.C.; Cui, G. Administrative changes and urban population in China. Ann. Assoc. Am. Geogr. 2015, 77, 373–395. [Google Scholar] [CrossRef]
- Martin, M.F. Defining China’s rural population. China Q. 1992, 130, 392–401. [Google Scholar] [CrossRef]
- Chan, K.W. Misconceptions and complexities in the study of China’s cities: Definitions, statistics, and implications. Eurasian Geogr. Econ. 2007, 48, 383–412. [Google Scholar] [CrossRef]
- Zhou, Y.S.Y. Toward establishing the concept of physical urban area in China. Acta Geogr. Sin. 1995, 62, 289–301. [Google Scholar]
- Mao, Q.; Ying, L.; Kang, W.; Qingfei, Z. Spatio-temporal changes of population density and urbanization pattern in China (2000–2010). China City Plan. Rev. 2016, 25, 8–14. [Google Scholar]
- Wang, F.; Zhou, Y. Modelling urban population densities in Beijing 1982–90: Suburbanisation and its causes. Urban Stud. 2014, 36, 271–287. [Google Scholar] [CrossRef]
- Luo, S.G.; Johnston, A.; Chen, D.C. Approach to delimiting metropolitan regions’ boundary and grading urban hierarchy within a metropolitan region—A case study of Shanghai metropolitan region. Chin. Geogr. Sci. 2008, 18, 197–205. [Google Scholar] [CrossRef]
- Clark, C. Urban population densities. J. R. Stat. Soc. 1951, 114, 490–496. [Google Scholar] [CrossRef]
- Masek, J.G.; Lindsay, F.E.; Goward, S.N. Dynamics of urban growth in the Washington DC metropolitan area, 1973–1996, from Landsat observations. Int. J. Remote Sens. 2000, 21, 3473–3486. [Google Scholar] [CrossRef]
- Hereher, M.E. Analysis of urban growth at Cairo, Egypt using remote sensing and GIS. Nat. Sci. 2012, 4, 355–361. [Google Scholar] [CrossRef]
- Abed, J.; Kaysi, I. Identifying urban boundaries: Application of remote sensing and geographic information system technologies. Can. J. Civ. Eng. 2003, 30, 992–999. [Google Scholar] [CrossRef]
- Li, Y.; Zhan, Q. Identification of urban boundaries based on geographic information system and land cover: A case in Wuhan. Urban. Land Use 2015, 2014, 63–70. [Google Scholar]
- Georg, I.; Blaschke, T.; Taubenböck, H. Are we in boswash yet? A multi-source geodata approach to spatially delimit urban corridors. ISPRS Int. Geo-Inf. 2018, 7, 15. [Google Scholar] [CrossRef]
- Taubenböck, H.; Ferstl, J.; Dech, S. Regions set in stone—Delimiting and categorizing regions in Europe by settlement patterns derived from EO-data. ISPRS Int. Geo-Inf. 2017, 6, 55. [Google Scholar] [CrossRef]
- Small, C.; Pozzi, F.; Elvidge, C.D. Spatial analysis of global urban extent from DMSP-OLS night lights. Remote Sens. Environ. 2005, 96, 277–291. [Google Scholar] [CrossRef]
- Liu, Z.F.; He, C.Y.; Zhang, Q.F.; Huang, Q.X.; Yang, Y. Extracting the dynamics of urban expansion in China using DMSP-OLS nighttime light data from 1992 to 2008. Landsc. Urban. Plan 2012, 106, 62–72. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Lawrence, W.T.; Stutzer, D.C.; Elvidge, C.D. A technique for using composite DMSP/OLS “city lights” satellite data to map urban area. Remote Sens. Environ. 1997, 61, 361–370. [Google Scholar] [CrossRef]
- Rozenfeld, H.D.; Rybski, D.; Andrade, J.S.; Batty, M.; Stanley, H.E.; Makse, H.A. Laws of population growth. Proc. Natl. Acad. Sci. USA 2008, 105, 18702–18707. [Google Scholar] [CrossRef] [PubMed]
- Rozenfeld, H.D.; Rybski, D.; Gabaix, X.; Makse, H.A. The area and population of cities: New insights from a different perspective on cities. Am. Econ. Rev. 2011, 101, 2205–2225. [Google Scholar] [CrossRef]
- Tan, X.; Chen, Y. Urban boundary identification based on neighborhood dilation. Prog. Geogr. 2015, 34, 1259–1265. [Google Scholar]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from tm imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Pesaresi, M.; Gerhardinger, A.; Kayitakire, F. A robust built-up area presence index by anisotropic rotation-invariant textural measure. IEEE J. Stars 2008, 1, 180–192. [Google Scholar] [CrossRef]
- Su, F.Z.; Gao, Y.; Zhou, C.H.; Yang, X.M.; Fei, X.Y. Scale effects of the continental coastline of China. J. Geogr. Sci. 2011, 21, 1101–1111. [Google Scholar] [CrossRef]
- Yan, G.J.; Hu, R.H.; Wang, Y.T.; Ren, H.Z.; Song, W.J.; Qi, J.B.; Chen, L. Scale effect in indirect measurement of leaf area index. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3475–3484. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote-sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Krehl, A.; Siedentop, S.; Taubenböck, H.; Wurm, M. A comprehensive view on urban spatial structure: Urban density patterns of German city regions. ISPRS Int. Geo-Inf. 2016, 5, 76. [Google Scholar] [CrossRef]
- Taubenböck, H.; Standfuß, I.; Klotz, M.; Wurm, M. The physical density of the city—Deconstruction of the delusive density measure with evidence from two European megacities. ISPRS Int. Geo-Inf. 2016, 5, 206. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M.; Alparone, L. Enhanced Gram-Schmidt Spectral Sharpening Based on Multivariate Regression of MS and Pan Data. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 3806–3809. [Google Scholar]
- Serpico, S.B. Support vector machines for remote sensing image classification. Proc. SPIE 2001, 4170, 160–166. [Google Scholar]
- Ghani, N.L.A.; Abidin, S.Z.Z.; Khalid, N.E.A. Accuracy Assessment of Urban Growth Pattern Classification Methods Using Confusion Matrix and ROC Analysis. In Proceedings of the 1st International Conference on Soft Computing in Data Science, Putrajaya, Malaysia, 2–3 September 2015. [Google Scholar]
- North, M.A. A Method for Implementing a Statistically Significant Number of Data Classes in the Jenks Algorithm. In Proceedings of the International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, China, 14–16 August 2009; pp. 35–38. [Google Scholar]
- Khan, F. An initial seed selection algorithm for k-means clustering of georeferenced data to improve replicability of cluster assignments for mapping application. Appl. Soft Comput. 2012, 12, 3698–3700. [Google Scholar] [CrossRef]
- Iglewicz, B.; Hoaglin, D. Use of boxplots for process evaluation. J. Qual. Technol. 1987, 19, 180–190. [Google Scholar] [CrossRef]


| Class | Buildings | Roads | Green Spaces | Water Bodies | Shadows | User’s Accuracy |
|---|---|---|---|---|---|---|
| Buildings | 207 | 19 | 4 | 0 | 4 | 88.46% |
| Roads | 14 | 131 | 3 | 0 | 5 | 85.62% |
| Green spaces | 3 | 8 | 291 | 4 | 11 | 91.80% |
| Water bodies | 0 | 0 | 0 | 76 | 6 | 92.68% |
| Shadows | 1 | 2 | 1 | 9 | 201 | 93.93% |
| Producer’s accuracy | 92% | 81.88% | 97.32% | 85.39% | 88.55% | |
| Overall accuracy: 90.60%; kappa coefficient: 87.83% | ||||||
| Class | Built-Up Area | Rural Settlements | User’s Accuracy |
|---|---|---|---|
| Built-up area | 572 | 33 | 94.55% |
| rural settlements | 26 | 369 | 93.42% |
| Producer’s accuracy | 95.65% | 91.79% | |
| Overall accuracy: 94.1%; kappa coefficient: 87.69% | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Tu, M.; Wang, S.; Liu, W. A Novel Approach for Identifying Urban Built-Up Area Boundaries Using High-Resolution Remote-Sensing Data Based on the Scale Effect. ISPRS Int. J. Geo-Inf. 2018, 7, 135. https://doi.org/10.3390/ijgi7040135
Zhou Y, Tu M, Wang S, Liu W. A Novel Approach for Identifying Urban Built-Up Area Boundaries Using High-Resolution Remote-Sensing Data Based on the Scale Effect. ISPRS International Journal of Geo-Information. 2018; 7(4):135. https://doi.org/10.3390/ijgi7040135
Chicago/Turabian StyleZhou, Yi, Mingguang Tu, Shixin Wang, and Wenliang Liu. 2018. "A Novel Approach for Identifying Urban Built-Up Area Boundaries Using High-Resolution Remote-Sensing Data Based on the Scale Effect" ISPRS International Journal of Geo-Information 7, no. 4: 135. https://doi.org/10.3390/ijgi7040135
APA StyleZhou, Y., Tu, M., Wang, S., & Liu, W. (2018). A Novel Approach for Identifying Urban Built-Up Area Boundaries Using High-Resolution Remote-Sensing Data Based on the Scale Effect. ISPRS International Journal of Geo-Information, 7(4), 135. https://doi.org/10.3390/ijgi7040135





