A Distance-Adaptive Refueling Recommendation Algorithm for Self-Driving Travel
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
2. Materials and Methods
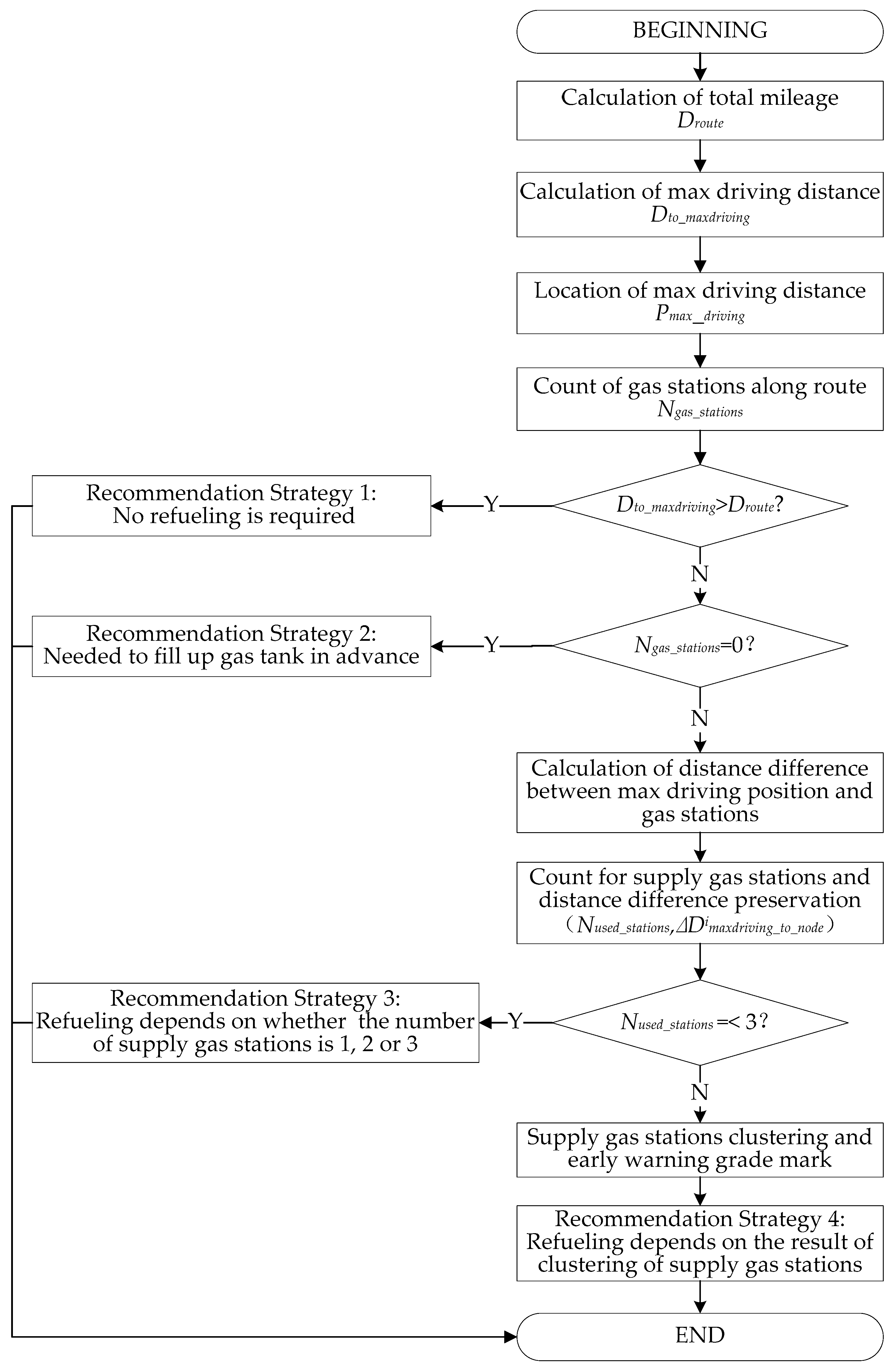
2.1. Algorithm Description
2.2. Key Decision Variables and Calculation Methods
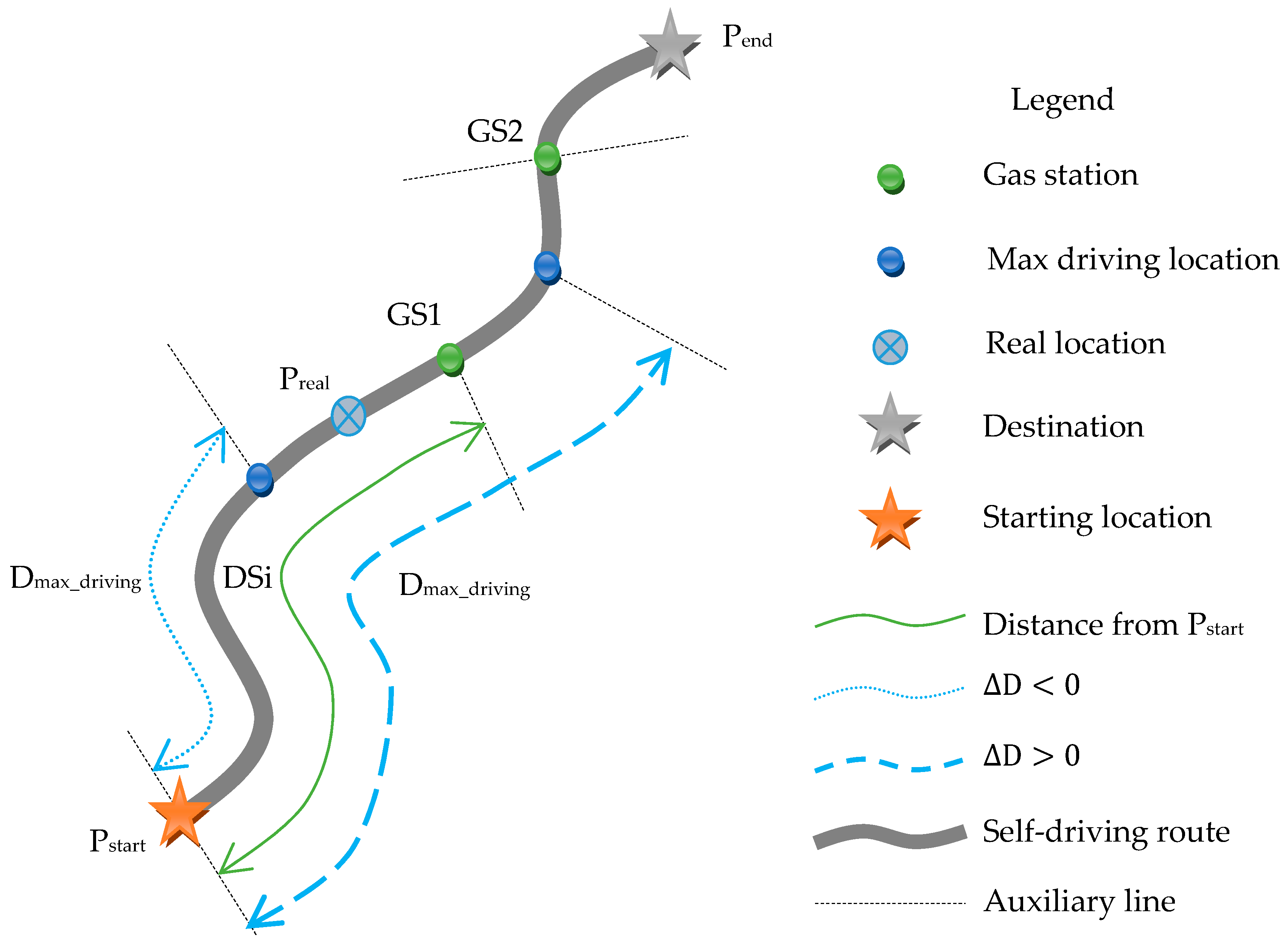
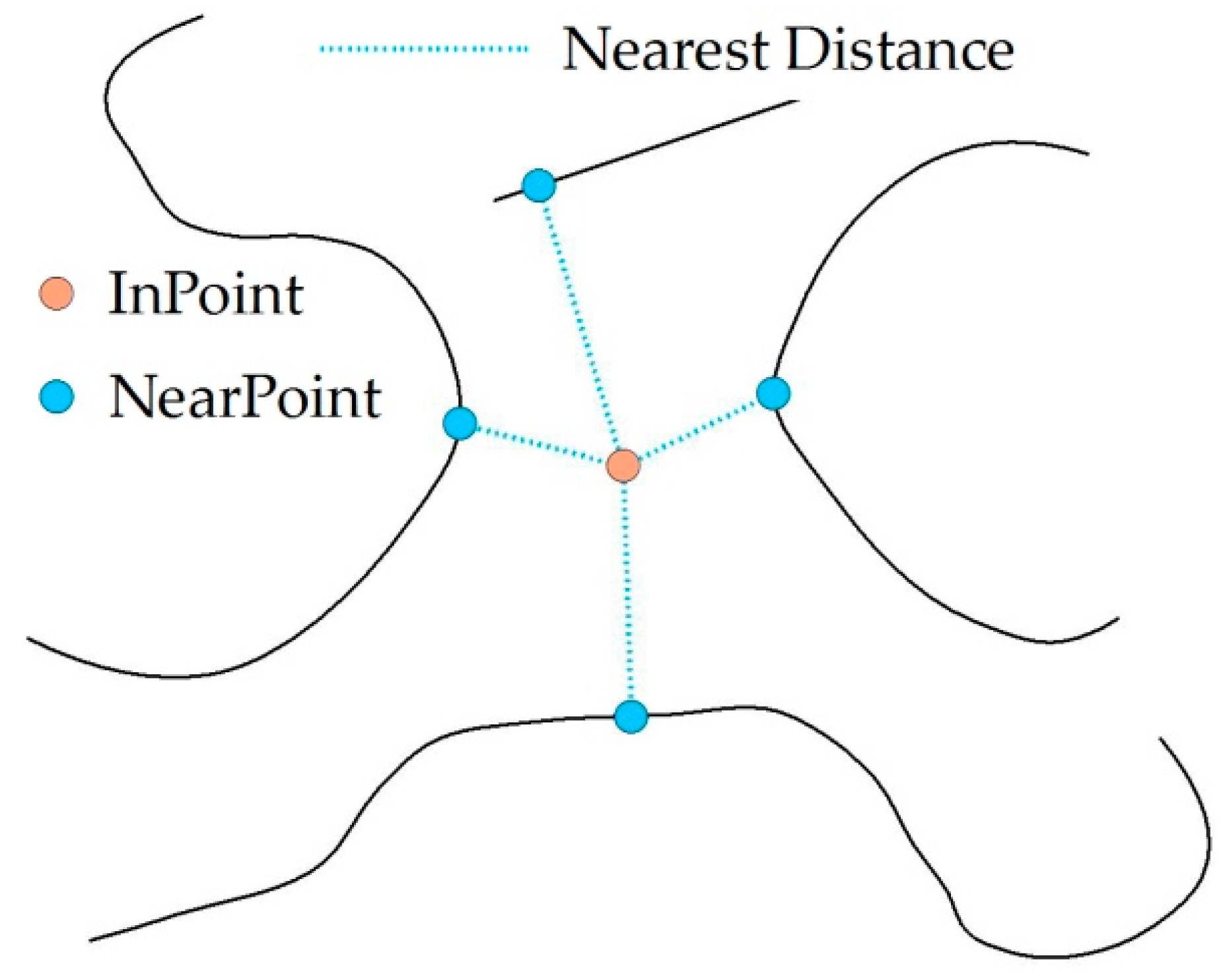
2.2.1. Calculation of the Three Distance Variables
2.2.2. Calculation of the Two Distance Differences
2.2.3. Calculation of the Two Counters of Gas Stations
2.3. Construction of Recommendation Rules and Design of Warning Mechanism
- When , there is one and only one refueling gas station along the route, which is marked with a red warning.
- When , beginning from the direction of the starting point, the first gas station is marked with an orange warning and the second gas station is marked with a red warning.
- When , beginning from the direction of the starting point, the first gas station is marked with a green warning, the second gas station is marked with an orange warning, and the third gas station is marked with a red warning.
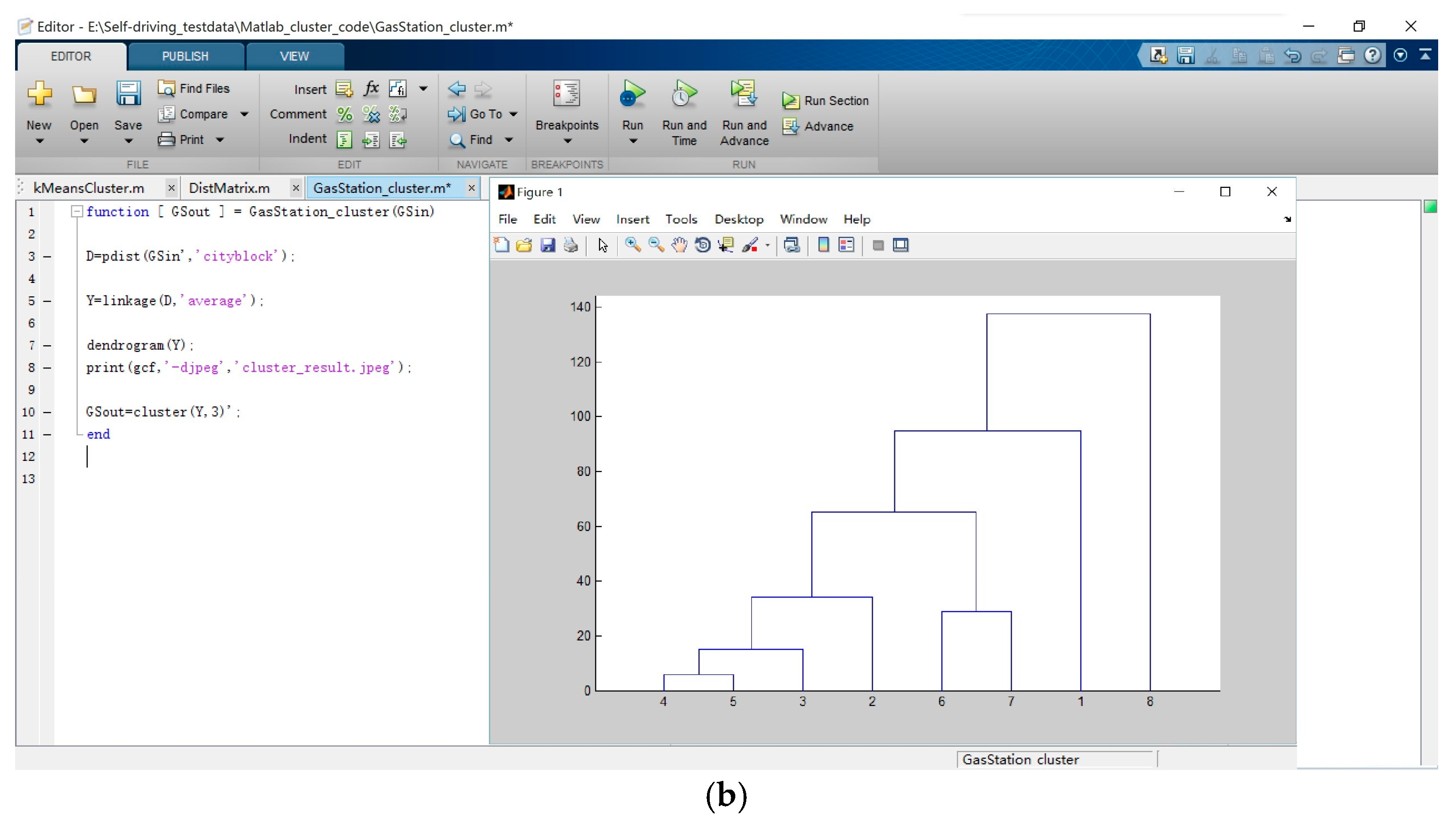
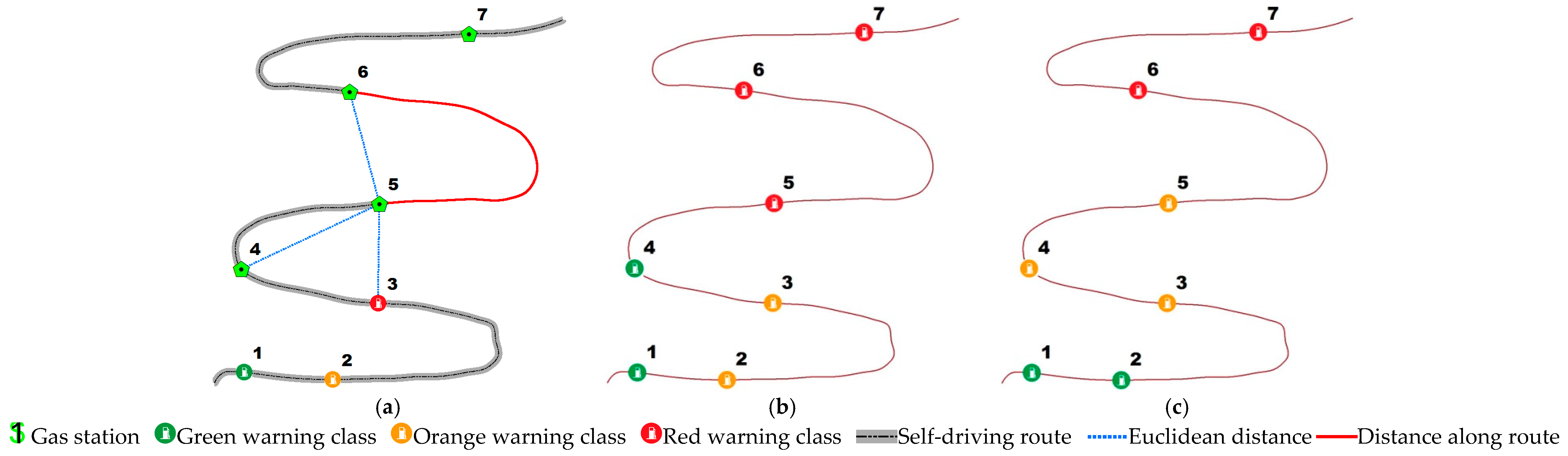
2.4. Layout Optimization of Refueling Service Based on Cluster Analysis
3. Results and Discussion
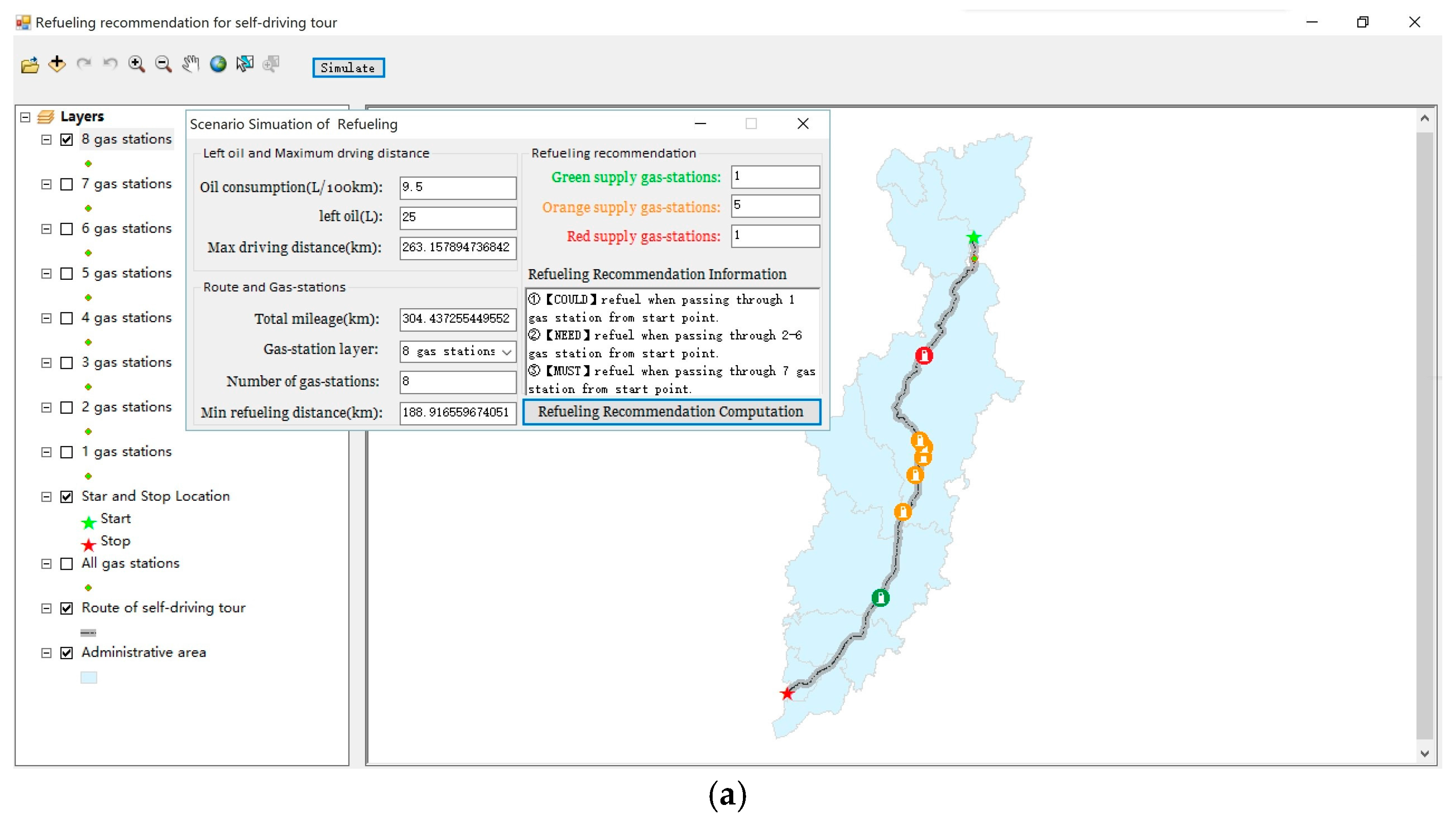
3.1. Design and Development of the Scenario Simulation System
3.2. Comparison and Sensitivity Analysis of Clustering Algorithm
3.2.1. Sensitivity Analysis of Clustering Attributes
3.2.2. Comparative Analysis of Clustering Algorithms
3.3. Test Data and Scenario Simulation Scheme
- (1)
- The self-driving route: A real path was used as the self-driving route, the starting point of which was located in Kunming, Yunnan Province, and the terminus of which was located in Zhaotong City, Yunnan Province, represented by red and blue stars, respectively.
- (2)
- Gas stations along the route: Several point elements representing gas stations were manually created near the route. According to the requirement for the scenario simulation, ten layers of gas stations were set up in this study; the number of gas stations per layer increased from 1 to 10, and these gas stations were located in different positions.
- (1)
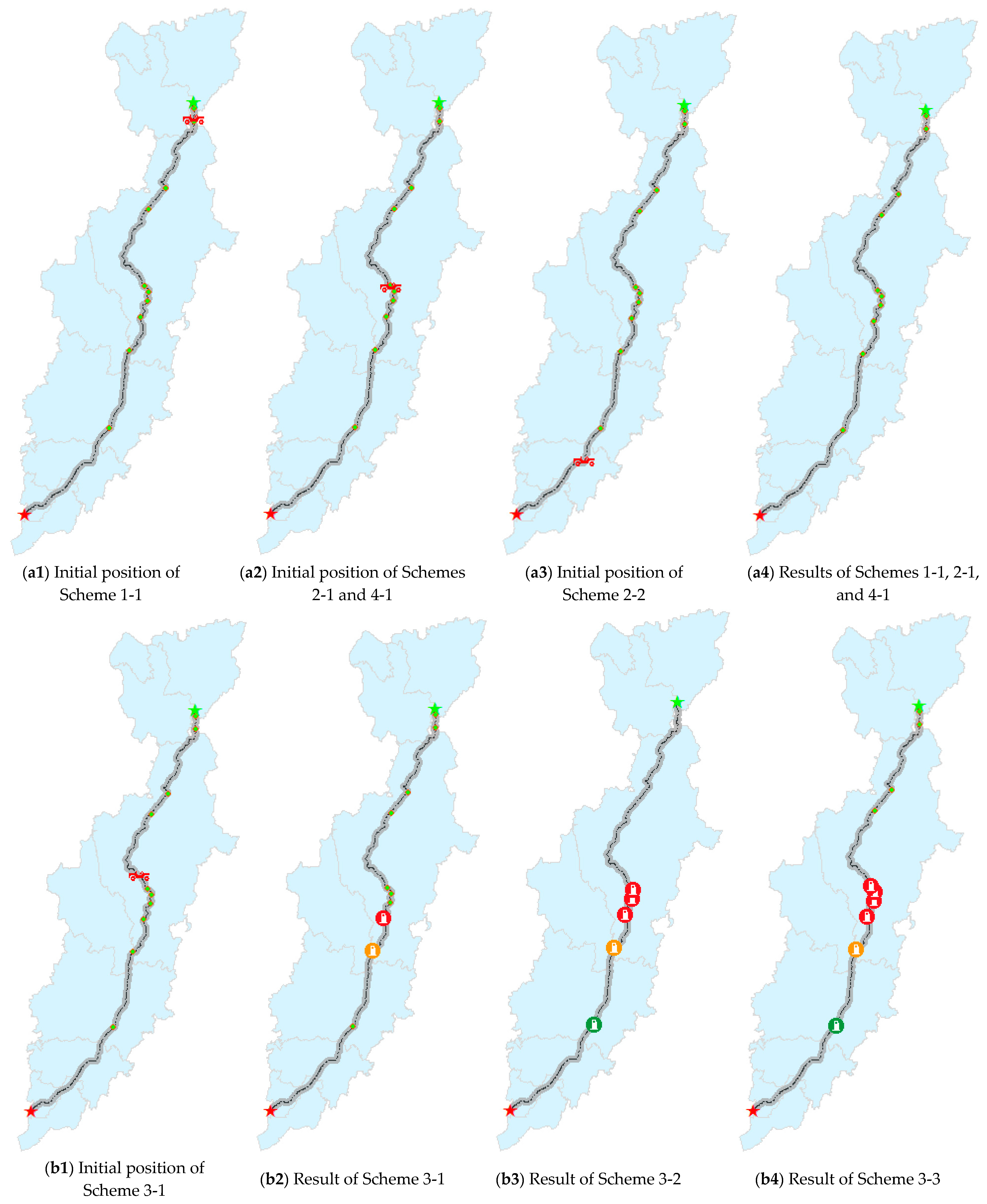
- Scenario 1: There was one testing scheme designed in Scenario 1. In this scenario, the maximum driving distance was greater than the aggregate mileage, and refueling was not required along the route. Scenario 1 was utilized to test the adaptability of recommendation Strategy 1.
- (2)
- Scenario 2: There were two testing schemes designed in Scenario 2 (Scheme 2-1 and Scheme 2-2). Scheme 2-1 indicated that the current remaining fuel was not enough for the vehicle to reach the nearest gas station along the way; Scheme 2-2 indicated that there was no refueling gas station along the route, recommending that the driver bring gas or fill up the gas tank in advance. The two testing schemes in Scenario 2 were utilized to test the adaptability of recommendation Strategy 2.
- (3)
- Scenario 3: There were three testing schemes designed in Scenario 3 (Scheme 3-1, Scheme 3-2, and Scheme 3-3). Supposing that the vehicle needed to refuel on the way, the impacts of a change in the number of refueling gas stations along the route on the recommendation strategy were explored in this scenario. The three testing schemes in Scenario 3 were mainly used to test the adaptability of mixed recommendations from Strategy 3 and Strategy 4.
- (4)
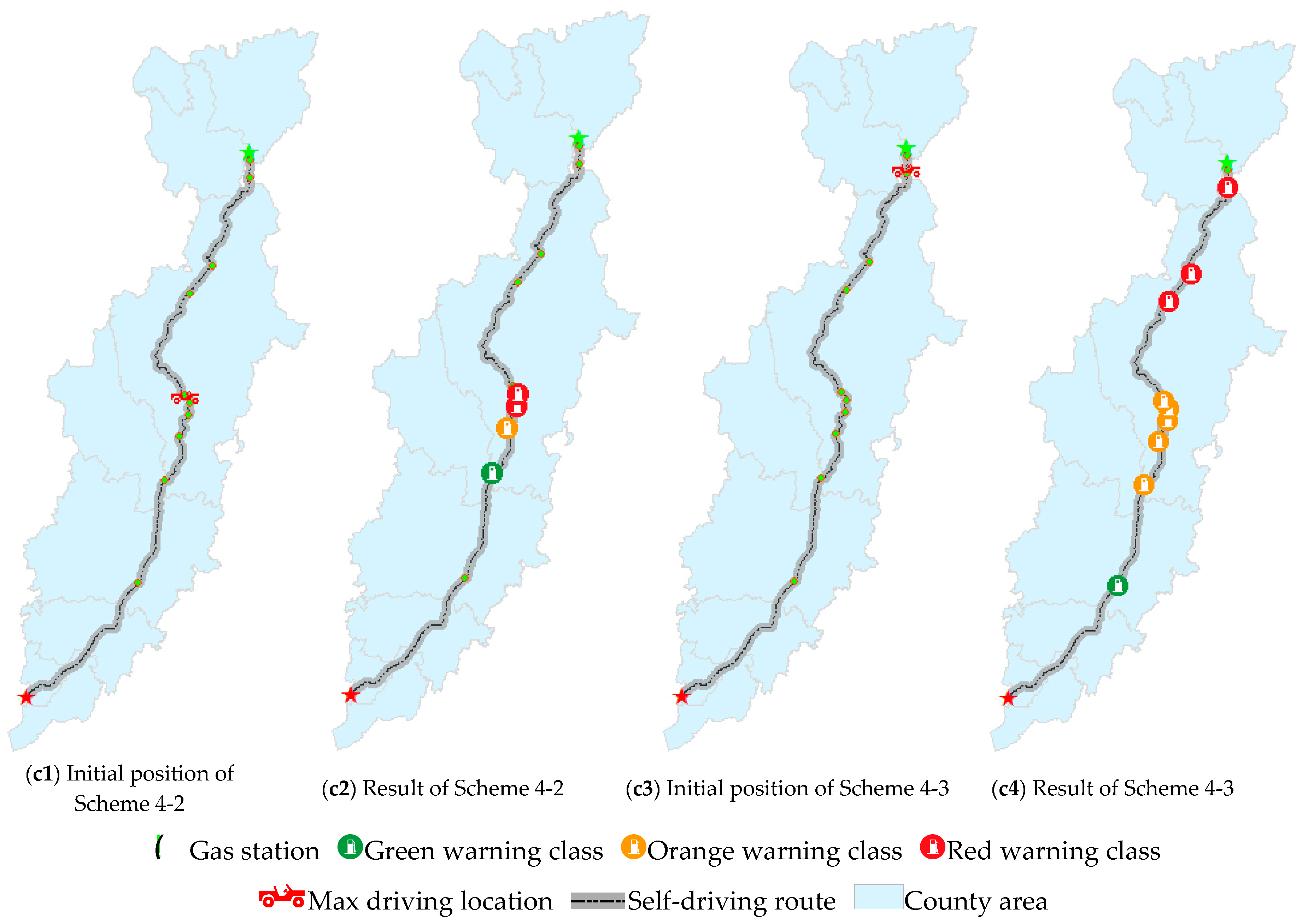
- Scenario 4: There were three testing schemes designed in Scenario 4 (Scheme 4-1, Scheme 4-2, and Scheme 4-3,). Supposing that the vehicle needed to refuel and that there were plenty of gas stations along the way, the influence of a change in the maximum driving distance of the vehicle and the number and layout of refueling gas stations on the recommendation strategy were explored in this scenario. The three testing schemes in Scenario 4 were mainly used to test the adaptability of mixed recommendations from Strategy 2 and Strategy 4.
3.4. Results and Evaluation of Scenario Simulation
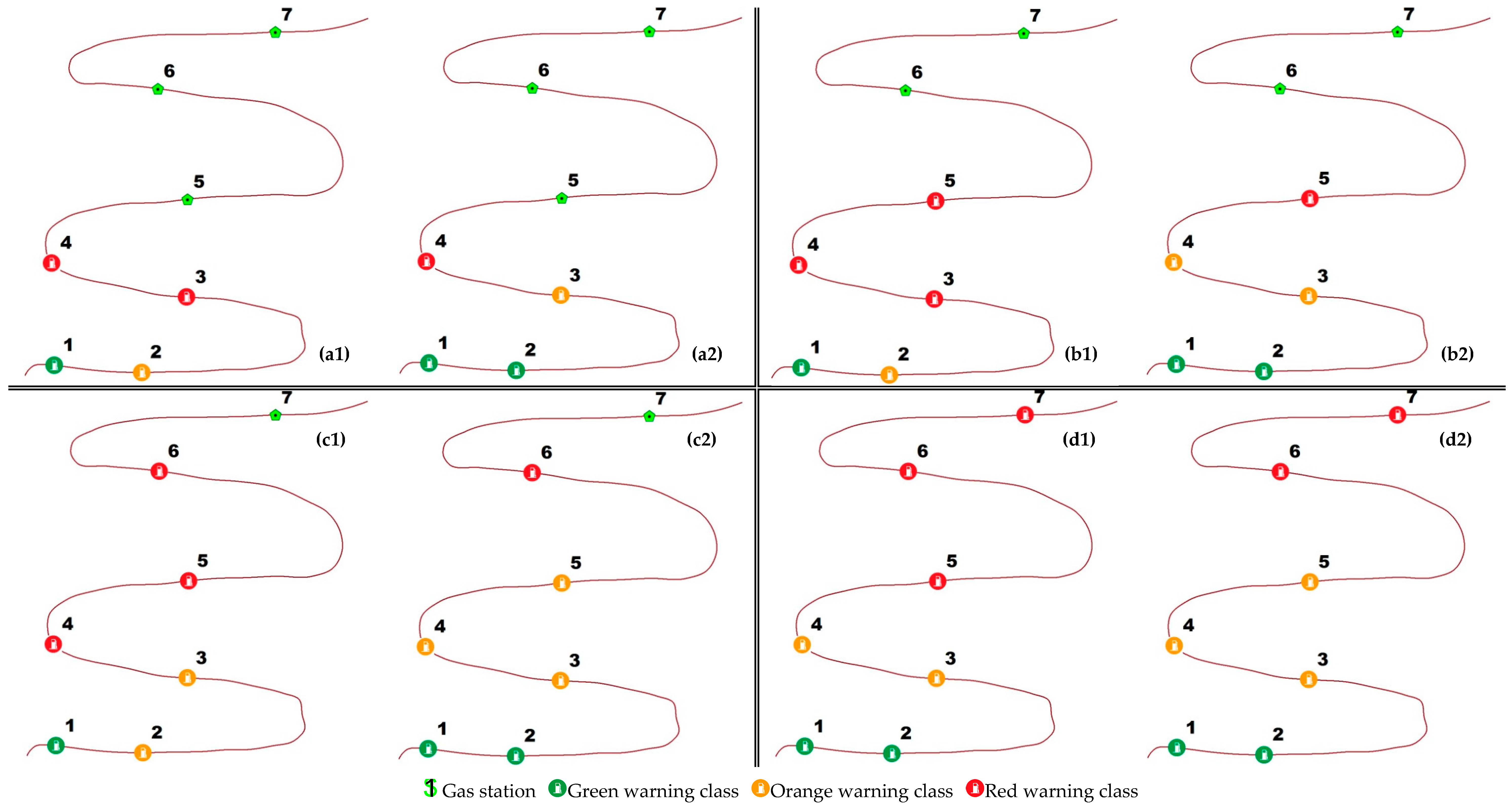
- Scheme 3-1: There were no more than three refueling gas stations along the route. Beginning from the direction of the starting point, the gas stations were marked with green, orange, and red warning levels in order from beginning to end; the simulated recommendation result is shown in Figure 8(b2).
- Scheme 3-2: There were more than three refueling gas stations along the route. Gas stations were divided into three categories, and the three categories were marked with green, orange, and red warning levels in order from beginning to end; the simulated recommendation result is shown in Figure 8(b3).
- Scheme 3-3: In this case, gas stations along the route were distributed ahead of and behind the initial accessible position of the vehicle, and “Scheme 3-1” or “Scheme 3-2” could be used to recommend the refueling strategy according to the number of refueling gas stations. The initial position is shown in Figure 8(b3), and the simulated recommendation result is shown in Figure 8(b4).
- Scheme 4-1: When the maximum driving distance of the vehicle was not sufficient to reach the nearest gas station along the route, the initial position and the simulated recommendation result were the same as in “Scheme 2-1”.
- Scheme 4-3: When the maximum driving distance of the vehicle was near the end of the route, the recommendation method was the same as in “Scheme 4-2”, while the difference in distance and the number of refueling gas stations within that road section resulted in a different recommendation strategy. The initial position is shown in Figure 8(c3), and the simulated recommendation result is shown in Figure 8(c4).
3.5. Discussion of Algorithm Applicability
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Narayanan, Y.; Macbeth, J.I.M. Deep in the desert: Merging the desert and the spiritual through 4wd tourism. Tour. Geogr. 2009, 11, 369–389. [Google Scholar] [CrossRef]
- Zhang, H. Global tourism boosts self-drive travel. Tour. Res. 2017, 9, 2–5. [Google Scholar]
- Liu, Y.H. A Car Broke down on the High Way Due to Fuel Exhaustion, then Fueling up and Driving away with the Help of Traffic Polices. NetEase News. Available online: http://bendi.news.163.com/shandong/17/0307/08/CETNRUJH04378EMR.html (accessed on 7 March 2017).
- Rachel, C. Bruce Highway crash: Woman Ran out of Fuel before Collision. Sydney Morning Herald. Available online: https://www.brisbanetimes.com.au/national/queensland/pedestrian-dead-after-bruce-highway-crash-20170102-gtklhg.html (accessed on 2 January 2017).
- Saarinen, M. One in 50 Drivers Ran out of Fuel in Past Year. 2015. Available online: http://xueshu.baidu.com/s?wd=paperuri%3A%2855c45ab8646ddb1d874f68203d3f12e2%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fconnection.ebscohost.com%2Fc%2Farticles%2F109248782%2Fone-50-drivers-ran-out-fuel-past-year&ie=utf-8&sc_us=1858252488442288911 (accessed on 8 March 2018).
- Wang, L.; Feng, B.Y.; Liu, C.G. Study on Countermeasures of Refueling Difficulty in Expressway Service Area. Hum. Commun. Sci. Technol. 2012, 38, 161–164. [Google Scholar]
- Daina, N.; Sivakumar, A.; Polak, J.W. Electric vehicle charging choices: Modelling and implications for smart charging services. Transp. Res. C Emerg. Technol. 2017, 81, 36–56. [Google Scholar] [CrossRef]
- Barajas, L.G. Behavior-Based Low Fuel Warning System. U.S. Patent 7,999,664 B2, 16 August 2011. [Google Scholar]
- Kitamura, R.; Sperling, D. Refueling behavior of automobile drivers. Transp. Res. A Gen. 1987, 21, 235–245. [Google Scholar] [CrossRef]
- Mcfarlane, B.L. Recreation specialization and site choice among vehicle-based campers. Leis. Sci. 2004, 26, 309–322. [Google Scholar] [CrossRef]
- Lin, C.; Choy, K.L.; Ho, G.T.S.; Chung, S.H.; Lam, H.Y. Survey of Green Vehicle Routing Problem: Past and future trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Jabbarpour, M.R.; Noor, R.M.; Khokhar, R.H. Green vehicle traffic routing system using ant-based algorithm. J. Netw. Comput. Appl. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Kwon, Y.; Choi, Y.; Lee, D. Heterogeneous fixed fleet vehicle routing problem considering carbon emission. Transp. Res. D Transp. Environ. 2013, 16, 81–89. [Google Scholar] [CrossRef]
- Montoya, A.; Guéret, C.; Mendoza, J.E.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. Part B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef]
- Sundar, K.; Rathinam, S. Algorithms for Routing an Unmanned Aerial Vehicle in the Presence of Refueling Depots. IEEE Trans. Autom. Sci. Eng. 2014, 11, 287–294. [Google Scholar] [CrossRef]
- Bruglieri, M.; Pezzella, F.; Pisacane, O.; Suraci, S. A Variable Neighborhood Search Branching for the Electric Vehicle Routing Problem with Time Windows. Electron. Notes Discret. Math. 2015, 47, 221–228. [Google Scholar] [CrossRef]
- Levy, D.; Sundar, K.; Rathinam, S. Heuristics for Routing Heterogeneous Unmanned Vehicles with Fuel Constraints. Math. Probl. Eng. 2014, 3, 282–290. [Google Scholar] [CrossRef]
- Hosseini, M.; MirHassani, S.A. Refueling-station location problem under uncertainty. Transp. Res. E Logist. Transp. Rev. 2015, 84, 101–116. [Google Scholar] [CrossRef]
- Hosseini, M.; MirHassani, S.A. A heuristic algorithm for optimal location of flow-refueling capacitated stations. Int. Trans. Oper. Res. 2017, 24, 1377–1403. [Google Scholar] [CrossRef]
- Miralinaghi, M.; Lou, Y.; Keskin, B.B.; Zarrinmehr, A.; Shabanpour, R. Refueling station location problem with traffic deviation considering route choice and demand uncertainty. Int. J. Hydrogen Energy. 2017, 42, 3335–3351. [Google Scholar] [CrossRef]
- Heng, H.J.; Yan, X.D.; Wang, F.; Li, H.F. Research on dynamic scheduling of airport fuel filling vehicle. J. Transp. Syst. Eng. Inf. Technol. 2017, 38, 1382–1388. [Google Scholar]
- Feng, X.; Ren, Z.Y. Collaborative Scheduling of Fuelling Vehicle and Ferry Vehicle Based on Genetic Algorithm. J. Transp. Syst. Eng. Inf. Technol. 2016, 16, 155–163. [Google Scholar]
- Suzuki, Y. A generic model of motor-carrier fuel optimization. Naval Res. Logist. 2008, 55, 737–746. [Google Scholar] [CrossRef]
- Suzuki, Y. A decision support system of dynamic vehicle refueling. Decis. Support Syst. 2009, 46, 522–531. [Google Scholar] [CrossRef]
- Suzuki, Y. A decision support system of vehicle routing and refueling for motor carriers with time-sensitive demands. Decis. Support Syst. 2012, 54, 758–767. [Google Scholar] [CrossRef]
- Suzuki, Y.; Dai, J. Decision Support System of Truck Routing and Refueling: A Dual-Objective Approach. Decis. Sci. 2013, 44, 817–842. [Google Scholar] [CrossRef]
- Suzuki, Y.; Montabon, F.; Lu, S.H. DSS of vehicle refueling: A new enhanced approach with fuel weight considerations. Decis. Support Syst. 2014, 68, 15–25. [Google Scholar] [CrossRef]
- Lin, S.H.; Gertsch, N.; Russell, J.R. A linear-time algorithm for finding optimal vehicle refueling policies. Oper. Res. Lett. 2007, 35, 290–296. [Google Scholar]
- Nicholas, M.A. Driving demand: What can gasoline refueling patterns tell us about planning an alternative fuel network? J. Transp. Geogr. 2010, 18, 738–749. [Google Scholar] [CrossRef]
- Kuby, M.J.; Kelley, S.B.; Schoenemann, J. Spatial refueling patterns of alternative-fuel and gasoline vehicle drivers in Los Angeles. Transp. Res. D Transp. Environ. 2013, 25, 84–92. [Google Scholar] [CrossRef]
- Kelley, S.; Kuby, M. On the way or around the corner? Observed refueling choices of alternative-fuel drivers in Southern California. J. Transp. Geogr. 2013, 33, 258–267. [Google Scholar] [CrossRef]
- Reddi, K.; Elgowainy, A.; Sutherland, E. Hydrogen refueling station compression and storage optimization with tube-trailer delveries. Int. J. Hydrog. Energy 2014, 39, 19169–19181. [Google Scholar] [CrossRef]
- Liu, W.B.; Deng, M.; Xia, X.G. Modeling Positional Errors of Geographical Lines in Vector GIS. J. Remote Sens. 2000, 4, 316–321. [Google Scholar]
- Abbaspour, R.A.; Shaeri, M.; Chehreghan, A. A method for similarity measurement in spatial trajectories. Spat. Inf. Res. 2017, 25, 491–500. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B. Assessment of the effects of expressway geometric design features on the frequency of accident crash rates using high-resolution laser scanning data and GIS. Geomat. Nat. Hazards Risk 2017, 8, 733–747. [Google Scholar] [CrossRef]
- Xing, Y.W.; Huang, T.; Yang, H.L. Optimization of liner refueling strategy based on ship speed adjustment. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 199–204. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining, 3rd ed.; Morgan Kaufmann: Boston, MA, USA, 2012. [Google Scholar]
- Chen, J.; Lin, X.; Zheng, H.; Bao, X. A novel cluster center fast determination clustering algorithm. Appl. Soft Comput. 2017, 57, 539–555. [Google Scholar]
- Ross, A.C.; Lehman, S.M. Applying spatial partitioning and K-Means clustering to habitat occupation in Propithecus perrieri. Am. J. Phys. Anthropol. 2011, 144, 257. [Google Scholar]
- Guha, S.; Rastogi, R.; Shim, K. Cure: An efficient clustering algorithm for large databases. Inf. Syst. 1998, 26, 35–58. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Date Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Estivill-Castro, V.; Lee, I. Argument free clustering for large spatial point-data sets via boundary extraction from delaunay diagram. Comput. Environ. Urban Syst. 2002, 26, 315–334. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Wei, R.; Murray, A.T. Spatial Clustering Overview and Comparison: Accuracy, Sensitivity, and Computational Expense. Ann. Assoc. Am. Geogr. 2014, 104, 1134–1155. [Google Scholar] [CrossRef]
- Nosovskiy, G.V.; Liu, D.; Sourina, O. Automatic clustering and boundary detection algorithm based on adaptive influence function. Pattern Recognit. 2008, 41, 2757–2776. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A comprehensive survey of clustering algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Zhan, Q.; Deng, S.; Zheng, Z. An Adaptive Sweep-Circle Spatial Clustering Algorithm Based on Gestalt. Isprs Int. J. Geo-Inf. 2017, 6, 272. [Google Scholar] [CrossRef]
- Murray, A.T. Spatial characteristics and comparisons of interaction and median clustering models. Geogr. Anal. 2000, 32, 1–18. [Google Scholar] [CrossRef]
- Kelley, S. AFV refueling stations and the complexity of freeway intersections: The scale dependency of network representation. Int. J. Geogr. Inf. Syst. 2016, 31, 346–363. [Google Scholar] [CrossRef]
- Sweda, T.M.; Dolinskaya, I.S.; Klabjan, D. Optimal Recharging Policies for Electric Vehicles. Transp. Sci. 2017, 52, 457–459. [Google Scholar] [CrossRef]
- Nicholas, M.A. Building an Alternative Fuel Refueling Network: How Many Stations are Needed and Where Should They be Placed? Bachelor’s Thesis, University of California, Davis, CA, USA, 2009. [Google Scholar]
- Wansink, B.; Ittersum, K.V. Stopping decisions of travelers. Tour. Manag. 2004, 25, 319–330. [Google Scholar] [CrossRef]
| Determination Condition | Value Range | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| The total number of gas stations | = 0 | T | ||||||
| The number of refueling gas stations | = 1 | T | ||||||
| = 2 | T | |||||||
| = 3 | T | |||||||
| > 3 | T | |||||||
| The distance from aggregate mileage | > 0 | T | F | F | F | F | F | |
| The distance from gas stations | > 0 | F | T | T | T | T | ||
| Recommendation strategy | Strategy 1 | Strategy 2 | Strategy 2 | Strategy 3 | Strategy 3 | Strategy 3 | Strategy 4 |
| Dij | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|
| 1 | 0 | D21 | D31 | D41 | Dn1 |
| 2 | D12 | 0 | D32 | D42 | Dn2 |
| 3 | D13 | D23 | 0 | D43 | Dn3 |
| 4 | D14 | D24 | D33 | 0 | Dn4 |
| n | D1n | D2n | D3n | D4n…… | 0 |
| Item | Original Data (×104) | Attributes and Results of Clustering | |||||
|---|---|---|---|---|---|---|---|
| Gas Station | X-Coordinate of the Gas Station/m | Y-Coordinate of the Gas Station/m | The Distance between the Gas Station and the Starting Point/km | The Clustering Result under the Constraint of Euclidean Distance and Route Distance | The Clustering Result of Euclidean Distance | The Clustering Result of Distances between the Gas Stations | |
| 1 | −6.6425 | −4.2083 | 0.0494 | c1 | c1 | c1 | |
| 2 | −3.6308 | −4.4530 | 0.0463 | c2 | c2 | c1 | |
| 3 | −2.0886 | −1.8608 | 0.0355 | c2 | c2 | c2 | |
| 4 | −6.7309 | −0.6905 | 0.0306 | c1 | c1 | c2 | |
| 5 | −2.0426 | 1.5114 | 0.0244 | c3 | c3 | c2 | |
| 6 | −3.0601 | 5.3208 | 0.0111 | c3 | c3 | c3 | |
| 7 | 0.9865 | 7.2768 | 0.0001 | c3 | c3 | c3 | |
| D (× 104)/km | Clustering Algorithm and Result Comparison | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| K-Means | Hierarchical Clustering Method | ||||||||
| 4 Gas Stations | 5 Gas Stations | 6 Gas Stations | 7 Gas Stations | 4 Gas Stations | 5 Gas Stations | 6 Gas Stations | 7 Gas Stations | ||
| 1 | 0.0494 | c1 | c1 | c1 | c1 | c1 | c1 | c1 | c1 |
| 2 | 0.0463 | c2 | c2 | c2 | c1 | c1 | c1 | c1 | c1 |
| 3 | 0.0355 | c3 | c3 | c2 | c2 | c2 | c2 | c2 | c2 |
| 4 | 0.0306 | c3 | c3 | c3 | c2 | c3 | c2 | c2 | c2 |
| 5 | 0.0244 | c3 | c3 | c3 | c3 | c2 | c2 | ||
| 6 | 0.0111 | c3 | c3 | c3 | c3 | ||||
| 7 | 0.0001 | c3 | c3 | ||||||
| Scenario Type | Testing Scheme | Adaptive Strategy | Aggregate Mileage/km | Maximum Driving Distance/km | Initial Accessible Position | Total Number of Gas stations | Number of Refueling Gas stations | Recommendation Result |
|---|---|---|---|---|---|---|---|---|
| 1 | 1-1 | 1 | 304.43 | 315.79 | Figure 8(a1) | NULL | NULL | Figure 8(a4) |
| 2 | 2-1 | 2 | 304.43 | 52.63 | Figure 8(a2) | NULL | NULL | Figure 8(a4) |
| 2-2 | 2 | 304.43 | NULL | Figure 8(a3) | 0 | 0 | Figure 8(a4) | |
| 3 | 3-1 | 3 | 304.43 | 178.95 | Figure 8(b1) | 2 | 2 | Figure 8(b2) |
| 3-2 | 4 | 304.43 | 178.95 | Figure 8(b1) | 5 | 5 | Figure 8(b3) | |
| 3-3 | 4 | 304.43 | 178.95 | Figure 8(b1) | 8 | 6 | Figure 8(b4) | |
| 4 | 4-1 | 2 | 304.43 | 52.63 | Figure 8(a2) | 10 | 0 | Figure 8(a4) |
| 4-2 | 4 | 304.43 | 157.89 | Figure 8(c1) | 10 | 4 | Figure 8(c2) | |
| 4-3 | 4 | 304.43 | 294.73 | Figure 8(c3) | 10 | 10 | Figure 8(c4) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Yang, K.; Peng, S.; Hong, L. A Distance-Adaptive Refueling Recommendation Algorithm for Self-Driving Travel. ISPRS Int. J. Geo-Inf. 2018, 7, 94. https://doi.org/10.3390/ijgi7030094
Xu Q, Yang K, Peng S, Hong L. A Distance-Adaptive Refueling Recommendation Algorithm for Self-Driving Travel. ISPRS International Journal of Geo-Information. 2018; 7(3):94. https://doi.org/10.3390/ijgi7030094
Chicago/Turabian StyleXu, Quanli, Kun Yang, Shuangyun Peng, and Liang Hong. 2018. "A Distance-Adaptive Refueling Recommendation Algorithm for Self-Driving Travel" ISPRS International Journal of Geo-Information 7, no. 3: 94. https://doi.org/10.3390/ijgi7030094
APA StyleXu, Q., Yang, K., Peng, S., & Hong, L. (2018). A Distance-Adaptive Refueling Recommendation Algorithm for Self-Driving Travel. ISPRS International Journal of Geo-Information, 7(3), 94. https://doi.org/10.3390/ijgi7030094





