Single-Frequency Kinematic Performance Comparison between Galileo, GPS, and GLONASS Satellite Positioning Systems Using an MMS-Generated Trajectory as a Reference: Preliminary Results
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiment Location and MMS POS/LV Description and Configuration
2.2. Survey Experimental Design
2.3. Data Processing and Comparison Method
- GS14 differential single constellations trajectory computation for all the possible combinations of four, five, and six satellites;
- Reference trajectory computation from MMS data;
- Solutions filtering and comparisons.
2.3.1. Trajectories Computations from GS14 Data
2.3.2. Reference Trajectory: MMS Output
2.3.3. Data Filtering and Comparisons
- (a)
- 16 vectors for the 4, 5, and 6 satellites combinations;
- (b)
- Among the 16 vectors for the considered combination (e.g., of 4 satellites), 8 vectors were generated for Galileo and GPS comparisons, and 8 vectors were generated for Galileo and GLONASS comparisons;
- (c)
- Considering, for example, Galileo and GPS comparisons (the same is valid for Galileo and GLONASS comparisons), the 8 vectors were produced by 4 couples of vectors finally used for the comparisons;
- (d)
- The 4 couples were built using, for each considered epoch (t), all the values found for the considered epoch t for planimetric and altimetric deviations, separated for fixed and float solutions. That is (e.g., for Galileo and GPS comparisons):
- (I): two vectors referred to the t-th epoch in case of fixed solutions (one for Galileo and one for GPS system);
- (II): two vectors referred to the t-th epoch in case of float solutions (one for Galileo and one for GPS system);
- (III): two vectors referred to the t-th epoch in case of fixed solutions (one for Galileo and one for GPS system);
- (IV): two vectors referred to the t-th epoch in case of float solutions (one for Galileo and one for GPS system);
- (e)
- Particularly, for each considered couple of vectors (e.g., couple I) related to a specific epoch t, the mean values for the Galileo analyzed parameter and for the same GPS (or GLONASS) parameter were computed and compared;
- (f)
- If the length of the considered GPS (or GLONASS) vector, referred to the t-th epoch, was greater than 15, a one-sample t-test [53] was executed to establish if the GPS (or Galileo and GLONASS) average parameter values were statistically different from the same Galileo parameters.
3. Results
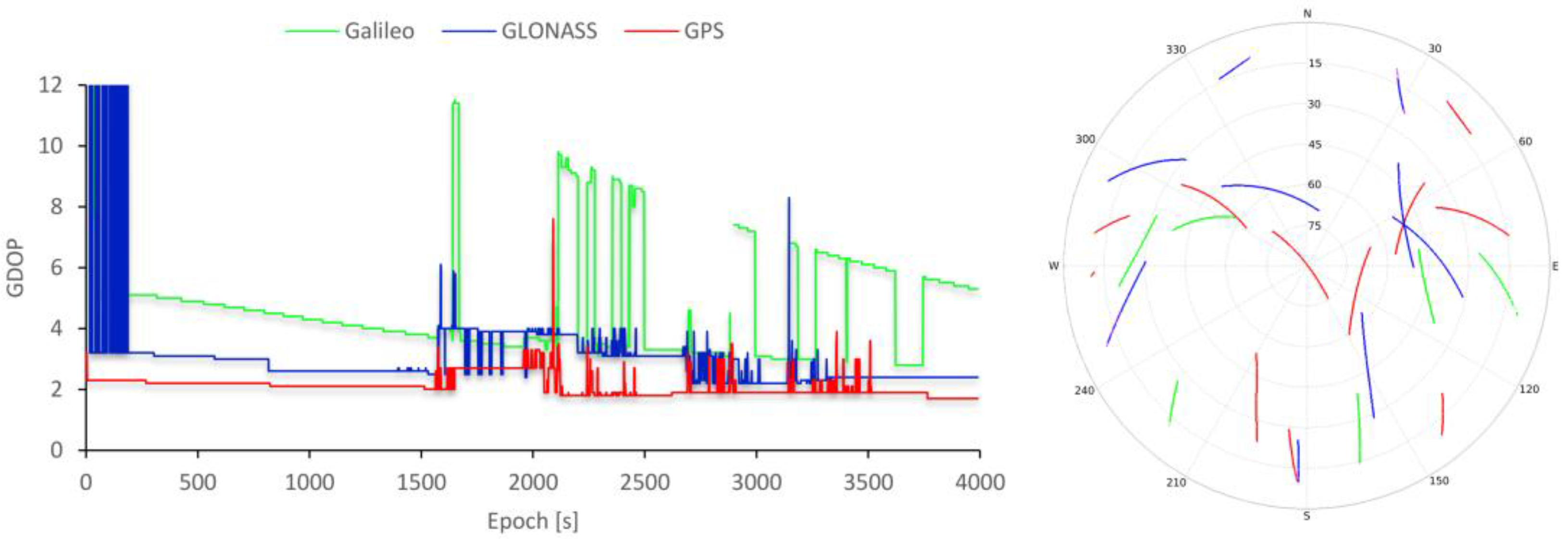
3.1. MMS Reference Trajectory and RKTLIB Results
3.2. Comparisons Results
- Each entry in the “comparison” column in Table 4 shows the object of the comparison: “ gal_vs_gps_4” and “ gal_vs_gps_4” are, respectively, the comparisons between the parameter for fixed ( and float () solutions for the combination of four satellites of the Galileo and GPS systems;
- The average values comparison (Avg. values comp.) columns report:
- ○
- the number of epochs for which it was possible to execute the simple comparisons between the average values of the two vectors;
- ○
- the number of times (gal score), expressed in percentage, in which the considered Galileo average planimetric or altimetric deviations performed better (thus was closer to the reference MMS trajectory for the t-th epoch).
- The columns related to the t-test summary report:
- ○
- the number of epochs in which it was possible to execute the one-sample t-test (point f) Section 2.3.3);
- ○
- the average p-value, introduced to provide a global vision of statistical significance of the tested differences;
- ○
- the number of epochs, expressed in percentage, in which the p-value was less than 0.5.
- Lastly, the Appendix/Supp. Material columns provide the references to the Appendix/Support Material figures. The reader should bear in mind that the presented figures and results derive from trajectories computed in post-processing with different accuracies (see Section 2.3.2).
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
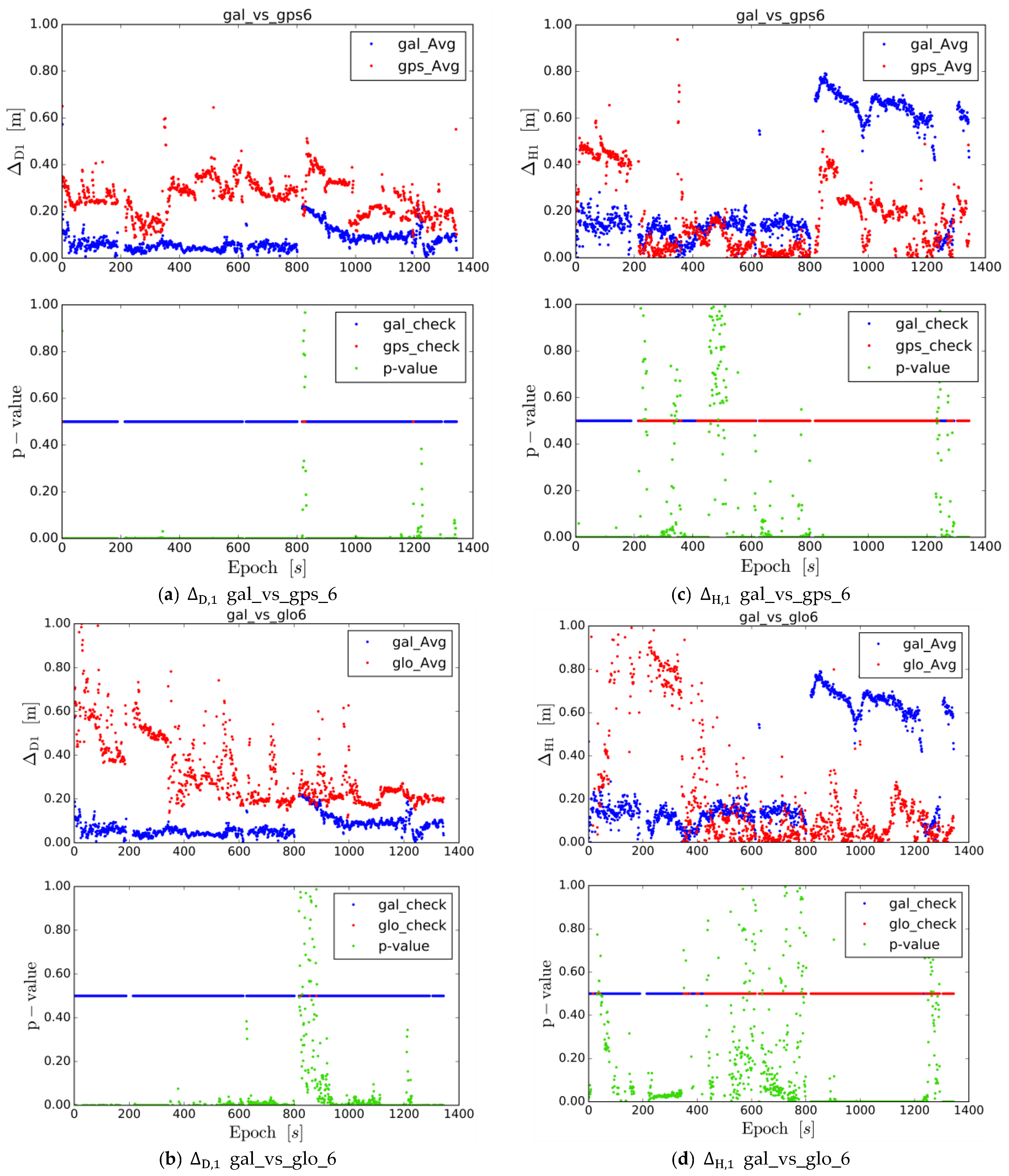
Appendix A
- The Galileo data are provided in blue, the GPS and GLONASS data in red, the p-values in green;
- The average values of the comparisons (“gal_Avg” for Galileo, gps_Avg for GPS, and glo_Avg for GLONASS) are provided in the upper subplot, whereas the statistical significance (p-value) of the differences is shown in the lower subplot;
- The lower subplot reports also additional information with a horizontal line placed at an ordinate of 0.5. This line is blue (gal_check) when the Galileo system performed better and is red (gps_check or glo_check) when the GPS of the GLONASS Systems performed better;
- The high degree of scattering of the p-value indicates a low statistical significance for the related epochs;
- The plots show the comparison for fixed solutions if the subscript of the parameter on the ordinate of the upper subplot is 1 (e.g., and );
- The plots show the comparison for float solutions if the subscript of the parameter on the ordinate of the upper subplot is 2 (e.g., and ).
References
- ESA: Galileo Fact Sheet. Available online: http://esamultimedia.esa.int/docs/galileo/GalileoFactsheet2017.pdf (accessed on 14 December 2017).
- Steigenberger, P.; Hugentobler, U.; Montenbruck, O. First demonstration of Galileo-only positioning. GPS World 2013, 24, 14–15. [Google Scholar]
- Simsky, A.; Mertens, D.; Sleewaegen, J.-M.; Hollreiser, M.; Crisci, M. Experimental results for the multipath performance of Galileo signals transmitted by GIOVE-A satellite. Int. J. Navig. Obs. 2008, 2008, 416380. [Google Scholar] [CrossRef]
- Simsky, A.; Mertens, D.; Sleewaegen, J.-M.; De Wilde, W.; Hollreiser, M.; Crisci, M. Multipath and tracking performance of Galileo ranging signals transmitted by GIOVE-B. In Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS), Savannah, GA, USA, 16–19 September 2008; pp. 1525–1536. [Google Scholar]
- Simsky, A.; Sleewaegen, J.-M.; Hollreiser, M.; Crisci, M. Performance assessment of Galileo ranging signals transmitted by GSTB-V2 satellites. In Proceedings of the ION GNSS, Fort Worth, TX, USA, 26–29 September 2006; pp. 1547–1559. [Google Scholar]
- Hellemans, A. A Simple Plumbing Problem Sent Galileo Satellites into Wrong Orbits. Available online: https://spectrum.ieee.org/tech-talk/aerospace/satellites/a-simple-plumbing-problem-sent-galileo-satellites-into-wrong-orbits (accessed on 14 December 2017).
- Langley, R.B. ESA Discusses Galileo Satellite Power Loss, Upcoming Launch. Available online: http://gpsworld.com/esa-discusses-galileo-satellite-power-loss-upcoming-launch/ (accessed on 14 December 2017).
- European Union. Galileo Open Service, Signal in Space Interface Control Document (OS SIS ICD); European Space Agency/European GNSS Supervisory Authority. Available online: https://www.gsc-europa.eu/system/files/galileo_documents/Galileo-OS-SIS-ICD.pdf (accessed on 14 December 2017).
- ESA. Galileo: A Constellation of Navigation Satellites. Available online: http://www.esa.int/Our_Activities/Navigation/Galileo/Galileo_a_constellation_of_navigation_satellites (accessed on 11 December 2017).
- Zaminpardaz, S.; Teunissen, P.J. Analysis of Galileo IOV+ FOC signals and E5 RTK performance. GPS Solut. 2017, 21, 1855–1870. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Galileo status: Orbits, clocks, and positioning. GPS Solut. 2017, 21, 319–331. [Google Scholar] [CrossRef]
- Ochieng, W.Y.; Sauer, K.; Cross, P.A.; Sheridan, K.F.; Iliffe, J.; Lannelongue, S.; Ammour, N.; Petit, K. Potential performance levels of a combined Galileo/GPS navigation system. J. Navig. 2001, 54, 185–197. [Google Scholar] [CrossRef]
- O’Keefe, K.; Julien, O.; Cannon, M.E.; Lachapelle, G. Availability, accuracy, reliability, and carrier-phase ambiguity resolution with Galileo and GPS. Acta Astronaut. 2006, 58, 422–434. [Google Scholar] [CrossRef]
- Diessongo, T.H.; Schüler, T.; Junker, S. Precise position determination using a Galileo E5 single-frequency receiver. GPS Solut. 2014, 18, 73–83. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J.; Huisman, L. First results of mixed GPS+ GIOVE single-frequency RTK in Australia. J. Spat. Sci. 2012, 57, 3–18. [Google Scholar] [CrossRef]
- Cai, C.; Luo, X.; Liu, Z.; Xiao, Q. Galileo signal and positioning performance analysis based on four IOV satellites. J. Navig. 2014, 67, 810–824. [Google Scholar] [CrossRef]
- Gaglione, S.; Angrisano, A.; Castaldo, G.; Freda, P.; Gioia, C.; Innac, A.; Troisi, S.; Del Core, G. The first Galileo FOC satellites: From useless to essential. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3667–3670. [Google Scholar]
- Gioia, C.; Borio, D.; Angrisano, A.; Gaglione, S.; Fortuny-Guasch, J. A Galileo IOV assessment: Measurement and position domain. GPS Solut. 2015, 19, 187–199. [Google Scholar] [CrossRef]
- Tegedor, J.; Øvstedal, O.; Vigen, E. Precise orbit determination and point positioning using GPS, Glonass, Galileo and BeiDou. J. Geod. Sci. 2014, 4. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.; Liu, J.; Li, X.; Li, X. Performance evaluation of single-frequency precise point positioning with GPS, GLONASS, BeiDou and Galileo. J. Navig. 2017, 70, 465–482. [Google Scholar] [CrossRef]
- Afifi, A.; El-Rabbany, A. Single Frequency GPS/Galileo Precise Point Positioning Using Un-Differenced and between-Satellite Single Difference Measurements. GEOMATICA 2014, 68, 195–205. [Google Scholar] [CrossRef]
- Cai, C.; He, C.; Santerre, R.; Pan, L.; Cui, X.; Zhu, J. A comparative analysis of measurement noise and multipath for four constellations: GPS, BeiDou, GLONASS and Galileo. Surv. Rev. 2016, 48, 287–295. [Google Scholar] [CrossRef]
- Pan, L.; Cai, C.; Santerre, R.; Zhang, X. Performance evaluation of single-frequency point positioning with GPS, GLONASS, BeiDou and Galileo. Surv. Rev. 2017, 49, 197–205. [Google Scholar] [CrossRef]
- Guo, F.; Li, X.; Zhang, X.; Wang, J. Assessment of precise orbit and clock products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]
- Odijk, D.; Teunissen, P.J.; Khodabandeh, A. Galileo IOV RTK positioning: Standalone and combined with GPS. Surv. Rev. 2014, 46, 267–277. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.; Odijk, D. Combined bds, galileo, qzss and gps single-frequency rtk. GPS Solut. 2015, 19, 151–163. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Nadarajah, N.; Teunissen, P.J.G. Instantaneous GPS/Galileo/QZSS/SBAS Attitude Determination: A Single-Frequency (L1/E1) Robustness Analysis under Constrained Environments. Navigation 2014, 61, 65–75. [Google Scholar] [CrossRef]
- Nadarajah, N.; Teunissen, P.J.; Raziq, N. Instantaneous GPS–Galileo attitude determination: Single-frequency performance in satellite-deprived environments. IEEE Trans. Veh. Technol. 2013, 62, 2963–2976. [Google Scholar] [CrossRef]
- Zajdel, R.; Sośnica, K.; Bury, G. A New Online Service for the Validation of Multi-GNSS Orbits Using SLR. Remote Sens. 2017, 9, 1049. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Amèzaga, A.; Vidal, D.; Olivé, R.; Munoz, J.F.; Camps, A. First polarimetric GNSS-R measurements from a stratospheric flight over boreal forests. Remote Sens. 2015, 7, 13120–13138. [Google Scholar] [CrossRef]
- Cefalo, R.; Grandi, G.; Roberti, R.; Sluga, T. Extraction of Road Geometric Parameters from High Resolution Remote Sensing Images Validated by GNSS/INS Geodetic Techniques. In Proceedings of the Computational Science and Its Applications—ICCSA 2017, Trieste, Italy, 3–6 July 2017; Springer: Cham, Switzerland, 2017; Volume 10407, pp. 181–195, ISBN 978-3-319-62400-6. [Google Scholar]
- Quan, W.; Li, J.; Gong, X.; Fang, J. INS/CNS/GNSS Integrated Navigation Technology; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-662-45158-8. [Google Scholar]
- Aicardi, I.; Gandino, F.; Grasso, N.; Lingua, A.M.; Noardo, F. A low-cost solution for the monitoring of air pollution parameters through bicycles. In Proceedings of the International Conference on Computational Science and Its Applications, Trieste, Italy, 3–6 July 2017; Springer: Cham, Switzerland, 2017; pp. 105–120. [Google Scholar]
- Takasu, T.; Yasuda, A. Development of the Low-Cost RTK-GPS Receiver with an Open Source Program Package RTKLIB; International Convention Centre: Jeju, Korea, 2009; pp. 4–6. [Google Scholar]
- Takasu, T. Real-time PPP with RTKLIB and IGS real-time satellite orbit and clock. In Proceedings of the GS Workshop 2010, Newcastle upon Tyne, UK, 28 June–2 July 2010; Volume 216, p. 2010. [Google Scholar]
- Piras, M.; Grasso, N.; Abdul Jabbar, A. Uav Photogrammetric Solution Using a Raspberry pi Camera Module and Smart Devices: Test and Results. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 289–296. [Google Scholar] [CrossRef]
- Abdul Jabbar, A.; Aicardi, I.; Grasso, N.; Piras, M. URBAN DATA COLLECTION USING A BIKE MOBILE SYSTEM WITH A FOSS ARCHITECTURE. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 3–9. [Google Scholar] [CrossRef]
- Takasu, T. RTKLIB Ver. 2.4. 2 Manual. Available online: http://www.rtklib.com/prog/manual_2.4.2.pdf (accessed on 15 March 2018).
- Caroti, G.; Piemonte, A. Measurement of cross-slope of roads: Evaluations, algorithms and accuracy analysis. Surv. Rev. 2010, 42, 92–104. [Google Scholar] [CrossRef]
- Leica Viva GS14—Professional Reliability When You Need the Most Demanding Accuracy—Leica Geosystems—Italia. Available online: http://www.leica-geosystems.it/it/Leica-Viva-GS14_102200.htm (accessed on 15 December 2017).
- Barzaghi, R.; Betti, B.; Biagi, L.; Pinto, L.; Visconti, M.G. Estimating the Baseline between CERN Target and LNGS Reference Points. J. Surv. Eng. 2016, 142, 04016012. [Google Scholar] [CrossRef]
- Leica Geosystems SmartNet ItalPoS. Available online: http://it.web.nrtk.eu/spiderweb/frmIndex.aspx (accessed on 13 December 2017).
- Takasu, T. RTKLIB: An Open Source Program Package for GNSS Positioning. Available online: http://www.rtklib.com/ (accessed on 15 March 2018).
- 17.1. Subprocess—Subprocess Management—Python 2.7.14 Documentation. Available online: https://docs.python.org/2/library/subprocess.html (accessed on 13 December 2017).
- 16.6. Multiprocessing—Process-Based “Threading” Interface—Python 2.7.14 Documentation. Available online: https://docs.python.org/2/library/multiprocessing.html (accessed on 13 December 2017).
- Novelli, A.; Aguilar, M.A.; Aguilar, F.J.; Nemmaoui, A.; Tarantino, E. C_AssesSeg Concurrent Computing Version of AssesSeg: A Benchmark Between the New and Previous Version. In Proceedings of the International Conference on Computational Science and Its Applications, Trieste, Italy, 3–6 July 2017; Springer: Cham, Switzerland, 2017; pp. 45–56. [Google Scholar]
- Pyproj 1.9.5.1: Python Package Index. Available online: https://pypi.python.org/pypi/pyproj? (accessed on 14 December 2017).
- Conversione Coordinate IGM. Available online: http://212.77.67.76/vol/index_coord.php (accessed on 14 December 2017).
- Applanix Corporation. PUBS-MAN-001768-POSPacTM MMSTM GNSS-Inertial Tools Software Version 7.2, Revision 12-User Guide; Applanix Corporation: Richmond Hill, ON, Canada, 2016. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Regione Autonoma Friuli-Venezia Giulia—Rete GNSS. Available online: http://www.regione.fvg.it/rafvg/cms/RAFVG/ambiente-territorio/conoscere-ambiente-territorio/FOGLIA1/ (accessed on 17 December 2017).

| n. of Solutions | Galileo | GPS | GLONASS | Total |
|---|---|---|---|---|
| 4 satellites | 15 × 9 | 330 × 9 | 126 × 9 | 4239 |
| 5 satellites | 6 × 9 | 462 × 9 | 126 × 9 | 5346 |
| 6 satellites | 1 × 9 | 462 × 9 | 84 × 9 | 4923 |
| n. of Solutions | Galileo | GPS | GLONASS |
|---|---|---|---|
| 4 satellites | 93 | 468 | 205 |
| 5 satellites | 34 | 1805 | 582 |
| 6 satellites | 9 | 2121 | 586 |
| Combination | n. of Combinations | Cut-Off | Ambiguity Fix | ||||
|---|---|---|---|---|---|---|---|
| 10° | 15° | 20° | Fix and Hold | Instantaneous | Continuous | ||
| best_gal_4 | 13 | 15% | 85% | ---- | 38% | 24% | 38% |
| best_gal_5 | 4 | ---- | 100% | ---- | 25% | 50% | 25% |
| best_gal_6 | 1 | ---- | ---- | 100% | 100% | ---- | ---- |
| best_glo_4 | 29 | 73% | 17% | 10% | 55% | 38% | 7% |
| best_glo_5 | 82 | 65% | 26% | 9% | 59% | 38% | 3% |
| best_glo_6 | 62 | 52% | 29% | 19% | 77% | 16% | 7% |
| best_gps_4 | 77 | 68% | 29% | 3% | 61% | 18% | 21% |
| best_gps_5 | 264 | 60% | 34% | 6% | 63% | 15% | 22% |
| best_gps_6 | 373 | 54% | 37% | 9% | 66% | 11% | 23% |
| Comparison | Avg. Values Comp. | t-Test Summary | ||||
|---|---|---|---|---|---|---|
| Epochs | Gal Score | Epochs | Avg. p | n. Epochs p < 0.05 | Appendix/Supp. Material | |
| gal_vs_gps_4 | 860 | 75.8% | 504 | 0.130 | 42.7% | Figure S1 |
| gal_vs_glo_4 | 847 | 76.5% | ---- | ---- | ---- | Figure S2 |
| gal_vs_gps_5 | 1287 | 90.8% | 1283 | 0.047 | 91.0% | Figure S3 |
| gal_vs_glo_5 | 1279 | 99.0% | 756 | 0.014 | 93.0% | Figure S4 |
| gal_vs_gps_6 | 1280 | 99.2% | 1280 | 0.008 | 98.0% | Figure A1a |
| gal_vs_glo_6 | 1280 | 99.8% | 998 | 0.041 | 89.2% | Figure A1b |
| gal_vs_gps_4 | 736 | 82.2% | 205 | 0.271 | 38.1% | Figure S5 |
| gal_vs_glo_4 | 463 | 90.9% | ---- | ---- | ---- | Figure S6 |
| gal_vs_gps_5 | 1176 | 97.9% | 1065 | 0.024 | 93.0% | Figure S7 |
| gal_vs_glo_5 | 1171 | 98.9% | 444 | 0.024 | 96.6% | Figure S8 |
| gal_vs_gps_6 | 32 | 93.8% | 30 | 0.036 | 93.3% | Figure S9 |
| gal_vs_glo_6 | 32 | 100% | 25 | 0.006 | 96.0% | Figure S10 |
| gal_vs_gps_4 | 860 | 6.7% | 504 | 0.049 | 86.9% | Figure S11 |
| gal_vs_glo_4 | 847 | 22.3% | ---- | ---- | ---- | Figure S12 |
| gal_vs_gps_5 | 1287 | 27.9% | 1283 | 0.056 | 85.7% | Figure S13 |
| gal_vs_glo_5 | 1279 | 40.5% | 756 | 0.068 | 80.4% | Figure S14 |
| gal_vs_gps_6 | 1280 | 26.0% | 1280 | 0.068 | 87.3% | Figure A1c |
| gal_vs_glo_6 | 1280 | 36.1% | 998 | 0.121 | 65.1% | Figure A1d |
| gal_vs_gps_4 | 736 | 12.2% | 206 | 0.005 | 98.5% | Figure S15 |
| gal_vs_glo_4 | 463 | 38.0% | ---- | ---- | ---- | Figure S16 |
| gal_vs_gps_5 | 1176 | 15.3% | 1065 | 0.060 | 82.8% | Figure S17 |
| gal_vs_glo_5 | 1171 | 42.4% | 444 | 0.072 | 82.2% | Figure S18 |
| gal_vs_gps_6 | 32 | 62.5% | 30 | 0.045 | 93.3% | Figure S19 |
| gal_vs_glo_6 | 32 | 59.4% | 25 | 0.451 | 16.0% | Figure S20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarantino, E.; Novelli, A.; Cefalo, R.; Sluga, T.; Tommasi, A. Single-Frequency Kinematic Performance Comparison between Galileo, GPS, and GLONASS Satellite Positioning Systems Using an MMS-Generated Trajectory as a Reference: Preliminary Results. ISPRS Int. J. Geo-Inf. 2018, 7, 122. https://doi.org/10.3390/ijgi7030122
Tarantino E, Novelli A, Cefalo R, Sluga T, Tommasi A. Single-Frequency Kinematic Performance Comparison between Galileo, GPS, and GLONASS Satellite Positioning Systems Using an MMS-Generated Trajectory as a Reference: Preliminary Results. ISPRS International Journal of Geo-Information. 2018; 7(3):122. https://doi.org/10.3390/ijgi7030122
Chicago/Turabian StyleTarantino, Eufemia, Antonio Novelli, Raffaela Cefalo, Tatiana Sluga, and Agostino Tommasi. 2018. "Single-Frequency Kinematic Performance Comparison between Galileo, GPS, and GLONASS Satellite Positioning Systems Using an MMS-Generated Trajectory as a Reference: Preliminary Results" ISPRS International Journal of Geo-Information 7, no. 3: 122. https://doi.org/10.3390/ijgi7030122
APA StyleTarantino, E., Novelli, A., Cefalo, R., Sluga, T., & Tommasi, A. (2018). Single-Frequency Kinematic Performance Comparison between Galileo, GPS, and GLONASS Satellite Positioning Systems Using an MMS-Generated Trajectory as a Reference: Preliminary Results. ISPRS International Journal of Geo-Information, 7(3), 122. https://doi.org/10.3390/ijgi7030122






