1.1. Introduction to the Multibeam Swath Bathymetry
Multibeam echosounders (MBESs) are widely used in marine environment surveillance, detailed bathymetry measurement and seafloor mapping, underwater object detection and imaging, or submerged infrastructure inspection. Current trends in their development involve the introduction of innovative transducer materials and the application of sophisticated processing techniques, including focusing algorithms that dynamically compensate for the curvature of the wavefront in the nearfield and thus allow for narrower beam widths (higher lateral resolution) at close ranges.
A “swath-sounding” echo system is one that is used to measure depth in a line extending outwards from the sounder transducer. Such a system acquires data at right angles in the direction of the motion of the transducer head. As the head moves forward, these profiles sweep out a ribbon-shaped surface of depth measurement, which is the so-called “swath.” Current swath sounding systems utilize two different technologies to achieve bathymetry measurements across a swath of a sea floor: (1) beam forming (MBESs) and (2) interferometric or phase discrimination (sonars). Both techniques have their advantages and disadvantages, but they lead to the same end results.
MBESs collect bathymetric soundings in a swath perpendicular to the ship track by electronically forming a series of transmit and receive beams in the transducer hardware, which measure the depth to the sea floor in discrete angular increments or sectors across the swath (see
Figure 1).
Based on measurement data collected during sea surveys, digital terrain models (DTMs) are created using appropriate data processing algorithms. Created DTMs, and subsequently derived seabed maps, must fulfill the norms specified in Special Publication No. 44 issued by the International Hydrographical Organizationn (IHO) [
2,
3]. The fundamental aim of that document is to specify the minimal hydrographic survey norms, to assure that the measurement data is collected in accordance with them, and, as a consequence, to ensure the accuracy of created models and maps. These norms also enable users to determine the spatial uncertainty of the data, and effective utilization of them ensures the safe use of measurement results.
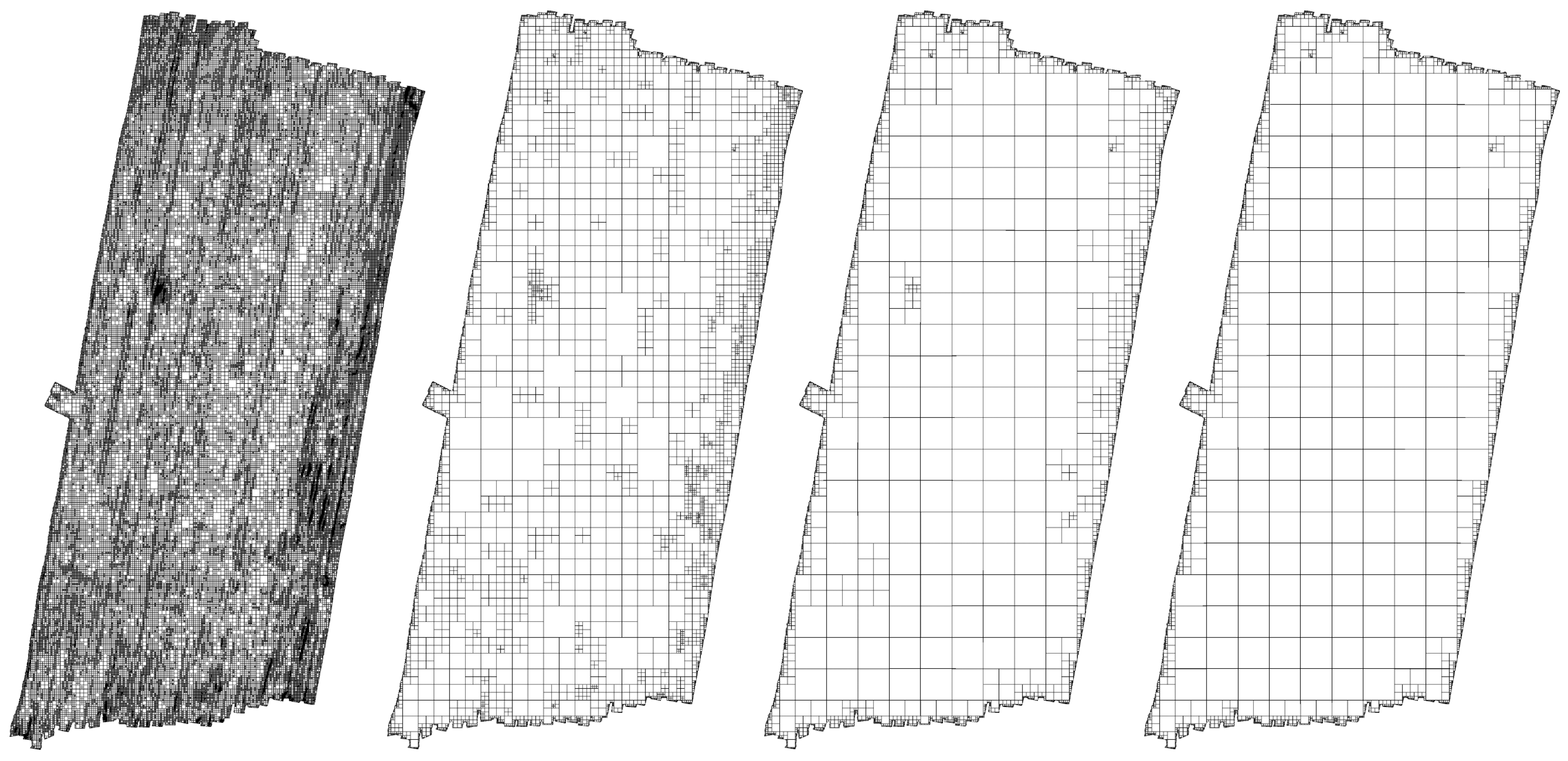
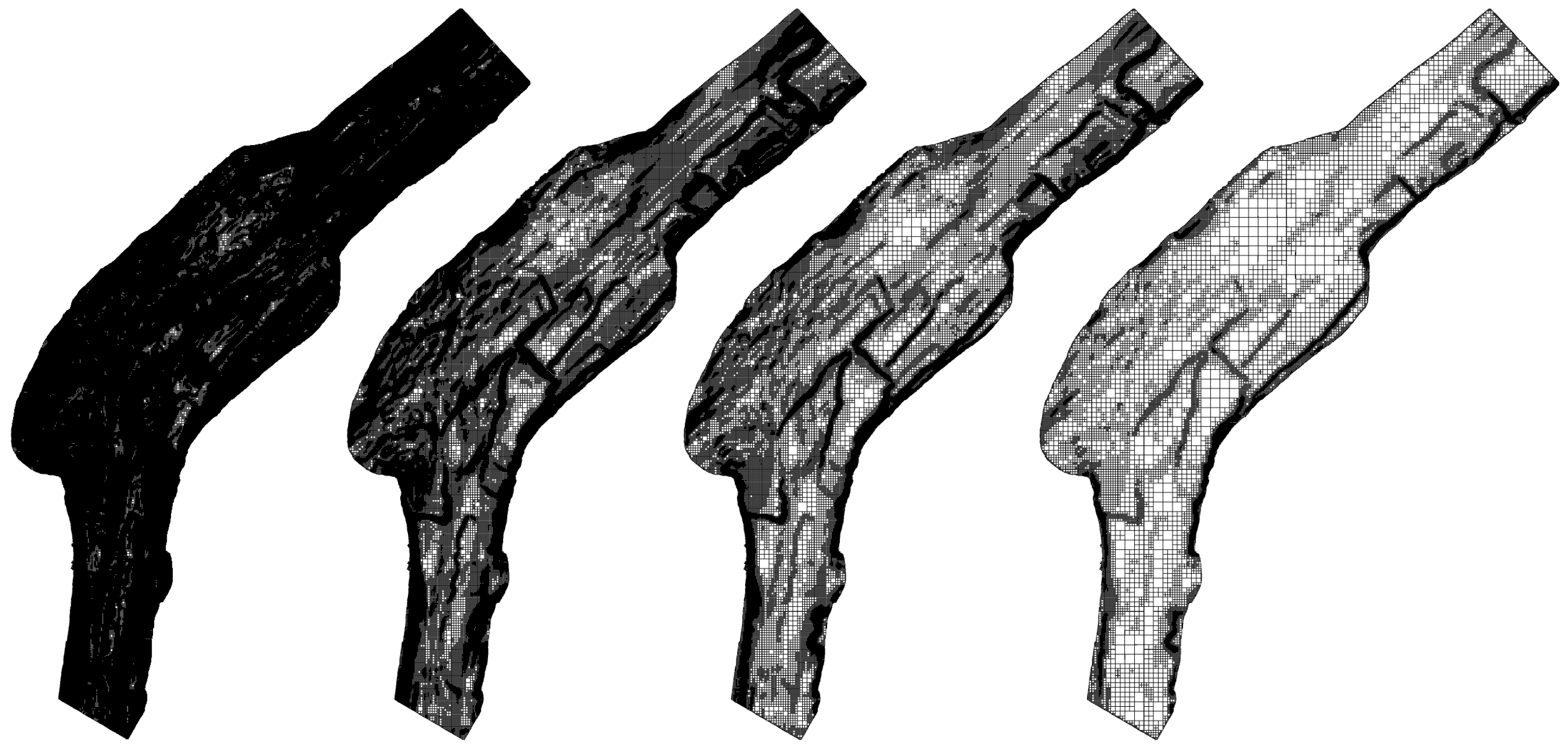
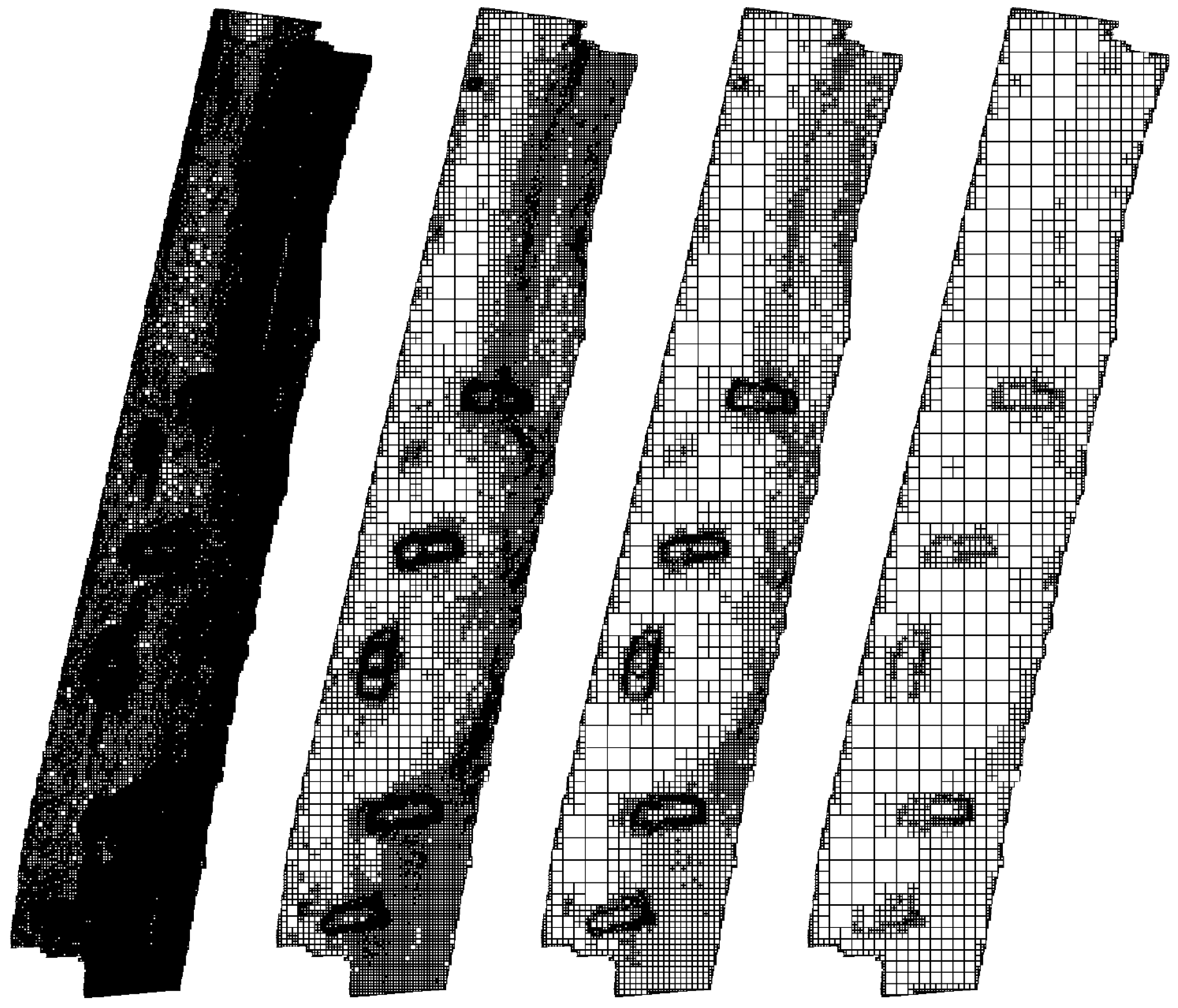
Taking into consideration a very large amount of data collected during the survey and the IHO requirements, a DTM is usually made on the basis of a grid structure (a regular net of squares) [
4,
5]. There are numerous methods of grid creation based on measurement data, the ones most often applied being kriging, a modified Shepard’s method, a radial basis function, the inverse distance to a power, triangulation with linear interpolation, moving average, wavelet methods [
6], and others based on artificial intelligence [
2].
In many practical hydrographic works, the native resolution of the grid structure is equal to one meter. It is easy to calculate because an area of one square kilometer described in this way contains one million points, stored on 3.8 or 7.6 MB (depending on the single precision floating-point representation, using 4 or 8 Bytes, respectively). Although mass storage devices make it possible to record an enormous amount of data, the other processes related to data transmission, retrieval, and processing are negatively influenced by their volume. Therefore, it is hard to imagine creating a model of a rather large area (a lake, bay, sea, or part of an ocean) with a high grid resolution. The volume of data in such a case seems to be beyond control.
1.2. Existing Methods
A number of approaches for mesh simplification and multiresolution surface triangulation have been developed over the last decades. Many general aspects of grids, multiresolution grids, nested grids, and all possible variations of quadtrees were presented by Samet [
7]. Detailed overviews on general mesh simplification and multiresolution modeling were given by Heckbert and Garland [
8], Cignoni et al. [
9], and Luebke [
10]. Gerstner [
11] proposed a hierarchical decomposition of the sphere by a recursive bisection triangulation in geographic coordinates is presented. Unfortunately, the author applied this method to a Triangulated Irregular Network (TIN) model only. Ben-Moshe et al. [
12] proposed a new terrain simplification algorithm based on several known digital image processing methods (e.g., DCT and wavelets compression), which were specially adjusted to fit digital elevation models (DEMs). The presented algorithm is based on the processing of integer numbers only (the elevation data are given as grayscale images), which may be not describe bathymetic data with sufficient accuracy. It should be noted that even TIFF-based formats such as GeoTIFF are limited with the accuracy of finite integer numbers. Hence, ASCII-based files, such as comma-separated values (csv) or ASCII-grid (txt) are more flexible. Parajola [
13] proved that hierarchical quad-tree-based terrain triangulation model is among the most efficient methods available. This method is based on a regular grid of triangles, and the output model is stored in a quad-tree structure, which is not particularly suitable for direct processing. Lau et al. [
14] presented a modified ODETLAP method for smoothing and evaluating reconstructed surfaces, and was extended to further process bathymetric data. This method may be applied in situations, when a very low amount of measurement data is collected (mainly by single-beam echosounders—SBESs). In addition, this method does not include an error control stage (called later parental error). Xie et al. [
15] applied a lossy surface compression technique to elevation datasets. The approach is based on two steps: first, it approximates the uncompressed terrain using an over-determined system of linear equations based on the Laplacian partial differential equation; second, an approximation is refined with respect to the uncompressed terrain using an error metric. In this case, the authors included the stage of error control performed for a developed model. The applied ODETLAP method can process continuous contour lines or isolated points. However, it is not well suited to dense data collected using MBESs. Parajola and Gobbetti [
16] analyzed multi-resolution approaches that exploit a certain semi-regularity of the data. This method is based on a quad-tree hierarchy, which is, however, not well adopted to further post-processing, especially in cases of large areas.
A general muliresolution grid structure is widely used in many fields of computer graphics and visualization. The level-of-detail (LOD) techniques, the basics, historical overview, and some new perspectives were described by Danovaro et al. [
17]. The method of creating muliresolution grid structures (called hierarchical grids) is proposed by Mahdavi-Amiri et al. [
18] and Weiss and De Floriani [
19]. Mahdavi-Amiri et al. [
20] described the use of these structures for representations of 3D objects (computer graphics). A comparison of different methods of smoothing in the decomposition of curves and tensor product surfaces was presented by Sadeghi and Samavati [
21]. Hierarchical grids appear in various applications in computer graphics such as subdivision and multiresolution surfaces, and terrain models. Since various grid types outperform others depending on the task, the use of multiple types, switching as needed, is desirable.
DTM compression as well as the use of multiresolution grid structures can be used for several techniques of collecting data (e.g., laser-scanners) that describe various types of surfaces (e.g., lands, and spatial objects). However, due to the different properties of the shape of the seabed surface and required accuracy, as well as the specific parameters of the compression method, results obtained for a different type of surface and data source in terms of data reduction may also be different.
In summary, the literature contains many methods oriented at the efficient description or reduction of the volume of elevation/depth data or other three-dimensional objects stored in TIN or grid models, including irregular or multiresolution structures. Most of them, however, do not include error control during the data reduction stage, and the information is presented in image form (which has obvious limitations). Many of the developed structures are quite complex, which makes it impossible to directly perform a further postprocessing of stored data.
The main goal of the research described in the paper was to check if it is possible to apply multiresolution grid to describing large data surfaces stored in the grid structure, taking into account the required standards set by the IHO, and whether the resulting reduction of data is competitive to other algorithms based on lossy compression in the frequency domain. The final result is a novel approach to store hydrographic data using an adaptive grid structure taking into consideration the required reconstruction accuracy.