Spatial Transformation of Equality – Generalized Travelling Salesman Problem to Travelling Salesman Problem
Abstract
1. Introduction
Problem Encountered
2. Transformation of the E-GTSP to TSP
- 1
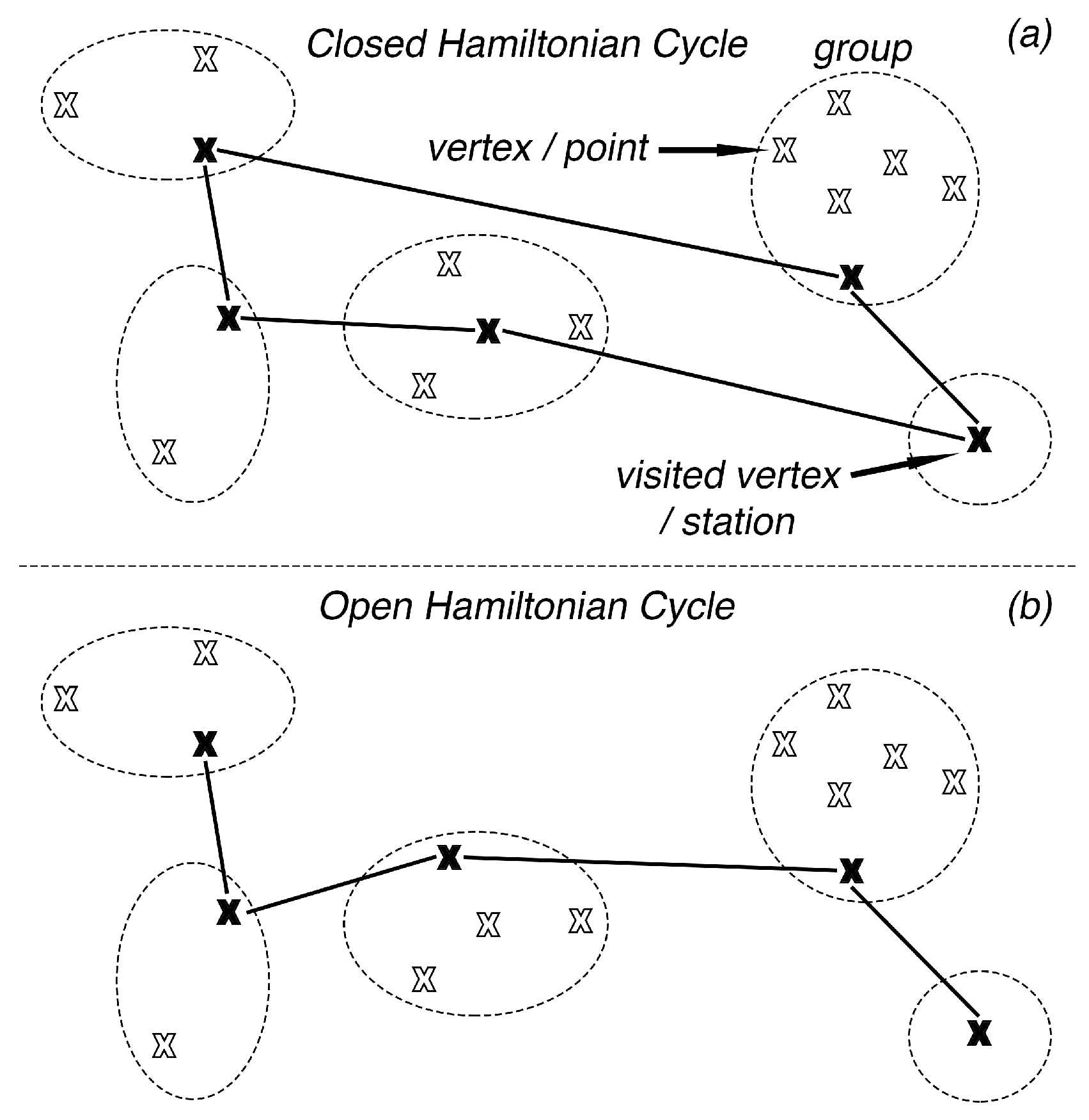
- Selection of a subset of vertices (), also termed as stations, such that and for all . Note that .
- 2
- Calculation of the minimum-cost Hamiltonian cycle in subgraph .
3. Methodology
3.1. E-Search and D-Search
| Algorithm 1 E-Search and D-Search pseudo-code | ||
| Require: Terminal points S and F, representing urban street-network, & , i.e., points’ groups set, where & ∀ & . | ||
| 1: | procedure E-GTSP ⇒ TSP | |
| 2: | if Algorithm 1 E-Search then Draw Euclidean Line | |
| 3: | end if | ▹ means corresponds to |
| 4: | if Algorithm 1 D-Search then Calculate Dijkstra Route | |
| 5: | end if | |
| 6: | Initialize an empty container | |
| 7: | for do | |
| 8: | Initialize an empty container . | |
| 9: | for do | |
| 10: | ← shortest Euclidean distance | ▹← means append |
| 11: | end for | |
| 12: | return | |
| 13: | ← v ∈ , with the smallest Euclidean distance | |
| 14: | end for | |
| 15: | return | |
| 16: | end procedure | |
| 17: | procedure TSP | |
| 18: | Calculate the minimum-cost Hamiltonian cycle induced by . Note: . | |
| 19: | end procedure | |
3.2. R-Search
| Algorithm 2 R-Search pseudo-code | |
| Require: Terminal points S and F, representing urban street-network, & , i.e., points groups set, where & ∀ & . | |
| 1: | procedure E-GTSP ⇒ TSP |
| 2: | Initialize an empty container |
| 3: | for do |
| 4: | Initialize an empty container . |
| 5: | for do |
| 6: | ← Euclidean distance |
| 7: | ← Euclidean distance |
| 8: | end for |
| 9: | return |
| 10: | ← v & ∈ , with the smallest Euclidean distance |
| 11: | end for |
| 12: | return |
| 13: | end procedure |
| 14: | procedure TSP |
| 15: | Calculate the minimum-cost Hamiltonian cycle for all pairs (i.e., ) induced by . |
| 16: | Select the pair with shortest minimum-cost cycle. |
| 17: | end procedure |
3.3. RE-Search and RD-Search
| Algorithm 3 RE-Search and RD-Search pseudo-code | |
| Require: Terminal points S and F, representing urban street-network, & , i.e., points groups set, where & ∀ & . | |
| 1: | procedure E-GTSP ⇒ TSP |
| 2: | Initialize an empty container |
| 3: | for do |
| 4: | Initialize an empty container . |
| 5: | for do |
| 6: | ← Euclidean distance |
| 7: | ← Euclidean distance |
| 8: | end for |
| 9: | return |
| 10: | ← Two v & ∈ , with least Euclidean distances |
| 11: | end for |
| 12: | return |
| 13: | if Algorithm 3 RE-Search then Run E-Search (Algorithm 1), treating ≡ |
| 14: | end if |
| 15: | if Algorithm 3 RD-Search then Run D-Search (Algorithm 1), treating ≡ |
| 16: | end if |
| 17: | Estimate (Filtered after E-Search or D-Search) |
| 18: | end procedure |
| 19: | procedure TSP |
| 20: | Calculate the minimum-cost Hamiltonian cycle for all pairs (i.e., ) induced by . |
| 21: | Select the pair with shortest minimum-cost cycle. |
| 22: | end procedure |
4. Study Area and Data-Set Used
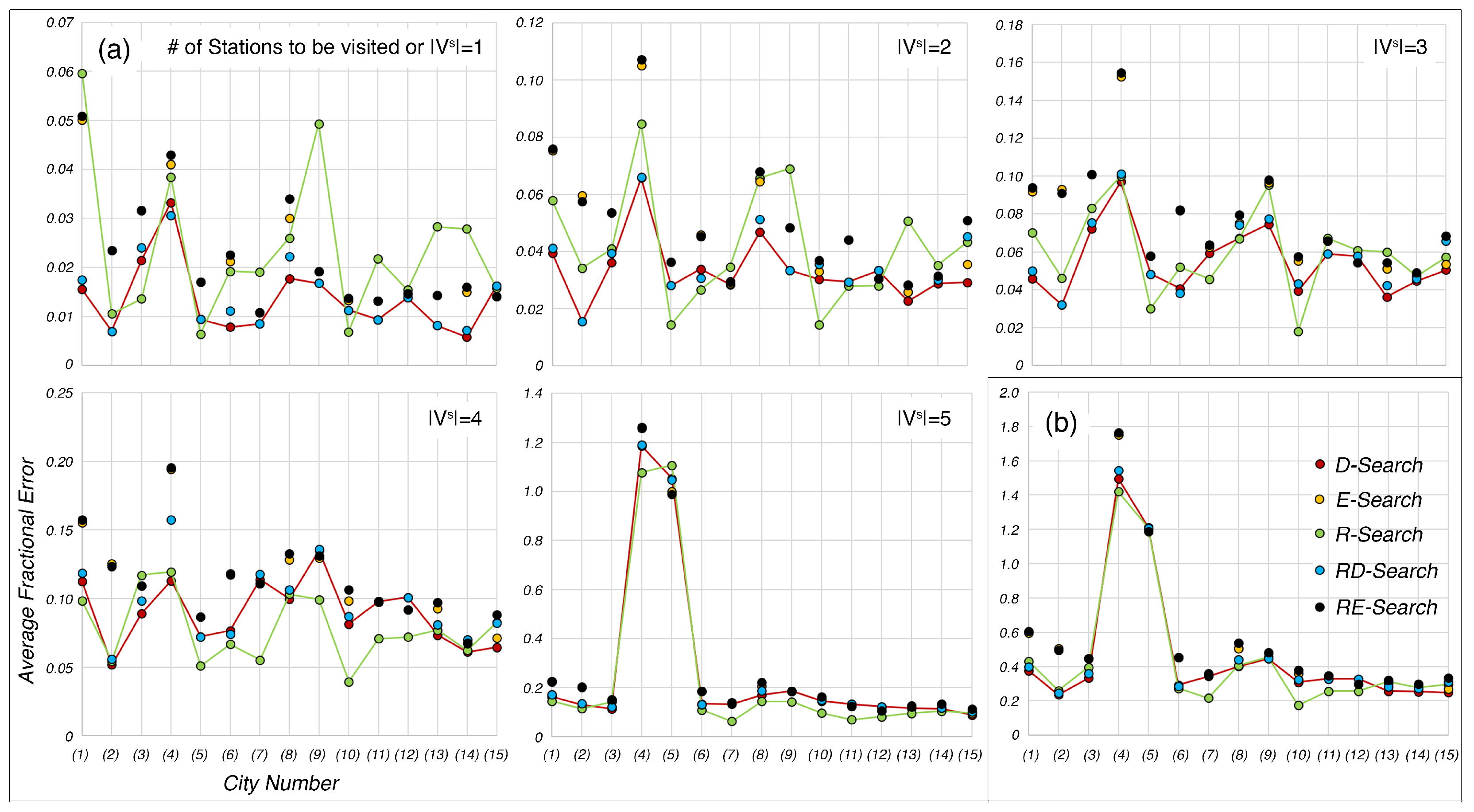
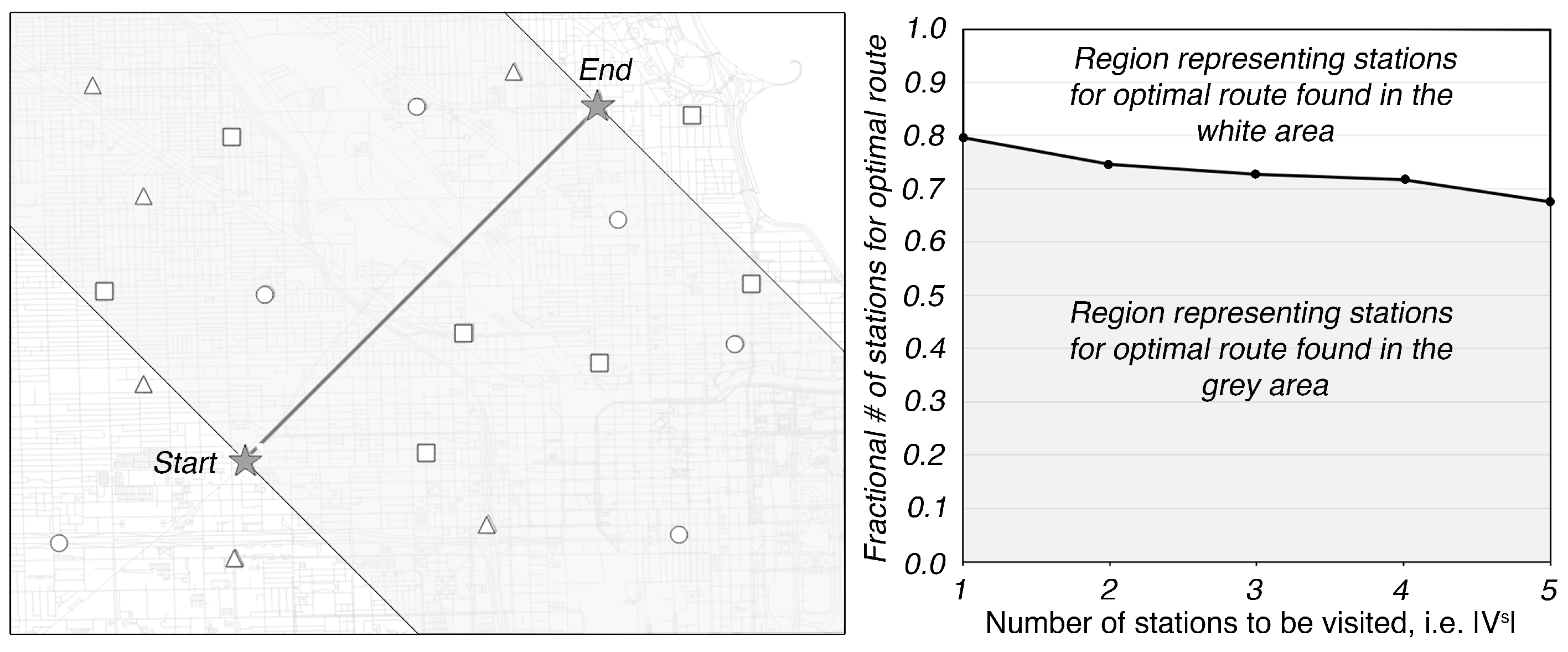
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| E-GTSP | Equality-Generalized Traveling Salesman Problem |
| GTSP | Generalized Traveling Salesman Problem |
| TSP | Traveling Salesman Problem |
| OSM | OpenStreetMap |
| GTSPLIB | Generalized Traveling Salesman Problem Library |
| E-Search | Euclidean Search |
| D-Search | Dijkstra Search |
| R-Search | Radial Search |
| RE-Search | Radial Euclidean Search |
| RD-Search | Radial Dijkstra Search |
References
- Hamilton, W.R. Memorandum respecting a new system of roots of unity. Philos. Mag. 1856, 12, 446. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, A.H.G.R. Some Simple Applications of the Travelling Salesman Problem. Oper. Res. Quart. 1975, 26, 717–733. [Google Scholar] [CrossRef]
- Psaraftis, H.N.; Wen, M.; Kontovas, C.A. Dynamic vehicle routing problems: Three decades and counting. Networks 2016, 67, 3–31. [Google Scholar] [CrossRef]
- Henry-Labor, A.L. The record balancing problem: A dynamic programming solution of a genera salesman problem. RAIRO-Oper. Res. 1969, 2, 43–49. [Google Scholar]
- Saksena, J.P. Mathematical model for scheduling clients through welfare agencies. Can. Oper. Res. Soc. 1970, 8, 185–200. [Google Scholar]
- Srivastava, S.S.; Kumar, S.; Garg, R.C.; Sen, P. Generalized travelling salesman problem through n sets of nodes. Can. Oper. Res. Soc. 1969, 7, 97–101. [Google Scholar]
- Laporte, G.; Nobert, Y. Generalized Travelling Salesman Problem Through n Sets Of Nodes: An Integer Programming Approach. INFOR Inf. Syst. Oper. Res. 1983, 21, 61–75. [Google Scholar] [CrossRef]
- Noon, C.E.; Bean, J.C. A Lagrangian Based Approach for the Asymmetric Generalized Traveling Salesman Problem. Int. J. Prod. Res. 1991, 39, 623–632. [Google Scholar] [CrossRef]
- Helsgaun, K. Solving the equality generalized traveling salesman problem using the Lin–Kernighan–Helsgaun Algorithm. Math. Program. Comput. 2015, 7, 269–287. [Google Scholar] [CrossRef]
- Karp, R.M. Reducibility among Combinatorial Problems. In 50 Years of Integer Programming 1958–2008; Springer: Berlin/Heidelberg, Germany, 2009; pp. 219–241. [Google Scholar]
- Laporte, G.; Asef-Vaziri, A.; Sriskandarajah, C. Some Applications of the Generalized Travelling Salesman Problem. J. Oper. Res. Soc. 1996, 47, 1461–1467. [Google Scholar] [CrossRef]
- Ben-Arieh, D.; Gutin, G.; Penn, M.; Yeo, A.; Zverovitch, A. Process planning for rotational parts using the generalized travelling salesman problem. Int. J. Prod. Res. 2010, 41, 2581–2596. [Google Scholar] [CrossRef]
- Gutin, G.; Punnen, A.P. The Traveling Salesman Problem and Its Variations. Comb. Optim. 2007, 12, 830. [Google Scholar] [CrossRef]
- Helsgaun, K. General k-opt submoves for the Lin–Kernighan TSP heuristic. Math. Program. Comput. 2009, 1, 119–163. [Google Scholar] [CrossRef]
- Lawler, E.L.; Lenstra, J.K.; Kan, A.H.G.R.; Shmoys, D.B. The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization; Wiley: Hoboken, NJ, USA, 1985; p. 476. ISBN 978-0-471-90413-7. [Google Scholar]
- Fu, C.; Cai, D. EFANNA: An Extremely Fast Approximate Nearest Neighbor Search Algorithm Based on kNN Graph. arXiv, 2016; arXiv:1609.07228. [Google Scholar]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N.; Kendall, D.G. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Zia, M.; Cakir, Z.; Seker, D.Z. A New Spatial Approach for Efficient Transformation of Equality—Generalized TSP to TSP. Free Open Source Softw. Geospat. (FOSS4G) Conf. Proc. 2017, 17, 15–22. [Google Scholar] [CrossRef]
- Laporte, G.; Mercure, H. Generalized travelling salesman problem through n sets of nodes: The asymmetrical case. Discret. Appl. Math. 1987, 18, 185–197. [Google Scholar] [CrossRef]
- Ben-Arieh, D.; Gutin, G.; Penn, M.; Yeo, A.; Zverovitch, A. Transformations of generalized ATSP into ATSP. Oper. Res. Lett. 2003, 31, 357–365. [Google Scholar] [CrossRef]
- Dimitrijevic, V.; Saric, Z. An efficient transformation of the generalized traveling salesman problem into the traveling salesman problem on digraphs. Inf. Sci. 1997, 102, 105–110. [Google Scholar] [CrossRef]
- Laporte, G.; Semet, F. Computational Evaluation Of A Transformation Procedure For The Symmetric Generalized Traveling Salesman Problem. INFOR Inf. Syst. Oper. Res. 2016, 37, 114–120. [Google Scholar] [CrossRef]
- Lien, Y.; Ma, E.; Wah, B.W.S. Transformation of the generalized traveling-salesman problem into the standard traveling-salesman problem. Inf. Sci. 1993, 74, 177–189. [Google Scholar] [CrossRef]
- Noon, C.E.; Bean, J.C. An Efficient Transformation Of The Generalized Traveling Salesman Problem. INFOR Inf. Syst. Oper. Res. 1993, 31, 39–44. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming Treatment of the Travelling Salesman Problem. J. ACM 1962, 9, 61–63. [Google Scholar] [CrossRef]
- Fischetti, M.; Salazar, J.J.; Toth, P. A Branch-and-Cut Algorithm for the Symmetric Generalized Traveling Salesman Problem. Oper. Res. Lett. 1997, 45, 378–394. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Munson, D. Which Street Pattern Represents Your Continent? 2013. Available online: https://munsonscity.com/2013/10/09 (accessed on 18 January 2018).
- Bourke, P. Fractal Dimension Calculator—FDC. 2003. Available online: http://paulbourke.net/fractals/fracdim (accessed on 18 January 2018).
- Overpass API. OpenStreetMap Overpass API. 2016. Available online: http://overpass-api.de (accessed on 18 January 2018).
- Hijmans, R.; Kapoor, J.; Wieczorek, J.; Garcia, N.; Maunahan, A.; Rala, A.; Mandel, A. GADM Database of Global Administrative Areas. 2015. Available online: http://www.gadm.org (accessed on 18 January 2018).
- Zverovitch, A. GTSP iNstances. 2008, Volume 2002. Available online: http://www.cs.rhul.ac.uk/home/zvero/GTSPLIB (accessed on 18 January 2018).
- Zia, M. E-GTSP-to-TSP-Tested-Instances. 2016. Available online: https://github.com/Zia-/E-GTSP-to-TSP-tested-instances (accessed on 18 January 2018).

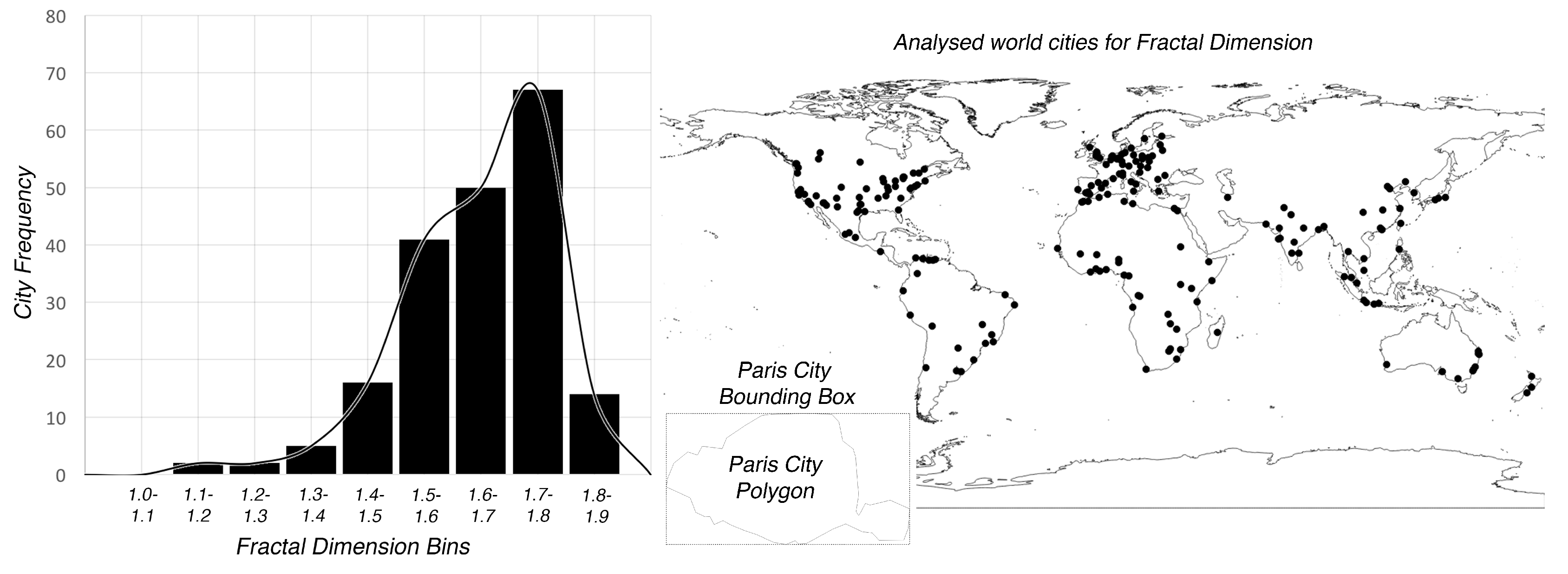



| ID | City | Fractal | Area | OSM | OSM | OSM | OSM | ∑Edge |
|---|---|---|---|---|---|---|---|---|
| (Country) | Dimension | (km) | # Vertex | Vertex | # Edge | Edge | (km) | |
| 1 | Hargeisa | 1.400 | 42,332 | 7267 | 0.17 | 10,839 | 0.26 | 7782 |
| (Somalia) | ||||||||
| 2 | Antananarivo | 1.413 | 42,291 | 26,955 | 0.64 | 33,188 | 0.78 | 10,455 |
| (Madagascar) | ||||||||
| 3 | La Paz | 1.432 | 14,454 | 55,239 | 3.82 | 83,209 | 5.76 | 11,012 |
| (Bolivia) | ||||||||
| 4 | Nairobi | 1.511 | 84 | 3,386 | 40.3 | 4469 | 53.2 | 482 |
| (Kenya) | ||||||||
| 5 | Mexico City | 1.517 | 1153 | 6839 | 5.93 | 7,819 | 6.78 | 1241 |
| (Mexico) | ||||||||
| 6 | Las Vegas | 1.537 | 81,440 | 154,289 | 1.89 | 205,164 | 2.52 | 40,971 |
| (USA) | ||||||||
| 7 | Seoul | 1.609 | 226 | 11,764 | 52.0 | 16,301 | 72.1 | 1394 |
| (S-Korea) | ||||||||
| 8 | Edmonton | 1.627 | 181,262 | 95,083 | 0.52 | 127,203 | 0.70 | 56,965 |
| (Canada) | ||||||||
| 9 | Calgary | 1.630 | 96,779 | 130,982 | 1.35 | 185,201 | 1.91 | 49,842 |
| (Canada) | ||||||||
| 10 | Amsterdam | 1.730 | 1152 | 62,630 | 54.4 | 88,977 | 77.2 | 8048 |
| (Holland) | ||||||||
| 11 | Brussels | 1.745 | 943 | 54,941 | 58.3 | 75,833 | 80.4 | 7273 |
| (Belgium) | ||||||||
| 12 | Delhi | 1.779 | 5078 | 198,972 | 39.2 | 270,302 | 53.2 | 27,063 |
| (India) | ||||||||
| 13 | Dallas | 1.800 | 4688 | 116,034 | 24.7 | 166,882 | 35.6 | 26,376 |
| (USA) | ||||||||
| 14 | Milan | 1.802 | 8043 | 265,604 | 33.0 | 356,506 | 44.3 | 36,666 |
| (Italy) | ||||||||
| 15 | Munich | 1.811 | 1817 | 188,387 | 103.7 | 253,015 | 139.2 | 17,380 |
| (Germany) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zia, M.; Cakir, Z.; Seker, D.Z. Spatial Transformation of Equality – Generalized Travelling Salesman Problem to Travelling Salesman Problem. ISPRS Int. J. Geo-Inf. 2018, 7, 115. https://doi.org/10.3390/ijgi7030115
Zia M, Cakir Z, Seker DZ. Spatial Transformation of Equality – Generalized Travelling Salesman Problem to Travelling Salesman Problem. ISPRS International Journal of Geo-Information. 2018; 7(3):115. https://doi.org/10.3390/ijgi7030115
Chicago/Turabian StyleZia, Mohammed, Ziyadin Cakir, and Dursun Zafer Seker. 2018. "Spatial Transformation of Equality – Generalized Travelling Salesman Problem to Travelling Salesman Problem" ISPRS International Journal of Geo-Information 7, no. 3: 115. https://doi.org/10.3390/ijgi7030115
APA StyleZia, M., Cakir, Z., & Seker, D. Z. (2018). Spatial Transformation of Equality – Generalized Travelling Salesman Problem to Travelling Salesman Problem. ISPRS International Journal of Geo-Information, 7(3), 115. https://doi.org/10.3390/ijgi7030115






