1. Introduction
Light Detection and Ranging (LiDAR) is one of the main measurement techniques used nowadays for the derivation of digital terrain models (DTM) in environmental applications. LiDAR, also referred to as laser scanning, provides highly accurate and dense 3D point measurements (point clouds) that can be acquired at different measurement scales. For example, terrestrial laser scanning (TLS) can measure micro-scale surface features (<1 m) such as pebbles or soil clods [
1,
2,
3]. Such data typically have a coverage of a few tens of meters. A coverage of, e.g., a few kilometers is possible when a TLS system is mounted on a moving vehicle or a riverboat [
4,
5]. These so-called mobile mapping systems also include a global navigation satellite system (GNSS) and/or an inertial measurement unit (IMU) for georeferencing the acquired points. Laser scanning performed from airplanes (ALS) constitutes another dynamic, mobile mapping system that provides an even larger coverage, but also features a lower resolution compared with TLS. However, such data are able to depict topographic signatures at the landscape scale relevant for hydrology and geomorphology [
5,
6,
7,
8,
9]. Therefore, LiDAR data are extremely useful for describing natural surfaces at several spatial scales.
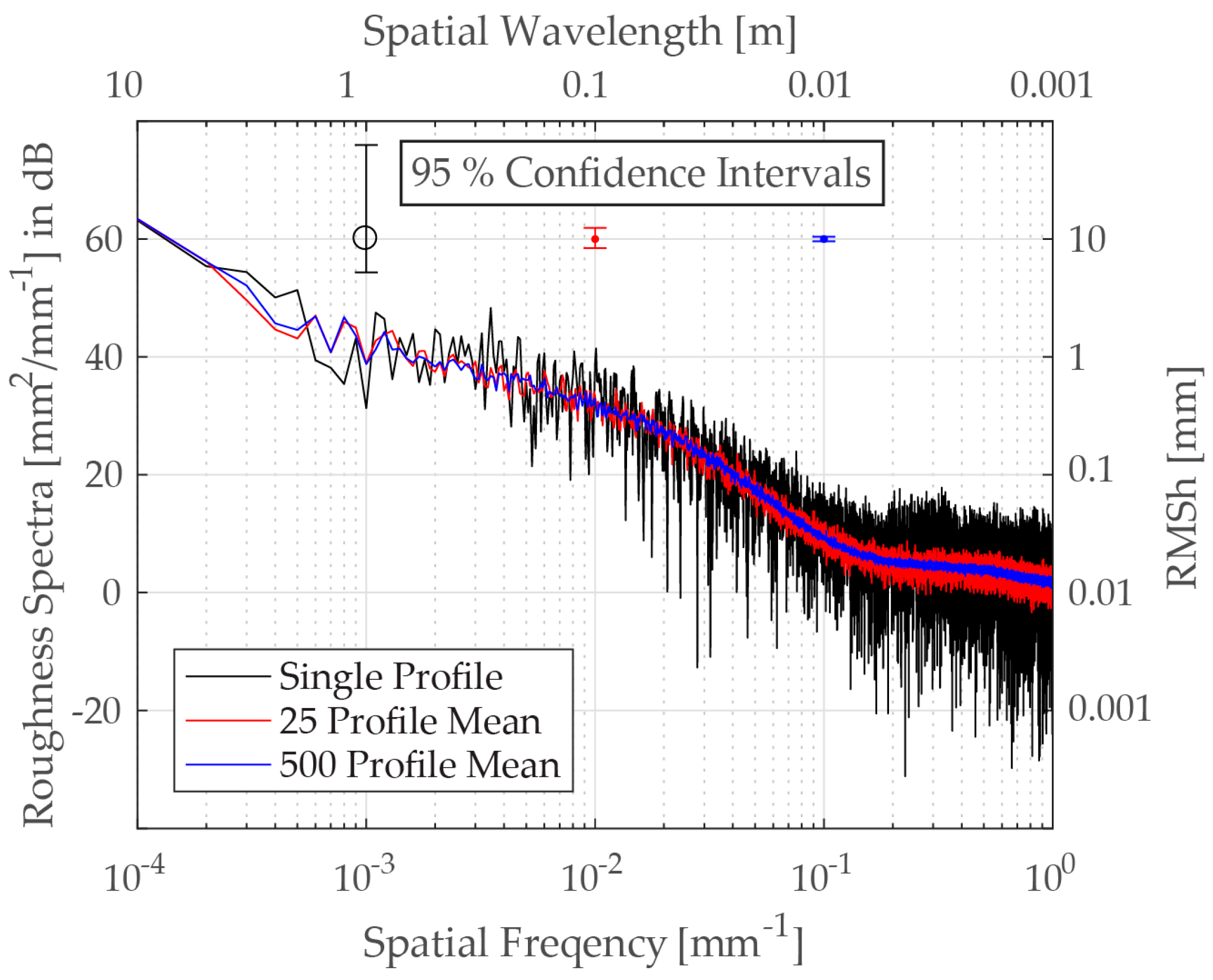
One way to describe natural surfaces over different spatial scales is by using the roughness spectrum [
8,
10,
11]. This is a DTM derivative that shows the distribution of the terrain variance over a certain range of spatial frequencies (wavelengths), where each frequency represents a sinusoidal component of the DTM in the spatial domain. More precisely, the roughness spectrum is the surface’s power spectral density; i.e., the Fourier transform of the surface’s autocorrelation function. The calculation of the roughness spectra is typically based on the Fast Fourier Transform (FFT) algorithm applied to a regularly-sampled elevation profile or a gridded DTM [
8,
12,
13]. Hedge and Masselink [
14] summarized the major steps of this methodology for time series data, but it is also valid in the case of gridded DTMs [
8]. As the elevation profiles are discrete and finite, a roughness spectrum has variances only in a certain span of discrete wavelengths (a particular frequency band). The longest (DC) and the smallest (Nyquist) wavelengths of this frequency band correspond exactly to the profile length and the double of the point spacing, respectively. Thus, for a LiDAR dataset, the DC and Nyquist wavelengths are defined by the spatial coverage and sampling distance, respectively.
Roughness spectra are extensively used to characterize surface roughness in many physical and environmental models. The radar backscattering models, for example, use the roughness spectrum to better define the scattering characteristics of certain natural surfaces and to predict the amount of backscatter energy from such surfaces [
15]. Furthermore, roughness spectra are used to describe the roughness length of the boundary surface and to analyze its wind velocity profile for different topographic scales [
16]. Similarly, in hydraulic models, the roughness spectrum and its slope are used to characterize grain roughness and local microtopography as well as to analyze the flow velocity spectrum [
17,
18]. Roughness spectra are also employed to quantify the influence of the Earth’s surface processes on landscape shapes [
8], or to describe the seafloor topography [
19].
For most of the above applications, roughness spectra are, or can be, derived from LiDAR point clouds. These LiDAR point clouds have to be interpolated into gridded DTMs first in order to apply the Fourier-based methodology and to derive the roughness spectra. It is, however, not known which frequencies of the resulting spectra are affected by the selected DTM interpolation method. Furthermore, multi-scale LiDAR datasets have different resolutions and coverages, and thus, provide spectra in different frequency bands. To combine such complementary data, it is important to know over which spatial scales the corresponding roughness spectra can be used interchangeably. Such an analysis is important to understand better how to measure surfaces with LiDAR and how to better combine these complementary LiDAR data to get the roughness spectra over a larger frequency band.
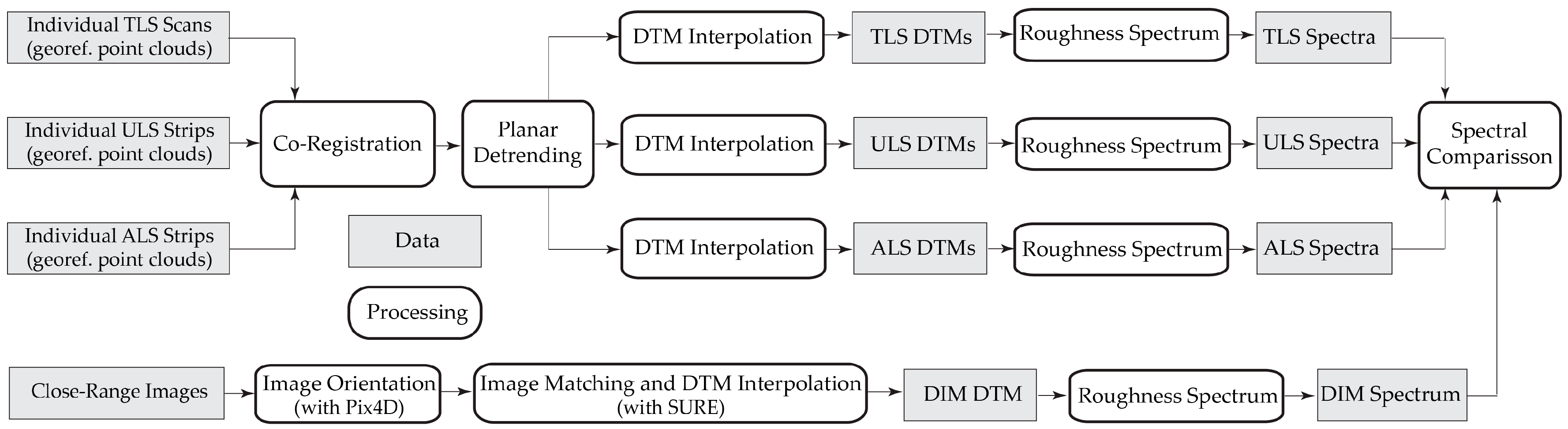
In this study, we sampled a 1 m × 10 m gravel plot with three different LiDAR techniques and analyzed and compared the corresponding roughness spectra. The LiDAR techniques used here comprise terrestrial laser scanning (TLS), laser scanning from an unmanned aerial vehicle (ULS), and laser scanning from an airplane (ALS). An unmanned aerial vehicle (UAV) is also referred to as a remotely piloted aircraft system (RPAS), or a drone. The gravel plot was extensively sampled with TLS (2.5 h of effective scanning with 14 high-resolution scans), whereas the ALS and ULS data were acquired in the course of a topographic survey campaign with the specific aim of covering a larger river section. Therefore, the focus of the analysis was more on the TLS data. In addition to these datasets, a set of high-resolution handheld images of the gravel plot was acquired and processed in order to have a non-LiDAR-based roughness spectrum for comparison. This dataset also served as a reference for the high-frequency surface components, as the ground sampling distance (GSD) of the images was 10 times smaller than the TLS footprint size. It is noted that the ULS data were acquired with a novel RIEGL VUX-1 UAV system that was applied in a surface roughness application for the first time.
Related Work and Objectives
In this study, roughness spectra and their confidence intervals are derived by applying the Fourier-based methodology standardized by Hedge and Masselink [
14]. Previous studies focused more on how particular Fourier-based steps such as profile windowing or detrending affect the shape of the roughness spectra [
10,
13]. Snapir et al. [
12] analyzed changes of roughness spectra of an agricultural soil surface derived from multi-temporal close-range images using structure from motion. Additionally, differences between the TLS roughness spectrum with roughness spectra derived from a triangulating laser scanner and images acquired by a UAV were analyzed in References [
3,
20], respectively. However, a comprehensive comparison of roughness spectra derived from several measurements techniques has not yet been done.
There exist several numerical roughness studies based on synthetic surfaces. These surfaces are typically simulated from a predefined shape of the roughness spectrum (or its autocorrelation function), applying the convolution of a random (uncorrelated) Gaussian surface (or a profile) with a moving window whose coefficients are derived from the predefined roughness spectrum [
21,
22]. The synthetic profiles are particularly used to understand the influence of the profile length, point spacing, and other sampling parameters on different roughness coefficients, as well as the radar backscattering coefficient [
23,
24]. Berti et al. [
25] analyzed the performance of different roughness assessment methods for automatic landslide detection on both synthetic and real surfaces. A synthetic sinusoidal surface is also used for testing the Fourier-based calculations of the autocorrelation function in a roughness analysis of seafloor roughness [
26]. Landy et al. [
27] developed a numerical model to simulate TLS measurements over a random, exponentially-correlated surface, which was then used to assess the influence of the occlusion errors and other TLS sampling errors. In these numerical studies, the theoretical roughness values of the synthetic surfaces are well approximated by the roughness methodology applied. However, real data and experiments come with additional complexities, which are also relevant to consider and quantify.
This study considers exclusively real, multiscale LiDAR data. As a reference, a very high-resolution DTM dataset acquired from handheld images is used. The analysis concentrates on how certain aspects of LiDAR data processing affect the shape of the resulting roughness spectrum and then compares the multiscale LiDAR spectra. More precisely, the objectives of this study are:
To analyze the influence of basic DTM interpolation methods on TLS, ULS, and ALS roughness spectra;
To analyze how the number of TLS scans affects the roughness spectrum;
To compare TLS, ULS, and ALS roughness spectra.
For the DTM interpolation analysis, TLS, ULS, and ALS point clouds are interpolated using basic interpolation methods and then the difference in the shape of the corresponding spectra is analyzed. The aim is to determine the spatial wavelengths that are not affected by the interpolation method. For the sake of simplicity, complex interpolation methods (e.g., the Kriging method) are not applied in this paper as their results depend on several parameters and impose stronger restrictions on the input data.
For analyzing the number of TLS scans, different combinations of TLS scans are selected and the corresponding roughness spectra are compared with the roughness spectrum derived using all 14 TLS scans (i.e., the reference roughness spectrum in this case). The aim is to determine if a 1 m × 10 m gravel plot can be measured with a smaller number of TLS scans, while still providing an equally accurate roughness spectrum as opposed to using all the TLS scans. An additional aim is to determine which frequency band can be covered by a single TLS scan with its roughness spectrum.
A comparison of the multiscale LiDAR spectra is done for the first time here. The aim of this analysis is to understand the differences in the TLS, ULS, and ALS spectra and to determine the spatial wavelengths over which they can be used interchangeably. The spectra based on TLS and novel ULS data are separately analyzed to assess to which degree the ULS spectrum can replace the TLS spectrum.
2. Study Site and Data
Table 1 gives an overview of the datasets (and their basic characteristics) used in this study. All the data were collected on 26 February 2015, and refer to the same area: the 1 m × 10 m gravel plot. The ALS and ULS data were already available as georeferenced point clouds for this study. Their georeferencing is performed with a rigorous strip adjustment procedure presented in [
28,
29], in detail. The TLS data are processed here from raw point clouds to georeferenced scans. Therefore, the input data for the roughness spectra calculation and all further analyses include individually georeferenced ALS, ULS, and TLS point clouds.
Figure 1 shows the basic properties of the study site. The 1 m × 10 m gravel plot is located at a point bar in the tailwater region of the pre-alpine Pielach River, a tributary of the Danube in Austria (48°12′50.70″ N, 15°22′27.50″ E, WGS 84). The microtopography of the gravel plot (
Figure 1d,e) mostly consists of unsorted fine (<2 cm in diameter) and medium (2–6 cm) pebbles, while several clusters of coarse (>6 cm) pebbles are also present. The plot also features microtopographic undulations at a cm to dm scale on top of a global planar slope.
2.1. ALS Data
The ALS data were acquired with a Riegl LMS-Q1560 dual-channel long-range laser scanning system which acquires two scans for each strip (x-shaped scan lines on the ground with a field of view (FoV): ±29°). The sensor additionally features a GNSS/IMU device to record the trajectory. The entire system was mounted on a Diamond DA42 aircraft. The ranging precision of this instrument is 20 mm, which is specified for a range of 250 m and estimated under the manufacturer test conditions [
30].
The scanning parameters were set to cover the whole river reach and provide at least 10 points per m2 for a single strip (i.e., two scans). The pulse repetition rate was 400 kHz and the flying speed was approximately 56 m/s (110 knots). The plot was covered with four strips, resulting in an average point density of 36 points per m2. This corresponds to an average point sampling of approximately 17 cm. As the flying height was 640 m above the terrain, the footprint diameter was also approximately 16 cm (the beam divergence being 0.25 mrad). This meant that the footprints of the individual ALS samples were (on average) touching, or just slightly overlapping one another.
The raw ALS data had already been preprocessed (cf. [
28,
29]), providing a georeferenced point cloud in the global coordinate system (ETRS89/UTM33N). The ALS preprocessing involved (a) the extraction of Gaussian echoes; (b) solving the range ambiguities due to the multiple-time-around ranging of the used sensor; and (c) direct georeferencing of the extracted echoes. The preprocessing was done in the sensor manufacturer software (RiPROCESS) [
29]. Additionally, a rigorous strip adjustment was done with the objective to minimize the point-to-plane distances in overlapping strip areas [
28]. The standard deviation of the residuals between the individual ALS strips was reported to be 1 cm [
29].
2.2. ULS Data
The ULS data were acquired with the Riegl VUX-1 UAV laser scanner mounted on the Riegl RiCOPTER, a remotely piloted octocopter. The sensor is equipped with an IMU/GNSS system to record the trajectory. The scanner itself performs online waveform processing, which provides additional attributes such as pulse shape deviation and calibrated reflectance readings for each laser echo [
31]. The ranging precision of this instrument is 5 mm, which is specified for a range of 150 m and estimated under the manufacturer test conditions [
32].
The scanning parameters were set to cover a larger area (~100 ha) and provide at least one point per dm
2 for a single ULS strip. The effective measurement rate was 350 kHz (cf. [
29]) and the flying speed was approximately 8 m/s (15.5 knots). The plot was covered with ten strips (the effective FoV: 230°, cf. [
29]), resulting in an average point density of 11.8 points per dm
2. This corresponds to an average point sampling of ~2.9 cm. As the flying height was 50 m above the terrain, the footprint diameter was ~2.5 cm (the beam divergence being 0.5 mrad). Thus, the footprints of the individual ULS samples were (on average) not overlapping with one another. As in the case of the ALS data, the raw ULS data had been preprocessed before (cf. [
28,
29]), providing a georeferenced point cloud in the same global coordinate system. The standard deviation of the point-to-plane residuals was reported to be below 2 cm for both the ULS strips only and the ULS and ALS strips combined [
28].
2.3. TLS Data
The gravel plot was extensively scanned with a Z+F IMAGER
® 5010c mounted on a high tripod. This scanner utilizes phase shift ranging and has a small beam divergence (0.3 mrad). The beam diameter at the exit (0.1 m range) is 3.5 mm, which allows for a high-resolution scanning of close objects (maximum range < 130 m). The ranging precision of this instrument is 0.3 mm, which is specified by the manufacturer for ranges smaller than 10 m and for grey targets [
33].
The scanning parameters were set to maximize the TLS sampling of the gravel plot and still have a reasonable scanning time to acquire as many scans as possible. The aim was for the footprints of the TLS samples to overlap one another in a single TLS scan. Therefore, the angular resolution was set to 0.036° (10,000 samples per full circle) and the ‘high’ scanning quality modus was selected. This TLS setting leads to a scanning time of 7 min per scan. The plot was scanned with 14 scans, 7 taken from each long side of the plot. This so-called opposite scanning minimizes occlusions due to object scan shadows. The average point density was 190.3 points per cm
2, which corresponds to an average point sampling of 0.7 mm. As the scanner height above the terrain was between 2.4 m and 2.6 m and the range was not larger than 4.5 m, the TLS footprint diameter was smaller than 5 mm within the plot. This meant that the TLS footprints were largely overlapping one another. For a single scan, the average sampling distance was ~2.4 mm (i.e., ~17 points per cm
2) and thus, the TLS footprints are largely overlapping one another even for the single scan samples. Such a scan maximizes the resolution of the TLS data and that scanning scheme is also known as correlated scanning [
34]. Furthermore, scanning from a high tripod ensured that the incidence angle was smaller than 52° for 90% of the data, which fulfilled the recommendations for soil roughness scanning [
3].
The raw TLS measurements were first preprocessed and then georeferenced. The preprocessing involved the following steps: (a) the elimination of erroneous range measurements (so-called mixed pixels) caused by phase-based ranging [
35]; (b) the georeferencing of the TLS scans; and (c) the export of the georeferenced points inside the gravel plot. All steps were performed using the Z+F LaserControl
® software (version 8.6) [
36]. The georeferencing of the TLS scans was done indirectly, using four ground control points (GCPs) and a ‘point block adjustment’ method implemented in the above software. The GCPs were located outside the plot and scan positions, ensuring target visibility in all scans and a favorable network geometry for the co-registration. The coordinates of the GCPs were derived from the total station measurements and in the global coordinate system of the ALS and ULS data. After georeferencing the individual TLS scans, the standard deviation of the 3D distance residuals at the GCPs was 1.6 mm. The same statistic derived for individual TLS scans was 0.8 mm. The georeferenced TLS scans were then exported for an improved, global co-registration with a version of the Iterative Closest Point (ICP) algorithm [
28]. The standard deviation of the point-to-plane distances between all scans after this global co-registration was 0.6 mm. This suggests a good co-registration as the ranging noise of the TLS scanner alone was ~0.3 mm [
33].
2.4. Handheld Images
A set of handheld images of the plot were also acquired to calculate an additional, non-LiDAR-based, roughness spectrum. In total, 117 images were collected with the full-frame Nikon D800 camera using a 28 mm lens. The images were taken with an overlap of 70–80% from ~1.8 m height above the ground, which resulted in a GSD not larger than 0.5 mm within the plot.
The images were first oriented and then dense image matching (DIM) was applied to derive a DTM. This will be referred to as the DIM DTM. The image orientation and self-calibration were done using a bundle block adjustment method implemented in the Pix4D software [
37]. The adjustment also included 18 3D GCPs uniformly distributed along the plot sides whose coordinates were measured by a total station in the global coordinate system. The resulting reprojection error was 0.13 pixels, whereas the standard deviation of the height residuals at the GCPs was 0.8 mm. Based on this camera orientation, the DIM DTM was calculated using the semi-global matching approach implemented in the SURE software [
38]. We used the option for automatic interpolation of a DTM and specified its grid size to be 0.5 mm, which corresponds to the GSD of our images. This is 10 times smaller than the TLS footprint diameter, which enables the DIM DTM to serve as the reference for the high-frequency surface features.
5. Discussion
5.1. Interpretation of the Results
This study analyses how the DTM interpolation, number of TLS scans, and multi-scale LiDAR data affect the shape of the roughness spectra. The aim of this paper was to quantify the wavelengths over which the roughness spectra can be used interchangeably.
5.1.1. DTM Interpolation
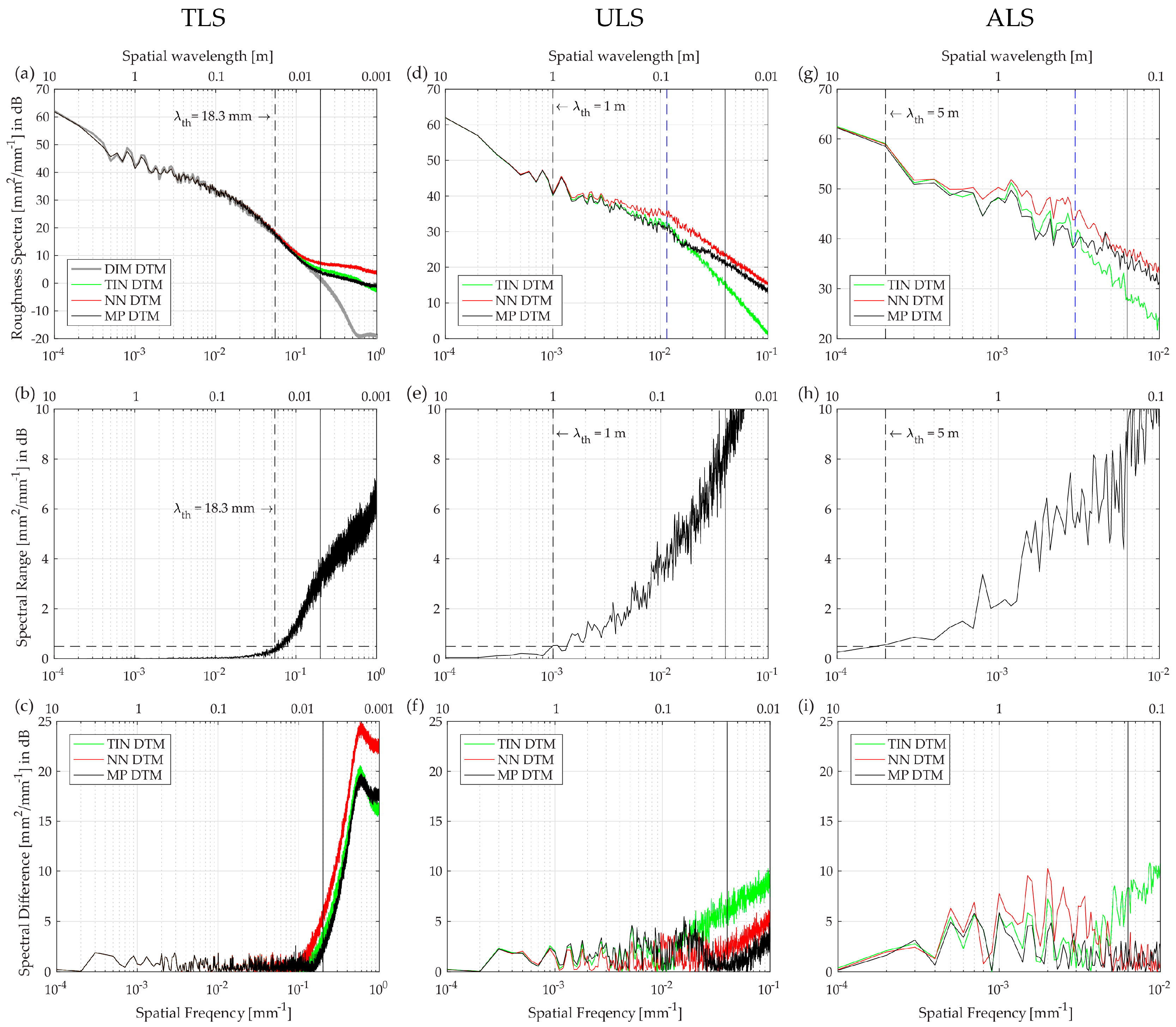
The three DTM interpolation methods (NN, TIN, and MP) affect the roughness spectrum only at the high frequencies (i.e., the spatial wavelengths close to the laser footprint diameter). The analyses from
Section 4.2 (
Figure 6) demonstrated that the ULS and ALS spectral ranges exceed the dB threshold much earlier (at wavelengths of 1 m and 5 m, respectively) compared with the TLS spectral range that exceeds at wavelengths of ~2 cm and smaller. This was expected as the ULS and ALS data are acquired at smaller measurement scales (coarser resolutions).
However, these results also show that the selection of the interpolation method is differently important for each LiDAR dataset. For the ULS data, the NN, TIN, or MP interpolations do not affect the roughness spectra at wavelengths larger than 1 m. Therefore, the optimization of the interpolation parameters is required to derive accurate ULS spectra at wavelengths smaller than 1 m. For the ALS data, the selection of interpolation method is particularly important as it affects almost all wavelengths. It is only the DC component and the first harmonic that are not affected by the interpolation method. One reason why these two surface components are not affected could be due to the fact that our plot length was too small for analyzing the ALS data. Therefore, a longer plot should be considered to determine accurately the threshold wavelength for the ALS data.
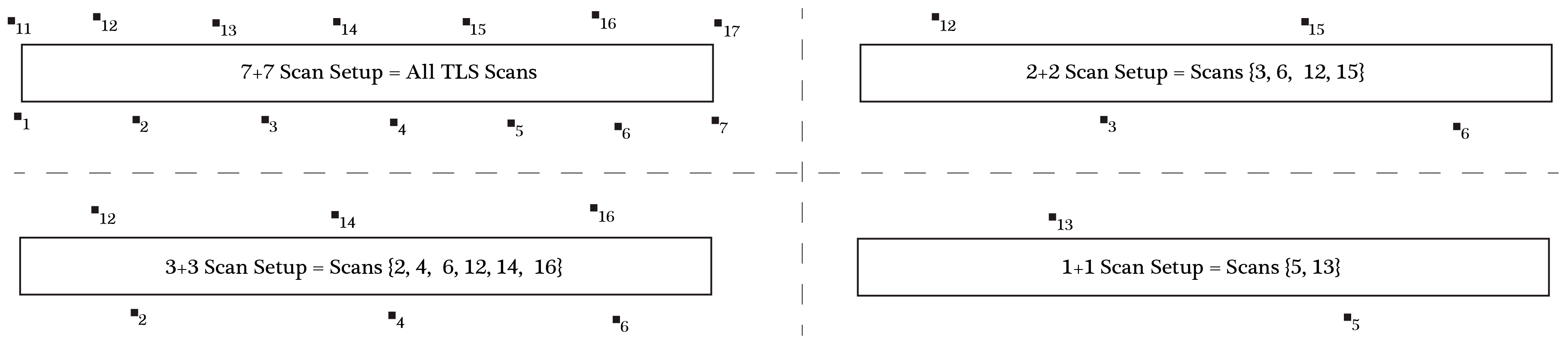
5.1.2. TLS Scan Setup
The analysis of the number of TLS scans is performed to further optimize the TLS setups for the measurement of the roughness spectrum. It was shown that a TLS scan taken from the plot corner may notably deform the shape of the roughness spectrum, whereas a center scan or two or more scans provide equally accurate roughness spectra as with all 14 TLS scans. It should be noted that a scan that is taken from the corner of a 1 m × 10 m plot can also be considered as a scan taken from the middle of a 1 m × 20 m plot. Based on this observation and the results shown in
Figure 7b,c, the following statements can be drawn:
It is noted that the 0.65 dB value of is just slightly violating the threshold based on the 95% confidence interval. In addition, the above statements are valid when TLS is applied from high tripods and from the center of the plot. It is expected that a roughness spectrum derived from TLS using classical geodetic tripods is more sensitive because of the larger occlusion effects. However, this is to be analyzed in further studies.
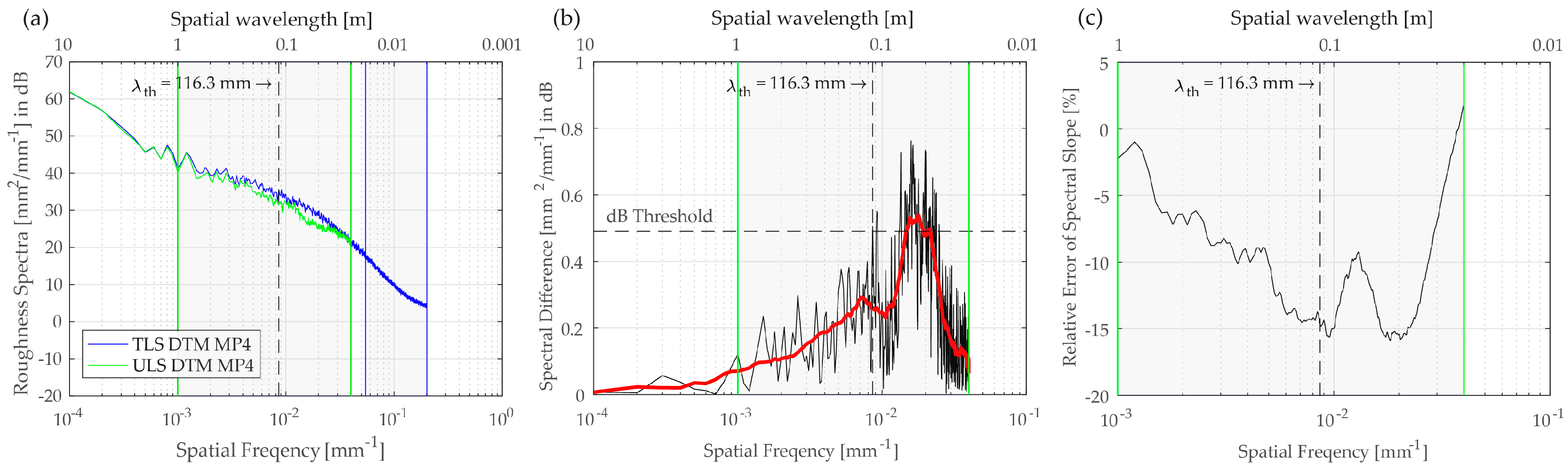
5.1.3. Multi-Scale Data and Spectral Differences
The differences between the TLS and ULS roughness spectra that are presented in
Figure 8b are linear at larger wavelengths (slightly smaller than the wavelength of 1 m) and then become more complex at smaller wavelengths (slightly larger than the ULS footprint diameter). Similar conclusions can be drawn from the relative differences
between the ULS and TLS spectral slopes (
Figure 8c). The slope differences linearly increase and reach a maximum around
. However, for wavelengths smaller than
, the slope differences become more complex and eventually change their sign. On the other hand, the differences between the TLS and DIM roughness spectra, presented in
Figure 8a and
Figure 9, are only linear. Therefore, one reason for the different behavior of the ULS spectrum for wavelengths larger and smaller than
is that the ULS data have less overlapping footprints.
It is also noted that the ULS spectral slope values (in
Figure 8c) overestimate the TLS spectral slope by about 15%, although the spectral differences are below 0.5 dB. This means that spectral slope values are more sensitive than the spectral differences. Therefore, the spectral slope may result in stronger measurement requirements compared with the requirements derived from the spectral differences.
5.2. Spectral Analysis
Investigating the roughness spectra is a method that can be used to analyze DTMs. It gives consistent results for the TLS data in the analysis of the scan setup and quantifies the loss of information when reducing the number of scans. Additionally, in the extreme case of using only one scan on the edge of the plot, the loss of quality is quantified. Likewise, the wavelength at which the spectra deviate significantly from each other due to different interpolation methods provides insight on the relevance of the choice of a certain method. The analysis of the spectra for different interpolation methods from LiDAR data at all investigated scales also allowed the conclusion that the four-point moving plane interpolation, which involves smoothing, is preferable over the NN and TIN interpolations. Therefore, the analysis of the difference to a reference spectrum provides a measure that concentrates on the resolution and damping of amplitudes of a specific DTM. This is additional information compared to other methods of DTM analysis such as the DEM of Differences (DoD), or the measures of the distribution of vertical height differences (mean, standard deviation, etc.).
5.3. The dB Threshold
In this paper, the dB threshold that corresponds to the 95% confidence interval of the ensemble averaged periodogram is used to determine the wavelengths over which the spectra can be used interchangeably. For our data, this dB threshold was 0.5 dB, which is a rather strict threshold value compared with other studies. For example, in an application of roughness spectra for microwave backscatter models, a spectral difference threshold of 2 dB was acceptable [
24]. Additionally, in a seafloor roughness application, the spectral differences were analyzed using a threshold of 1 dB [
19]. Therefore, the
values reported in this paper should be considered as rather conservative estimates.
A dB threshold that is tailored to a particular application would exactly define the requirements for the LiDAR measurements and the roughness spectrum calculation, but only for that particular application. A threshold based on the confidence interval of the roughness spectrum has the advantage of being application independent and furthermore, accounts for the variance of the ensemble averaged spectrum.
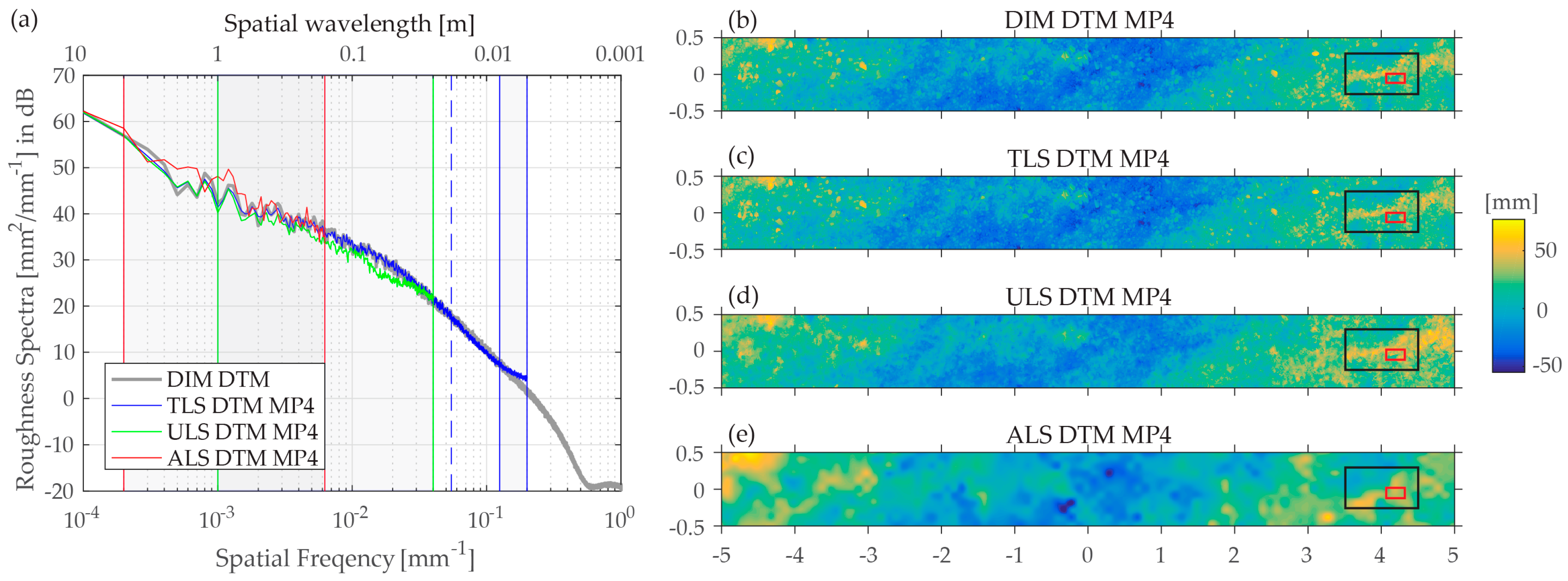
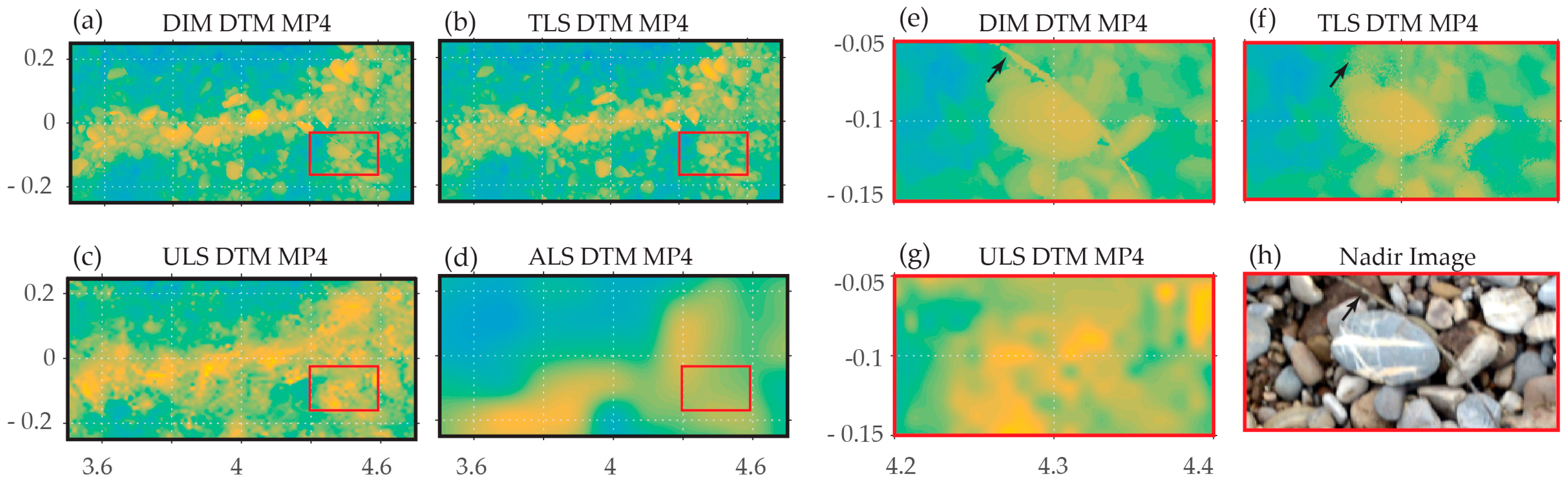
5.4. ALS and ULS Data
The comparison of the multi-scale LiDAR data is always challenging as such measurements involve many setup parameters. Our TLS data, for example, were optimal for the analysis because the plot was oversampled by a large number of scans and we scanned in the correlated sampling mode (i.e., with highly overlapping footprints within a single scan). This then allowed for optimizing the TLS setup for the roughness spectrum calculation. On the other hand, ALS and ULS did not offer an as extensive sampling of the plot as in the case of TLS. Therefore, to optimize the ALS and ULS setups for roughness spectra calculation, it would be important to acquire ALS and ULS data that have both highly overlapping footprints within the scan line and a large number of scans (strips) that cover the plot.
We posit the hypothesis that an extensive sampling of the plot with ALS and ULS would certainly result in more optimistic
values than the ones reported here for the ULS and ALS data. For example, in
Figure 6, the spectral range value
at the footprint wavelength is almost 8 dB for the ALS and ULS data, whereas, for the TLS data, this value is about 3 dB. This shows that the ULS and ALS spectra are more sensitive to the interpolation method than the TLS spectra. One reason for this could be the lower footprint overlap of the ULS and ALS data compared with the TLS data. It would be interesting to see, e.g., if both the
and
values would be smaller than the values reported in
Section 4.1 when derived from the ULS and ALS data with highly overlapping footprints. In addition, it would be interesting to see if the complex differences observed between the TLS and ULS spectra (
Figure 9b) could become linear as with the differences observed between the TLS and DIM spectra (the grey rectangle with blue edges,
Figure 9a). Highly overlapping footprints correspond to an extremely dense sampling of surface heights and thus, the roughness spectra will be less affected by the interpolation method. This means that an agreement between the TLS and ULS spectra can be expected to improve even to the sub-decimeter wavelengths (e.g., when the sampling distance of the ULS points is notably smaller than the ULS footprint diameter). Bearing in mind that our dB threshold is rather strict compared to other publications, it can be concluded that the ULS data has a high potential to replace the TLS data for the roughness spectrum calculation in many applications. This should be, however, shown in further experiments.
5.5. Limitations and Suggested Further Experiments
The idea behind this work was to initiate a quality analysis of the roughness spectrum calculation from LiDAR data. The outcome provided valuable conclusions on the TLS setup and the comparison of the TLS, ULS, and ALS spectra (and the range of their interchangeability). However, the experiment also revealed that both the experimental setup and the roughness spectra analysis could be improved in further studies.
One way to extend the analysis of the roughness spectra could be by propagating them further through geophysical models and analyzing how the model predictions are sensitive to changes in the roughness spectrum. This analysis could help in defining better dB thresholds for particular applications. In addition to this, further analysis could consider more complex interpolation methods, such as the Kriging method. As
Section 4.2 showed, the TLS spectrum can be used as the reference in optimizing the interpolation parameters for ULS data by minimizing the differences between the ULS- and TLS-spectrum at wavelengths smaller than 1 m. Similarly, the ULS spectrum can then be used as the reference to optimize the interpolation parameters for ALS data.
Further experiments would also require improvements to the experimental setup and data acquisition. For example, the plot size should be much longer than 10 m for analyzing the ALS spectra. A plot size of 100 m, for example, would be feasible for TLS, as it can be surveyed with 10 TLS scans (according to the conclusions from
Section 4.3). The ULS and ALS data should be acquired with a point spacing (both within and between the scan lines) notably smaller than their footprint diameters (the correlated scanning [
34]). This means that the plot should be scanned from a large number of overlapping strips (flight lines). Such data would allow for the optimization of the ALS and ULS setups for the roughness spectrum calculation as was done here for our TLS data.
Another variable in further experiments can be the natural surface itself. Soil surface roughness is, for example, relevant for understanding the radar backscattering signal and for modelling the runoff overland flow hydraulics [
12,
46]. Therefore, it would be interesting to analyze whether the interpolation effects and the multi-scale data affected the roughness spectrum of a soil surface differently compared to the gravel surface.
6. Conclusions
In this paper, we used TLS, ULS, and ALS point clouds of a 1 m × 10 m gravel plot to derive and analyze roughness spectra from interpolated DTMs. The TLS, ULS, and ALS spectra were calculated as ensemble averaged periodograms. The spectral comparison was done using the dB threshold that was based on a 95% confidence interval of the ensemble averaged periodograms. The aim was to determine the scales (spatial wavelengths) over which the spectra can be used interchangeably. Furthermore, the extensive sampling of the plot with TLS allowed us to optimize the TLS measurement setup for roughness spectra calculation.
The analysis showed that one TLS scan can be used to measure 10 m long plots and to derive roughness spectra that are reliable for wavelengths larger than 5 cm (10 times the TLS footprint size). One TLS scan can also measure 20 m long plots, but then the roughness spectrum is only reliable for wavelengths larger than 4 dm. However, one TLS scan can also measure roughness spectra over 1 cm (two times the TLS footprint size) to 10 m wavelengths, but with spectral differences reaching up to 0.65 dB.
The results also showed that a TLS setup with six scans (three each for the two longer plot sides) provides equally accurate roughness spectra as any other setup that includes more than six TLS scans. Furthermore, it was shown that the TLS spectrum (based on all the scans) is not affected by the basic interpolation methods at wavelengths larger than about 2 cm (four times the TLS footprint size). Finally, the comparison of the TLS and DIM spectra showed that they agree well with one another for wavelengths larger than 1 cm (two times the TLS footprint size). These conclusions refer to a TLS scanning performed using large tripods (scan heights of about 2.5 m) and in the correlated sampling mode (overlapping footprints within a single scan).
The comparison of the ULS and TLS spectra showed that they agreed well with one another for wavelengths larger than about 1.2 dm (about five times the ULS footprint size). At these wavelengths, the ULS spectral slope overestimates the TLS spectral slope by about 15%, although the spectral difference is below 0.5 dB. To get accurate ULS spectra at wavelengths smaller than 1 m, the optimization of the interpolation parameters is required. The plot size was too small to derive more conclusions about the ALS spectrum. However, the analysis showed that only the DC component and the first harmonic (5 m wavelength) of the ALS spectrum were not affected by the interpolation methods.
The above results refer to a dB threshold that is strict compared with the dB thresholds used in other applications (e.g., 1 dB or 2 dB in seafloor roughness and microwave backscatter modelling, respectively). Thus, the above conclusions are rather conservative and show that ULS data has high potential to replace TLS data for roughness spectra calculation in many applications.