1. Introduction
Spatial autocorrelation (SA) is a common phenomenon of spatial data analyses, where there is a common naive hypothesis that SA is zero (e.g., [
1,
2,
3]) for datasets involving, for example, georeferenced demographic, social economic, and remotely sensed image variables. A more reasonable postulate would be nonzero SA. Gotelli and Ulrich [
4] (p. 171) also pointed out that one of the important challenges in null modeling testing in ecology is “creating null models that perform well with … varying degrees of SA in species occurrence data”. This is a challenge that is not unique to ecology. A main problem hindering the positing of a nonzero SA hypothesis, or varying degrees of SA, is the unknown sampling distribution of the SA parameter, which may be denoted by
of the simultaneous autoregressive (or SAR, which is called the “spatial error model” in spatial econometrics [
5] (p. 5)) model in this paper. This parameter quantifies the degree of self-correlation in the error term (e.g., [
6] (p. 42, which can be rewritten as Equation (1)); as when it deviates further from zero, its distribution becomes more skewed and peaked, and its variance decreases.
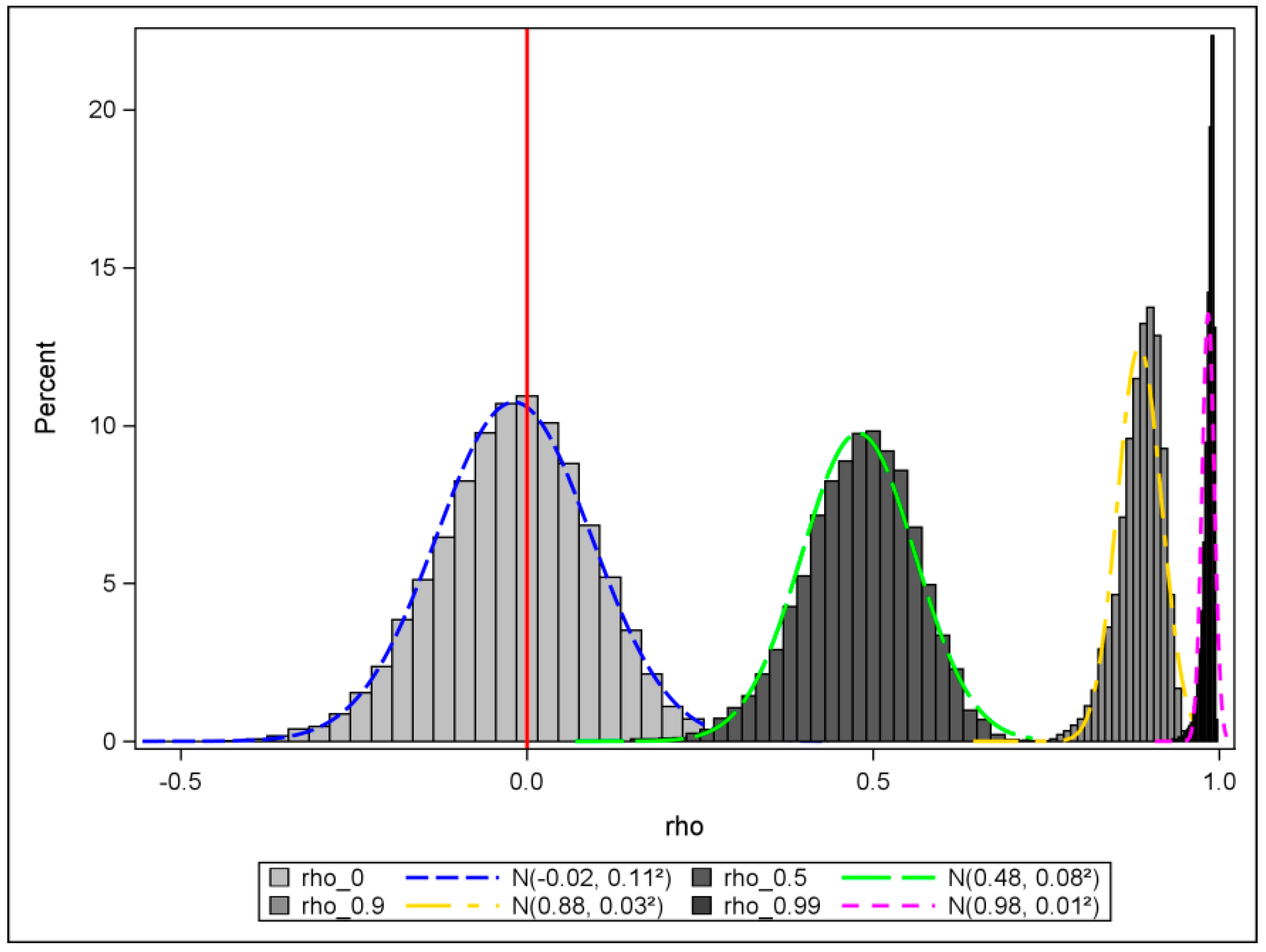
Figure 1 shows this phenomenon, where its connectivity matrix comes from the Wuhan census block data that are employed in the moderate SA case. Four histograms with density curves for different
values of 0, 0.5, 0.9, and 0.99 reveal that as
increases, the distribution moves further from zero (see the red reference line perpendicular to the horizontal axis), and its shape becomes narrower.
To gain an understanding of the complications related to figuring out the sampling distribution of the test statistic under the nonzero hypothesis, it is always enlightening to look back to Pearson’s r (i.e., correlation coefficient) in standard statistics and the autocorrelation coefficient in time series models, because the SA coefficient resembles the “auto” version of the former, and extends the latter from a uni-direction (time dimension) to a multi-directions (space dimension) case. A parallel to what is commonly done in spatial scenarios is that a routine null hypothesis often sets the (auto)correlation coefficient to zero in classical statistics or time series (e.g., [
7,
8]). In order to test the nonzero correlation coefficient in standard statistics, a Fisher’s Z-transformation is used so that the transformed statistic is approximately normally distributed and its variance is stabilized (e.g., [
9] (pp. 55–56); [
10] (p. 487); [
11]). However, for the original
, the distribution becomes skewed as
approaches its extreme values. Fortunately, Provost [
12] suggests closed-form representations of the density function and integer moments of the sample correlation coefficient to furnish a solution for the distribution problem. For time series autocorrelations, the research on a statistical distribution of a nonzero coefficient was developed from a more practical viewpoint. For example, Ames and Reiter [
13] established the distribution of autocorrelation coefficients in economic time series by using empirical datasets so that hypothesis testing for the significance of (auto)correlation among economic variables could have “a more appropriate basis” (p. 638) than the null hypothesis on a basis of zero (auto)correlation. More recent literature [
14] pertaining to this topic focused on the effect of the nonzero coefficient on the distribution of the Durbin-Watson test estimator. Similarly to the time series literature, studies on the distribution of the nonzero autocorrelation coefficient/parameter are rare in spatial statistics. One related work dates back to 1967, in which Mead [
15] verified that the Fisher’s Z-transformation did not help to obtain a stabilized variance, and even its generalized form could only help in instances of a very small
(i.e., 0, ±0.05, ±0.1). This earlier work provides evidence that the variance problem seems to be a major obstacle for establishing a sampling distribution for nonzero
. This paper furnishes a possible solution for this problem by representing the variance of
as a function of
, and validates the asymptotic normality of this distribution through Monte Carlo simulation experiments. Moreover, it also establishes a function between
and the Moran Coefficient (MC, also known as Moran’s I, [
16]), which bridges the most widely used SA statistic and spatial autoregressive model.
This paper contributes to the literature by establishing properties of the sampling distribution of nonzero
, supplementing the asymptotic variance known for zero
in a regression framework. Its results also pertain to the conditional autoregressive (CAR) model, which is called the conditionally specified Gaussian (CSG) in spatial econometrics [
17] (pp. 197 and 201), as well as the autoregressive response (AR) model, which is called the spatial lag model in spatial econometrics [
5] (p. 5). A SAR model can also be written as a CAR model (e.g., [
18] (p. 149); [
19] (p. 123); [
20] (p. 68)), both SAR and AR are of second-order (i.e., they also specify spatial correlation in terms of neighbors of neighbors), and their pure SA versions with no independent variables are the same model. The focus is on the SAR here because it is the most commonly used specification in spatial statistics, and the SAR uses the row standardized spatial weights matrix
, not matrix
(see
Section 2).
It is also necessary to explain the motivation of this paper from a more general perspective. Because Cliff and Ord [
21] systematically introduced hypothesis testing for the existence of SA latent in spatial data, SA-related research, in terms of both its theoretical and applied aspects, has flourished in a wide range of domains employing datasets with geographical or locational information. Sokal and Oden [
22,
23] introduced SA into biology, which inspired biologists to take SA into account in their work because most biological or ecological datasets are closely related to geographical locations. Legendre [
24] constructed a paradigm for ecologists to describe and test for SA, as well as to introduce spatial structure into ecological models. Other fields dealing with SA include, for example, spatial epidemiology (see [
25] for a thorough overview), spatial econometrics (e.g., [
26]), and urban planning (e.g., [
27]), which often use Geographical Information Science (GIS, [
28]) methods or tools. In all of these domains, testing the existence or presence of SA is a solved problem, where the next question which naturally arises is how the degree of SA could be tested. This paper furnishes an answer to this question.
This article consists of five sections.
Section 2 presents model specification and parameter estimation.
Section 3 furnishes the sampling distribution of the SA parameter estimate.
Section 4 gives one simulated example for zero SA by setting the null hypothesis to be
, as well as two empirical examples. Empirical analyses from over the years disclose that most socio-economic/demographic attributes have a degree of correlation ranging from 0.4 to 0.6, which indicates a relevant range for
within 0.65 to 0.85 [
29]; thus, a moderate SA case sets the null hypothesis as
, whereas a strong SA case sets the null hypothesis as
.
Section 5 presents conclusions and discussion. There are also appendices with some supplementary materials.
2. Model Specification and Parameter Estimation
This paper focuses on the SAR model and its SA parameter
. The first use of the word
simultaneous as a descriptor of an
autoregressive model was by Whittle [
30], whose seminal article introduced an expression known as the SAR model for two-dimensional stationary processes. Concomitantly with the development of spatial statistics, the SAR model was frequently used by geographers, econometricians, ecologists, and other spatial researchers as one of the very popular specifications for describing georeferenced data.
This SAR model is specified as follows:
where
is a response variable whose realizations
can be observations of a geographic attribute (e.g., average house price) distributed across
regions,
is a SA parameter,
is a stochastic version (row standardized) of the n-by-n (
entries) binary contiguity matrix
(the entry of the ith row and jth column is 1 if region i and j are adjacent, and 0 otherwise)—both
and
reflect the spatial adjacency of a geographical phenomenon,
is the n-by-n (
entries) identity matrix,
is a n-by-(m+1) (
entries) matrix with m explanatory variables (i.e., covariates) and one unit vector for the intercept,
is a coefficient vector of the order (m+1)-by-1, and
is a n-by-1 white-noise error term, which conforms to a standard multivariate normal distribution,
. In Equation (1),
appears on both sides of the equal sign, which is why the regression has the prefix,
auto; when the equation is rewritten for individual observations,
similar equations
simultaneously appear.
Without loss of generality,
can be void of covariates and contain only the intercept term, rendering a pure SA specification. Then, Equation (1) is reduced to:
where
is the n-by-1 vector of ones contained in matrix
. Equation (2) is also known as a pure SAR model, and is the specification employed in this paper. For the pure SAR specification, the error model and lag model are equivalent.
The parameters that need to be estimated in an SAR model are
,
(for Equation (2), it is only
), and
. As pointed out by Ord [
31] (p. 122), the least squares estimator of
is inconsistent, and even if this problem is revised by choosing an auxiliary matrix, the estimator is less efficient than a maximum likelihood estimator (MLE). Thus, ML estimation is a commonly used technique to estimate
(e.g., [
18,
21]; [
32]). Griffith [
33] (pp. 176–177) provides explicit MLEs of these parameters, and furnishes an equivalent form for the MLE of
that can be executed with the SAS code employed by this paper, and
for square tessellation and the rook’s adjacency (for regular square queen, and hexagonal adjacencies, see §3.1). However, a well-known problem of the MLE is the computing burden of its logarithm determinant constituting its Jacobian term, i.e.,
, which becomes especially troublesome when a sample size becomes large. Griffith [
34,
35,
36,
37,
38] (This work includes finding approximations of the Jacobian for regular, as well as irregular surface partitioning, exploring analytical or approximated expressions of eigenvalues of matrix
and matrix
, and figuring out a simplified algorithm for calculating MLEs for massive sample sizes. In addition, this work establishes criteria to check the rationality of posited eigenvalue approximations, and to evaluate the Jacobian term approximations. Analyses summarized in this paper are based upon these contributions.) contributed some simplifications that reduced the computational burden of this factor. Another issue meriting attention here is the sampling variance of the model estimated
(i.e.,
, which is simplified to
hereafter), because it measures the uncertainty or quantifies the precision of the ML estimate. Capturing how this variance changes is helpful for evaluating the efficiency of the estimator; in addition, it is always necessary to know at least the first- and the second-order central moments of a sampling distribution of a parameter estimator so that statistical inference can be conducted. Ord [
31] (p. 124) suggests an asymptotic variance-covariance matrix of
and
, from which an expression of the asymptotic variance of
can be obtained. This lays the foundation for exploring the analytical expression of the sampling variance of
in this paper.
Another approach that can be used to estimate the SA parameter is the general method of moments (GMM) furnished by, among others, Kelejian and Prucha [
39,
40]. Walde et al. [
41] present a thorough comparison between GMM- and MLE-based methods for very large-data spatial models, and suggest employing the former. A very important reason that led them to choose the GMM for large spatial data model estimation was that the GMM had a “directly computable” (p. 164) standard error of
, which is also implemented in a MLE framework in this paper.
Section 3 describes this implementation in detail.
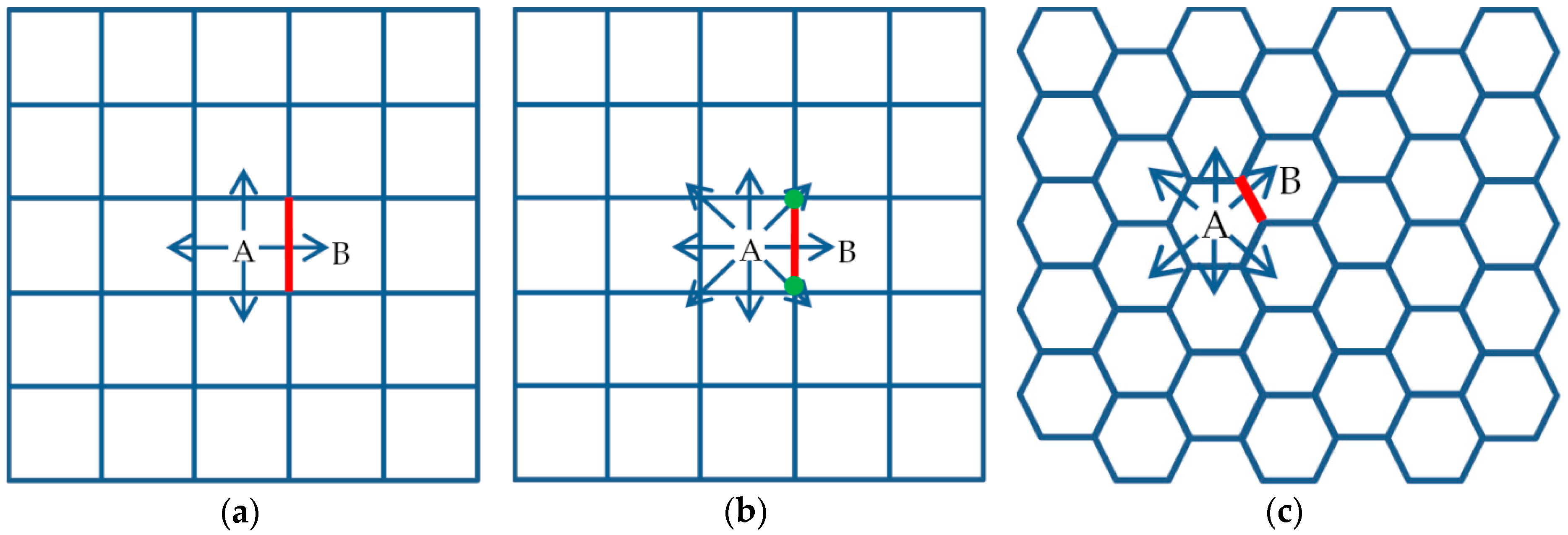
3. The Sampling Distribution of
Before discussing the sampling distribution, it is necessary to introduce three surface partitionings on which all works of this paper are based: a regular square tessellation with rook connectivity (squares A and B are defined to be neighbors if they have a common edge), a regular square tessellation with queen connectivity (squares A and B are defined to be neighbors if they have a common edge or a common vertex), and a regular hexagonal tessellation with rook connectivity (hexagons A and B are defined to be neighbors if they have a common edge). There are definitely many types of geographical configurations, e.g., some theoretical types that have been discussed in [
42], a more practical one that is used to construct grids for the earth’s surface (i.e., ISEA3H, [
43]), a soccer ball-like configuration (i.e., a combination of hexagons and pentagons). However, only these three were employed, because the rook and queen are frequently-used criteria in many GIS and spatial data analysis-related software or packages (e.g., Esri ArcMap; spdep in R, [
6]); moreover, these two adjacency schemes with a more regular square lattice relate to increasingly used, remotely sensed images. Also, a hexagonal configuration is often used in spatial sampling design [
44] (pp. 24–25) and aggregation [
43]. In summary, these three configurations are frequently used in practice, and many irregular lattices tend to have connectivities that are between a regular square and hexagon lattice (e.g., [
42]). As shown in
Figure 2, for a square tessellation,
A has four neighbors for a rook adjacency, eight neighbors for a queen adjacency, and six neighbors for a hexagonal tessellation. Suppose there are
observations of a geographical attribute distributed over one of these landscapes, considering the regularity, and let
, where
is the number of rows,
is the number of columns, and the dimension of the connectivity matrix is n-by-n (i.e.,
).
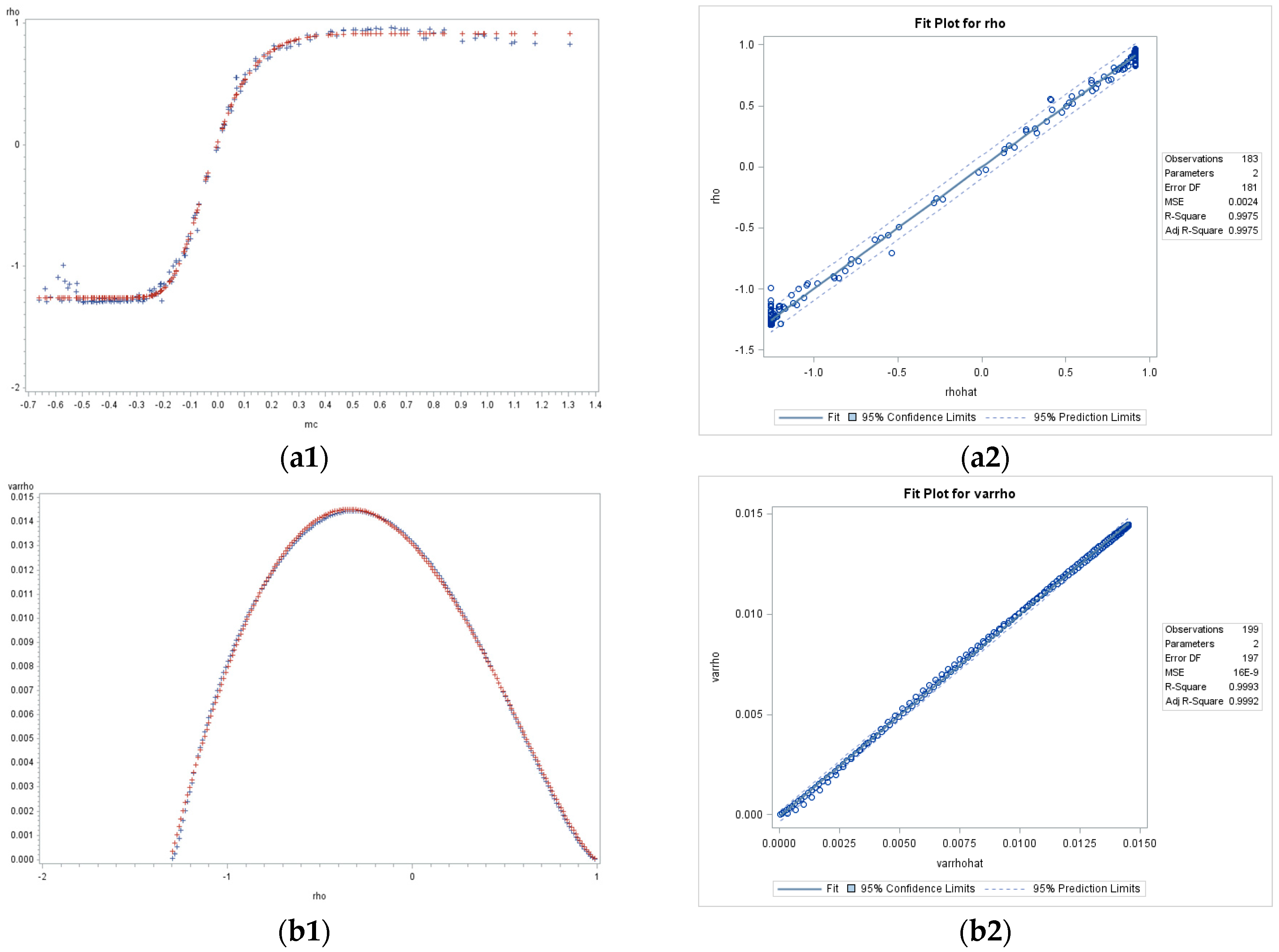
3.1. The Relationship between and the MC
In the literature, the most widely used statistic for quantifying SA is the MC. From a model perspective,
is the parameter that has the same function as the MC. Although these two quantities are related, they are not equivalent, and thus should not be interchangeably used [
1]. Establishing their explicit relationship quantitatively supports evaluation of the SA level latent in georeferenced data. Griffith [
45] (pp. 33–34) points out that the relationship curve of
against the MC is logistic (or sigmoid). This paper explores their relationship function further so that
can be quantitatively described by the MC for the three surface partitionings discussed in this paper.
Suppose a geographical configuration has
units. The estimates of
and the MC are closely related to matrix
, where
is defined as done previously,
is the projection matrix defined as
, and
is a n-by-n matrix whose entries are all ones. Jong et al. [
46] (pp. 21–22) demonstrated that
, which is indicative of the relationship between extreme MC values and extreme eigenvalues (denoted by
) of
; in other words, the maximum eigenvalue corresponds to the maximum MC value, while the minimum eigenvalue corresponds to the minimum MC value. Because this equation restricts the feasible range of the MC, it is reasonable to generate a set of sample MC values by:
Ordering the eigenvalues such that
, the corresponding
can be estimated for each by employing eigenvectors
to replace
in Equation (2). That is:
The eigenvalue
and eigenvector
correspond to the ith MC value, and this
is also the response variable in the pure SAR model rendering an estimate for the
ith
value.
To explore the relationship between the MC and
, 14 groups of experiments with different sample sizes were conducted for the three configurations (i.e., regular square rook, regular square queen, and hexagonal cases), where
ranged from 25 to 4900 (that is,
, where
and
increase in increments of five). The theoretical relationship functions for different spatial configurations were defined, and the parameters were estimated.
Table 1 summarizes the resulting expressions. The bold
is the base of the natural logarithm, and
is the minimum eigenvalue of matrix
(rook connectivity
is about −1, queen
is approximately −0.53, whereas
of the hexagonal tessellation is around −0.57).
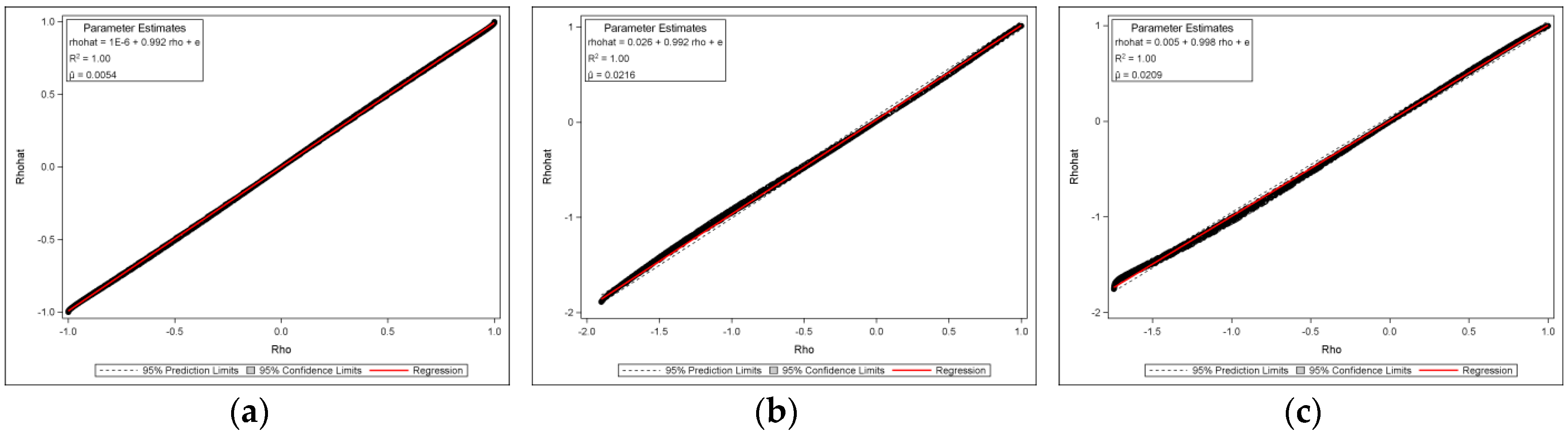
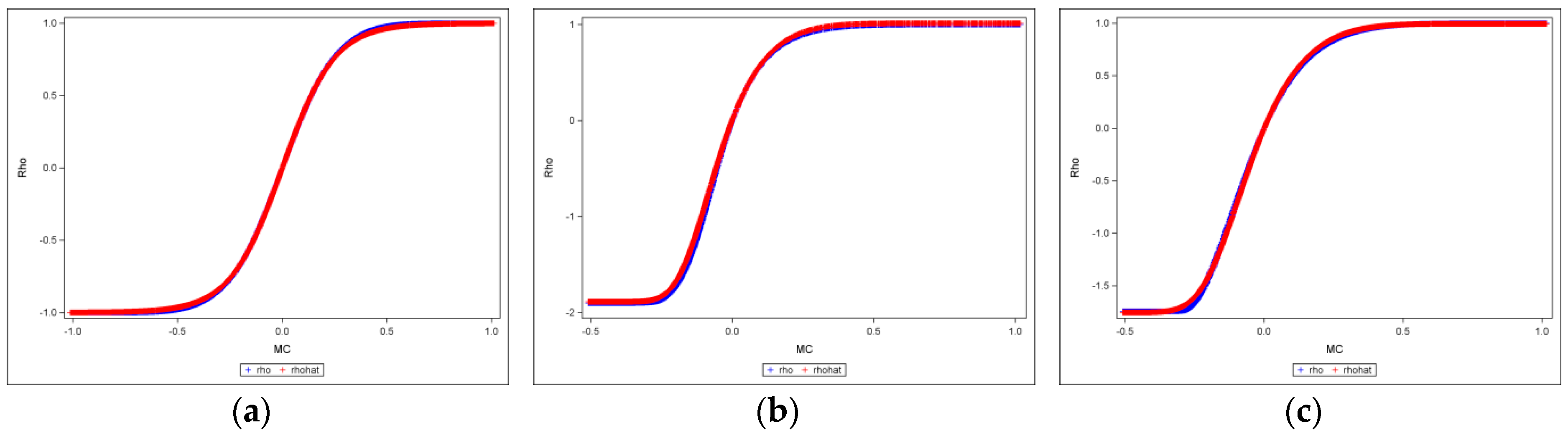
Figure 3 presents the selected fitted curves. This figure depicts the 70-by-70 (
) configuration results for the square-rook, square-queen, and hexagonal cases. It presents the fitted curves (red), computed with the theoretical equation, superimposed on the observed data (blue), where the horizontal axis indicates the values of MC, and the vertical axis stands for the values of
(here,
denotes both the MC-estimated
and the SAR-estimated
.); the regression lines of
(estimated by the functions of the MC in
Table 1) versus
are shown in
Appendix A.
Figure 3a reveals that for the square rook connectivity, the feasible range of the MC is approximately
, and the range of
is
. For the square queen (
Figure 3b) and hexagonal (
Figure 3c) cases, the MC is about
;
is approximately
and
, respectively (These intervals of
verify the inequality
(Ord, 1975, p124). While the most frequently used interval is
(refer to
Section 2), intervals beyond this range can be transformed onto it.). These theoretical and original scatter plots match perfectly, with bivariate regression
s of nearly 1 (see
Appendix A Figure A1).
3.2. The Sampling Variance of
The sampling variance of
is important because it quantifies the uncertainty with which
is estimated. Ord [
31] (p. 124) proposes the asymptotic variance-covariance matrix
1 of
and
(the value of diagonal entries of the variance-covariance matrix of error term
); for illustrative purposes, it is rewritten as:
where
,
is the
ith eigenvalue of matrix
, “tr” is the matrix trace operator, and superscript “T” is the matrix transpose operator. An asymptotic formula of the sampling variance of
derived from Equation (5) by inverting the 2-by-2 matrix is
, where
. Hence, the variance expansion may be written as:
This equation is still not easy to compute because it involves (inverse) matrix operations, as well as eigenvalues. The following sub-sections present some simplifications which only consist of sample size (or number of observations)
, and the extreme eigenvalues of matrix
(specifically, for zero SA cases, only
and
).
3.2.1. The Sampling Variance of at Zero
When
, Equation (6) becomes
. Because
(
. is a diagonal matrix whose
diagonal entries are inverse row sums of matrix
),
and
are square matrices, and
because
is binary,
, then the asymptotic variance of
at zero is:
Table 2 summarizes this variance for different surface partitionings; the formulae for summation of the inverse row sum of matrix
and summation of squared eigenvalues of matrix
are listed in
Appendix B.
The expressions in
Table 2 make Equation (7) extremely easy to compute, especially when the sample size is large. However, functions for
at nonzero points are more complex. As has been argued by [
15], the variance of the inter-plant competition coefficient (which is the sampling variance of
that is discussed in this paper) cannot be stabilized by the Fisher Z-transformation, and even its generalized form only works on very weak spatial interactions (0, ±0.05, ±0.1) for three specific spatial configurations (i.e., 7, 12, and 19 hexagonally arranged points; see
Figure 1 on p. 193). More recently, Griffith and Chun [
47] emphasized that better quantifying the spatial variability of SA estimates is still a challenge. By exploring the distribution of the variance, this paper finds that the sampling variance of
is a function of
(which is implemented with
), which is depicted by a Beta distribution curve with equal parameters larger than 1.
3.2.2. The Sampling Variance of at Nonzero Values
To conduct the experiments, 30 groups of different sample sizes, ranging from 5-by-5 to 150-by-150 with
and
increasing in increments of five, were employed; the sample size of each group was
. The SA parameter
was uniformly sampled across its feasible ranges, namely,
, where
is an eigenvalue of matrix
. Theoretical functions of asymptotic variance versus
are presented in
Table 3. In the formulae,
is the variance at zero (see
Table 2),
is the standardized
with form
, and
and
are the maximum and minimum eigenvalues of matrix
, respectively.
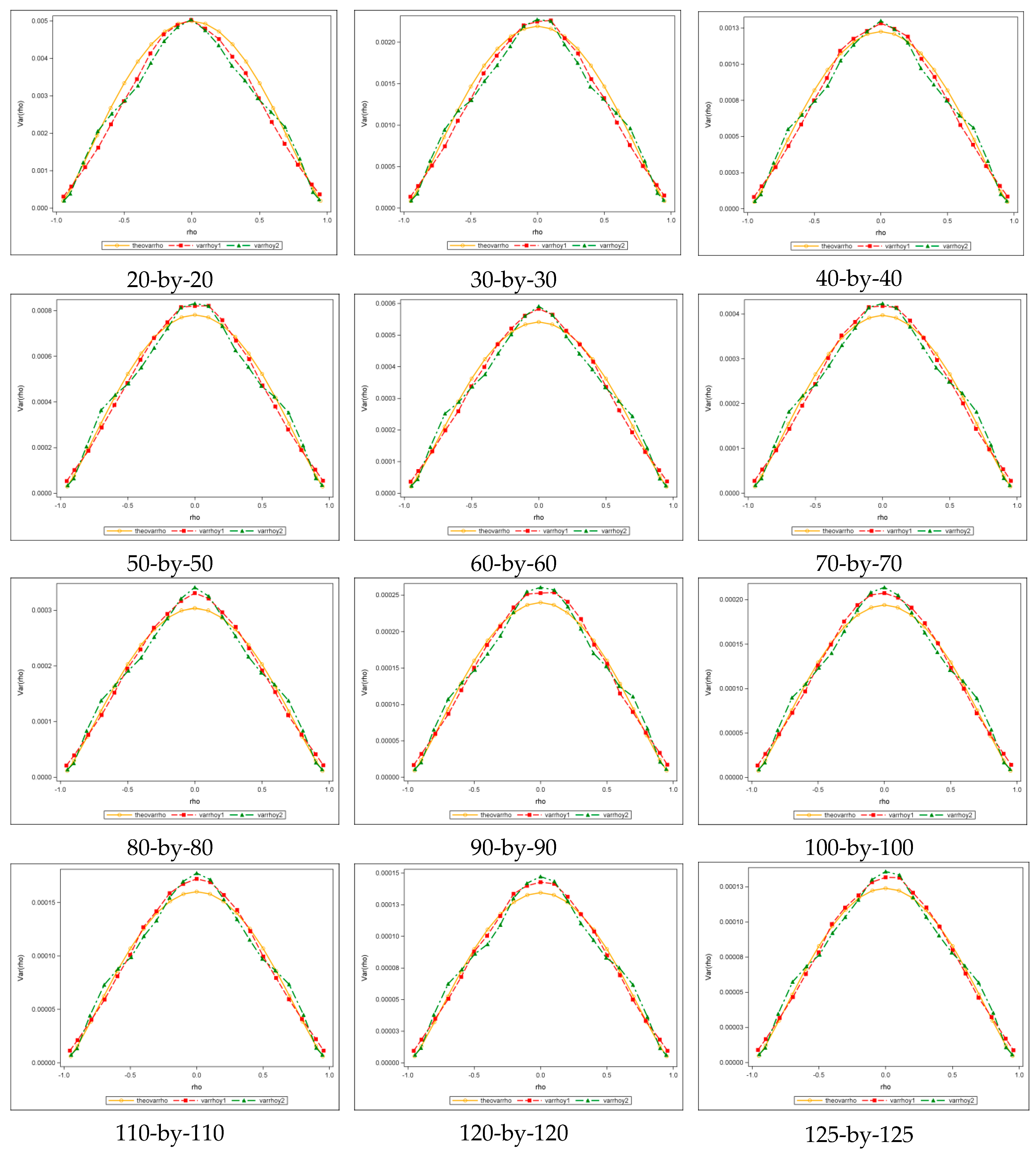
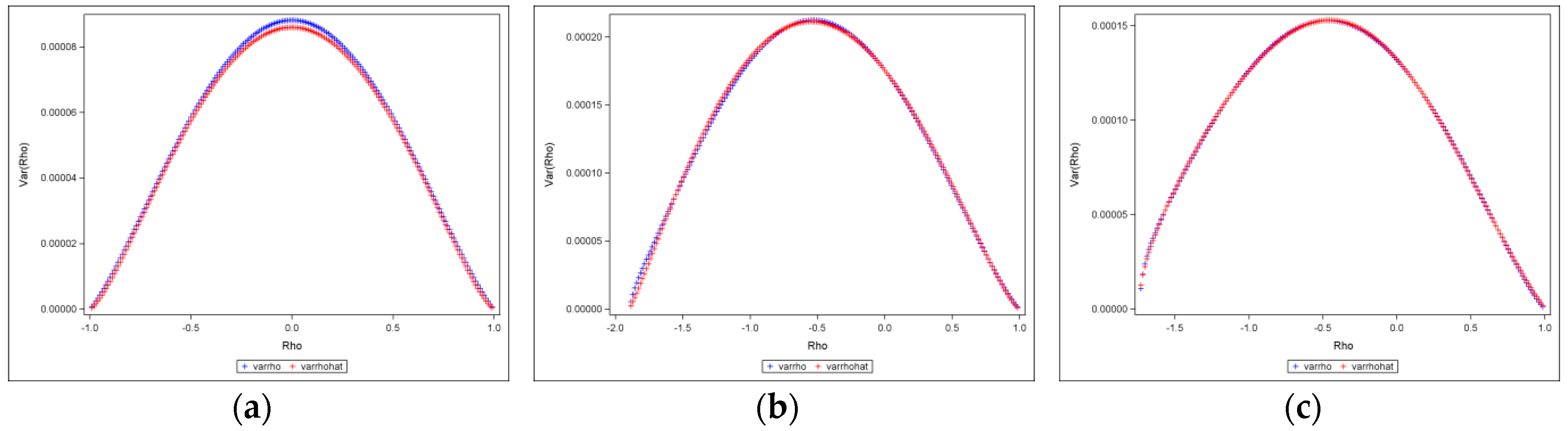
Figure 4 shows selected results of 150-by-150 (
) lattices for the square rook, square queen, and hexagonal cases. It presents theoretical plots (red) superimposed on the original scatter plots (blue), showing that the sampling variance of
is Beta-distributed with equal shape and scale parameters, and that the theoretical and the original plots closely correspond, which is also corroborated by the bivariate regression plots and their accompanying
values of nearly 1 (see
Appendix A Figure A2).
To evaluate the validity of the theoretical equations listed in
Table 3, simulation experiments were conducted.
3.2.3. Simulation Experiments
For each of the three cases, 24 groups of experiments of different sample sizes (from 10-by-10 to 125-by-125) were done, and for each sample size, combinations of two treatments (i.e., employing an approximated Jacobian term [
36,
37] and employing [
35] a new algorithm for MLEs) were applied for the pure SAR model. For a square rook case,
took 21 values (from −0.9 to 0.9 with a 0.1 increment, and ±0.95) within its feasible range
, and 10,000 replications were executed per value per method. For a square queen case,
took 29 values (from −1.8 to 0.9 with a 0.1 increment, and 0.95) within its feasible range
, and 10,000 replications were executed per value per method. For a hexagonal case,
took 28 values (from −1.6 to 0.9 with a 0.1 increment, and −1.65, 0.95) within its feasible range
, and 10,000 replications were executed per value per method.
Table 4 shows different treatment combinations that were employed by the three cases with sample size 100 (i.e., 10-by-10 lattice). Full information about the simulations appears in
Appendix C (
Table A2). For a specific
, 10,000 simulated values were generated whose frequency distribution was approximately normal, and from which its mean and variance were extracted.
These experiments contend with two complications: approximating the Jacobian term, and clarifying its derivation for the nonlinear regression model in SAS. For the square rook adjacency case, two forms of approximation furnished by [
36] were employed. For the square queen and hexagon adjacency cases, the following approximation [
37] was used:
where
denotes an approximated Jacobian term. The default derivative of the Jacobian term employed in SAS is misleading. Its correct form, Equation (A2), is presented in
Appendix D. Griffith [
35] (p. 2149) furnishes a new algorithm to avoid the massive matrix calculation in the MLEs, which effectively reduces the execution time. This algorithm is employed in this paper.
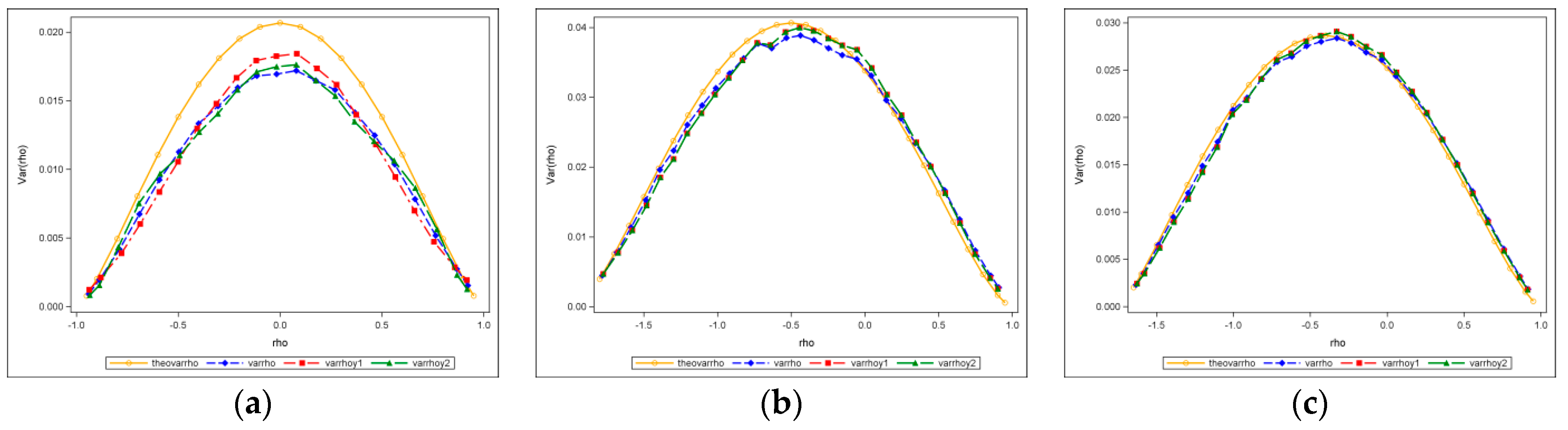
Figure 5 includes 10-by-10 results for the regular square rook, regular square queen, and regular hexagonal tessellation cases. In all these figures, the theoretical values are presented by smooth orange curves. Selected sampling distributions of weak, moderate, and strong positive
for a 10-by-10 lattice are presented in
Appendix E to illustrate the asymptotic normality of its sampling distribution.
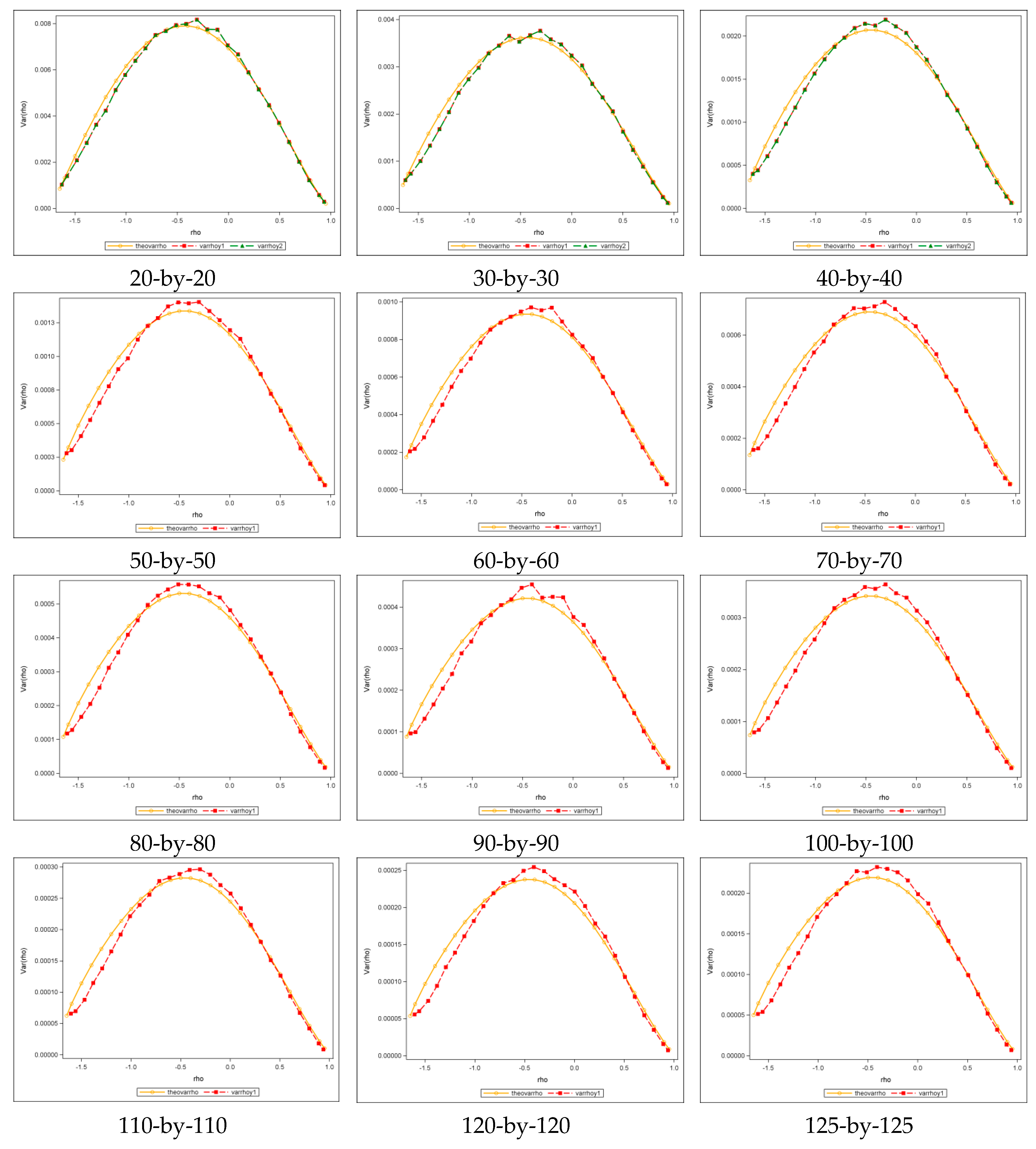
Figure 5a portrays variance values for a systematic sample of 21 points (from −0.95 to 0.95) and a square rook case. Not including the orange graph, there are three other colored graphs in
Figure 5a, where the blue stands for the exact values, and the red and green represent two different approximated calculations. The exact and approximated values are close, while a small gap appears between the blue-red-green and the orange graphs around the peak. The gap almost disappears when the sample size becomes 400 (20-by-20, see
Appendix FFigure A4), and then appears again, but has no big change as the sample size increases. The gap is the difference between the theoretical and the exact values, and depicts the accuracy of the theoretical formulae—a smaller gap indicates a better approximation.
Figure 5b portrays variance values for a systematic sample of 29 points (from −1.8 to 0.95) and a square tessellation with a queen adjacency case. To obtain the two results, one (the red) was calculated by approximating the Jacobian term and using a simplified algorithm for ML estimation [
35], whereas the other (the green) was calculated by approximating the Jacobian term and using the conventional ML estimation implementation. Results calculated by these two methods are coincident, and they are not only considerably close to the exact graph (the blue in
Figure 5b), but also close to the theoretical curves; the variance plots for larger sample sizes are shown in
Appendix F (
Figure A5), in which the theoretical (orange) and one approximation (red) are portrayed (except for the 20-by-20 case) because executing the nonlinear regression without the simplified algorithm is extremely time-consuming, and the gaps between the orange and the red are negligible.
Figure 5c portrays variance values for a systematic sample of 28 points (from −1.65 to 0.95) computed for the hexagonal case. Here, the two approximations almost perfectly match the exact and theoretical values; variance plots for larger sample sizes appear in
Appendix F (
Figure A6); the exact variances would be slightly bigger around the maximum values than the theoretical ones when sample size exceeds 1600 (40-by-40), whereas values along the two sides match reasonably well.
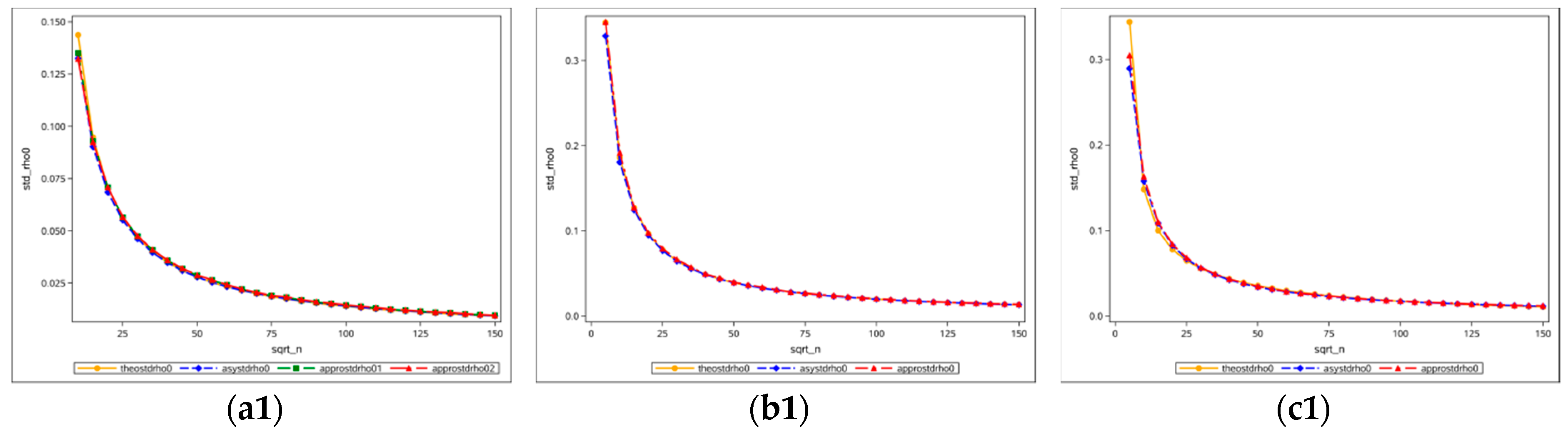
Figure 6 presents convergence plots of variances at
. The top row presents convergence curves whose horizontal axis is the square root of the sample size (from 5 to 150), and whose vertical axis is the standard deviation. Different colors indicate different calculation methods; for example, the orange denotes the theoretical calculated variance of
at zero, the blue denotes the asymptotic (formulae in
Table 2) computed variance, the green and red respectively denote variance calculated with simulation experiments using the two methods approximating the Jacobian term (two methods exist for the square rook adjacency, whereas only one for the square queen and hexagonal adjacencies). The bottom row shows the standard-deviation-to-square-root-of-sample-size ratio (from 5 to 150); the green and red lines denote those standard deviations calculated with simulation experiments versus the asymptotically calculated standard deviations.
Figure 6(a1,a2) are from the results of a square rook case,
Figure 6(b1,b2) display the results from a square queen case, and
Figure 6(c1,c2) portray the results from a hexagonal case. All of the trajectory curves appear to converge to zero, and all standard deviation ratios fluctuate around 1, when sample size goes to infinity.
5. Conclusions and Discussion
The main contribution of this paper is furnishing the sampling distribution of the nonzero SA parameter of the SAR model, which is frequently employed in a wide range of disciplines whose study observations are connected with geographical attributes or locations. More specifically, the sampling distribution was constructed for three specific spatial structures (i.e., regular square rook and queen, and hexagonal tessellations); the former two are usually used for remotely sensed images (raster data), while the latter is preferred for spatial sampling designs and aggregations. As shown with graphics and functions, the curve shape of the parameter against the MC is sigmoid, which indicates that the MC should better differentiate SA levels and is more coincident with intuition (e.g., a MC value of 0.5 quantifies moderate SA, whereas the value for the same level may be larger than 0.7, which conjures up a vision of moderate-to-strong SA at first glance). This may suggest that the MC could be better for assessing the level of SA. In addition, the sampling variance of the parameter seems to conform to a beta distribution with equal scale and shape parameters (larger than 1). A difference in these distributions between the square rook and the other two is that the parabola-shaped curve is symmetric at zero for the square rook adjacency, whereas the symmetry is at negative points for the square queen and hexagonal adjacencies.
One merit of this contribution is that it implements hypothesis testing for a nonzero null hypothesis. For illustrative purposes, two empirical examples for moderate and strong SA were selected, as was a zero null hypothesis case employing simulated data exhibiting a random map pattern. For this random case, the result indicates a failure to reject the null hypothesis, which is in accordance with our expectation. For the moderate case, prior knowledge that
and the MC have a logistic relationship (i.e., MC values beyond, e.g., (−0.3, 0.3) correspond to extreme
values) results in positing a null hypothesis of
; thus, the null hypothesis is not rejected. For the strong SA case, the null hypothesis of
is rejected mainly because of the large sample size (i.e.,
) and the closeness between 0.95 and 1, both of which result in an extremely small variance. These examples verify that the uncovered sampling distribution results are credible (the standard error for
is 0.0141, corresponding to a z-score of 0.7188, which has a very small difference of 0.0066 with the z-score 0.7254 appearing in
Table 5). In addition, a by-product of this contribution is the visualization of statistical power curves for SA statistics [
42]. Because the SA parameter can be expressed in terms of the MC, their power curves can be plotted with a common measurement scale (see
Appendix I).
Future work needs to refine, and hopefully simplify, the variance expression for the hexagonal case; one way to achieve this end is to increase the number of experiments (the current variance-
function is based upon 14 groups of datasets (i.e., 7-by-7 to 70-by-70) to estimate its parameters). Extensions can be made for more complicated landscapes, such as a combination of hexagons and pentagons, partitionings with distorted hexagons (i.e., ISEA3H as a hexagonal Discrete Global Grid System; [
43]); these may be described with appropriate spatial weights matrices, where for the former, expressions like those listed in
Table 2 need to be derived, and for the latter, a spatial weights matrix containing metrics based upon side length or hexagon area may be more reasonable than a binary version. An important issue illustrated by the last example meriting emphasis is that the formal hypothesis testing or its p-value may no longer make sense because of the large-to-massive sample size involved. For example, the “confidence interval” of 0.9697 is [0.9659, 0.9735], in which the null hypothesis value should be contained; otherwise, the null hypothesis is rejected. A cause of this “always significant” phenomenon is the extremely small variance for a very big sample size, which creates the necessity to develop a new criterion to substitute for statistical significance when analyzing spatial data with large-to-massive sample sizes. This is a meaningful research theme that needs attention in the future.