Abstract
Citrus is considered one of the most important fruit crops globally due to its contribution to food and nutritional security. However, the production of citrus has recently been in decline due to many biological, environmental, and socio-economic constraints. Amongst the biological ones, pests and diseases play a major role in threatening citrus quantity and quality. The most damaging disease in Kenya, is the African citrus greening disease (ACGD) or Huanglongbing (HLB) which is transmitted by the African citrus triozid (ACT), Trioza erytreae. HLB in Kenya is reported to have had the greatest impact on citrus production in the highlands, causing yield losses of 25% to 100%. This study aimed at predicting the occurrence of ACT using an ecological habitat suitability modeling approach. Specifically, we tested the contribution of vegetation phenological variables derived from remotely-sensed (RS) data combined with bio-climatic and topographical variables (BCL) to accurately predict the distribution of ACT in citrus-growing areas in Kenya. A MaxEnt (maximum entropy) suitability modeling approach was used on ACT presence-only data. Forty-seven (47) ACT observations were collected while 23 BCL and 12 RS covariates were used as predictor variables in the MaxEnt modeling. The BCL variables were extracted from the WorldClim data set, while the RS variables were predicted from vegetation phenological time-series data (spanning the years 2014–2016) and annually-summed land surface temperature (LST) metrics (2014–2016). We developed two MaxEnt models; one including both the BCL and the RS variables (BCL-RS) and another with only the BCL variables. Further, we tested the relationship between ACT habitat suitability and the surrounding land use/land cover (LULC) proportions using a random forest regression model. The results showed that the combined BCL-RS model predicted the distribution and habitat suitability for ACT better than the BCL-only model. The overall accuracy for the BCL-RS model result was 92% (true skills statistic: TSS = 0.83), whereas the BCL-only model had an accuracy of 85% (TSS = 0.57). Also, the results revealed that the proportion of shrub cover surrounding citrus orchards positively influenced the suitability probability of the ACT. These results provide a resourceful tool for precise, timely, and site-specific implementation of ACGD control strategies.
1. Introduction
Citrus is considered one of the most important fruit crops in the world due to its contribution to food and nutritional security [1]. Also, citrus is the top-ranked fruit crop with regard to its international trade value [2]. The commercially important citrus species are sweet oranges (Citrus sinensis), lemons (Citrus limon), limes (Citrus aurantifolia), grapefruit (Citrus paradisi), and tangerines (Citrus reticulata). Globally, sweet oranges represent approximately 70% of citrus production. In 2016, the global total production of sweet oranges was about 73 million tons [3]. In Kenya, citrus is a valuable fruit crop used mainly for domestic consumption as a fresh produce with only a small quantity being processed into juice and jams [4]. Citrus provides some minerals and vitamins like vitamin C, carotenoids, and polyphenols that are essential for human health. In terms of the area of production, citrus (mainly oranges) ranks third (7268 ha) after bananas (63,299 ha) and mangoes (54,332 ha) in the country [5].
Citrus plants can prosper in a wide range of environmental conditions from tropical to subtropical climatic conditions [6]. However, the best citrus production conditions are found in subtropical climate zones in elevations ranging from sea level up to 2100 m above mean sea level (m.a.s.l.), with an optimal growth temperature ranging from 20 °C to 30 °C. In Kenya, citrus fruits’ quantity and quality have been considerably declining. For instance, oranges yields at 11.73 ton ha−1 are far below (23% less) the global mean yield of 18.45 ton ha−1 [7,8]. Two of the major production constraints that hinder citrus production in Kenya are insect pests and diseases, among which the African citrus triozid (ACT), Trioza erytreae, plays a key role [9]. Direct feeding by ACT results in leaf curling and, furthermore, causes deposition of honeydews on infested plants [10]. In Africa, ACT is known for transmission of the devastating phloem-limited bacterium Candidatus Liberibacter africanus (CLaf), responsible for the African citrus greening disease (ACGD) or Huanglongbing (HLB) [11]. In addition to ACT, HLB is also transmitted by the Asian citrus psyllid (ACP) (Diaphorina citri), which is the primary vector in Asia [12,13] but was also recently discovered in eastern Africa [14]. These two psyllids are distributed according to their temperature requirements, with ACT being highly temperature sensitive and thus restricted to cooler elevated areas [15,16]. The common symptoms of ACGD are mottling and yellowing of the leaves, reduced tree foliage which results in small and bitter-tasting fruits, and the eventual death of severely infected citrus trees [17]. In Kenya, ACGD is reported to have had the greatest impact on citrus production in the highlands, causing yield losses of 25% to 100% [18]. The yield of affected trees is not only considerably reduced by continuous fruit drop, dieback, and tree stunting, but also by the poor quality of fruits that remain on the trees which are inedible.
Over the years, different approaches have been used for implementing various ACGD preventive and control measures [19]. This includes strict regulations of nurseries through a registered disease-free certification scheme to prevent the spread of ACGD and its vectors [20]. Little is known on the spatial distribution of the disease vectors, yet such information could greatly assist in developing precise geo- and time-referenced vector distribution maps. Such maps can be useful in monitoring the spatial spread and suitable areas for the vectors, enabling for a more targeted implementation of interventions. Vector-transmitted disease propagation follows vector ecological principles as an indirect explanation of disease cycles, outbreaks, and prevalence [21]. One of the most frequently used approaches for producing vector distribution maps is the ecological niche (EN) modeling approach [22]. EN models statistically link spatial variabilities in a set of predictor variables to the distribution of species of interest that can be a plant disease vector like ACT [23,24]. The dependence of plant disease propagation on spatio-temporal environmental niche factors of the disease vector has recently received considerable attention [25]. Yet, studies focusing on the ways in which geographical environmental factors affect the habitat suitability and host-vector dynamics are still limited. In addition, there is a need for studies that employ a multi-source variable (e.g., vegetation phenology and climate) approach to predict the spatial distribution of plant disease vectors.
Models have been developed to provide information about diseases and the distribution of associated environmental variables that are used as proxies for habitat suitability. The best known EN models used in insect-based distribution modeling include Generalized Linear Models (GLM), Generalized Additive Models (GAM), Genetic Algorithm for Rule-Set Production (GARP), Boosted Regression Trees (BRT), and Maximum Entropy (MaxEnt) [26]. Studies have compared the performance of several EN modeling algorithms to predict the distribution of different species and found that MaxEnt was the best-performing model using presence-only data [27]. In addition, MaxEnt is the most utilized EN model for estimating the distribution of plant insect pests like stink bugs (Halyomorphahalys spp.) [28], large pine weevil (Hylobius abietis), and horse-chestnut leaf miner (Cameraria ohridella) [29], boreal forest insect pests [30], fruit flies [31], and disease vector ticks (Ixodes ricinus) [32].
For HLB, a number of studies employed mathematical, and geostatistical simulation, life table, and conceptual modeling routines [33,34,35], to study the distribution of ACP using environmental variables as predictors (i.e., temperature and rainfall) in regard to the biology of the vector (e.g., developmental stages and their populations) and host plant interactions (e.g., number of susceptible or infectious orange trees). These studies demonstrated the possibility of estimating the distribution, progression and optimal temperature ranges for ACP in countries like the USA, Mexico, Brazil, Vietnam, and Australia. In Africa, Shimwela et al. [36] and Narouei-Khandan et al. [37] employed two correlative MaxEnt and support vector machine modeling approaches to map the potential distribution of ACP using global-scale environmental predictors. These two studies reported that Eastern African countries like Kenya and Tanzania would be highly suitable for the psyllid. To the best of our knowledge, no other study has employed an EN modeling approach to predict the distribution of ACGD vectors in Africa.
Yet, there is a need for an explicit ACT distribution mapping routine in countries such as Kenya, where the transmission of ACGD is mainly due to this vector. Moreover, previous studies looked at the relevance and influence of environmental variables in predicting the distribution of ACGD vectors but did not consider the expected relevance of vegetation patterns and phenology, resulting through interactions between climatic, topographic, and vegetation patterns at a landscape scale, which can considerably improve the performance of EN models like MaxEnt [30]. Moreover, vegetation patterns and phenology play a key role in influencing vector-host-pathogen transmission, including vector distribution, abundance, and diversity [38]. These vegetation-related patterns and phenological variables can only be extracted from temporal remotely-sensed datasets. When used in EN models, the remotely-sensed vegetation pattern and phenological variables are useful additional predictors for the spatial distribution of pests and diseases since EN models rely on the correlation between a habitat’s characteristics and the biophysical properties of the studied pest and disease [39].
Further, much research has focused on the biology of ACT and its dispersal [40]; however, little is known regarding how land use/land cover (LULC) features influence the habitat suitability of the vector and its dispersal. However, remotely-sensed datasets from different systems have been widely used for the identification and separation of citrus orchards from other LULC types for appropriate policy making and citrus production forecasting [41,42,43]. More efforts concerning understanding the influence of the landscape on the survival of pests and diseases like ACT using remotely-sensed variables are crucial. For instance, the context of the landscape has been reported to affect the population of crop insects directly, or more frequently, indirectly, through its effects on the physical environment around the host plants [44]. For instance, landscape heterogeneity has been reported to influence the direction and distance moved by a dispersed pest and pathogens, in addition to the infestation rate [45]. For example, Rizzo et al. [46] reported that the proximity to the forest edge was associated with an increase in the infestation of sudden oak death disease in California. Avellino et al. [47] tested the relationship between the landscape context and three highly differentiated focal coffee pests and pathogens. They found a positive relationship between the studied coffee pest and disease incidences and the proportion of different LULC classes at different radii around coffee sample plots. Thies et al. [48] studied the correlation between the local proportion of destroyed oilseed canola buds and the characteristics of landscape context. They showed that an increase in the landscape complexity was associated with a decrease in damage caused to oilseed canola by Meligethes. aeneus. All these studies alluded to the fact that the surrounding vegetation provides a refuge for the vectors during periods of time when the conditions are unfavorable for the spreading of the disease. Despite this strong influence that the landscape properties have on the spread of pests and diseases, no research has explored the relationship between ACT habitat suitability with the surrounding landscape composition for a better understanding of the ecology and spread of ACGD.
The objectives of this study were, (i) to explore the potential and contribution of vegetation phenological variables and Land Surface Temperature (LST) derived from remotely-sensed data combined with environmental variables to predict the distribution and habitat suitability for ACT at a test site in Kenya using a MaxEnt model and, (ii) to test the effect of the surrounding landscape context on the habitat suitability for ACT. This was achieved by relating a set of bio-climatic and topographic environmental (BCL) variables and remotely-sensed (RS) variables to ACT presence-only distributions over a region-specific, i.e., representative agro-ecological gradient.
2. Methods
2.1. Study Area
The study site consists of 35 administrative counties in three main agro-ecological zones in Kenya lying in low-, mid-, and high- elevation zones, see Figure 1. The study area covers parts of the Coastal, Eastern, Central, and Western regions of Kenya. The Central and Western regions exhibit cooler and wetter climatic conditions which are particularly favorable for citrus growing. The two regions experience a bi-modal rainfall distribution with the major crops being maize and beans, which in most cases are interspersed with mangoes and citrus trees, in addition to tea and coffee. Generally, citrus growing across the entire country is commonly practiced in small orchards and backyards, with only a few big citrus plantations in Kenya.
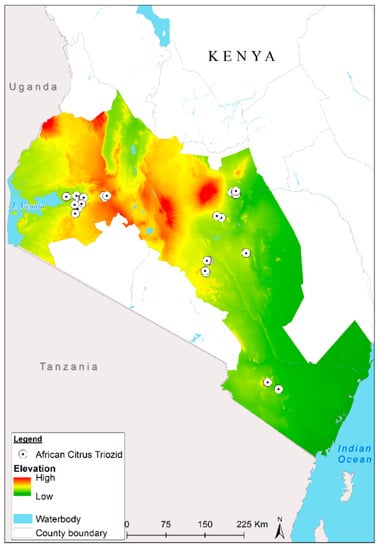
Figure 1.
Study area (major citrus-growing regions) in Kenya where the African citrus triozid (Trioza erytreae) presence data were collected.
In the low-lying coastal region with higher humidity levels, farmers cultivate a wide range of food as well as tree crops like coconut palms, mango, citrus, and pawpaw. The major citrus-growing areas in the coastal region are Kwale Kilifi and Taita Taveta [49]. The Eastern region is located in the hot and dry semi-arid savannah biome and has similar cropping patterns as the coastal region. It is dominated by steep slopes with elevations ranging from 500 to 1200 m above mean sea level (m. a. m. s. l.).
2.2. ACT Occurrence Data
Field surveys were conducted along a clearly defined transect within the citrus-growing regions from the lowlands to the highlands in Kenya. In general, horticultural farming in Kenya is mainly carried out by small-scale producers because of the scarcity of productive land for horticultural production. Thus, citrus is grown in a wide range of elevations ranging from the lowlands to the highlands of Kenya [50]. The study area was divided into three elevation zones: Low (0–500 m. a. m. s. l.), middle (501–1000 m. a. m. s. l.), and high (>1000 m. a. m. s. l.). Each elevation zone was regarded as a stratum; therefore, we followed a stratified random sampling protocol to collect the ACT presence data. In each stratum (i.e., elevation zone), we randomly selected citrus orchards and nurseries, including backyards of small farms with a minimum orchard-to-orchard distance of 2 km for sampling. At least 30 citrus orchards in each stratum were sampled and with the aid of a hand-held Global Positioning System (GPS) device with a positional accuracy of ±2 m, the location of the citrus orchard, nursery, or backyard farm where ACT was present was recorded as an occurrence point. Specifically, for sample citrus orchard and backyard farms ≤ 0.5 ha, all citrus trees were inspected for ACT symptoms, while in orchards > 0.5 ha only 20 randomly selected trees were sampled in each orchard by moving across the orchard in a W-pattern [36]. Presence-only observations (n = 47) were collected across the study area, see Figure 1, between January 2015 and September 2016. This number of presence-only observations is regarded as acceptable in a MaxEnt modeling routine [51,52]. A subset of the ACT presence-only observations was used for training the MaxEnt model (75% of the sample observations), and 25% of the sample observations were used for model evaluation [53]. We also collected information on the representative sample vegetation cover and type surrounding citrus orchards and backyard farms where the ACT was present using geotagged photographs that were taken from the main four cardinal directions of the orchards for further inspection on how the landscape context could affect the presence of ACT.
2.3. Predictor Variables
We considered 35 variables as potential predictors for estimating ACT distribution and habitat suitability. The variables were categorized into BCL and RS variables, see Table 1. For the BCL variables, we selected variables based on the ecological requirements of the vector as reported in previous studies: temperature, humidity, and elevation [36]. Temperature and precipitation were represented by 19 “bioclimatic” variables, see Table 1, available from the WorldClim database (www.worldclim.org) [54]. WorldClim projects current climatic conditions at 1-km spatial resolutions based on observations gathered from different weather stations between 1950 and 2000; the point datasets are interpolated using a thin plate smoothing spline algorithm to create a seamless raster dataset [54]. We also used topographical variables related to the potential ACGD vectors’ habitat. These included elevation, slope, hill shade, and aspect in degrees, see Table 1. Hill shade was included as a proxy for relative solar radiation load that accounts for the effect of topographic shading [55]. We observed in the field that the majority of ACT presence points were on the windward side for mountainous regions as opposed to the leeward side; hence, we included hill shade as a predictor variable in our ACT distribution model. The topographical variables were extracted from a void-filled 90 m digital elevation model (DEM) data set from the Shuttle Radar Topographical Mission (SRTM) [56]. Using the Environment for Visualizing Images (ENVI) version 4.8 (Exelis Visual Information Solutions, Boulder, CO, USA), both bio-climatic and topographical variables were resampled using a bilinear interpolation method to fit the 250m pixel size of the remotely-sensing variables [57].

Table 1.
Predictor variables used for modeling the ecological niche for the African citrus triozid (Trioza erytreae). The variables were divided into two sets; environmental (bio-climatic and topographical) and remote-sensing variables. Bold text refers to variables which were selected through a multi-collinearity test using the Findcorrelation function in the caret package in the R software and finally used in the MaxEnt model.
RS variables on vegetation phenological metrics and vegetation productivity dynamics were derived from a Moderate Resolution Imaging Spectroradiometer (MODIS) Enhanced Vegetation Index (EVI) time-series data at a 250-m spatial resolution. MODIS products such as Normalized Difference Vegetation Index (NDVI) and EVI are the most widely used indices for monitoring of the vegetation phenological pattern [58]. Matsushita et al [59] pointed out that NDVI is easily affected by soil background and low vegetation coverage and easily saturated in high vegetation coverage. On the other hand, EVI minimizes the noise of soil background and adjusts atmospheric aerosol interference, thus improving the sensitivity of mimicking densely vegetated sites as compared to NDVI [60,61,62]. In the present study, MODIS 16-day EVI composites for the years 2014 to 2016 from the National Aeronautics and Space Administration (NASA) Land Processes Distributed Active Archive Center (LP DAAC—https://lpdaac.usgs.gov/) were downloaded and preprocessed using the MODISTools package in R [63]. MODISTools provides a function for mosaicking and sub-setting the downloaded data to a selected geographical extent. Then, we calculated 11 vegetation phenological metrics, see Table 1, using the TIMESAT software [64]. Namely, we calculated (1) start of the season (start of season) which is the time of initial vegetation green up, (2) end of the season (end of season) representing time of initial vegetation senescence, (3) the length of growing season from green up to senescence (length of season), (4) base level, which was calculated by averaging the left and right minimum values (base value) that represent the baseline of the seasonal phenology curve, (5) time for the middle of the growing season (mid of season), (6) the highest EVI value of the season (max fitted value), (7) seasonal amplitude calculated as the difference between the peak EVI value and the average of the left and right minimum values corresponding to the amount of EVI change (amplitude), (8) the rate of vegetation green up (left derivative), (9) the rate of vegetation senescence (right derivative), (10) proxy for the relative amount of vegetation biomass without regarding the minimum EVI values (large integral), and (11) the proxy for the relative amount of vegetation biomass while regarding the minimum EVI values (small integral). All 11 vegetation phenological metrics [64,65,66] were calculated for the two growing seasons within each year. TIMESAT extracts vegetation phenological variables by fitting a local function to the time-series datasets [67]. We fitted the Savitzky-Golay smoothing model function that replaces the data value by values in a window using a second-order polynomial function with optimum smoothing parameters [64,68]. The Savitzky-Golay function reduces the effects of residual signals and smooths the time-series EVI dataset to a degree determined by the size of the smoothing window and reduces the noise caused primarily by cloud contamination and atmospheric variability [67]. The start and end of season threshold parameters for the smoothing function were set at 20%, as suggested by Jonsson and Eklundh [64], to optimize the error that could be caused by varying start and end of season dates in different locations across the study area [69]. Only variables for the first season were used in this study since data from the second season were not consistent throughout all the years across the study area [69]. Our study area cuts across different climatic zones in Kenya with a varying number of rainy seasons; hence, some of our sample sites commonly experience unimodal rainfall (one rainy season), while others have bi-modal rainfall (two rainy seasons) in a calendar year. This variability in the rainy seasons could have caused the variation and inconsistency in the vegetation phenological variable across the entire study area during the second rainy season. In addition to the vegetation phenological metrics, LST has proved to have a major influence on the spread and development of pests and diseases [70]. LST variables extracted from time-series MODIS data for the years 2014 to 2016 were averaged for each year and included in the set of predictor variables. MODIS LST has a high spatial characteristic that enables the capture of the spatial variability of land surface fluxes within a finer scale as opposed to point observations taken on the ground.
2.4. Predictor Variable Selection
To examine the expected multi-collinearity among the predictor variables, we performed a Pearson correlation test, see Figure 2, between all the predictor variables shown in Table 1. Furthermore, the “Findcorrelation” function in the Caret package in R was used to eliminate highly correlated variables using the mean absolute error score. A correlation coefficient of |r| > 0.7 was set as a collinearity indicator for variables that would severely affect our model [17]. Variables that met this criterion were eliminated from the analysis, and only the uncorrelated predictor variables were used in the MaxEnt model.
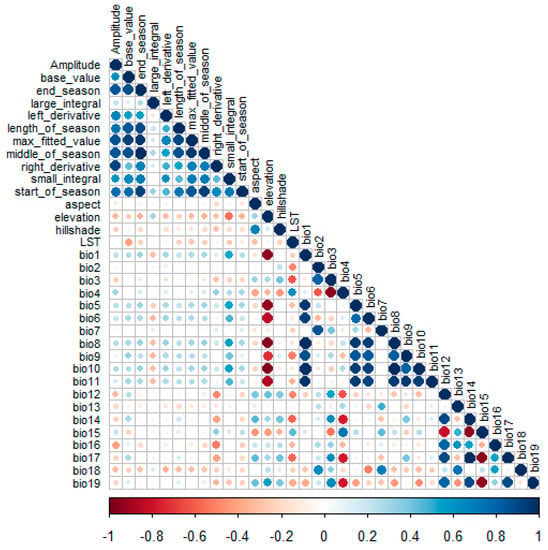
Figure 2.
Collinearity matrix for predictor variables. Darker shades of blue and red colors indicate high variable collinearity while light shades indicate low collinearity between variables.
2.5. EN Modeling
A MaxEnt model algorithm [71] was used to predict the distribution and likely suitable sites for ACT. MaxEnt is a presence background machine-learning approach that estimates species’ distribution that has maximum entropy subject to a set of constraints based upon a user’s knowledge of the environmental conditions at known occurrence sites [27]. Like most maximum-likelihood estimation methods, the MaxEnt algorithm adopts a uniform distribution and performs several iterations in which the weights related to the environmental variables are adjusted to maximize the average probability of point localities. These weights are then used to compute the distribution over the entire geographical space [72].
To minimize overfitting in the MaxEnt model, we implemented a regularization method to penalize the model in proportion to the coefficient magnitude [73]. Further, we ran MaxEnt models using the default variable responses setting and a logistic output format which results in the ACT distribution suitability prediction ranging from 0 (less suitable) to 1 (highly suitable). However, a default regularization multiplier was doubled to reduce the chance of under or over prediction [74]. In addition, we used the 10th percentile training presence threshold which predicts the 10% most extreme presence observations as absent to eliminate ‘outliers’ from the final model [75]. To study the effects of the vegetation phenology and dynamics for predicting ACT distribution, we performed two MaxEnt models, one included the environmental variables only (BCL model) and the other included both the environmental and remote-sensing variables (BCL-RS model).
2.6. EN Models Validation
Commonly, the accuracy of the MaxEnt distribution suitability maps is assessed using conventional accuracy measures such as the area under the curve (AUC) and chi-squared (X2) statistics. However, these accuracy statistics are somehow biased and highly sensitive to the proportional extent of the predicted presence observations [76], as a result of an overestimation of the pseudoabsence samples. Hence, in this study, we employed more reliable and adequate measures to evaluate the overall MaxEnt model performance. Specifically, we used true skill statistic (TSS) and Cohen’s kappa coefficient (Khat) to evaluate the accuracy of the ACT distribution suitability maps [77]. As compared to TSS, kappa inherently depends on prevalence. However, an ideal measure of model performance should not be affected by prevalence but combine sensitivity and specificity [78]. Thus, TSS combines both sensitivity and specificity to account for both omission and commission errors and is not affected by prevalence and the size of the validation set and, therefore, is the best parameter to measure model performance. Both TSS and Khat range from −1 to +1, where +1 indicates perfect agreement between the observed and predicted ACT observations, whereas values <0 indicate no agreement or that most of the predicted ACT observations were produced by chance [79]. In addition, we used a Jackknife procedure to assess the relative importance of each individual predictor variable to the ACT distribution suitability model [80]. To test the null hypothesis that there was no statistical (p ≤ 0.05) difference between the predictions of the BCL and the BCL-RS MaxEnt models, a two-sample t-test was performed. Herein, using ‘ArcGIS create random points’ tool, we generated 500 random sample points throughout the study area and compared their predictive power for each of the two models (i.e., BCL and BCL-RS).
2.7. Landscape Context Calculation
To describe the landscape context, we used a LULC map at a 20-m spatial resolution over the study area based on one year of Sentinel-2A observations ranging from December 2015 to December 2016 developed and validated by Climate Change Initiative (CCI) Land Cover (LC) team [81]. Since ACT is likely to spread locally up to a distance of 1500 m by natural dispersal [82], we extracted the LULC proportion within a 1500 m radius buffer from the center for each of the 24 ACT occurrence points collected from the field which were not overlapped within each buffer, see Figure 3. The proportions of the four major LULC classes (tree cover, shrubs cover, grassland, and cropland) within each buffer were calculated. We hypothesize that these four major LULC classes could influence the occurrence of ACT within a landscape scale. The same buffers were also used to extract the corresponding average habitat suitability scores from the suitability map generated by the MaxEnt algorithm. Random forest (RF) regression [83,84] analysis was performed to determine the most relevant LULC classes for the ACT habitat suitability scores using the RF variable importance by-product. An RF regression model was performed using the default settings suggested by Breiman [83], and the importance of the LULC classes was assessed using the RF mean decrease in accuracy (%) metric.
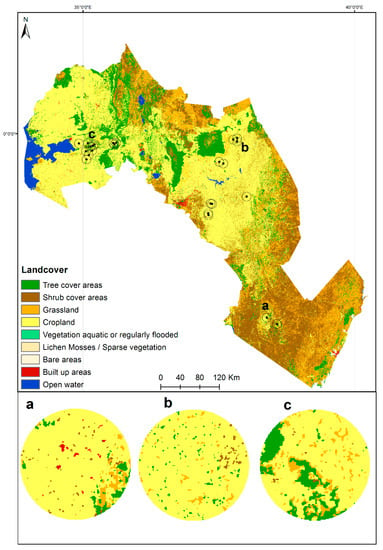
Figure 3.
A 20-m spatial resolution land use/land cover map for the study area generated by the Climate Change Initiative (CCI) Land Cover (LC) team. Using yearly Sentinel-2 observations. (a–c) represent zoomed buffers of 1500 m radius each around certain representative African citrus triozid (ACT) occurrence points.
3. Results
3.1. EN Models
The Pearson correlation test for multi-collinearity resulted in selecting only six BCL and six RS uncorrelated predictor variables, respectively, see Table 1. The overall accuracy, TSS, and Khat for both the BCL and BCL-RS MaxEnt models are shown in Table 2. A combined BCL-RS model gave the highest accuracy of 92% with a TSS score of 0.83 compared to the model with only environmental variables (BCL model), which had an overall accuracy of 85% and a TSS score of 0.572. TSS and Khat statistics showed a prediction better than expected at random (TSS = 0.5) for both models, with the BCL-RS model performing better than the BCL model.

Table 2.
Accuracy assessment statistics for the developed African citrus triozid (Trioza erytreae) MaxEnt models.
3.2. Variable Importance
Figure 4 and Figure 5 show the results of the jackknife test of variable importance for the BCL and BCL-RS models, respectively. Blue shades show the individual importance of each variable when used in isolation, while green shows the model performance when the variables are exempted from the model. The figures also show the variables which caused the greatest decreases in the gain when omitted, indicating that they provided a significant portion of information that was not contained in the other variables. For both models (BCL and BCL-RS), the variable with the highest gain (relevance) when used in isolation was Bio 18; therefore, Bio 18 appears to have the most useful information individually, followed by Bio 16 (for variable definitions see Table 1). Likewise, the variables that decreased the gain the most when they were omitted were Bio 16 and Bio 18 for the BCL model and Bio 16 and LST for the BCL-RS model. These variables appear to have the most influence on the models compared to the other variables.
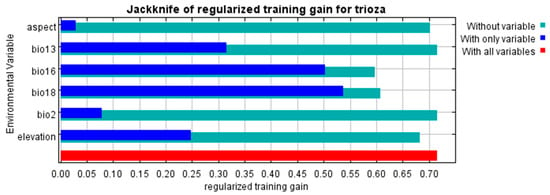
Figure 4.
Jackknife variable importance test of regulated gains for the BCL model. The dark blue shades show the regularized training gain for the specific variable, light blue shows the relevance when the variable is omitted, while red shows the regularized training gain with all the variables combined.
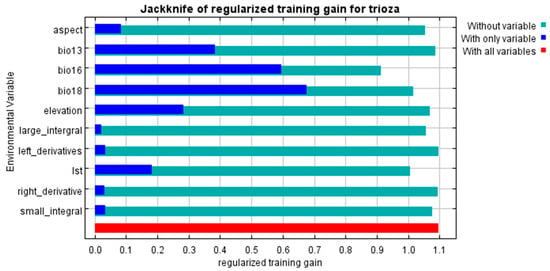
Figure 5.
Jackknife variable importance test of regulated gains for the BCL-RS model. The dark blue shades show the regularized training gain for the specific variable, light blue illustrates gains without the variable, while red shows the regularized training gain with all the variables combined.
Table 3 presents the percentage that each variable contributed and its permutation importance in the BCL and BCL-RS models, respectively. In the BCL model, Bio 16 was the variable that contributed the most (48.3%) followed by Bio 18 (44.5%), Elevation (4.0%), and Aspect (2.2%), respectively. Similarly, in the BCL-RS model, Bio 16 contributed the most (41%), followed by Bio 18 (36.3%), while the contributions for LST, Elevation, and Aspect ranged from 4.9% to 6.6%.

Table 3.
Percentage contributions and permutation importance for each variable to the BCL and BCL-RS models, respectively.
3.3. Habitat Suitability Mapping
Figure 6 shows the predicted habitat suitability map for ACT based on the BCL, see Figure 6a, and the BCL-RS, see Figure 6b, models. The maps indicate the more suitable predicted sites with warmers colors (red) and less suitable predicted sites with cooler colors (blue). Both models show better predicted conditions in Western, Central, and small parts of Eastern Kenya. These areas have a higher elevation above mean sea level. The least suitable sites are mostly towards the coastal region which has lower elevations.
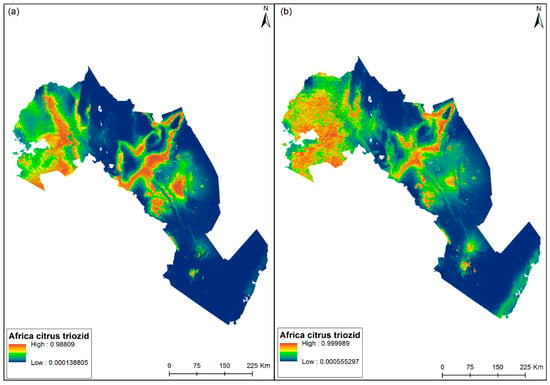
Figure 6.
Predicted distribution suitability map for African citrus triozid (Trioza erytreae) using environmental (BCL model) variables (a), and environmental and remotely-sensed (BCL-RS model) variables (b). Blue indicates low distribution suitability, while red represents high distribution suitability.
The t-test result showed that the BCL-RS model produced significantly (t-statistic = 2.8279 and p = 0.005) higher AUC values compared to the BCL model. The t-test difference in the means, indicated that RS variables contributed 18% to the prediction model when combined with environmental variables.
3.4. Relationship between ACT Habitat Suitability and Landscape Context
We realized that there are diverse and multiscale responses of landscape context (i.e., LULC) to the habitat suitability of ACT. Using the mean decrease in accuracy (%) in the RF variable importance rank, the “shrubs” class was found to be the most relevant LULC class to ACT habitat suitability followed by “trees”, “grassland”, and “cropland”, respectively, as shown in Figure 7.
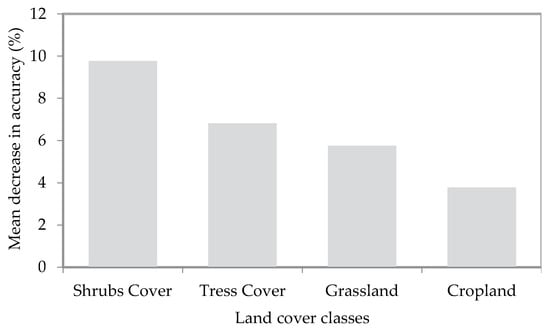
Figure 7.
The relevance of the four major land use/land cover classes to the habitat suitability of African citrus triozid (Trioza erytreae) using a random forest variable importance rank.
4. Discussion
This study tests the applicability of an EN modeling approach for predicting the distribution and suitable habitat for ACT in citrus-growing regions in Kenya. This was achieved through nesting ACT habitat variables with a MaxEnt modeling framework for generating distribution information that is fundamental for prioritizing sites in which the management of ACGD is most needed or feasible [85]. A reliable and accurate ACT distribution map is a valuable information source for monitoring vector infestation rates and disease spread. Such a spatial data set can also be used to prioritize interventions that prohibit the spread of the disease to unaffected areas [86]. The “near-real-time” aspect of the remotely-sensing data means that the largely neglected aspect of early response can be addressed within integrated pest management (IPM) strategies [87].
In general, our study shows that both the uncorrelated BCL and RS variables were well-associated with the occurrence of ACT in typical Eastern African landscapes with their heterogeneous agro-ecologies. The results showed the importance of fusing RS with BCL variables in reducing the overestimated spatial variability in the predictor variables and in enhancing the predictive power of the model [69]. For the best performing models, Bio 16 (annual precipitation) had the highest contribution towards predicting the habitat suitability for ACT followed by Bio 18 (precipitation of the warmest quarter), LST, elevation, aspect, and small integral (MODIS-derived vegetation productivity). Precipitation of both the wettest and warmest quarter were important variables in defining the habitat suitability of ACT since they regulate the optimal temperature ranges within which the triozid survives [88]. In addition, precipitation and temperature regulate citrus flushing circles which are known to be highly correlated with the occurrence of ACT [10]. The significance of the precipitation related variables in describing habitat suitability for ACT was more pronounced than elevation, which has been linked with the distribution of the vector in a previous study [36]. This could be due to the micro-climatic aspect which is not entirely dependent on elevation but also landscape heterogeneity, among other aspects. In the BCL model, Bio 16 and Bio 18 alone contributed more than 92% to the model performance, while in the BCL-RS model, the contribution from these variables was reduced to 77% indicating that inclusion of RS variables contributes immensely to the model. Since our aim was to start from known BCL variables that are commonly used to predict the spatial distribution of crop pests, then explore the contribution of RS variables to the predictive model performance, we did not create a model without bioclimatic variables. Also, we did not create any bootstrapped MaxEnt models, which could have allowed the quantification of the effect sampling variability had on our model results (ACT distribution map).
Makori et al. [69] reported that RS information used within habitat suitability models is known to better account for explicit landscape patterns, that define habitats, thereby reducing model over-fitting and essentially increasing the accuracy and precision of habitat suitability models. In addition, our results showed that LST played a key role in defining the niche of the ACT vector. This is in agreement with previous studies which have shown LST to be a main parameter in pest modeling routines [89]. The influence of RS variables in modeling the habitat suitability of ACT was considerable. The BCL model, as shown in Figure 6a, had over-predicted the distribution of ACT compared to the BCL-RS model, as shown in Figure 6b. In our ACT prediction distribution map, areas with high occurrence probabilities are characterized by high precipitation, high elevation, lower temperature regimes, and relatively similar vegetation productivity patterns.
The ACT distribution maps using BCL-RS variables show high occurrences of ACT in specific locations of the coastal region of Kenya. This disagrees with the findings of previous studies that ACT is unlikely to be present in coastal ecosystems. This could be related to vegetation dynamics and landscape context (i.e., LULC), which are very distinct in some specific areas along the coastal region, such as Wundanyi sub-county in Taita-Taveta county where the habitat suitability was reported to be high compared to other coastal regions of Kenya using the MaxEnt model. Despite the climate conditions being very similar to other regions where the model has predicted a high suitability of ACT, vegetation patterns in regions where the habitat suitability is high are very distinct and of similar productivities since they have common climatic conditions in terms of rainfall and temperature. This is in alignment with the finding from the literature that vegetation dynamics play a key role in defining the niche of crop pests and diseases [90]. This result reinforced the importance of both BCL and RS variables for modeling the distribution of ACT. Further, our study is a step towards the understanding of how the spread of insect pests is enhanced by BCL (both bio-climatic and topographic) and RS (vegetation phenological variables and LST), that influence the spread and multiplication of the vector in African agro-ecosystems.
Furthermore, the results from this study revealed that landscape context should not be ignored regarding understanding the distribution and dispersal pattern of ACT. However, we did not include landscape context in our MaxEnt model since from our field observation, we realized that the majority of the citrus orchards in our study area are within a cropland class. In our case, a presence-only MaxEnt model would have extracted only ‘cropland’ features for all ACT presence points. Therefore, we opted to look at the effect of the landscape context on ACT habitat suitability based on the dispersal capability of the pest (which is 1500 m). The relationship between ACT habitat suitability and the four major LULC classes across the major citrus-growing regions showed that there is an association between the surrounding shrub cover proportion and habitat suitability for ACT. Shrub cover near citrus orchards could provide alternative host plants for the vector during the time when citrus trees are not flushing since ACT is correlated with the flushing rhythm of the citrus host [91]. In addition, from field observations, it became clear that the majority of the ACT-infected citrus trees were within shaded areas, and thus trees and shrubs surrounding the citrus orchards most likely provide more suitable temperature conditions for the survival of ACT.
To the best of our knowledge, our study is the first attempt to predict the distribution of ACT using an enhanced and optimized EN modeling algorithm with BCL and RS variables and habitat suitability relationships with the surrounding landscape classes. Previous studies have only investigated the role of various environmental variables for mapping ACP distribution, but in these studies, links between localized factors captured in more sophisticated modeling routines and better consideration of landscape patterns were not considered [36]. Future studies should explore the relationship between vegetation phenological and other localized pest classification factors and ACT densities (i.e., number of insets per unit area) to better understand the survival and dispersal patterns of the vector as there is a need for a better and more concerted implementation of vector management practices.
5. Conclusions
The impact of spatially heterogeneous environmental factors on ACT population dynamics are complex to model. However, understanding the inter-relationship between vectors, hosts, and their niches environment can provide valuable information for identifying conditions suitable for pathogen introduction and transmission in citrus-growing regions. By exploring the spatial distribution of ACT, we identified a set of BCL factors that are favorable for its development, predicted its spatial occurrence, and identified potential areas that, due to their BCL conditions, would be suitable for its introduction.
The BCL-RS model showed higher accuracy metrics and was deemed appropriate for predicting the distribution and potentially suitable areas for ACT. Though less important, the influence of vegetation phenological variables and LST for determining the habitat suitability of ACT was considerable. Our results revealed that apart from the BCL variables like temperature, rainfall, and elevation, which have previously been found to define the EN of ACT, vegetation patterns and dynamics at a landscape level play a key role in influencing vector-host-pathogen transmission and distribution. The ACT distribution prediction maps are an important tool for identifying risk zones and understanding risk drivers. Also, the distribution maps can provide baseline information for the development and implementation of effective IPM strategies. Future studies should look at modeling the density of ACT on a landscape scale for the precise application of prevention and control measures.
Author Contributions
R.K. analyzed the data and wrote the manuscript. He is also the main author of all sections in this manuscript. All co-authors provided valuable input regarding fieldwork, data analysis, and manuscript preparation. Conceptualization, R.K., E.M.A.-R. and T.L.; Formal analysis, R.K.; Funding acquisition, S.A.M. and S.E.; Methodology, R.K.; Project administration, T.L. and E.M.A.-R.; Software, R.K.; Supervision, B.C. and T.L.; Validation, R.K.; Writing – original draft, R.K.; Writing – review & editing, E.M.A.-R, B.C., S.A.M. and S.E. and T.L.
Funding
This research was funded by Ministry for Economic Cooperation and Development (BMZ) and Deutsche Gesellschaft für Internationale Zusammenarbeit Advisory Service on Agricultural Research for Development (GIZ/BEAF)grant number 81180346 and the APC was funded by GIZ/BMZ.
Acknowledgments
We gratefully acknowledge the financial support for this research by Germany – Ministry for Economic Cooperation and Development (BMZ) and Deutsche Gesellschaft für Internationale Zusammenarbeit Advisory Service on Agricultural Research for Development (GIZ/BEAF) for the project “Citrus pest management in Kenya and Tanzania”. We also acknowledge the International Centre for Insect Physiology and Ecology (icipe) core funding provided by UK’s Department for International Development (DFID), Swedish International Development Cooperation Agency (Sida), the Swiss Agency for Development and Cooperation (SDC), the BMZ, and the Kenyan Government. The views expressed herein do not necessarily reflect the official opinion of the donors. Our appreciation also extends to the Plant Health Theme of icipe for helping in field identification and data collection. Special thanks to Mr. Jackson Kimani for preparing the final maps.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Franco-Vega, A.; Reyes-Jurado, F.; Cardoso-Ugarte, G.A.; Sosa-Morales, M.E.; Palou, E.; López, M. Chapter 89—Sweet Orange (Citrus sinensis) Oils A2. In Essential Oils in Food Preservation, Flavor and Safety; Preedy, V.R., Ed.; Academic Press: San Diego, CA, USA, 2016; pp. 783–790. [Google Scholar]
- Liu, Y.; Heying, E.; Tanumihardjo, S.A. History, Global Distribution, and Nutritional Importance of Citrus Fruits. Compr. Rev. Food Sci. Food Saf. 2012, 11, 530–545. [Google Scholar] [CrossRef]
- FAO, Food and Agriculture Organization of the United. FAOSTAT Statistics Database; FAO: Rome, Italy, 2016. [Google Scholar]
- Ouma, G. Challenges and approaches to sustainable citrus production in Kenya. Afr. J. Plant Sci. Biotechnol. 2008, 2, 49–51. [Google Scholar]
- Adhikari, U.; Nejadhashemi, A.P.; Woznicki, S.A. Climate change and eastern Africa: A review of impact on major crops. Food Energy Secur. 2015, 4, 110–132. [Google Scholar] [CrossRef]
- Nicholas, I.D. 26—Plantings in Tropical and Subtropical Areas A2. In Windbreak Technology; Brandle, J.R., Hintz, D.L., Sturrock, J.W., Eds.; Elsevier: Amsterdam, The Netherlands, 1988; pp. 465–482. [Google Scholar]
- Asharaf, S.; Khan, A.G.; Ali, S.; Iftikhar, M. An Assessment of the Socio-Economic Factors Affecting the Adoption of Citrus Tissue Culture Technology in Kenya; Ciencia Rural: Santa Maria, Brazil, 2002. [Google Scholar]
- Waithaka, K. Consultant’s Report on Tropical Fruit Production in East and Southern Africa; Food and Agriculture Organization of the United Nations: Rome, Italy, 1991. [Google Scholar]
- ICIPE. SCIPM: Project by ICIPE and Partners to Improve Citrus Farming. 2015. Available online: http://www.icipe.org/news/scipm-project-icipe-and-partners-improve-citrus-farming (accessed on 17 April 2018).
- Michaud, J.P. Natural mortality of Asian citrus psyllid (Homoptera: Psyllidae) in Central Florida. Biol. Control 2004, 29, 260–269. [Google Scholar] [CrossRef]
- Zou, H.; Gowda, S.; Zhou, L.; Hajeri, S.; Chen, G.; Duan, Y. The Destructive Citrus Pathogen, ‘Candidatus Liberibacter asiaticus’ Encodes a Functional Flagellin Characteristic of a Pathogen-Associated Molecular Pattern. PLoS ONE 2012, 7, e46447. [Google Scholar] [CrossRef] [PubMed]
- Boykin, L.M.; De Barro, P.; Hall, D.G.; Hunter, W.B.; McKenzie, C.L.; Powell, C.A.; Shatters, R.G. Overview of worldwide diversity of Diaphorina citri Kuwayama mitochondrial cytochrome oxidase 1 haplotypes: Two Old World lineages and a New World invasion. Bull. Entomol. Res. 2012, 102, 573–582. [Google Scholar] [CrossRef] [PubMed]
- Jagoueix, S.; Bove, M.J.; Garnier, M. The phloem-limited bacterium of greening disease of citrus is a member of the α subdivision of the proteobacteria. Int. J. Syst. Bacteriol. 1994, 44, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Khamis, F.M.; Rwomushana, I.; Ombura, L.O.; Cook, G.; Tanga, C.M.; Ekesi, S. DNA Barcode Reference Library for the African Citrus Triozid, Trioza erytreae (Hemiptera: Triozidae): Vector of African Citrus Greening. J. Econ. Entomol. 2017, 110, 2637–2646. [Google Scholar] [CrossRef] [PubMed]
- Catling, H.D. Notes on the biology of the South African citrus psylla, Trioza erytreae (Del Guercio) (Homoptera: Psyllidae). J. Entomol. Soc. S. Afr. 1973, 36, 299–306. [Google Scholar]
- Aubert, B. Trioza erytreae Del Guercio and Diaphorina citri Kuwayama (Homoptera: Psyllidae), the two vectors of citrus greening disease: Biological aspects and possible control strategies. Fruits 1987, 42, 149–162. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Pole, F.N.; Ndung’u, J.M.; Kimani, J.M. Citrus farming in Kwale district: A case study of Lukore location. In Proceedings of the 12th KARI Biennial Conference: Transforming Agriculture for Improved Livelihoods through Agricultural Product Value Chains, Nairobi, Kenya, 8–12 November 2010. [Google Scholar]
- Alvarez, S.; Rohrig, E.; Solís, D.; Thomas, M.H. Citrus Greening Disease (Huanglongbing) in Florida: Economic Impact, Management and the Potential for Biological Control. Agric. Res. 2016, 5, 109–118. [Google Scholar] [CrossRef]
- Grafton-Cardwell, E.E.; Stelinski, L.L.; Stansly, P.A. Biology and Management of Asian Citrus Psyllid, Vector of the Huanglongbing Pathogens. Annu. Rev. Entomol. 2013, 58, 413–432. [Google Scholar] [CrossRef] [PubMed]
- Moore, S.M.; Borer, E.T.; Hosseini, P.R. Predators indirectly control vector-borne disease: Linking predator–prey and host–pathogen models. J. R. Soc. Interface 2010, 7, 161–176. [Google Scholar] [CrossRef] [PubMed]
- Peterson, A.T. Ecologic Niche Modeling and Spatial Patterns of Disease Transmission. Emerg. Infect. Dis. 2006, 12, 1822–1826. [Google Scholar] [CrossRef] [PubMed]
- Brownstein, J.S.; Holford, T.R.; Fish, D. A climate-based model predicts the spatial distribution of the Lyme disease vector Ixodes scapularis in the United States. Environ. Health Perspect. 2003, 111, 1152–1157. [Google Scholar] [CrossRef] [PubMed]
- Lord, C.C. Modeling and biological control of mosquitoes. J. Am. Mosq. Control Assoc. 2007, 23, 252–264. [Google Scholar] [CrossRef]
- Hol, W.H.; Bezemer, T.M.; Biere, A. Getting the ecology into interactions between plants and the plant growth-promoting bacterium Pseudomonas fluorescens. Front. Plant Sci. 2013, 4, 81. [Google Scholar] [CrossRef] [PubMed]
- Shabani, F.; Kumar, L.; Ahmadi, M. A comparison of absolute performance of different correlative and mechanistic species distribution models in an independent area. Ecol. Evol. 2016, 6, 5973–5986. [Google Scholar] [CrossRef] [PubMed]
- Yackulic, C.B.; Chandler, R.; Zipkin, E.F.; Royle, J.A.; Nichols, J.D.; Campbell Grant, E.H.; Veran, S. Presence-only modelling using MAXENT: When can we trust the inferences? Methods Ecol. Evol. 2013, 4, 236–243. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Potential Geographic Distribution of Brown Marmorated Stink Bug Invasion (Halyomorpha halys). PLoS ONE 2012, 7, e31246. [Google Scholar] [CrossRef] [PubMed]
- Barredo, J.I.; Strona, G.; Rigo, D.; Caudullo, G.; Stancanelli, G.; San-Miguel-Ayanz, J. Assessing the potential distribution of insect pests: Case studies on large pine weevil (Hylobius abietis L) and horse-chestnut leaf miner (Cameraria ohridella) under present and future climate conditions in European forests. EPPO Bull. 2015, 45, 273–281. [Google Scholar] [CrossRef]
- Hof, A.R.; Svahlin, A. The potential effect of climate change on the geographical distribution of insect pest species in the Swedish boreal forest. Scand. J. For. Res. 2016, 31, 29–39. [Google Scholar] [CrossRef]
- Marchioro, C.A. Global Potential Distribution of Bactrocera carambolae and the Risks for Fruit Production in Brazil. PLoS ONE 2016, 11, e0166142. [Google Scholar] [CrossRef] [PubMed]
- Alkishe, A.A.; Peterson, A.T.; Samy, A.M. Climate change influences on the potential geographic distribution of the disease vector tick Ixodes ricinus. PLoS ONE 2017, 12, e0189092. [Google Scholar] [CrossRef] [PubMed]
- Chiyaka, C.; Singer, B.H.; Halbert, S.E.; Morris, J.G.; van Bruggen, A.H.C. Modeling huanglongbing transmission within a citrus tree. Proc. Natl. Acad. Sci. USA 2012, 109, 12213–12218. [Google Scholar] [CrossRef] [PubMed]
- Vilamiu, R.G.d.A.; Ternes, S.; Braga, G.A.; Laranjeira, F.F. A model for Huanglongbing spread between citrus plants including delay times and human intervention. Proc. Natl. Acad. Sci. USA 2012, 1479, 2315–2319. [Google Scholar]
- Ramirez, G.R.G.; Medina, H.C.P.B.; Trujillo, T.J.R. Agroclimatic risk of development of Diaphorina citri in the citrus region of Nuevo Leon, Mexico. Afr. J. Agric. Res. 2016, 11, 3254–3260. [Google Scholar]
- Shimwela, M.M.; Narouei-Khandan, H.A.; Halbert, S.E.; Keremane, M.L.; Minsavage, G.V.; Timilsina, S.; Massawe, D.P.; Jones, J.B.; van Bruggen, A.H.C. First occurrence of Diaphorina citri in East Africa, characterization of the Ca. Liberibacter species causing huanglongbing (HLB) in Tanzania, and potential further spread of D. citri and HLB in Africa and Europe. Eur. J. Plant Pathol. 2016, 146, 349–368. [Google Scholar] [CrossRef]
- Narouei-Khandan, H.A.; Halbert, S.E.; Worner, S.P.; van Bruggen, A.H.C. Global climate suitability of citrus huanglongbing and its vector, the Asian citrus psyllid, using two correlative species distribution modeling approaches, with emphasis on the USA. Eur. J. Plant Pathol. 2016, 144, 655–670. [Google Scholar] [CrossRef]
- Paull, S.H.; Song, S.; McClure, K.M.; Sackett, L.C.; Kilpatrick, A.M.; Johnson, P.T.J. From superspreaders to disease hotspots: Linking transmission across hosts and space. Front. Ecol. Environ. 2012, 10, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, N.E.; Edwards, T.C., Jr.; Moisen, G.G.; Frescino, T.S.; Blackard, J.A. Remote sensing-based predictors improve distribution models of rare, early successional and broadleaf tree species in Utah. J. Appl. Ecol. 2007, 44, 1057–1067. [Google Scholar] [CrossRef] [PubMed]
- Green, G.C.; Catling, H.D. Weather induced mortality of the citrus psylla, trioza erytreae (del guercio) (homoptera: Psyllidae), a vector of greening virus, in some citrus producing areas of Southern Africa. Agric. Meteorol. 1971, 8, 305–317. [Google Scholar] [CrossRef]
- Amoros Lopez, J. Land cover classification of VHR airborne images for citrus grove identification. ISPRS J. Photogramm. Remote Sens. 2011, 66, 115–123. [Google Scholar] [CrossRef]
- Ozdemir, L. Separation of Citrus Plantations from forest cover using Landsat Imagery. Allg. For. Jagdztg. 2007, 178, 208–212. [Google Scholar]
- Shrivastava, R.J.; Gebelein, J.L. Landcover classification and economic assessment of citrus groves using remote sensing. ISPRS J. Photogramm. Remote Sens. 2007, 61, 341–353. [Google Scholar] [CrossRef]
- Plantegenest, M.; Le May, C.; Fabre, F.D.R. Landscape epidemiology of plant diseases. J. R. Soc. Interface 2007, 4, 963–972. [Google Scholar] [CrossRef] [PubMed]
- Margosian, M.L.; Garrett, K.A.; Hutchinson, J.M.S.; With, K.A. Connectivity of the American Agricultural Landscape: Assessing the National Risk of Crop Pest and Disease Spread. BioSci 2009, 59, 141–151. [Google Scholar] [CrossRef]
- Rizzo, D.M.; Garbelotto, M. Sudden oak death: Endangering California and Oregon forest ecosystems. Front. Ecol. Environ. 2003, 1, 197–204. [Google Scholar] [CrossRef]
- Avelino, J.; Romero-Gurdian, A.; Cruz-Cuellar, H.F.; Declerck, F.A. Landscape context and scale differentially impact coffee leaf rust, coffee berry borer, and coffee root-knot nematodes. Ecol. Appl. 2012, 22, 584–596. [Google Scholar] [CrossRef] [PubMed]
- Thies, C.; Steffan-Dewenter, I.; Tscharntke, T. Effects of landscape context on herbivory and parasitism at different spatial scales. Oikos 2003, 101, 18–25. [Google Scholar] [CrossRef]
- Oosten, C.V. Farming Systems and Food Security in Kwale District Kenya; MOPAN Development, Ed.; Africa Studies Centre: Leiden, The Netherlands, 1989. [Google Scholar]
- Anonymous. Horticulture Crops Protection Handbook; Ministry of Agriculture: Nairobi, Kenya, 1984.
- Wisz, M.S.; Hijmans, R.J.; Li, J.; Peterson, A.T.; Graham, C.H.; Guisan, A. Effects of sample size on the performance of species distribution model. Divers. Distrib. 2008, 14, 763–773. [Google Scholar] [CrossRef]
- Amirpour Haredasht, S.; Barrios, M.; Farifteh, J.; Maes, P.; Clement, J.; Verstraeten, W.W.; Tersago, K.; Van Ranst, M.; Coppin, P.; Berckmans, D.; et al. Ecological niche modelling of bank voles in Western Europe. Int. J. Environ. Res. Public Health 2013, 10, 499–514. [Google Scholar] [CrossRef] [PubMed]
- Qin, A.; Liu, B.; Guo, Q.; Bussmann, R.W.; Ma, F.; Jian, Z.; Xu, G.; Pei, S. Maxent modeling for predicting impacts of climate change on the potential distribution of Thuja sutchuenensis Franch., an extremely endangered conifer from southwestern China. Glob. Ecol. Conserv. 2017, 10, 139–146. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Pierce, K.B.; Lookingbill, T.; Urban, D. Urban, A simple method for estimating potential relative radiation (PRR) for landscape-scale vegetation analysis. Landscape Ecology. Landsc. Ecol. 2005, 20, 137–147. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. The CGIAR Consortium for Spatial Information (CGIAR-CSI). 2008. Available online: http://srtm.csi.cgiar.org/ (accessed on 16 May 2018).
- Usery, E.L.; Finn, M.P.; Scheidt, D.J.; Ruhl, S.; Beard, T.; Bearden, M. Geospatial data resampling and resolution effects on watershed modeling: A case study using the agricultural non-point source pollution model. J. Geogr. Syst. 2004, 6, 289–306. [Google Scholar] [CrossRef]
- Li, Z.; Li, X.; Wei, D.; Xu, X.; Wang, H. An assessment of correlation on MODIS-NDVI and EVI with natural vegetation coverage in Northern Hebei Province, China. Procedia Environ. Sci. 2010, 2, 964–969. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-Density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, C.; Chen, W.; Lin, X. Preliminary Comparison of MODIS-NDVI and MODIS-EVI in Eastern Asia; Geomatics and Information Science of Wuhan University: Wuhan, China, 2006; Volume 31, pp. 407–410. [Google Scholar]
- Liu, S.; Liu, X.; Liu, M.; Wu, L.; Ding, C.; Huang, Z. Extraction of Rice Phenological Differences under Heavy Metal Stress Using EVI Time-Series from HJ-1A/B Data. Sensors 2017, 17, 1243. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Tuck, S.L.; Phillips, H.R.P.; Hintzen, R.E.; Scharlemann, J.P.W.; Purvis, A.; Hudson, L.N. MODISTools—Downloading and processing MODIS remotely sensed data in R. Ecol. Evol. 2014, 4, 4658–4668. [Google Scholar] [CrossRef] [PubMed]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Wei, H.; Heilman, P.; Qi, J.; Nearing, M.A.; Gu, Z.; Zhang, Y. Assessing phenological change in China from 1982 to 2006 using AVHRR imagery. Front. Earth Sci. 2012, 6, 227–236. [Google Scholar] [CrossRef]
- Penatti, N.; Isnard, T. Subdivision of pantanal quaternary wetlands: Modis NDVI timeseries in the indirect detection of sediments granulometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B8, 311–316. [Google Scholar] [CrossRef]
- Cai, Z.; Jönsson, P.; Jin, H.; Eklundh, L. Performance of Smoothing Methods for Reconstructing NDVI Time-Series and Estimating Vegetation Phenology from MODIS Data. Remote Sens. 2017, 9, 1271. [Google Scholar] [CrossRef]
- Chen, J. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Makori, D.; Fombong, A.; Abdel-Rahman, E.; Nkoba, K.; Ongus, J.; Irungu, J.; Mosomtai, G.; Makau, S.; Mutanga, O.; Odindi, J.; et al. Predicting Spatial Distribution of Key Honeybee Pests in Kenya Using Remotely Sensed and Bioclimatic Variables: Key Honeybee Pests Distribution Models. ISPRS Int. J. Geo-Inf. 2017, 6, 66. [Google Scholar] [CrossRef]
- Chabot-Couture, G.; Nigmatulina, K.; Eckhoff, P. An Environmental Data Set for Vector-Borne Disease Modeling and Epidemiology. PLoS ONE 2014, 9, e94741. [Google Scholar] [CrossRef] [PubMed]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Buermann, W.; Saatchi, S.; Smith, T.B.; Zutta, B.R.; Chaves, J.A.; Milá, B.; Graham, C.H. Predicting species distributions across the Amazonian and Andean regions using remote sensing data. J. Biogeogr. 2008, 35, 1160–1176. [Google Scholar] [CrossRef]
- Royle, J.A.; Chandler, R.B.; Yackulic, C.; Nichols, J.D. Likelihood analysis of species occurrence probability from presence-only data for modelling species distributions. Methods Ecol. Evol. 2012, 3, 545–554. [Google Scholar] [CrossRef]
- Sahlean, T.C.; Gherghel, I.; Papeş, M.; Strugariu, A.; Zamfirescu, Ş.R. Refining Climate Change Projections for Organisms with Low Dispersal Abilities: A Case Study of the Caspian Whip Snake. PLoS ONE 2014, 9, e91994. [Google Scholar] [CrossRef] [PubMed]
- Cord, A.F.; Klein, D.; Gernandt, D.S.; de la Rosa, J.A.P.; Dech, S. Remote sensing data can improve predictions of species richness by stacked species distribution models: A case study for Mexican pines. J. Biogeogr. 2014, 41, 736–748. [Google Scholar] [CrossRef]
- Anderson, R.P.; Lew, D.; Peterson, A.T. Evaluating predictive models of species’ distributions: Criteria for selecting optimal models. Ecol. Model. 2003, 162, 211–232. [Google Scholar] [CrossRef]
- Jorge Soberon, B. Mapping Species Distributions: Spatial Inference and Prediction. Q. Rev. Biol. 2011, 86, 219–220. [Google Scholar]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, S.; Sun, P.; Wang, T.; Wang, G.; Zhang, X.; Wang, L. Consensus Forecasting of Species Distributions: The Effects of Niche Model Performance and Niche Properties. PLoS ONE 2015, 10, e0120056. [Google Scholar] [CrossRef] [PubMed]
- Matyukhina, D.S.; Miquelle, D.G.; Murzin, A.A.; Pikunov, D.G.; Fomenko, P.V.; Aramilev, V.V.; Litvinov, M.N.; Salkina, G.P.; Seryodkin, I.V.; Nikolaev, I.G.; et al. Assessing the Influence of Environmental Parameters on Amur Tiger Distribution in the Russian Far East Using a MaxEnt Modeling Approach. Achiev. Life Sci. 2014, 8, 95–100. [Google Scholar] [CrossRef]
- ESA CCI Land Cover-S2 Prototype Land Cover Map of Africa. Available online: http://www.2016africalandcover20m.esrin.esa.int/ (accessed on 23 May 2018).
- Van Den Berg, M.A.; Anderson, S.H.; Deacon, V.E. Population studies of the citrus psylla, trioza erytreae: Factors influencing dispersal. Phytoparasitica 1991, 19, 283. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Forkuor, G.; Hounkpatin, O.K.L.; Welp, G.; Thiel, M. High Resolution Mapping of Soil Properties Using Remote Sensing Variables in South-Western Burkina Faso: A Comparison of Machine Learning and Multiple Linear Regression Models. PLoS ONE 2017, 12, e0170478. [Google Scholar] [CrossRef] [PubMed]
- Tonnang, H.E.Z.; Hervé, B.D.B.; Biber-Freudenberger, L.; Salifu, D.; Subramanian, S.; Ngowi, V.B.; Guimapi, R.Y.A.; Anani, B.; Kakmeni, F.M.M.; Affognon, H.; et al. Advances in crop insect modelling methods—Towards a whole system approach. Ecol. Model. 2017, 354, 88–103. [Google Scholar] [CrossRef]
- De Meyer, M.; Robertson, M.P.; Mansell, M.W.; Ekesi, S.; Tsuruta, K.; Mwaiko, W.; Vayssieres, J.F.; Peterson, A.T. Ecological niche and potential geographic distribution of the invasive fruit fly Bactrocera invadens (Diptera, Tephritidae). Bull. Entomol. Res. 2010, 100, 35–48. [Google Scholar] [CrossRef] [PubMed]
- Bové, J.M. Huanglongbing or yellow shoot, a disease of Gondwanan origin: Will it destroy citrus worldwide? Phytoparasitica 2014, 42, 579–583. [Google Scholar] [CrossRef]
- Blum, M.; Lensky, I.M.; Rempoulakis, P.; Nestel, D. Modeling insect population fluctuations with satellite land surface temperature. Ecol. Model. 2015, 311, 39–47. [Google Scholar] [CrossRef]
- Ratnadass, A.; Fernandes, P.; Avelino, J.; Habib, R. Plant species diversity for sustainable management of crop pests and diseases in agroecosystems: Review. Agron. Sustain. Dev. 2012, 32, 273–303. [Google Scholar] [CrossRef]
- Cook, G.; Maqutu, V.Z.; Vuuren, S.P.V. Population Dynamics and Seasonal Fluctuation in the Percentage infection of Trioza erytreae with ‘Candidatus’ Liberibacter Africanus, the African Citrus Greening Pathogen, in an Orchard Severely Infected with African Greening and Transmission by Field-Collected Trioza erytreae. Afr. Entomol. 2013, 22, 127–135. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).