Identifying Urban Neighborhood Names through User-Contributed Online Property Listings
Abstract
1. Introduction
- RQ1
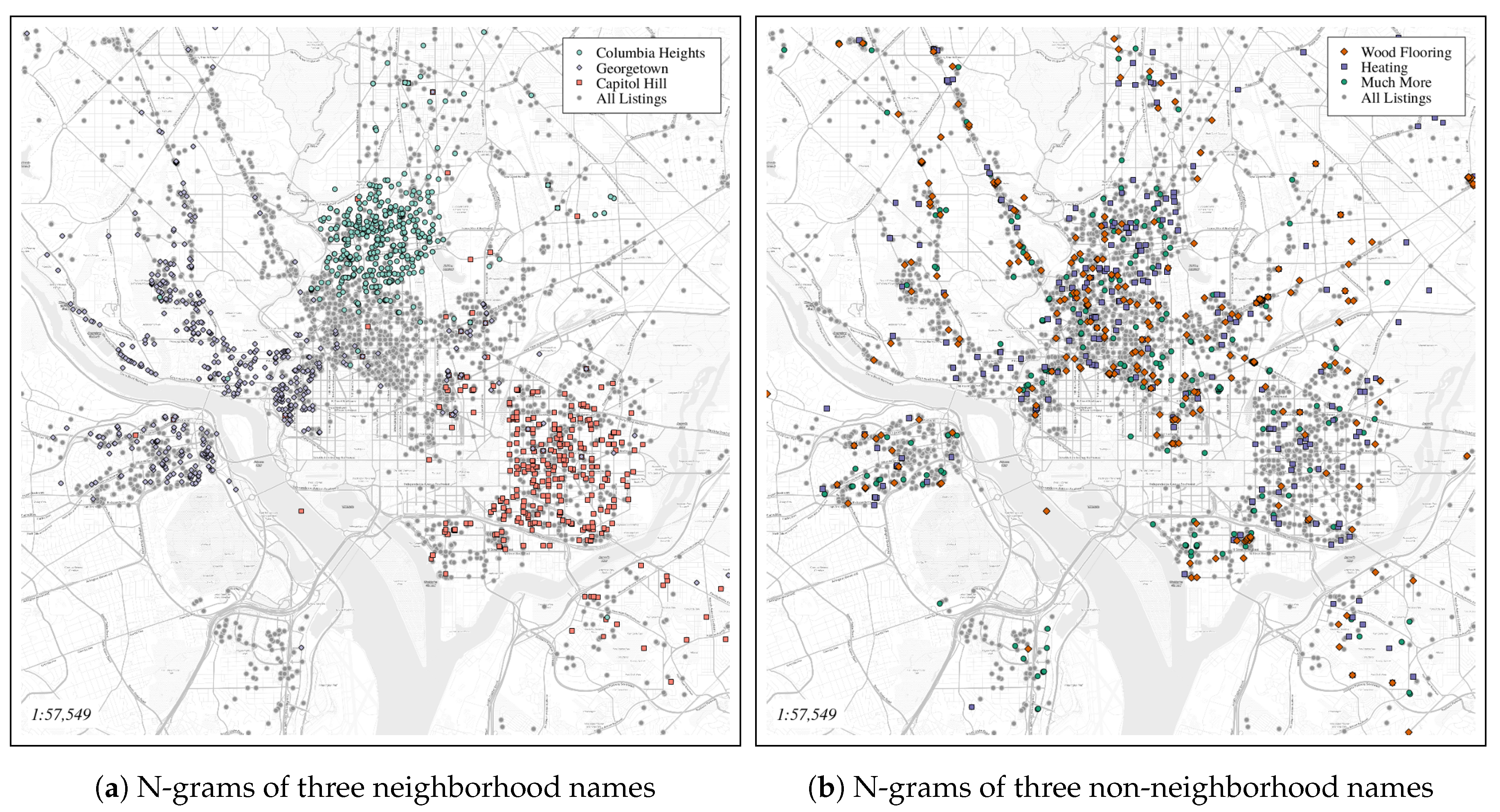
- Can neighborhood names be identified from natural language text within housing rental listings? Specifically, can spatially descriptive measures of geo-tagged n-grams be used to separate neighborhood names from other terms? A set of spatial statistical measures is calculated for all n-grams (An n-gram is a sequence of n items (often words) identified in text. For example ’kitchen’ is a uni-gram, ’small kitchen’ a bi-gram, etc.) in a set of listings and used to identify neighborhoods names.
- RQ2
- Does an ensemble learning approach based on spatial distribution measures more accurately identify neighborhood names than the spatial distribution measures alone? Given spatial statistics for each n-gram in a set of listings, we show that combining these in a random forest model produces higher accuracy than individual measures alone.
- RQ3
- Can an identification model trained on a known set of neighborhood names be used to identify uncommon neighborhood names or previously unidentified neighborhoods? Training a random forest model on spatial statistics of common neighborhood names within a city, we demonstrate that lesser known neighborhood names can be identified. In some cases, alternative names or other descriptive terms are proposed through the use of such a model.
- RQ4
- Can a neighborhood name identification model trained on data from one city be used to identify neighborhood names in a different city? A random forest model constructed from neighborhood names in Washington, DC, is used in the identification of neighborhood names in Seattle, WA, and Montréal, QC.
- RQ5
- What are the biases associated with neighborhood names mentioned in rental property listings? Lastly, we report on the spatial distribution biases associated with craigslist rental listings in Washington, DC.
2. Related Work
3. Data
3.1. Rental Property Listings
3.1.1. n-Grams
3.1.2. Geotagged n-Grams
3.2. Neighborhood Names and Boundaries
4. Methodology
4.1. Spatial Statistics
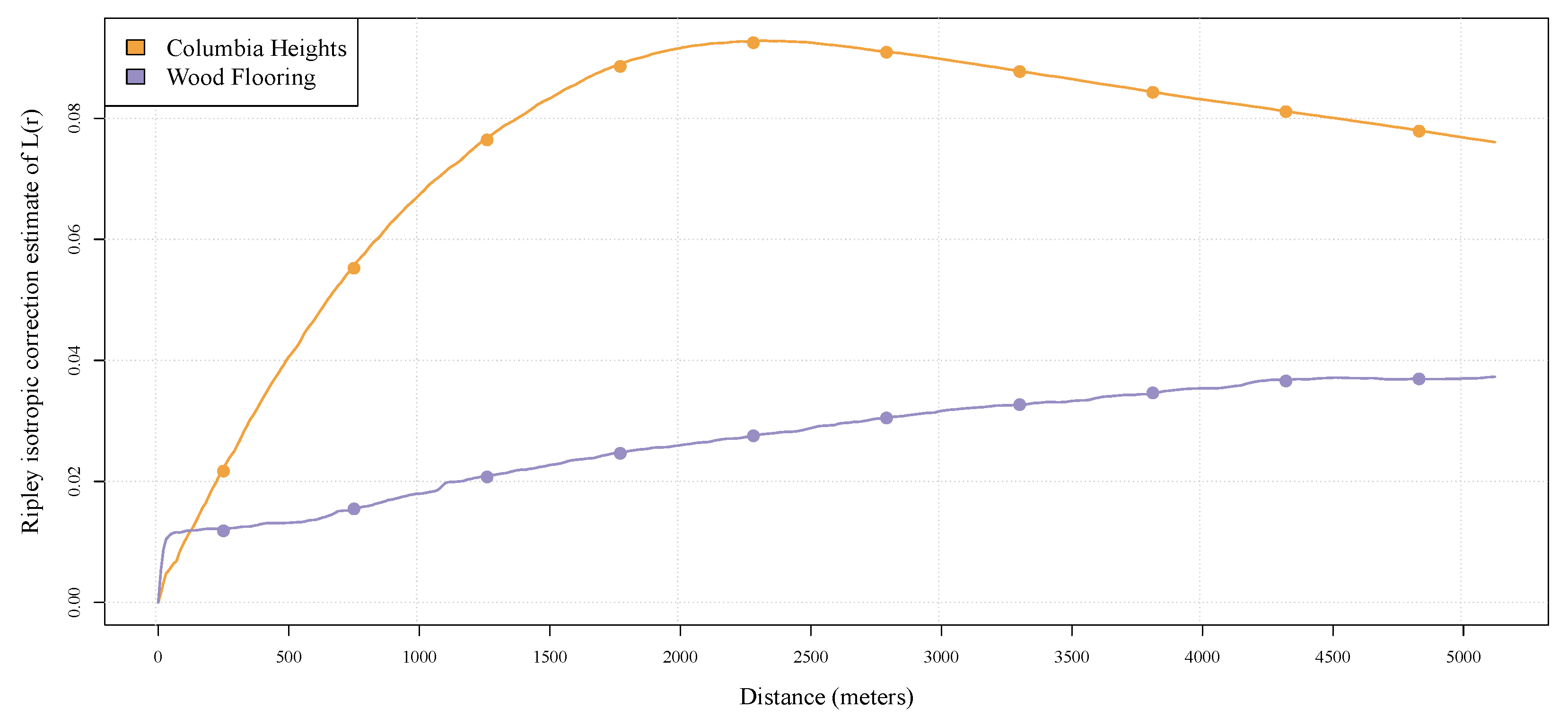
4.1.1. Spatial Dispersion
4.1.2. Spatial Homogeneity
4.1.3. Convex Hull
4.1.4. Spatial Autocorrelation
4.2. Data Setup
4.3. Individual Predictors
4.4. Random Forest Ensemble Learning
4.4.1. Training and Testing
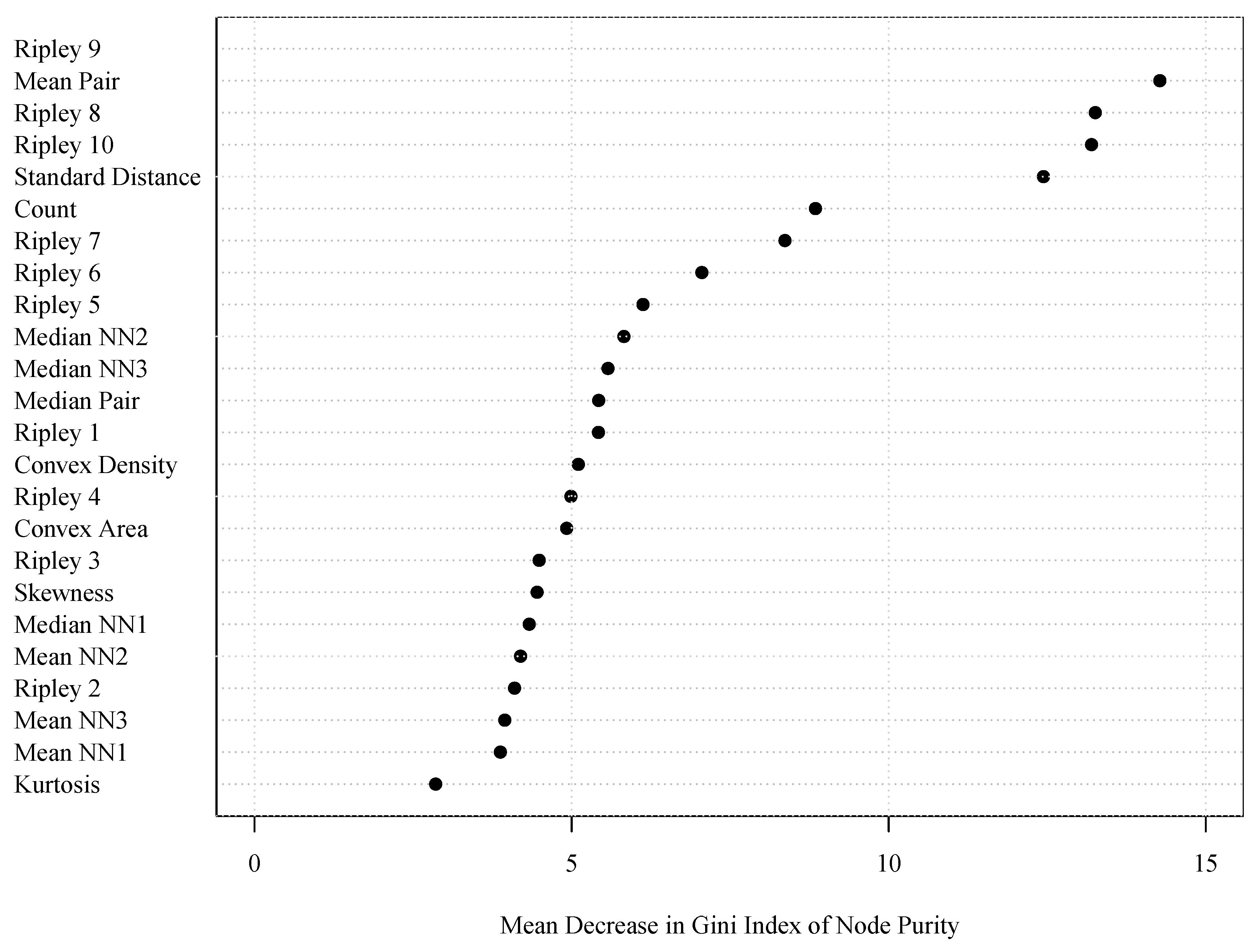
4.4.2. Variable Importance
4.5. Evaluation
5. Results
5.1. Individual Predictors
5.2. Ensemble Learning
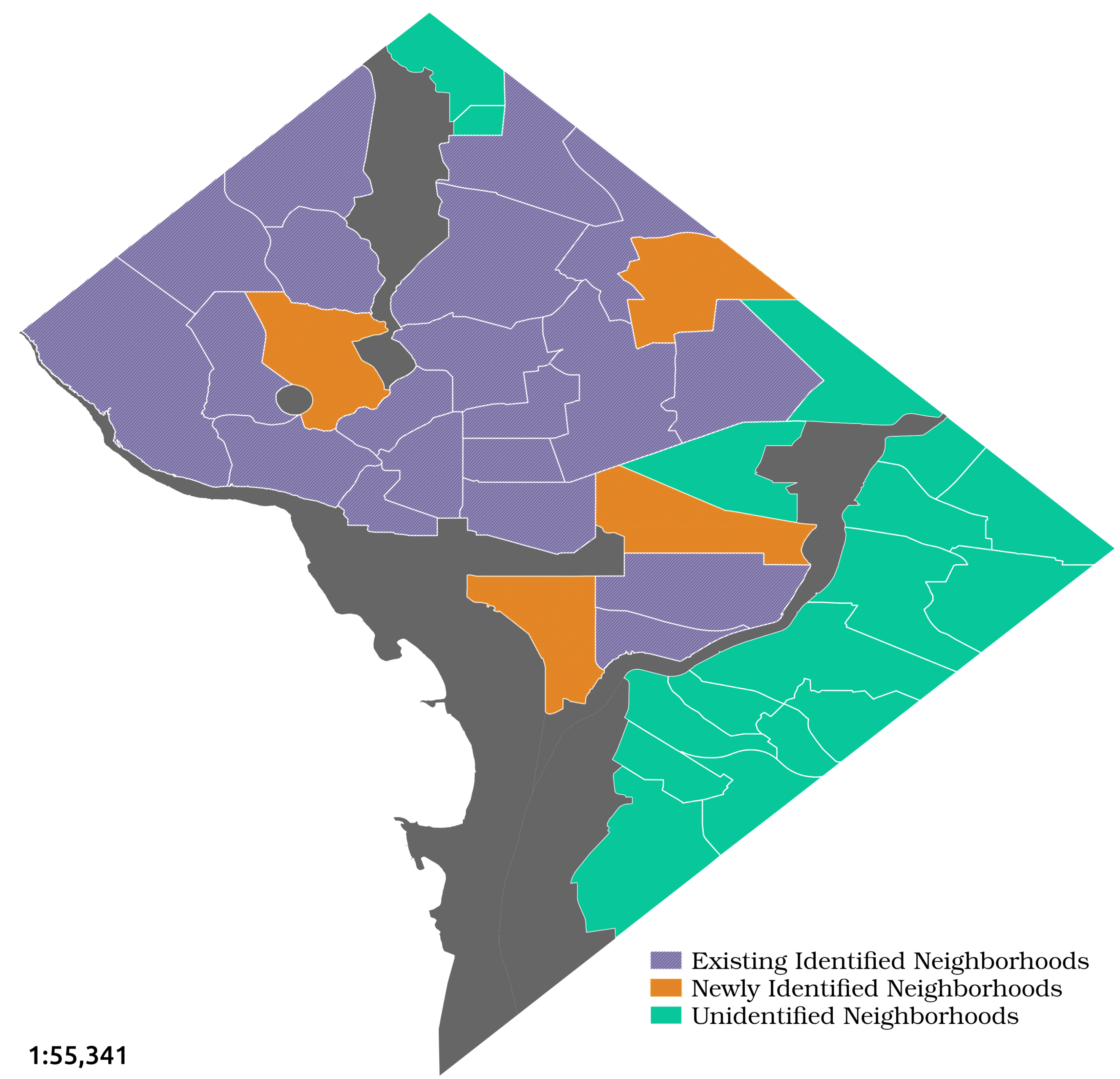
5.3. Identifying Neighborhoods in Other Cities
5.3.1. Predicting Seattle Neighborhoods
5.3.2. Predicting Montréal Neighborhoods
6. Discussion
6.1. False Positives
6.1.1. Washington, DC
6.1.2. Seattle, WA
6.1.3. Montréal, QC
6.2. Listing Regional Bias and False Negatives
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| N Match | SD | Count | Mean NN1 | Mean NN2 | Mean NN3 | Med. NN1 | Med. NN2 | Med. NN3 | Mean Pair | Med. Pair | Ripley 1 | Ripley 2 | Ripley 3 | Ripley 4 | Ripley 5 | Ripley 6 | Ripley 7 | Ripley 8 | Ripley 9 | Ripley 10 | Kurtosis | Skewness | Convex Area | Convex Density | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N Match | 1.000 | −0.363 | 0.029 * | −0.125 | −0.131 | −0.136 | −0.089 | −0.108 | −0.114 | −0.371 | −0.337 | 0.109 | 0.289 | 0.381 | 0.427 | 0.447 | 0.443 | 0.435 | 0.429 | 0.422 | 0.402 | 0.0212 *** | −0.121 | −0.201 | −0.001 *** |
| SD | −0.363 | 1.000 | −0.041 * | 0.179 | 0.201 | 0.210 | 0.137 | 0.213 | 0.237 | 0.981 | 0.932 | −0.166 | −0.362 | −0.505 | −0.611 | −0.683 | −0.738 | −0.774 | −0.802 | −0.823 | −0.844 | 0.056 | 0.017 *** | 0.419 | −0.309 |
| Count | 0.029 * | −0.041 * | 1.000 | −0.793 | −0.820 | −0.831 | −0.428 | −0.510 | −0.570 | 0.010 *** | −0.039 * | −0.296 | −0.219 | −0.139 | −0.086 | −0.047 | −0.010 *** | 0.022 *** | 0.044 | 0.053 | 0.065 | −0.174 | −0.029 * | 0.676 | 0.857 |
| Mean NN1 | −0.125 | 0.179 | −0.793 | 1.000 | 0.961 | 0.948 | 0.779 | 0.807 | 0.824 | 0.169 | 0.165 | −0.138 | −0.204 | −0.237 | −0.234 | −0.233 | −0.244 | −0.259 | −0.255 | −0.234 | −0.221 | −0.083 | 0.101 | −0.257 | −0.921 |
| Mean NN2 | −0.131 | 0.201 | −0.820 | 0.961 | 1.000 | 0.984 | 0.739 | 0.824 | 0.842 | 0.188 | 0.184 | −0.117 | −0.198 | −0.241 | −0.243 | −0.245 | −0.261 | −0.280 | −0.278 | −0.259 | −0.246 | −0.095 | 0.126 | −0.276 | −0.943 |
| Mean NN3 | −0.136 | 0.210 | −0.831 | 0.948 | 0.984 | 1.000 | 0.732 | 0.813 | 0.852 | 0.194 | 0.186 | −0.104 | −0.186 | −0.234 | −0.240 | −0.245 | −0.263 | −0.281 | −0.280 | −0.263 | −0.252 | −0.081 | 0.123 | −0.291 | −0.944 |
| Med. NN1 | −0.089 | 0.137 | −0.428 | 0.779 | 0.739 | 0.732 | 1.000 | 0.906 | 0.871 | 0.178 | 0.126 | −0.533 | −0.539 | −0.495 | −0.417 | −0.360 | −0.337 | −0.321 | −0.292 | −0.249 | −0.218 | −0.335 | 0.143 | 0.011 *** | −0.607 |
| Med. NN2 | −0.108 | 0.213 | −0.510 | 0.807 | 0.824 | 0.813 | 0.906 | 1.000 | 0.964 | 0.254 | 0.209 | −0.446 | −0.505 | −0.505 | −0.456 | −0.417 | −0.401 | −0.393 | −0.366 | −0.323 | −0.295 | −0.317 | 0.171 | −0.021 *** | −0.703 |
| Med. NN3 | −0.114 | 0.237 | −0.570 | 0.824 | 0.842 | 0.852 | 0.871 | 0.964 | 1.000 | 0.273 | 0.235 | −0.369 | −0.445 | −0.468 | −0.437 | −0.412 | −0.406 | −0.404 | −0.382 | −0.342 | −0.316 | −0.262 | 0.162 | −0.077 | −0.742 |
| Mean Pair | −0.371 | 0.981 | 0.010 *** | 0.169 | 0.188 | 0.194 | 0.178 | 0.254 | 0.273 | 1.000 | 0.955 | −0.242 | −0.445 | −0.591 | −0.694 | −0.762 | −0.810 | −0.838 | −0.857 | −0.870 | −0.881 | −0.001 | 0.047 | 0.465 | −0.276 |
| Med. Pair | −0.337 | 0.932 | −0.039 * | 0.165 | 0.184 | 0.186 | 0.126 | 0.209 | 0.235 | 0.955 | 1.000 | −0.147 | −0.352 | −0.510 | −0.627 | −0.710 | −0.768 | −0.811 | −0.847 | −0.877 | −0.903 | 0.072 *** | 0.004 *** | 0.364 | −0.285 |
| Ripley 1 | 0.109 | −0.166 | −0.296 | −0.138 | −0.117 | −0.104 | −0.533 | −0.446 | −0.369 | −0.242 | −0.147 | 1.000 | 0.906 | 0.749 | 0.589 | 0.478 | 0.414 | 0.370 | 0.319 | 0.268 | 0.230 | 0.578 | −0.189 | −0.555 | −0.042 * |
| Ripley 2 | 0.289 | −0.362 | −0.219 | −0.204 | −0.198 | −0.186 | −0.539 | −0.505 | −0.445 | −0.445 | −0.352 | 0.906 | 1.000 | 0.930 | 0.808 | 0.708 | 0.641 | 0.588 | 0.532 | 0.479 | 0.440 | 0.639 | −0.337 | −0.581 | 0.071 |
| Ripley 3 | 0.381 | −0.505 | −0.139 | −0.237 | −0.241 | −0.234 | −0.495 | −0.505 | −0.468 | −0.591 | −0.510 | 0.749 | 0.930 | 1.000 | 0.948 | 0.875 | 0.809 | 0.754 | 0.698 | 0.646 | 0.607 | 0.569 | −0.393 | −0.544 | 0.156 |
| Ripley 4 | 0.427 | −0.611 | −0.086 | −0.234 | −0.243 | −0.240 | −0.417 | −0.456 | −0.437 | −0.694 | −0.627 | 0.589 | 0.808 | 0.948 | 1.000 | 0.969 | 0.916 | 0.862 | 0.812 | 0.767 | 0.731 | 0.429 | −0.371 | −0.503 | 0.204 |
| Ripley 5 | 0.447 | −0.683 | −0.047 | −0.233 | −0.245 | −0.245 | −0.360 | −0.417 | −0.412 | −0.762 | −0.710 | 0.478 | 0.708 | 0.875 | 0.969 | 1.000 | 0.974 | 0.930 | 0.888 | 0.850 | 0.817 | 0.298 | −0.310 | −0.469 | 0.238 |
| Ripley 6 | 0.443 | −0.738 | −0.010 *** | −0.244 | −0.261 | −0.263 | −0.337 | −0.401 | −0.406 | −0.810 | −0.768 | 0.414 | 0.641 | 0.809 | 0.916 | 0.974 | 1.000 | 0.979 | 0.946 | 0.912 | 0.878 | 0.192 | −0.236 | −0.445 | 0.271 |
| Ripley 7 | 0.435 | −0.774 | 0.022 *** | −0.259 | −0.280 | −0.281 | −0.321 | −0.393 | −0.404 | −0.838 | −0.811 | 0.370 | 0.588 | 0.754 | 0.862 | 0.930 | 0.979 | 1.000 | 0.984 | 0.954 | 0.920 | 0.112 | −0.160 | −0.425 | 0.300 |
| Ripley 8 | 0.429 | −0.802 | 0.044 | −0.255 | −0.278 | −0.280 | −0.292 | −0.366 | −0.382 | −0.857 | −0.847 | 0.319 | 0.532 | 0.698 | 0.812 | 0.888 | 0.946 | 0.984 | 1.000 | 0.986 | 0.957 | 0.039 * | −0.090 | −0.401 | 0.314 |
| Ripley 9 | 0.422 | −0.823 | 0.053 | −0.234 | −0.259 | −0.263 | −0.249 | −0.323 | −0.342 | −0.870 | −0.877 | 0.268 | 0.479 | 0.646 | 0.767 | 0.850 | 0.912 | 0.954 | 0.986 | 1.000 | 0.986 | −0.012 *** | −0.050 | −0.380 | 0.312 |
| Ripley 10 | 0.402 | −0.844 | 0.065 | −0.221 | −0.246 | −0.252 | −0.218 | −0.295 | −0.316 | −0.881 | −0.903 | 0.230 | 0.440 | 0.607 | 0.731 | 0.817 | 0.878 | 0.920 | 0.957 | 0.986 | 1.000 | −0.037 * | −0.035 * | −0.360 | 0.312 |
| Kurtosis | 0.0212 *** | 0.056 | −0.174 | −0.083 | −0.095 | −0.081 | −0.335 | −0.317 | −0.262 | −0.001 *** | 0.072 | 0.578 | 0.639 | 0.569 | 0.429 | 0.298 | 0.192 | 0.112 | 0.039 * | −0.012 *** | −0.037 * | 1.000 | −0.764 | −0.277 | −0.042 * |
| Skewness | −0.121 | 0.017 *** | −0.029* | 0.101 | 0.126 | 0.123 | 0.143 | 0.171 | 0.162 | 0.047 | 0.004 *** | −0.189 | −0.337 | −0.393 | −0.371 | −0.310 | −0.236 | −0.160 | −0.090 | −0.050 | −0.035 * | −0.764 | 1.000 | 0.060 | −0.077 |
| Convex Area | −0.201 | 0.419 | 0.676 | −0.257 | −0.276 | −0.291 | 0.011 *** | −0.021 *** | −0.077 | 0.465 | 0.364 | −0.555 | −0.581 | −0.544 | −0.503 | −0.469 | −0.445 | −0.425 | −0.401 | −0.380 | −0.360 | −0.277 | 0.060 | 1.000 | 0.294 |
| Convex Density | −0.001 *** | −0.309 | 0.857 | −0.921 | −0.943 | −0.944 | −0.607 | −0.703 | −0.742 | −0.276 | −0.285 | −0.042 * | 0.071 | 0.156 | 0.204 | 0.238 | 0.271 | 0.300 | 0.314 | 0.312 | 0.312 | −0.042 * | −0.077 | 0.294 | 1.000 |
Appendix B
References
- Riesz, M. Borders Disputed! Brooklynites Take Issue with Google’s Neighborhood Maps. 2014. Available online: https://www.brooklynpaper.com/stories/37/18/all-google-maps-neighborhoods-2014-04-25-bk_37_18.html (accessed on 1 July 2018).
- Folven, E. Residents Voice Anger of Redistricting Maps. 2012. Available online: http://beverlypress.com/2012/02/residents-voice-anger-of-redistricting-maps/ (accessed on 1 July 2018).
- Usborne, S. Disputed Territories: Where Google Maps Draws the Line. 2018. Available online: https://www.theguardian.com/technology/shortcuts/2016/aug/10/google-maps-disputed-territories-palestineishere (accessed on 1 July 2018).
- Sutter, J. Google Maps Border Becomes Part of International Dispute. 2010. Available online: http://edition.cnn.com/2010/TECH/web/11/05/nicaragua.raid.google.maps/index.html (accessed on 1 July 2018).
- Nicas, J. As Google Maps Renames Neighborhoods, Residents Fume. 2018. Available online: https://www.nytimes.com/2018/08/02/technology/google-maps-neighborhood-names.html (accessed on 1 July 2018).
- Taylor, R.B.; Gottfredson, S.D.; Brower, S. Neighborhood naming as an index of attachment to place. Popul. Environ. 1984, 7, 103–125. [Google Scholar] [CrossRef]
- Mitrany, M.; Mazumdar, S. Neighborhood design and religion: Modern Orthodox Jews. J. Archit. Plan. Res. 2009, 26, 44–69. [Google Scholar]
- Knopp, L. Gentrification and gay neighborhood formation in New Orleans. In Homo Economics: Capitalism, Community, and Lesbian and Gay Life; Psychology Press: Hove, UK, 1997; pp. 45–59. [Google Scholar]
- Alderman, D.H. A street fit for a King: Naming places and commemoration in the American South. Prof. Geogr. 2000, 52, 672–684. [Google Scholar] [CrossRef]
- Hernandez, J. Redlining revisited: Mortgage lending patterns in Sacramento 1930–2004. Int. J. Urban Reg. Res. 2009, 33, 291–313. [Google Scholar] [CrossRef]
- Northcraft, G.B.; Neale, M.A. Experts, amateurs, and real estate: An anchoring-and-adjustment perspective on property pricing decisions. Organ. Behav. Hum. Decis. Process. 1987, 39, 84–97. [Google Scholar] [CrossRef]
- Altschuler, A.; Somkin, C.P.; Adler, N.E. Local services and amenities, neighborhood social capital, and health. Soc. Sci. Med. 2004, 59, 1219–1229. [Google Scholar] [CrossRef] [PubMed]
- Calem, P.S.; Gillen, K.; Wachter, S. The neighborhood distribution of subprime mortgage lending. J. Real Estate Financ. Econ. 2004, 29, 393–410. [Google Scholar] [CrossRef]
- Romero, M. How Real Estate Websites Define Fishtown’s Boundaries. 2016. Available online: https://philly.curbed.com/2016/10/31/13458206/fishtown-neighborhood-boundaries-map (accessed on 2 June 2018).
- Grether, D.M.; Mieszkowski, P. Determinants of real estate values. J. Urban Econ. 1974, 1, 127–145. [Google Scholar] [CrossRef]
- Mumford, L. The neighborhood and the neighborhood unit. Town Plan. Rev. 1954, 24, 256–270. [Google Scholar] [CrossRef]
- Talen, E. Constructing neighborhoods from the bottom up: The case for resident-generated GIS. Environ. Plan. B Plan. Des. 1999, 26, 533–554. [Google Scholar] [CrossRef]
- Sieber, R. Public participation geographic information systems: A literature review and framework. Ann. Assoc. Am. Geogr. 2006, 96, 491–507. [Google Scholar] [CrossRef]
- United States Department of Housing and Urban Development; Office of Policy Development and Research. The Behavioral Foundations of Neighborhood Change; University of Michigan Library: Ann Arbor, MI, USA, 1979.
- Keller, S.I. The Urban Neighborhood: A Sociological Perspective; Random House: New York, NY, USA, 1968; Volume 33. [Google Scholar]
- Hoyt, H. The Structure and Growth of Residential Neighborhoods in American Cities; Washington, U.S. Govt.: Washington, DC, USA, 1939.
- Coulton, C.J.; Korbin, J.; Chan, T.; Su, M. Mapping residents’ perceptions of neighborhood boundaries: A methodological note. Am. J. Community Psychol. 2001, 29, 371–383. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.A.; Reardon, S.F.; Firebaugh, G.; Farrell, C.R.; Matthews, S.A.; O’Sullivan, D. Beyond the census tract: Patterns and determinants of racial segregation at multiple geographic scales. Am. Sociol. Rev. 2008, 73, 766–791. [Google Scholar] [CrossRef] [PubMed]
- Sampson, R.J.; Morenoff, J.D.; Gannon-Rowley, T. Assessing “neighborhood effects”: Social processes and new directions in research. Ann. Rev. Sociol. 2002, 28, 443–478. [Google Scholar] [CrossRef]
- Schockaert, S.; De Cock, M. Neighborhood restrictions in geographic IR. In Proceedings of the 30th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Amsterdam, The Netherlands, 23–27 July 2007; pp. 167–174. [Google Scholar]
- Hollenstein, L.; Purves, R. Exploring place through user-generated content: Using Flickr tags to describe city cores. J. Spat. Inf. Sci. 2010, 2010, 21–48. [Google Scholar]
- Hu, Y.; Gao, S.; Janowicz, K.; Yu, B.; Li, W.; Prasad, S. Extracting and understanding urban areas of interest using geotagged photos. Comput. Environ. Urban Syst. 2015, 54, 240–254. [Google Scholar] [CrossRef]
- Gao, S.; Janowicz, K.; Montello, D.R.; Hu, Y.; Yang, J.A.; McKenzie, G.; Ju, Y.; Gong, L.; Adams, B.; Yan, B. A data-synthesis-driven method for detecting and extracting vague cognitive regions. Int. J. Geogr. Inf. Sci. 2017, 31, 1245–1271. [Google Scholar] [CrossRef]
- Gao, S.; Janowicz, K.; Couclelis, H. Extracting urban functional regions from points of interest and human activities on location-based social networks. Trans. GIS 2017, 21, 446–467. [Google Scholar] [CrossRef]
- McKenzie, G.; Adams, B. Juxtaposing Thematic Regions Derived from Spatial and Platial User-Generated Content. In Leibniz International Proceedings in Informatics (LIPIcs), Proceedings of the 13th International Conference on Spatial Information Theory (COSIT 2017), L’Aquila, Italy, 4–8 September 2017; Clementini, E., Donnelly, M., Yuan, M., Kray, C., Fogliaroni, P., Ballatore, A., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2017; Volume 86, pp. 1–14. [Google Scholar]
- Cranshaw, J.; Schwartz, R.; Hong, J.I.; Sadeh, N. The Livehoods Project: Utilizing Social Media to Understand the Dynamics of a City. In Proceedings of the Sixth International AAAI Conference on Weblogs and Social Media, Dublin, Ireland, 4–7 June 2012. [Google Scholar]
- Wahl, B.; Wilde, E. Mapping the World...One Neighborhood at a Time. Directions Magazine, 4 December 2008. [Google Scholar]
- McKenzie, G.; Hu, Y. The “Nearby” Exaggeration in Real Estate. In Proceedings of the Cognitive Scales of Spatial Information Workshop (CoSSI 2017), L’Aquila, Italy, 4–8 September 2017. [Google Scholar]
- Chisholm, M.; Cohen, R. The Neighborhood Project. 2005. Available online: https://hood.theory.org/ (accessed on 2 June 2018).
- Hu, Y.; Mao, H.; McKenzie, G. A natural language processing and geospatial clustering framework for harvesting local place names from geotagged housing advertisements. Int. J. Geogr. Inf. Sci. 2018. [Google Scholar] [CrossRef]
- Zhu, R.; Hu, Y.; Janowicz, K.; McKenzie, G. Spatial signatures for geographic feature types: Examining gazetteer ontologies using spatial statistics. Trans. GIS 2016, 20, 333–355. [Google Scholar] [CrossRef]
- Zhu, R.; Janowicz, K.; Yan, B.; Hu, Y. Which kobani? a case study on the role of spatial statistics and semantics for coreference resolution across gazetteers. In Proceedings of the International Conference on Geographic Information Science, Montreal, QC, Canada, 27–30 September 2016. [Google Scholar]
- Brindley, P.; Goulding, J.; Wilson, M.L. A data driven approach to mapping urban neighbourhoods. In Proceedings of the 22nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Fort Worth, TX, USA, 4–7 November 2014; pp. 437–440. [Google Scholar]
- Brindley, P.; Goulding, J.; Wilson, M.L. Generating vague neighbourhoods through data mining of passive web data. Int. J. Geogr. Inf. Sci. 2018, 32, 498–523. [Google Scholar] [CrossRef]
- Jones, C.B.; Purves, R.S.; Clough, P.D.; Joho, H. Modelling vague places with knowledge from the Web. Int. J. Geogr. Inf. Sci. 2008, 22, 1045–1065. [Google Scholar] [CrossRef]
- Derungs, C.; Purves, R.S. Mining nearness relations from an n-grams web corpus in geographical space. Spat. Cogn. Comput. 2016, 16, 301–322. [Google Scholar] [CrossRef]
- Vasardani, M.; Winter, S.; Richter, K.F. Locating place names from place descriptions. Int. J. Geogr. Inf. Sci. 2013, 27, 2509–2532. [Google Scholar] [CrossRef]
- Buscaldi, D.; Rosso, P. A conceptual density-based approach for the disambiguation of toponyms. Int. J. Geogr. Inf. Sci. 2008, 22, 301–313. [Google Scholar] [CrossRef]
- Gelernter, J.; Mushegian, N. Geo-parsing messages from microtext. Trans. GIS 2011, 15, 753–773. [Google Scholar] [CrossRef]
- Inkpen, D.; Liu, J.; Farzindar, A.; Kazemi, F.; Ghazi, D. Location detection and disambiguation from Twitter messages. J. Intell. Inf. Syst. 2017, 49, 237–253. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Kang, C.; Gao, Y.; Lu, Y. Analyzing Relatedness by Toponym Co-O ccurrences on Web Pages. Trans. GIS 2014, 18, 89–107. [Google Scholar] [CrossRef]
- Santos, J.; Anastácio, I.; Martins, B. Using machine learning methods for disambiguating place references in textual documents. GeoJournal 2015, 80, 375–392. [Google Scholar] [CrossRef]
- Melo, F.; Martins, B. Automated geocoding of textual documents: A survey of current approaches. Trans. GIS 2017, 21, 3–38. [Google Scholar] [CrossRef]
- Bird, S.; Klein, E.; Loper, E. Natural Language Processing with Python: Analyzing Text with the Natural Language Toolkit; O’Reilly Media, Inc.: Newton, MA, USA, 2009. [Google Scholar]
- Baddeley, A.; Rubak, E.; Turner, R. Spatial Point Patterns: Methodology and Applications with R; Chapman and Hall/CRC Press: London, UK, 2015. [Google Scholar]
- Ripley, B.D. The second-order analysis of stationary point processes. J. Appl. Probab. 1976, 13, 255–266. [Google Scholar] [CrossRef]
- Besag, J.E. Comment on ‘Modelling spatial patterns’ by BD Ripley. JR Stat. Soc. B 1977, 39, 193–195. [Google Scholar]
- McKenzie, G.; Janowicz, K.; Gao, S.; Yang, J.A.; Hu, Y. POI pulse: A multi-granular, semantic signature–based information observatory for the interactive visualization of big geosocial data. Cartographica 2015, 50, 71–85. [Google Scholar] [CrossRef]
- Graham, R.L. An efficient algorithm for determining the convex hull of a finite planar set. Inf. Process. Lett. 1972, 1, 132–133. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chesnokova, O.; Nowak, M.; Purves, R.S. A crowdsourced model of landscape preference. In LIPIcs-Leibniz International Proceedings in Informatics; Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik: Wadern, Germany, 2017; Volume 86. [Google Scholar]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manag. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Hayes, M.M.; Miller, S.N.; Murphy, M.A. High-resolution landcover classification using Random Forest. Remote Sens. Lett. 2014, 5, 112–121. [Google Scholar] [CrossRef]
- George-Cosh, D. July 1 Is Day for Mass, Messy Moves in Montreal. 2013. Available online: https://www.wsj.com/articles/SB10001424127887323300004578559722182821246 (accessed on 2 June 2018).
- Boeing, G.; Waddell, P. New insights into rental housing markets across the united states: web scraping and analyzing craigslist rental listings. J. Plan. Educ. Res. 2017, 37, 457–476. [Google Scholar] [CrossRef]

| City | Listings | Unique Locations | Unique n-Grams | Cleaned n-Grams |
|---|---|---|---|---|
| Washington, DC | 60,167 | 13,307 | 1,294,747 | 3612 |
| Seattle, WA | 68,058 | 17,795 | 1,053,297 | 5554 |
| Montréal, QC | 10,425 | 4836 | 571,223 | 2914 |
| Source | Washington, DC | Seattle, WA | Montréal, QC |
|---|---|---|---|
| Wikipedia | 129 | 134 | 73 |
| Zillow | 137 | 115 | N/A |
| Zetashapes/Who’s On First | 182 | 124 | N/A |
| City Government/AirBnB | 46 * | 106 | 23 |
| Common Neighborhoods | 95 | 79 | 23 |
| Measure | Max F-Score |
|---|---|
| Standard Distance | 0.047 |
| Count | 0.083 |
| Mean NN1 | 0.047 |
| Mean NN2 | 0.047 |
| Mean NN3 | 0.047 |
| Med.NN1 | 0.050 |
| Med. NN2 | 0.050 |
| Med. NN3 | 0.050 |
| Mean Pair | 0.047 |
| Med. Pair | 0.047 |
| Ripley 1 | 0.099 |
| Ripley 2 | 0.279 |
| Ripley 3 | 0.405 |
| Ripley 4 | 0.500 |
| Ripley 5 | 0.548 |
| Ripley 6 | 0.570 |
| Ripley 7 | 0.587 |
| Ripley 8 | 0.624 |
| Ripley 9 | 0.633 |
| Ripley 10 | 0.624 |
| Kurtosis | 0.101 |
| Skewness | 0.047 |
| Convex Area | 0.047 |
| Convex Density | 0.144 |
| Model | F-Score | Precision | Recall |
|---|---|---|---|
| Common matched neighborhoods | 0.807 | 0.845 | 0.777 |
| Common + secondary matches | 0.872 | 0.863 | 0.882 |
| Randomly assigned matches | 0.047 | 0.063 | 0.037 |
| Model | F-Score | Precision | Recall |
|---|---|---|---|
| Common matched neighborhoods | 0.671 | 0.625 | 0.724 |
| Common + secondary matches | 0.733 | 0.702 | 0.767 |
| Trained on Seattle (common) | 0.786 | 0.782 | 0.791 |
| Model | F-Score | Precision | Recall |
|---|---|---|---|
| Common matched neighborhoods | 0.397 | 0.353 | 0.453 |
| Common + secondary matches | 0.483 | 0.412 | 0.583 |
| Trained on Montréal (common) | 0.655 | 0.559 | 0.792 |
| Category | Washington, DC | Seattle, WA | Montréal, QC |
|---|---|---|---|
| Landmarks | Capitol Building | Space Needle | Place Jacques-Cartier |
| Academic Institution | Catholic University | University of Washington | McGill University |
| Streets | Wisconsin Ave. | Summit Ave. | Cavendish Blvd. |
| Broader Regions | National Mall | Waterfront | Saint-Laurent River |
| Transit Stations | Union Train Station | King Street Station | Jolicoeur Station |
| Companies | Yes, Organic | Amazon | Atwater Market |
| Misc. | blvd | concierge | du vieux |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McKenzie, G.; Liu, Z.; Hu, Y.; Lee, M. Identifying Urban Neighborhood Names through User-Contributed Online Property Listings. ISPRS Int. J. Geo-Inf. 2018, 7, 388. https://doi.org/10.3390/ijgi7100388
McKenzie G, Liu Z, Hu Y, Lee M. Identifying Urban Neighborhood Names through User-Contributed Online Property Listings. ISPRS International Journal of Geo-Information. 2018; 7(10):388. https://doi.org/10.3390/ijgi7100388
Chicago/Turabian StyleMcKenzie, Grant, Zheng Liu, Yingjie Hu, and Myeong Lee. 2018. "Identifying Urban Neighborhood Names through User-Contributed Online Property Listings" ISPRS International Journal of Geo-Information 7, no. 10: 388. https://doi.org/10.3390/ijgi7100388
APA StyleMcKenzie, G., Liu, Z., Hu, Y., & Lee, M. (2018). Identifying Urban Neighborhood Names through User-Contributed Online Property Listings. ISPRS International Journal of Geo-Information, 7(10), 388. https://doi.org/10.3390/ijgi7100388





