Study of a Gray Genetic BP Neural Network Model in Fault Monitoring and a Diagnosis System for Dam Safety

Abstract

In this paper, a self-diagnosis system of observer fault with linear and non-linear combination is studied in light of the unstable performance of the automatic monitoring system and the drift of the measured value. The system makes a prediction step ahead of time, compares it with the online measured value, and makes a logical judgment based on the residual error to achieve the purpose of real-time diagnosis of the automatic monitoring system. We developed a novel combined algorithm for dam deformation prediction using two traditional models and one optimization model. The developed algorithm combines two sub-algorithms: the gray model (GM) (1, 1) and the back-propagation neural network (BPNN) model. The GM (1, 1) addresses the effects of the automated monitoring of data from unstable situations; the BPNN model addresses the internal non-linear regularity of the dam displacement. The connection weights and thresholds of the BPNN model can be optimized and determined via the genetic algorithm (GA), which can decrease the uncertainties within the model predictions and improve the prediction accuracy. The results show that the fault self-diagnosis system based on the GM-GA-BP combined model can realize online fault diagnosis better than the traditional single models.

1. Introduction

With the rapid development of science and technology, dam safety automation monitoring has undergone a qualitative leap [1,2,3,4]. While dam safety automatic monitoring has been vigorously promoted, this also necessitates new requirements for monitoring the stability and reliability of the automation system. In the actual project, the performance of the automated monitoring system is unstable, and there is the problem of drift of the measured value, which affects the stability and reliability of the monitoring data. To obtain timely feedback, address the safety performance of dam safety monitoring, and ensure that the monitoring system works properly, an observer fault self-diagnosis system combined with a non-linear model is evaluated in this work. The system is composed of two parts: residual generation and residual judgment. The self-diagnosis system works in parallel with the actual monitoring system. When the monitoring system is fault-free, the residual value between the two is relatively small, and its amplitude is close to zero. When the system deviates from normal operation or fails, the residuals deviate from zero and exhibit a large residual error. If the corresponding residual value of the predicted value and the online measured value exceeds the threshold, the system will activate an alarm to realize the real-time diagnosis of the performance of the automated monitoring system. However, dam deformation is influenced primarily by the water level and temperature, it has a complex non-linearity, and automated monitoring data are not stable. These factors are unstable and challenging to analyze, hindering the accurate prediction of dam deformation. For this reason, over the past several decades, many researchers have focused on addressing these challenges, and several studies of dam deformation have been published based on cases worldwide [5,6,7,8]. Many methods have been proposed for forecasting dam deformation, including the use of statistical regression models, deterministic models, and hybrid models.

Statistical regression models [9,10,11,12,13,14,15,16] have been proposed to quantitatively process dam deformation data [9]. For example, researchers have used improved models employing the average temperature to analyze the Castelo Arch Dam [10]. Rocha used a power polynomial of the reservoir water level to formulate a hydrostatic pressure factor [9]. Statistical regression models based on the finite-element method have been widely used to predict dam deformation [11]. Deterministic models [17,18,19,20,21,22,23], on the other hand, can be used to analyze the dam time observation sequence [12]. Many researchers have used multiple linear regression approaches analyzing the relationship between the environmental quantity and effect size [13]. For the hybrid models [24,25,26,27], a combination of deterministic models and purely statistical (regression) models can be used to analyze dam displacements. According to the system identification viewpoint, deterministic relational models belong to the positive problem research category of system identification, and the current deterministic models often use single models. To ensure a good fit and forecast, two elements must be considered: the program set (the choice of modeling method) and the environmental set (the learning of historical experience). From the viewpoint of information theory, each type of fitting and forecasting method has a unique information characteristic, which is the exploration of objects inside. If multiple different models are used for the same positive problem of system identification and are effectively integrated, various types of information can be fully utilized, and the accuracy of the prediction can be improved. In recent years, because the back-propagation neural network (BPNN) has a strong self-learning ability and adaptive ability and can approach any non-linear system, it is widely used in various simulations and prediction fields as an excellent non-linear tool. However, the BPNN is intrinsically limited by slow convergence rates and local minima and has limited generalization capabilities. In addition, the design and structure optimization performed for the BPNN generally relies on a time-consuming iterative trial-and-error approach [28,29,30,31,32,33,34]. To solve these problems, many researchers have used the model combination method to improve and optimize the neural network (NN). The combination models can offer better and more robust performance than that of single conventional NNs. More specifically, using fuzzy math theory to quantify and aggregate influential factors, it is possible for an NN to achieve improved prediction accuracy. This combined model is termed a “fuzzy neural network” [35,36,37,38,39,40,41,42,43]. In addition, a chaotic NN was proposed to investigate non-linear features and uses chaos mapping and wavelet transformation. The low correlation of wavelet neurons makes the NN have a faster convergence rate and, to a certain extent, whitens the “black box” method of the NN model. Wavelet neurons have better localized characteristics and a higher learning resolution, making the NN have a stronger adaptive ability and higher prediction accuracy [44]. When using the particle swarm optimization algorithm or the genetic algorithm (GA), a global search for the optimal solution can be performed to optimize the network architecture and the connection weights of the BPNN [45,46,47,48,49,50,51,52,53,54]. Zemin Fu combined GA-BPNN prediction and finite-element model simulation to improve the process of the multiple-step incremental air-bending forming of sheet metal [49]. Fei Yin proposed the use of GA-BP to optimize the parameters of the injection molding process [50]. Furthermore, Guangying Chen suggested that a GA-based BPNN is a promising approach for anticipating MMP (minimum miscibility pressure) in the CO₂-EOR (enhanced oil recovery) process [51].

This paper first addresses the performance instability of the dam monitoring automation system and the problem of measured value drift. The gray model (GM) is used to optimize the dataset and solve the problem of instability of the monitoring data of the automated monitoring system, in addition to increasing the smoothness and stability of the monitoring data. At the same time, due to the complex non-linear characteristics of dam deformation, the water level and temperature of the dam area are adopted to correct the residual values of the GM (1, 1). In this paper, the GA-BP model is adopted to establish the relationship between the influencing factors and the gray residual values. Next, the new residuals can be predicted by the GA-BP model. Finally, the dam displacement prediction is obtained by subtracting the new residuals from the prediction of GM (1, 1). The details are as follows:

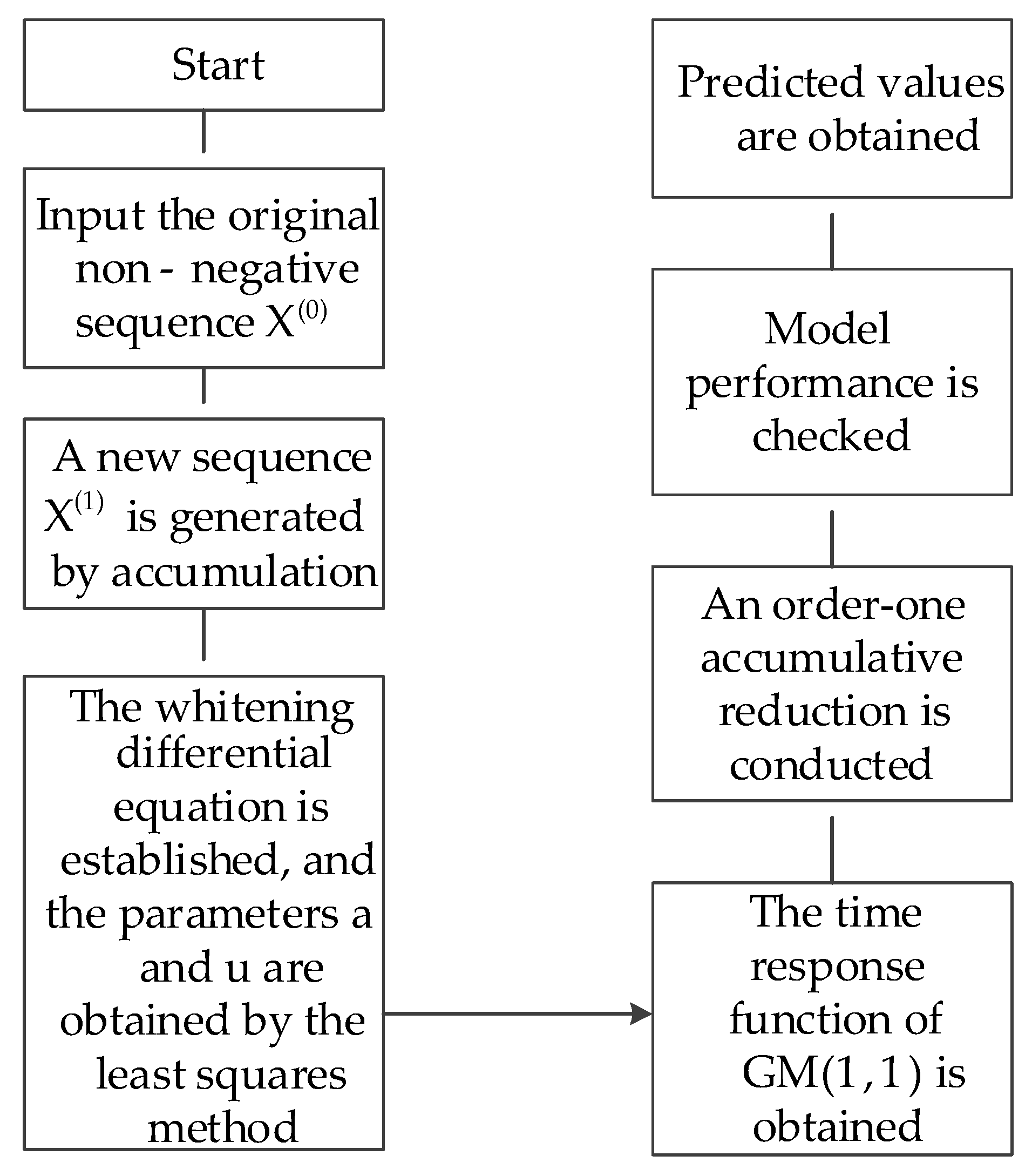
(1)

The GM (1, 1) was used to fit and predict the automated monitoring sequences, resulting in the fitting value and the predicted value. The fitting value and the predicted value represent the main trend of the dam, and their values are reliable and almost linear.

(2)

The residual sequences of the GM (1, 1) can be obtained by subtracting the original values from the predicted values. The residual sequences reflect the volatility of the dam, and their values are unstable and non-linear.

(3)

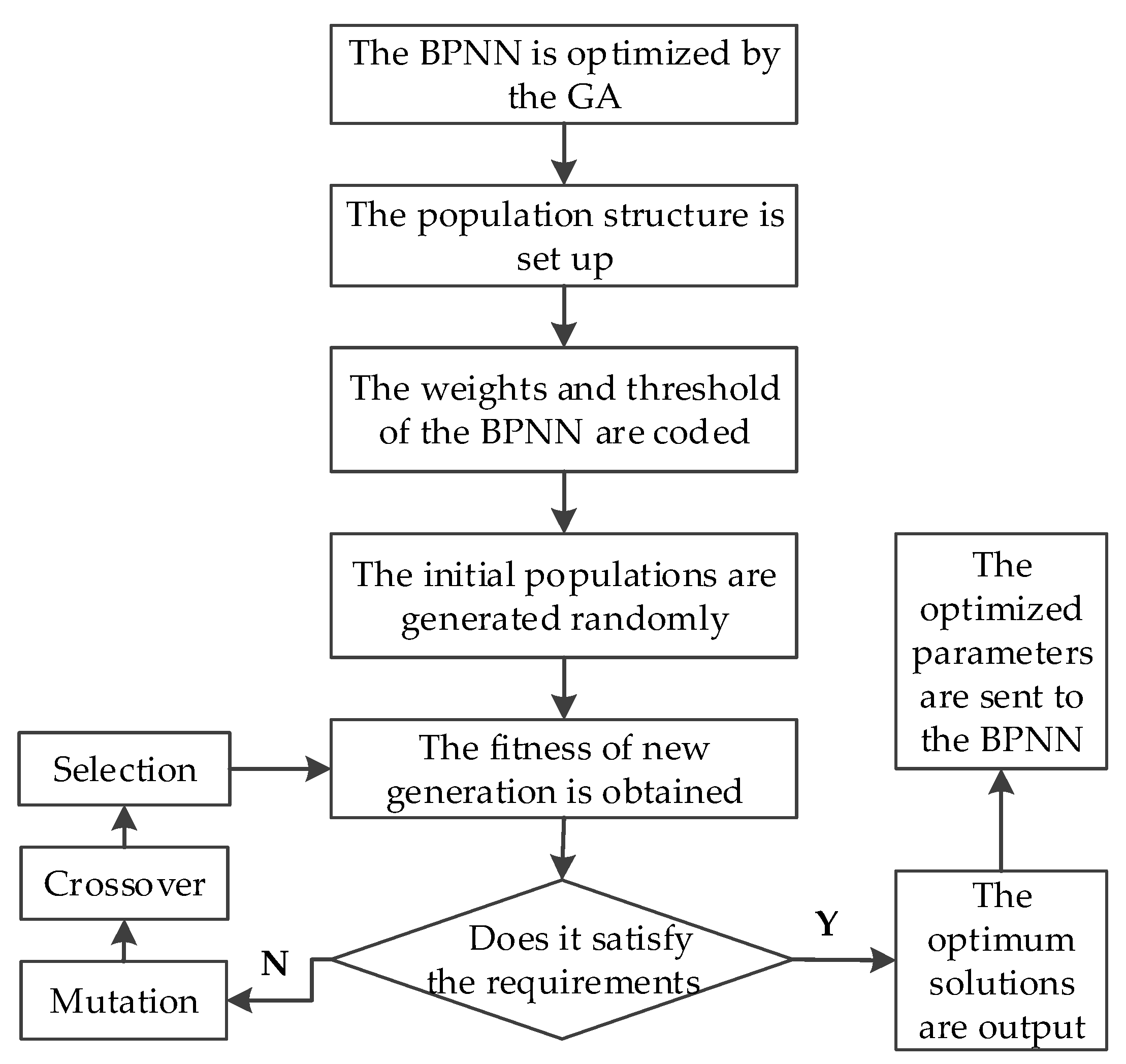
The GA is used to optimize the structure of the BPNN, and the GA-BP is built.

(4)

The GA-BP is trained by the influence factors (water level and temperature) and the residual values of the GM (1, 1): the input values of the GA-BP model are the influencing factors, and the output values are the residual values of the GM (1, 1).

(5)

The GA-BP is found to be trained well and can be adopted to predict new residuals; when the influencing factors (water level and temperature) are entered, the model will output the new residuals.

(6)

The dam displacement prediction is obtained by subtracting the new residuals from the prediction of the GM (1, 1).

As mentioned above, the GM-GA-BP model considers the characteristics of linear and non-linear variation of the dam so that the higher accuracy prediction value can be obtained. The rest of this paper is organized as follows: Section 2 describes the study area, including the modeling methods of the GM (1, 1), BPNN, GA-BP model, GM-BP model, and GM-GA-BP models. Section 3 presents a validation and comparison of model performance, including the model parameter setting methods, the datasets used in this study, and the experimental results and analysis. Finally, Section 4 contains the conclusions, including the applicability of the model and future work.

2. Model Principles

2.1. Modeling with a GM

The GM is used to describe changes in gray systems. In a gray system, the information is partially known and partially unknown, and the unknown information is calculated using the known information through various methods. Thus, a gray system reveals the inherent regularity of a given data sequence through data mining and collation [55,56]. For GM (1, 1), the original sequence is accumulated to generate an accumulation generation sequence that is then used to generate an accumulative reduction sequence. The GM (1, 1), a first-order, one-variable GM, is an effective forecasting method employed for issues with uncertain and imperfect information. The sample data can contain as few as four observations when using the GM (1, 1) for prediction [20]. The current process for GM (1, 1) modeling is described below.

The original forecasted sequence $X_1^{(0)}$ is written as:

$$X_1^{(0)}=\left\{x^{(0)}(1),x^{(0)}(2),\dots ,x^{(0)}(n)\right\},x^{(0)}(k)\ge 0,(k=1,2,\dots ,n)$$

(1)

where $x^{(0)}(k)$ represents the original data (such as dam deformation data). Then, the accumulation generation sequence $X_1^{(1)}$ is generated from the original forecasted sequence as:

$$X_1^{(1)}=\left\{x^{(1)}(1),x^{(1)}(2),\dots ,x^{(1)}(n)\right\},x^{(1)}(k)={\displaystyle {\sum }_{i=1}^k{x}^{(0)}}(i)$$

(2)

where $x^{(1)}(k)$ is accumulated using the original data. Next, the mean sequence $Z^{(1)}$ is generated with the accumulation generation sequence $X_1^{(1)}$ as:

$$\begin{array}{l}{Z}^{(1)}=\frac{1}{2}\left\{z^{(1)}(2),z^{(1)}(3),\dots ,z^{(1)}(n)\right\}\\ z^{(1)}(m)=\frac{1}{2}\left\{x^{(1)}(m)+x^{(1)}(m-1)\right\},(m=2,3,\dots ,n)\end{array}$$

(3)

where $z^{(1)}(m)$ is the mean value and can be generated with the accumulation generation sequence; finally, the gray differential equation of the GM (1, 1) is constructed as:

$$\frac{d{x}^{(1)}(k)}{dt}+a{x}^{(1)}(k)=u$$

(4)

where the parameters a and u must be estimated and can be calculated using the least squares method as:

$$\widehat{a}={[a,u]}^T={(B^{T}B)}^{-1}{B}^T{Y}_N$$

(5)

where B is a matrix and can be written as follows:

$$B=\left[\begin{array}{ll}-z^{(1)}(2)& 1\\ -z^{(1)}(3)& 1\\ \hspace{1em} ⋮& ⋮\\ -z^{(1)}(3)& 1\end{array}\right]$$

(6)

and Y_N can be written as:

$$Y_N={[x_1^{(0)}(2),x_1^{(0)}(3),\dots ,x_1^{(0)}(n)]}^T$$

(7)

By introducing the parameters Y_N and B into Equations (4) and (5), the time response function of GM (1, 1) can be obtained as follows:

$${\widehat{X}}^{(1)}(k+1)=\left\{x^{(0)}(1)-\frac{u}{a}\right\}\cdot e^{-ak}+\frac{u}{a},(k=1,2,\dots ,n)$$

(8)

By applying first-order accumulative reduction, the following modeling and forecasting values are obtained:

$${\widehat{X}}^{(0)}(k+1)={\widehat{x}}^{(1)}(k+1)-{\widehat{x}}^{(1)}(k)=(1-e^a)(x^{(0)}(1)-\frac{u}{a})e^{-ak}$$

(9)

In summary, the GM (1, 1) modeling procedure can be presented in a straightforward and intuitive manner, as shown in Figure 1.

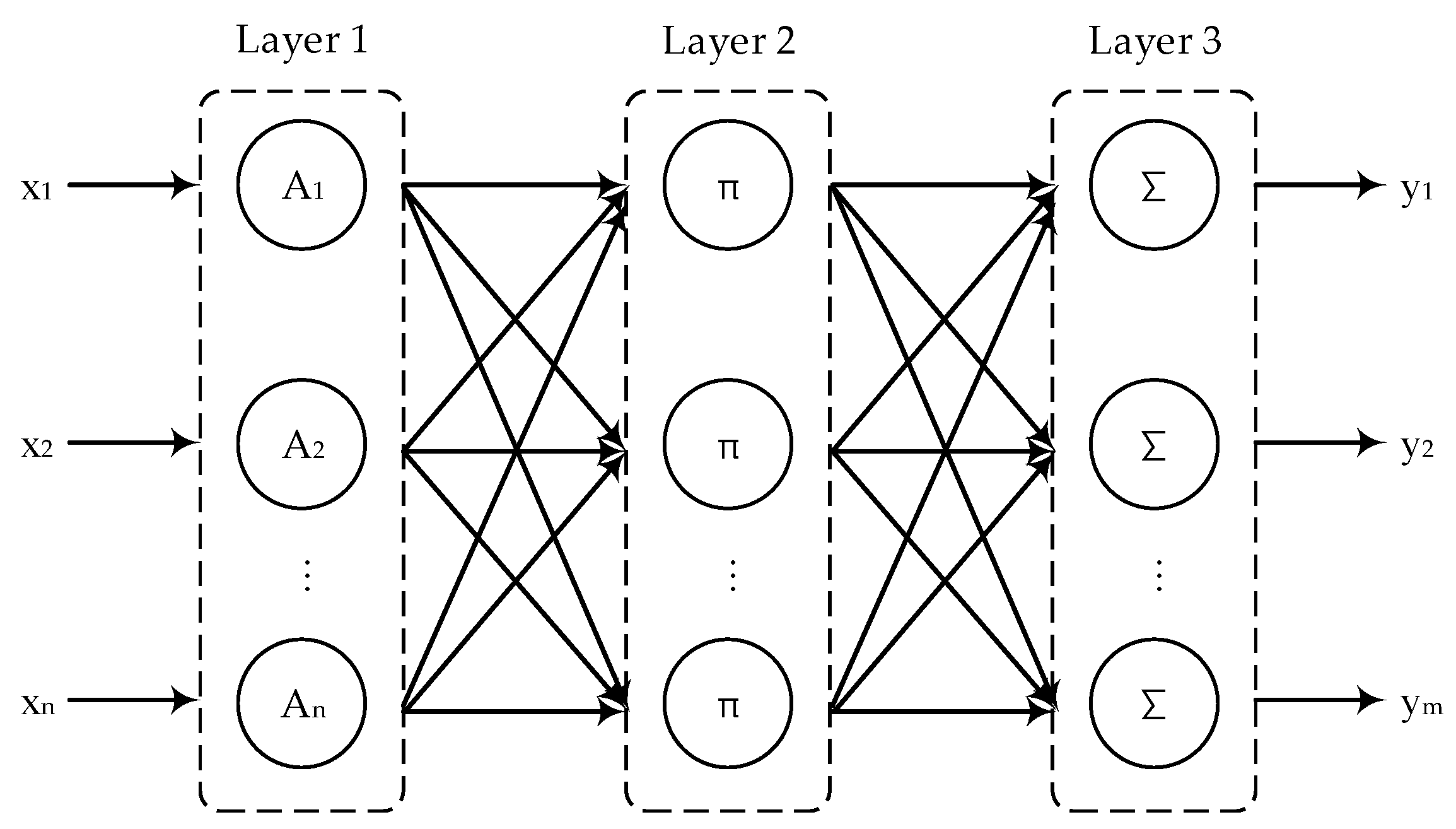
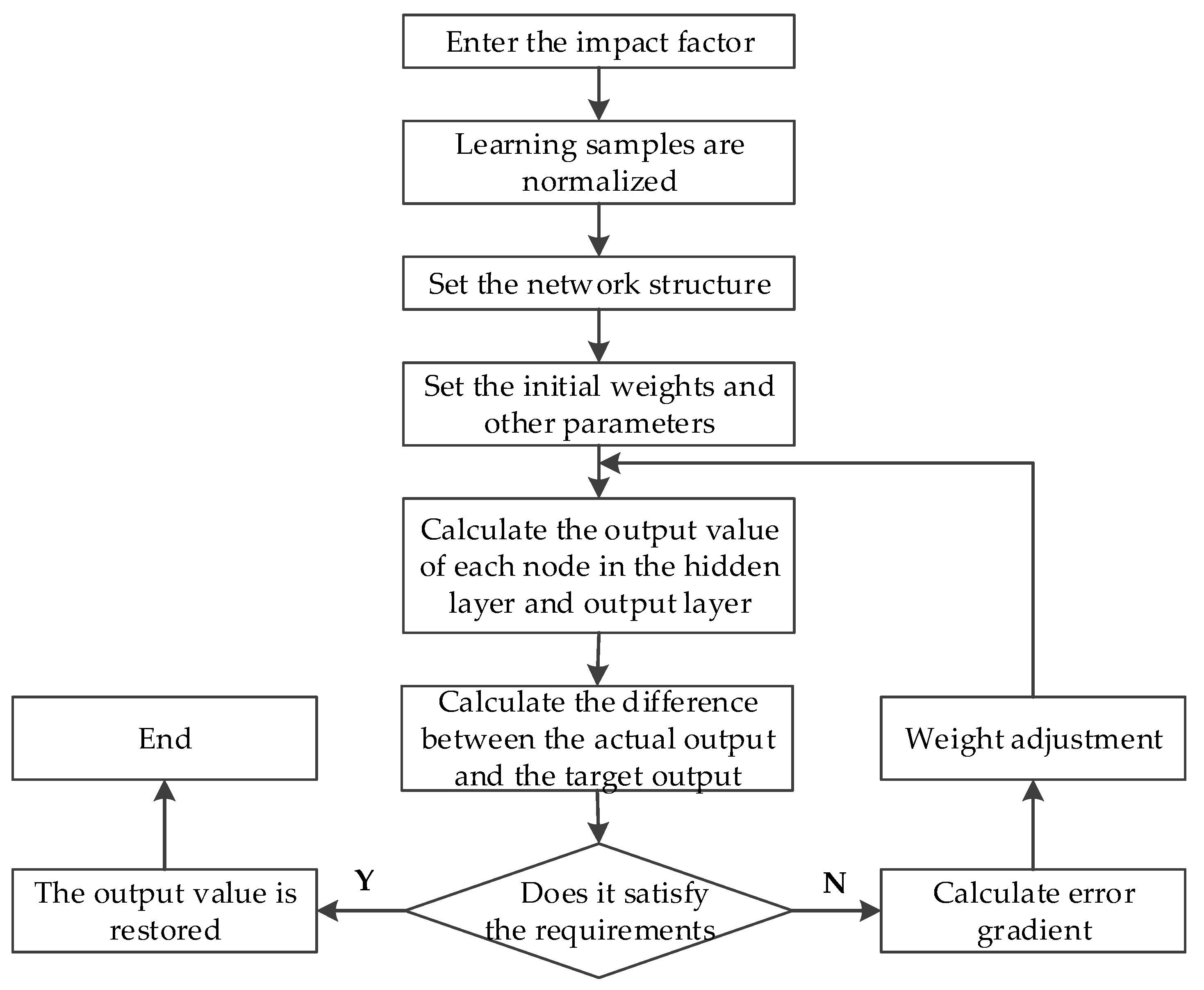
2.2. Modeling with the BPNN Model

Artificial NNs are a relatively new type of information processing system that imitates the structure and function of the human brain [30]. An artificial NN is composed of extensively interconnected neurons that have functional features. An NN uses these functions to achieve connected memory and self-adaptive learning, allowing it to learn the connections between inputs and outputs. More specifically, the weights and thresholds of the network connections are adjusted by the inputs and outputs. Eventually, the NNs can converge and correctly map the inputs and outputs. Substantial evidence shows that NNs can be adapted to complex non-linear situations and achieve higher degrees of success, fault tolerance, and robustness than conventional mathematical models. NNs can be divided into two categories based on the type of interconnection mode between the neurons: the feedforward NN and the feedback network.

The BPNN is a widely used, multilayer feedforward NN based on error back-propagation [32,34]. A complete BPNN model includes at least three layers of neurons: an input layer, a hidden layer, and an output layer. The neurons in these layers are connected to each other and signals propagate through the layers. The inputs of the nodes in each layer are affected only by the outputs of the previous layer, and the nodes in the same layer do not affect each other; each layer is affected only by the nodes and the transfer functions. In this framework, input values are sent forward through the network, and then the differences between the calculated and expected outputs from the training dataset are computed. The differences (i.e., the errors) are then propagated backward through the network to adjust the weights, which are repeatedly adjusted during several iterations. The framework of the BPNN model is shown in Figure 2.

Figure 2 shows the framework of a three-layer BPNN model. Assume that the input layer has n neurons, the hidden layer has u neurons, and the output layer has m neurons. The input value of the NN is $X={(x_1,x_2,\cdots x_i,\cdots ,x_n)}^T$, and the output vector of the output layer is $Y=(y_0,y_1,y_2,\dots ,y_m)$. Then, the input vector of hidden layer is

$$I_i={\displaystyle \sum _{j=1}^n{w}_{ij}\cdot x_j+{\theta }_i}(i=1,2,\dots ,u),$$

(10)

where $w_{ij}$ is the weight of the network connection between the $j$th neuron in the input layer and the $i$th neuron in the hidden layer. ${\theta }_i$ is the threshold of the $i$th neuron in the hidden layer. The network chooses the sigmoid function as the excitation function $f$ of hidden layer neurons; then, the output vector of the hidden layer neurons is:

$$C_i=\frac{1}{1+e^{-I_i}}$$

(11)

Taking the output layer neuron threshold as $\gamma$ and the output layer neuron excitation function as a linear function, then the output vector of output layer neurons is:

$$y={\displaystyle \sum _{i=1}^m{v}_i{C}_i}+\gamma$$

(12)

where $v_i$ is the network weight of the hidden layer to the output layer.

Assuming that there are $P$ training sample $X={(x_1,x_2,\cdots x_i,\cdots ,x_p)}^T$, after the sample is input into the network, the network randomly gives the connection weight vector $W$ composed of $w_{ij},{\theta }_i,\gamma ,v_i$. In this way, the output value $y$ of the network can be obtained, while the expected output of the network is $t$, and for the sample $p$, the output error of the network is:

$$e_p=t_p-y_p$$

(13)

and the error function is defined as:

$$E_p=\frac{1}{2}{(t_p-y_p)}^2$$

(14)

As $W$ network initializations are given randomly, the $E_p$ value is relatively large, and the network accuracy is not high. When the network structure is determined, only the weights and threshold of each layer can be adjusted to optimize the network to reduce the network output error and improve the network accuracy.

In the standard BP algorithm, according to the principle-of-gradient-descent method, the change in the corresponding weights of neurons in each layer is proportional to the negative derivative of the error function to the value, and the correction formula of network weights is

$$\Delta W=-\eta \frac{\partial E_p}{\partial W}$$

(15)

where $\eta$ is the learning rate, and the value range is generally (0,1).

By substituting Equations (11), (12) and (14) into Equation (15), we obtain:

$$\begin{array}{l}\Delta W=\eta e_p\frac{\partial y_p}{\partial W}\\ \Delta W=(\Delta w_{ij},\Delta {\theta }_i,\Delta v_i,\Delta \gamma )\end{array}$$

(16)

According to Equation (16), the value of each element in $W$ for a given sample $P$ is:

$$\begin{array}{l}\Delta w_{ij}=\eta e_p\frac{\partial y_p}{\partial w_{ij}}=\eta e_p{v}_i{C}_{ip}(1-C_{ip})x_{ip}\\ \Delta {\theta }_i=\eta e_p\frac{\partial y_p}{\partial {\theta }_i}=\eta e_p{v}_i{C}_{ip}(1-C_{ip})\\ \Delta v_i=\eta e_p\frac{\partial y_p}{\partial v_i}=\eta e_p{C}_{ip}\\ \Delta \gamma =\eta e_p\frac{\partial y_p}{\partial \gamma }=\eta e_p\end{array}\}$$

(17)

Since the output $C_{ip}$ of each neuron in the hidden layer and the output error $e_p$ of the network have been calculated after the forward calculation is completed, the value of $\Delta W$ can be obtained by Equation (17). Finally, the iteration formula $w^{\prime }=w+\Delta w$ is used to modify the original $w$ and obtain the new connection weight vector $w^{\prime }$. For all of the learning samples, the above calculation process is performed according to the sample arrangement order, and then the value of the weight vector $W^{\prime }$ is determined. For each of the $P$ samples, a forward calculation is performed to find the sum of the errors, $E={\displaystyle \sum _1^P{E}_P}$, thus completing a round of iterative calculation.

The purpose of calculating $E$ is to evaluate the accuracy of the network; circuit training repeats the above steps many times, and the BPNN connection weights are continually updated. The output error will tend toward a minimum. When $E$ reaches a set value, the loop is complete; if it is not reached, the cycle training will continue many times. The detailed BPNN calculation process is shown in Figure 3 below:

2.3. Modeling with the GA-BP Model

In this study, the GA-BP model consists of the GA and BPNN model. The prediction accuracy of the BPNN model is determined from the connection weights and threshold values, which are typically set based on operator experience; therefore, the prediction accuracy of the BPNN is subjective. Fortunately, the GA, an ecological system algorithm proposed by Professor Holland [47], can be adopted to search for a globally optimal solution for the BPNN connection weights and thresholds to obtain the values that are appropriate for optimizing the NN structure.

The GA overcomes the disadvantage of the BPNN model, which easily falls into local extremum. The individuals are filtered according to a certain fitness function and a series of genetic operations, so that individuals with a high fitness are retained and form a new group. The fitness of each individual in the new group is continuously improved until a certain limit condition is satisfied. In this case, the individual with the highest degree of adaptation is the optimal solution of the parameter to be optimized. In this paper, the parameters to be optimized are the weights and thresholds of the BPNN. There are six main factors in using the GA to optimize parameters: parameter coding, initial population setting, fitness function design, genetic operation, setting of algorithm control parameters, and handling of constraints.

(1) Parameter coding

Chromosome coding is the expression of the solution of a problem by a code, so that the state space of the problem corresponds to the code space of the GA, which depends to a large extent on the nature of the problem and will affect the design of the genetic operation. Because the optimization process of the GA is not directly related to the problem parameter itself but to the code space corresponding to a certain encoding mechanism, the selection of coding is the important factor that affects the performance and efficiency of the algorithm. The traditional GA adopts binary encoding. When dealing with complex problems, there are many independent variables and a long chromosome length, which leads to the increase of search space, thereby reducing search efficiency. Considering the network size in this paper, real number coding is used in this paper. That is, a real number is directly used as a gene position of a chromosome, so that the length of the chromosome is greatly shortened, which not only saves the complexity of the round-trip coding and decoding but also simplifies the genetic operation. The code string consists of four parts: input layer and hidden layer connection weights, hidden layer and output layer connection weights, hidden layer threshold, and output layer threshold. For a BPNN to be optimized, assuming that the number of input layer nodes is $n$, the number of hidden layer nodes is $u$, and the number of output layer nodes is $m$, the mapping relationship of the encoding is:

$$Y=(w_{11},w_{12},\dots ,w_{nu},v_{11},v_{12},\dots ,v_{um},{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_u,{\beta }_1,{\beta }_2,\dots ,{\beta }_m)$$

(18)

where $w$ is the weight of the connection between the input layer and the hidden layer, $v$ is the weight of the connection between the hidden layer and the output layer, $\alpha$ is the threshold of the hidden layer, and $\beta$ is the output layer threshold. The subscripts represent the corresponding neuron serial number. Such a long string (each position on the string corresponds to a weight and threshold of the network) constitutes a chromosome individual. $N$ such individuals make up a group; that is, the size of the population is $N$. The length of the code string can be calculated using the following formula:

$$s=n\cdot u+u\cdot m+u+m$$

(19)

(2) Initialize the group

To establish the initial solution space, we must design $m$ initial code strings (individuals), each of which has its own range of variation. The larger the scope of the design, the lower the search efficiency, but if the design is too small, there may be no solution. The BP algorithm often uses interval (−1, 1) to generate the initial weight. In this paper, the initial population ‘popu’ (N, L) (that is, the matrix of $N$ rows and $L$ columns) is randomly generated in the MATLAB environment; $N$ is the population size, and $L$ is the code string length. Each individual ‘popu’ (n, :) represents an independent forward network, $n\in [1,N]$. The population size affects the final result of genetic optimization and the efficiency of the GA.

(3) Determine the fitness function

The connection weights and thresholds represented on the code string are assigned to the corresponding parts of the NN. The weights and thresholds optimized by the GA are brought into the NN for training, and the errors between the actual output and the expected output of the network are calculated after the operation. The search objective of the GA is to find the weight and the threshold that minimize the square sum of errors. However, since the GA can evolve only in the direction of increasing the value of the fitness function, the fitness function uses the reciprocal of the sum of squared errors.

The fitness function can be written as follows:

$$f(x)=\frac{1}{E}$$

(20)

where $E$ reflects the output error of the BPNN, and can be written as follows:

$$E=\frac{1}{2}{\displaystyle \sum _{k=1}^N{(y_k-{\stackrel{⏜}{y}}_k)}^2},$$

(21)

where $y_k$ and ${\stackrel{⏜}{y}}_k$ represent the desired output value and the actual output value of the $k$th node of the output layer, respectively.

(4) Evolutionary computation of populations, genetic manipulation, and evolutionary termination conditions

In this paper, the uniform ranking method is adopted as a mechanism of selection. The mechanism of this method is to rank all of the individuals in a group according to their fitness level. Based on this ranking, the probability that each individual is selected is determined, and each chromosome is selected by the roulette wheel selection method; the selected chromosome will enter the next generation of the population.

For the operation of the GA, this paper uses an arithmetic cross method and a non-uniform mutation method. The choice of crossover probability $P_c$ and mutation probability $P_m$ are the keys that affect the behavior and performance of the algorithm: If $P_c$ is too large, the structural model of fitness will soon be destroyed, whereas a too-small $P_c$ will stop the search; at the same time, if $P_m$ is too small, new gene blocks will not be easily generated, whereas if it is too large, the GA will become a random search, thereby losing its excellent features. Therefore, this paper adopts the adaptive genetic algorithm (Adaptive GA, AGR) proposed by Srinvias [57]. $P_c$ and $P_m$ can automatically change with the degree of fitness.

Because the output of the GA in this paper is the initial weight of the BP network, this group of values is further modified by the BP network in training, and thus the accuracy of the GA is not very high. To reduce the complexity of the actual operation, this article sets the number of iterations $T$ as a termination condition.

Figure 4 shows the framework of the GA-BP approach presented in this paper.

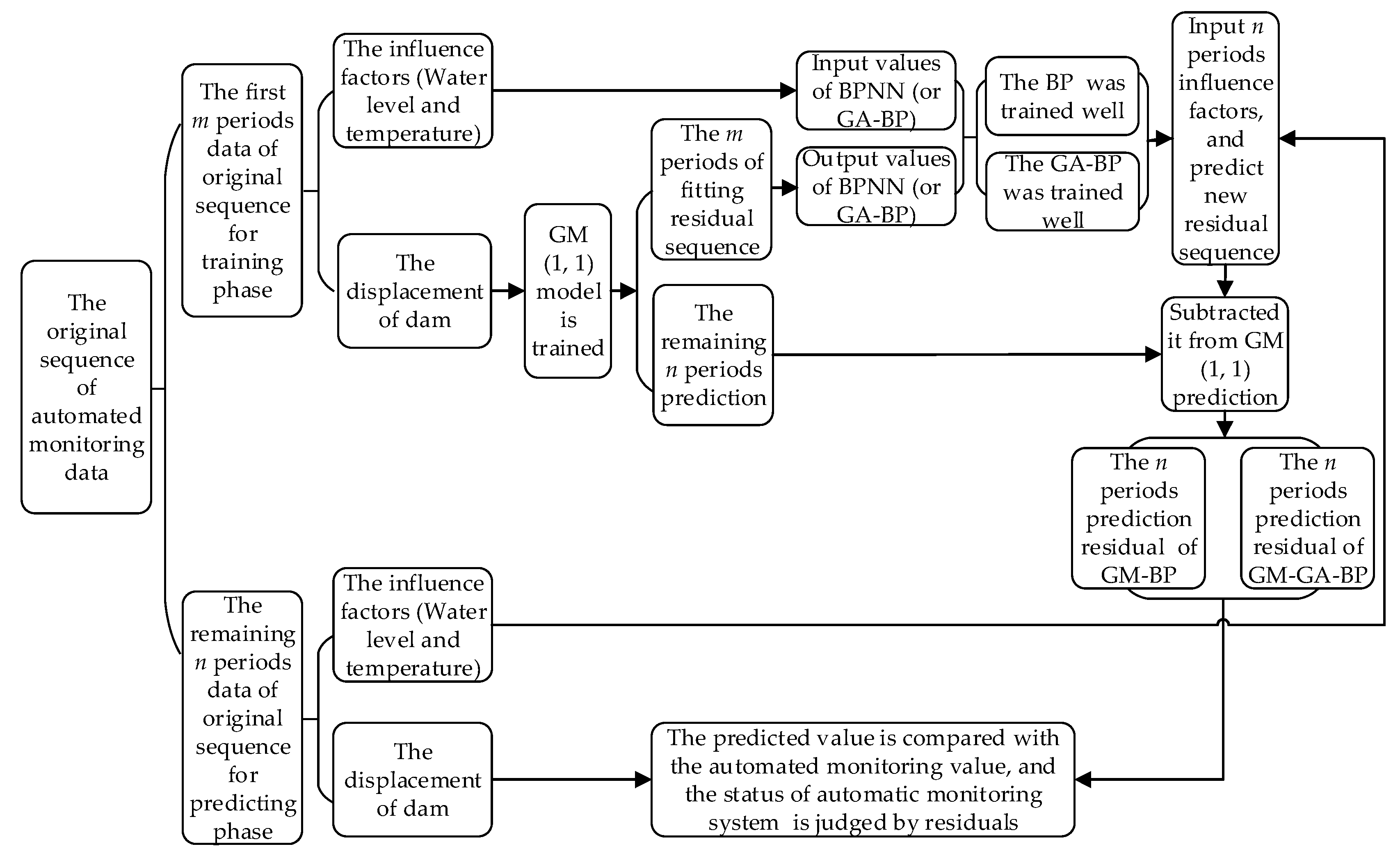
2.4. Modeling with the GM-BP Model and GM-GA-BP Model

In this study, the GM-BP model consists of the GM (1, 1) and BPNN models, and the GM-GA-BP model consists of the GM (1, 1) and GA-BP model. The combination principle of GM-BP and GM-GA-BP is the same; they are combined with the GM (1, 1) using the series connection method. Using the original data series, the GM (1, 1) produces a residual series that offers more realistic and more regular deformation characteristics. Then, the BPNN model (or the GA-BP model) is trained using the residual series and the influencing factors, which finally establishes the GM-BP (or GM-GA-BP) model. Figure 5 shows the data processing flow of the GM-BP model and the GM-GA-BP model.

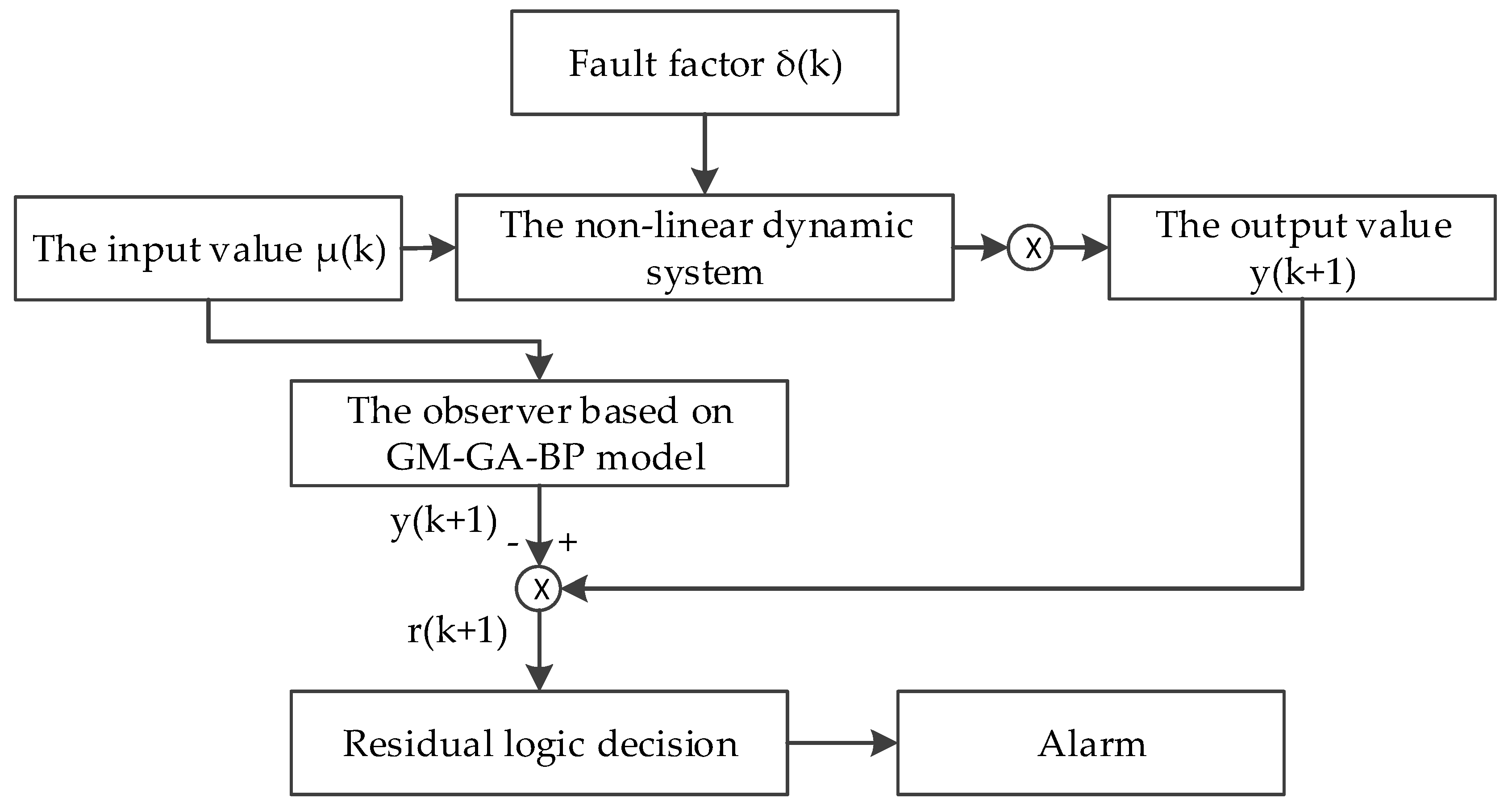
2.5. Design of a Dam Safety Fault Monitoring and Diagnosis System

An online dam monitoring fault self-diagnosis system includes three parts: the acquisition system, the communication system, and the software system. The acquisition system includes the laying of measuring points on the slope of the dam, and the use of automated measurement robots, water-level sensors, and temperature gauges for data acquisition. The function of the communication system is to connect the monitoring equipment and the collection equipment through the optical fiber to achieve the real-time data transmission. The software system installed in the dam monitoring equipment is mainly used to complete the data acquisition and analysis, real-time system monitoring, and diagnosis tasks. The monitoring device is connected by the optical fiber to the acquisition system, and then the original data on the collector can be read in real time through the configuration of the communication software. When the data transmission is normal, every time the data are collected, the database of the monitoring station will be updated and saved in real time, and it will serve as a learning sample of the models used in this paper. When the database is updated, the system program triggers a model prediction event. The prediction event includes the use of GA to calculate network parameters and the use of prediction models to predict dam deformation. When the genetic algorithm calculates the new network structure parameters according to the new sample data, the original structural parameters of the BPNN will be replaced by new parameters, and finally the predicted value of the new sample will be obtained through the prediction model. The well-trained network predicts the displacement of the dam by inputting the influencing factors collected in real time. If there is no fault in the acquisition system, the residual between the predicted value and the dam displacement collected in real time is relatively small. When the acquisition system deviates from the normal working state or fails, the residual error between the predicted value and the real-time displacement of the dam is large. When the residual error is greater than the set limit, the monitoring system will give an alarm. The principle of the automatic fault diagnosis system for dam safety automation monitoring based on the gray genetic BPNN model is shown in Figure 6.

3. Validation and Comparison of Model Performances

3.1. Setting of Model Parameters

In this study, the same training and test datasets were used for each model as control variables, and the model parameters were set to the same values to the extent possible. In this paper, the input factors include two influencing factors, the water level and temperature, and the output factor is the residual sequence. Thus, the number of input neurons in the network is 2, the number of output neurons is 1, and the number of hidden nodes can be obtained according to the following empirical formula [58]:

$$J_c={(0.43mn+0.12n^2+2.54m+0.77n+0.35)}^{\frac{1}{2}}+0.51$$

(22)

where $J_c$ represents the number of hidden nodes, and $m$ and $n$ are the numbers of input and output nodes, respectively. The result of the calculation is rounded up, and the number of hidden layer nodes set in this paper is 3. The sigmoid function is used as an activation function for the input layer. Considering the characteristics of the sigmoid function, and according to the original data trends, the training sample sequence is scaled within (–1, 1). This method can effectively avoid the two saturation regions of the minimum and maximum values of the sigmoid function, and it expedites the learning rate of the network to maintain the original relationship of the data.

In addition, the transfer function for the hidden layer is a continuously differentiable function (“tansig”), and the output layer adopts a linear function (“purelin”).

Because of the non-linearity of the BP network, the initial value affects whether the learning of the network is locally minimized and whether it can converge. Therefore, to ensure that each neuron changes in the maximum area of its transfer function, rather than falling in a small area, the initial weight is required to bring the state of each neuron close to zero when the input is accumulated. In this paper, the GA was used to optimize the initial weights of the BPNNs. The learning rate and momentum coefficient of the network were both set to 0.01, and the number of training samples was set to 10,000. Following Schaffer’s recommendations [46,59], the ranges of the optimal GA parameters were set as follows: n = 20–30, P_c = 0.75–0.95, and P_m = 0.05–0.01. In reference to these factors, the GA parameters were set as follows: the initial population size was 20, the crossover rate was 0.75, the mutation rate was 0.01, and the maximum generation was 20 according to the actual situation.

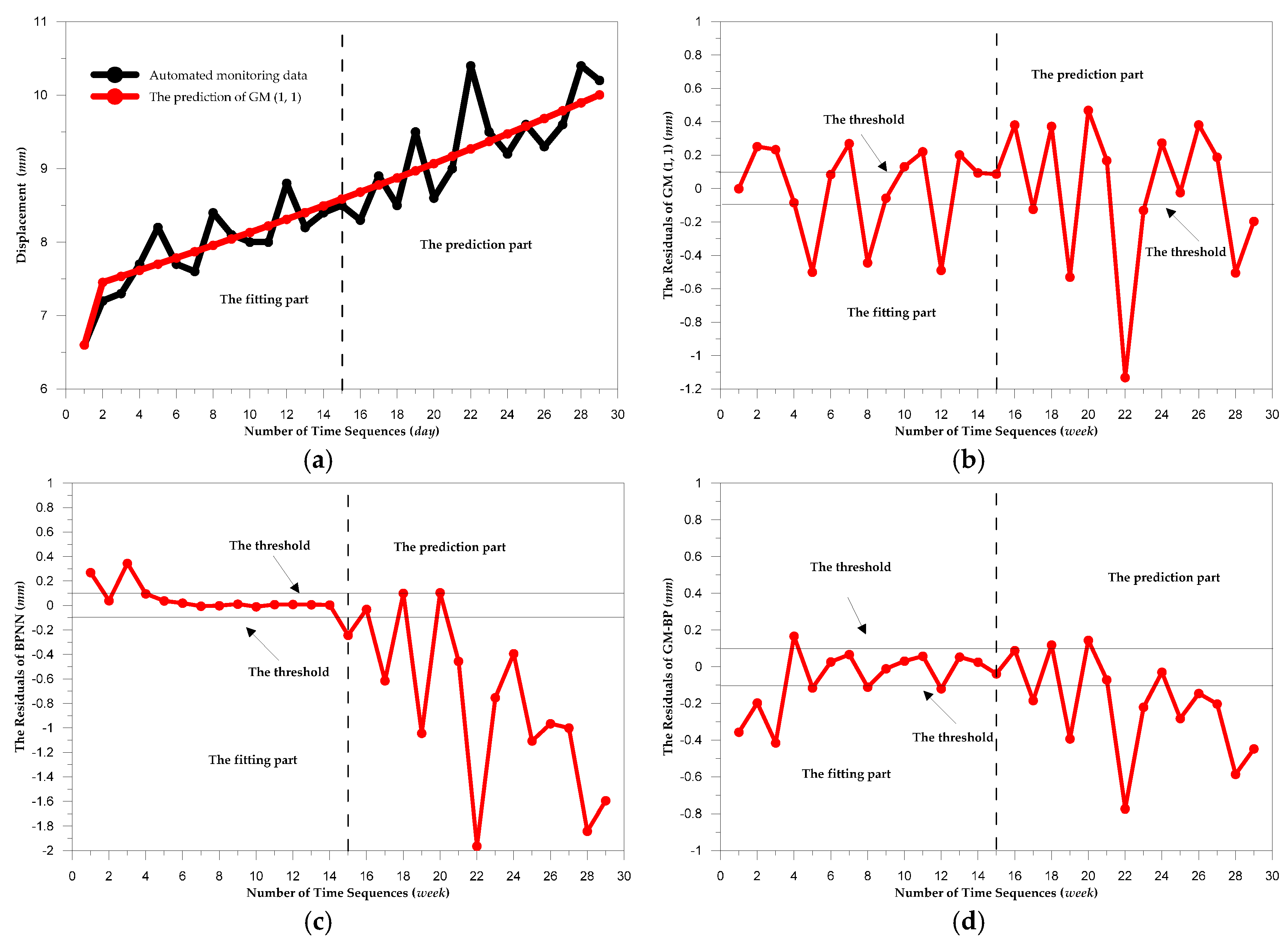
3.2. Analysis of the Models for Predicting the Displacement of Dam Deformation

Figure 7 shows the images of the dam at the Ertan Hydropower Station, which is located in the downstream reaches of the Yalong River in the boundary area between Yanbian County and Miyi County. Situated 33 km away from Panzhihua City, southwest of Sichuan Province, the Ertan Dam is a double-curvature arch dam that is 240 m tall and 774.69 m long. At an elevation of 1205 m, the dam’s crest is 11 m wide, and the base of the dam is 55.7 m in width.

To observe the stress state and displacement of the dam, 41 sets of strain gauges were buried. Tension wire alignment and the plumb-line method were adopted in the automatic monitoring of horizontal displacement. Hydrostatic leveling was adopted in the automatic monitoring of vertical displacement. To detect the stability and reliability of automated monitoring, some automated monitoring points were also monitored manually. In this paper, taking the X16 measuring point of 4# tension wire as an example, the horizontal displacement observation values of 29 weeks in the automatic observation data were selected, as shown in

Table 1. Original automated monitoring data of the Ertan Hydropower Station Dam.

Cycle (Week)	Displacement (mm)	Upstream Water Level (m)	Temperature (°C)
1	6.6	1198.49	31.4
2	7.2	1198.73	29.9
3	7.3	1198.81	29.7
4	7.7	1199.03	26.3
5	8.2	1199.61	25.7
6	7.7	1199.05	27.3
7	7.6	1199.03	27.1
8	8.4	1200.22	25.2
9	8.1	1200.13	26.1
10	8	1200.07	27
11	8	1200.09	26.1
12	8.8	1200.87	24.6
13	8.2	1200.31	28.3
14	8.4	1200.53	28.9
15	8.5	1200.66	29.3
16	8.3	1200.36	29.2
17	8.9	1201.05	28.7
18	8.5	1200.74	29.4
19	9.5	1201.06	25
20	8.6	1200.71	31.4
21	9	1201.07	30.2
22	10.4	1201.06	31.3
23	9.5	1201.08	29.8
24	9.2	1201.03	30.2
25	9.6	1201.08	27.6
26	9.3	1201.02	28.4
27	9.6	1201.12	25.3
28	10.4	1201.64	24.7
29	10.2	1201.55	25.2

.

As shown in Table 1, the monitoring data include 29 monitoring periods that lasted for 29 weeks. The water level increased from 1198.49 m to 1201.55 m during the monitoring periods (a total increase of 3.06 m), and the weekly average water level was approximately 0.1 m. The total dam displacement during the monitoring periods was approximately 3.6 mm, and the weekly average displacement was approximately 0.1 mm. However, on some days, the weekly increase in horizontal displacement reached approximately 1 mm, which is 10 times the average, indicating that there may be a large degree of instability in the automated monitoring data, and there is a possibility that the measured value drifts. Particularly, during the 22nd week of the observation period, the horizontal displacement of the dam increased by 1.4 mm compared to the previous week. However, Table 1 shows that the water level and temperature did not change abnormally during this phase. In addition, compared with the artificial measurement of the point, the artificial measurement changed smoothly, and no mutation occurred. Therefore, this mutation should be generated by random interference, which influenced the automated monitoring sensor, and should belong to the automatic monitoring failure.

In this paper, the fault self-diagnosis system consists of residual generation and residual judgment. The prediction is made by the proposed model, and the predicted value is compared with the automatic monitoring value to obtain the residual. When the residual is large and exceeds the set threshold (0.1 mm), according to a certain method of fault separation strategy, it will be able to achieve the online diagnosis of fault. To prove the validity and superiority of the proposed model, the GM (1, 1), the BPNN model, the GM-BP model, the GA-BP model, and the GM-GA-BP model proposed in this paper were used to predict the dam displacement. The prediction and the residual response curve are shown in Figure 8.

In Figure 8, the “fitting part” refers to the network output value obtained by inputting the influencing factor during the training process of the network. Because, during training, there is an error between the actual output and the expected output, the correction direction of the actual output value is the expected output value, so the output of the training process is called the fitted part of the output value. The “prediction part” refers to the network output value obtained by inputting the influence factor after the network is well trained.

Figure 8a shows the relationship between the dam automation monitoring data and the GM (1, 1) prediction. It can be seen that the GM (1, 1) predictions reflect the overall displacement trend of the dam. Compared between the two curves, the dam displacement automation monitoring data has an abnormal mutation in the 22nd week of the observation period. As explained above, the abnormal mutation is generated by random interference and is a drift value of the automated monitoring sensor.

Figure 8b shows the residual curve of the GM (1, 1). It can be seen that the curve is non-linear and reflects the volatility of the dam automation monitoring data. However, the residuals of the GM (1, 1) model are easily beyond the set threshold. Therefore, the GM (1, 1) is not feasible for the observer fault self-diagnosis system.

Figure 8c shows the residual curve of the BPNN model. It can be seen that the residual values of the BPNN model are smaller than the set threshold in the fitting part, but due to the weak generalization ability of the BPNN model, the BPNN residuals are easily beyond the set threshold in the prediction part, which did not meet the actual situation. Therefore, the BPNN is not feasible for the observer fault self-diagnosis system.

Figure 8d shows the residual curve of the GM-BP model. Compared with Figure 8b, the residual of the GM-BP model is smaller than that of the GM (1, 1), which indicates that the BPNN model can give full play to its non-linear approximation function in the non-linear dam safety monitoring fault diagnosis system. It also indicates that considering the influence of water level and temperature on dam fluctuation can effectively correct the residual of the GM (1, 1). Compared with Figure 8c, the residual of the GM-BP model is smaller than that of BPNN, which indicates that the GM (1, 1) can optimize the dataset, solve the problem of instability of the monitoring data, and then provide the main trend of dam displacement for the BPNN model to ensure that the BPNN prediction does not deviate from the actual trend of dam displacement. However, due to the weak generalization ability and low convergence rate of the BPNN model, the residuals of the GM-BP model are easily beyond the set threshold in most of the observation periods.

Figure 8e shows the residual curve of the GA-BP model. Compared with Figure 8c, the residuals of the GA-BP model were significantly reduced relative to the traditional BPNN model. This result indicates that the GA adopted to optimize the weights of BPNN can improve the capabilities of the global search and local extreme value processing, filter and compress the redundant information of the sample, and extract the eigenvalues of the sample space comprehensively. Thus, the GA-BP model can obtain highly precise prediction values. However, dam displacement is the result of the combined effect of various comprehensive factors; the GA-BP model established only the relationship between two influencing factors (the water level and the temperature) and dam displacement value, and this relationship is not comprehensive. Therefore, the prediction accuracy of GA-BP is uns.

Figure 8f shows the residual curve of the GM-GA-BP model. For the GM-GA-BP model, the GM (1, 1) model was first adopted to extract the main trend of dam displacement, ensuring that the prediction of the GM-GA-BP model does not deviate from the dam displacement trend and improving the stability of the model prediction. Then, the BPNN optimized by the GA was adopted to establish the relationship between the influencing factors and the residuals of the GM (1, 1), to correct the residuals, and improve the prediction accuracy of the model. Therefore, the GM-GA-BP model can provide both stable and highly predictive values. Figure 8f reveals that the GM-GA-BP residual is small and within the set threshold. When the automated monitoring system is unstable and drift occurs in the 22nd period, the residual is beyond the set threshold. Therefore, the GM-GA-BP model can produce more accurate predictions that are in line with the actual situation and evaluate the failure of an automated monitoring system.

3.3. Evaluation for the Models

In order to compare the forecasting results, a statistical regression model (SRM), a support vector machine (SVM), the GM (1, 1) model, the traditional BPNN model, the GM-BP model, the GA-BP model, and the GM-GA-BP model are established, respectively, for the sample data. Using the mean absolute error (MAE) and root mean square error (RMSE), the dam deformation predictions of the three models are validated and compared.

(1)

The MAE is calculated using the following formula:

$$MAE=\frac{1}{n}{\displaystyle {\sum }_{t=1}^n\left|Yt-\widehat{Y}t\right|}$$

(23)

(2)

The RMSE is calculated using the following formula:

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{t=1}^n{(Yt-\widehat{Y}t)}^2}}$$

(24)

where Y_t represents the actual deformation values from dam monitoring, ${\widehat{Y}}_t$ represents the deformation prediction values of the model, and n represents the number of monitoring periods.

The precision of each tested model is listed in

Table 2. The precision of each tested model is analyzed using the MAE and RMSE.

Evaluation Index	SRM	SVM	GM(1,1)	BP	GM-BP	GA-BP	GM-GA-BP
MAE (mm)	0.584	0.358	0.277	0.451	0.189	0.289	0.045
RMSE (mm)	0.347	0.540	0.363	0.640	0.229	0.370	0.052

.

As shown in Table 2, the precision index values for the SRM, the SVM, the GM (1, 1), and the traditional BPNN model are relatively poor (with MAE values of 0.584 mm, 0.358 mm, 0.277 mm, and 0.451 mm and RMSE values of 0.347 mm, 0.540 mm, 0.363 mm, and 0.640 mm, respectively). For the statistical regression model, it belongs to the posterior model, and requires a lot of sample data as a basis. However, the sample data in this article is limited, so it is not suitable for this article. For the SVM model, the kernel functions used in this paper are sigmoid functions. Since SVM has many unique advantages in solving small samples and nonlinear problems, its accuracy is superior to statistical regression model and traditional BP model. However, due to the complexity of the deformation of the dam, the single invariant kernel function cannot fully reflect and predict the deformation of the dam. Therefore, the prediction accuracy is not stable, and the RMSE value is large. For a single GM (1, 1), due to its lack of non-linear approximation ability, the prediction error is large. Its prediction curve can reflect only the main linear deformation of the dam but is not sensitive to fluctuation of the dam. Combining the GM and the non-linear BPNN model to form the GM-BP combination model, the prediction error is reduced (the average absolute value is 0.189 mm, and the RMSE value is 0.229 mm). It is proved that the non-linear capability of the BPNN can make up for the deficiency of the GM (1, 1). For the traditional BPNN model, the prediction error is large because of its disadvantage of easily falling into local extreme points and weak generalization ability. The GA is used to optimize the connection weight and threshold of the BPNN to improve the generalization ability of the network and prevent it from falling into the local extreme point. Therefore, the prediction error of the combined model GA-BP decreases relative to the BPNN (with an MAE value of 0.289 mm and an RMSE value of 0.370 mm). The above two methods optimize the model from different aspects. The BPNN optimizes the non-linear processing capability of the GM, while the GA optimizes the internal structure of the BP. Therefore, the two optimization methods are combined organically to form the GM-GA-BP model. Since the new model combines the advantages of the above model, its prediction accuracy is higher than that of all the above models; the average absolute value is 0.045 mm, and the RMSE value is 0.052 mm.

In the experiments, the GM (1, 1), the BPNN model, the GM-BP model, and the GA-BP model were first used to conduct the fitting and predict dam displacement. However, the results show that the prediction of these models is unsatisfactory. For the proposed GM-GA-BP model, we optimized the automated monitoring data to obtain the realistic regularity of the dam displacement using the GM (1, 1) and optimized the weights and thresholds to improve the generalization ability of the BPNN and prevent it from falling into local extrema using the GA. When extracting the regularity, the GA-BP effectively considers the real changing trends of the dam and learns the rules in a reasonable fashion with high simulation accuracy. In comparison with the other models in this study, the prediction of the proposed model is relatively accurate, proving that the combination of the models is reliable. In order to compare with more traditional models, this paper studies the accuracy of the statistical regression model and SVM model in dealing with this prediction problem. The results show that the statistical regression model, which depends on the sample information amount, and the SVM, which is based on a single kernel function, have low prediction accuracy and unstable performance. However, due to the combination of the GM (1, 1) and the GA-BP model, the proposed GM-GA-BP model has higher prediction accuracy when dealing with this kind of problem. Also, due to the adaptive learning characteristics of the BPNN model, the proposed model can adjust the network structure according to the samples at any time to maintain stable performance. The results show that the GM-GA-BP model, which is well trained by online automatic monitoring data, can provide highly precise predictions one step early under the conditions of the normally functioning automated monitoring system. The prediction is compared with the online measured value and makes a logical judgment based on the residual error. When the residual exceeds the pre-set threshold, the system is judged to be faulty.

4. Conclusions

In this paper, a fault self-diagnosis system for the automatic monitoring of dam safety based on the GM-GA-BP model is proposed. Its purpose is to solve the problem of instability and drift data preprocessing and the problem of BPNN optimization and prediction. The automated dam safety monitoring system is a non-linear system that exhibits unstable performance and drifting of the measured values. This study applies the methods of the GM (1, 1), BPNN, and GA to the self-diagnosis system of automated fault monitoring. A combined model of GM-GA-BP was proposed to accommodate the performance instability of the automated monitoring system, the drift of measurement values, and the local extremum problem. A case study using the automated monitoring data of the Ertan Hydropower Station Dam in China is presented and discussed to examine the performance of the proposed model. In this study, the proposed GM-GA-BP model addresses two issues: (1) solving the automatic monitoring system problem of instability performance and measurement drift so that the characteristics of the dam deformation are more easily detectable, and (2) solving the weights and thresholds of the NNs, to improve the generalization ability of the network and prevent it from falling into local extrema, making it fully achieve its non-linear approximation function and correct the residuals. The results show that the self-diagnosis system of the automatic fault monitoring of dam safety based on the GM-GA-BP model can realize the online diagnosis and real-time isolation of faults, and that the proposed model has higher prediction accuracy and more stable prediction performance than the traditional prediction models.

There are certain limitations of this study. The first limitation is related to the GM (1, 1). Because the GM (1, 1) is a linear model, the GM-GA-BP model is more suitable for dam displacement, for which the trend is similar to linearity, than the continuous changes of the water level and temperature caused by drought, rain, and season changes. The second limitation is that this study analyzes only the fault diagnosis system of automated displacement monitoring. Therefore, the fault diagnosis system of comprehensive automation monitoring (including the monitoring of dam deformation and uplift pressure) and the associated thresholds remain to be studied. To resolve the remaining problems and determine the further performance of the proposed model, additional investigations must be conducted in future work.