Comparison of Split Window Algorithms for Retrieving Measurements of Sea Surface Temperature from MODIS Data in Near-Land Coastal Waters
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. In Situ and Satellite Data
3. Methods
3.1. Operational Algorithms for Retrieving Global Data of Sea Surface Temperature (SST) from Moderate Resolution Imaging Spectroradiometer (MODIS) Data
3.2. Algorithms for Retrieving SST Data from MODIS Data
3.3. Current Operational Algorithm for Retrieving Land Surface Temperature (LST) Data from MODIS Data
3.4. Algorithms for Retrieving LST Data from MODIS Data
3.5. Estimation of Input Data
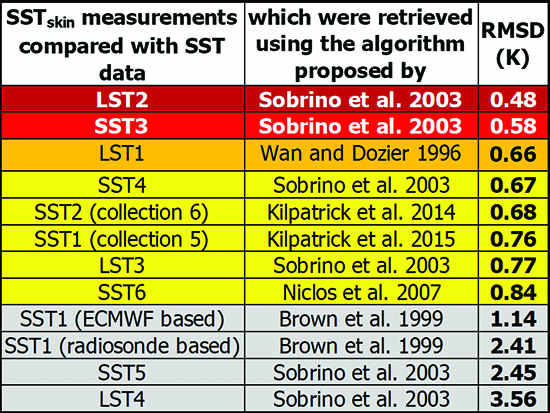
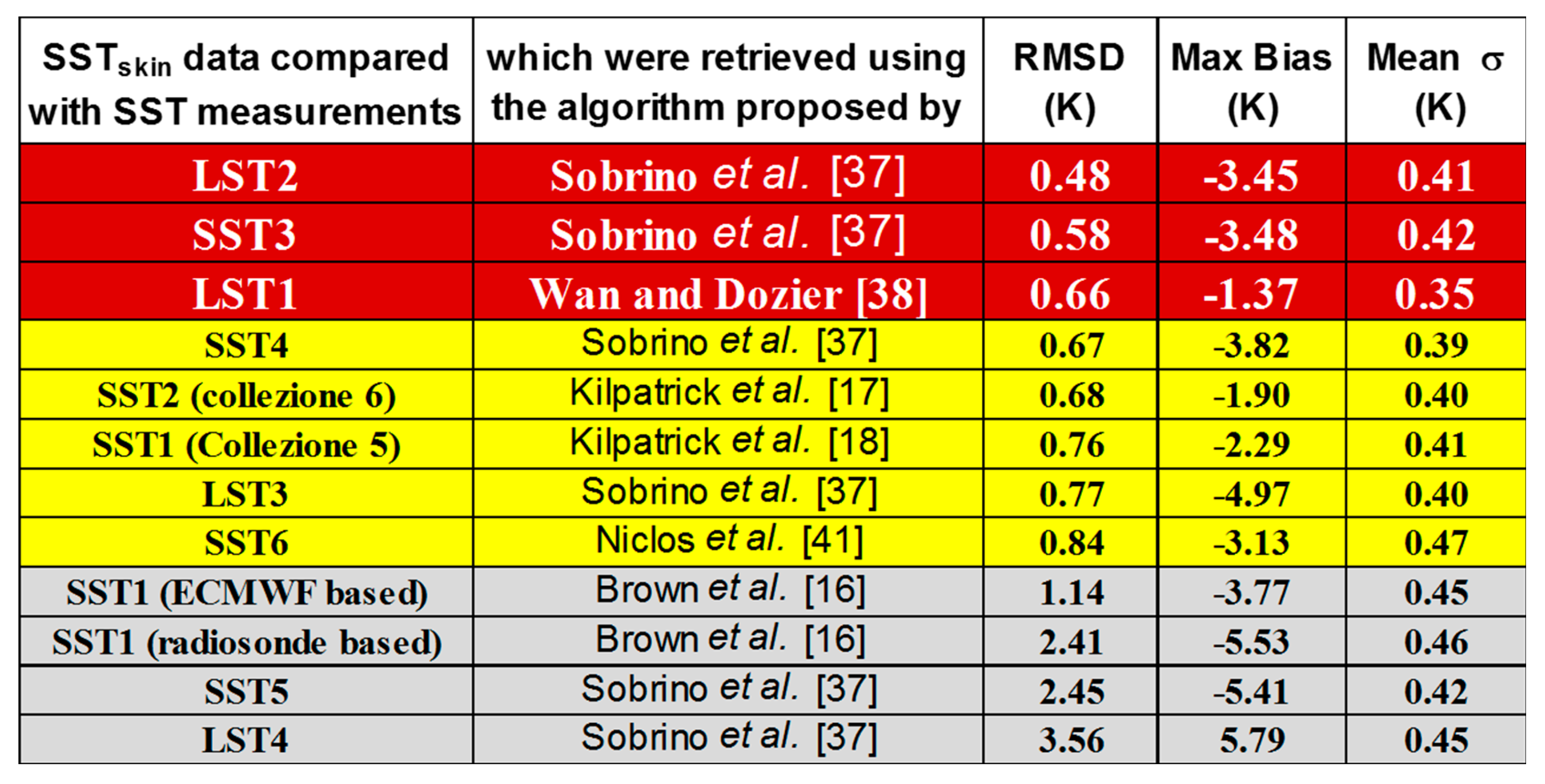
4. Results and Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Blanchette, C.A.; Miner Melis, C.; Raimondi, P.T.; Lohse, D.; Heady, K.E.; Broitman, B.R. Biogeographical patterns of rocky intertidal communities along the Pacific coast of North America. J. Biogeogr. 2008, 35, 1593–1607. [Google Scholar] [CrossRef]
- Ahuja, S. Monitoring Water Quality: Pollution Assessment, Analysis, and Remediation; Elsevier: Waltham, MA, USA, 2013; pp. 1–379. [Google Scholar]
- Smale, D.A.; Wernberg, T. Satellite-derived SST data as a proxy for water temperature in nearshore benthic ecology. Mar. Ecol. Prog. Ser. 2009, 387, 27–37. [Google Scholar] [CrossRef]
- Valentini, E.; Filipponi, F.; Nguyen Xuan, A.; Passarelli, F.M.; Taramelli, A. Earth Observation for Maritime Spatial Planning: Measuring, Observing and Modeling Marine Environment to Assess Potential Aquaculture Sites. Sustainability 2016, 8, 519. [Google Scholar] [CrossRef]
- McCaul, M.; Barland, J.; Cleary, J.; Cahalane, C.; McCarthy, T.; Diamond, D. Combining Remote Temperature Sensing with in-Situ Sensing to Track Marine/Freshwater Mixing Dynamics. Sensors 2016, 16, 1402. [Google Scholar] [CrossRef] [PubMed]
- Narváez, D.A.; Poulin, E.; Leiva, G.; Hernández, E.; Castilla, J.C.; Navarrete, S.A. Seasonal and spatial variation of nearshore hydrographic conditions in central Chile. Cont. Shelf Res. 2004, 24, 279–292. [Google Scholar] [CrossRef]
- De Boer, G.J.; Pietrzak, J.D.; Winterwerp, J.C. SST observations of upwelling induced by tidal straining in the Rhine ROFI. Cont. Shelf Res. 2009, 29, 263–277. [Google Scholar] [CrossRef]
- Tang, D.; Kester, D.R.; Wang, Z.; Lian, J.; Kawamura, H. AVHRR satellite remote sensing and shipboard measurements of the thermal plume from the Daya Bay, nuclear power station, China. Remote Sens. Environ. 2003, 84, 506–515. [Google Scholar] [CrossRef]
- Dufois, F.; Penven, P.; Whittle, C.P.; Veitch, J. On the warm nearshore bias in Pathfinder monthly SST products over Eastern Boundary Upwelling Systems. Ocean Model. 2012, 47, 113–118. [Google Scholar] [CrossRef]
- Castillo, K.D.; Lima, F.P. Comparison of in situ and satellite-derived (MODIS-Aqua/Terra) methods for assessing temperatures on coral reefs. Limnol. Oceanogr. Methods 2010, 8, 107–117. [Google Scholar] [CrossRef]
- Leichter, J.J.; Helmuth, B.; Fischer, A.M. Variation beneath the surface: Quantifying complex thermal environments on coral reefs in the Caribbean, Bahamas and Florida. J. Mar. Res. 2006, 64, 563–588. [Google Scholar] [CrossRef]
- Thomas, A.; Byrne, D.; Weatherbee, R. Coastal sea surface temperature variability from Landsat infrared data. Remote Sens. Environ. 2002, 81, 262–272. [Google Scholar] [CrossRef]
- Cavalli, R.M. Retrieval of Sea Surface Temperature from MODIS Data in Coastal Waters. Sustainability 2017, 9, 2032. [Google Scholar] [CrossRef]
- Pearce, A.; Faskel, F.; Hyndes, G. Nearshore sea temperature variability off Rottnest Island (Western Australia) derived from satellite data. Int. J. Remote Sens. 2006, 27, 2503–2518. [Google Scholar] [CrossRef]
- Smit, A.J.; Roberts, M.; Anderson, R.J.; Dufois, F.; Dudley, S.F.; Bornman, T.G.; Bolton, J.J. A Coastal Seawater Temperature Dataset for Biogeographical Studies: Large Biases between In Situ and Remotely-Sensed Data Sets around the Coast of South Africa. PLoS ONE 2013, 8, e81944. [Google Scholar] [CrossRef] [PubMed]
- Brown, O.B.; Minnett, P.J.; Evans, R.; Kearns, E.; Kilpatrick, K.; Kumar, A.; Sikorski, R.; Závody, A. MODIS Infrared Sea Surface Temperature Algorithm Algorithm Theoretical Basis Document; Version 2.0; University of Miami: Miami, FL, USA, 1999; pp. 1–91. [Google Scholar]
- Kilpatrick, K.; Podesta, G.; Walsh, S.; Evans, R.; Minnett, P. Implementation of Version 6 AQUA and TERRA SST Processing; White Paper; University of Miami: Coral Gables, FL, USA, 2014. [Google Scholar]
- Kilpatrick, K.A.; Podestá, G.; Walsh, S.; Williams, E.; Halliwell, V.; Szczodrak, M.; Brown, O.B.; Minnett, P.J.; Evans, R. A decade of sea surface temperature from MODIS. Remote Sens. Environ. 2015, 165, 27–41. [Google Scholar] [CrossRef]
- Szczodrak, M.; Minnett, P.J.; Evans, R.H. The effects of anomalous atmospheres on the accuracy of infrared sea-surface temperature retrievals: Dry air layer intrusions over the tropical ocean. Remote Sens. Environ. 2014, 140, 450–465. [Google Scholar] [CrossRef]
- Fiedler, L.; Bakan, S. Interferometric measurements of sea surface temperature and emissivity. Deutsch. Hydrogr. Z. 1997, 49, 357–365. [Google Scholar] [CrossRef]
- Friedman, D. Infrared characteristics of ocean water (1.5–15 μ). Appl. Opt. 1969, 8, 2073–2078. [Google Scholar] [CrossRef] [PubMed]
- Konda, M.; Imasato, N.; Nishi, K.; Toda, T. Measurement of the sea surface emissivity. J. Oceanogr. 1994, 50, 17–30. [Google Scholar] [CrossRef]
- Masuda, K.; Takashima, T.; Takayama, Y. Emissivity of pure and sea waters for the model sea surface in the infrared window regions. Remote Sens. Environ. 1988, 24, 313–329. [Google Scholar] [CrossRef]
- Masuda, K. Influence of wind direction on the infrared sea surface emissivity model including multiple reflection effect. Meteorol. Geophys. 2012, 63, 1–13. [Google Scholar] [CrossRef]
- Newman, S.M.; Smith, J.A.; Glew, M.D.; Rogers, S.M.; Taylor, J.P. Temperature and salinity dependence of sea surface emissivity in the thermal infrared. Q. J. R. Meteorol. Soc. 2005, 131, 2539–2557. [Google Scholar] [CrossRef]
- Niclòs, R.; Caselles, V. Angular variation of the sea surface emissivity. In Recent Research Development in Thermal Remote Sensing; Research Signpost: Thiruvananthapuram, Indian, 2005; pp. 37–65. [Google Scholar]
- Niclòs, R.; Caselles, V.; Coll, C.; Valor, E.; Rubto, E. Autonomous Measurements of Sea Surface Temperature Using In Situ Thermal Infrared Data. J. Atmos. Ocean. Technol. 2004, 21, 683–692. [Google Scholar] [CrossRef]
- Niclòs, R.; Valor, E.; Caselles, V.; Coll, C.; Sánchez, J.M. In situ angular measurements of thermal infrared sea surface emissivity—Validation of models. Remote Sens. Environ. 2005, 94, 83–93. [Google Scholar] [CrossRef]
- Salisbury, J.W. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Watts, P.D.; Allen, M.R.; Nightingale, T.J. Wind speed effects on sea surface emission and reflection for the along track scanning radiometer. J. Atmos. Ocean. Technol. 1996, 13, 126–141. [Google Scholar] [CrossRef]
- Wen-Yao, L.; Field, R.T.; Gantt, R.G.; Klemas, V. Measurement of the surface emissivity of turbid waters. Remote Sens. Environ. 1987, 21, 97–109. [Google Scholar] [CrossRef]
- Wei, J.A.; Wang, D.; Gong, F.; He, X.; Bai, Y. The Influence of Increasing Water Turbidity on Sea Surface Emissivity. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3501–3515. [Google Scholar] [CrossRef]
- Wu, X.; Smith, W.L. Emissivity of rough sea surface for 8–13 μm: Modeling and verification. Appl. Opt. 1997, 36, 2609–2619. [Google Scholar] [CrossRef] [PubMed]
- Mueller, J.L.; Austin, R.W.; Morel, A.; Fargion, G.S.; McClain, C.R. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4, Volume I: Introduction, Background and Conventions; NASA Technical Memorandum 2003-21621; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003; pp. 1–56.
- Wolfe, R.E.; Roy, D.P.; Vermote, E. MODIS land data storage, gridding, and compositing methodology: Level 2 grid. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1324–1338. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Towards a local split window method over land surfaces. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Sobrino, J.A.; El Kharraz, J.; Li, Z.L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens. 2003, 24, 5161–5182. [Google Scholar] [CrossRef]
- Wan, Z.M.; Dozier, J. A generalized split-window algorithm for retrieving land surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Wan, Z. MODIS Land-Surface Temperature Algorithm Theoretical Basis Document (LST ATBD); Version 3.3; University of California: Santa Barbara, CA, USA, 1999. [Google Scholar]
- Emery, W.J.; Yu, Y.; Wick, G.A.; Schluessel, P.; Reynolds, R.W. Correcting infrared satellite estimates of sea surface temperature for atmospheric water vapor attenuation. J. Geophys. Res. Oceans 1994, 99, 5219–5236. [Google Scholar] [CrossRef]
- Niclòs, R.; Caselles, V.; Coll, C.; Valor, E. Determination of sea surface temperature at large observation angles using an angular and emissivity-dependent split-window equation. Remote Sens. Environ. 2007, 111, 107–121. [Google Scholar] [CrossRef]
- Cavalli, R.M.; Betti, M.; Campanelli, A.; Di Cicco, A.; Guglietta, D.; Penna, P.; Piermattei, V. A methodology to assess the accuracy with which remote data characterize a specific surface, as a Function of Full Width at Half Maximum (FWHM): Application to three Italian coastal waters. Sensors 2014, 14, 1155–1183. [Google Scholar] [CrossRef] [PubMed]
- Cattaneo, A.; Correggiari, A.; Langone, L.; Trincardi, F. The late-Holocene Gargano subaqueous delta. Adriatic shelf: Sediment pathways and supply fluctuations. Mar. Geol. 2003, 193, 61–91. [Google Scholar] [CrossRef]
- Monticelli, L.S.; Caruso, G.; Decembrini, F.; Caroppo, C.; Fiesoletti, F. Role of prokaryotic biomasses and activities in carbon and phosphorus cycles at a coastal. thermohaline front and in offshore waters (Gulf of Manfredonia. Southern Adriatic Sea). Microb. Ecol. 2014, 67, 501–519. [Google Scholar] [CrossRef] [PubMed]
- Spagnoli, F.; Dell’Anno, A.; De Marco, A.; Dinelli, E.; Fabiano, M.; Gadaleta, M.V.; Iannig, C.; Loiaconoc, F.; Maninia, M.; Mongelli, G.; et al. Biogeochemistry, grain size and mineralogy of the central and southern Adriatic Sea sediments: A review. Chem. Ecol. 2010, 26 (Suppl. 1), 19–44. [Google Scholar] [CrossRef]
- Rebesco, M.; Neagu, R.C.; Cuppari, A.; Muto, F.; Accettella, D.; Dominici, R.; Caburlotto, A. Morphobathymetric analysis and evidence of submarine mass movements in the western Gulf of Taranto (Calabria margin. Ionian Sea). Int. J. Earth Sci. 2009, 98, 791–805. [Google Scholar] [CrossRef]
- Buccolieri, A.; Buccolieri, G.; Cardellicchio, N.; Dell’Atti, A.; Di Leo, A.; Maci, A. Heavy metals in marine sediments of Taranto Gulf (Ionian Sea. southern Italy). Mar. Chem. 2006, 99, 227–235. [Google Scholar] [CrossRef]
- Cardellicchio, N.; Buccolieri, A.; Di Leo, A.; Giandomenico, S.; Spada, L. Levels of metals in reared mussels from Taranto Gulf (Ionian Sea. Southern Italy). Food Chem. 2008, 107, 890–896. [Google Scholar] [CrossRef]
- Cattaneo, A.; Trincardi, F.; Asioli, A.; Correggiari, A. The Western Adriatic shelf clinoform: Energy-limited bottomset. Cont. Shelf Res. 2007, 27, 506–525. [Google Scholar] [CrossRef]
- Roselli, L.; Fabbrocini, A.; Manzo, C.; D’Adamo, R. Hydrological heterogeneity, nutrient dynamics and water quality of a non-tidal lentic eco system (Lesina Lagoon, Italy). Estuar. Coast. Shelf Sci. 2009, 84, 539–552. [Google Scholar] [CrossRef]
- Crease, J.; Dauphinee, T.; Grose, P.L.; Lewis, E.L.; Fofonoff, N.P.; Plakhin, E.A.; Striggow, K.; Zenk, W. The Acquisition, Calibration and Analysis of CTD Data; UNESCO Technical Papers in Marine Sciences: Paris, France, 1988; Volume 54, pp. 1–105. [Google Scholar]
- Webster, P.J.; Clayson, C.A.; Curry, J.A. Clouds, radiation, and the diurnal cycle of sea surface temperature in the tropical western Pacific. J. Clim. 1996, 9, 1712–1730. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air–sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Donlon, C.J.; Keogh, S.J.; Baldwin, D.J.; Robinson, I.S.; Ridley, I.; Sheasby, T.; Barton, I.J.; Bradley, E.F.; Nightingale, T.J.; Emery, W. Solid-State Radiometer Measurements of Sea Surface Skin Temperature. J. Atmos. Ocean. Technol. 1998, 15, 775–787. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Godfrey, J.S.; Wick, G.A.; Edson, J.B.; Young, G.S. Cool-skin and warm-layer effects on sea surface temperature. J. Geophys. Res. Oceans 1996, 101, 1295–1308. [Google Scholar] [CrossRef]
- Kawai, Y.; Wada, A. Diurnal sea surface temperature variation and its impact on the atmosphere and ocean: A review. J. Oceanogr. 2007, 63, 721–744. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Minnett, P.J.; Ward, B. Profiles of ocean surface heating (POSH): A new model of upper ocean diurnal warming. J. Geophys. Res. Oceans 2009, 114, C07017. [Google Scholar] [CrossRef]
- Mueller, J.L.; McClain, G.; Bidigare, R.; Trees, C.; Balch, W.; Dore, J.; Drapeau, D.; Karl, D.; Van, L. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 5, Volume V: Biogeochemical and Bio-Optical Measurements and Data Analysis Protocols; NASA Technical Memorandum 2003-21621; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003; pp. 1–36.
- Pegau, S.; Zaneveld, J.R.V.; Mitchell, B.G.; Mueller, J.L.; Kahru, M.; Wieland, J.; Stramska, M. Ocean Optics Protocols For Satellite Ocean Color Sensor Validation, Revision 4, Volume IV: Inherent Optical Properties: Instruments, Characterizations, Field Measurements and Data Analysis Protocols; NASA Technical Memorandum 2003-211621; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003; pp. 1–76.
- Walton, C.C. A review of differential absorption algorithms utilized at NOAA for measuring sea surface temperature with satellite radiometers. Remote Sens. Environ. 2016, 187, 434–446. [Google Scholar] [CrossRef]
- François, C.; Brisson, A.; Le Borgne, P.; Marsouin, A. Definition of a radiosounding database for sea surface brightness temperature simulations: Application to sea surface temperature retrieval algorithm determination. Remote Sens. Environ. 2002, 81, 309–326. [Google Scholar] [CrossRef]
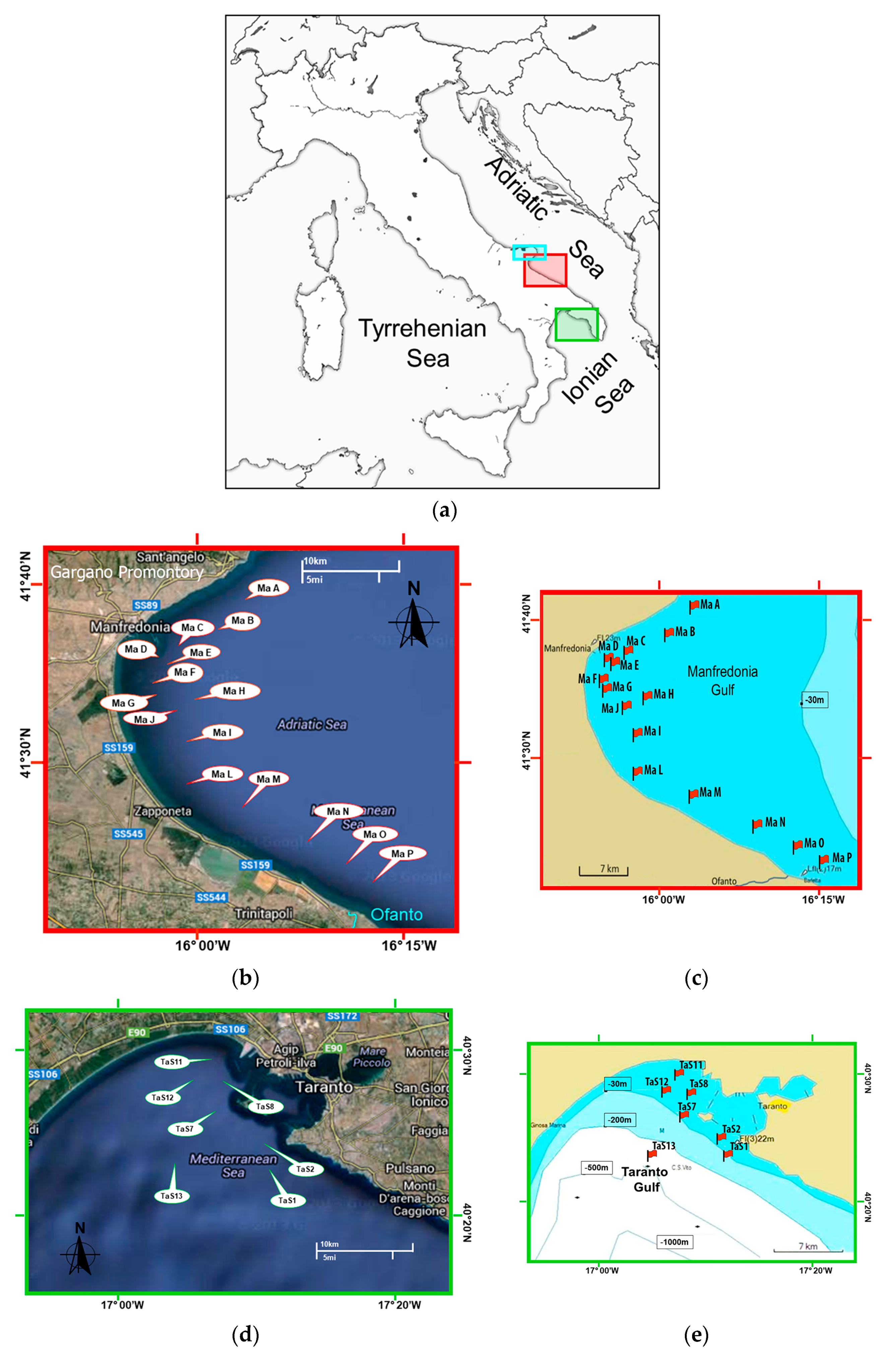
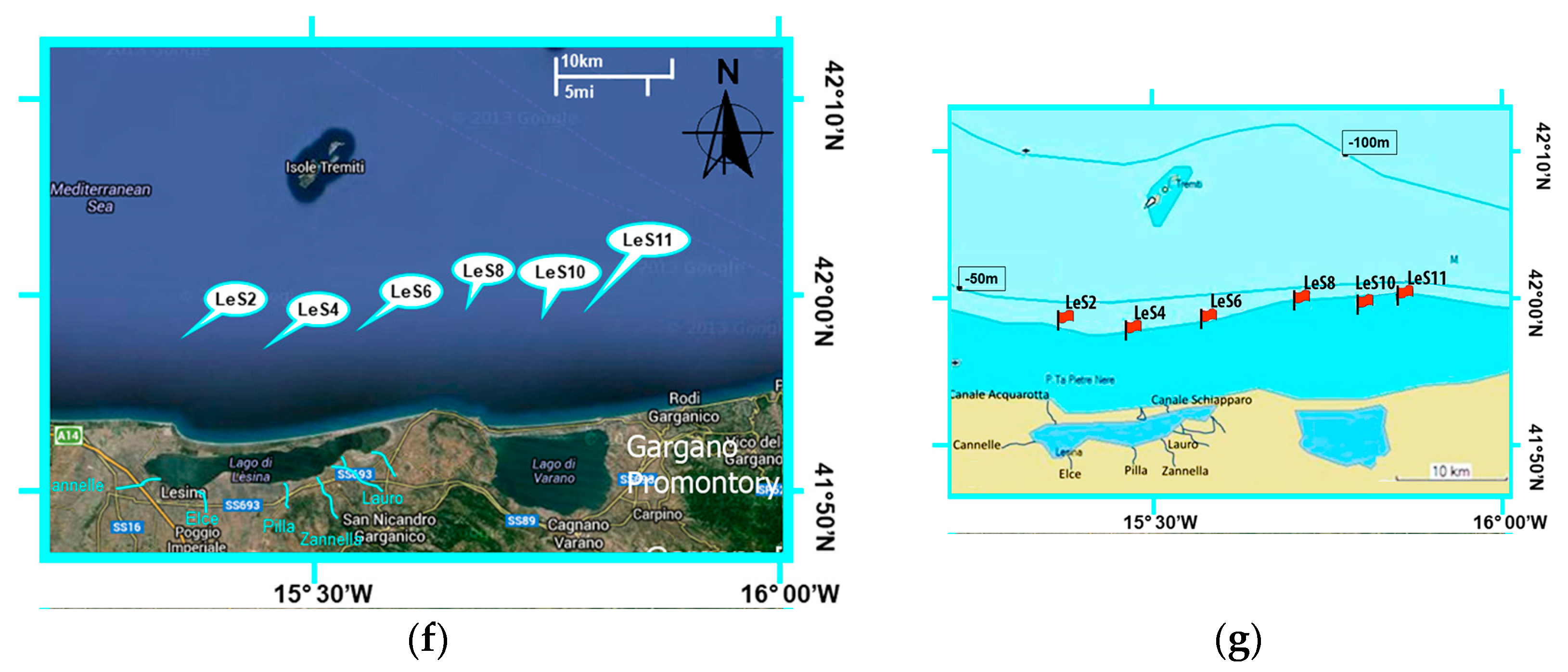
| Coastal Waters of the Manfredonia Gulf | ||||||
| Date | Start Time (UTC) | Number of Locations | SPM (mg/L) | Salinity (g/L) | SSTskin (K) | |
| 08/08/2011 | 11:45 | 5 | Mean | 3.01 | 38.22 | 301.10 |
| σ | 1.82 | 0.06 | 0.69 | |||
| 09/08/2011 | 12:25 | 7 | Mean | 3.16 | 38.17 | 301.22 |
| σ | 0.75 | 0.04 | 0.55 | |||
| 12/08/2011 | 11:20 | 8 | Mean | 5.42 | 38.33 | 299.79 |
| σ | 2.24 | 0.07 | 0.38 | |||
| 24/08/2011 | 11:40 | 11 | Mean | 7.44 | 38.41 | 301.86 |
| σ | 0.86 | 0.04 | 0.51 | |||
| Coastal Waters of the Taranto Gulf | ||||||
| Date | Start Time (UTC) | Number of Locations | SPM (mg/L) | Salinity (g/L) | SSTskin (K) | |
| 13/08/2011 | 12:00 | 5 | Mean | 2.36 | 38.31 | 299.47 |
| σ | 0.58 | 0.01 | 0.34 | |||
| 14/08/2011 | 12:45 | 6 | Mean | 1.93 | 38.29 | 300.25 |
| σ | 0.63 | 0.04 | 0.42 | |||
| 15/08/2011 | 11:50 | 6 | Mean | 2.37 | 38.30 | 299.81 |
| σ | 0.56 | 0.06 | 0.42 | |||
| 16/08/2011 | 12:30 | 2 | Mean | 1.69 | 38.23 | 299.99 |
| σ | 0.11 | 0.01 | 0.26 | |||
| Coastal Waters of the Area Close to Lesina Lagoon | ||||||
| Date | Start Time (UTC) | Number of Locations | SPM (mg/L) | Salinity (g/L) | SSTskin (K) | |
| 07/08/2011 | 12:40 | 6 | Mean | 1.50 | 37.86 | 300.12 |
| σ | 0.41 | 0.08 | 0.21 | |||
| Date Start Time | SST1(radiosonde based) (K) | SST1(ECMWF based) (K) | SST1(collection 5) (K) | SST2(collection 6) (K) | |
|---|---|---|---|---|---|
| Coastal Waters of the Manfredonia Gulf | |||||
| 08/08/2011 11:45 UTC | Bias | −2.19 ** | −0.78 ** | −0.28 # | 0.25 # |
| σ | 0.33 | 0.35 | 0.67 | 0.65 | |
| RMSD | 2.21 | 0.84 | 0.67 | 0.65 | |
| 09/08/2011 12:25 UTC | Bias | −2.57 ** | −0.93 ** | −0.19 # | 0.27 # |
| σ | 0.94 | 0.97 | 0.91 | 0.95 | |
| RMSD | 2.71 | 1.30 | 0.88 | 0.93 | |
| 12/08/2011 11:20 UTC | Bias | −4.19 ** | −1.16 ** | 0.64 * | 1.02 * |
| σ | 0.30 | 0.27 | 0.30 | 0.31 | |
| RMSD | 4.20 | 1.18 | 0.70 | 1.06 | |
| 24/08/2011 11:40 UTC | Bias | −1.26 ** | −0.76 ** | 0.66 * | 0.30 * |
| σ | 0.30 | 0.31 | 0.34 | 0.32 | |
| RMSD | 1.30 | 0.82 | 0.74 | 0.43 | |
| Coastal Waters of the Taranto Gulf | |||||
| 13/08/2011 12:00 UTC | Bias | −2.46 ** | −1.42 ** | −0.84 ** | −0.59 ** |
| σ | 0.15 | 0.13 | 0.12 | 0.12 | |
| RMSD | 2.47 | 1.42 | 0.85 | 0.60 | |
| 14/08/2011 12:45 UTC | Bias | −3.12 ** | −1.37 ** | 0.83 * | 0.61 * |
| σ | 1.16 | 1.10 | 0.23 | 0.22 | |
| RMSD | 3.30 | 1.70 | 0.85 | 0.65 | |
| 15/08/2011 11:50 UTC | Bias | −2.12 ** | −1.02 ** | −0.74 ** | −0.48 ** |
| σ | 0.37 | 0.35 | 0.32 | 0.31 | |
| RMSD | 2.15 | 1.07 | 0.80 | 0.56 | |
| 16/08/2011 12:30 UTC | Bias | −1.59 ** | −0.82 ** | 0.46 * | 0.41 * |
| σ | 0.03 | 0.06 | 0.11 | 0.11 | |
| RMSD | 1.59 | 0.82 | 0.47 | 0.42 | |
| Coastal Waters of the Area Close to Lesina Lagoon | |||||
| 07/08/2011 12:40 UTC | Bias | −1.46 ** | −1.11 ** | 0.57 # | 0.52 # |
| σ | 0.27 | 0.28 | 0.47 | 0.44 | |
| RMSD | 1.48 | 1.14 | 0.71 | 0.66 | |
| Date Start Time | SST3 (K) | SST4 (K) | SST5 (K) | SST6 (K) | |
|---|---|---|---|---|---|
| Coastal Waters of the Manfredonia Gulf | |||||
| 08/08/2011 11:45 UTC | Bias | −0.36 # | 0.48 # | 0.63 * | −0.72 # |
| σ | 0.39 | 0.41 | 0.47 | 0.43 | |
| RMSD | 0.51 | 0.61 | 0.76 | 0.82 | |
| 09/08/2011 12:25 UTC | Bias | −0.49 # | 0.43 # | 4.21 * | −0.72 # |
| σ | 0.99 | 1.01 | 1.09 | 1.09 | |
| RMSD | 1.05 | 1.04 | 9.67 | 1.26 | |
| 12/08/2011 11:20 UTC | Bias | −0.35 # | −0.50 # | −1.91 ** | −0.79 # |
| σ | 0.29 | 0.30 | 0.27 | 0.52 | |
| RMSD | 0.45 | 0.58 | 1.92 | 0.93 | |
| 24/08/2011 11:40 UTC | Bias | −0.34 # | −0.55 # | −0.73 ** | −0.69 ** |
| σ | 0.32 | 0.31 | 0.31 | 0.31 | |
| RMSD | 0.46 | 0.63 | 0.79 | 0.75 | |
| Coastal Waters of the Taranto Gulf | |||||
| 13/08/2011 12:00 UTC | Bias | −0.27 ** | −0.43 ** | −1.45 ** | −1.03 ** |
| σ | 0.12 | 0.13 | 0.13 | 0.12 | |
| RMSD | 0.29 | 0.44 | 1.45 | 1.03 | |
| 14/08/2011 12:45 UTC | Bias | −1.06 ** | −0.99 ** | −2.60 ** | −0.54 ** |
| σ | 0.25 | 0.25 | 0.41 | 0.25 | |
| RMSD | 1.09 | 1.01 | 2.63 | 0.59 | |
| 15/08/2011 11:50 UTC | Bias | −0.14 # | −0.31 # | −0.94 ** | −0.72 ** |
| σ | 0.31 | 0.30 | 0.33 | 0.32 | |
| RMSD | 0.32 | 0.42 | 0.99 | 0.78 | |
| 16/08/2011 12:30 UTC | Bias | −0.60 ** | −0.59 ** | −1.55 ** | −0.51 ** |
| σ | 0.16 | 0.12 | 0.05 | 0.07 | |
| RMSD | 0.61 | 0.60 | 1.55 | 0.52 | |
| Coastal Waters of the Area Close to Lesina Lagoon | |||||
| 07/08/2011 12:40 UTC | Bias | −0.27 # | 0.40 # | −1.56 ** | −0.49 # |
| σ | 0.41 | 0.45 | 0.48 | 0.48 | |
| RMSD | 0.46 | 0.57 | 1.62 | 0.66 | |
| Date Start Time | LST1 (K) | LST2 (K) | LST3 (K) | LST4 (K) | |
|---|---|---|---|---|---|
| Coastal Waters of the Manfredonia Gulf | |||||
| 08/08/2011 11:45 UTC | Bias | −0.70 ** | −0.36 # | −0.89 # | 5.25 * |
| σ | 0.29 | 0.44 | 0.35 | 0.37 | |
| RMSD | 0.75 | 0.54 | 0.94 | 5.26 | |
| 09/08/2011 12:25 UTC | Bias | −0.11 # | −0.29 # | −2.43 ** | 4.76 * |
| σ | 0.76 | 0.99 | 1.14 | 0.46 | |
| RMSD | 0.75 | 0.93 | 2.95 | 9.36 | |
| 12/08/2011 11:20 UTC | Bias | −0.91 ** | −0.04 # | −0.06 # | 1.12 # |
| σ | 0.27 | 0.40 | 0.30 | 1.02 | |
| RMSD | 0.94 | 0.38 | 0.30 | 1.48 | |
| 24/08/2011 11:40 UTC | Bias | −0.65 ** | −0.30 # | 0.00 # | 2.89 * |
| σ | 0.31 | 0.31 | 0.31 | 0.32 | |
| RMSD | 0.72 | 0.42 | 0.30 | 2.90 | |
| Coastal Waters of the Taranto Gulf | |||||
| 13/08/2011 12:00 UTC | Bias | −0.69 ** | −0.16 ** | −0.12 ** | 2.29 * |
| σ | 0.12 | 0.13 | 0.12 | 0.13 | |
| RMSD | 0.64 | 0.20 | 0.16 | 2.29 | |
| 14/08/2011 12:45 UTC | Bias | −0.34 # | −0.60 ** | −1.20 ** | 1.97 # |
| σ | 0.36 | 0.31 | 0.33 | 0.24 | |
| RMSD | 0.47 | 0.66 | 1.24 | 1.98 | |
| 15/08/2011 11:50 UTC | Bias | −0.55 # | −0.04 # | −0.04 # | 3.10 * |
| σ | 0.33 | 0.30 | 0.32 | 0.30 | |
| RMSD | 0.63 | 0.28 | 0.30 | 3.12 | |
| 16/08/2011 12:30 UTC | Bias | −0.47 # | −0.33 ** | −0.13 | 2.17 * |
| σ | 0.21 | 0.13 | 0.08 | 0.05 | |
| RMSD | 0.49 | 0.34 | 0.15 | 2.17 | |
| Coastal Waters of the Area Close to Lesina Lagoon | |||||
| 07/08/2011 12:40 UTC | Bias | −0.19 # | −0.05 # | −0.13 # | 2.06* |
| σ | 0.39 | 0.44 | 0.32 | 0.73 | |
| RMSD | 0.40 | 0.41 | 0.32 | 2.17 | |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavalli, R.M. Comparison of Split Window Algorithms for Retrieving Measurements of Sea Surface Temperature from MODIS Data in Near-Land Coastal Waters. ISPRS Int. J. Geo-Inf. 2018, 7, 30. https://doi.org/10.3390/ijgi7010030
Cavalli RM. Comparison of Split Window Algorithms for Retrieving Measurements of Sea Surface Temperature from MODIS Data in Near-Land Coastal Waters. ISPRS International Journal of Geo-Information. 2018; 7(1):30. https://doi.org/10.3390/ijgi7010030
Chicago/Turabian StyleCavalli, Rosa Maria. 2018. "Comparison of Split Window Algorithms for Retrieving Measurements of Sea Surface Temperature from MODIS Data in Near-Land Coastal Waters" ISPRS International Journal of Geo-Information 7, no. 1: 30. https://doi.org/10.3390/ijgi7010030
APA StyleCavalli, R. M. (2018). Comparison of Split Window Algorithms for Retrieving Measurements of Sea Surface Temperature from MODIS Data in Near-Land Coastal Waters. ISPRS International Journal of Geo-Information, 7(1), 30. https://doi.org/10.3390/ijgi7010030