A Knowledge Base for Automatic Feature Recognition from Point Clouds in an Urban Scene
Abstract
1. Introduction
2. Related Works
3. Building a Knowledge Base for Automatic Feature Recognition
- (1)
- identification of motivating scenarios and the scope of ontology;
- (2)
- definition of competency questions;
- (3)
- building the ontology (ontology capture, ontology coding and integrating the existing ones);
- (4)
- validation of the ontology according to the requirements set by competency question;
- (5)
- maintenance of ontology after verification.
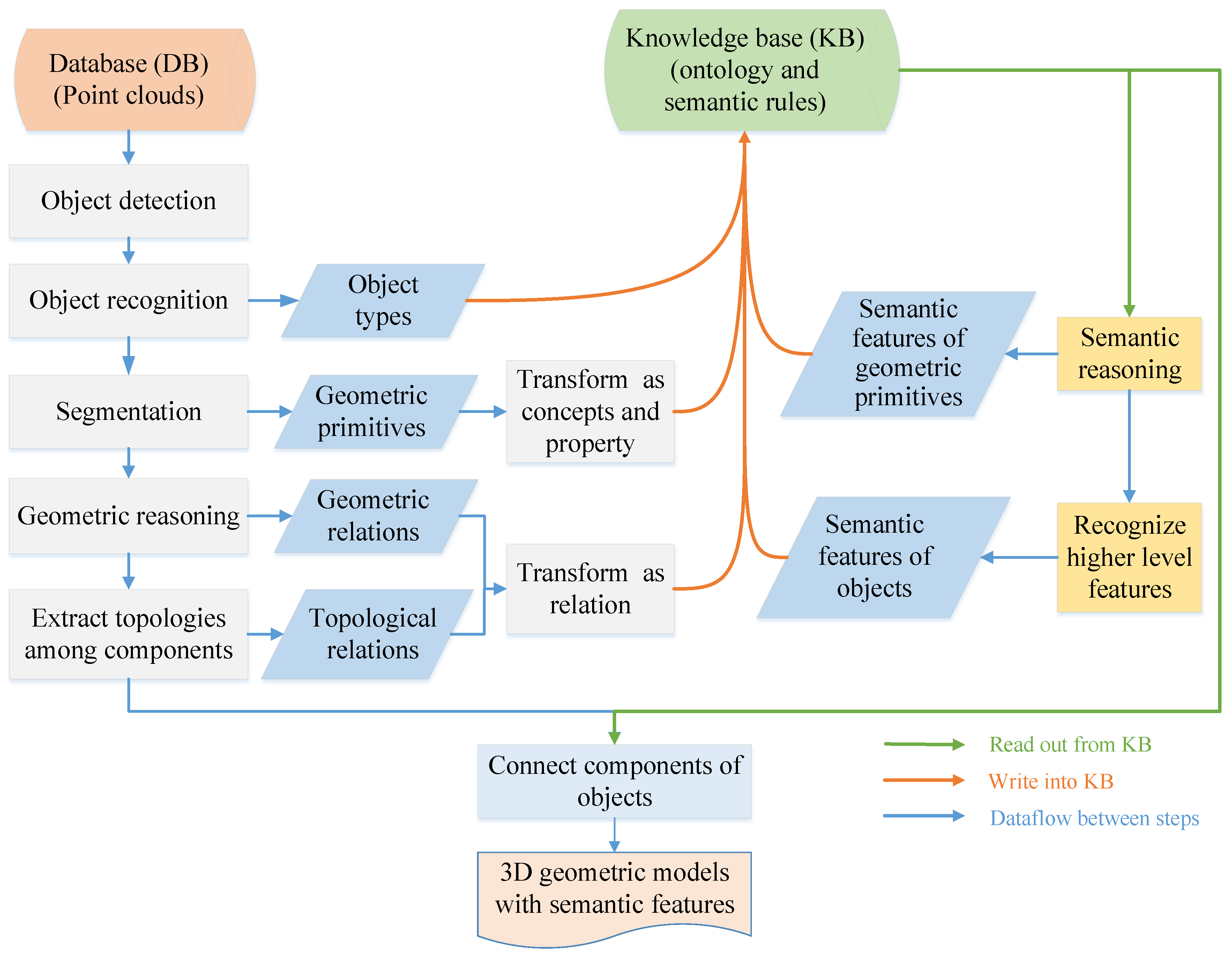
3.1. Conceptual Framework for Automatic 3D Modeling and Feature Recognition from Point Clouds of Urban Scenes
3.2. Definition of Concepts
3.3. Modularity of Concept in an Urban Scene
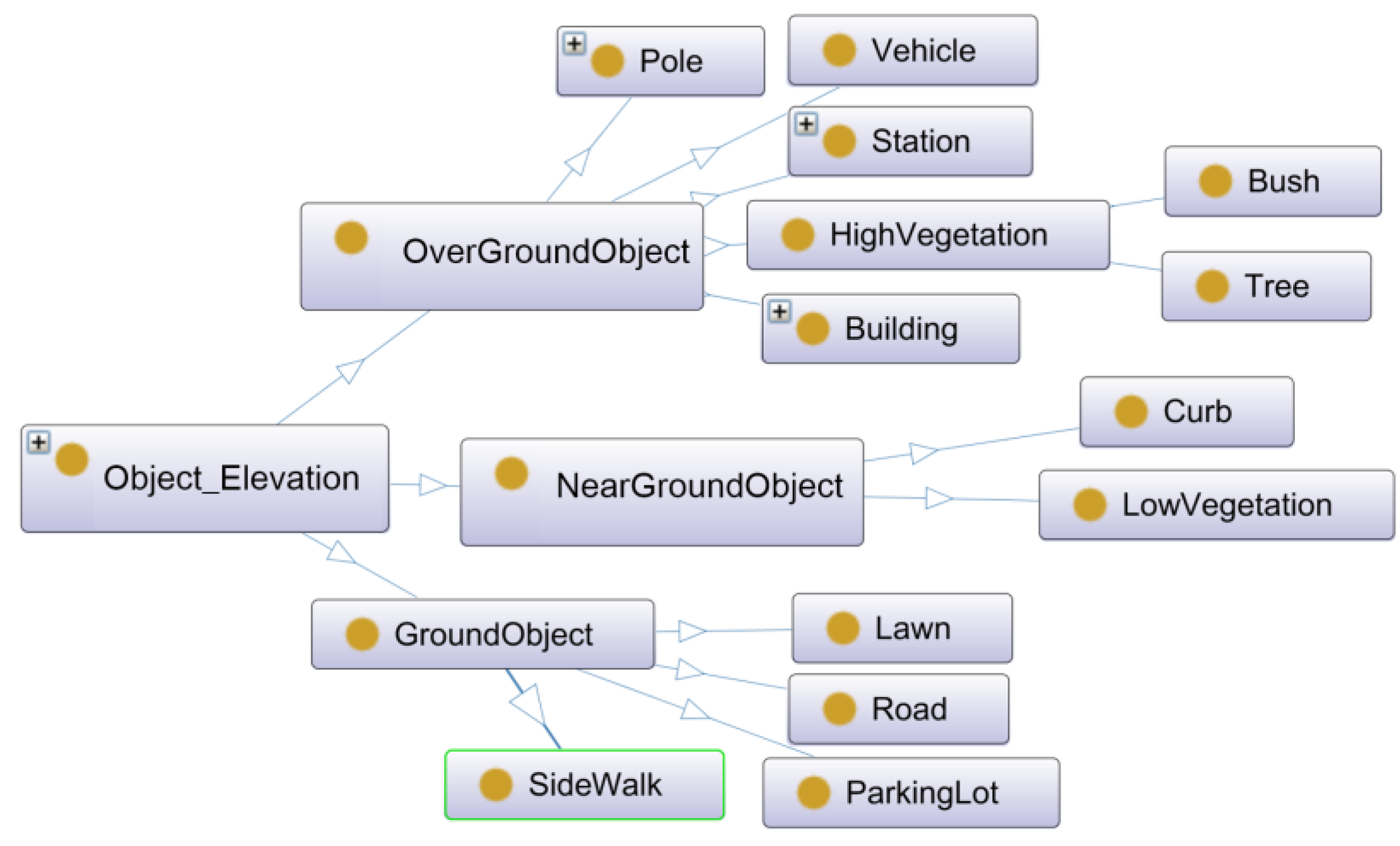
3.3.1. Elevation Perspective
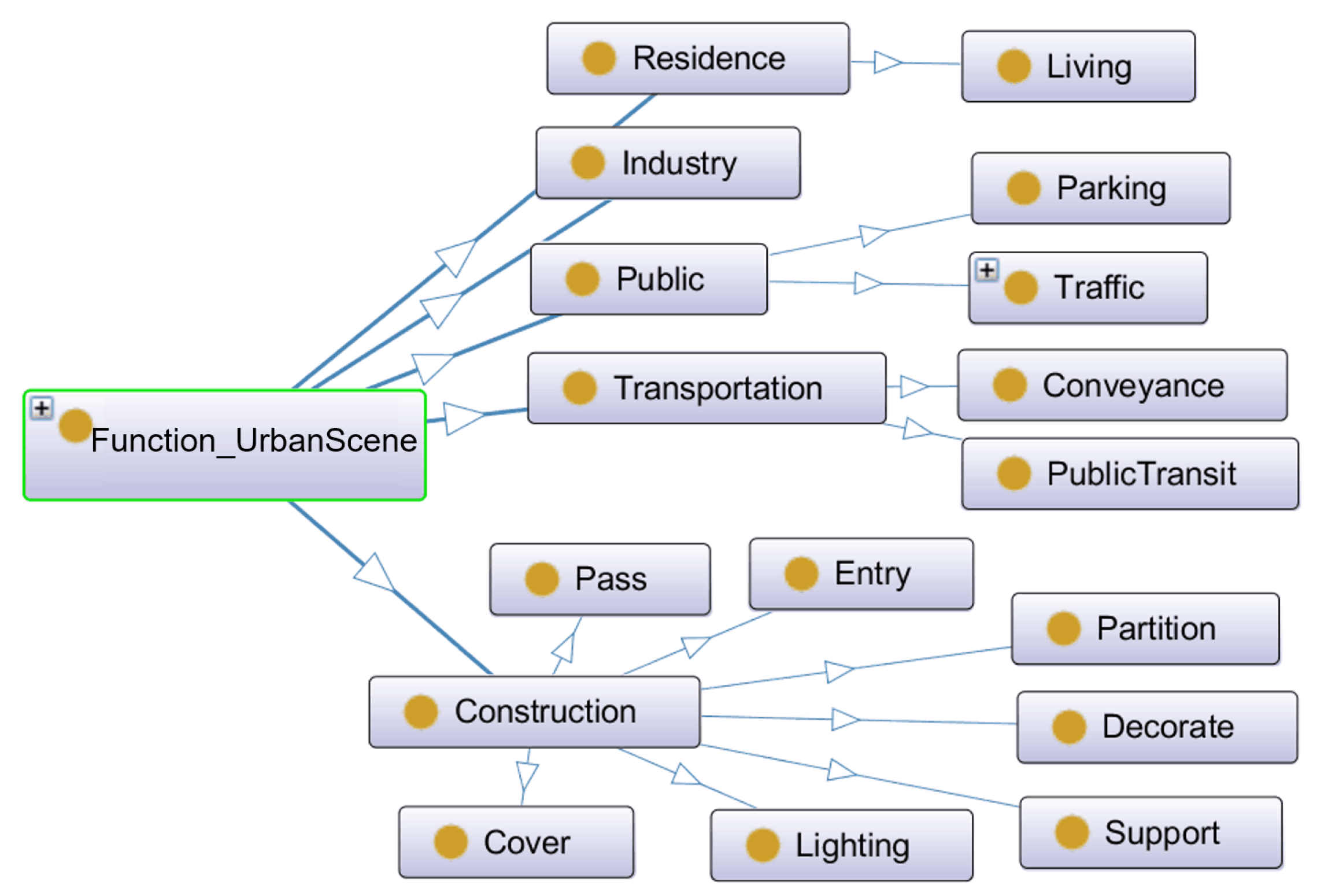
3.3.2. Functionality Perspective
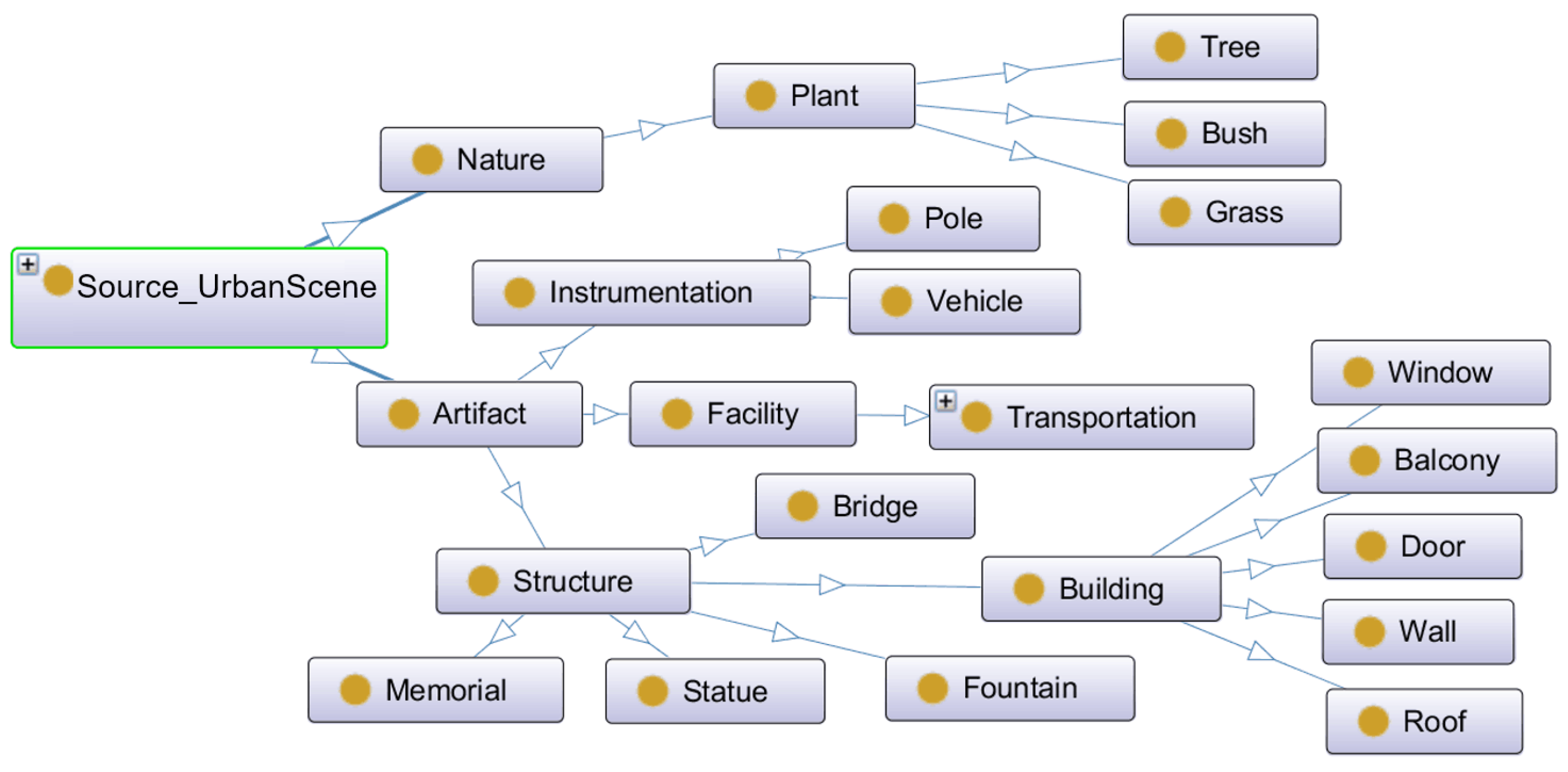
3.3.3. Nature of Objects Perspective
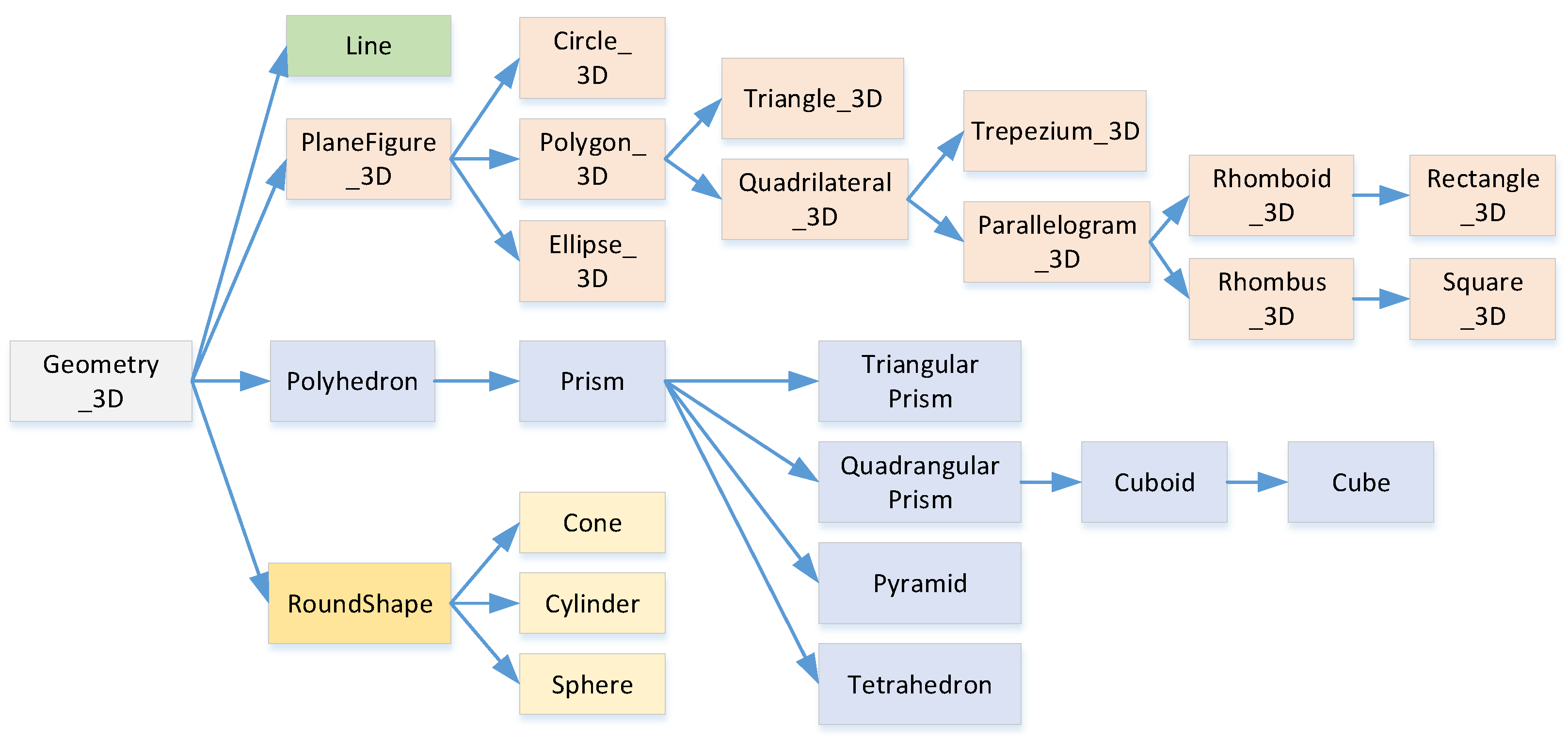
3.3.4. Geometry Module
3.3.5. Composition Module
- Components aggregation: an individual object can be broken down into some components that cannot be decomposed into any small parts. For example, in geometric model of a building, the patch representing a wall may not be divided into smaller pieces.
- Subsystem aggregation: this relationship indicates the abstract concepts for representing functionally relevant sets. For example, a parking lot area comprises of a piece of ground with some vehicles, some sign poles and some poles for paying the parking fee.
- System aggregation: this level is used to represent the top-level aggregation relationships among objects in an independent scene or objects in a network. Examples include transportation system containing many parts severing for transportation.
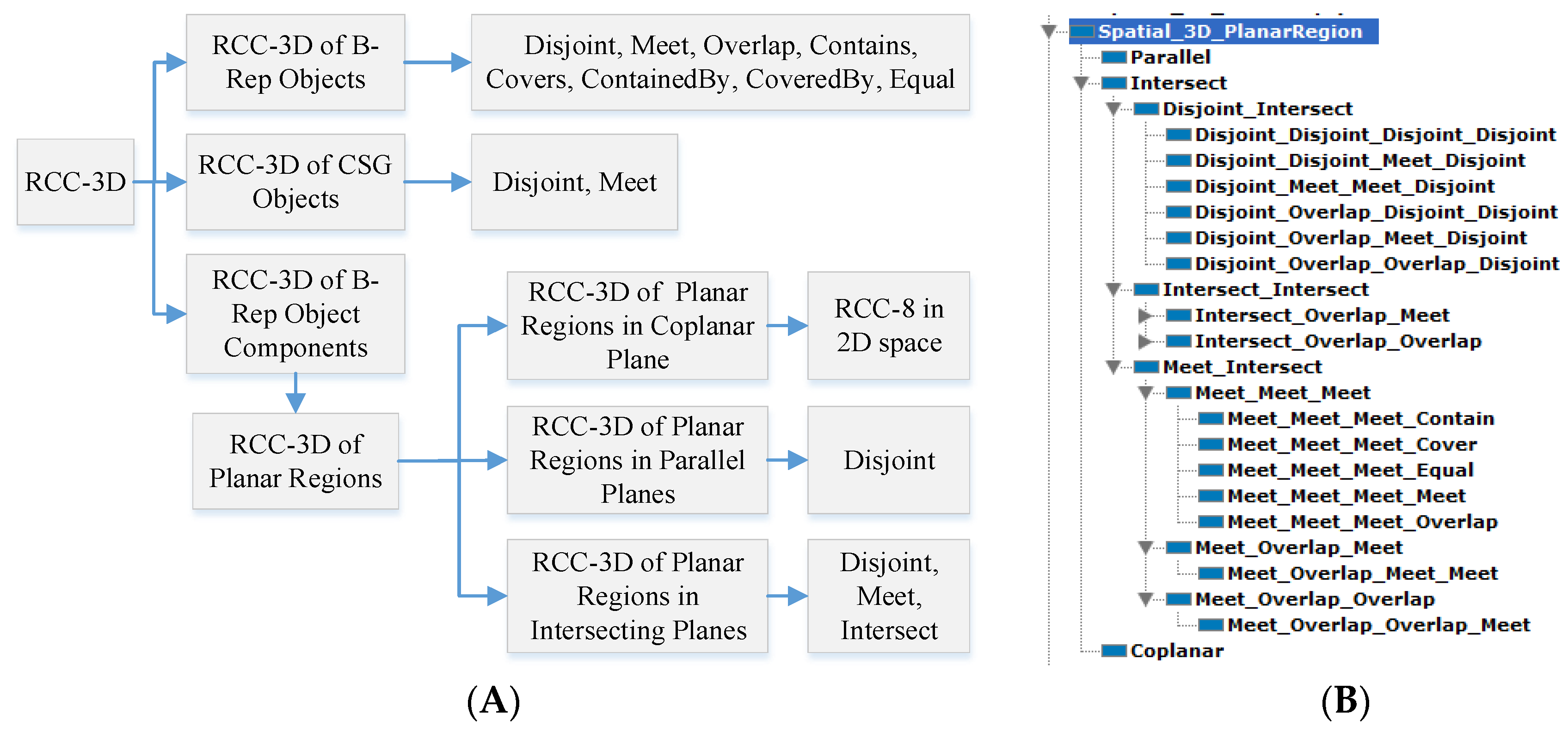
3.3.6. Spatial Relations Module
- If the planes are parallel, these two planar regions are disjoint.
- If the planes are coplanar, the relation between two planar regions is determined as in 2D space.
- If the planes are intersecting, two planar regions can have many possible topological relations.
- = indicates the interior of the region A;
- = the boundary of the region A;
- = the interior of the region B;
- = the boundary of the region B;
- = intersection of two planes containing planar regions A and B;
- records the topological relations of the primitives comprised of the common parts between the planar region A and B and intersection line. The primitives are all located on the intersection line;
- dim() = dimension operator.
- (1)
- The relation between the planar region A and the intersection line Il, including Disjoint, Meet and Overlap;
- (2)
- The relation between the planar region B and the intersection line Il;
- (3)
- The relations between primitives on the intersection line IL that are the common part comprised of planar region A and the intersection line and the common part comprised of planar region B and the intersection line.
3.4. Objects Attributes
3.5. Constraints
- Geometric dimensional constraints: for feature recognition, the essential and intrinsic attributes of objects, including measurable attributes, geometry shape attributes, limit the rough classification of objects.
- Spatial relations constraints: spatial constraints link objects in a local part of the urban scene. For some objects belonging to the transportation system, cars are moving on the road surface. Sidewalks are extending following the road or connected to roads. Traffic sign pole or light pole located near to the roads or sidewalks. Especially for man-made objects, components of objects have some topological relations constraints in the aspect of design or functional requirements. These constraints also can be represented as rules in the knowledge base.
- Logical constraints: some constraints are given not for the measurable or spatial constraints but from the view of logic. An example for interpreting logical constraints is that a parking lot is a piece of ground where accommodates a large amount of orderly arranged vehicles. Because logical constraints could associate concepts according to their logical relations of functions, locations, and system relevance, they are defined in the level of relevance among components of objects. Similarly, they can be defined in the level of subsystem consisting of objects.
3.6. Relationships Definition
- Hyponymy: it is the “is-a” relationship. It is the semantic relation of being subordinate or belonging to a lower rank or class [42]. Relationships including the definition of the kinds of concept constitute the backbone of ontological taxonomy tree structure. “is-a” relationship also contains some converted relationships, including synonymy and antonymy relations. “isEquivalentTo” and “isSimiliarTo” belong to synonymy relations. At the same time, “isDisjoint” and “isOpposite” are main relationships of antonymy [57].
- Meronymy: it is the “whole-part” relationship. It indicates the relationship of grouping concepts as a whole or decomposing concepts into parts. The relationships of “isPartof” and “isComposedof” are commonly defined in whole-part relations among concepts. In OWL ontologies, there are listed use cases of whole-part relations, such as defining “whole-part” relationships for individuals and class definition. Although the relationship “subclassOf” and “kind of” all are used to organize concepts hierarchically, their distinction must be made to decide the relationship in hierarchical concepts [58], including descriptive relations, possessive attributes (“has” relation), spatial relationship (locateAt, connect, align, parallel, vertical, direction, above, on, in), function relationship (hasFunction), and composition relations (must-beComposedOf, could-beComposedOf).
3.7. Axioms
| Plane(?P1), Plane(?P2), Line(?L1), isPerpendicularTo(?P1,?L1), isPerpendicularTo(?P2,?L1) -> isParallel(?P1,?P2) |
| Line(?L1), Line(?L2), Line(?L3), isPerpendicularTo(?L1,?L3), isPerpendicularTo(?L2,?L3) -> isParellel(?L1,?L2) |
| Plane(?P1), Plane(?P2), Plane(?P3), Plane(?P4), isPerpendicularTo(?P1,?P3), isPerpendicularTo(?P1,?P4), isPerpendicularTo (?P3,?P4), isPerpendicularTo(?P2,?P3), isPerpendicularTo (?P2,?P4) -> isParallel(P1,?P2) |
4. Experimentation and Results
4.1. Consistency Check in Protégé
4.2. Reasoning Experiments Based on Knowledge Base
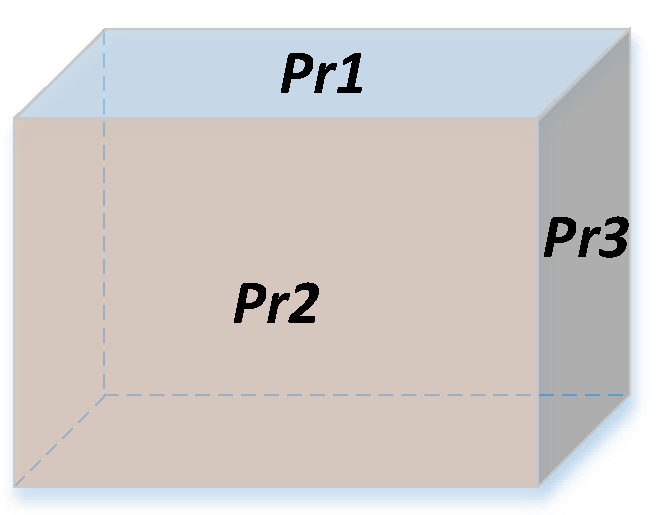
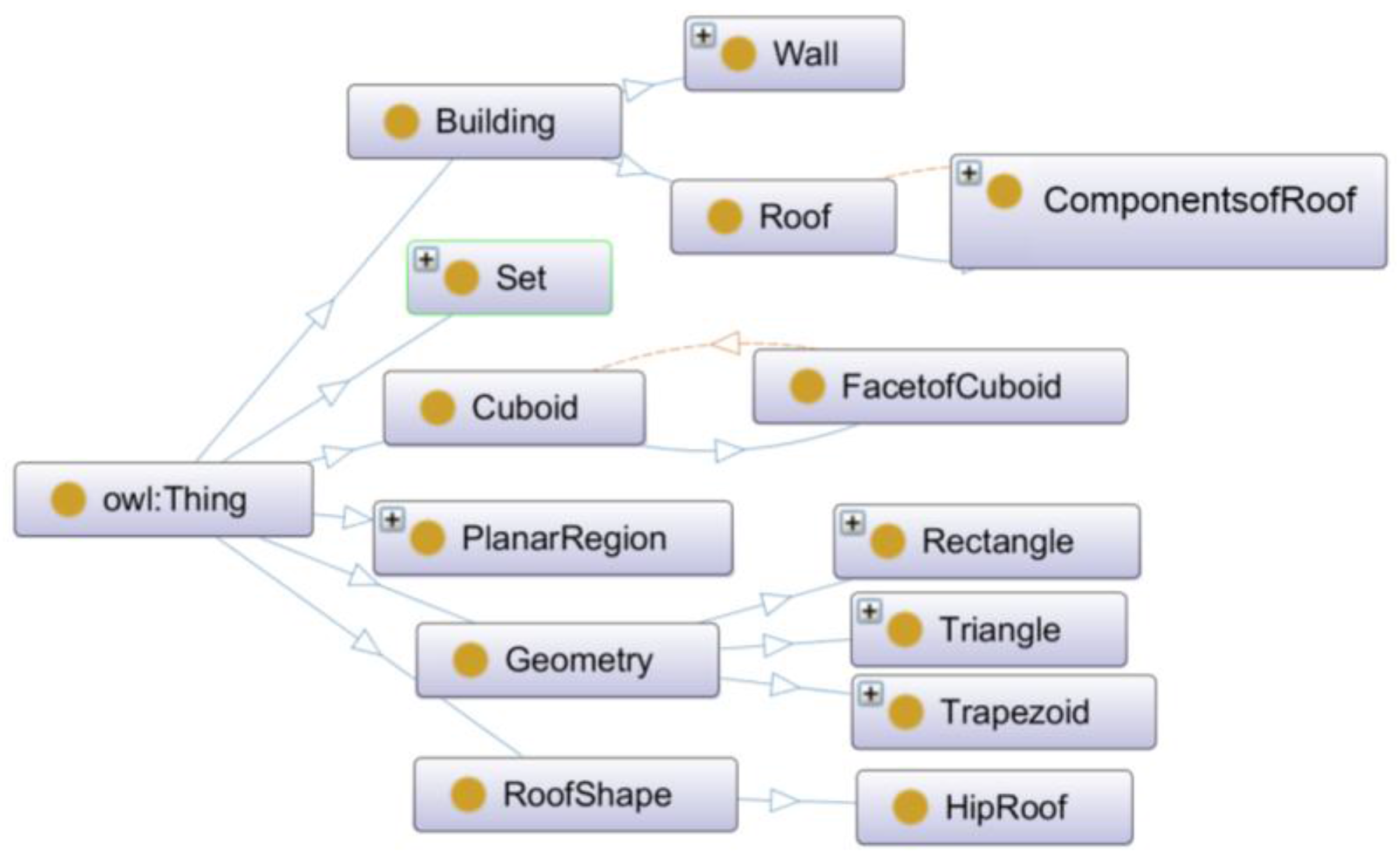
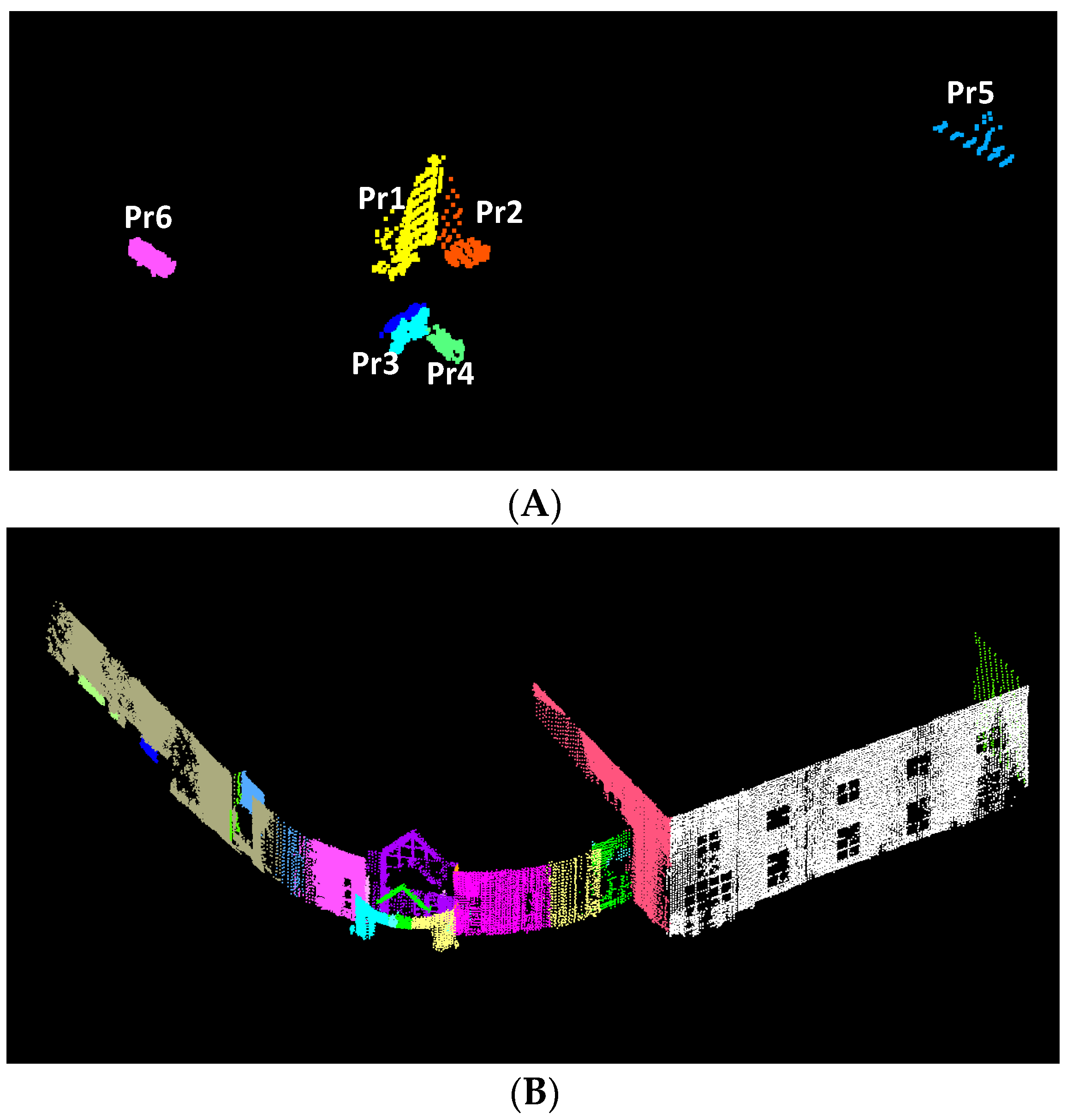
4.2.1. Experiment of Recognizing a Cuboid from Planar Regions
| PlanarRegion(?Pr1), PlanarRegion(?Pr2), isNeighboringTo(?Pr1,?Pr2), isMeet_Meet_Meet_Equal(?Pr1,?Pr2), isVerticalTo(?Pr1,?Pr2) -> isMeet_Equal_Vertical(?Pr1,?Pr2) | (1) |
| PlanarRegion(?Pr1), PlanarRegion(?Pr2), PlanarRegion(?Pr3), PlanarRegion(?Pr4), PlanarRegion(?Pr6), Rectangle(?Pr1), isNeighboringTo(?Pr2,?Pr1), isNeighboringTo(?Pr2,?Pr3), isNeighboringTo(?Pr2,?Pr4), isNeighboringTo(?Pr2,?Pr5), isMeet_Equal_Vertical(?Pr2,?Pr1), isMeet_Equal_Vertical(?Pr2,?Pr3), isMeet_Equal_Vertical(?Pr2,?Pr4), isMeet_Equal_Vertical(?Pr2,?Pr6) -> FacetofCuboid(?Pr2) | (2) |
| Set(?A), PlanarRegion(?Pr1), PlanarRegion(?Pr2), PlanarRegion(?Pr3), PlanarRegion(?Pr4), PlanarRegion(?Pr5), PlanarRegion(?Pr6), isInSet(?Pr1,?A), isInSet(?Pr2,?A), isInSet(?Pr3,?A), isInSet(?Pr4,?A), isInSet(?Pr5,?A), isInSet(?Pr6,?A), FacetofCuboid(?Pr1), FacetofCuboid(?Pr2), FacetofCuboid(?Pr3), FacetofCuboid(?Pr4), FacetofCuboid(?Pr5), FacetofCuboid(?Pr6) -> Cuboid(?A) | (3) |
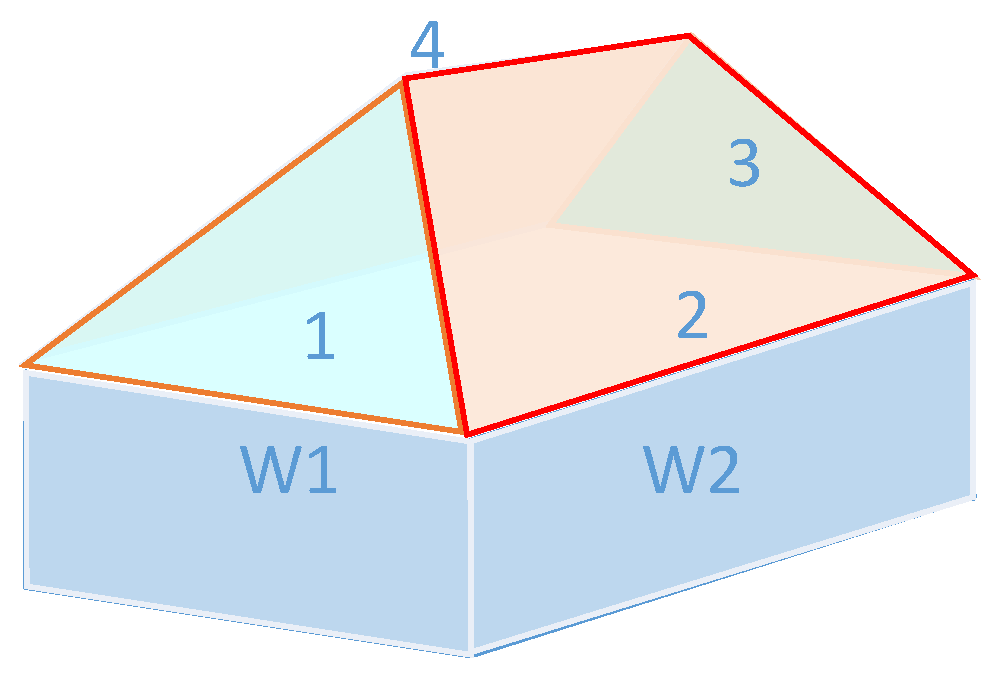
4.2.2. Axioms and Rules to Formally Define a Hip Roof from Planar Regions
| Set(?B), Wall(?W1), Wall(?W2), Wall(?W3), Wall(?W4), Trapezoid(?Trap), Triangle(?Tri), PlanarRegion(?Pra1), isInSet(?Pra1,?B), ComponentsofRoof(?Pra1), PlanarRegion(?Pra2), isInSet(?Pra2,?B), ComponentsofRoof(?Pra2), PlanarRegion(?Pra3), isInSet(?Pra3,?B), ComponentsofRoof(?Pra3), PlanarRegion(?Pra4), isInSet(?Pra4,?B), ComponentsofRoof(?Pra4), hasShape(?Pra1,?Tri), hasShape(?Pra2,?Trap), hasShape(?Pra3,?Tri), hasShape(?Pra4,?Trap), isMeet_Meet_Meet_Equal(?Pra1,?Pra4), isMeet_Meet_Meet_Equal(?Pra1,?Pra2), isMeet_Meet_Meet_Equal(?Pra3,?Pra4), isMeet_Meet_Meet_Equal(?Pra3,?Pra2), isMeet_Meet_Meet_Equal(?Pra2,?Pra3), isMeet_Meet_Meet_Equal(?Pra2,?Pra1), isMeet_Meet_Meet_Equal(?Pra2,?Pra4), isMeet_Meet_Meet_Equal(?Pra4,?Pra3), isMeet_Meet_Meet_Equal(?Pra4,?Pra1), isMeet_Meet_Meet_Equal(?Pra4,?Pra2), isSlopeTo(?Pra1,?W1), isSlopeTo(?Pra2,?W2), isSlopeTo(?Pra3,?W3), isSlopeTo(?Pra4,?W4) -> HipRoof(?B) | (4) |
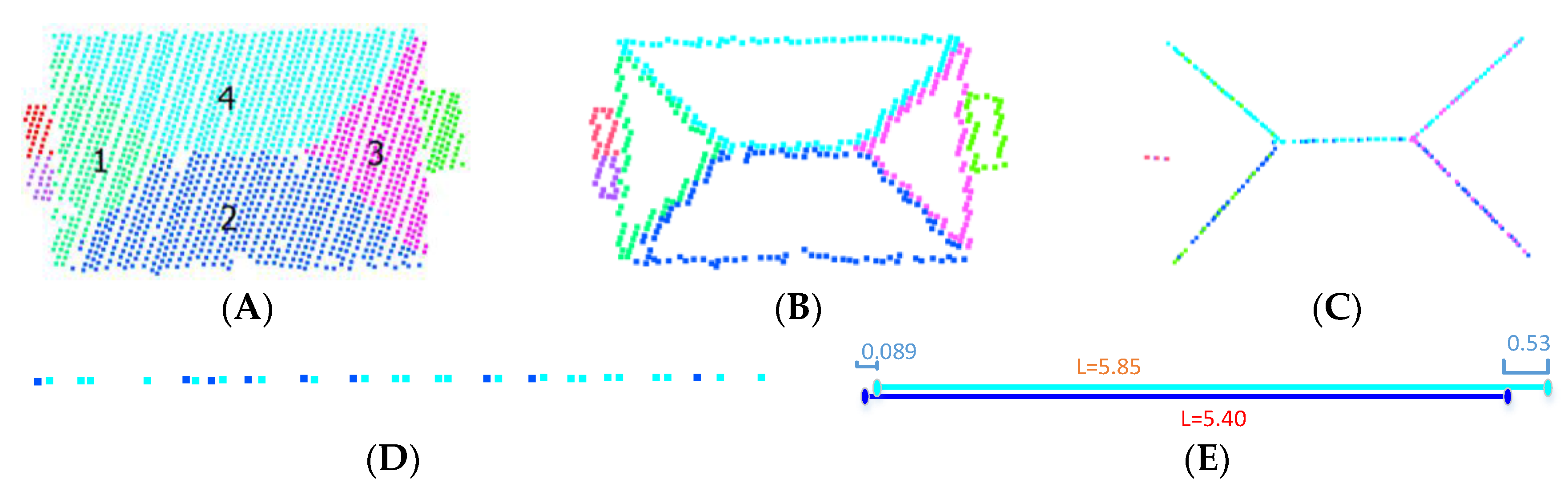
4.2.3. Experiment for Recognizing a Hip Roof from Point Clouds
| Set(?B), Ground(?g), Trapezoid(?Trap), Triangle(?Tri), PlanarRegion(?Pra1), isInSet(?Pra1,?B), ComponentsofRoof(?Pra1), PlanarRegion(?Pra2), isInSet(?Pra2,?B), ComponentsofRoof(?Pra2), PlanarRegion(?Pra3), isInSet(?Pra3,?B), ComponentsofRoof(?Pra3), PlanarRegion(?Pra4), isInSet(?Pra4,?B), ComponentsofRoof(?Pra4), hasShape(?Pra1,?Tri), hasShape(?Pra2,?Trap), hasShape(?Pra3,?Tri), hasShape(?Pra4,?Trap), isMeet_Meet_Meet_Equal(?Pra1,?Pra4), isMeet_Meet_Meet_Equal(?Pra1,?Pra2), isMeet_Meet_Meet_Equal(?Pra3,?Pra4), isMeet_Meet_Meet_Equal(?Pra3,?Pra2), isMeet_Meet_Meet_Equal(?Pra2,?Pra3), isMeet_Meet_Meet_Equal(?Pra2,?Pra1), isMeet_Meet_Meet_Equal(?Pra2,?Pra4), isMeet_Meet_Meet_Equal(?Pra4,?Pra3), isMeet_Meet_Meet_Equal(?Pra4,?Pra1), isMeet_Meet_Meet_Equal(?Pra4,?Pra2), isSlopeTo(?Pra1,?g), isSlopeTo(?Pra2,?g), isSlopeTo(?Pra3,?g), isSlopeTo(?Pra4,?g) -> HipRoof(?B) | (5) |
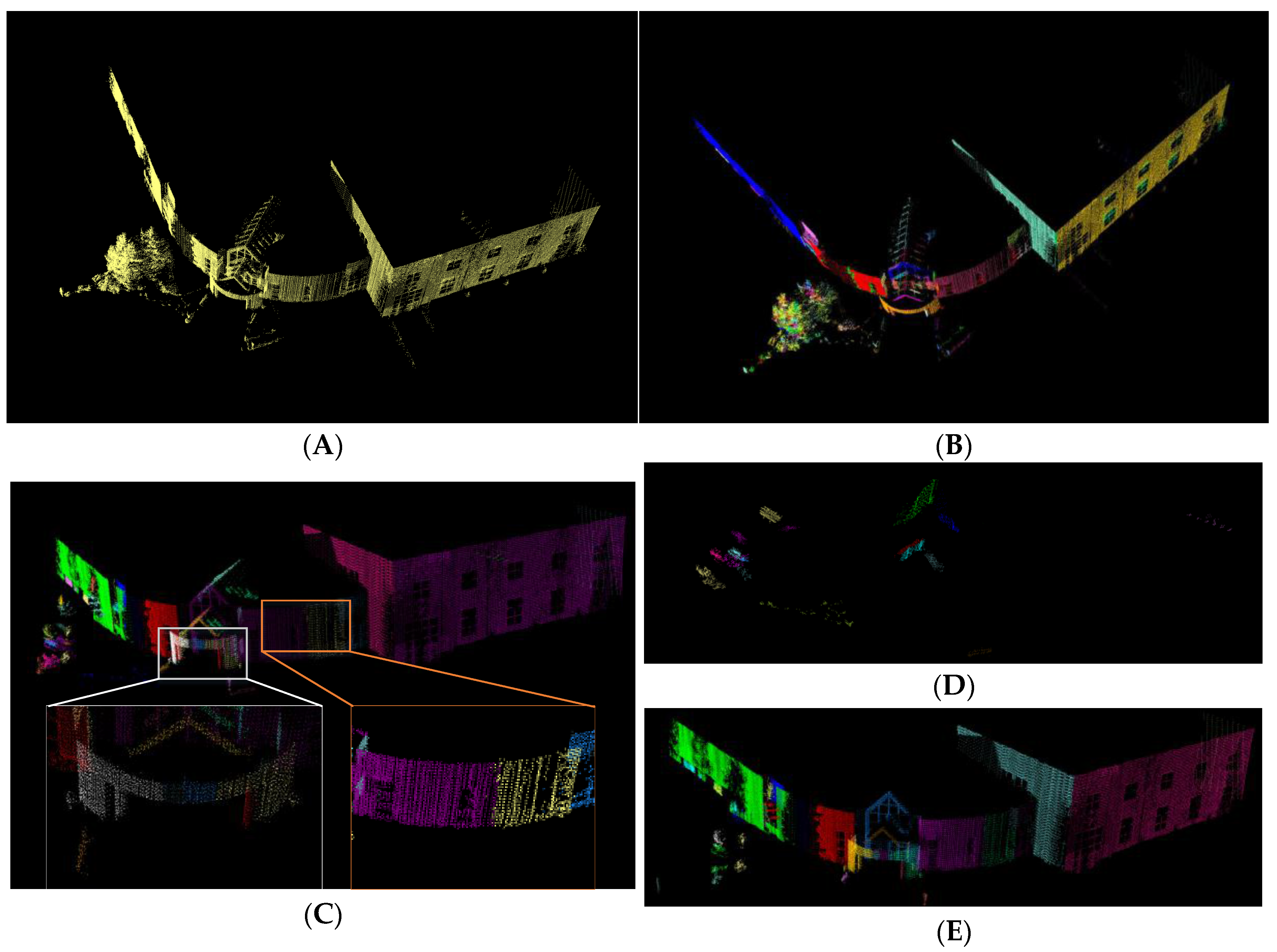
4.2.4. Experiment for Recognizing Semantic Features of Buildings from Point Clouds
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lin, H.; Chen, M.; Lu, G.; Zhu, Q.; Gong, J.; You, X.; Wen, Y.; Xu, B.; Hu, M. Virtual geographic environments (VGEs): A new generation of geographic analysis tool. Earth-Sci. Rev. 2013, 126, 74–84. [Google Scholar] [CrossRef]
- Lin, H.; Chen, M.; Lu, G. Virtual geographic environment: A workspace for computer-aided geographic experiments. Ann. Assoc. Am. Geogr. 2013, 103, 465–482. [Google Scholar] [CrossRef]
- Li, X.; Lv, Z.; Wang, W.; Wu, C.; Hu, J. Virtual reality gis and cloud service based traffic analysis platform. In Proceedings of the 23rd International Conference on Geoinformatics, Wuhan, China, 19–21 June 2015; pp. 1–6. [Google Scholar]
- Xu, B.; Lin, H.; Gong, J.; Tang, S.; Hu, Y.; Nasser, I.A.; Jing, T. Integration of a computational grid and virtual geographic environment to facilitate air pollution simulation. Comput. Geosci. 2013, 54, 184–195. [Google Scholar] [CrossRef]
- Xu, B.; Lin, H.; Chiu, L.; Hu, Y.; Zhu, J.; Hu, M.; Cui, W. Collaborative virtual geographic environments: A case study of air pollution simulation. Inf. Sci. 2011, 181, 2231–2246. [Google Scholar] [CrossRef]
- Torrens, P.M. Slipstreaming human geosimulation in virtual geographic environments. Ann. GIS 2015, 21, 325–344. [Google Scholar] [CrossRef]
- Mekni, M. Automated Generation of Geometrically-Precise and Semantically-Informed Virtual Geographic Environnements Populated with Spatially-Reasoning Agents. Ph.D. Thesis, Université Laval, Ville de Québec, QC, Canada, 2010. [Google Scholar]
- Pu, S.; Vosselman, G. Knowledge based reconstruction of building models from terrestrial laser scanning data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 575–584. [Google Scholar] [CrossRef]
- Tang, P.; Huber, D.; Akinci, B.; Lipman, R.; Lytle, A. Automatic reconstruction of as-built building information models from laser-scanned point clouds: A review of related techniques. Autom. Constr. 2010, 19, 829–843. [Google Scholar] [CrossRef]
- Guarino, N. Formal ontology, conceptual analysis and knowledge representation. Int. J. Hum.-Comput. Stud. 1995, 43, 625–640. [Google Scholar] [CrossRef]
- Gruber, T.R. Toward principles for the design of ontologies used for knowledge sharing. Int. J. Hum.-Comput. Stud. 1995, 43, 907–928. [Google Scholar] [CrossRef]
- Guarino, N. Formal Ontology and Information Systems. In Proceedings of the First International Conference (FOIS’98), Trento, Italy, 6–8 June 1998; IOS Press: Trento, Italy, 1998; Volume 46, pp. 3–15. [Google Scholar]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Holzbach, A.; Beetz, M. Model-based and learned semantic object labeling in 3D point cloud maps of kitchen environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 3601–3608. [Google Scholar]
- Cantzler, H. Improving Architectural 3D Reconstruction by Constrained Modelling. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2003. [Google Scholar]
- Loch-Dehbi, S.; Plümer, L. Automatic reasoning for geometric constraints in 3D city models with uncertain observations. ISPRS J. Photogramm. Remote Sens. 2011, 66, 177–187. [Google Scholar] [CrossRef]
- Hmida, H.B.; Cruz, C.; Boochs, F.; Nicolle, C. Knowledge base approach for 3D objects detection in point clouds using 3D processing and specialists knowledge. Int. J. Adv. Intell. Syst. 2012, 5, 1–14. [Google Scholar]
- Truong, Q.H. Knowledge-Based 3D Point Clouds Processing. Ph.D. Thesis, Université de Bourgogne, Dijon, France, 2013. [Google Scholar]
- Xiong, X.; Adan, A.; Akinci, B.; Huber, D. Automatic creation of semantically rich 3D building models from laser scanner data. Autom. Constr. 2013, 31, 325–337. [Google Scholar] [CrossRef]
- Truong, H.Q.; Hmida, H.B.; Boochs, F.; Habed, A.; Cruz, C.; Voisin, Y.; Nicolle, C. Automatic detection and qualification of objects in point clouds using multi-layered semantics. Photogramm. Fernerkund. Geoinform. 2013, 2013, 221–237. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.; Yu, J. Ontological inference of work item based on BIM data. KSCE J. Civil Eng. 2015, 19, 538–549. [Google Scholar] [CrossRef]
- Zhong, B.; Li, Y. An ontological and semantic approach for the construction risk inferring and application. J. Intell. Robot. Syst. 2014, 79, 1–15. [Google Scholar] [CrossRef]
- Pauwels, P.; Terkaj, W. Express to owl for construction industry: Towards a recommendable and usable ifcowl ontology. Autom. Constr. 2016, 63, 100–133. [Google Scholar] [CrossRef]
- Pauwels, P.; Krijnen, T.; Terkaj, W.; Beetz, J. Enhancing the ifcowl ontology with an alternative representation for geometric data. Autom. Constr. 2017, 80, 77–94. [Google Scholar] [CrossRef]
- Isikdag, U.; Zlatanova, S.; Underwood, J. A bim-oriented model for supporting indoor navigation requirements. Comput. Environ. Urban Syst. 2013, 41, 112–123. [Google Scholar] [CrossRef]
- Shayeganfar, F.; Anjomshoaa, A.; Tjoa, A. A smart indoor navigation solution based on building information model and google android. In Computers Helping People with Special Needs; Miesenberger, K., Klaus, J., Zagler, W., Karshmer, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5105, pp. 1050–1056. [Google Scholar]
- Hadzic, M.; Chang, E.; Wongthongtham, P.; Dillon, T. Ontology-Based Multi-Agent Systems; Springer: Berlin/Heidelberg, Germany, 2009; pp. 37–60. [Google Scholar]
- Guarino, N. Semantic matching: Formal ontological distinctions for information organization, extraction, and integration. In Information Extraction a Multidisciplinary Approach to an Emerging Information Technology, Proceedings of the International Summer School, Frascati, Italy, 14–18 July 1997; Pazienza, M.T., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 139–170. [Google Scholar]
- Grüninger, M.; Fox, M.S. Methodology for the design and evaluation of ontologies. In Workshop on Basic Ontological Issues in Knowledge Sharing; IJCAI-95: Montreal, QC, Canada, 1995. [Google Scholar]
- Fernández-López, M.; Gómez-Pérez, A.; Juristo, N. Methontology: From ontological art towards ontological engineering. In Proceedings of the Symposium on Ontological Engineering of AAAI, Stanford, CA, USA, 24–26 March 1997. [Google Scholar]
- Fernández-López, M.; Gómez-Pérez, A. Overview and analysis of methodologies for building ontologies. Knowl. Eng. Rev. 2002, 17, 129–156. [Google Scholar] [CrossRef]
- Wang, L.; Shi, J.; Song, G.; Shen, I.-F. Object detection combining recognition and segmentation. In Computer Vision–ACCV 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 189–199. [Google Scholar]
- Dorninger, P.; Nothegger, C. 3D segmentation of unstructured point clouds for building modelling. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Vienna University of Technology: Vienna, Austria, 2007; Volume 35, pp. 191–196. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D is here: Point cloud library (PCL). In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Shapiro, L.G.; Stockman, G.C. Computer Visión; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Jochem, A.; Höfle, B.; Rutzinger, M.; Pfeifer, N. Automatic roof plane detection and analysis in airborne lidar point clouds for solar potential assessment. Sensors 2009, 9, 5241–5262. [Google Scholar] [CrossRef] [PubMed]
- Nurunnabi, A.; West, G.; Belton, D. Outlier detection and robust normal-curvature estimation in mobile laser scanning 3D point cloud data. Pattern Recognit. 2015, 48, 1404–1419. [Google Scholar] [CrossRef]
- Gavrilova, T.; Laird, D. Practical design of business enterprise ontologies. In Industrial Applications of Semantic Web; Bramer, M., Terziyan, V., Eds.; Springer: New York, NY, USA, 2005; Volume 188, pp. 65–81. [Google Scholar]
- Gavrilova, T.; Carlucci, D.; Schiuma, G. Art of visual thinking for smart business education. In Proceedings of the 8th International Forum on Knowledge Asset Dynamics (IFKAD-2013), Zagreb, Croatia, 12–14 June 2013; pp. 12–14. [Google Scholar]
- Stuckenschmidt, H.; Parent, C.; Spaccapietra, S. Modular Ontologies: Concepts, Theories and Techniques for knowledge Modularization; Springer: Berlin/Heidelberg, Germany, 2009; p. 378. [Google Scholar]
- Pu, S.; Rutzinger, M.; Vosselman, G.; Oude Elberink, S. Recognizing basic structures from mobile laser scanning data for road inventory studies. ISPRS J. Photogramm. Remote Sens. 2011, 66, S28–S39. [Google Scholar] [CrossRef]
- Hois, J.; Bhatt, M.; Kutz, O. Modular ontologies for architectural design. In Formal Ontologies Meet Industry; IOS Press: Amsterdam, The Netherlands, 2009; pp. 66–77. [Google Scholar]
- Miller, G.; Fellbaum, C. Wordnet: An Electronic Lexical Database; MIT Press Cambridge: Cambridge, UK, 1998. [Google Scholar]
- Kresse, W.; Fadaie, K. ISO Standards for Geographic Information; Springer: Berlin/Heidelberg, Germany, 2004; Volume 11, p. 322. [Google Scholar]
- Mark, D.M.; Egenhofer, M.J. Modeling spatial relations between lines and regions: Combining formal mathematical models and human subjects testing. Cartogr. Geogr. Inf. Syst. 1994, 21, 195–212. [Google Scholar]
- Egenhofer, M.J.; Herring, J. A mathematical framework for the definition of topological relationships. In Proceedings of the Fourth International Symposium on Spatial Data Handling, Zurich, Switzerland, 23–27 July 1990; pp. 803–813. [Google Scholar]
- Egenhofer, M.J.; Herring, J. Categorizing Binary Topological Relations between Regions, Lines, and Points in Geographic Databases; Technical Report; University of Maine: Orono, ME, USA, 1990; pp. 94–122. [Google Scholar]
- Roeper, P. Region-based topology. J. Philos. Log. 1997, 26, 251–309. [Google Scholar] [CrossRef]
- Egenhofer, M. A formal definition of binary topological relationships. In Foundations of Data Organization and Algorithms; Litwin, W., Schek, H.-J., Eds.; Springer: Berlin Heidelberg, Germany, 1989; Volume 367, pp. 457–472. [Google Scholar]
- Randell, D.A.; Cui, Z.; Cohn, A.G. A spatial logic based on regions and connection. In Proceeding of the 3rd International Comference on Knowledge Representation and Reasoning, Morgan, Kaufmann, 25–29 October 1992; pp. 1–12. [Google Scholar]
- Clementini, E.; Sharma, J.; Egenhofer, M.J. Modelling topological spatial relations: Strategies for query processing. Comput. Graph. 1994, 18, 815–822. [Google Scholar] [CrossRef]
- Egenhofer, M. Reasoning about binary topological relations. In Advances in Spatial Databases; Günther, O., Schek, H.-J., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; Volume 525, pp. 141–160. [Google Scholar]
- Zlatanova, S.; Rahman, A.A.; Shi, W. Topological models and frameworks for 3D spatial objects. Comput. Geosci. 2004, 30, 419–428. [Google Scholar] [CrossRef]
- Albath, J.; Leopold, J.L.; Sabharwal, C.L.; Maglia, A.M. Rcc-3d: Qualitative spatial reasoning in 3d. In Proceedings of the 23rd International Conference on Computer Applications in Industry and Engineering (CAINE 2010), Las Vegas, NV, USA, 8–10 November 2010; pp. 74–79. [Google Scholar]
- Sabharwal, C.L.; Leopold, J.L.; Eloe, N. A More Expressive 3D Region Connection Calculus. In Proceedings of the 2011 International Workshop on Visual Languages and Computing, Florence, Italy, 18–20 August 2011; pp. 307–311. [Google Scholar]
- Freeman, J. The modelling of spatial relations. Comput. Graph. Image Process. 1975, 4, 156–171. [Google Scholar] [CrossRef]
- Xing, X.F.; Mostafavia, M.A.; Wang, C. Extension of rcc topological relations for 3D complex objects components extracted from 3D lidar point clouds. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B3, 425–432. [Google Scholar] [CrossRef]
- El-Diraby, T.E.; Osman, H. A domain ontology for construction concepts in urban infrastructure products. Autom. Constr. 2011, 20, 1120–1132. [Google Scholar] [CrossRef]
- Natasha, N.; Evan, W. Simple Part-Whole Relations in OWL Ontologies. Available online: http://www.w3.org/2001/sw/BestPractices/OEP/SimplePartWhole/#ref-FMA (accessed on 23 November 2017).
- Sirin, E.; Parsia, B.; Grau, B.C.; Kalyanpur, A.; Katz, Y. Pellet: A practical OWL-DL reasoner. Web Semant. Sci. Serv. Agents World Wide Web 2007, 5, 51–53. [Google Scholar] [CrossRef]
- Horridge, M.; Bechhofer, S. The owl API: A java api for owl ontologies. Semant. Web 2011, 2, 11–21. [Google Scholar]
- Curl, J.S. A Dictionary of Architecture and Landscape Architecture; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Design Buidling Ltd. Design Buidlings Wiki. Available online: https://www.designingbuildings.co.uk/wiki/Wall_types#Wall_definition (accessed on 23 November 2017).




| Information Type | Terms | Examples |
|---|---|---|
| Quantitative Elements | Geometric Dimension | length, width, height, radius, thickness, area, volume |
| Geographic Coordinate | latitude, longitude, elevation | |
| Local Coordinates | X, Y, Z | |
| Properties of Point Clouds | intensity, return number, point source ID, classification, color | |
| Qualitative Elements | Object Types | building, car, road, tree, pole, etc. |
| Geometric Shape | circle, rectangle, ellipsoidal, cross-sectional shape, line, cylinder, cuboid | |
| Surface Type | plane, curved surface | |
| Dependence | logical dependence, geographic dependence, physical dependence | |
| Topology | 2D and 3D topology | |
| Function Relevance | interrelated relation for functions | |
| Surrounding Attributes | the neighboring information and their relations | |
| Architecture Components | wall, roof, floor, door, windows, balcony, etc. | |
| Roof Shapes | flat, shed, gable, hip, barrel, etc. | |
| Material Attributes | concrete, wood, asphalt | |
| Geometric Relations | parallel, perpendicular, intersecting, coplanar, etc. |
| Type of Relations | Graphical Representation | Topological Relations |
|---|---|---|
| Point-point relations |  | Disjoint, Equal |
| Line segment-point relations |  | Disjoint, Meet, Contain |
| Line segment-line segment relations | 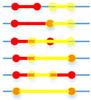 | Disjoint, Meet, Overlap, Cover, Contain, Equal |
| Attribute Types | Explanation | Examples |
|---|---|---|
| Dimensional attributes | measurable quantitative dimension of objects | size, height, length, width, area |
| Geometric shape attributes | describe geometric shapes | normal, boundary, surface type (plane, curved), shape(rectangle, square, circle) |
| Spatial attributes | location-related attributes and spatial relations | X-coordinate, Y-coordinate, Z-coordinate, latitude, longitude |
| Function attributes | object functions in a system or the roles of objects in a scene | lighting (for light pole), control traffic (for traffic sign), passing (for door) |
| Dependency attributes | attributes representing the interdependency between components or objects | logical dependency, geographic dependency, location dependency |
| System (combination) attributes | attributes are the terms for a group of objects or a subsystem | roof styles (such as gable, hip, shed, flat, and mansard and so on), traffic system, intersection |
| Semantic Features | Rules | Explanation | Rule ID |
|---|---|---|---|
| Wall | PlanarRegion(?pr_i), isVerticalTo(?pr_i,?ground), Ground(?ground), hasDirection(?ground,(0,0,1)), hasArea(?pr_i,?area_i), greaterThan(?area_i,2) -> Wall(?pr_i) | A wall is a plane that is vertical to ground and its area it greater than 2 m2 | (6) |
| PlanarRegion(?pr_j), isCoplanarTo(?pr_j,?plane_i), Wall(?pr_j) -> Wall(?pr_j) | If a plane is coplanar to a wall, it is wall | (7) | |
| PlanarRegion(?pr_k), isConnectTo(?pr_k,?pr_i), Wall(?pr_i), isVerticalTo(?pr_k,?ground), Ground(?ground), hasDirection(?ground,(0,0,1)) -> Wall(?pr_k) | If a plane connects to a wall and is vertical to ground, it is wall | (8) | |
| PlanarRegion(?pr_j), Wall(?pr_i), isConnectTo(?pr_j,?pr_i), isCoplanarTo(?pr_j,?pr_i), -> isSameWall(?pr_j,?pr_i) | If a plane connects to a wall and is coplanar to this wall, they belong to same wall | (9) | |
| Roof | PlanarRegion(?pr_i), hasArea(?pr_i,?area_i), greaterThan(?area_i,2), isSlopeTo(?pr_i,?ground), Ground(?ground), hasDirection(?ground,(0,0,1)), hasSlopeAngle(?pr_i,?ang_i), lessThan(?ang _i,70), hasHeightAttribute(?pr_i,?upperMost) -> ComponentsofRoof(?pr_i) | A roof component has covering function on the uppermost part of a building | (10) |
| PlanarRegion(?pr_i), ComponentsofRoof(?pr_j), isSlopeTo(?pr_i,?ground), Ground(?ground), hasDirection(?ground,(0,0,1)), isConnectTo(?pr_i,?pr_j), hasSlopeAngle(?pr_i,?ang_i), lessThan(?ang _i,70), hasHeightAttribute(?pr_i,?upperMost) -> ComponentsofRoof(?pr_i) | (11) | ||
| Gable roof style | Set(?B), isInSet(?pr1,?B), isInSet(?pr2,?B), ComponentsofRoof(?pr1), ComponentsofRoof(?pr2), isMeet_Meet_Meet(?pr1,?pr2), Line(?line1) -> hasIntersectLine(?B,?line) | A gable roof consists of two roof sections sloping in opposite directions and the highest, horizontal edges meet to form the roof ridge. (v_g = (0,0,1)) | (12) |
| Set(?B), isInSet(?pr1,?B), isInSet(?pr2,?B), ComponentsofRoof(?pr1), ComponentsofRoof(?pr2), hasDirection(?pr1,?v1), isLeftSide(?v1,?v_g), hasDirection(?pr2,?v2), isRightSide(?v2,?v_g), Line(?line1), isParallelTo(?line1,?ground), Ground(?ground), hasDirection(?ground,?v_g), higherThan(?line1,?pr1), higherThan(?line1,?pr2) -> GableRoof(?B) | (13) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, X.-F.; Mostafavi, M.-A.; Chavoshi, S.H. A Knowledge Base for Automatic Feature Recognition from Point Clouds in an Urban Scene. ISPRS Int. J. Geo-Inf. 2018, 7, 28. https://doi.org/10.3390/ijgi7010028
Xing X-F, Mostafavi M-A, Chavoshi SH. A Knowledge Base for Automatic Feature Recognition from Point Clouds in an Urban Scene. ISPRS International Journal of Geo-Information. 2018; 7(1):28. https://doi.org/10.3390/ijgi7010028
Chicago/Turabian StyleXing, Xu-Feng, Mir-Abolfazl Mostafavi, and Seyed Hossein Chavoshi. 2018. "A Knowledge Base for Automatic Feature Recognition from Point Clouds in an Urban Scene" ISPRS International Journal of Geo-Information 7, no. 1: 28. https://doi.org/10.3390/ijgi7010028
APA StyleXing, X.-F., Mostafavi, M.-A., & Chavoshi, S. H. (2018). A Knowledge Base for Automatic Feature Recognition from Point Clouds in an Urban Scene. ISPRS International Journal of Geo-Information, 7(1), 28. https://doi.org/10.3390/ijgi7010028






