Collaborative Geodesign and Spatial Optimization for Fragmentation-Free Land Allocation
Abstract
:1. Introduction
2. General Problem Definition: Fragmentation-Free Land Allocation
2.1. Basic Concepts
2.2. Formal Problem Definition
- –
- A watershed (study area) containing a set of spatial locations in a two-dimensional space, where are coordinates on two mutually-orthogonal directions;
- –
- Boundary of unchangeable landscapes within the watershed;
- –
- A set L of choices of land management practices {};
- –
- A list of ecosystem objectives {} and a weight of each objective;
- –
- For each objective , its profit value of LMP choice at location ;
- –
- A cost value of LMP choice at location ;
- –
- A budget limit ;
- –
- A minimum area and regular shape (e.g., rectangle);
- –
- Each spatial location can only have one choice of LMP:
- –
- The budget for the land allocation is less than or equal to :
- –
- Every patch formed by a homogeneous LMP in the land allocation map satisfies the minimum area and width constraint, and the regular-shape constraint.
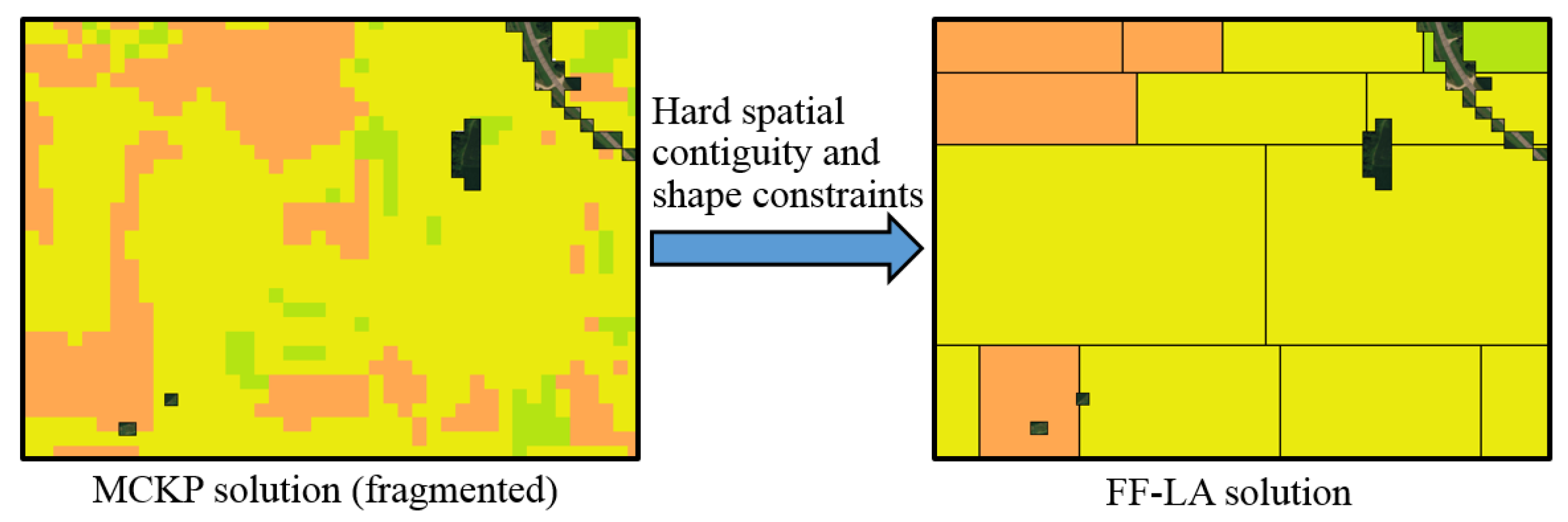
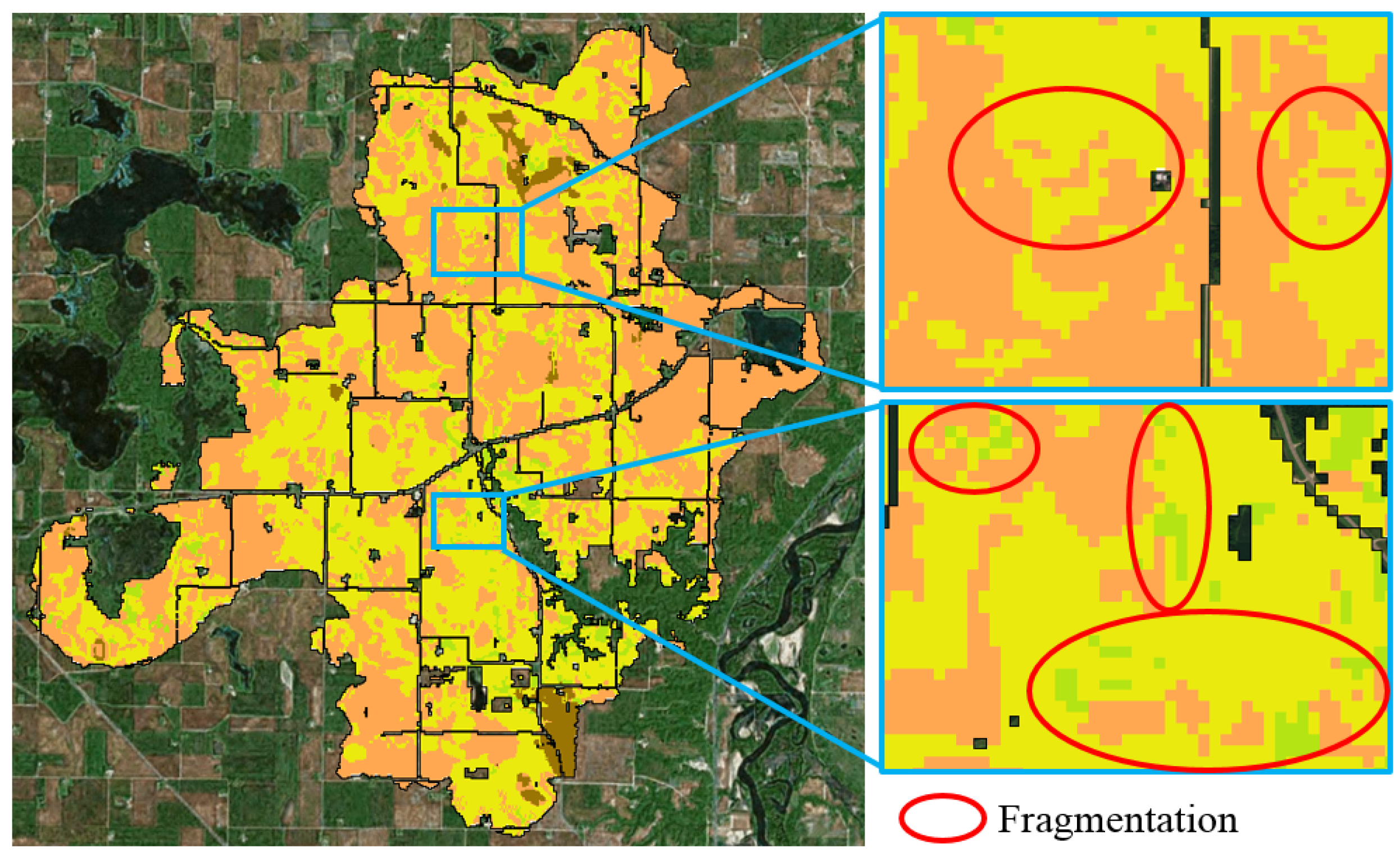
3. Challenges
4. Related Work and Novelty
4.1. Limitations of Related Work
4.2. Novelty
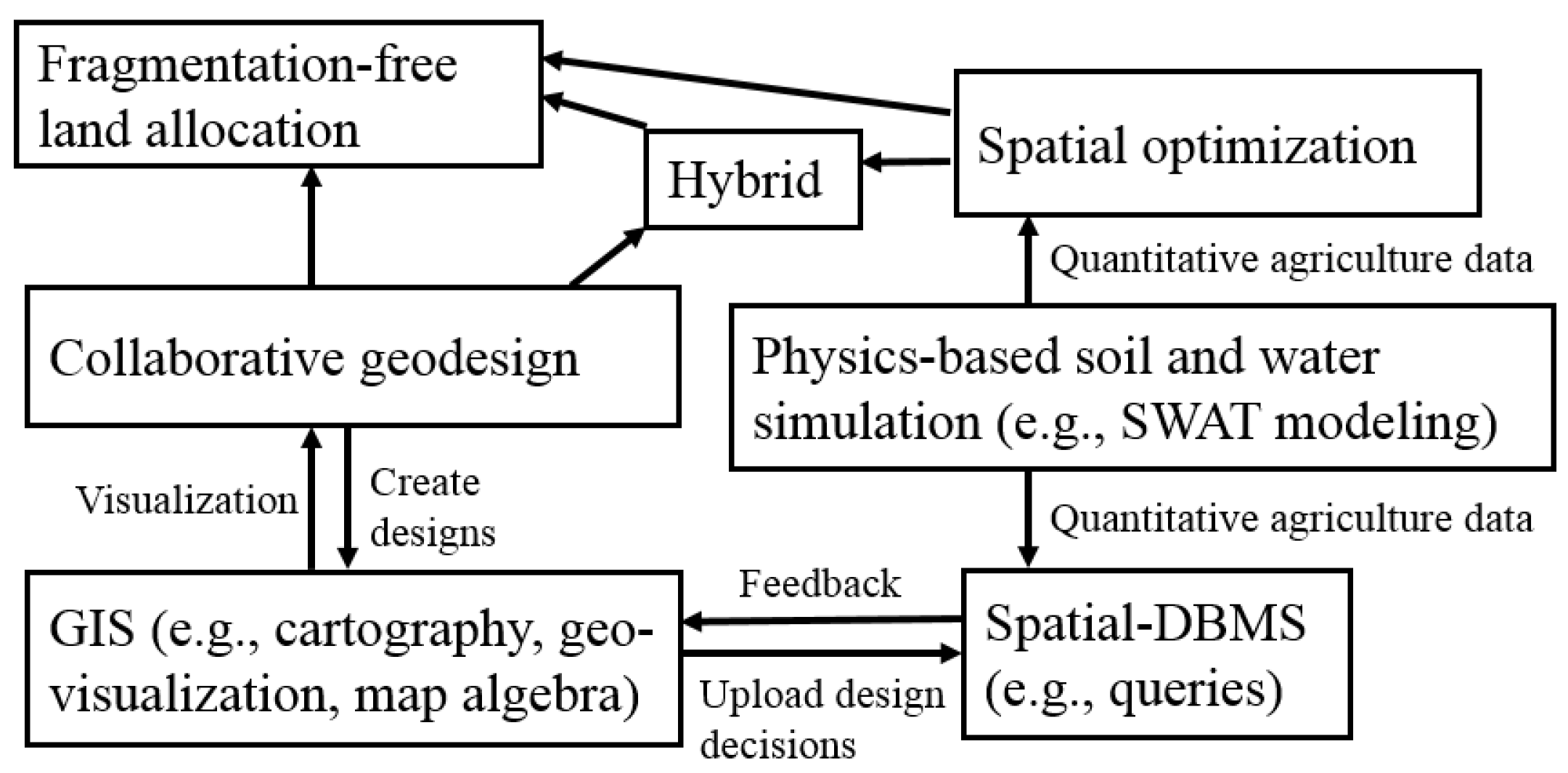
5. Frameworks for Fragmentation-Free Land Allocation
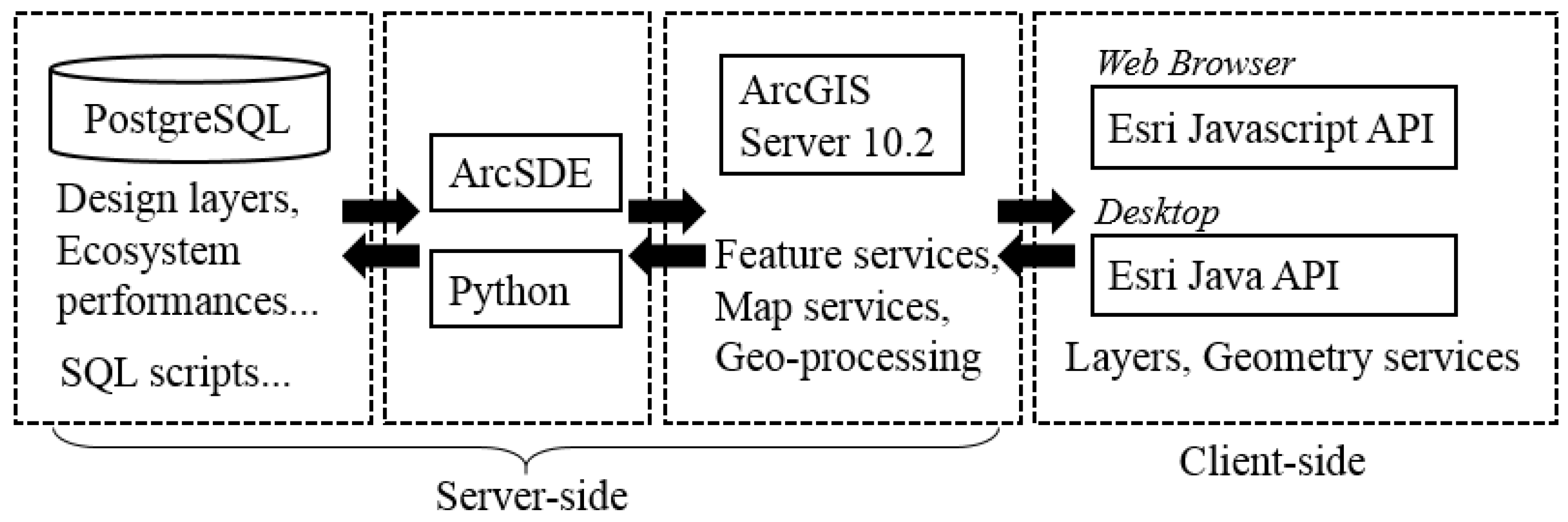
5.1. Overall Architecture
5.2. Collaborative Geodesign
5.3. Spatial Optimization
- –
- A grid partition G of the study area, where each grid cell is identified by its row i and column j.
- –
- A list L of LMP choices.
- –
- A full list Z of combinations of tile, LMP choice and the corresponding profit p and cost c:, where defines the top-left grid cell of the tile and ) defines the bottom right.
- –
- A budget limit , a minimum area and a minimum width ;
- –
- Binary choice on :
- –
- The cost is less than or equal to :
- –
- Each tile belonging to satisfies the minimum area and minimum width :
- –
- The tiles of selected elements in are non-overlapping. For all () in :
5.4. Towards the Future: A Hybrid Framework
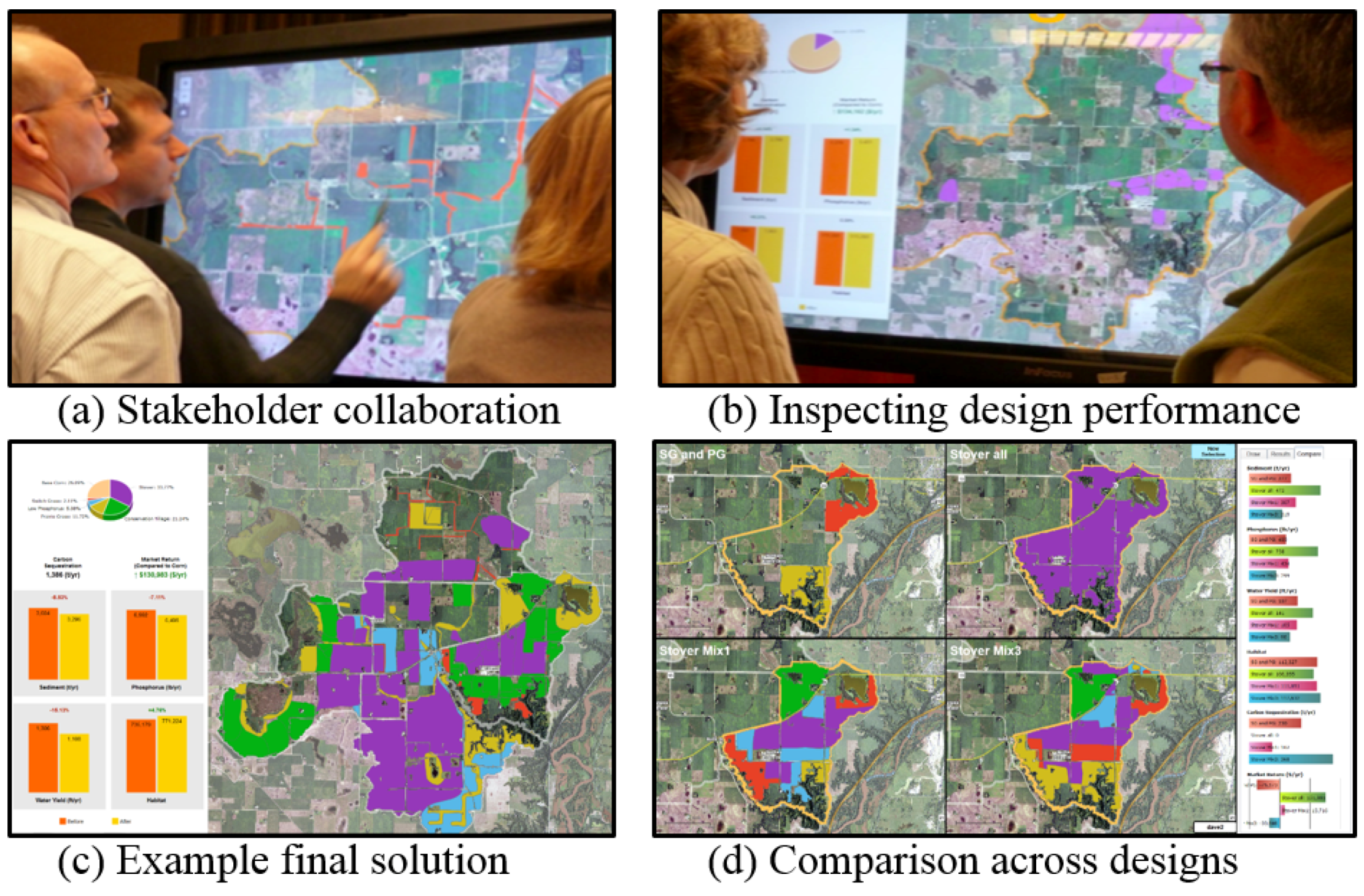
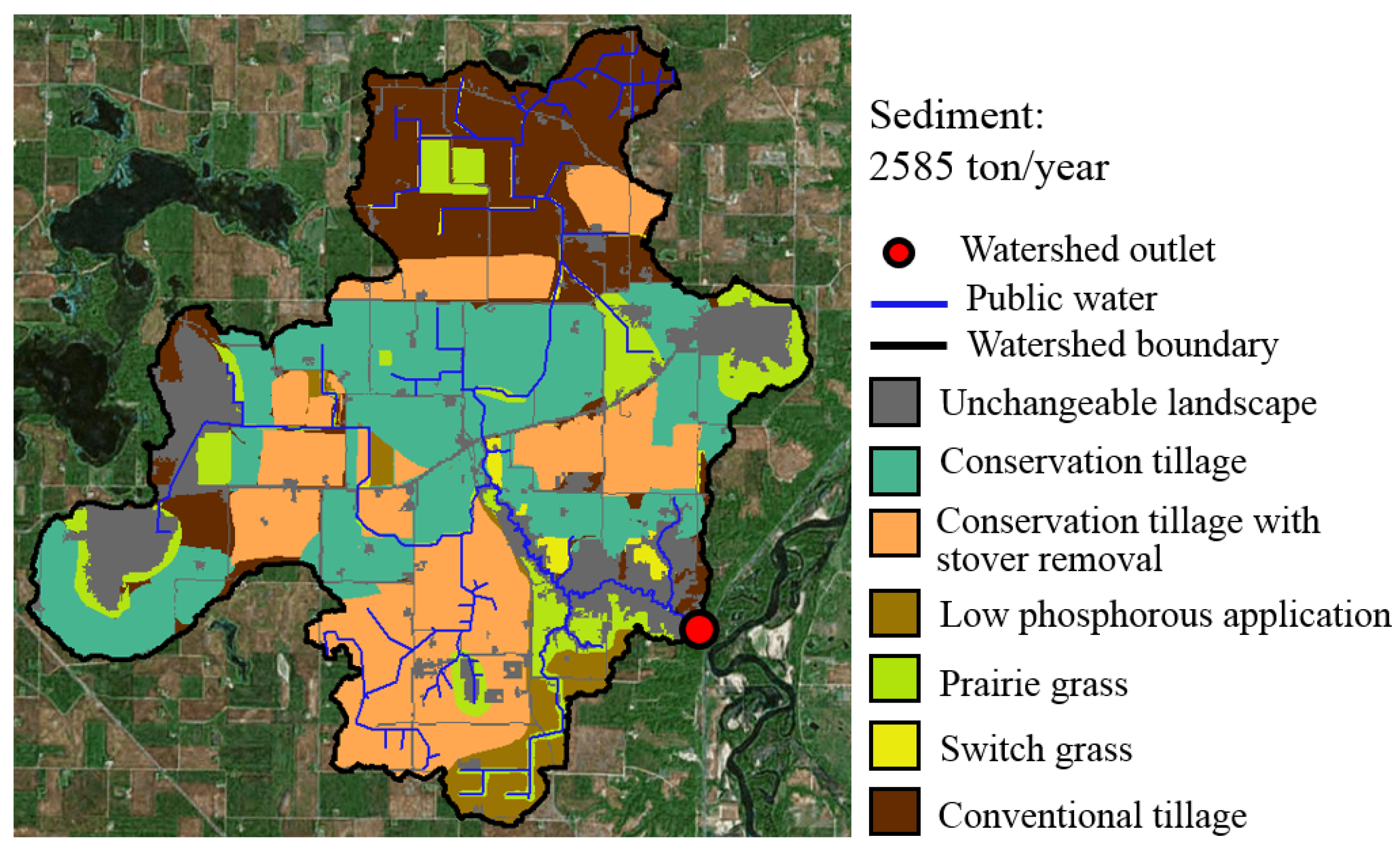
6. Case Study: Seven Mile Creek Watershed
6.1. Stakeholder Solution with Collaborative Geodesign
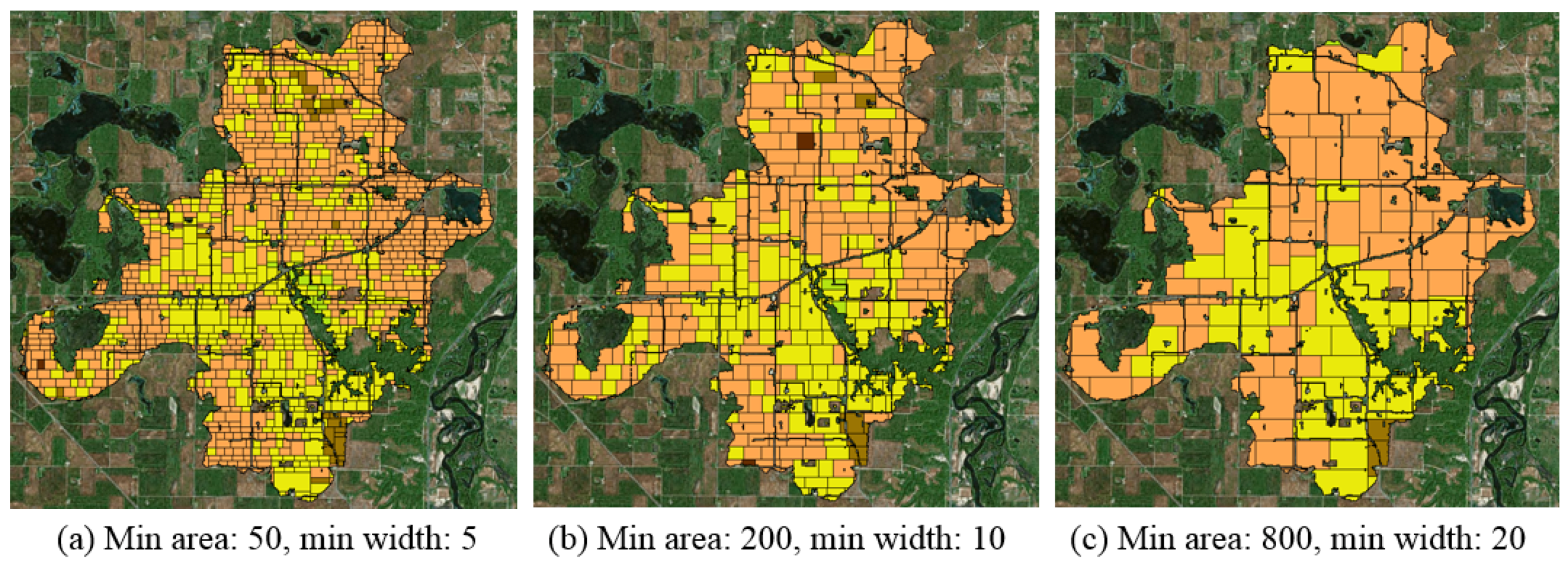
6.2. Computer-Suggested Solutions with Spatial Optimization
6.3. Comparison of Land Allocation Approaches
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- United Nations. World Population Prospects, 2015 Revision. Available online: https://esa.un.org/unpd/wpp/publications/files/key_findings_wpp_2015.pdf (accessed on 10 July 2017).
- Schively, C.; Runck, B.; Pitt, D.; Kne, L.; Jordan, N.; Mulla, D.J.; Zerger, C.; Reichenbach, M. Collaborative geodesign to advance multifunctional landscapes. Lands. Urban Plan. 2016, 156, 71–80. [Google Scholar]
- Van Dijk, T. Scenarios of Central European land fragmentation. Land Use Policy 2003, 20, 149–158. [Google Scholar] [CrossRef]
- Niroula, G.S.; Thapa, G.B. Impacts and causes of land fragmentation, and lessons learned from land consolidation in South Asia. Land Use Policy 2005, 22, 358–372. [Google Scholar] [CrossRef]
- Kellerer, H.; Pferschy, U.; Pisinger, D. The multiple-choice knapsack problem. In Knapsack Problems; Springer: Berlin/Heidelberg, Germany, 2004; pp. 317–347. [Google Scholar]
- Jordan, N.R.; Slotterback, C.S.; Cadieux, K.V.; Mulla, D.J.; Pitt, D.G.; Olabisi, L.S.; Kim, J.O. TMDL implementation in agricultural landscapes: A communicative and systemic approach. Environ. Manag. 2011, 48, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Galzki, J.; Birr, A.S.; Mulla, D.J. Identifying critical agricultural areas with 3-meter LiDAR elevation data for precision conservation. J. Soil Water Conserv. 2011, 66, 423–430. [Google Scholar] [CrossRef]
- Kalcic, M.M.; Chaubey, I.; Frankenberger, J. Defining Soil and Water Assessment Tool (SWAT) hydrologic response units (HRUs) by field boundaries. Int. J. Agric. Biol. Eng. 2015, 8, 69–80. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool—Historical development applications, and future research directions. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 1211–1240. [Google Scholar] [CrossRef]
- Nelson, E.; Mendoza, G.; Regetz, J.; Polasky, S.; Tallis, H.; Cameron, D.; Chan, K.; Daily, G.C.; Goldstein, J.; Kareiva, P.M.; et al. Modeling multiple ecosystem services, biodiversity conservation, commodity production, and tradeoffs at landscape scales. Front. Ecol. Environ. 2009, 7, 4–11. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, K.; Shekhar, S.; Dalzell, B.; Mulla, D. Geodesign optimization (GOP) towards improving agricultural watershed sustainability. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17): Workshop on AI and OR for Social Good, San Francisco, CA, USA, 4–5 February 2017. [Google Scholar]
- Muthukrishnan, S.; Poosala, V.; Suel, T. On rectangular partitionings in two dimensions: Algorithms, complexity and applications. In Proceedings of the International Conference on Database Theory, Jerusalem, Israel, 10–12 January 1999; pp. 236–256. [Google Scholar]
- Berman, P.; DasGupta, B.; Muthukrishnan, S.; Ramaswami, S. Improved approximation algorithms for rectangle tiling and packing. In Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA ’01), Washington, DC, USA, 7–9 January 2001; pp. 427–436. [Google Scholar]
- Cao, K.; Ye, X. Coarse-grained parallel genetic algorithm applied to a vector based land use allocation optimization problem: The case study of Tongzhou Newtown, Beijing, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 1133–1142. [Google Scholar] [CrossRef]
- Wang, X.; Yu, S.; Huang, G. Land allocation based on integrated GIS-optimization modeling at a watershed level. Landsc. Urban Plan. 2004, 66, 61–74. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, X. Land use allocation based on a multi-objective artificial immune optimization model: An application in Anlu County, China. Sustainability 2015, 7, 15632–15651. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, Y.; Jin, X.; Shu, B.; Zhou, Y.; Yang, X. Simulating multi-objective land use optimization allocation using multi-agent system—A case study in Changsha, China. Ecol. Model. 2016, 320, 334–347. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, W.; He, J.; Liu, Y.; Ai, T.; Liu, D. A land-use spatial optimization model based on genetic optimization and game theory. Comput. Environ. Urban Syst. 2015, 49, 1–14. [Google Scholar] [CrossRef]
- Ligmann-Zielinska, A.; Church, R.L.; Jankowski, P. Spatial optimization as a generative technique for sustainable multiobjective land-use allocation. Int. J. Geogr. Inf. Sci. 2008, 22, 601–622. [Google Scholar] [CrossRef]
- Cao, K.; Huang, B.; Zhao, Q.; Wang, S. Land Use Allocation Optimization towards Sustainable Development Based on Genetic Algorithm. In Proceedings of the 2009 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; pp. 1–5. [Google Scholar]
- Liu, Y.; Peng, J.; Jiao, L.; Liu, Y. PSOLA: A heuristic land-use allocation model using patch-level operations and knowledge-informed rules. PLoS ONE 2016, 11, e0157728. [Google Scholar] [CrossRef] [PubMed]
- Ligmann-Zielinska, A.; Church, R.; Jankowski, P. Sustainable urban land use allocation with spatial optimization. In Proceedings of the 8th International Conference on Geocomputation, Ann Arbor, MI, USA, 31 July–3 August 2005; pp. 1–3. [Google Scholar]
- PostgreSQL. 2017. Available online: https://www.postgresql.org/ (accessed on 10 July 2017).
- CPLEX Solver User Manual. 2016. Available online: https://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.3/ilog.odms.studio.help/pdf/opl_languser.pdf (accessed on 10 July 2017).
- Anderson, J.L. Industrializing the Corn Belt; Northern Illinois University Press: DeKalb, IL, USA, 2016; p. 248. [Google Scholar]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Runck, B.C.; Shekhar, S.; Kne, L.; Mulla, D.; Jordan, N.; Wiringa, P. Collaborative Geodesign and Spatial Optimization for Fragmentation-Free Land Allocation. ISPRS Int. J. Geo-Inf. 2017, 6, 226. https://doi.org/10.3390/ijgi6070226
Xie Y, Runck BC, Shekhar S, Kne L, Mulla D, Jordan N, Wiringa P. Collaborative Geodesign and Spatial Optimization for Fragmentation-Free Land Allocation. ISPRS International Journal of Geo-Information. 2017; 6(7):226. https://doi.org/10.3390/ijgi6070226
Chicago/Turabian StyleXie, Yiqun, Bryan C. Runck, Shashi Shekhar, Len Kne, David Mulla, Nicolas Jordan, and Peter Wiringa. 2017. "Collaborative Geodesign and Spatial Optimization for Fragmentation-Free Land Allocation" ISPRS International Journal of Geo-Information 6, no. 7: 226. https://doi.org/10.3390/ijgi6070226
APA StyleXie, Y., Runck, B. C., Shekhar, S., Kne, L., Mulla, D., Jordan, N., & Wiringa, P. (2017). Collaborative Geodesign and Spatial Optimization for Fragmentation-Free Land Allocation. ISPRS International Journal of Geo-Information, 6(7), 226. https://doi.org/10.3390/ijgi6070226





