Abstract
Demand for agricultural food production is projected to increase dramatically in the coming decades, putting at risk our clean water supply and prospects for sustainable development. Fragmentation-free land allocation (FF-LA) aims to improve returns on ecosystem services by determining both space partitioning of a study area and choice of land-use/land-cover management practice (LMP) for each partition under a budget constraint. In the context of large-scale industrialized food production, fragmentation (e.g., tiny LMP patches) discourages the use of modern farm equipment (e.g., 10- to 20-m-wide combine harvesters) and must be avoided in the allocation. FF-LA is a computationally challenging NP-hard problem. We introduce three frameworks for land allocation planning, namely collaborative geodesign, spatial optimization and a hybrid model of the two, to help stakeholders resolve the dilemma between increasing food production capacity and improving water quality. A detailed case study is carried out at the Seven Mile Creek watershed in the midwestern US. The results show the challenges of generating near-optimal solutions through collaborative geodesign, and the potential benefits of spatial optimization in assisting the decision-making process.
1. Introduction
The rising human population, projected to reach 9 billion by 2050 [1], is expected to dramatically increase the demand for agricultural food production, placing significant pressure on soil and water sustainability. Conventional farming loosens soil structure and increases the risk of soil being washed away during irrigation and rainfall. Soil erosion carries sediments into surface water and leads to water quality degradation. In addition, application of phosphorus, an important practice in agricultural land management, leaves fertilizer residues, further aggravating water pollution.
In recent years, land allocation has been recognized as an important methodology to find a better balance between food production and water conservation [2]. In an agricultural watershed, soil and water properties vary across spatial locations (e.g., water downstream contains more fertilizer residues due to accumulation). Placing different land management practices at different locations has critical impacts on food production and water quality. For example, allocation of grassland near water bodies can significantly filter out fertilizer residues and strengthen surface soil structure, improving water quality. On the other hand, replacing food crops with grassland leads to reduced production of food. Thus, modeling the interactions among land management practices, food production and water quality at different locations, and identifying more effective land allocations are important for improving agricultural watershed sustainability. This has also been identified by conservation groups, agricultural producers, and agribusiness as a core strategy for sustainable development.
When planning land allocation, it is important that farmland is not divided into parcels that are irregularly shaped or too small to accommodate modern farm equipment. Otherwise, land fragmentation can greatly reduce farming efficiency as suggested by many studies [3,4].
Solving fragmentation-free land allocation (FF-LA) demands both social collaboration (e.g., among stakeholders) and algorithmic optimization approaches. While algorithms aim to quantitatively optimize the ecosystem service objectives, the final implementation plan depends on stakeholder opinions and implementation. Stakeholder (e.g., farmers, watershed managers) discussions about conflicting objectives and desired land-uses are difficult to formulate into the algorithmic optimization problem. In optimization, the problem is a computationally challenging NP-hard problem. In fact, just determining land management practice (LMP) choices over a set of fixed space partitions is already an NP-hard problem (0–1 integer programming problem [5]). Fragmentation-free land allocation needs to determine both space partitioning and an LMP choice for each partition, making it a computationally demanding problem. The problem is similarly a challenging social problem at the planning and implementation stages. While it is widely recognized that diverse groups of people need to work together to solve complex agricultural problems at the landscape scale [6], these groups often value different aspects of the landscape in different ways, and see different changes in land use as more or less desirable. The typical result has been a significant conflict between more environmentally-oriented and agricultural production-oriented groups of people.
Currently, agricultural landscapes are largely determined by individuals seeking to make the best choices for their farming operation under market and government pressures. While cases of community-level decision-making exist, land management is primarily handled by individual farmers on individual parcels. Environmental conservation practices are determined by local government and nongovernmental organizations that target conservation practices heuristically. For example, changes are made either ad hoc or at locations which produce the highest amount of pollution (as suggested by a recent work [7]). As a result, land use is often far from optimal at the watershed scale, and results in both high public costs for conservation and low levels of pollution control. Existing optimization approaches either consider flexible space partitioning with fixed properties at each spatial location (e.g., no multiple-choice to make) or consider fixed space partitioning with combinatorial choices (e.g., different combinations of land management practices in FF-LA), but do not address both problems during optimization. Spatial optimization for FF-LA aims to deal with both space partitioning and assignment of land management practices. In addition, related work in the land allocation domain does not consider both geometric regularity constraint (e.g., rectangular shape) and contiguity constraint (e.g., minimum patch size), which may still be acceptable in land-use zoning in urban areas, but can lead to a fragmented plan that is difficult for implementation in agricultural landscape management. Details are discussed in Section 4.
We propose three frameworks to solve FF-LA, namely collaborative geodesign, spatial optimization and a hybrid of the two. Collaborative geodesign is a stakeholder-driven approach, where the land allocation solutions are created by a group of human experts using our decision-support software system. The collaborative geodesign tools have been fully implemented and made publicly available. Spatial optimization is a computer-driven approach which heuristically solves FF-LA with a dynamic-growth tiling framework which guarantees no fragmentation is generated during optimization. The hybrid approach builds a bridge between stakeholder designs and computer generated designs, allowing stakeholders to start with a promising initial solution, which can help significantly reduce the complexity of the design process.
The proposed frameworks are evaluated through a detailed case study at the Seven Mile Creek watershed in the mid-western US. The results revealed the difficulty of social learning in collaborative geodesign when stakeholders have to deal with conflicting objectives (e.g., water quality and market return). Spatial optimization offered promising solutions which could potentially help stakeholders balance conflicting objectives and assist their discussion towards a final implementation plan. This motivates further study on the hybrid framework which integrates spatial optimization into collaborative geodesign.
2. General Problem Definition: Fragmentation-Free Land Allocation
2.1. Basic Concepts
Watershed: A basin where all surface water converges to a single outlet on its boundary.
Unchangeable landscape: Places in a watershed where the land use and land cover cannot be changed (e.g., water bodies and roads). These places are not within the scope of land allocation.
Spatial location: In this paper, a watershed consists of a finite collection of non-overlapping spatial locations. Each location is a region. Examples of spatial locations are cells in an orthogonal grid or hydrological response units [8].
Ecosystem services: Benefits from an ecosystem, such as water, carbon sequestration, habitat, economic market return, etc.
Land management practices (LMP): Methods of managing agricultural land, such as conventional tillage, conservation tillage, low-phosphorus application and grassland. A management practice directly interacts with properties of a farm (e.g., soil type, water quality) and affects the quality of ecosystem services. Geographic variation plays an important role in the interaction. For example, allocating grassland at places near water bodies can significantly filter out fertilizer residues and protect water quality.
Profit and cost: In this research, the value of an ecosystem service is quantified using the Soil and Water Assessment Tool (SWAT) and InVEST modeling [9,10]. Multiple ecosystem service objectives are linearly combined into a single objective (profit). The cost includes economic losses from decreases in food production and investment needed for re-purposing lands (e.g., change management practices).
Land fragmentation: Small or irregularly shaped patches of land management practices, where a patch is a contiguous region with homogeneous choice of land management practices. Land fragmentation prohibits efficient use of large farm equipment (e.g., 10- to 20-m-wide combine harvester heads) [3,4].
Spatial constraints: Spatial constraints are used to avoid land fragmentation. In this research, we use a minimum patch area to guarantee each patch of land management practice is large enough to be farmed efficiently. In addition, we use a regular-shaped constraint, where the shape is defined based on user preference (e.g., rectangle).
2.2. Formal Problem Definition
Inputs:
- –
- A watershed (study area) containing a set of spatial locations in a two-dimensional space, where are coordinates on two mutually-orthogonal directions;
- –
- Boundary of unchangeable landscapes within the watershed;
- –
- A set L of choices of land management practices {};
- –
- A list of ecosystem objectives {} and a weight of each objective;
- –
- For each objective , its profit value of LMP choice at location ;
- –
- A cost value of LMP choice at location ;
- –
- A budget limit ;
- –
- A minimum area and regular shape (e.g., rectangle);
Output: A land allocation map with assignment of land management practices for all spatial locations. The solution at each location is denoted by , where if is selected; otherwise 0.
Objective: Maximize overall profit in the watershed.
Constraints:
- –
- Each spatial location can only have one choice of LMP:
- –
- The budget for the land allocation is less than or equal to :
- –
- Every patch formed by a homogeneous LMP in the land allocation map satisfies the minimum area and width constraint, and the regular-shape constraint.
The goal of spatial land allocation is to maximize ecosystem profit for the entire watershed under certain economic and spatial geometric constraints. The economic constraint defines the maximum available budget available to stakeholders (e.g., from government subsidies). The spatial constraints guarantee the solution allows efficient use of large farm equipment (e.g., combine harvesters), thereby ensuring the solution meets the practical needs of farmers.
The problem definition is general in order to be flexible for different types of spatial locations and spatial constraints. For example, in a concrete problem instance, the locations can be defined as orthogonal grid cells inside the study area, and the size of a grid cell can be chosen based on the data resolution or user preference. The locations can also be defined as irregularly shaped or non-identically sized regions, such as hydrological response units [8].
For the spatial constraints, the shape definition is flexible for different cases and applications. For example, farms in the midwestern US are often rectangular in shape (Figure 1a) due to the ease of operating farm equipment in straight lines and the abundance of water supply. On the other hand, farms in a relatively dry climate (e.g., Idaho, US) are often circular in shape due to the use of central pivot irrigation systems (Figure 1b).

Figure 1.
Aerial images showing farm shapes in Google Maps. (a) shows rectangular-shaped farms and (b) shows circular-shaped farms.
3. Challenges
Collaborative geodesign and algorithmic optimization methods are complementary approaches to allocating land use at the landscape scale. Optimization methods can identify solutions that humans may struggle to find because of the overall complexity of the decision-making context. However, optimization methods struggle to incorporate qualitative information about the local cultural context because it is difficult to measure. On the other hand, human-driven design approaches are good at capturing many of the qualitative concerns related to local cultural practices and practical constraints that may be difficult to incorporate into an optimization routine. Taken together, both approaches have strengths and weakness that could complement one another.
From the perspective of human decision-making, land allocation at the landscape scale is a complex problem for stakeholder groups because of the large number of variables for individuals to consider and because of the social conflict associated with the situation. For example, some individuals will perceive certain factors as being of little value compared to others, which will cause them to prefer one land use over another. The classic case of this is the stereotypical environmentalist who may care primarily about water quality compared to a farmer who cares primarily about economic profit. Different stakeholder’s values and perceptions also add considerable complexity to the land allocation process. While environmental stakeholders may perceive perennial grasses to be a very reasonable land use, farmers may see this land use as unrealistic. This leads to considerable social complexity in the process of allocating different land uses over the extent of a watershed with the intention of increasing the public good from the landscape. In addition, stakeholders have to consider highly difficult to measure metrics such as community well-being and overall regional economic health.
From the algorithmic optimization perspective, the fragmentation-free land allocation (FF-LA) problem is computationally challenging (formally, NP-hard) as we proved in [11]. Figure 2 shows that FF-LA can be reduced from the multiple-choice knapsack problem (MCKP). Here we also show a concrete special case of FF-LA that is equivalent to MCKP. In MCKP, we are given a finite set of classes, and each class has multiple choices. Each choice in each class has a profit value and a cost value. The goal is to select one and only one choice from each class that maximizes the profit under a cost constraint. In the general version of the FF-LA problem, we have a finite set of spatial locations, and each location has a set of multiple choices, where each choice has a profit value (e.g., a linear combination of multiple objectives) and a cost value. Each spatial location can be considered as a class in MCKP. As a special case, we can define the minimum area as 0, and the shape as any arbitrary shape. This special case is equivalent to a MCKP problem. Thus, given any MCKP instance, we can always construct an instance of this FF-LA special case in polynomial time. In addition, the solution of FF-LA can be mapped to MCKP by assigning the choice at each spatial location to each class, so this mapping can also be done in polynomial time. Thus, the general version of FF-LA is at least as hard as MCKP, which is NP-hard.

Figure 2.
Reduction from the multiple-choice knapsack problem (MCKP) to the fragmentation-free land allocation (FF-LA). LMP: land management practices.
4. Related Work and Novelty
4.1. Limitations of Related Work
The multiple-choice knapsack problem (MCKP) [5] deals with combinatorial optimization, which corresponds to the assignment of land management practices among space-partitions in fragmentation-free land allocation. However, MCKP does not consider space partitioning during optimization.
Rectangular partitioning problems (e.g., R-TILE, R-PACk) [12,13] study space partitioning of a given grid to optimize a predefined objective function (e.g., minimize the total number of partitions). However, each grid cell has a fixed value and there is no multiple-choice to make at a grid cell level or combinatorial choices to make among grid cells, whereas in fragmentation-free land allocation, each spatial location has multiple choices of land management practices. In addition, rectangular partitioning problems do not consider spatial contiguity constraints (e.g., minimum tile area).
More general than the MCKP and rectangular partitioning problems, fragmentation-free land allocation needs to consider both space partitioning and combinatorial LMP assignment.
In state-of-the-art land allocation work, both fixed and flexible space partitioning have been explored. However, existing formulations (e.g., [14,15,16,17,18,19]) often consider constraints on the total allocated area of each land-use type, and do not consider the regular-shape constraint (e.g., rectangle) and the minimum patch size constraint at a patch level. In several improved formulations (e.g., [20,21,22]), patch-level area constraints were modeled using soft constraints (e.g., penalty terms) or heuristic approaches were designed to prefer more contiguous landscapes over fragmented ones. These methods recognized the importance of avoiding fragmentation in several application domains and were able to reduce fragmentation. However, they cannot guarantee that both hard geometric-shape and size constraints will be satisfied while effectively improving objective functions. Thus, their allocation solutions can still be non-feasible for implementation when applied to agriculture landscape management, especially at high resolutions (e.g., 3 m, 10 m).
4.2. Novelty
For the fragmentation-free land allocation (FF-LA) problem, related work is mainly limited by not enforcing hard spatial contiguity and shape constraints, which can cause fragmentation in a land allocation plan (example in Figure 3). In our work, we explicitly model and enforce hard spatial constraints (i.e., minimum patch area, regular shape such as rectangle) to completely eliminate fragmentation in the results.
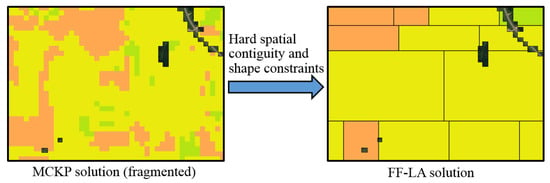
Figure 3.
Fragmentation elimination with hard spatial constraints.
More importantly, compared to the state-of-the-art, our work provides a more complete solution to the FF-LA problem by considering both stakeholder-driven collaborative design and computer-driven optimization. The solution consists of: (1) a collaborative geodesign system that aims to engage stakeholders, who are the actual decision-makers, into the land allocation process; and (2) a spatial optimization approach to suggest high quality land allocation plans that satisfy all the spatial constraints. In addition, we propose a hybrid framework that integrates the collaborative geodesign system and the optimization algorithms, and we identify the major building blocks of this hybrid approach.
5. Frameworks for Fragmentation-Free Land Allocation
5.1. Overall Architecture
The overall architecture of fragmentation-free land allocation (FF-LA) is shown in Figure 4. Our three proposed frameworks to solve FF-LA are collaborative geodesign, spatial optimization and a hybrid model of both.
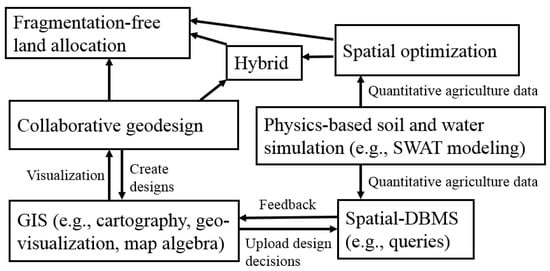
Figure 4.
Overall architecture of fragmentation-free land allocation. SWAT: Soil and Water Assessment Tool. GIS: Geographic Information System. DBMS: Database Management System.
5.2. Collaborative Geodesign
Collaborative geodesign provides a technology supported system that assists stakeholders to make complex and collaborative decisions on land allocations. The stakeholders come from multiple sectors, both public and private, including agriculture, water conservation, habitat protection, etc. Much social conflict exists around agricultural land use and its effects on water and other resources. The goal of collaborative geodesign is to reduce conflict by engaging stakeholders in collaboration, facilitating knowledge sharing, and helping them design landscapes that provide better social welfare with a better balance of food production, resource conservation, and climate resilience.
We have developed a collaborative geodesign system to help multiple stakeholders negotiate the inevitable trade-offs that arise with changes in land planning, management or policy. The system is composed of a client-side application and a back-end server that: (1) supports geo-processing and visualization services; and (2) hosts a spatial database for query processing. A detailed architecture of the collaborative geodesign system is shown in Figure 5.
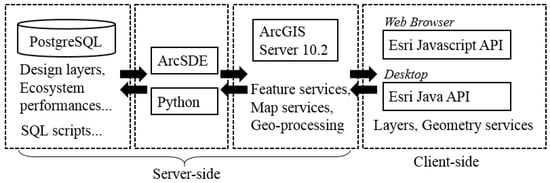
Figure 5.
Detailed architecture of the collaborative geodesign system.
The client-side application was implemented using Esri JavaScript/Java API for visualization and geometry processing. Multiple data layers are provided to support collaborative decision-making among stakeholders. For example, risk maps of water and soil quality are provided to help stakeholders determine where to allocate water and soil conservation practices such as grassland. The layers can be turned on/off with adjustable transparency settings, which makes it possible to overlay multiple layers to support complex decision-making. All of the layers are published using Esri ArcGIS Server 10.2 through its map and feature services. As stakeholders allocate patches of land management practices on the base-map, a geometry-service is called to fix geometry errors (e.g., self-intersecting polygons) and automatically remove the parts that overlap with unchangeable landscapes (e.g., water bodies, roads as discussed in Section 2.1).
The land allocation designs hand-crafted by stakeholders can be saved a any time and uploaded to the server for analysis and feedback. The uploaded designs are stored in a spatial database implemented with a PostgreSQL database [23]. The quantitative performance values of all ecosystem services under different combinations of spatial locations and land management practices (Section 2.1) are precomputed (e.g., using SWAT and InVEST modeling) and stored in the spatial database. Once a design is uploaded, its performance is immediately evaluated using the precomputed quantitative values and returned to stakeholders with a chart representation. Since stakeholders may explore different design strategies, the application provides functionality to display and compare up to four different designs at a time. The comparison includes both a map visualization and an integrated performance chart. Stakeholders will iterate through a series of design scenarios until they reach consensus and converge on a final land allocation plan.
Figure 6 shows an example session of the collaborative geodesign system, where the system is deployed on a 55-inch multi-touch display. In Figure 6a,b, stakeholders (e.g., farmers, water specialists) are going through a social learning process to collaborate and resolve conflicting objectives on ecosystem services related to water quality and economic return. Different design scenarios created by stakeholders were evaluated (Figure 6b,c) and compared using the quantitative feedback (Figure 6d).
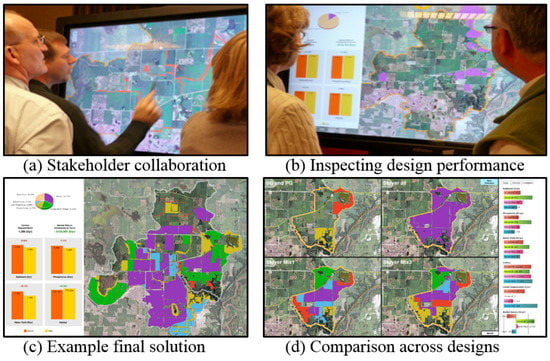
Figure 6.
Software developed to engage stakeholders in creating and evaluating land allocations. (a) Stakeholders work together to hand-craft designs using the interactive interface. (b) Design performance is evaluated and returned to stakeholders for discussion. (c) An example design with charts showing performances. (d) Stakeholders can compare multiple designs and evaluate trade-offs.
Publicly available implementation : We have fully implemented and documented the collaborative geodesign tools and made them publicly available. The newest web-based tool is available at: http://maps.umn.edu/geodesign/, where users can interact with the collaborative geodesign tools in a web-browser. The instructions and overall description are available at: http://newagbioeconomy.umn.edu/collaborativegeodesign/. The desktop versions implemented using Java (both 32-bit and 64-bit) are available at: http://www-users.cs.umn.edu/~xiexx347/cg.
5.3. Spatial Optimization
Our second framework for solving the fragmentation-free land allocation (FF-LA) problem is based on spatial optimization. Section 2.2 provides a general problem formulation for FF-LA where the definitions for spatial locations and spatial constraints are flexible. Here we present concrete problem formulation using integer programming, in which the spatial locations are defined as orthogonal grid cells, and each LMP patch is constrained to have a rectangular shape and satisfy a minimum area and width.
In order to mathematically define the spatial constraints, we previously proposed a tile-based problem formulation in [11]. Tiles are defined as a rectangular region formed by adjacent grid cells and all grid cells in each tile share a homogeneous LMP choice. Thus, in this formulation, our decision variables are LMP choices on tiles rather than on grid cells. The profit and cost values of each LMP choice on a tile can be precomputed as the sum of all profit and cost values of the grid cells contained in the tile. For profit value, the multiple ecosystem services are combined into a single profit value using user-defined weights, which is the same as Section 2.2. Supposing there are N grid cells, we then have tiles in total since each pair of grid cells can uniquely determine a tile (e.g., one grid cell as the top-left corner and the other as the bottom-right). The land allocation solution is composed of a collection of non-overlapping tiles and one LMP choice on each tile. With the modeling of tiles, the shape constraint is implicitly imposed on all patches. In addition, the minimum area constraint can also be easily defined on each tile. The new formulation is:
Inputs:
- –
- A grid partition G of the study area, where each grid cell is identified by its row i and column j.
- –
- A list L of LMP choices.
- –
- A full list Z of combinations of tile, LMP choice and the corresponding profit p and cost c:, where defines the top-left grid cell of the tile and ) defines the bottom right.
- –
- A budget limit , a minimum area and a minimum width ;
Output: A subset of Z (tile-partitioning and LMP assignment)
Objective: To maximize overall profit in the watershed:
where is 1 if and otherwise 0.
Constraints:
- –
- Binary choice on :
- –
- The cost is less than or equal to :
- –
- Each tile belonging to satisfies the minimum area and minimum width :
- –
- The tiles of selected elements in are non-overlapping. For all () in :
Constraints (8)–(10) guarantee that all LMP patches in the final land allocation are large enough for farm equipment operations, so the solution is fragmentation-free. In practice, these constraints can be pre-processed by removing all unsatisfied elements in Z. Constraints (11) and (12) are additional constraints needed to avoid overlapping tiles in the space partitioning. Here () is considered to be different than (). By adding the constraints for all pairs, the selected tiles in the solution are disjointed either horizontally or vertically.
Since the boundaries of a real-world watershed and of the unchangeable landscape within it are often irregular in shape, the spatial constraints are relaxed at a boundary. Our previous work in [11] dealt with a rectangular shaped study area. In this paper, we apply our approach to a real-world watershed with irregularly shaped boundaries: (1) We construct a grid of this irregularly-shaped watershed by using its minimum bounding rectangle (MBR); (2) We assign profit and cost values of 0 to all grid cells outside the watershed boundary or within unchangeable landscape so that these regions do not affect the decisions; and (3) After a land allocation plan is obtained, the LMP assigned to locations outside the watershed or inside the unchangeable landscape are removed by post-processing.
As discussed in [11], it is computationally prohibitive to solve the optimization problem exactly for a large-scale watershed (e.g., a grid with 1000 rows and 1000 columns), and a dynamic-growth tiling framework (DGTF) was proposed to heuristically search for a land allocation solution that satisfies all the spatial constraints. The idea is to start from a baseline (one side of the grid), and iteratively grow tiles on top of the baseline or existing tiles until the entire grid is filled up. In each step, we make sure the new tile satisfies the minimum area and width. As we proved in [11], if we always grow a new tile from the unoccupied place that is closest to the baseline, then we always have: (1) enough space to grow a new tile satisfying the spatial constraints; or (2) an adjacent tile which can be extended to fill up the space left. This process is illustrated in Figure 7. One property of DGTF is that it has a complete potential search space, which means any arbitrary rectangular tiling scheme can be reproduced by following the steps in DGTF [11].
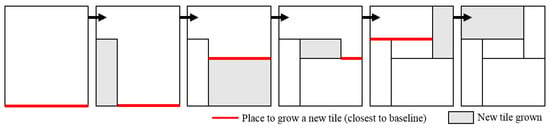
Figure 7.
Dynamic-growth tiling: the baseline is the bottom side (grid lines are not shown).
Phase 1: Tile growth: At each step, the size of the new tile and the corresponding LMP choice is determined by a local guidance function. The local optimizer will enumerate all the potential new tiles that can be grown and select the one that locally maximizes the guidance function value. In [11], we pre-computed a linear programming solution in which the spatial constraints and binary choice constraints are relaxed. The relaxed linear programming solution was used as an upper-bound on the optimal solution of FF-LA. For the rectangular region defined by a tile, denote the profit and cost achieved in the linear programming solution as and (the LMP choices in a tile may not be the same in the relaxed linear programming solution), and denote those achieved by a homogeneous choice of as and . The score of the guidance function is computed as . The local optimizer selects the new tile and LMP choice by maximizing the score. The aim of this guidance function is to make a decision to locally best approach the upper-bounding solution.
Phase 2: LMP rearrangement: After Phase 1 is completed, a tile-partitioning is obtained with initial LMP assignment. The goal of Phase 2 is to rearrange the LMP assignment on tiles to further improve the objective function. In [11], we used a heuristic pair-wise trading method. In each step, we enumerate a pair of tiles and explore potential LMP changes on the two tiles that can improve the objective function without violating the cost constraint. The trading continues until no further improvement can be made.
Solution quality improvement: Here we use an exact solver to replace the heuristic pair-wise trader in Phase 2. Since the tile-partitioning is already fixed after Phase 1, we are left with a set of fixed tiles. Thus, the spatial constraints (e.g., minimum area, shape, non-overlapping) are no longer binding or effective. This change makes the problem much easier to solve since we can treat each tile as an independent variable. In addition, since the number of tiles in the final solution is always smaller than or equal to the number of grid cells, the scale of the problem is also reduced. In practice, the problem can be efficiently solved by standard integer programming solvers (e.g., CPLEX solver [24] or dynamic programming [5]). The use of exact solvers guarantees the optimality of LMP assignment in Phase 2 and thus can always produce a higher objective function value than our previous Phase 2 approach in [11].
5.4. Towards the Future: A Hybrid Framework
A hybrid framework is needed to fully address the fragmentation-free land allocation problem. The information that humans consider in making land allocation decisions is often richer than what a computer considers; it can include hard-to-quantify information like cultural values, land owner preferences, and technical implementation feasibility. As a result, humans often make decisions using a larger information set than can be easily quantified through data. By contrast, optimization methods focus on the trade-offs that are captured by the quantitative information available (e.g., water risk, market return).
We propose a hybrid approach that integrates the spatial optimization algorithm into the collaborative geodesign system. This would allow solutions from spatial optimization to serve as promising starting points or suggestions that stakeholders could consider during their deliberations. We introduce three building blocks of the hybrid approach, namely stakeholder intervention, sub-problem optimization and interactivity.
Stakeholder intervention: Stakeholders are allowed to intervene in the solution of the optimization algorithm. They can constrain both space partitioning and choices of land management practices at certain locations based on their discussion and expert knowledge, which is part of a social learning process and is hard to know beforehand using the optimization algorithm. The algorithm then guarantees that solutions at those places are fixed and not changed. Alternatively, stakeholders can directly choose a specific sub-region where decisions are difficult to make and seek suggestions from the optimization algorithm only for that region.
Sub-problem optimization: With stakeholder intervention, the optimization algorithm needs to solve a specific sub-problem (e.g., at a certain region) instead of the original problem (e.g., entire watershed). In order to solve the sub-problem, the algorithm needs to determine the feasibility of the sub-problem and identify a solution. In scenarios where stakeholder interventions create a non-feasible problem (e.g., insufficient budget or space to satisfy the constraints), the algorithm should suggest several modifications to stakeholder interventions so stakeholders can discuss and reconfigure the interventions to make them feasible.
Interactivity: The use of an optimization algorithm in collaborative geodesign requires interactions between stakeholders and the algorithm. In a geodesign session, this requires real-time or quick (e.g., several seconds to minutes) feedback/suggestions from the algorithm. To meet the processing speed requirement, the algorithm needs to be accelerated or it can optimize at a coarse resolution to allow interactive decision-making. Between sessions (e.g., overnight), the optimization algorithm is given plenty of time to search a larger space of solutions, and it can run on fine-resolution to help identify new opportunities for stakeholders to discuss in the next session.
6. Case Study: Seven Mile Creek Watershed
We evaluated the collaborative geodesign and spatial optimization frameworks through a case study of land allocation in the Seven Mile Creek watershed, located in southwestern Minnesota. The total area of the watershed is about 25,000 acres. Water run-off here converges directly to the Minnesota River, a tributary of the Mississippi River. Since the watershed is located around the head of the Mississippi River, fertilizer application and soil erosion in this area can severely affect water quality downstream by introducing fertilizer residues and sediments. In fact, food production in agricultural areas inside the Mississippi River watershed is a dominant source of pollution in the Gulf of Mexico, and a major cause of the well-known “Dead Zone”.
As part of the “Corn Belt” [25], the Seven Mile Creek watershed has undergone intensive maize–soybean production, which has led to water quality degradation. New demand for cellulosic feedstocks for advanced biofuels and other bioproducts could generate a market for other crops such as switchgrass and corn stover. This would present a major economic opportunity for rural communities, but could also generate additional environmental harm. It is an opportune time to redesign the agricultural landscape to improve its sustainability for food and clean water production. In this case study, the goal was to maximize water quality improvement under a cost constraint (e.g., cost for re-purposing land management practices, decrease in food production).
As an approximation of the real-world watershed, the study area was discretized into an orthogonal grid with 30 m by 30 m grid cells. Quantifying water quality improvement and modeling the economic cost of applying each LMP to each grid cell requires detailed soil and physics modeling. In this study, quantitative coefficients for water quality and economic cost were computed using the state-of-the-art Soil and Water Assessment Tool (SWAT) and the InVEST model. These physical models employ hundreds of inputs (e.g., precipitation, solar radiation, wind speed) to correctly simulate real-world scenarios. As a standard practice, the models were very carefully calibrated by domain experts to yield accurate coefficients.
Figure 8 shows the boundary of the Seven Mile Creek watershed. The streams inside converge to the outlet at the bottom-right. Overall, the grid partition was 455 by 447 in size with 203,385 grid cells. Each grid cell has six possible LMPs: conventional tillage, conservation tillage, conservation tillage with stover removal, low-phosphorus application, switch grass, and prairie grass. The baseline scenario was conventional tillage, which is the current LMP applied in the entire study area.
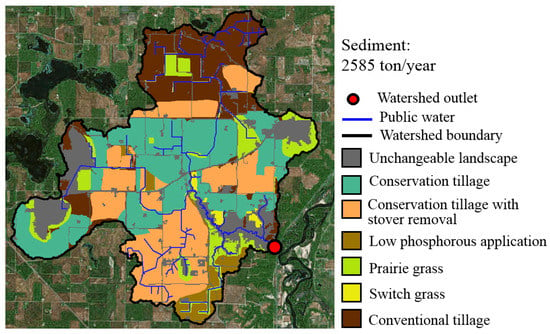
Figure 8.
Stakeholder solution with collaborative geodesign.
6.1. Stakeholder Solution with Collaborative Geodesign
The collaborative geodesign approach was utilized in the Seven Mile Creek watershed by a group of diverse stakeholders from agriculture, conservation, nonprofit, and for-profit sectors, including individual farmers, commodity crop representatives, state and federal regulators, and local community groups. Through a series of eight meetings, stakeholders engaged in social learning; four of the meetings used the geodesign system (further details on the social process are described in [2]).
In the workshop, stakeholders identified a common objective to better sustain the environmental and economic well-being of the landscape. To reduce the complexity of the human design process, the stakeholders were divided into five groups of four to five individuals of diverse backgrounds. Each group was given a different sub-portion of the watershed so that less information needed to be considered given the smaller spatial extent. In this session, the number of iterations that stakeholders took to reach the final design was in the range of 7 to 22. The final land allocation plan generated by the collaboration across all stakeholder groups is shown in Figure 8.
The result of the collaborative geodesign process was that different groups used a wide variety of land-use choices. Together, all of the different practices were used and included results that were not as efficient. Sediment (tons/year) was used to evaluate the water quality impact of the stakeholder design. As shown in Figure 8, the stakeholder design yielded a total sediment of 2585 tons per year, a reduction of 182 tons per year compared to the baseline scenario. Expert knowledge involved in this design can be seen at multiple places. For example, vegetative buffer strips of prairie grass were allocated along drainage ditches (Figure 8 bottom), to help filter out fertilizer residues and improve water quality. Conservation tillage with corn stover removal was allocated in large areas for greater economic return.
6.2. Computer-Suggested Solutions with Spatial Optimization
To demonstrate the importance of spatial constraints, we first show the integer programming solution without spatial constraints in Figure 9. The market return achieved by stakeholders was used as a cost constraint here so that the integer programming solution must have at least the same amount of market return. Without the spatial constraints, the choice on each grid cell was treated as an independent variable (its spatial adjacency was ignored). In Figure 9, we can see much evidence of land fragmentation. The boundaries of LMP patches tend to be curving with a large amount of local variations, which is difficult for farm equipment to maneuver through. When zoomed in, a large number of small LMP patches can be observed. This type of land fragmentation can significantly reduce the efficiency of farm equipment operations.
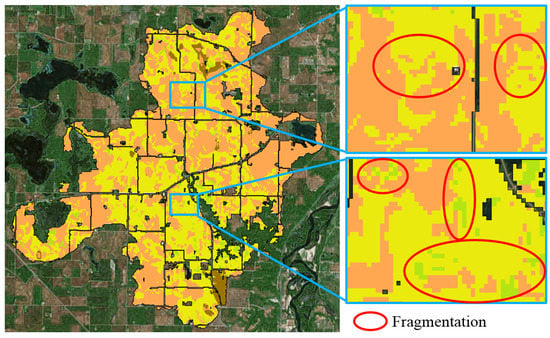
Figure 9.
Example of land fragmentation in integer programming solution without spatial constraints.
Computer-suggested land allocation maps are shown in Figure 10. The land allocation maps were generated under three different sets of spatial constraints: (1) minimum area of 50 grid cells and minimum width (also height) of 5 grid cells; (2) minimum area of 200 and minimum width of 10; and (3) minimum area of 800 and minimum width of 20. Each grid cell measured 30 m by 30 m. The economic cost constraint was obtained from the stakeholder design, which means the economic return needed to be at least as high as that of the stakeholder design. The goal was to evaluate the performance gain of sediment reduction by using spatial optimization.
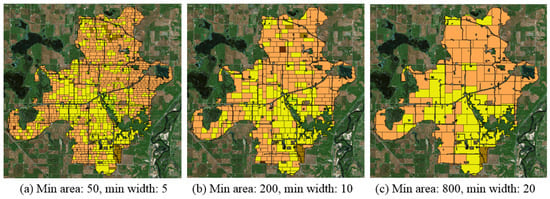
Figure 10.
Fragmentation-free land allocation results with different spatial constraints. The minimum tile area and width gradually increase from (a–c). The total sediment of (a) is 1508 ton/year, (b) is 1597 ton/year and (c) is 1664 ton/year.
The total sediment achieved by our algorithm ranged from 1508 to 1664 tons per year under different minimum area and width constraints. The general trend was that the amount of sediment increased as the minimum area and width increased. In order to maintain a higher level of spatial contiguity (e.g., larger LMP patches), the algorithm had to make more non-optimal choices at places to eliminate small LMP patches that did not satisfy the minimum area and width constraints. Overall, spatial optimization showed a significantly lower amount of sediment compared to the stakeholder design.
6.3. Comparison of Land Allocation Approaches
Collaborative geodesign and spatial optimization generated markedly different land allocation solutions both in terms of the distribution of land management practices over space and the overall proportion of land uses chosen. This is illustrated most clearly in the greater proportion of conservation tillage (without stover removal) used across stakeholder designs compared to the solutions from the optimization approach. Stakeholders relied heavily on the common practice of conservation tillage whereas the optimization approach used the land management practice minimally. Another advantage of the optimization approach is that it can, depending on the spatial constraints used, suggest landscapes that fit either a precision agriculture or a conventional agriculture vision.
In terms of overall performance, spatial optimization did better than this current set of stakeholder designs in reducing sediment loading while maintaining economic performance (Figure 8 and Figure 10). Despite this significant improvement, collaborative geodesign is still a necessary step towards a final implementation plan because: (1) it involves the stakeholders (e.g., farmers) who are the actual decision-makers and implementers of the plan; and (2) stakeholder discussion resolves critical issues such as cultural values, land owner preferences, and feasibility of technical implementation (e.g., individual level, community level). These problems remain hard to quantify and model in an optimization algorithm.
This case study shows that spatial optimization is indeed able to provide valuable land allocation insights to help stakeholders explore new opportunities to improve return on ecosystem services (e.g., water quality). This motivates and validates the use of a hybrid approach which incorporates both stakeholder collaboration and algorithmic optimization. In future, the hybrid framework discussed in Section 5.4 will be further studied and implemented towards an integrated system.
7. Conclusions and Future Work
Fragmentation-free land allocation (FF-LA) is important for improving the efficiency of allocating land management practices (LMPs) within a watershed, balancing water quality improvements with the need for meaningful clustering of LMPs while avoiding LMP fragmentation on too fine a scale to manage practically. The FF-LA problem is challenging from both computational (i.e., NP-hard) and social perspectives. We discuss three frameworks to solve the FF-LA problem. Geodesign’s technology-supported framework engages stakeholders in creating and evaluating various land allocation designs (the fully-implemented system is available online). The spatial optimization framework provides an algorithmic solution that guarantees no fragmentation exists in land allocation solutions. Our case study in the Seven-Mile-Creek watershed showed the importance of both collaborative geodesign and spatial optimization, and motivates us to further research a third hybrid framework which aims to integrate the optimization methods into the geodesign system.
In future work, we will explore: (1) new interactive algorithms needed in the hybrid framework; and (2) extending the shape constraints from rectangle to a variety of regular shapes.
Acknowledgments
This material is based upon work supported by the National Science Foundation under Grants No. 1541876, 1029711, IIS-1320580, 0940818 and IIS-1218168, the USDOD under Grants No. HM1582-08-1-0017 and HM0210-13-1-0005, ARPA-E under Grant No. DE-AR0000795, and the OVPR Infrastructure Investment Initiative and Minnesota Supercomputing Institute (MSI) at the University of Minnesota. We also thank Kim Koffolt for improving the readability of this article.
Author Contributions
Y. Xie, P. Wiringa, B. Runck and L. Kne developed the geodesign system. D. Mulla and S. Shekhar raised the research problem on developing a fragmentation-free land allocation (FF-LA) algorithm. Y. Xie proposed the detailed FF-LA formulation and algorithm, advised by S. Shekhar. Y. Xie, B. Runck, S. Shekhar and D. Mulla contributed to related work. Y. Xie and B. Runck designed the case study. D. Mulla and N. Jordan provided agricultural concepts, interpretation, modeling and data. Y. Xie and B. Runck wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- United Nations. World Population Prospects, 2015 Revision. Available online: https://esa.un.org/unpd/wpp/publications/files/key_findings_wpp_2015.pdf (accessed on 10 July 2017).
- Schively, C.; Runck, B.; Pitt, D.; Kne, L.; Jordan, N.; Mulla, D.J.; Zerger, C.; Reichenbach, M. Collaborative geodesign to advance multifunctional landscapes. Lands. Urban Plan. 2016, 156, 71–80. [Google Scholar]
- Van Dijk, T. Scenarios of Central European land fragmentation. Land Use Policy 2003, 20, 149–158. [Google Scholar] [CrossRef]
- Niroula, G.S.; Thapa, G.B. Impacts and causes of land fragmentation, and lessons learned from land consolidation in South Asia. Land Use Policy 2005, 22, 358–372. [Google Scholar] [CrossRef]
- Kellerer, H.; Pferschy, U.; Pisinger, D. The multiple-choice knapsack problem. In Knapsack Problems; Springer: Berlin/Heidelberg, Germany, 2004; pp. 317–347. [Google Scholar]
- Jordan, N.R.; Slotterback, C.S.; Cadieux, K.V.; Mulla, D.J.; Pitt, D.G.; Olabisi, L.S.; Kim, J.O. TMDL implementation in agricultural landscapes: A communicative and systemic approach. Environ. Manag. 2011, 48, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Galzki, J.; Birr, A.S.; Mulla, D.J. Identifying critical agricultural areas with 3-meter LiDAR elevation data for precision conservation. J. Soil Water Conserv. 2011, 66, 423–430. [Google Scholar] [CrossRef]
- Kalcic, M.M.; Chaubey, I.; Frankenberger, J. Defining Soil and Water Assessment Tool (SWAT) hydrologic response units (HRUs) by field boundaries. Int. J. Agric. Biol. Eng. 2015, 8, 69–80. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool—Historical development applications, and future research directions. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 1211–1240. [Google Scholar] [CrossRef]
- Nelson, E.; Mendoza, G.; Regetz, J.; Polasky, S.; Tallis, H.; Cameron, D.; Chan, K.; Daily, G.C.; Goldstein, J.; Kareiva, P.M.; et al. Modeling multiple ecosystem services, biodiversity conservation, commodity production, and tradeoffs at landscape scales. Front. Ecol. Environ. 2009, 7, 4–11. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, K.; Shekhar, S.; Dalzell, B.; Mulla, D. Geodesign optimization (GOP) towards improving agricultural watershed sustainability. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17): Workshop on AI and OR for Social Good, San Francisco, CA, USA, 4–5 February 2017. [Google Scholar]
- Muthukrishnan, S.; Poosala, V.; Suel, T. On rectangular partitionings in two dimensions: Algorithms, complexity and applications. In Proceedings of the International Conference on Database Theory, Jerusalem, Israel, 10–12 January 1999; pp. 236–256. [Google Scholar]
- Berman, P.; DasGupta, B.; Muthukrishnan, S.; Ramaswami, S. Improved approximation algorithms for rectangle tiling and packing. In Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA ’01), Washington, DC, USA, 7–9 January 2001; pp. 427–436. [Google Scholar]
- Cao, K.; Ye, X. Coarse-grained parallel genetic algorithm applied to a vector based land use allocation optimization problem: The case study of Tongzhou Newtown, Beijing, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 1133–1142. [Google Scholar] [CrossRef]
- Wang, X.; Yu, S.; Huang, G. Land allocation based on integrated GIS-optimization modeling at a watershed level. Landsc. Urban Plan. 2004, 66, 61–74. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, X. Land use allocation based on a multi-objective artificial immune optimization model: An application in Anlu County, China. Sustainability 2015, 7, 15632–15651. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, Y.; Jin, X.; Shu, B.; Zhou, Y.; Yang, X. Simulating multi-objective land use optimization allocation using multi-agent system—A case study in Changsha, China. Ecol. Model. 2016, 320, 334–347. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, W.; He, J.; Liu, Y.; Ai, T.; Liu, D. A land-use spatial optimization model based on genetic optimization and game theory. Comput. Environ. Urban Syst. 2015, 49, 1–14. [Google Scholar] [CrossRef]
- Ligmann-Zielinska, A.; Church, R.L.; Jankowski, P. Spatial optimization as a generative technique for sustainable multiobjective land-use allocation. Int. J. Geogr. Inf. Sci. 2008, 22, 601–622. [Google Scholar] [CrossRef]
- Cao, K.; Huang, B.; Zhao, Q.; Wang, S. Land Use Allocation Optimization towards Sustainable Development Based on Genetic Algorithm. In Proceedings of the 2009 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009; pp. 1–5. [Google Scholar]
- Liu, Y.; Peng, J.; Jiao, L.; Liu, Y. PSOLA: A heuristic land-use allocation model using patch-level operations and knowledge-informed rules. PLoS ONE 2016, 11, e0157728. [Google Scholar] [CrossRef] [PubMed]
- Ligmann-Zielinska, A.; Church, R.; Jankowski, P. Sustainable urban land use allocation with spatial optimization. In Proceedings of the 8th International Conference on Geocomputation, Ann Arbor, MI, USA, 31 July–3 August 2005; pp. 1–3. [Google Scholar]
- PostgreSQL. 2017. Available online: https://www.postgresql.org/ (accessed on 10 July 2017).
- CPLEX Solver User Manual. 2016. Available online: https://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.3/ilog.odms.studio.help/pdf/opl_languser.pdf (accessed on 10 July 2017).
- Anderson, J.L. Industrializing the Corn Belt; Northern Illinois University Press: DeKalb, IL, USA, 2016; p. 248. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).