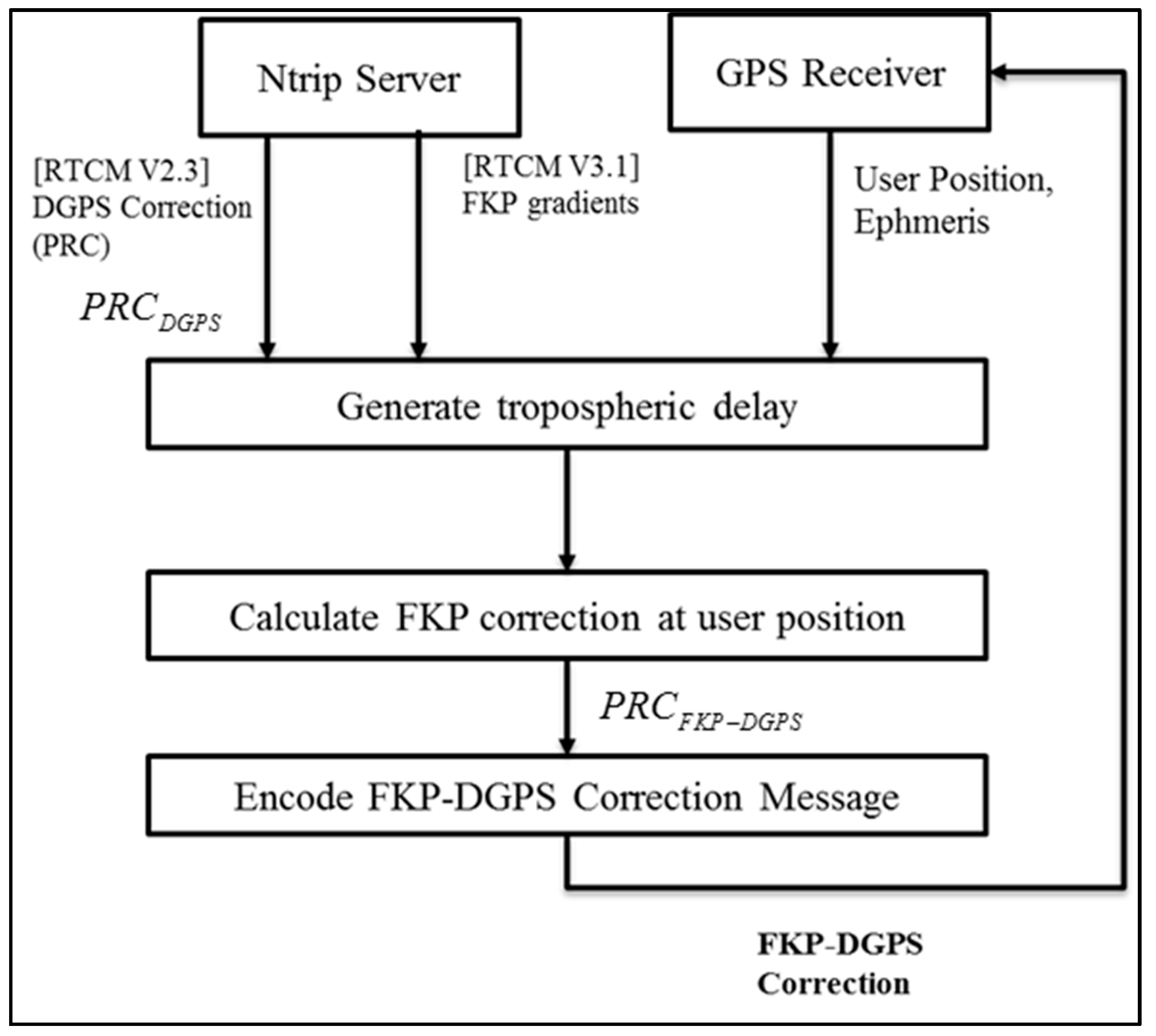
4.3. Static Test
To confirm the improvement in the accuracy of the DGPS of the low-cost single frequency GPS receiver using the modified FKP corrections in the position domain, static and dynamic user tests were conducted. First, the static test is introduced.
In the static test,
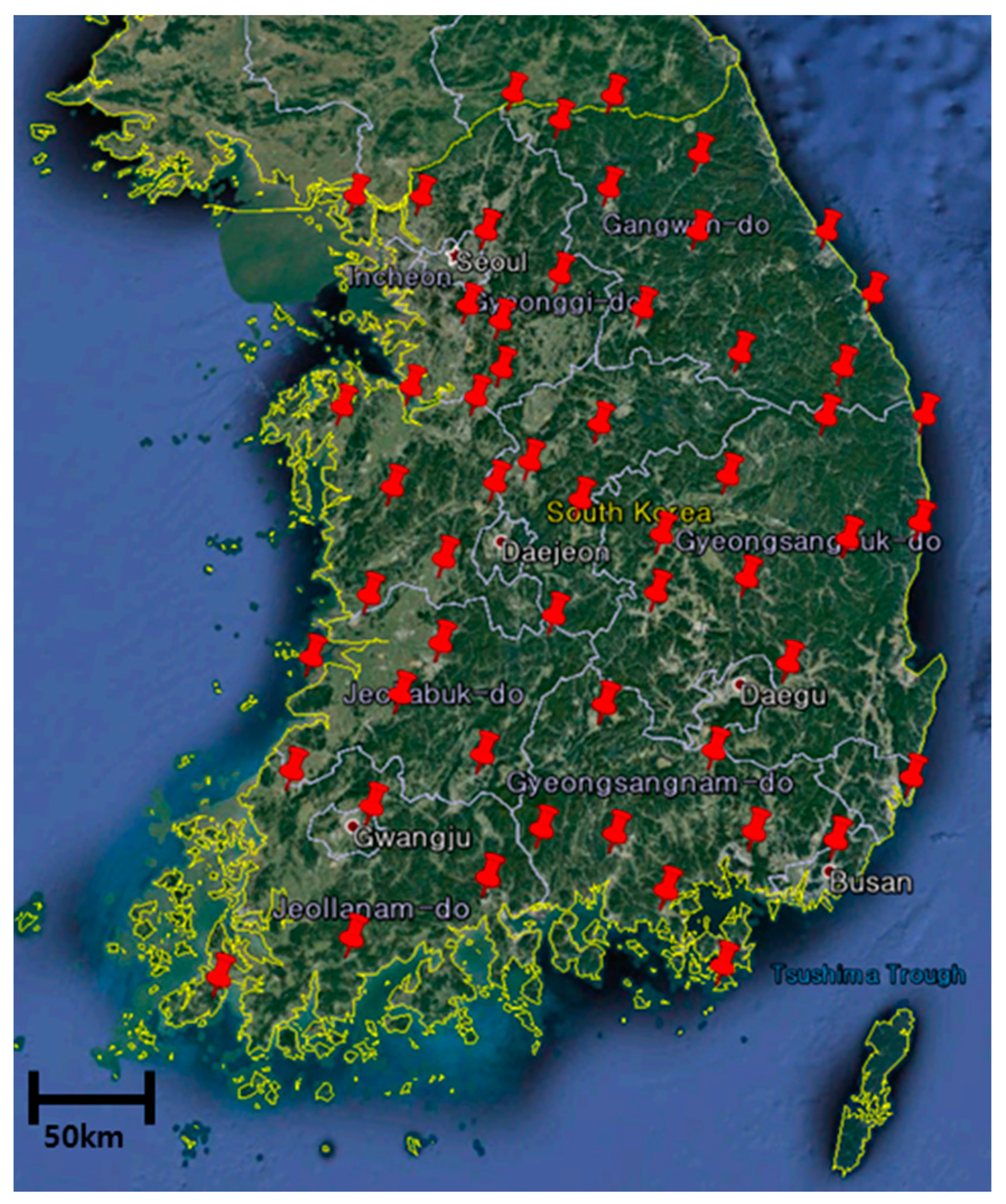
Figure 8a shows the u-blox LEA-6T evaluation kit selected as the low-cost GPS receiver, which is one of the most popular and inexpensive commercial GPS receivers. It can be applied for the DGPS messages in the RTCM version 2.3. The static user is located at Bldg. 312 in Seoul National University in Korea. In addition, to confirm the effect of the FKP corrections corresponding to the baseline lengths which is the distance between the user and the RS, four RSs (YANP, WNJU, YOWL, and WULJ) were selected which are at distances of 50, 90, 140, and 225 km south–east of the user in sequence, as shown in
Figure 8b.
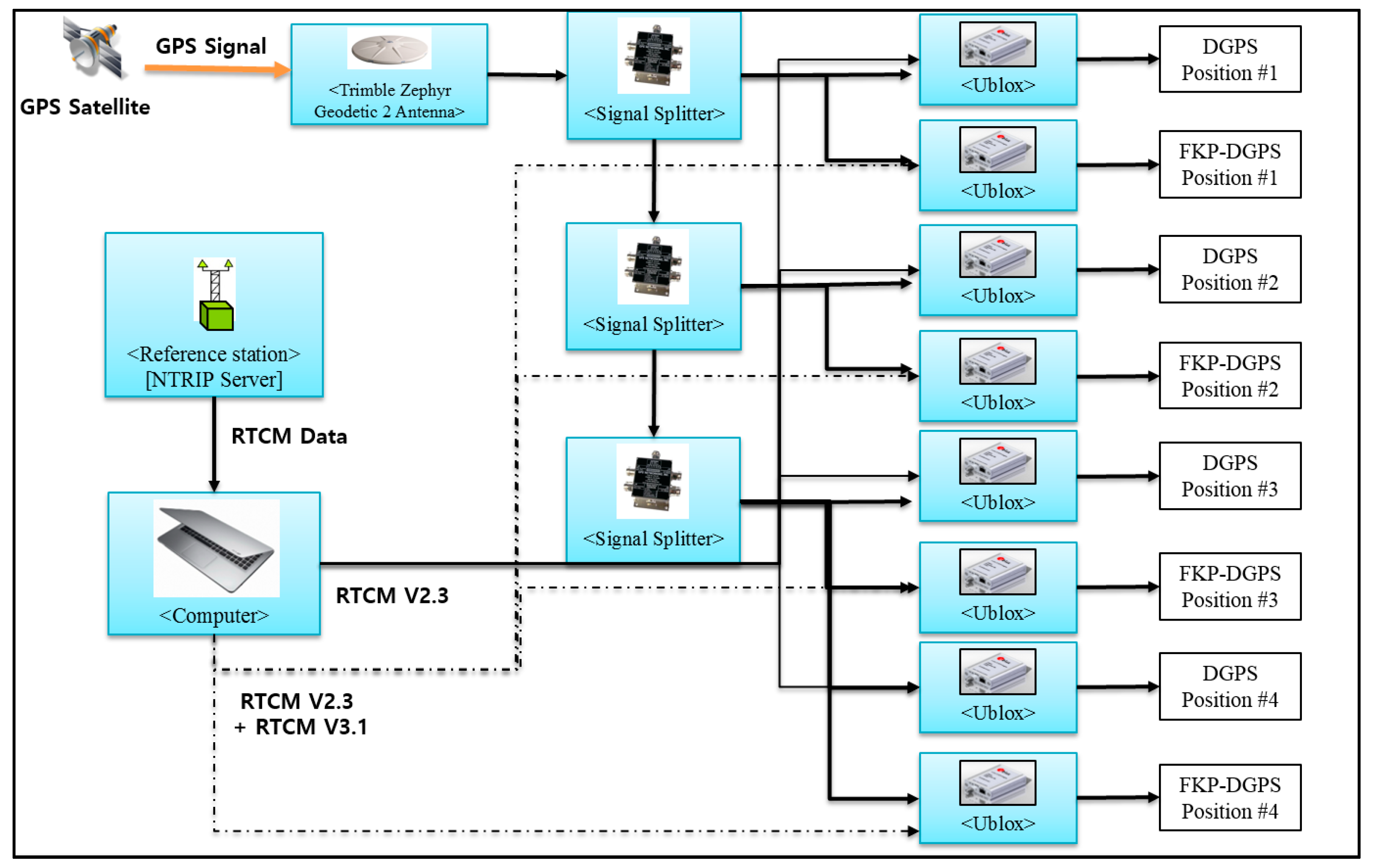
The test was conducted for approximately 12 h from 4 April 2017 10:30 in local time (UTC+09). To obtain the data from the four RSs simultaneously and let the receivers operate the DGPS and FKP-DGPS, eight receivers were used as the static user. In the test, an RS receiver of Trimble NetR9 and the eight u-blox receivers were connected to a Trimble Zephyr geodetic 2 antenna as shown in
Figure 9. Using the measurements from the NetR9 and Zephyr antenna, a precise position was determined. Although the geodetic antenna reduces the noise level of the u-blox receiver compared to the original patch antenna, it does not reduce the bias error due to the spatial decorrelation, which can help in distinguishing the bias error from the noise-related error. In addition,
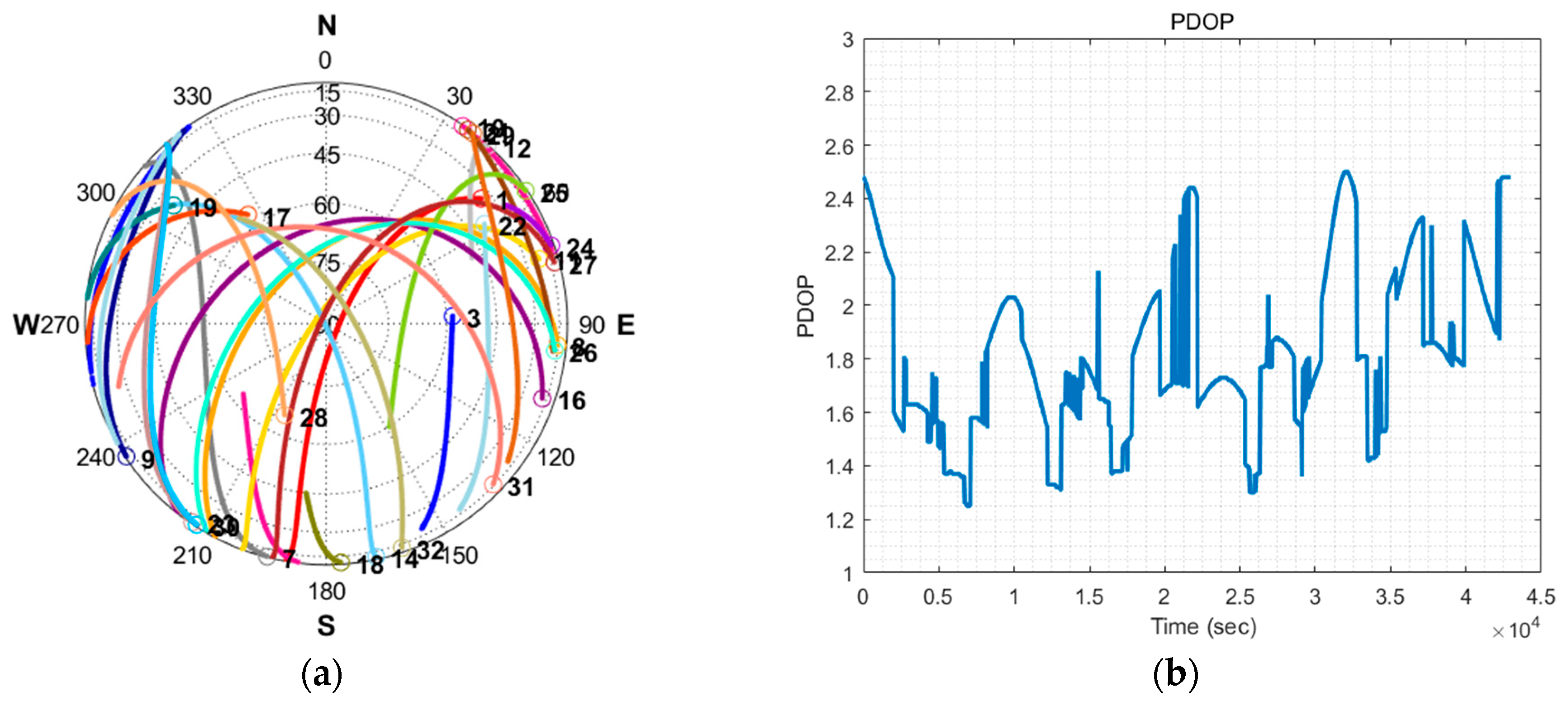
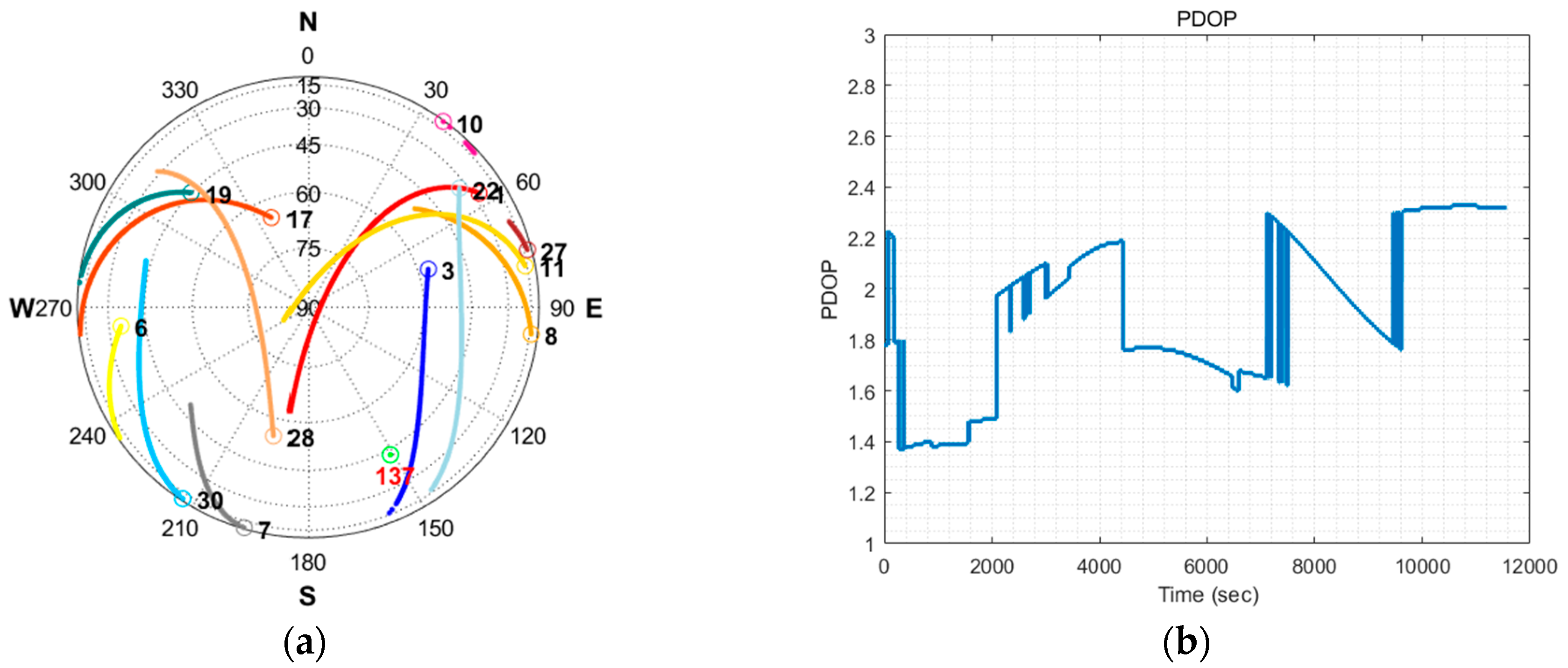
Figure 10a shows the visible satellites in the sky during the test.
Figure 10b shows the position dilution of precision (PDOP). The geometry of satellites affects the positioning accuracy and the dilution factor (DOP) depends solely on the geometry. Thus, the PDOP is normally presented with the positioning results in the field of GPS error analysis [
28].
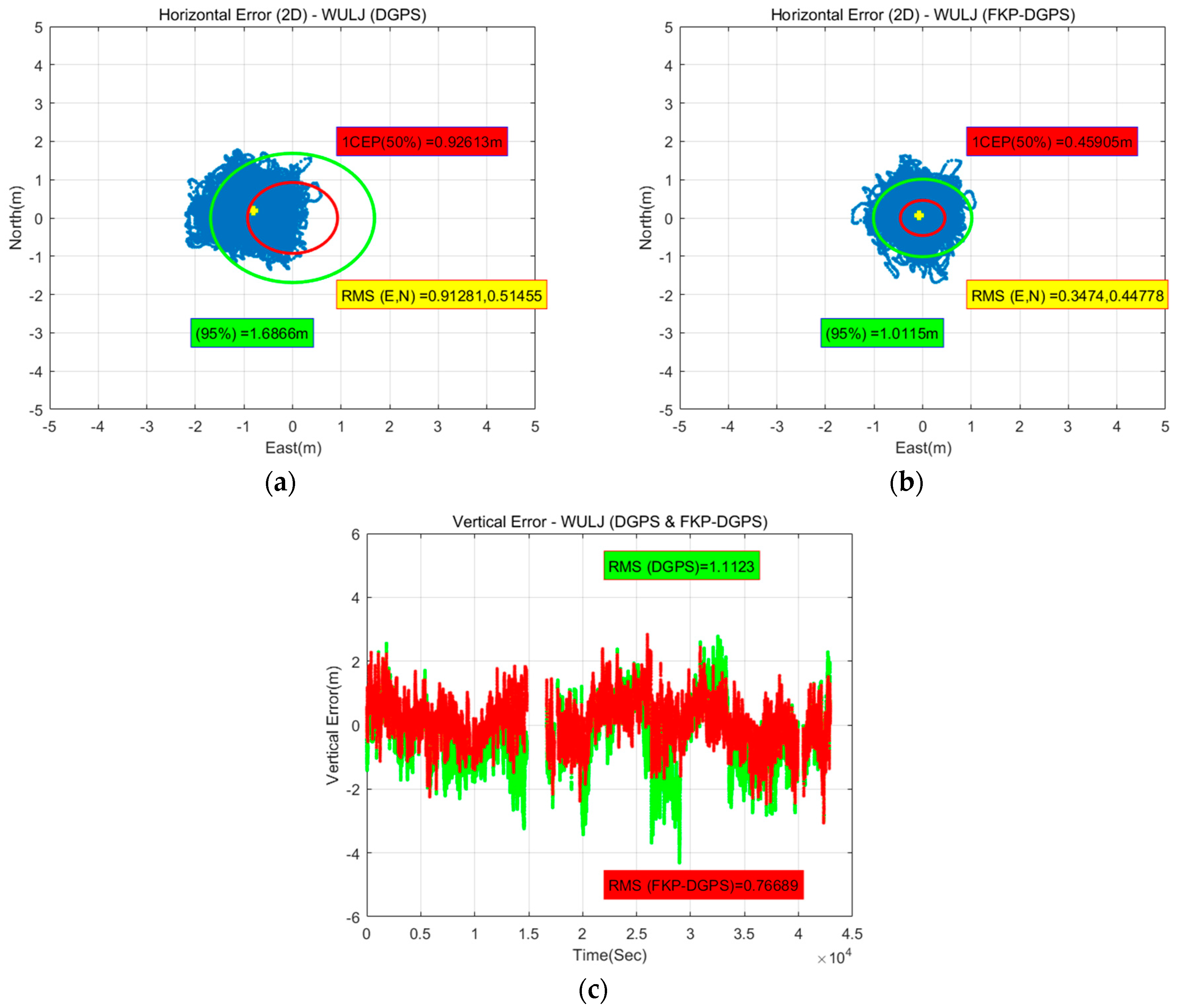
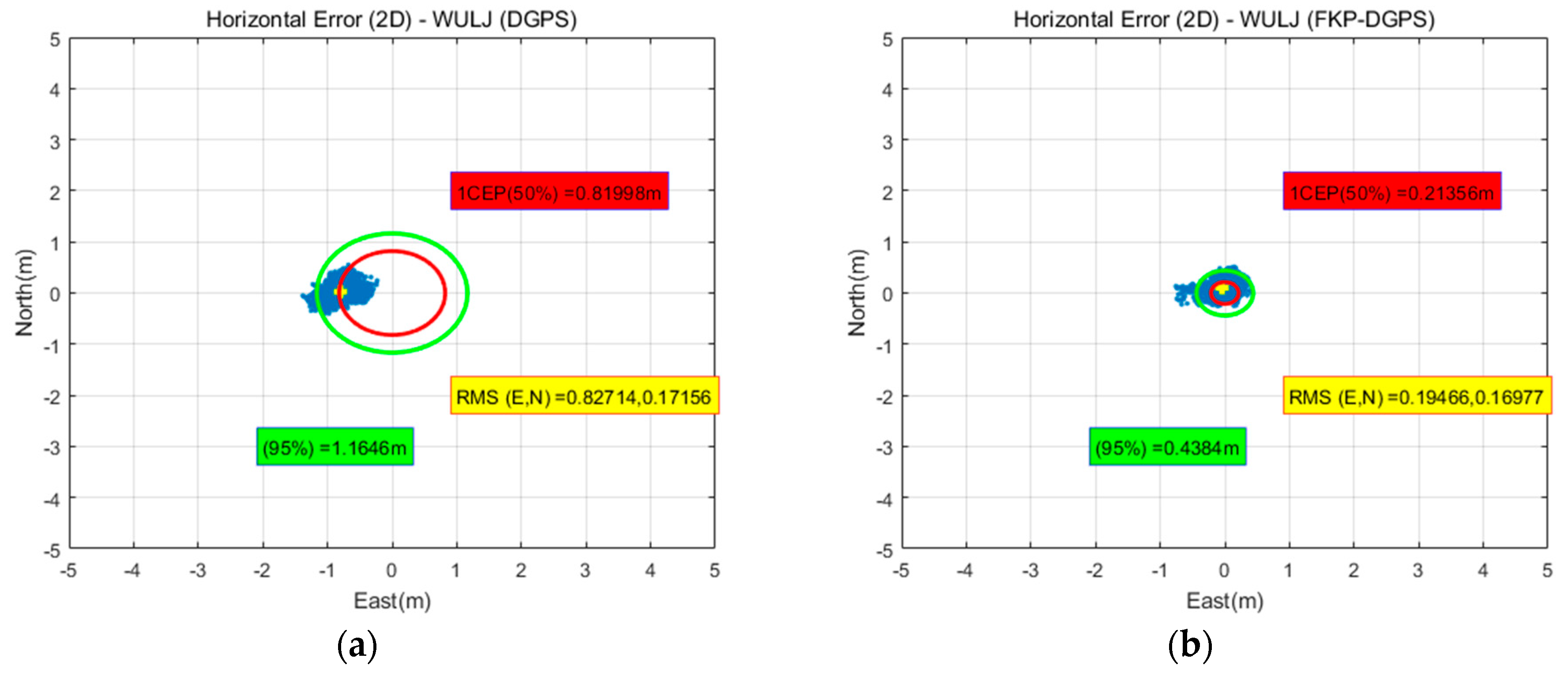
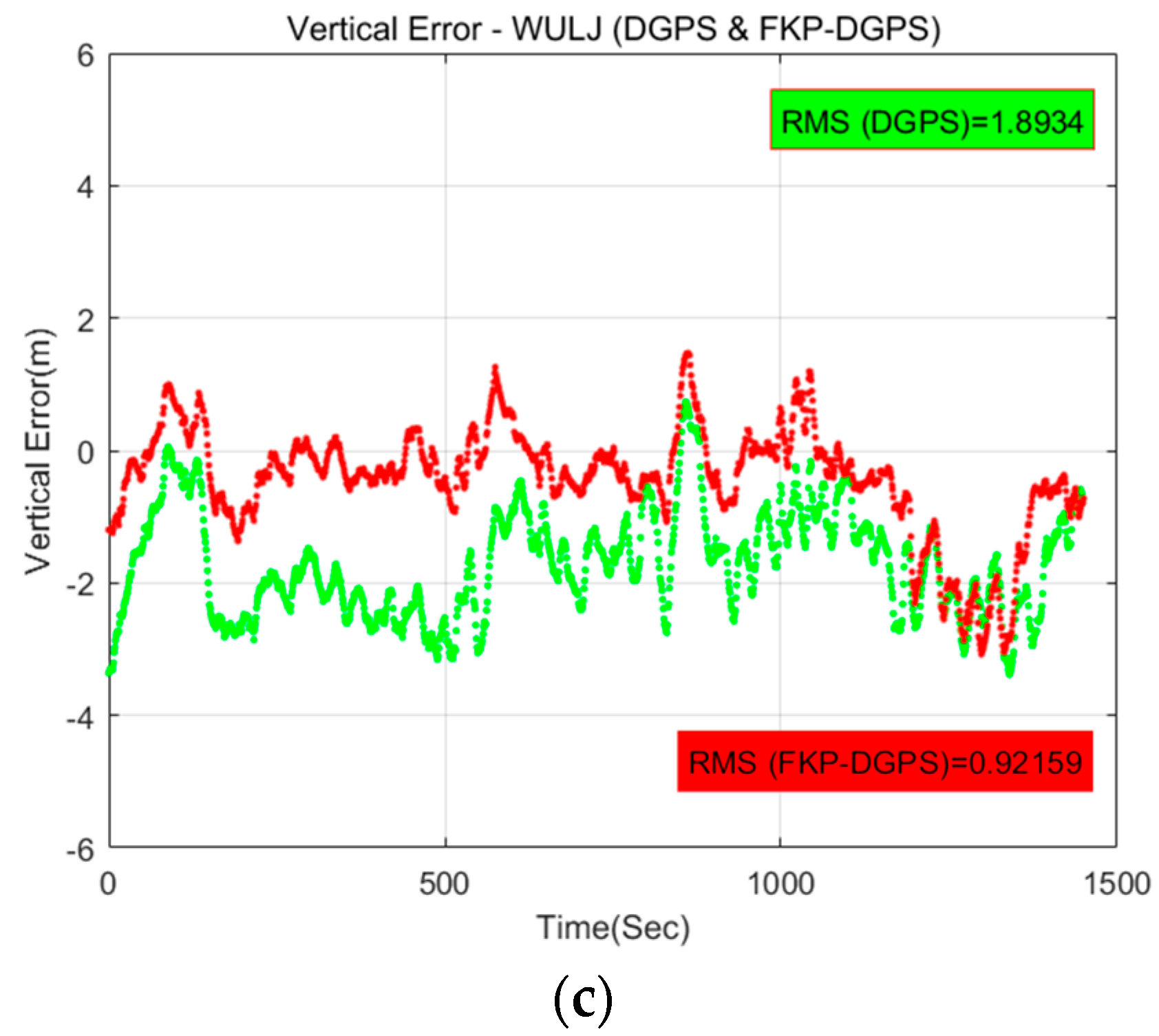
Figure 11 shows the horizontal and vertical position errors of the DGPS and FKP-DGPS results of the WULJ RS, which is located farthest from the static user in the east-north-up (ENU) coordinate. It is easily confirmed that the horizontal result of the DGPS is slightly biased on the left side. However, the horizontal result of the FKP-DGPS seems unbiased, but slightly noisy. Furthermore, the positive effect of the FKP correction can be confirmed from the vertical result. The blank in the vertical results occurred when the correction data are not received from the NGII FKP server because of the server-side problem. The data in the blank are excluded from the analysis.
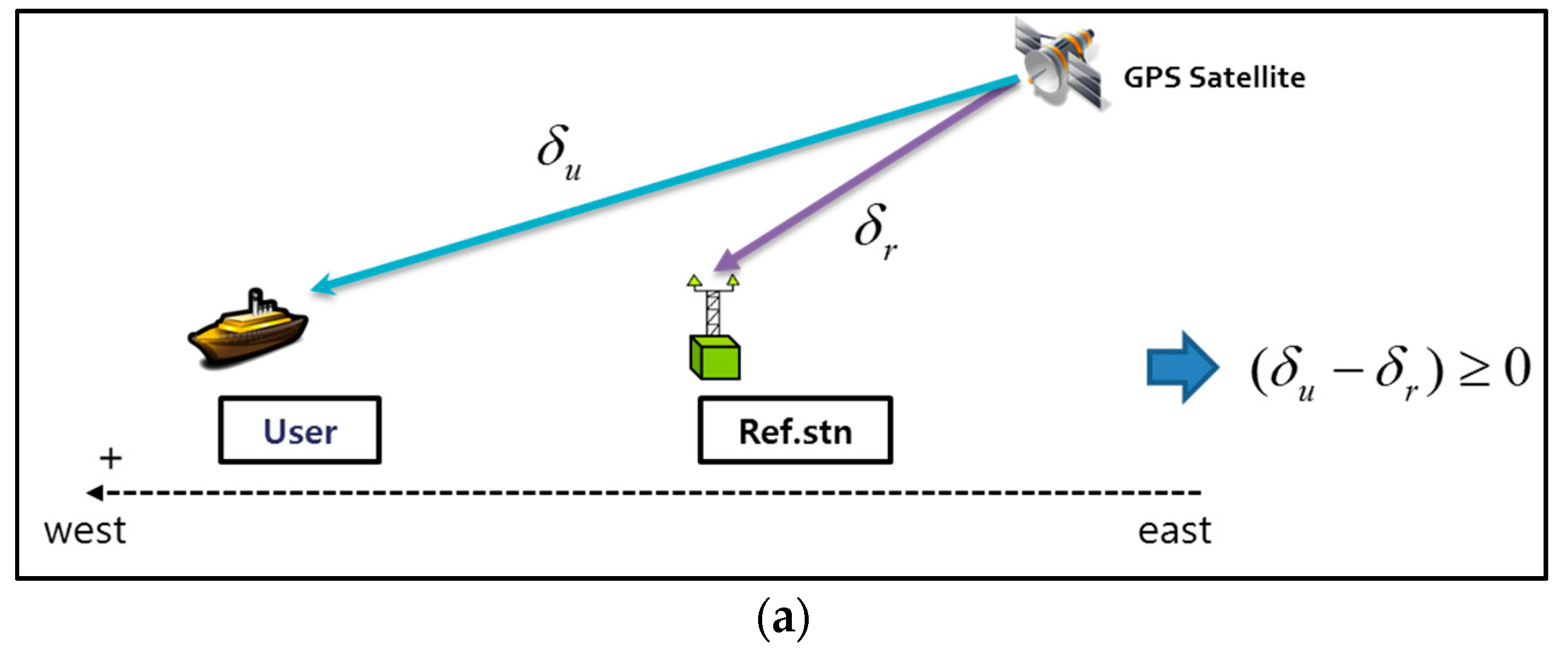
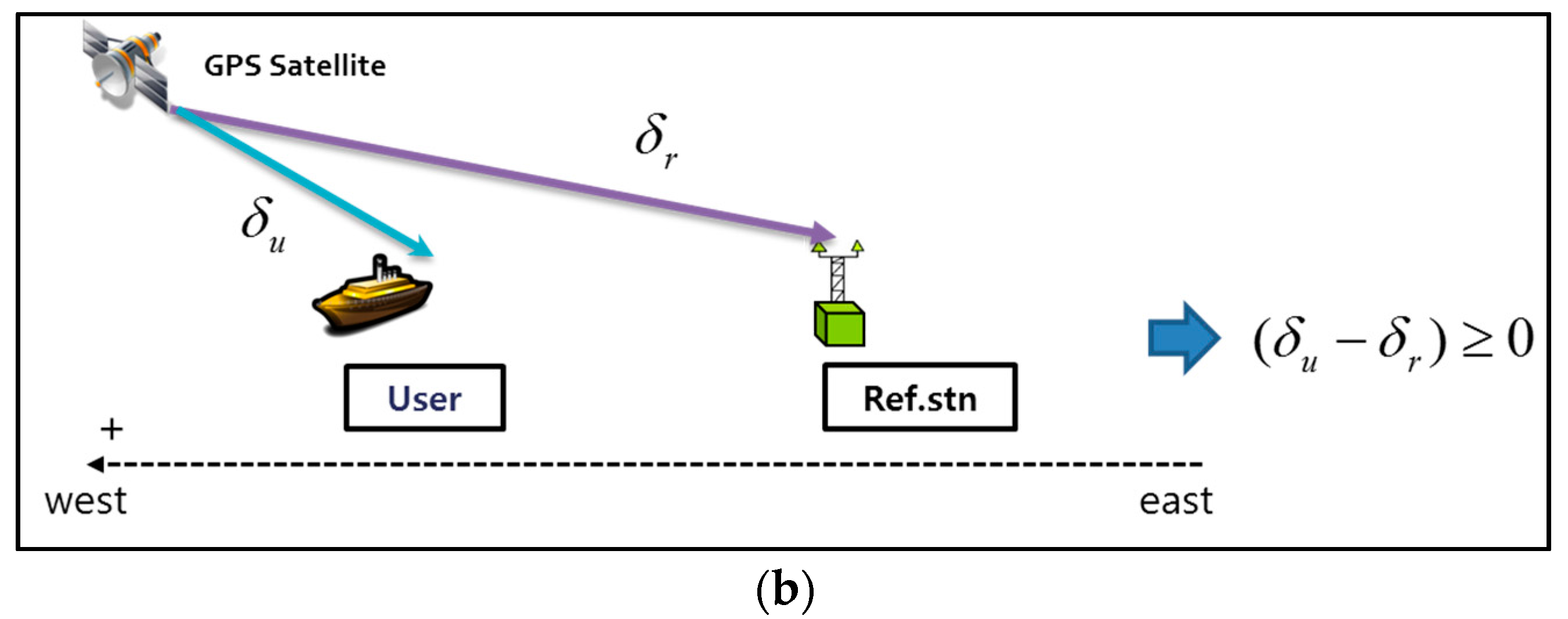
Figure 12 shows the reason for the bias in the horizontal result of the DGPS on the west side. Considering the rotation of the Earth, the appearance of satellites is in the east-west direction. Moreover, satellites with low elevation angles more significantly affect positioning results. In
Figure 12, it is assumed that the west direction is positive, and the GPS satellite has low elevation angle. If
are the measurement errors of the user and RS, respectively, and
is equal to the correction from the DGPS RS, the residual error of the user after applying the correction from the DGPS RS can be positive, implying that the positioning error lies in the west direction.
Figure 12a shows the case wherein the GPS satellite is on the east side of the user and RS.
Figure 12b shows the case wherein the GPS satellite is on the west side of the user and RS.
Table 4 and
Table 5 present the detailed numerical results including the results of other stations. The results show that the FKP-DGPS has more accurate positioning accuracy than the DGPS. With the increase in the baseline length, the effect of the FKP correction on the errors due to the spatial decorrelation increases with respect to the positioning accuracy. Thus, in cases of the FKP-DGPS, the improvements of the 95% horizontal accuracy of all stations are 3%, 18%, 26%, and 40% for the corresponding baseline lengths of the RSs compared to the accuracy of the DGPS. In particular, the error components of the east direction are visibly reduced when the FKP-DGPS is applied, which were large when the corrections were used from an RS far apart from the user in the east direction of DGPS. Based on the statistics in
Table 4 and
Table 5,
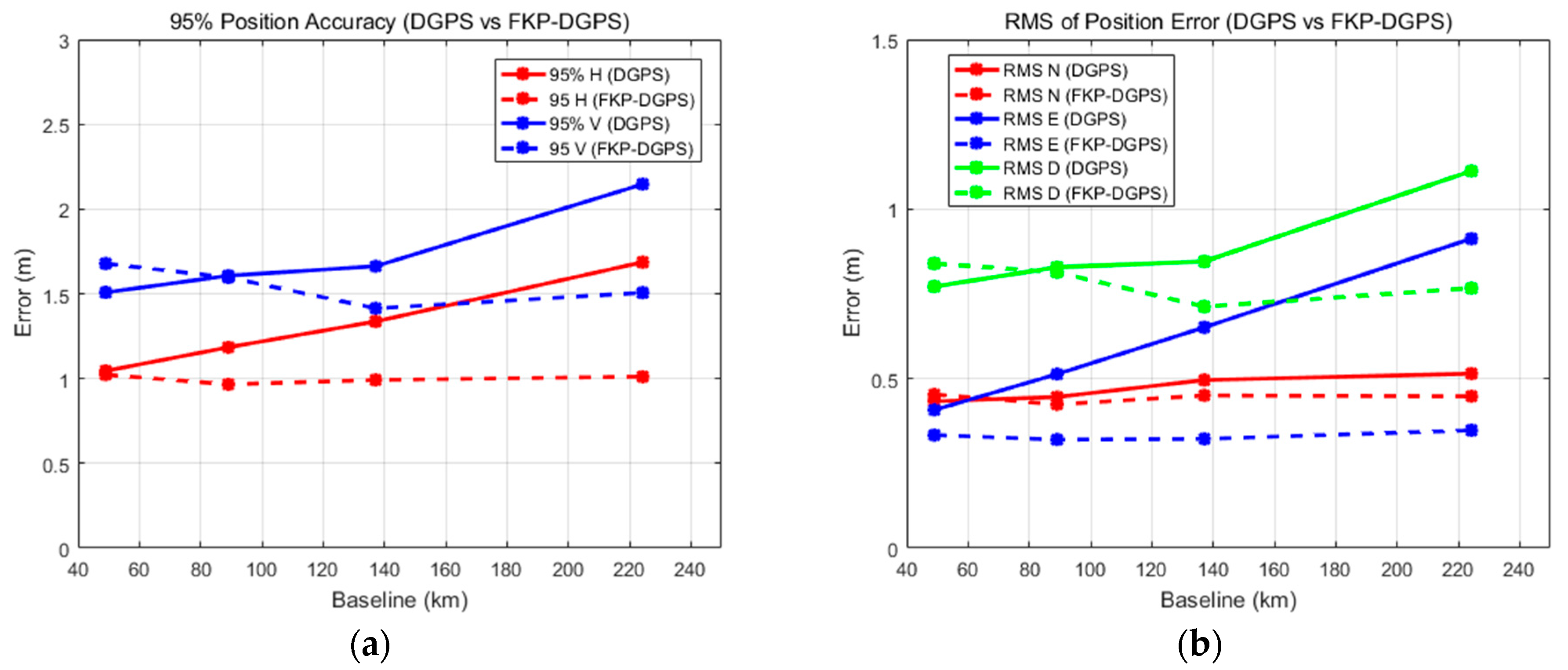
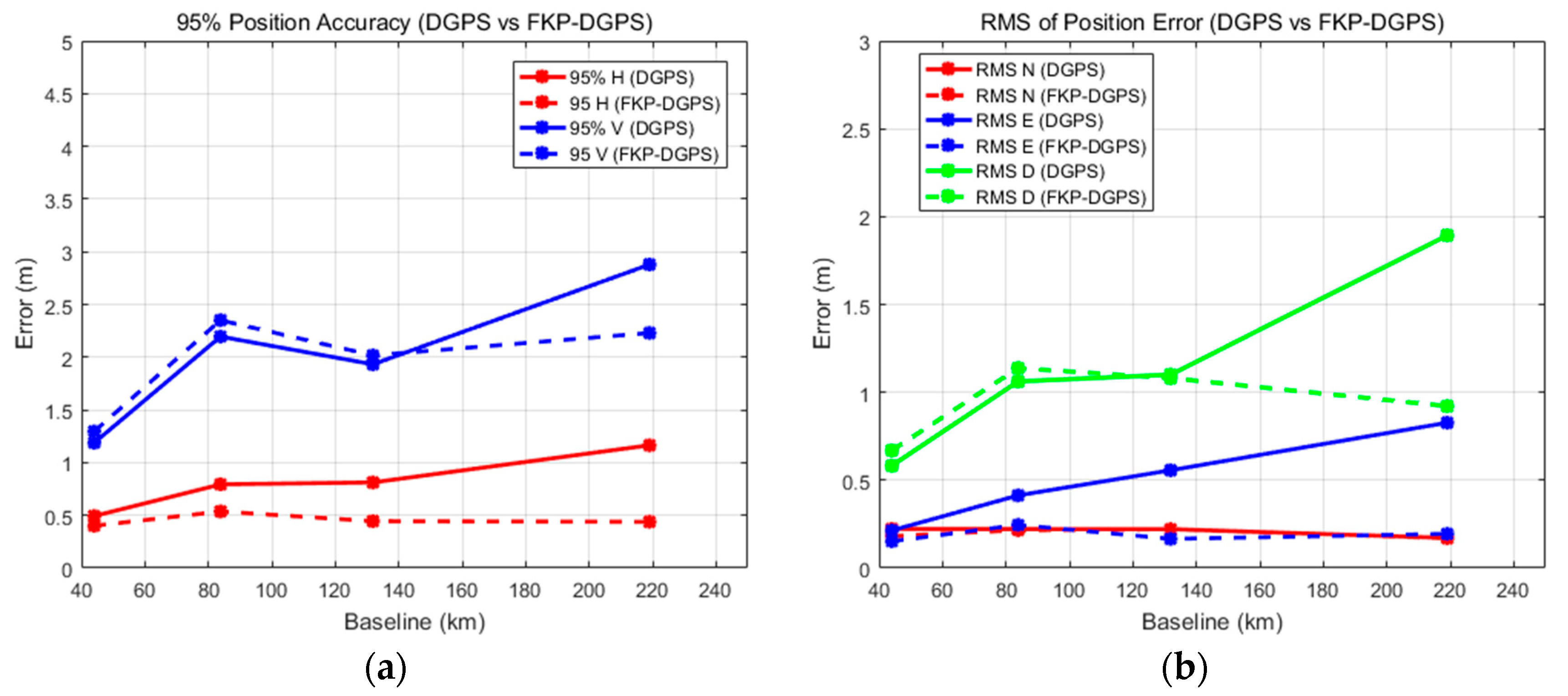
Figure 13a shows the 95% horizontal and vertical results corresponding to the baseline lengths. In addition,
Figure 13b shows the RMS errors in the north, east, and downward directions. In
Figure 13, the dashed line indicates the FKP-DGPS and the solid line indicates the DGPS. The results show that the accuracies of the FKP-DGPS remain largely constant even if the baseline lengths increase. The valid baseline length of the FKP correction for the pseudorange measurements is clearly above 200 km.
An additional test was conducted to compare the performance of the user-oriented FKP-DGPS with those of other alternatives, such as SBAS or VRS-DGPS. The configuration of the additional test is largely similar to that of the static test; the u-blox LEA-6T evaluation kit is used, and the user is located at Bldg. 312 in Seoul National University.
Figure 14a shows the visible satellites in the sky during the test.
Figure 14b shows the PDOP. The test was conducted for approximately 3 h from 1 July 2017 13:30 in local time (UTC+09). For the SBAS test, PRN 137 satellite of MSAS was used, which is observed at the elevation of 43° and the azimuth of 151° in Korea. For the VRS-DGPS test, we need an assumption on the dynamic user and its situation to compare the performance with VRS-DGPS, because there is no infrastructure for VRS-DGPS in Korea.
The SBAS mode of the U-blox receiver had been set to be enabled via the u-center program. Once the configuration was set to the SBAS mode, the rover can apply the augmentation message to generate the range correction appropriate to the rover’s real-time position, because the same SBAS message is broadcast to all the users in the service area regardless their location.
On the other hand, a generic VRS system provides the rover’s proper correction only after it got the rover’s approximate position. Moreover, a VRS user without multi-channel datalinks to nearby VRSs might experience performance degradation or discontinuity due to the absence of the correction during the handover from the previous VRS to a new one. Assuming a user who left from WULJ and arrived at Seoul without updating its real-time position because of privacy problem or RS handover issue, the static DGPS accuracy using WULJ correction is equivalent to the VRS-DGPS accuracy of the rover at Seoul, because its VRS was not changed from the initial VRS, WULJ, through the entire journey.
In general, the SBAS has much wider coverage, but it has similar or lower positioning accuracy than the local area DGPS whose coverage is within 150 km [
29].
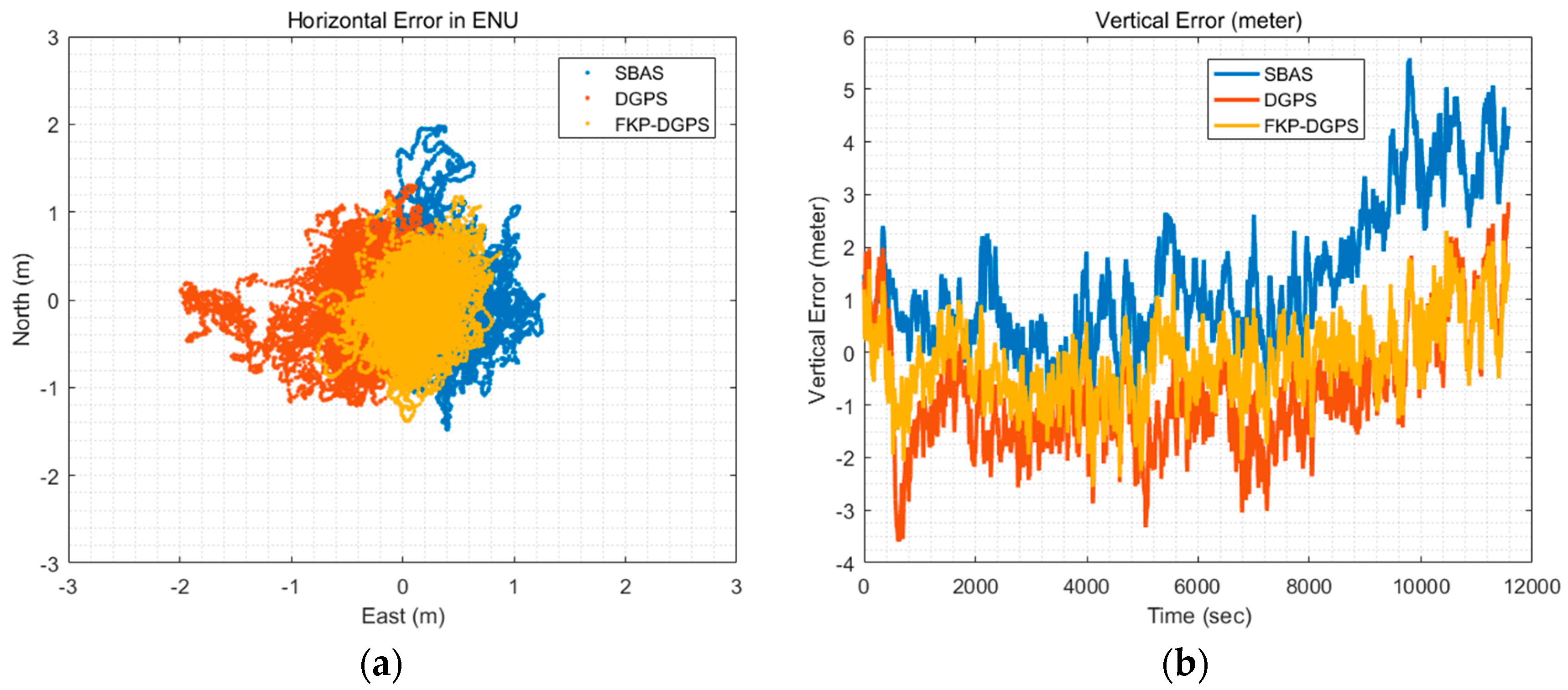
Figure 15 shows the horizontal and vertical position errors of the SBAS, DGPS and FKP-DGPS results in the east-north-up (ENU) coordinate. In this test, the DGPS show the position error of the user of the previous VRS-DGPS assumption at Seoul, wherein the correction from the WULJ RS is used. We can easily confirm that the horizontal and vertical results of the FKP-DGPS are much better than those of the SBAS and DGPS.
Table 6 lists the detailed numerical results.
4.4. Dynamic Test
Using the developed real-time FKP-DGPS software, we conducted a dynamic test to verify the feasibility of the FKP corrections for the dynamic user. The configuration of the dynamic test is largely similar to that of the static test. The u-blox LEA-6T evaluation kit is selected as the low-cost GPS receiver. Moreover, a Trimble zephyr model 2 antenna was used as the antenna. In the dynamic test, four RSs (YANP, WNJU, YOWL, and WULJ) were selected located at distances of 50, 90, 140, and 225 km south–east of the user in sequence. The dynamic test system was implemented in a land vehicle as shown in
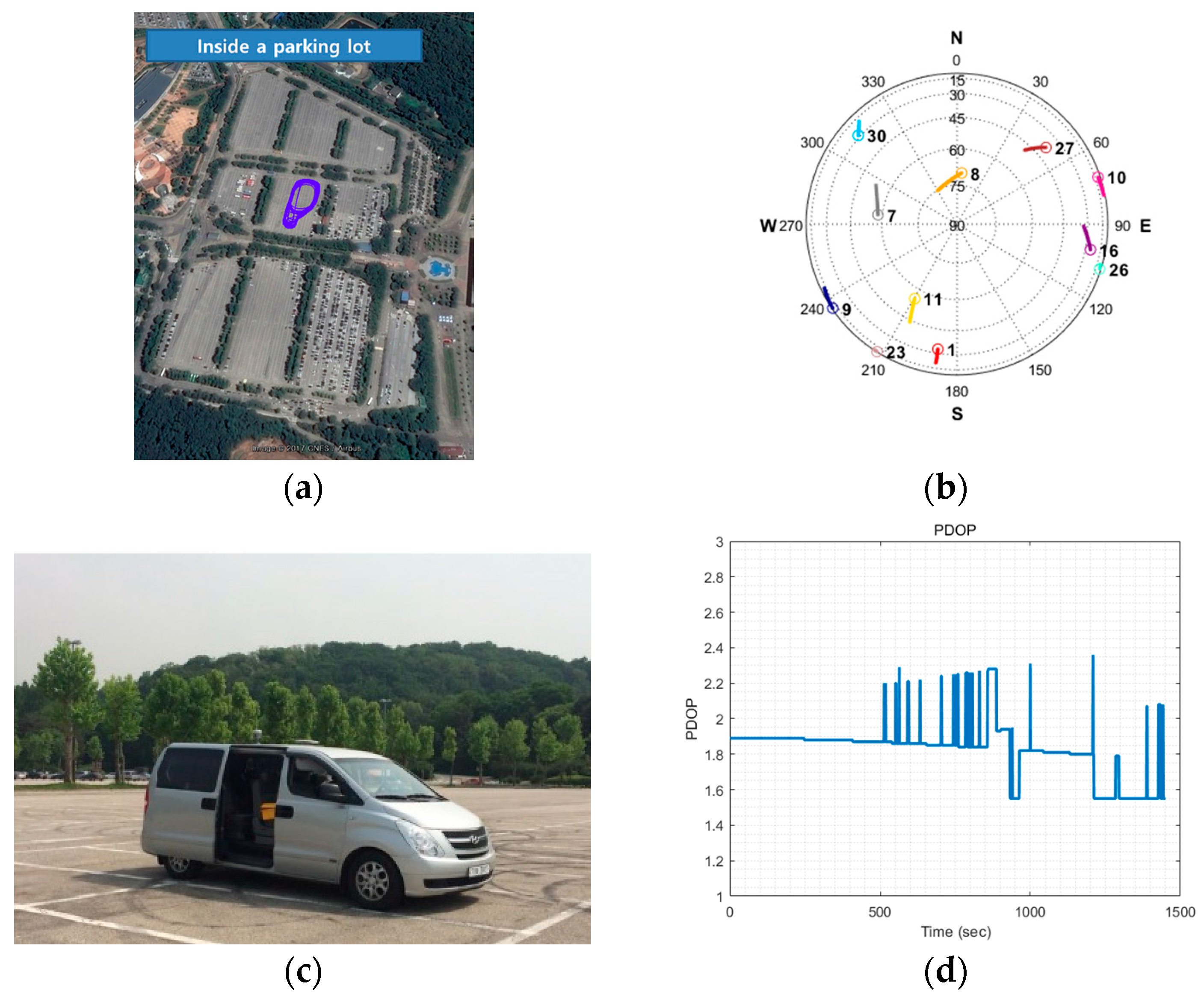
Figure 16c, which was driven inside the parking lot of Seoul Grand Park, as shown in
Figure 16a. The blue line describes the trajectory of the dynamic user. The test was conducted for approximately 25 min from 25 May 2017 15:00 in local time (UTC+09).
Figure 16b,d show the visible satellites in the sky and PDOP during the test.
Figure 17 shows the horizontal and vertical position errors of the DGPS and FKP-DGPS of the WULJ RS, which is the farthest from the static user, in the ENU coordinate compared to the reference positions obtained using the Trimble NetR9 receiver with post-processing Trimble Business Center (TBC) software. The results are similar to the static test results. We can easily confirm that the horizontal result of the DGPS is slightly biased to the west side, whereas the FKP-DGPS obtains a more accurate horizontal positioning than the DGPS.
Table 7 and
Table 8 list the detailed numerical results along with the results of other stations.
Like the static test, the FKP-DGPS has more accurate positioning accuracy than the DGPS for most of the results because of the compensate error factors due to the spatial decorrelation. Thus, in the cases of the FKP-DGPS, the improvements of the 95% horizontal accuracy of all stations are 18%, 32%, 46%, and 62% for the corresponding baseline lengths of the RSs compared to the accuracy of the DGPS. Although it is not clear to show the vertical accuracy improvement via the FKP-DGPS in a short-time period of the dynamic test, the error components of the east have definitely reduced.
Figure 18a shows the 95% horizontal and vertical error tendency to the baseline length.
Figure 18b describes the RMS of the error for each direction based on the result of
Table 7 and
Table 8. In
Figure 18, the dashed lines indicate the FKP-DGPS and the solid lines indicate the DGPS. From these figures, we can confirm that the FKP-DGPS can significantly contribute to the reduction in the spatial decorrelation effect in the position-domain and the improvement in the position accuracy.