SCMDOT: Spatial Clustering with Multiple Density-Ordered Trees
Abstract
:1. Introduction
- We propose an innovative method to represent a dataset by constructing a series of constrained Multiple Density-Ordered Trees (MDOT) in the proper order. During the process of generating MDOT, a high spatial similarity of each cluster can be ensured. In this way, our algorithm is capable of not only handling the problem of separating clusters with complex structures, but also increasing the robustness and reliability of the clustering result.
- Our method introduces a novel approach based on MDOT to identify noises and cluster centres. Noises which included in the inappropriate start points before constructing MDOT and can be further confirmed rely on the deviation from the final clusters. In addition, cluster centres can be recognised as the roots of MDOT.
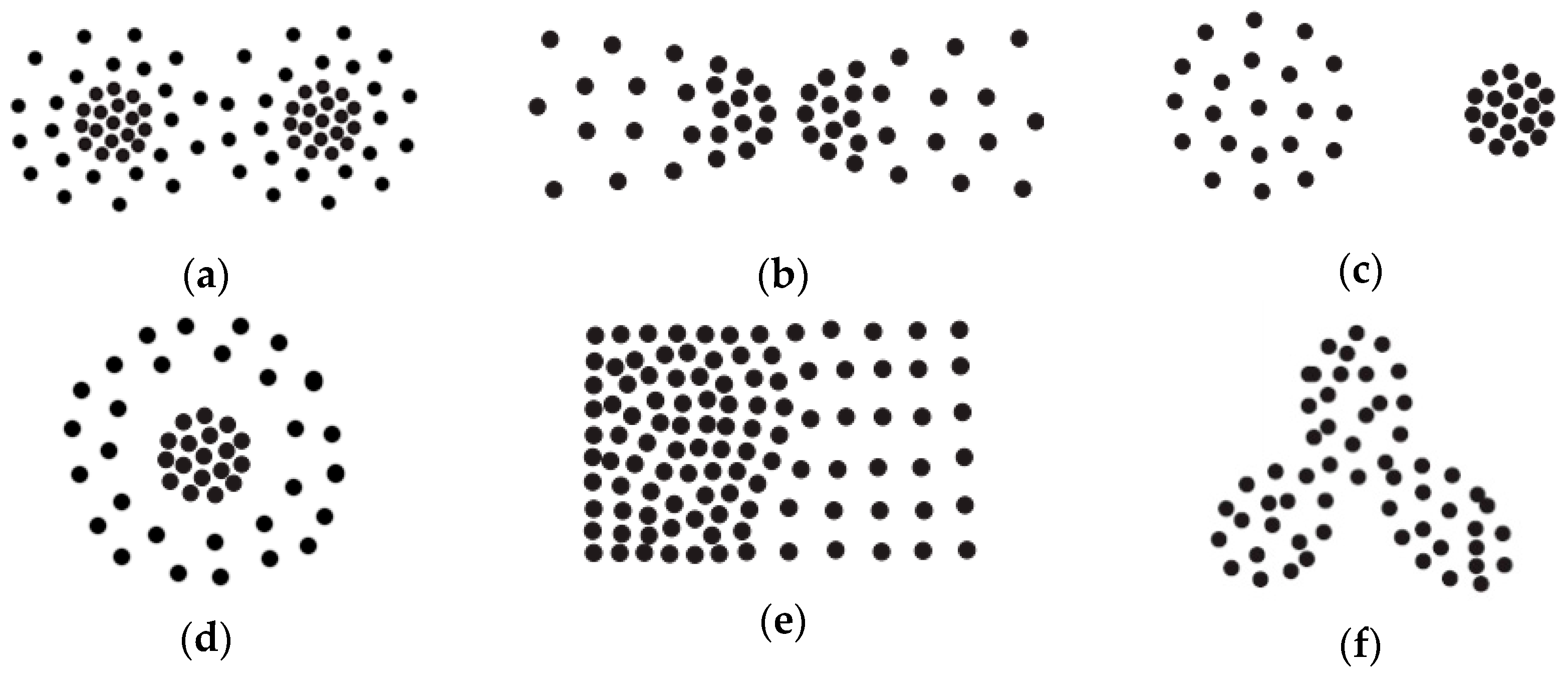
- The proposed method can be adapted to the detection of clusters with different shapes and uneven density, which has been especially proved effective in the case of adjacent clusters with distinctly varied densities.
2. Related Works
3. SCMDOT Algorithm
- We introduce an innovative way of developing a dynamic agglomerative model to represent the original dataset. Being different from the method employed by SCDOT, a series of clusters can be successively generated from regions of sparse areas to the dense areas rather than partitioning a whole DOT into several sub-clusters, which can circumvent the issues of splitting clusters.
- With the goal of ensuring a high spatial similarity for each cluster, we adopt a new tactic to control the growth of DOT in terms of edge growth and density change by imposing certain restrictions. From another point of view, the spatial similarity of each cluster will be guaranteed consistently during the procedure of construction.
- An improved criterion of merging clusters is proposed in this paper. Due to the improvement mentioned above providing an effective way to acquire internal proximity of each cluster, we are able to use it as an important indicator to measure the intra-similarity of clusters in the merging process so as to adapt to the change in local density among clusters.
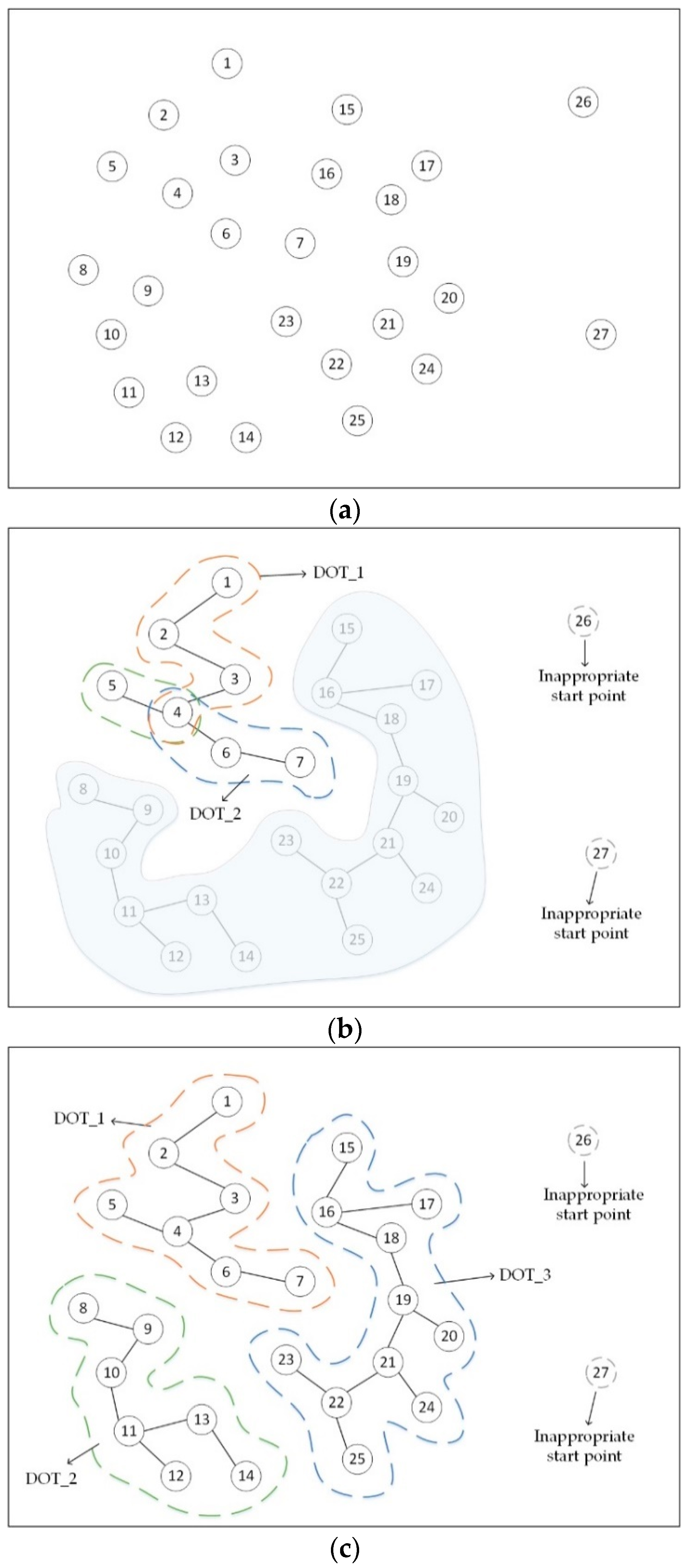
3.1. Prune Inappropriate Start Points
3.2. Construct Multiple Density-Ordered Trees (MDOT)
3.3. Merge MDOT into Final Clusters
3.4. Algorithm and Performance Analysis
| Algorithm 1. SCMDOT |
| Input: DB, , , , , , goal. Output: C . |
|
| Algorithm 2. ConstructSubTrees(ASP, DB′, , , ) |
| Input: ASP, DB′, , , . Output: all points in DB′ marked with cluId. |
| list_CP.add(SearchConnectionPoint(ASP, DB′, , , )); // By Equations (6)–(9) CP SelectConnectionPoint(list_CP); currentPoint ASP; while CP ! = NULL do if CP is unvisited then mark CP as visited; CP.cluId currentPoint.cluId; IdentifySubTree(currentPoint).AppendChild(CP); // IdentifySubTree(i) returns the sub-tree containing point i currentPoint CP; list_CP.clear(); list_CP.add(SearchConnectionPoint(currentPoint, DB′, , , )); CP SelectConnectionPoint(list_CP); else established_subTree IdentifySubTree(CP); new_subTree IdentifySubTree(currentPoint); for each j in established_subTree do j.cluId currentPoint.cluId; end for Combine_SubTrees(established_subTree, new_subTree); CP NULL; end if end while |
| Algorithm 3. MergeClusters (DB′, ) |
| Input: DB′, . Output: C . |
| C FindClusters(DB′); // FindClusters(DB′) returns clusters where points in each cluster with the same cluId for each Cluster Ci in C do for each Cluster Cj in C do if CalculateMergeValue(Ci, Cj). MergeValue > 0 then // By Equations (10)–(12) list_MergeValue < cluId1, cluId2, MergeValue > CalculateMergeValue(Ci, Cj); end if end for end for K C.size(); T list_MergeValue.size(); while K > goal and T > 0 do bestPairClusters SelectBestMergeClusters(list_MergeValue); MergeBestClusters(bestPairClusters); list_MergeValue.delete(bestPairClusters); K K – 1; T T – 1; end while return C; |
4. Experiments and Results
4.1. Experiments on Synthetic Datasets
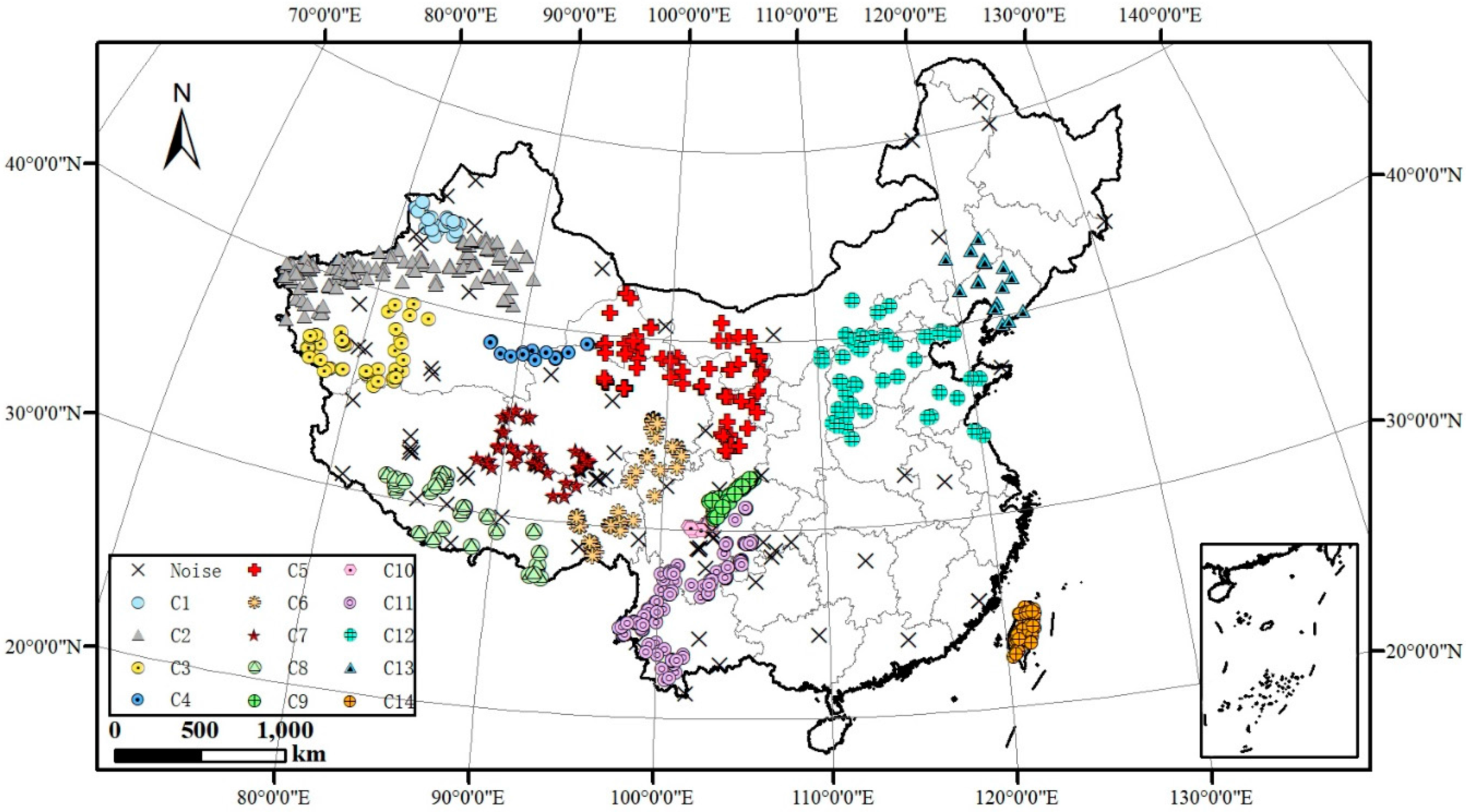
4.2. Practical Applications of SCMDOT
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, L.; Tian, F.; Smith, J.A.; Hu, H. Urban signatures in the spatial clustering of summer heavy rainfall events over the Beijing metropolitan region. J. Geophys. Res. Atmos. 2014, 119, 1203–1217. [Google Scholar] [CrossRef]
- Estivill-Castro, V.; Lee, I. Multi-level clustering and its visualization for exploratory spatial analysis. GeoInformatica 2002, 6, 123–152. [Google Scholar] [CrossRef]
- Sluydts, V.; Heng, S.; Coosemans, M.; Roey, K.V.; Gryseels, C.; Canier, L.; Kim, S.; Khim, N.; Siv, S.; Mean, V. Spatial clustering and risk factors of malaria infections in ratanakiri province, cambodia. Malar. J. 2014, 13, 387. [Google Scholar] [CrossRef] [PubMed]
- Jagla, E.A.; Kolton, A.B. A mechanism for spatial and temporal earthquake clustering. J. Geophys. Res. Atmos. 2010, 115, 100–104. [Google Scholar] [CrossRef]
- Deng, M.; Liu, Q.; Cheng, T.; Shi, Y. An adaptive spatial clustering algorithm based on delaunay triangulation. Comput. Environ. Urban Syst. 2011, 35, 320–332. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; pp. 281–297. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Lu, X.; Liu, Z.; Huang, J.; Cheng, G. Spatial clustering with density-ordered tree. Phys. A Stat. Mech. Appl. 2016, 460, 188–200. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Mehmood, R.; Zhang, G.; Bie, R.; Dawood, H.; Ahmad, H. Clustering by fast search and find of density peaks via heat diffusion. Neurocomputing 2016, 208, 210–217. [Google Scholar] [CrossRef]
- Xu, J.; Wang, G.; Deng, W. DenPEHC: Density peak based efficient hierarchical clustering. Inf. Sci. 2016, 373, 200–218. [Google Scholar] [CrossRef]
- Schaeffer, S.E. Graph clustering. Comput. Sci. Rev. 2007, 1, 27–64. [Google Scholar] [CrossRef]
- Karypis, G.; Han, E.H.; Kumar, V. Chameleon: A hierarchical clustering algorithm using dynamic modeling. Computer 1999, 32, 68–75. [Google Scholar] [CrossRef]
- Zahn, C.T. Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Trans. Comput. 1971, C-20, 68–86. [Google Scholar] [CrossRef]
- Zhong, C.; Miao, D.; Wang, R. A graph-theoretical clustering method based on two rounds of minimum spanning trees. Pattern Recognit. 2010, 43, 752–766. [Google Scholar] [CrossRef]
- Zhong, C.; Miao, D.; Nti, P. Minimum spanning tree based split-and-merge: A hierarchical clustering method. Inf. Sci. 2011, 181, 3397–3410. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. Automatic region building for spatial analysis. Trans. GIS 2011, 15, 29–45. [Google Scholar] [CrossRef]
- Guha, S.; Rastogi, R.; Shim, K. CURE: An Efficient Clustering Algorithm for large Databases. In Proceedings of the ACM-SIGMOD International Conference on Management of Data, Seattle, WA, USA, 1–4 June 1998; pp. 73–84. [Google Scholar]
- Guha, S.; Rastogi, R.; Shim, K. ROCK: A robust clustering algorithm for categorical attributes. Inf. Syst. 2000, 25, 345–366. [Google Scholar] [CrossRef]
- Lee, J.S.; Olafsson, S. A meta-learning approach for determining the number of clusters with consideration of nearest neighbors. Inf. Sci. 2013, 232, 208–224. [Google Scholar] [CrossRef]
- Lee, J.-S.; Olafsson, S. Data clustering by minimizing disconnectivity. Inf. Sci. 2011, 181, 732–746. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Fu, L.; Medico, E. Flame, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioinform. 2007, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Law, M.H.C. Data clustering: A user′s dilemma. In Proceedings of the Pattern Recognition and Machine Intelligence, First International Conference, Kolkata, India, 20–22 December 2005; pp. 1–10. [Google Scholar]
- Chang, H.; Yeung, D.Y. Robust path-based spectral clustering. Pattern Recognit. 2008, 41, 191–203. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. In Proceedings of the ACM-SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 31 May–3 June 1999; pp. 49–60. [Google Scholar]
- Rand, W.M. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]


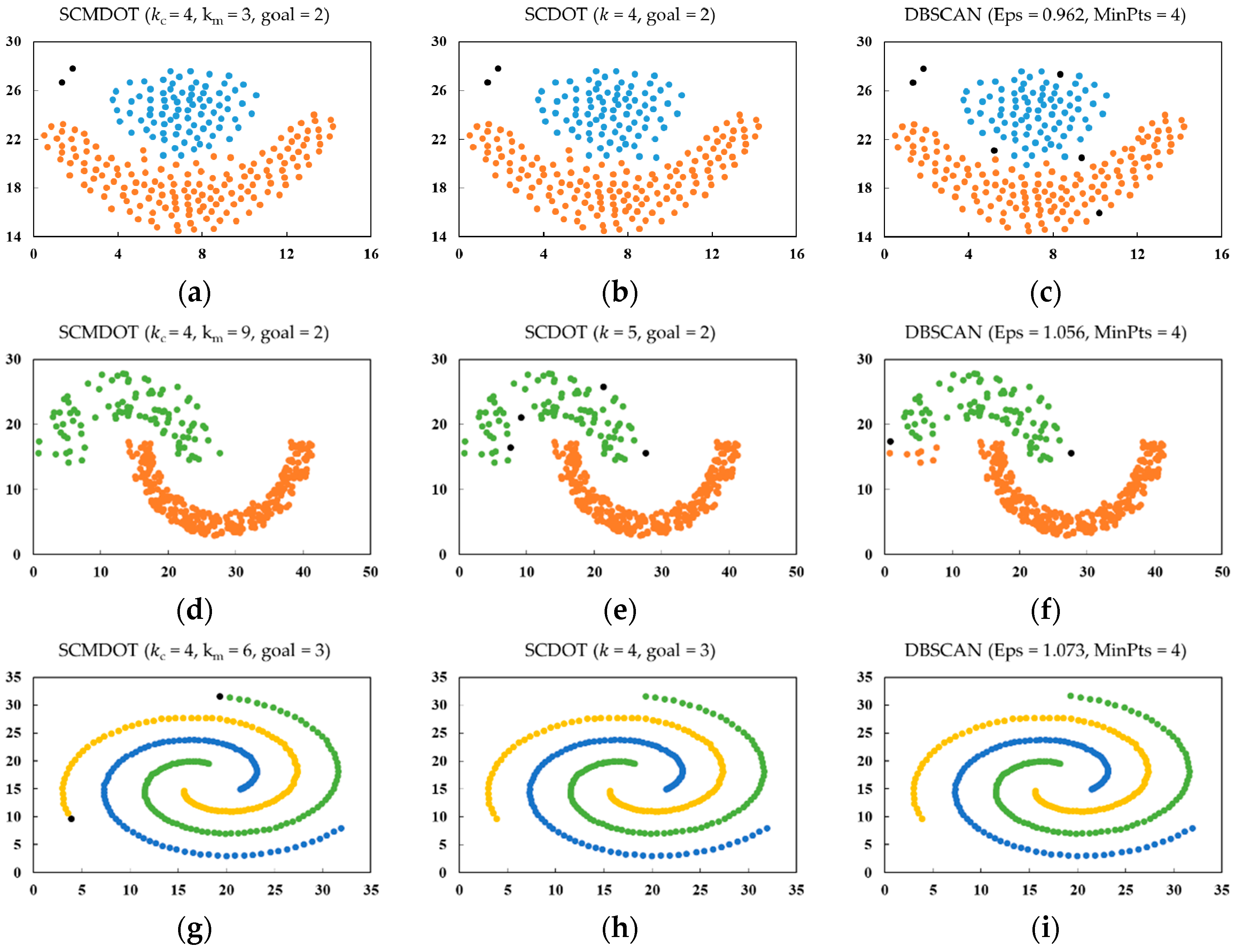
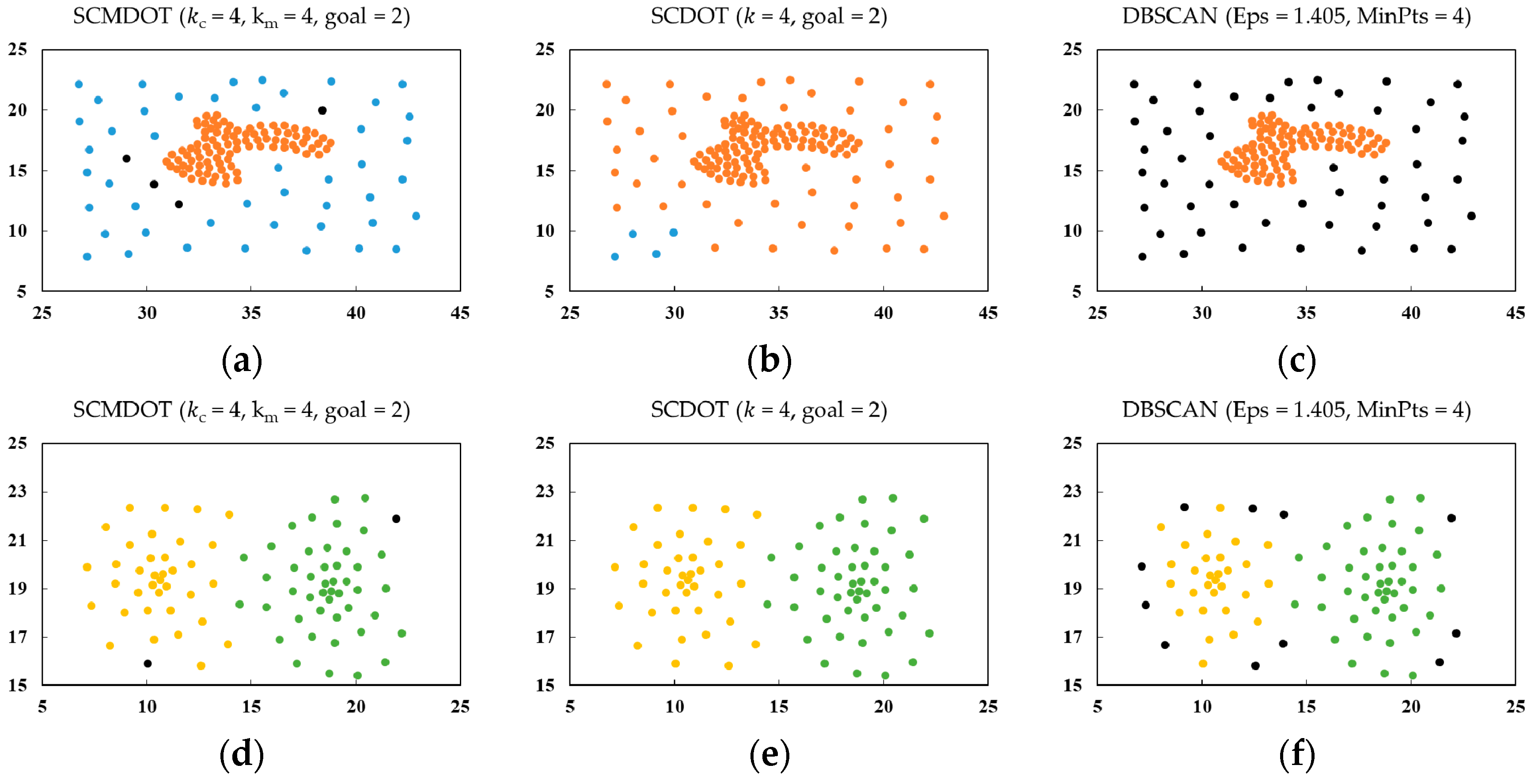
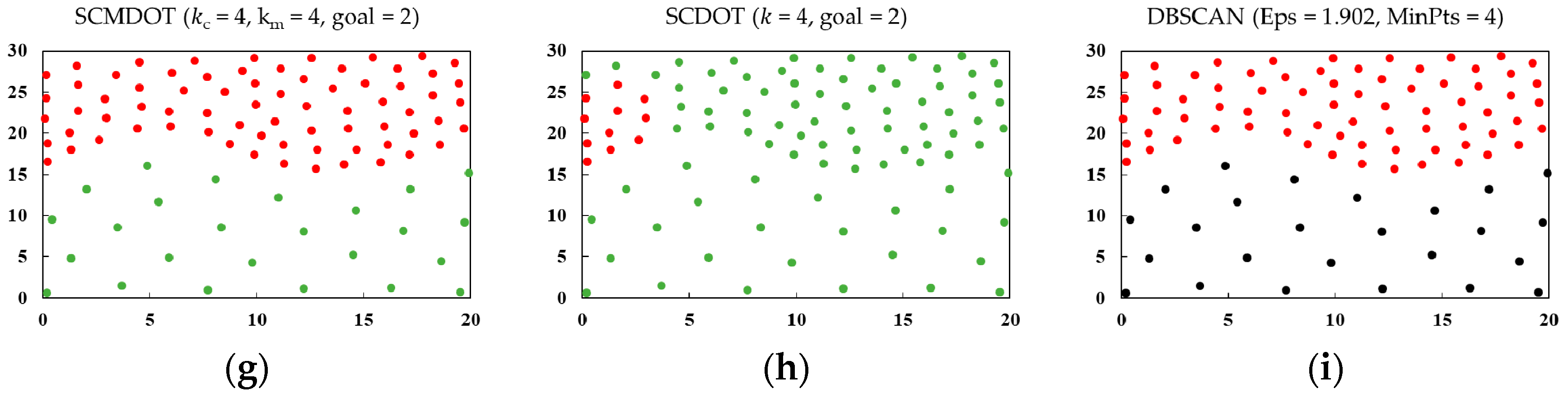

| Data Set | Data Size (N) | Dimensionality (d) | Number of Clusters (K) |
|---|---|---|---|
| DS1 | 240 | 2 | 2 |
| DS2 | 373 | 2 | 2 |
| DS3 | 312 | 2 | 3 |
| DS4 | 142 | 2 | 2 |
| DS5 | 83 | 2 | 2 |
| DS6 | 97 | 2 | 2 |
| SCMDOT | SCDOT | DBSCAN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ARI | AMI | Noise Number | ARI | AMI | Noise Number | ARI | AMI | Noise Number | |
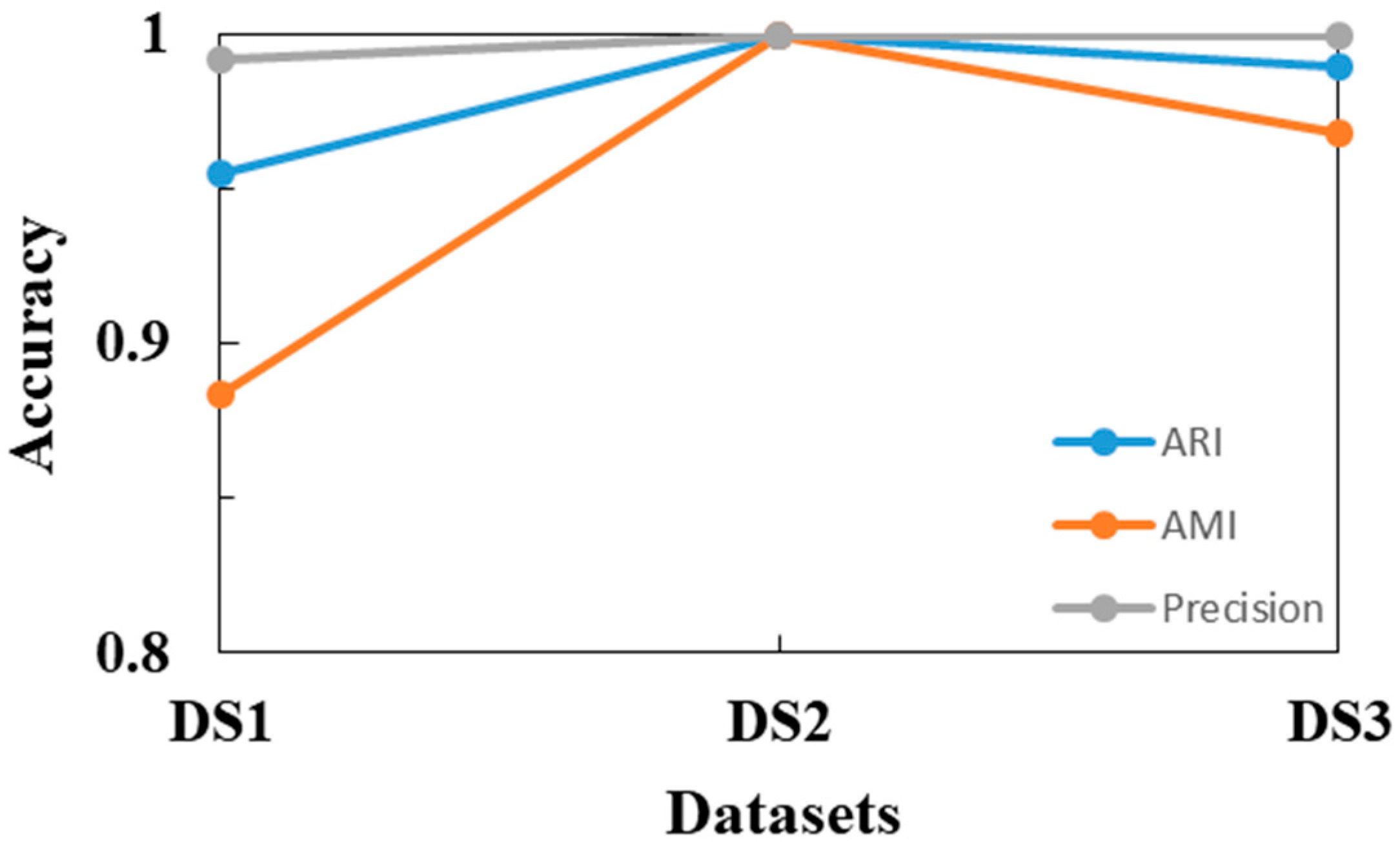
| DS1 | 0.955 | 0.884 | 2 | 0.988 | 0.942 | 2 | 0.939 | 0.817 | 6 |
| DS2 | 1 | 1 | 0 | 0.989 | 0.927 | 4 | 0.976 | 0.859 | 2 |
| DS3 | 0.990 | 0.968 | 2 | 1 | 1 | 0 | 1 | 1 | 0 |
| SCMDOT | SCDOT | DBSCAN | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ARI | AMI | Noise Number | ARI | AMI | Noise Number | ARI | AMI | Noise Number | |
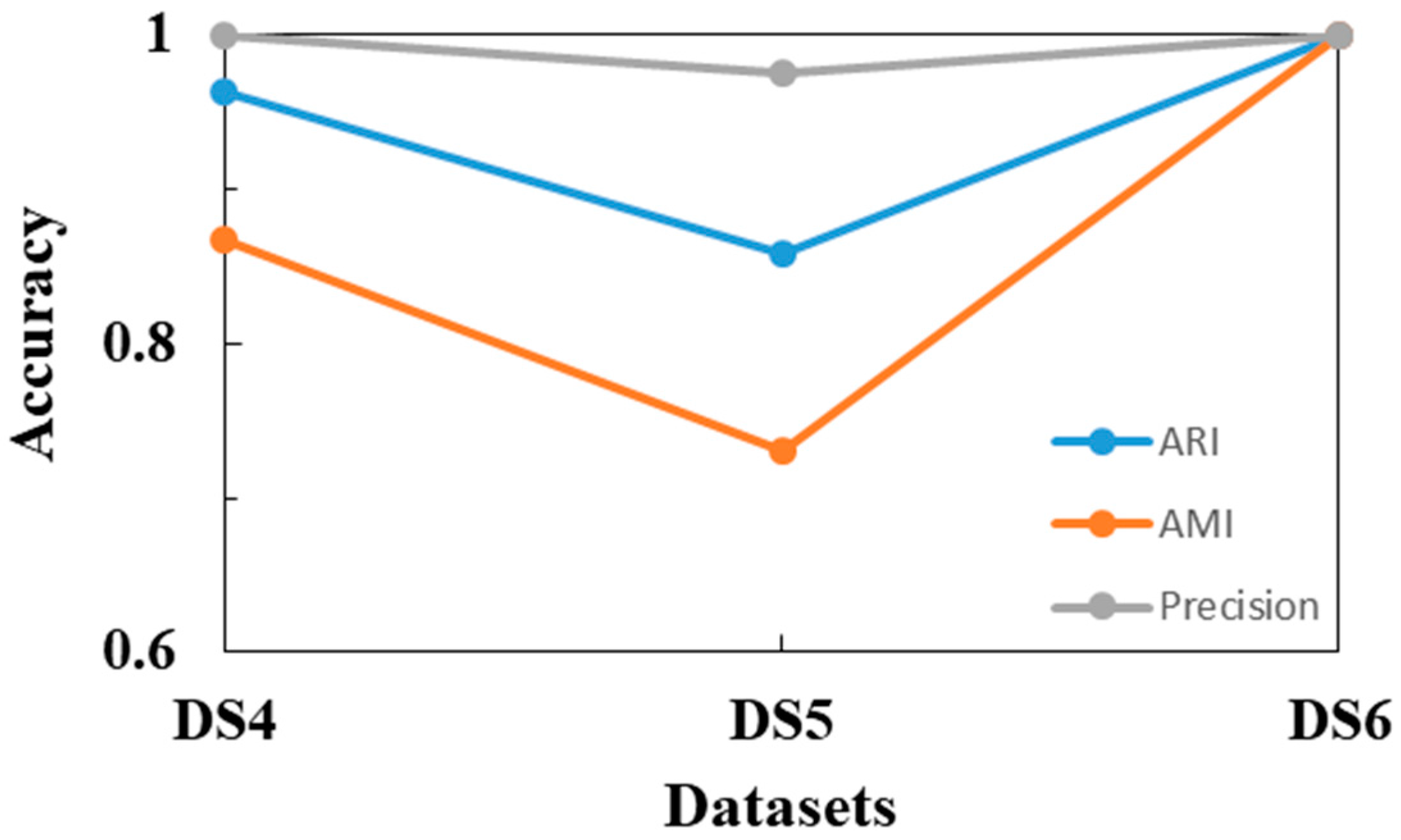
| DS4 | 0.963 | 0.867 | 4 | 0.049 | 0.040 | 0 | 0 | 0 | 50 |
| DS5 | 0.859 | 0.730 | 2 | 0.905 | 0.855 | 0 | 0.729 | 0.563 | 11 |
| DS6 | 1 | 1 | 0 | −0.090 | 0.054 | 0 | 0 | 0 | 25 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Jiang, H.; Chen, C. SCMDOT: Spatial Clustering with Multiple Density-Ordered Trees. ISPRS Int. J. Geo-Inf. 2017, 6, 217. https://doi.org/10.3390/ijgi6070217
Wu X, Jiang H, Chen C. SCMDOT: Spatial Clustering with Multiple Density-Ordered Trees. ISPRS International Journal of Geo-Information. 2017; 6(7):217. https://doi.org/10.3390/ijgi6070217
Chicago/Turabian StyleWu, Xiaozhu, Hong Jiang, and Chongcheng Chen. 2017. "SCMDOT: Spatial Clustering with Multiple Density-Ordered Trees" ISPRS International Journal of Geo-Information 6, no. 7: 217. https://doi.org/10.3390/ijgi6070217
APA StyleWu, X., Jiang, H., & Chen, C. (2017). SCMDOT: Spatial Clustering with Multiple Density-Ordered Trees. ISPRS International Journal of Geo-Information, 6(7), 217. https://doi.org/10.3390/ijgi6070217





