1. Introduction
Video surveillance systems have rapidly expanded due to the technology’s important role in traffic monitoring, crime prevention, security, and post-incident analysis [
1]. As a consequence of increasing safety concerns, camera surveillance has been widely adopted as a way to monitor public spaces [
2]. Currently, there are tens of thousands of cameras in cities collecting a huge amount of data on a daily basis [
3]. Video surveillance systems were originally designed for human operators to watch concurrently and to record a video for later analysis. As the number of cameras is significantly increasing and the quantity of the archived video data becomes unmanageable by a human operator, intelligent video surveillance systems have been introduced [
2].
Real-time video monitoring is playing an increasingly significant role in surveillance systems for numerous security, law enforcement, and military applications [
4]. However, conventional video monitoring systems have various problems with multi-point surveillance [
5]. A typical system for conventional video surveillance directly connects each video camera to a corresponding monitor. When the scale of the surveillance system grows larger than the human capacity for monitoring, serious problems can occur. Security operators must mentally map each surveillance monitor image to a corresponding area in the real world, and this complex task requires training and experience [
5]. To facilitate multi-camera coordination and tracking, Sankaranarayanan and Davis [
6] highlighted the significance of establishing a common reference frame to which these cameras can be mapped. They recommended the use of GIS as a common frame of reference because it not only presents a solid ground truth but—more importantly—is also used to store semantic information (e.g., the locations of buildings, roads, sensitive areas, etc.) for use in applications such as tracking and activity analysis.
In order to integrate a video and GIS, that video must be geographically referenced. Since a video represents a sequence of separate images (frames), to georeference it, each frame must be supplemented with information that maps the frame’s pixels with corresponding geographic locations. One way to do that is to record the camera position, orientation, and field-of-view at the moment of frame capture, so that at a later time, the frame image can be projected into the virtual 3D GIS scene. Since measuring these parameters can be both inaccurate and complex, in this paper we will present a method for their indirect estimation. The method relies on matching distinct points from video frames with georeferenced orthophoto maps and digital elevation models (DEM) to obtain their 3D coordinates. Once an adequate number of distinct points are matched, Levenberg–Marquardt iterative optimization [
7,
8] is applied to find the most suitable video georeference, i.e., position and orientation of the camera. The measure of suitability is a sum of the least square errors between the input and obtained image coordinates of the chosen points.
The paper is organized as follows:
Section 2 presents related work regarding video surveillance, camera calibration, and image georegistration.
Section 3 presents details regarding surveillance camera video georeferencing, focusing on explaining the parameters that are used to georeference a single video frame. In
Section 4, the proposed estimation method is described, covering both fixed and Pan-Tilt-Zoom (PTZ) camera variations.
Section 5 presents the software implementation of the proposed method and the obtained experimental results. Finally,
Section 6 presents the conclusions.
2. Related Work
User interfaces for video surveillance systems are traditionally based on matrices of video displays, maps, and indirect controls. Spatial navigation, especially for the real-time tracking of complex events involving many cameras, can be very difficult. In such situations, an operator must make quick, accurate decisions on which cameras to use to navigate among the many cameras available. To cope with the increasing number of installed cameras, modern video surveillance systems rely on automation through intelligent video surveillance [
3] and a better presentation of surveillance data through context-aware solutions [
9] and integration with virtual GIS environments [
10,
11].
The goal of intelligent video surveillance is to efficiently extract useful information from the huge amount of video created by surveillance cameras by automatically detecting, tracking, and recognizing objects of interest and by understanding and analyzing activities detected in the video [
3]. Intelligent video surveillance aims to minimize video processing, transmission, and storage requirements, making it suitable for usage on a large scale as an integrated safety and security solution in smart cities. Calavia et al. [
12] proposed such a system to detect and identify abnormal and alarming situations by analyzing objects’ trajectories. The integration of a video and GIS, on the other hand, aims to unify the representations of video information collected from different geographic locations [
13]. As such, it does not conflict with the techniques of intelligent and context-aware video surveillance. On the contrary, many innovative features, such as a GIS-based user interface for better situation awareness, the automatic pointing of one or more PTZ cameras to a given geolocation, integration with geolocated sensors, and geolocation-based automation for event handling, can emerge [
10].
The potential of spatial video, i.e., geographically referenced videographic data, as an additional data type within GIS was considered by Lewis et al. [
14]. Their research focused on representing video frames using Viewpoint data structures in order to enable geospatial analysis. In recent years, an increasing number of papers have addressed the different problems of large-scale video surveillance and integration with GIS. The estimation of visual coverage, as one of the most important quality indexes for depicting the usability of a camera network, was addressed by Wang et al. [
15] and Yaagoubi et al. [
16]. Dealing with a similar problem, Choi and Lee [
1] proposed an approach to evaluate the surveillance coverage index to quantitatively measure how effectively a video surveillance system can monitor a targeted area. The problem of organizing and managing real-time geospatial data for public security video surveillance was addressed by Wu et al. [
17]. They proposed a hybrid NoSQL—SQL approach for real-time data access and structured on-the-fly analysis which can meet the requirements of increased spatio-temporal big data linking analysis. Trying to overcome the limitations of conventional video surveillance systems, such as the low efficiency in video searching, redundancy in video data transmission, and insufficient capability to position video content in geographic space, Xie et al. [
13] proposed the integration of a GIS and moving objects in surveillance videos by using motion detection and spatial mapping.
A prerequisite for the fusion of video and GIS is that video frames are geographically referenced. Georeferencing video is, in many ways, related to the problems of camera calibration (or camera pose estimation) and video georegistration. Camera calibration is a fundamental problem in computer vision and is indispensable in many video surveillance applications [
3]. Camera calibration is the process of estimating intrinsic and/or extrinsic parameters. Intrinsic parameters deal with the camera’s internal characteristics, such as the focal length, principal point, skew coefficients, and distortion coefficients. Extrinsic parameters describe its position and orientation in the world.
The problem of camera calibration has been well covered in the literature. Zhang [
18] proposed a simple camera calibration technique to determine radial distortion by observing a planar pattern shown at a few different orientations. Lee and Nevatia [
2] developed a video surveillance camera calibration tool for urban environments that relies on vanishing points extraction. Vanishing points are easily obtainable in urban environments since there are many parallel lines such as street lines, light poles, buildings, etc. The calibration of environmental camera images by means of the Levenberg—Marquardt method has been studied by Muñoz et al. [
19]. They proposed a procedure that relies on a low number of ground control points (GCP) to estimate all the pinhole camera model parameters, including the lens distortion parameters. Camera calibration techniques are essential for many other computer vision and photogrammetric related problems such as 3D reconstruction from multiple images [
20], visual odometry [
21], and visual SLAM (simultaneous localization and mapping) [
22].
Video georegistration is the spatial registration of video imagery to geodetically calibrated reference imagery so that the video can inherit the reference coordinates [
23]. The ability to assign geodetic coordinates to video pixels is an enabling step for a variety of operations that can benefit large-scale video surveillance. In the photogrammetric community, the prevailing approach for the accurate georegistration of geospatial imagery from mobile platforms is referred to as direct georeferencing [
24]. The required camera position and orientation for such applications is obtained from a geodetic grade global navigation satellite system (GNSS) receiver in combination with a high-quality navigation grade inertial navigation system (INS). The achievable accuracy of the direct georeferencing can be further increased with the additional integration of ground control information. Neumann et al. [
25] introduced an approach which stabilizes a directly georeferenced video stream based on data fusion with available 3D models. Morse et al. [
26], as part of their research dedicated to creating maps of geospatial video coverage quality, reported the use of terrain models and aerial reference imagery to refine the pose estimate of the unmanned aerial vehicle’s (UAV) camera.
Georegistration of ground imagery or stationary videos, such as surveillance cameras videos, usually relies on homography matrix-based methods [
27,
28]. These methods assume a planar ground in a geographic space, so they require four or more matching points to determine the corresponding homography matrix. Since they are based on the assumption of a planar ground, homography matrix-based methods are not suitable for large-scale scenes or scenes with a complex terrain. In these cases, the terrain model is usually taken into account and georegistration is equivalent to the camera pose estimation in geographic space [
19]. In recent years, other methods based on a georegistered 3D point cloud have emerged. Li et al. [
29] proposed a method for the global camera pose estimation using a large georegistered 3D point cloud, covering many places around the world. Their method directly establishes a correspondence between image features and 3D points and then computes a camera pose consistent with these feature matches. A similar approach has been applied by Qi Shan et al. [
30] with the additional warping of a ground-level image into target view used for achieving more reliable feature correspondence.
The proposed method for georeferencing a surveillance video relies on matching 2D image coordinates from video frames with 3D geodetic coordinates to estimate the camera’s position and orientation in geographic space. The main advantage of such an approach is its generality, i.e., the surveillance area doesn’t have to be planar and 3D geodetic coordinates of identified points can be obtained in different ways. The second important advantage of the method is its simplicity since the only two prerequisites for applying the method are georeferenced orthophoto maps and DEM. Finally, the third and the most distinct advantage is that it supports the georeferencing of PTZ cameras.
4. Estimation of Camera Georeference
The proposed method for camera georeferencing relies on matching distinct points in the video with their respective 3D geodetic coordinates. To acquire these coordinates, we relied on matching these points with locations on georeferenced orthophoto maps and reading their altitude from digital elevation models (DEM) of the area of interest. Other methods for acquiring geodetic coordinates are also possible.
Once an adequate number of distinct points are matched, Levenberg–Marquardt iterative optimization [
7,
8] is applied to find the most suitable video georeference, i.e., position and orientation of the camera. The measure of the process accuracy is a sum of the least square errors between the input and obtained image coordinates of the chosen points. Since image coordinates are specified in pixels, the error represents a measure of ‘visual quality’ of the estimated georeference.
The proposed method can be applied for both fixed and PTZ cameras. First, we will discuss fixed cameras and later we will introduce the modification required so the method can be applied to PTZ cameras.
4.1. Fixed Camera Case
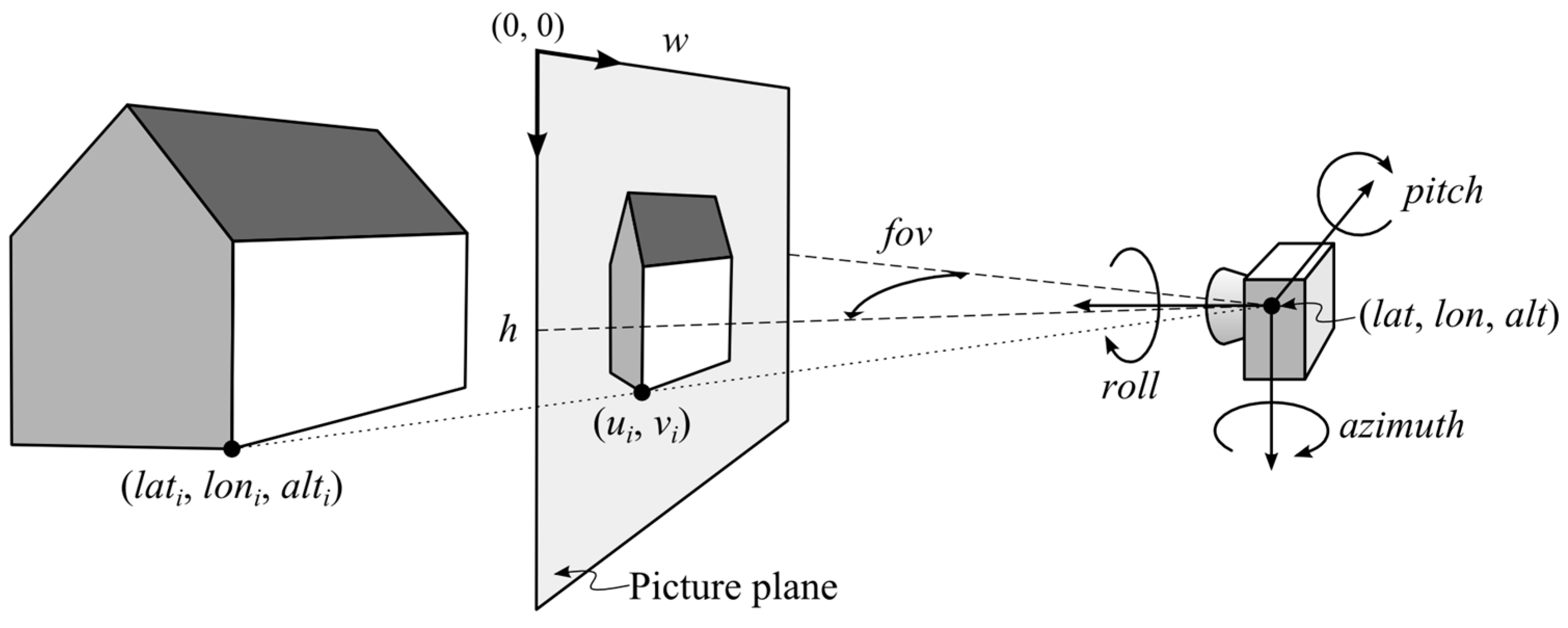
To better understand the inputs and outputs of the proposed method, let us again consider the example depicted in
Figure 1. The output of the method is the camera georeference, i.e., the parameters
lat,
lon,
alt,
azimuth,
pitch, and
roll. The last parameter
fov can also be estimated, or it can be premeasured [
35] and taken as a constant during this process. The method inputs are a certain number (
i = 1, ...,
N) of paired world (
lati,
loni,
alti) and image coordinates (
ui,
vi). Since we rely on iterative optimization, we will also need some initial georeference to start the process. Some rough estimation of the camera position and orientation is required. Finally, we need a mathematical model of the camera that will transform the input 3D geodetic coordinates (
lati,
loni,
alti) using the current georeference (
lat,
lon,
alt,
azimuth,
pitch,
roll,
fov) to the estimated image coordinates (
). To do so, we adopted the previously described pinhole camera model (see Equations (1)–(3)).
Since the pinhole model operates with 3D world coordinates in Cartesian space, input geodetic coordinates must be internally converted to an appropriate Cartesian form. To ensure uniform applicability of our method to any place on Earth, we used geocentric coordinates obtained using geodetic-to-geocentric transformation [
36]:
where parameter
a represents the semi-major axis (equatorial radius) and parameter
f represents the flattening of the ellipsoid (for WGS84 ellipsoid
a = 6,378,137 m and
f = 1/298.257223563).
The next step in applying the pinhole camera model is to specify the camera’s extrinsic ([
R t]
T) and intrinsic (
K) parameters using seven parameters of the observer viewpoint model. Parameters
fu,
fv,
cu, and
cv of the intrinsic camera matrix (
K) are calculated using the
fov parameter and frame’s width (
w) and height (
h) in pixels by employing the following equations:
The rotation matrix
R is calculated using the
azimuth,
pitch, and
roll parameters, while
lat and
lon are used to rotate the coordinate system:
Rx,
Ry, and
Rz are the basic rotation matrices that rotate the vectors by an angle
θ about the
x,
y, or
z-axis using the right-hand rule:
Finally, the translation vector
t is calculated from the geocentric camera position, obtained by transforming the
lat,
lon, and
alt parameters, and the previously calculated rotation matrix
R:
Once we have initialized the pinhole model parameters and converted the input geodetic coordinates (
lati,
loni,
alti) to geocentric coordinates (
xi,
yi,
zi), it is possible to transform those coordinates to image coordinates (
). The mean square error that is minimized during the process is calculated between the obtained image coordinates (
) and input, i.e., expected image coordinates (
ui,
vi):
In each cycle of the iterative process, the modification of the georeference parameters β is carried out in order to decrease the error. The process ends when the error falls below a certain value or when the increment in all parameters falls below a certain value. We should emphasize that the fov parameter can be excluded from the optimization process if it is predetermined.
To begin the iterative process, it is necessary to define the initial values of the estimating parameters, i.e., the camera georeference. In the case where a function has only one minimum, the initial values do not affect the outcome. However, if there are multiple local minima, the initial values should be close to the expected solution. When applied to our case, given the complexity of the transformation, this means that it is necessary to provide approximate values of the camera position and orientation, i.e., roughly determine the camera georeference.
Finally, let us summarize the list of steps through which the proposed method for georeferencing fixed cameras is carried out:
Setting initial georeference: An initial georeference can be obtained by measuring the camera position using GPS or reading it from a map. Camera orientation can be roughly estimated using a compass (azimuth parameter) or by matching surrounding objects with a map.
Identification of distinct points in the video: About ten or more evenly distributed points should be identified from the video, and their image coordinates should be recorded. Selected points should not change with time and should lay on the ground (this is not mandatory if a point’s altitude can be provided).
Obtaining 3D geodetic coordinates for the identified points: Geodetic coordinates can be obtained using high-resolution orthophoto maps and DEM. There is also a possibility to measure those coordinates using differential GPS in the case when maps are not available.
Refinement of georeference parameters using iterative process: Iterative optimization is applied in order to find georeference parameters with the smallest mean square error between the identified image coordinates and the ones obtained by the transformation. If optimization gets locked into a local minimum, and the error of the estimation is too high, the process should be restarted with a new initial georeference and possibly a new set of points.
Verification of the obtained georeference: Once the optimal georeference is estimated, it can be applied and verified by observing the differences between the input and obtained image coordinates.
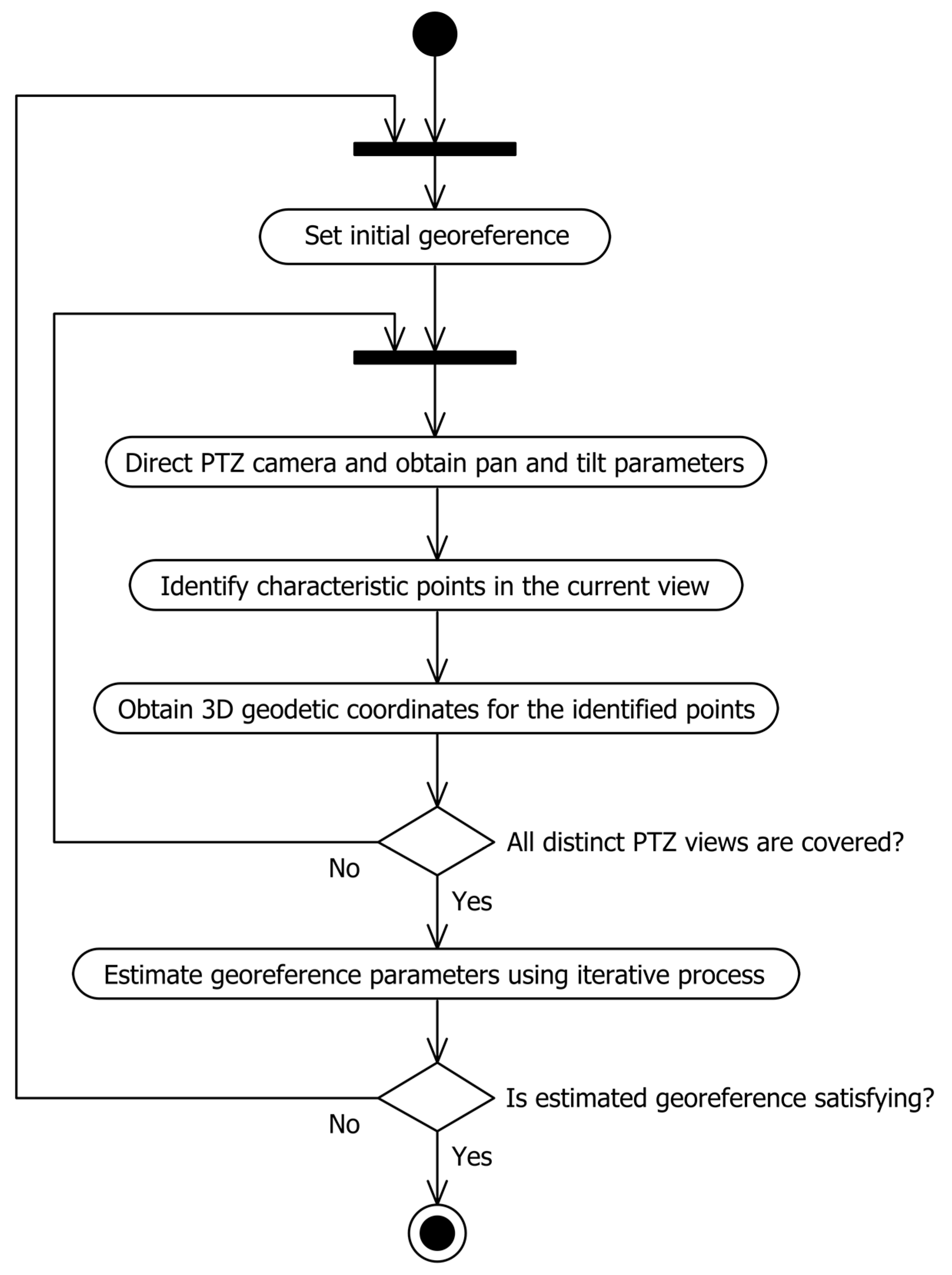
4.2. PTZ Camera Case
PTZ is an acronym for Pan-Tilt-Zoom and in video surveillance terminology denotes a class of cameras that can be rotated horizontally (pan) and vertically (tilt), and that can change the field-of-view by changing the zoom level. A method for calculating the absolute camera orientation (
azimuth,
pitch, and
roll) from the current relative camera orientation (
pan and
tilt) and absolute camera orientation when
pan and
tilt parameters are zero (
azimuth0,
pitch0, and
roll0) is introduced by Milosavljević et al. [
31]. Regarding the previous discussion on initializing the pinhole model parameters, the only difference is how the rotation matrix
R is calculated:
Since the extrinsic camera matrix now depends on the
pan and
tilt parameters, and the
fov parameter is no longer fixed, these must be included, along with geodetic and image coordinates, as an input measure (
pani,
tilti,
fovi). For that reason, the optimization parameters
β and transformation
f defined in Equation (10) are now modified to:
Since the current camera field-of-view (
fovi) is no longer estimated, it is necessary to determine it from the corresponding value of the
zoom parameter. Appropriate transformation can be done analytically [
35], or it can be empirically measured for a certain camera model and kept within the lookup table. A UML activity diagram that illustrates the process of PTZ camera georeferencing is shown in
Figure 2.
5. Implementation and Experimental Results
In order to validate the proposed estimation method, we implemented an application called Camera Calibration for georeferencing surveillance cameras. The application supports both fixed and PTZ network (i.e., IP) cameras. Video retrieval is done using HTTP protocol, so for fixed cameras, it is enough to enter the URL that is used to retrieve the current video frame. Optionally, it is possible to enter the username and password to access the camera API. In the case of PTZ cameras, besides video frames, it is necessary to additionally retrieve the current pan, tilt, and zoom values. Currently, we support only AXIS PTZ cameras through VAPIX protocol, but further upgrades are possible.
Besides dependence on the camera, this application also relies on the use of Web Map Service (WMS) to retrieve the orthophoto map of the area surrounding camera, so as to retrieve the elevation of the chosen points. That is why the application relies on two standard WMS requests: GetMap and GetFeatureInfo. GetMap, as the name suggests, is used to retrieve a georeferenced image (a map) of the requested area, while GetFeatureInfo is used to retrieve additional information (elevation in our case) for the certain point on that map.
The application is implemented in C++ using Qt framework version 4.8.5. The user interface (UI) is shown in
Figure 3, and it is divided into three separate parts (windows). The main window is used to control the application. Here, the user can setup the WMS server and camera parameters, enter the initial georeference, start the georeference estimation, and view the calculated results. The second part is the camera view that is used to display the video and points that are identified in it. This view is also used to identify points, show corresponding output points, and in the case of the PTZ camera, it allows the user to control the camera. Finally, the third part is map view, which is used to display and navigate the orthophoto of the area of interest, so as to enter and display identified points.
Figure 3 depicts how different parts of the application are used in the real-life scenario of camera georeferencing using 15 points. The result of the obtained georeference is depicted in the camera view with points in blue along with input points in red. To illustrate the accuracy achieved using the proposed method,
Figure 4 depicts the corresponding camera output displayed in the projected video mode of our GIS-based video surveillance solution [
10]. Several other examples of georeferences depicted in the same way are shown in
Figure 5. Georeferencing of these examples is done using an orthophoto map with a pixel size of 0.1 m and DEM with a ground sample distance (GSD) of 1 m.
We already stated that for the estimation of camera georeferences we rely on Levenberg–Marquardt iterative optimization. This technique is a standard one for nonlinear least-squares problems and can be thought of as a combination of steepest descent and the Gauss-Newton method [
37]. To implement it in our application, we used an open-source C/C++ library called levmar [
38]. One advantage of levmar is that it supports the use of both analytic and approximate Jacobian. Since the transformation we used for mapping the input 3D geodetic coordinates into output image coordinates is rather complex, finding analytic Jacobian would not be a simple task. That is why we relied on the feature of levmar to approximate Jacobian using the finite-difference method.
The levmar library offers several interface functions which offer unconstraint and constraint optimization, the use of single and double precision, and as previously mentioned, analytic and approximate Jacobian. In our implementation, we used function dlevmar_dif that offers double precision, unconstrained optimization, and approximate Jacobian. A full description of the corresponding input parameters is given in [
38], but in general, it requires an initial parameters’ estimate, measurement vector, an optional pointer to additional data, and a pointer to a function that implements appropriate transformation. In our case, the initial parameters correspond to initial georeference, measurements to a set of input video coordinates, while additional data hold the corresponding 3D geodetic coordinates, frame width (
w), and height (
h), and optionally, the
fov,
pan, and
tilt values for each measurement.
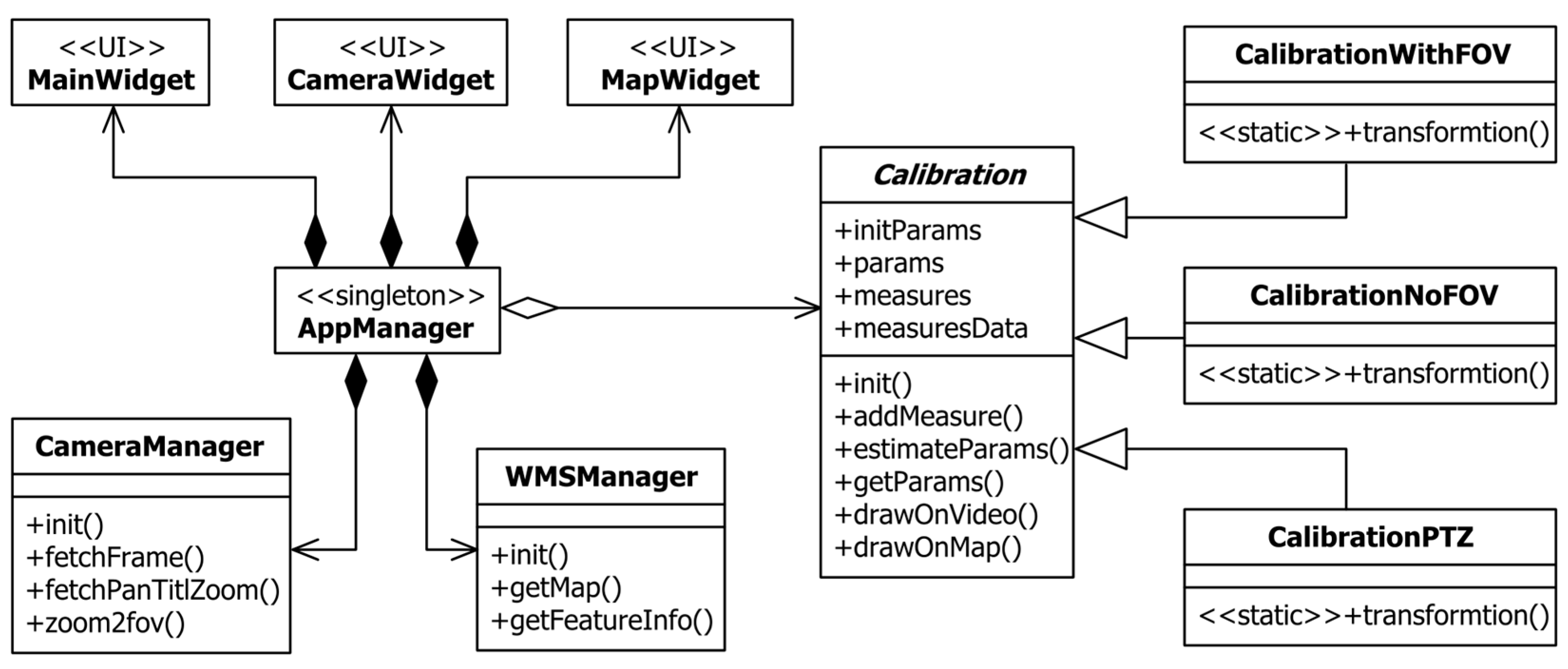
Finally, to complete this overview, let us consider an architecture of the implemented application. The corresponding UML class diagram is shown in
Figure 6. As it can be seen, the whole application is built around singleton class AppManager, which is used for communication between other classes. There are three widget classes (MainWidget, CameraWidget, and MapWidget) for each of the previously described UI parts. Class CameraManager represents an interface toward the surveillance camera, while class WMSManager represents an interface toward the WMS server. Finally, the most important part of the application is encapsulated in the Calibration abstract class and its derivatives. Class CalibrationWithFOV implements a full georeference estimation of fixed cameras when
fov is included. Similarly, class CalibrationNoFOV is used with fixed cameras when
fov is known and excluded from the estimation. Finally, CalibrationPTZ is used to estimate the georeference of PTZ cameras. These three subclasses contain specific transformations for each of the specified subdomains, while the abstract superclass exposes a common interface for this process and holds necessary data.
Accuracy Analyses
The examples presented in
Figure 4 and
Figure 5 give us some idea of the achievable accuracy in estimating camera georeferences. Nevertheless, since we lack ground truth values, it is hard to determine how much-estimated values differ. Additionally, it would be interesting to know how the precision of determining the world and image coordinates influences the results.
To cope with specified challenges, we developed a series of synthetic experiments that relate measurement errors of the 3D world and image coordinates to errors in the estimated position, orientation, and field-of-view. The experiments are conducted using the following methodology:
Creating ground truth dataset: Based on the real-life example that included mapping between 15 geodetic and image coordinates, we estimated the camera georeference, i.e., the camera’s position, orientation, and field-of-view. Then, we transformed our input geodetic coordinates using the obtained georeference and we got the output image coordinates. These image coordinates, along with the input geodetic coordinates and chosen georeference, represent our ideal, zero-error, data set that would be considered a ground truth for all other estimations.
Adding variations and estimating georeference: To simulate errors in the process of obtaining geodetic and image coordinates, we added randomly generated values from a certain range (plus/minus the amount of the variation) to input coordinates. To simulate an error in map reading, we generated variations in meters and added them to geocentric coordinates that are calculated from the ground truth geodetic coordinates. To simulate errors in the image coordinates reading, we generated variations in pixels and added them to the ground truth image coordinates. Once we had made a sample dataset in this way, we applied our estimation method to determine the most suitable georeference. Squares of the differences between parameters were recorded.
Averaging the results: Since a single measurement heavily depends on picked random values, to average the results and get an estimate of the error, we applied 10,000 such measurements. Based on the accumulated squared differences, we calculated the standard deviation of the position (in meters), orientation, and field-of-view (in degrees).
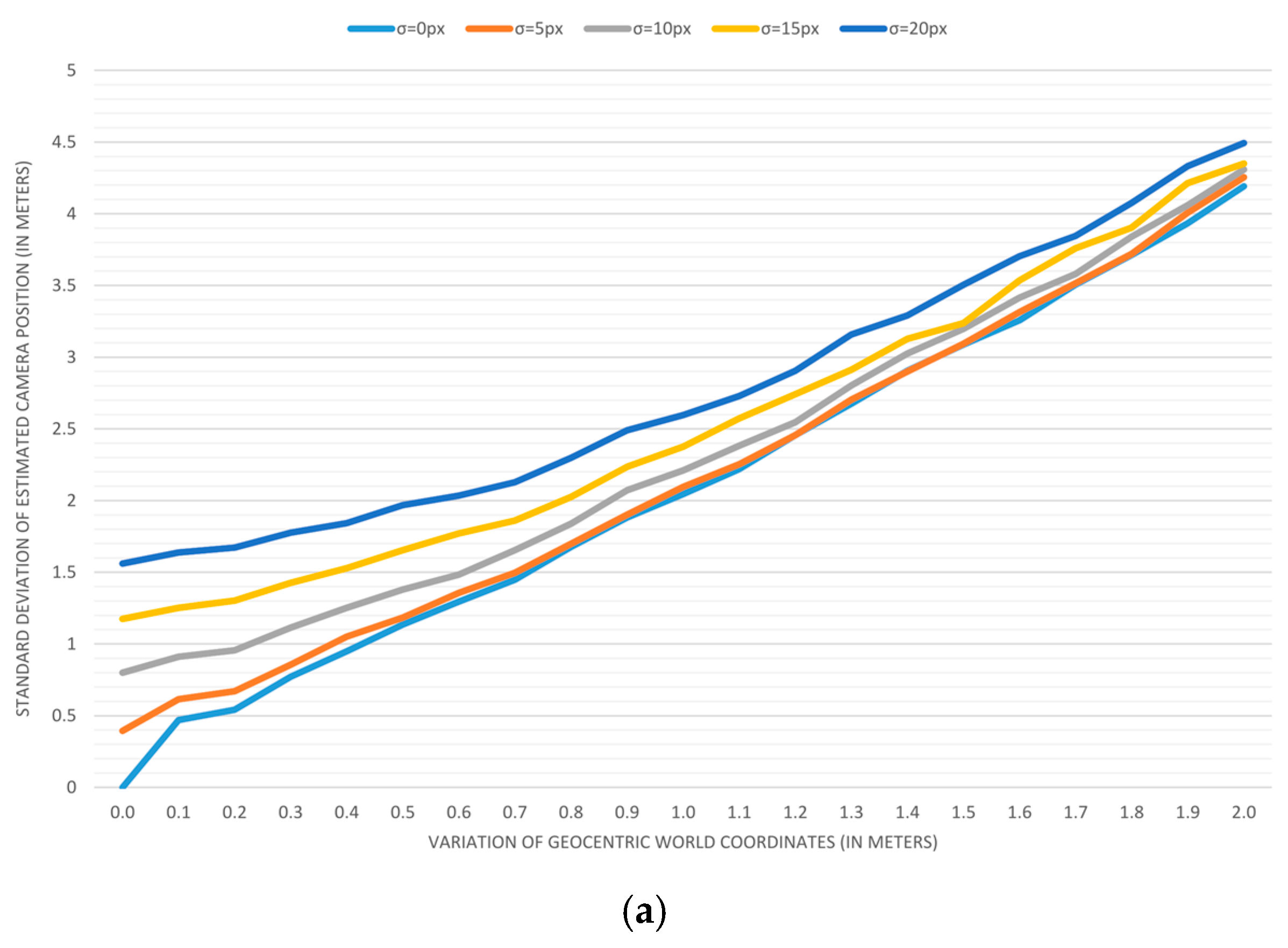
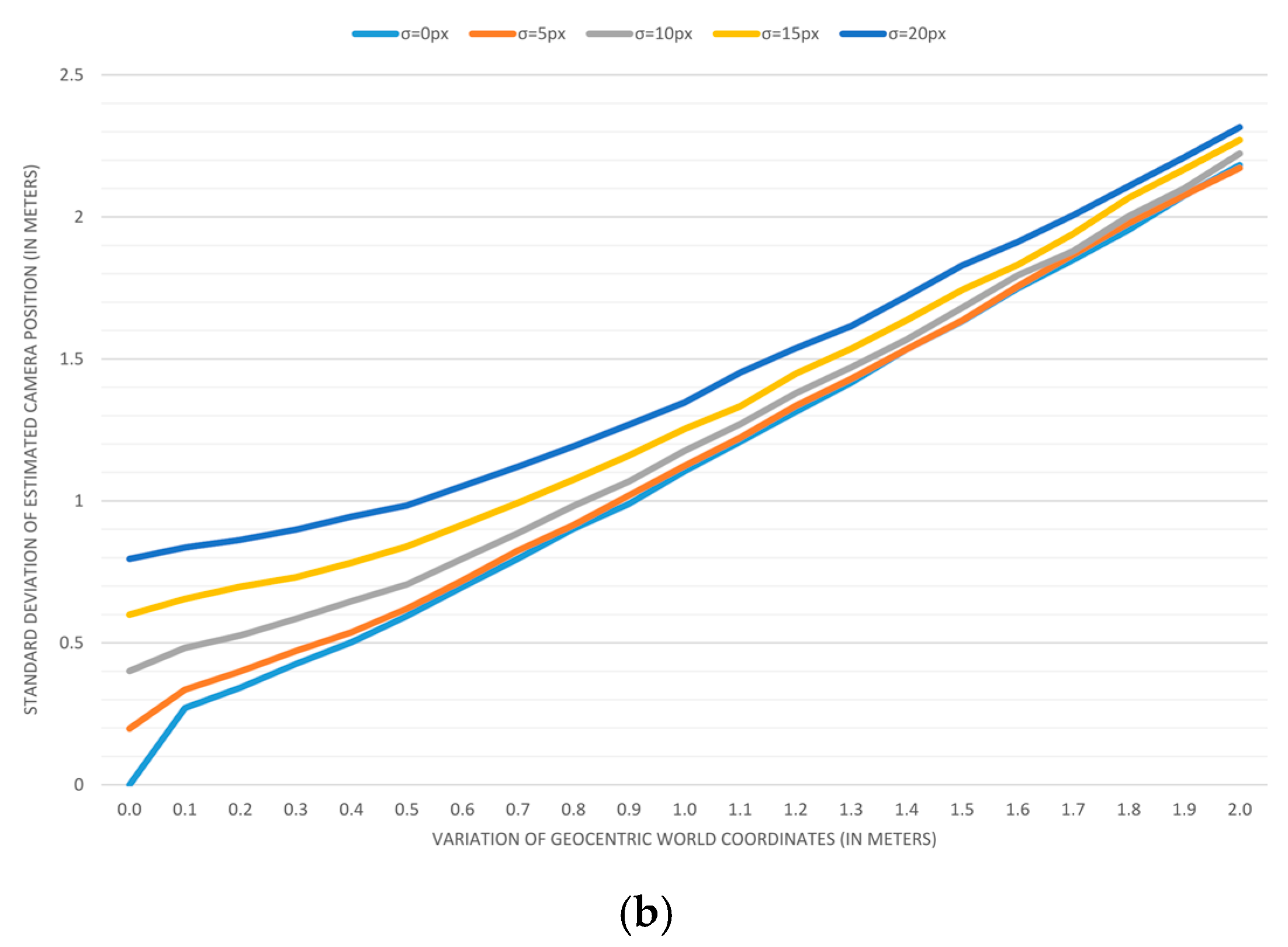
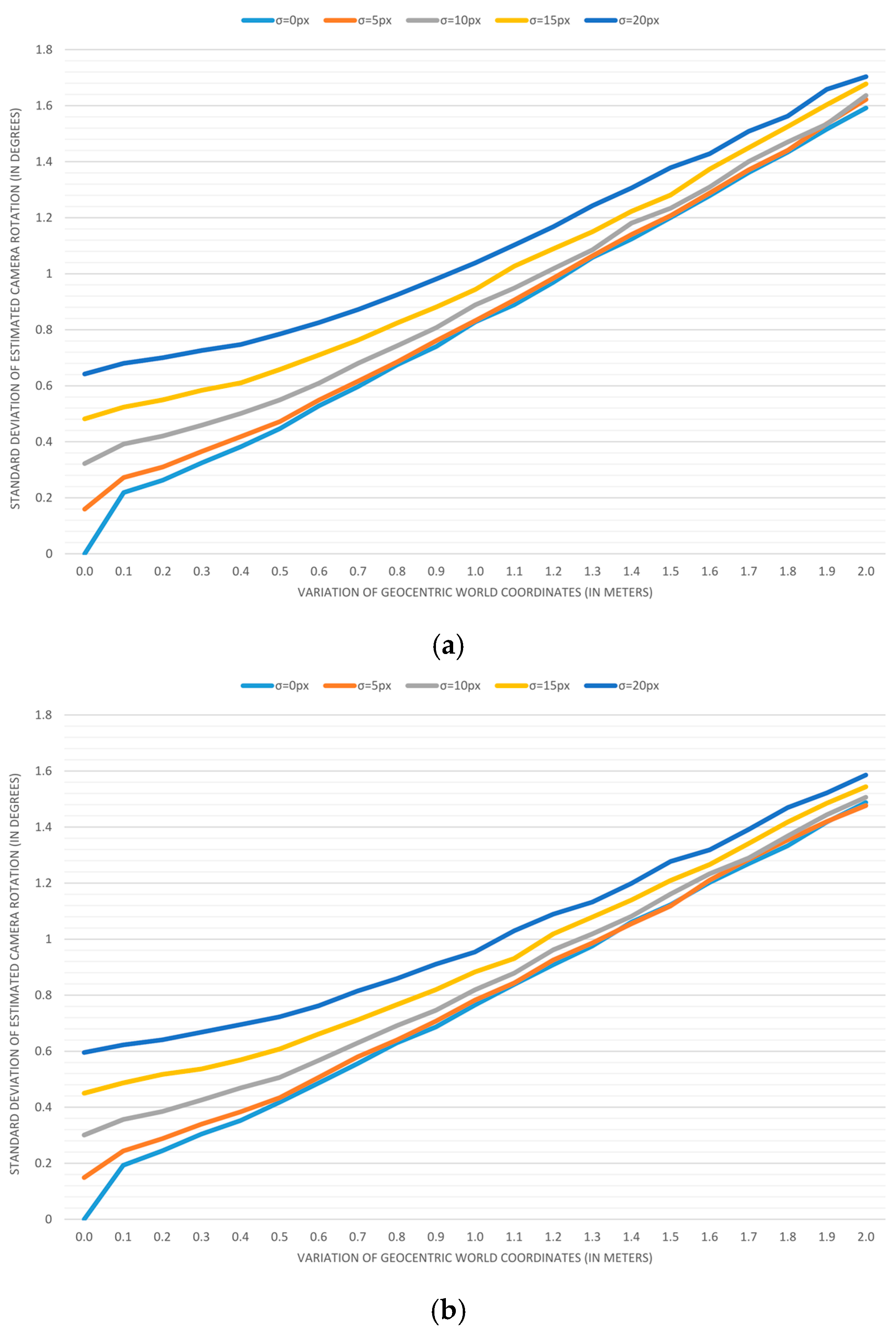
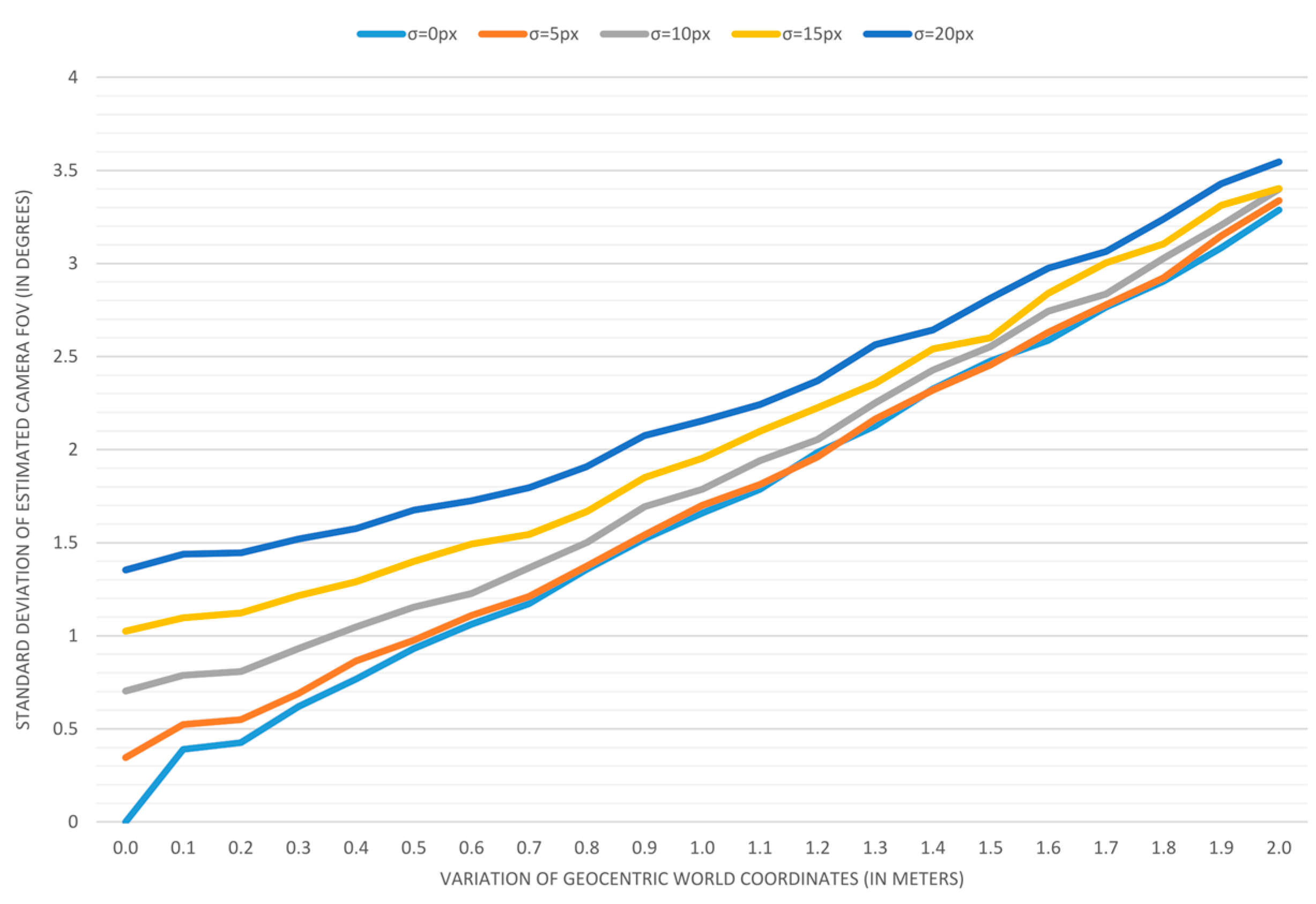
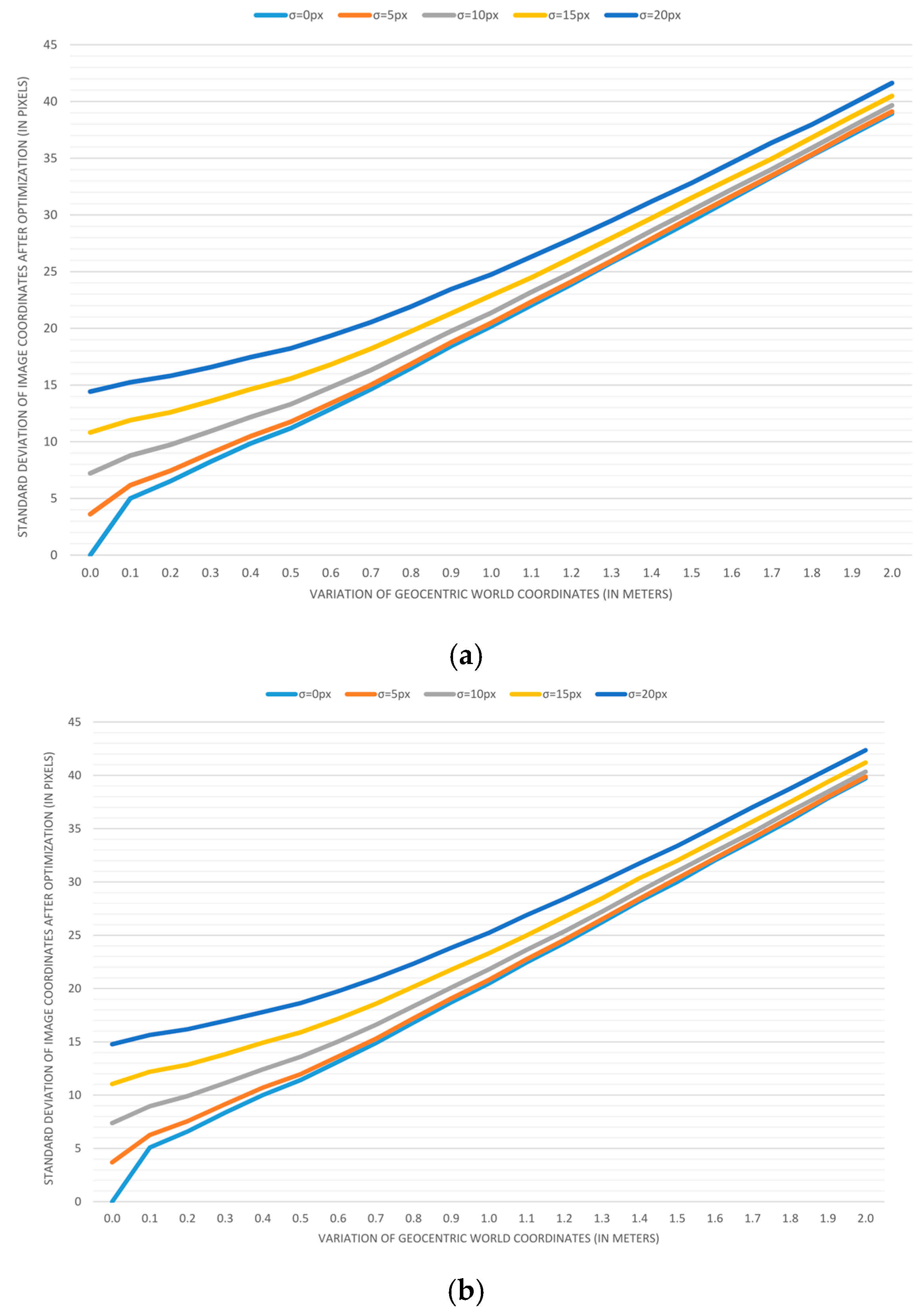
Plotting the results: To visualize trends, we applied previous measurements for variations in geocentric coordinates that range from 0 to 2 m, with a step of 0.1 m. Variations in image coordinates of 0, 5, 10, 15, and 20 pixels are used to create five different series displayed on each graph.
The results of accuracy analyses are displayed in
Figure 7,
Figure 8,
Figure 9 and
Figure 10.
Figure 7 depicts the error in estimating the camera position when the field-of-view is estimated (a) and when it is predetermined (b). As it can be seen, one additional parameter in the estimation process doubles the positioning error. In a similar form,
Figure 8 depicts the error in estimating the camera orientation. In this case, estimating the field-of-view again leads to a bigger error, but in this case, the difference is almost insignificant. The estimation error for a camera’s field-of-view is depicted in the next graph (
Figure 9). Finally,
Figure 10 depicts the estimation process error in terms of the standard deviation of image coordinates when the field-of-view is estimated (a) and when it is predetermined (b). As it can be assumed, having the field-of-view as an additional estimation parameter results in a smaller overall process error, but surprisingly, the difference is hardly noticeable.
The presented results lead to the conclusion that the independent and accurate determining of a camera’s field-of-view should be taken into account whenever it is possible. The second interesting discovery is that the variation of input image coordinates of up to 5 pixels has almost no effect on the accuracy when a map reading error is above 0.3 m.
6. Conclusions
The integration of video surveillance and 3D GIS paves the way for new opportunities that were not possible with conventional surveillance systems [
20]. The ability to acquire the geolocation of each point in the video, or to direct a PTZ camera to the given geolocation, relies on the quality of the provided video georeference. Since a video represents a sequence of images (frames), to georeference it, we need to know the exact parameters that determine the camera view at the moment each frame is captured. An appropriate set of seven parameters that specify the camera position, orientation, and field-of-view has previously been defined by Milosavljević et al. [
31] as the observer viewpoint model. Since GIS-based video surveillance relies on the overlapping of video frames with a virtual 3D GIS scene, even small errors in georeference parameters become apparent. Therefore, it is necessary to accurately determine the camera georeference. Although it is possible to measure these parameters, the required procedures are complicated and the results do not always guarantee a satisfactory accuracy. The goal of the research presented in this paper was to come up with an alternative by developing a method for the indirect estimation of these parameters.
The proposed method is based on pairing the image coordinates of certain static point features, which can be recognized in a video, with their 3D geographic locations obtained from high-resolution orthophotos and DEM. Once we pair enough evenly distributed points, Levenberg–Marquardt iterative optimization is applied to find the most suitable camera georeference, i.e., to estimate the position and orientation of the camera. To do so, the process tries to minimize the sum of least square errors between the input image coordinates and image coordinates obtained transforming input 3D geodetic coordinates using current georeference parameters.
The proposed method can be used to estimate the georeference of both fixed and PTZ cameras. With fixed cameras, we have a simpler case, where the video frame georeference is constant and can be treated as a camera georeference. On the other hand, PTZ cameras introduce a ‘dynamical’ video frame georeference that depends on the current values for pan, tilt, and zoom. In that case, the camera georeference is equal to the video frame georeference where pan and tilt are set to zero. The current frame georeference is calculated based on the camera georeference and current pan and tilt values. In this paper, we also discussed how this method can be applied for estimating the PTZ camera georeference.
Based on the proposed method, we implemented an application for georeferencing fixed and PTZ surveillance cameras. This application not only provided validation of the described approach, but proved that it was very efficient in the assigned tasks. The advantages of the proposed method can be summarized as follows:
Very good accuracy of the resulting georeferences compared to measured values
Simplified georeferencing procedure (without leaving the office)
Ability to determine the camera georeference even when it is not possible to access it for on-site measuring (e.g., distant location, restricted area)
Ability to estimate the fixed camera field-of-view when it is not possible to measure it (e.g., pre-mounted cameras)
Support for PTZ cameras
Finally, we would like to emphasize that, even though these results are satisfying, this method is human dependent, and as such, it has great potential for automation. The ability to automatically identify and pair points would be a great improvement that could lead to the integration of a video and GIS beyond video surveillance.