Trajectory Data Mining via Cluster Analyses for Tropical Cyclones That Affect the South China Sea
Abstract
:1. Introduction
2. Research Methods
2.1. Research Data
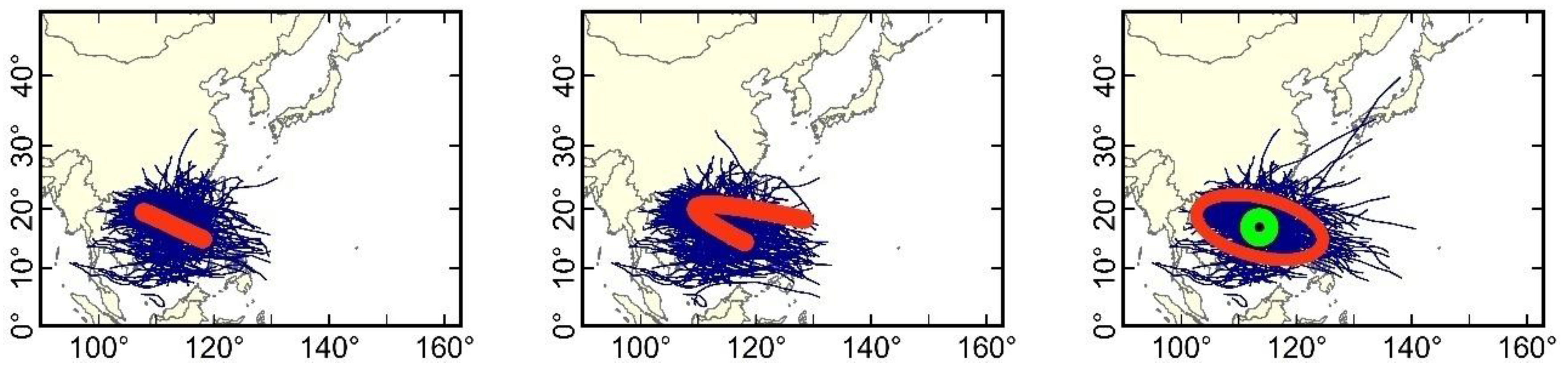
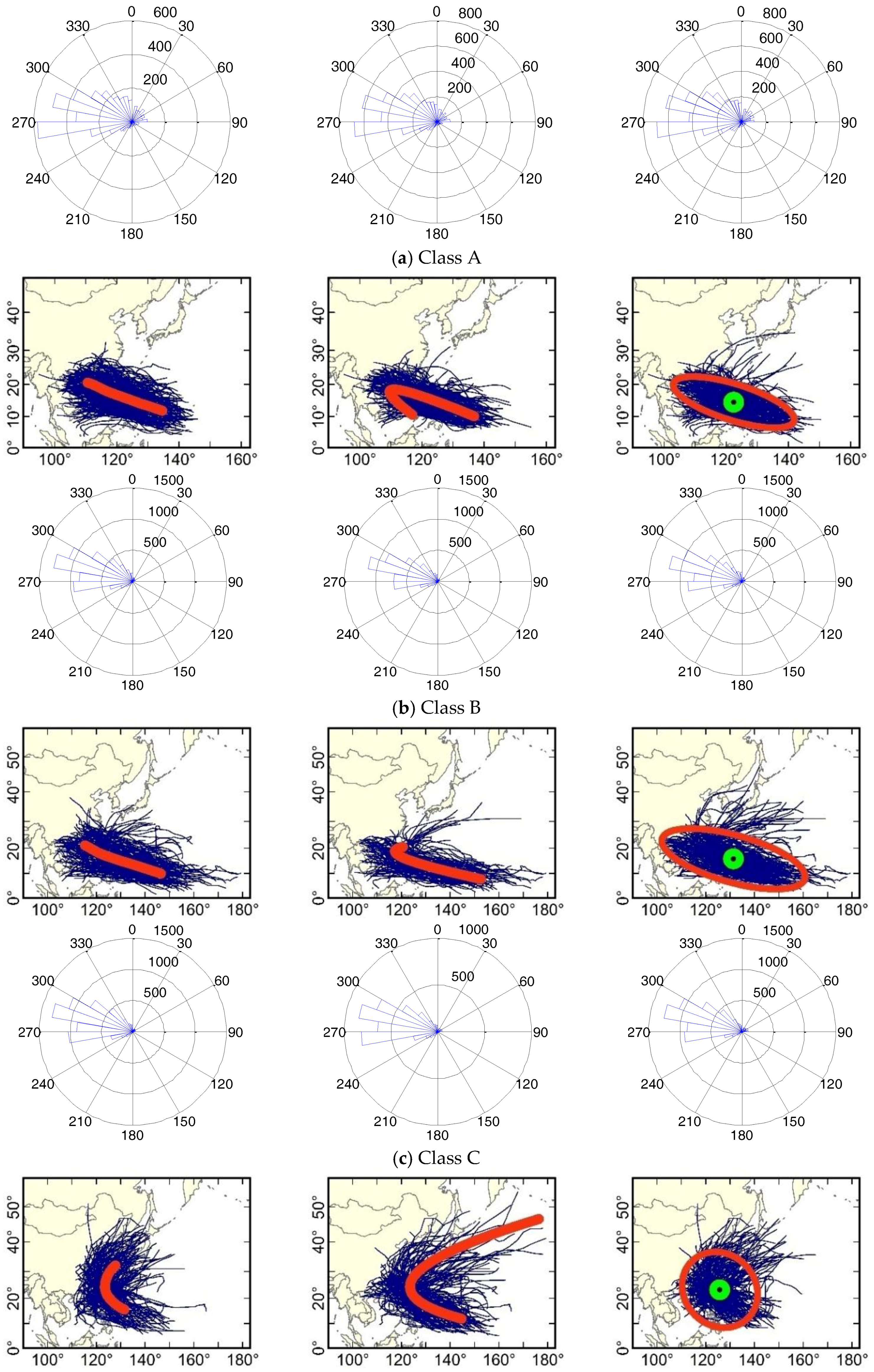
2.2. Equal Division of TC Trajectory Method
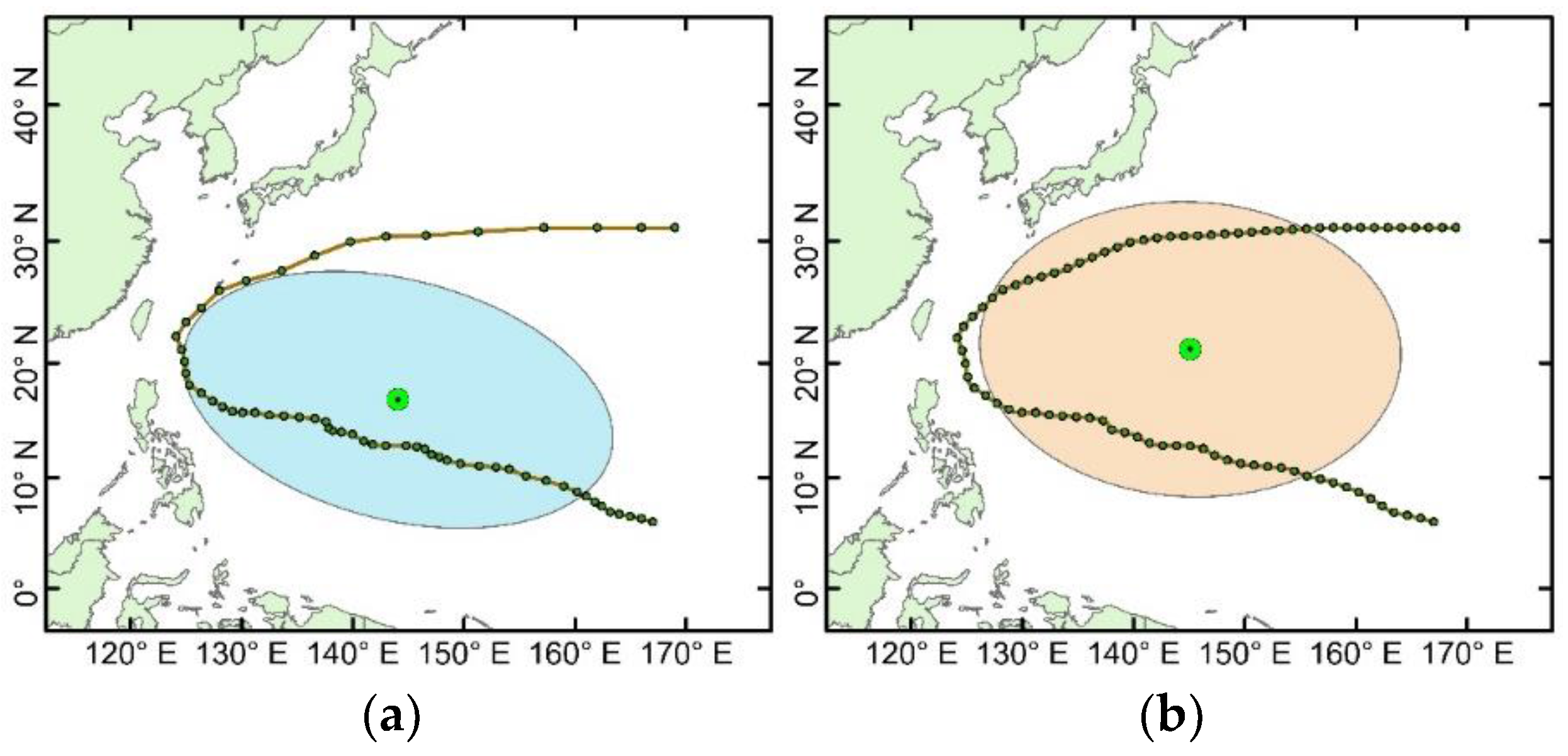
2.3. Mass Moment of the TC Trajectory Method
2.4. Mixed Regression Model Method
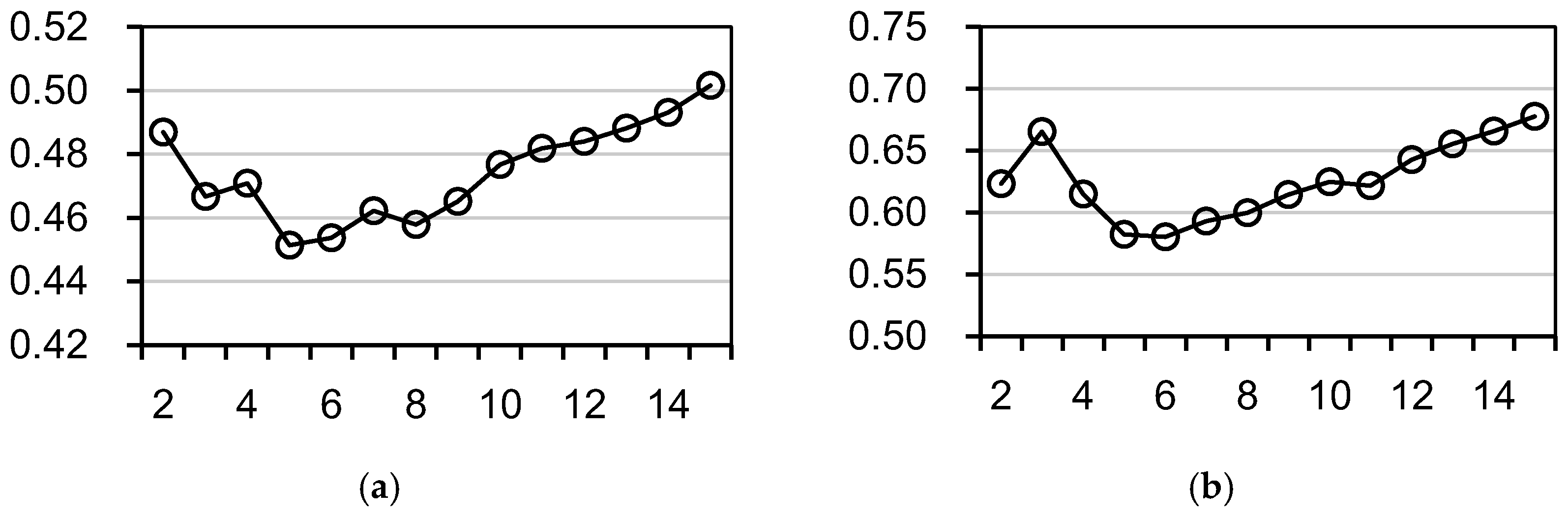
2.5. Selection of the Number of Clusters
3. Results
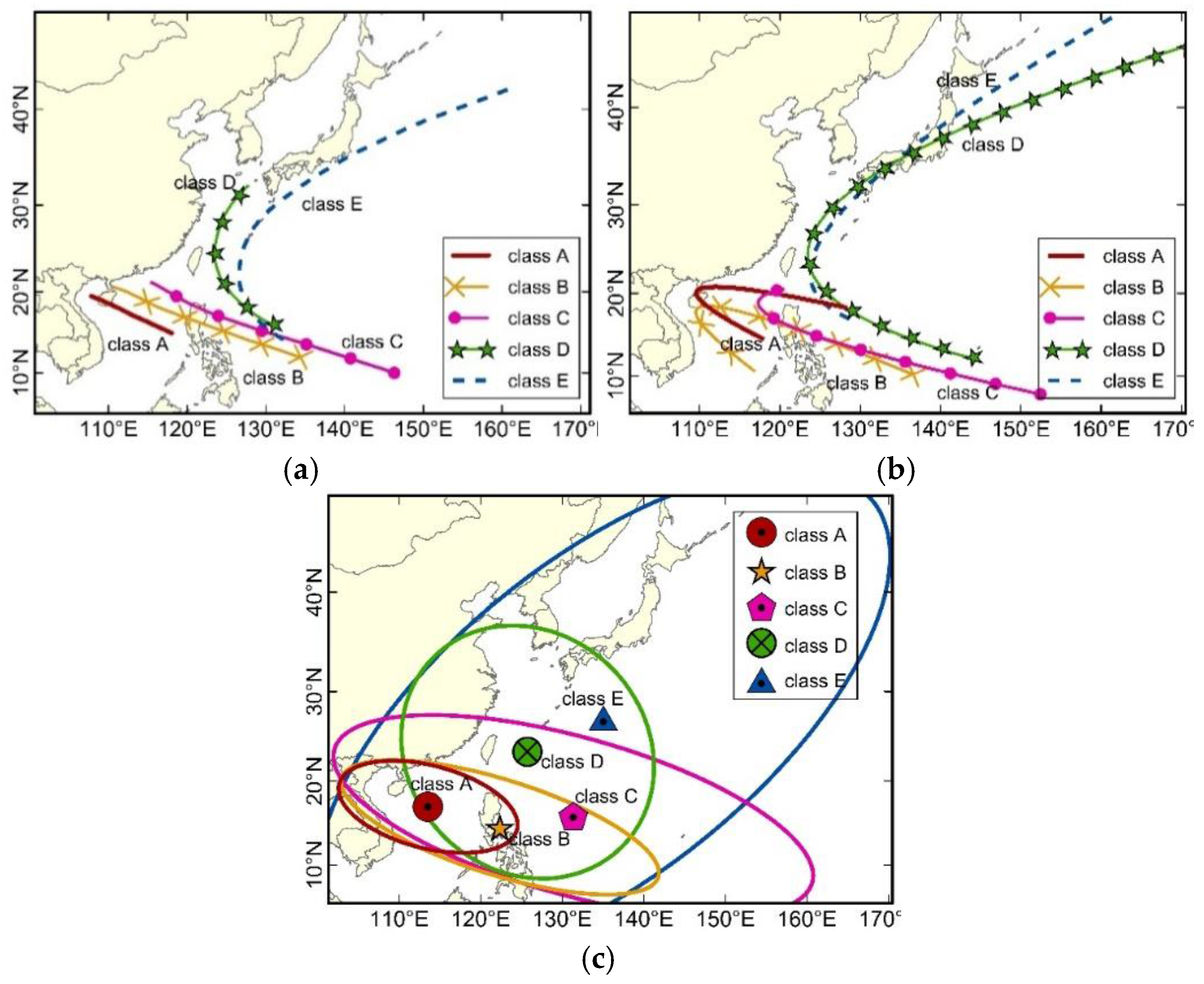
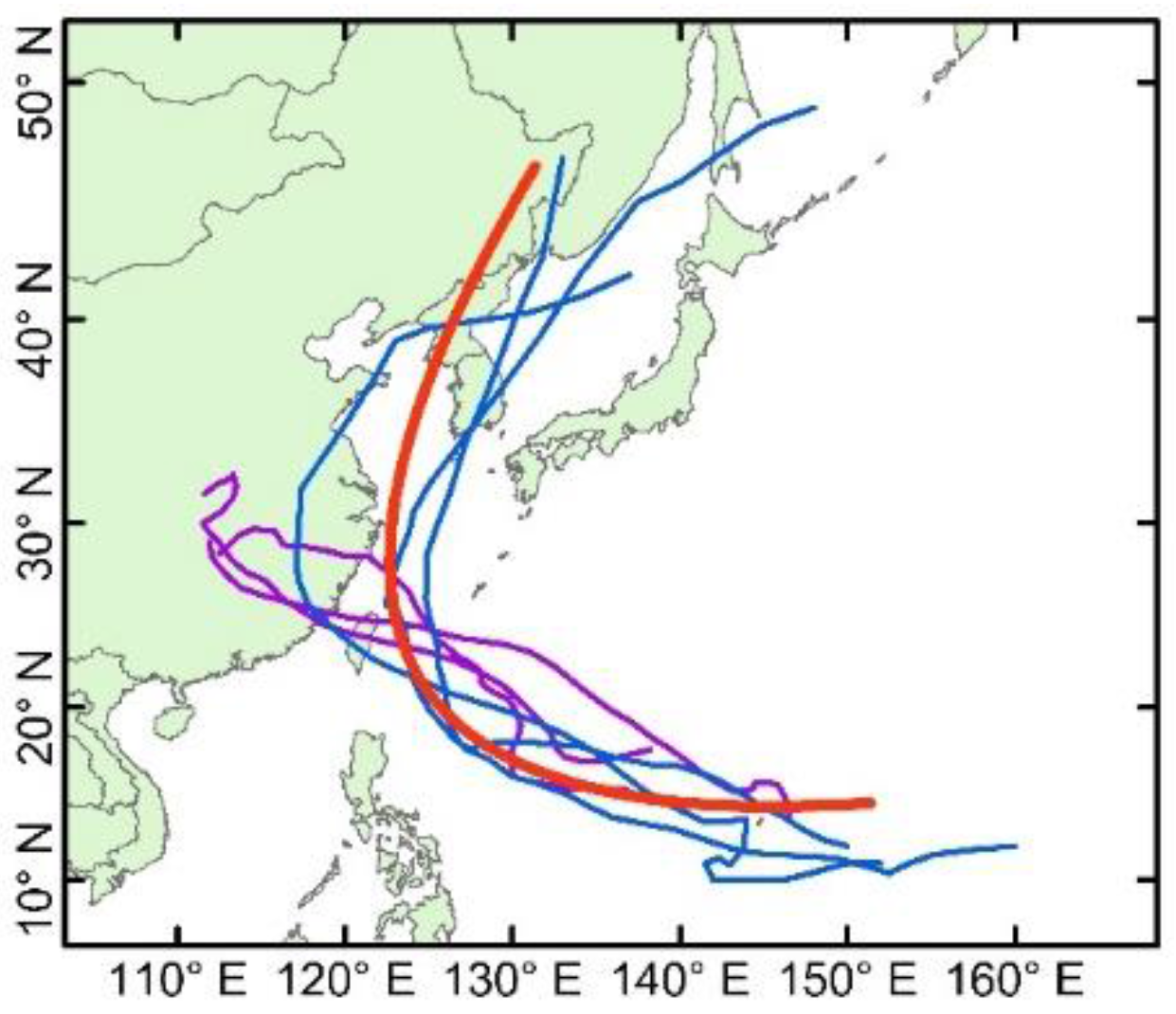
3.1. Clustering Results for the TC Trajectories
3.2. Trajectory Features of Different TC Classes
3.3. Genesis Locations of Different TC Classes
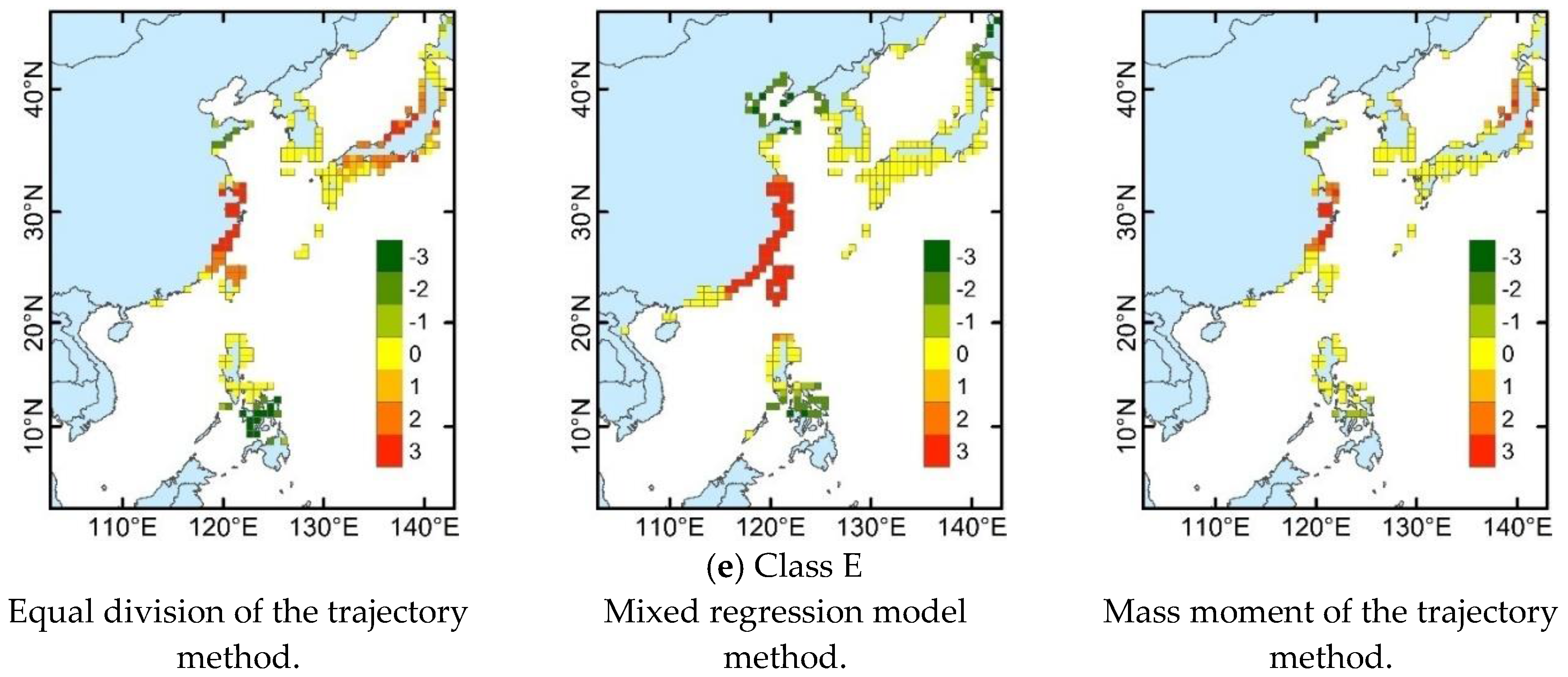
3.4. Landfall Locations for Different TC Classes
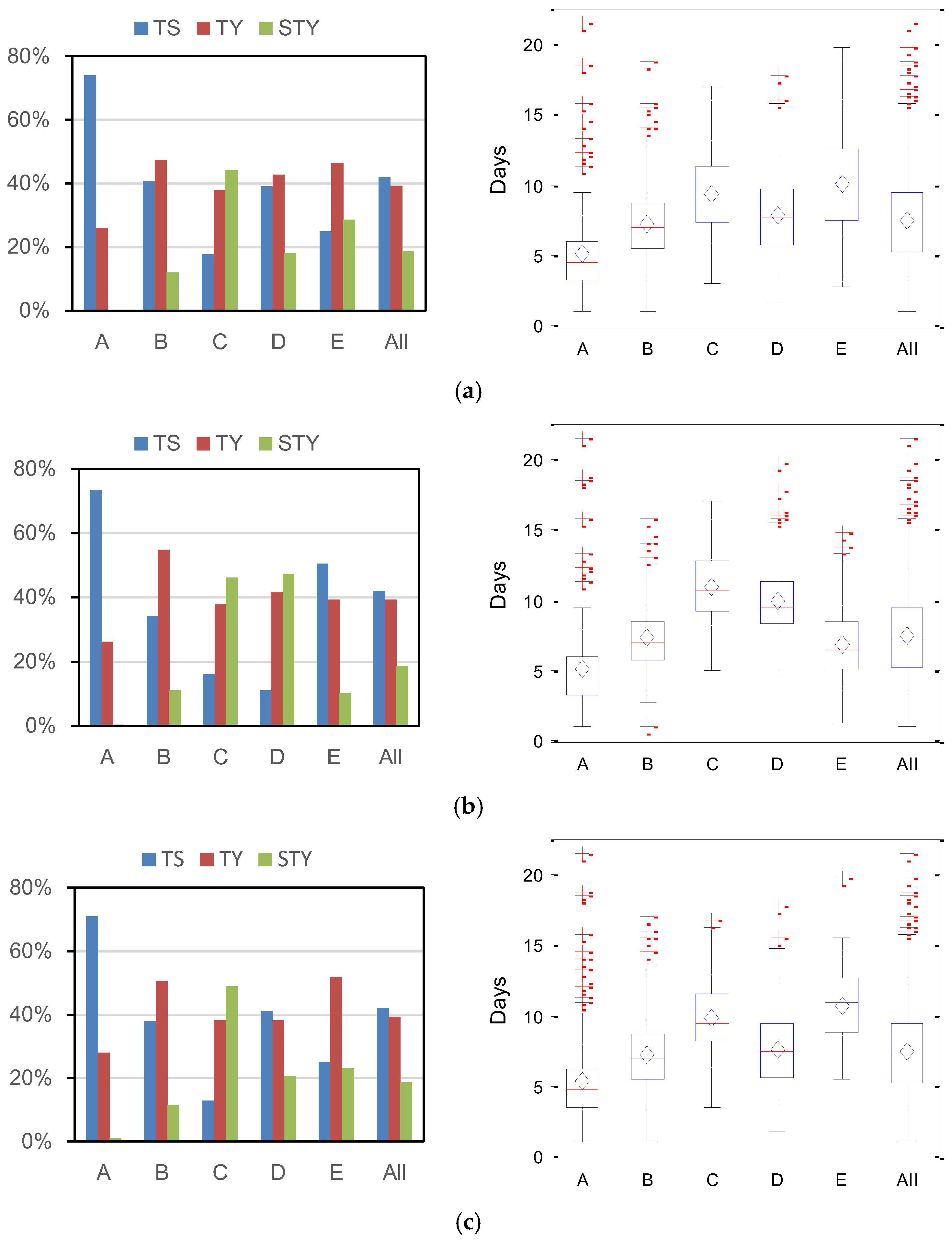
3.5. Intensity and Lifetime of Different TC Classes
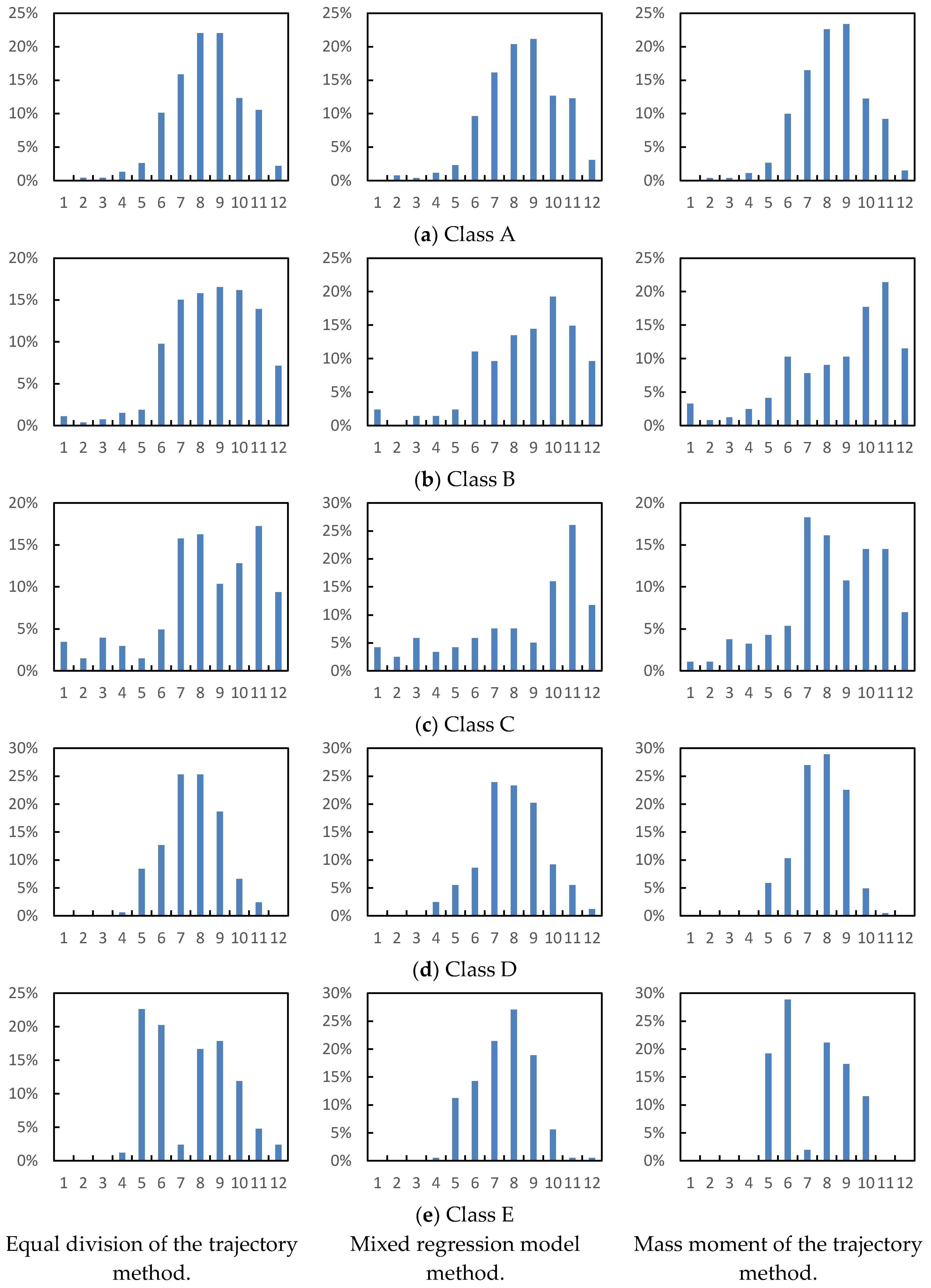
3.6. Seasonal Distribution of Different TC Classes
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Y.; Wu, C.-C. Current understanding of tropical cyclone structure and intensity changes—A review. Meteorol. Atmos. Phys. 2004, 87, 257–278. [Google Scholar] [CrossRef]
- Chan, J.C.L.; Liu, K.S.; Ching, S.E.; Lai, E.S.T. Asymmetric distribution of convection associated with tropical cyclones making landfall along the South China Coast. Mon. Weather Rev. 2004, 132, 2410–2420. [Google Scholar] [CrossRef]
- McGregor, G.R. The tropical cyclone hazard over the South China Sea 1970–1989. Appl. Geogr. 1995, 15, 35–52. [Google Scholar] [CrossRef]
- Gemmer, M.; Yin, Y.; Luo, Y.; Fischer, T. Tropical cyclones in China: County-based analysis of landfalls and economic losses in Fujian Province. Quat. Int. 2011, 244, 169–177. [Google Scholar] [CrossRef]
- Li, X.; Ren, F.; Yang, X.; Wang, C. A study of the regional differences of the tropical cyclone activities over the South China Sea and the Western North Pacific. Clim. Environ. Res. 2010, 15, 504–510. (In Chinese) [Google Scholar]
- Kim, H.S.; Kim, J.H.; Ho, C.H.; Chu, P.S. Pattern classification of typhoon tracks using the fuzzy c-means clustering method. J. Clim. 2011, 24, 488–508. [Google Scholar] [CrossRef]
- Saunders, M.A.; Chandler, R.E.; Merchant, C.J.; Roberts, F.P. Atlantic hurricanes and NW Pacific typhoons: ENSO spatial impacts on occurrence and landfall. Geophys. Res. Lett. 2000, 27, 1147–1150. [Google Scholar] [CrossRef]
- Wang, B.; Chan, J.C.L. How strong ENSO events affect tropical storm activity over the western north Pacific. J. Clim. 2002, 15, 1643–1658. [Google Scholar] [CrossRef]
- Hodanish, S.; Gray, W.M. An observational analysis of tropical cyclone recurvature. Mon. Weather Rev. 1993, 121, 2665–2689. [Google Scholar] [CrossRef]
- Elsner, J.B.; Liu, K.-B. Examining the ENSO-typhoon hypothesis. Clim. Res. 2003, 25, 43–54. [Google Scholar] [CrossRef]
- Harr, P.A.; Elsberry, R.L. Tropical cyclone track characteristics as a function of large-scale circulation anomalies. Mon. Weather Rev. 1991, 119, 1448–1468. [Google Scholar] [CrossRef]
- Harr, P.A.; Elsberry, R.L. Large-scale circulation variability over the tropical western north Pacific. Part I: Spatial patterns and tropical cyclone characteristics. Mon. Weather Rev. 1995, 123, 1225–1246. [Google Scholar] [CrossRef]
- Harr, P.A.; Elsberry, R.L. Large-scale circulation variability over the tropical western north Pacific. Part II: Persistence and transition characteristics. Mon. Weather Rev. 1995, 123, 1247–1268. [Google Scholar] [CrossRef]
- Lander, M.A. Specific tropical cyclone track types and unusual tropical cyclone motions associated with a reverse-oriented monsoon trough in the western North Pacific. Weather Forecast. 1996, 11, 170–186. [Google Scholar] [CrossRef]
- Liu, K.; Chan, J.C. Climatological characteristics and seasonal forecasting of tropical cyclones making landfall along the South China coast. Mon. Weather Rev. 2003, 131, 1650–1662. [Google Scholar] [CrossRef]
- Li, Y.; Chen, L.-S.; Zhang, S.-J. Statistical characteristics of tropical cyclone making landfalls on China. J. Trop. Meteorol. 2004, 20, 14–23. (In Chinese) [Google Scholar]
- Liu, X.; Ban, Y. Uncovering spatio-temporal cluster patterns using massive floating car data. ISPRS Int. J. Geo-Inf. 2013, 2, 371–384. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, R. Road map inference: A segmentation and grouping framework. ISPRS Int. J. Geo-Inf. 2016, 5, 130. [Google Scholar] [CrossRef]
- Shi, Y.; Deng, M.; Yang, X.; Liu, Q.; Zhao, L.; Lu, C.-T. A framework for discovering evolving domain related spatio-temporal patterns in Twitter. ISPRS Int. J. Geo-Inf. 2016, 5, 193. [Google Scholar] [CrossRef]
- Markman, V. Unsupervised discovery of fine-grained topic clusters in Twitter posts. In Proceedings of the Analyzing Microtext: Papers from the 2011 AAAI Workshop, San Francisco, CA, USA, 8 August 2011. [Google Scholar]
- Sun, Y.; Fan, H.; Li, M.; Zipf, A. Identifying the city center using human travel flows generated from location-based social networking data. Environ. Plan. B Plan. Des. 2016, 43, 480–498. [Google Scholar] [CrossRef]
- Sârbu, C.; Einax, J.W. Study of traffic-emitted lead pollution of soil and plants using different fuzzy clustering algorithms. Anal. Bioanal. Chem. 2008, 390, 1293–1301. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.-C.; Lin, K.-Y. Diagnosis for monitoring system of municipal solid waste incineration plant. Expert Syst. Appl. 2008, 34, 247–255. [Google Scholar] [CrossRef]
- Cheng, S.Y.; Wang, F.; Li, J.B.; Chen, D.S.; Li, M.J.; Zhou, Y.; Ren, Z.H. Application of Trajectory Clustering and Source Apportionment Methods for Investigating Trans-Boundary Atmospheric PM10 Pollution. Aerosol Air Qual. Res. 2013, 13, 333–342. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkely, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Elsner, J.B. Tracking hurricanes. Bull. Am. Meteorol. Soc. 2003, 84, 353–356. [Google Scholar] [CrossRef]
- Blender, R.; Fraedrich, K.; Lunkeit, F. Identification of cyclone-track regimes in the North Atlantic. Q. J. R. Meteorol. Soc. 1997, 123, 727–741. [Google Scholar] [CrossRef]
- Corporal-Lodangco, I.; Leslie, L. Cluster analysis of Philippine tropical cyclone climatology: Applications to forecasting. J. Climatol. Weather Forecast. 2016, 4, 2. [Google Scholar] [CrossRef]
- Gaffney, J.S. Probabilistic Curve-Aligned Clustering and Prediction with Regression Mixture Models. Ph.D. Thesis, University of California, Oakland, CA, USA, 2004. [Google Scholar]
- Camargo, S.J.; Robertson, A.W.; Gaffney, S.J.; Smyth, P.; Ghil, M. Cluster analysis of typhoon tracks. Part I: General properties. J. Clim. 2007, 20, 3635–3653. [Google Scholar] [CrossRef]
- Gaffney, S.; Smyth, P. Trajectory clustering with mixtures of regression models. In Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; pp. 63–72. [Google Scholar]
- Camargo, S.J.; Robertson, A.W.; Gaffney, S.J.; Smyth, P.; Ghil, M. Cluster analysis of typhoon tracks. Part II: Large-scale circulation and ENSO. J. Clim. 2007, 20, 3654–3676. [Google Scholar] [CrossRef]
- Kossin, J.P.; Camargo, S.J.; Sitkowski, M. Climate modulation of North Atlantic hurricane tracks. J. Clim. 2010, 23, 3057–3076. [Google Scholar] [CrossRef]
- Nakamura, J.; Lall, U.; Kushnir, Y.; Camargo, S.J. Classifying North Atlantic tropical cyclone tracks by mass moments. J. Clim. 2009, 22, 5481–5494. [Google Scholar] [CrossRef]
- Camargo, S.J.; Robertson, A.W.; Barnston, A.G.; Ghil, M. Clustering of Eastern North Pacific tropical cyclone tracks: ENSO and MJO effects. Geochem. Geophys. Geosyst. 2008, 9. [Google Scholar] [CrossRef]
- Paliwal, M.; Patwardhan, A. Identification of clusters in tropical cyclone tracks of North Indian Ocean. Nat. Hazards 2013, 68, 645–656. [Google Scholar] [CrossRef]
- Yang, L.; Du, Y.; Wang, D.; Wang, C.; Wang, X. Impact of intraseasonal oscillation on the tropical cyclone track in the South China Sea. Clim. Dyn. 2014, 44, 1505–1519. [Google Scholar] [CrossRef]
- Goh, A.Z.-C.; Chan, J.C.L. Interannual and interdecadal variations of tropical cyclone activity in the South China Sea. Int. J. Climatol. 2010, 30, 827–843. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Ren, F.; Liang, J.; Wu, G.; Dong, W.; Yang, X. Reliability Analysis of Climate Change of Tropical Cyclone Activity over the Western North Pacific. J. Clim. 2011, 24, 5887–5898. [Google Scholar] [CrossRef]
- Chu, H.-J.; Liau, C.-J.; Lin, C.-H.; Su, B.-S. Integration of fuzzy cluster analysis and kernel density estimation for tracking typhoon trajectories in the Taiwan region. Expert Syst. Appl. 2012, 39, 9451–9457. [Google Scholar] [CrossRef]
- Gaffney, S.J.; Robertson, A.W.; Smyth, P.; Camargo, S.J.; Ghil, M. Probabilistic clustering of extratropical cyclones using regression mixture models. Clim. Dyn. 2007, 29, 423–440. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Bensaid, A.M.; Hall, L.O.; Bezdek, J.C.; Clarke, L.P.; Silbiger, M.L.; Arrington, J.A.; Murtagh, R.F. Validity-guided (re) clustering with applications to image segmentation. IEEE Trans. Fuzzy Syst. 1996, 4, 112–123. [Google Scholar] [CrossRef]
- Abonyi, J.; Feil, B. Cluster Analysis for Data Mining and System Identification; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Chen, S.-R. Source regions of tropical Pacific storms over north west ocean. Meteorol. Mon. 1990, 16, 23–26. (In Chinese) [Google Scholar]
- Camargo, S.J.; Sobel, A.H. Western North Pacific tropical cyclone intensity and ENSO. J. Clim. 2005, 18, 2996–3006. [Google Scholar] [CrossRef]
- Chan, J.C. Decadal Variations of Intense Typhoon Occurrence in the Western North Pacific. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 2008; pp. 249–272. [Google Scholar]
- Mei, W.; Xie, S.-P.; Primeau, F.; McWilliams, J.C.; Pasquero, C. Northwestern Pacific typhoon intensity controlled by changes in ocean temperatures. Sci. Adv. 2015, 1, e1500014. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Ding, Y. An Introduction to Typhoons in the Northwest Pacific; Science Press Ltd.: Beijing, China, 1979; p. 491. (In Chinese) [Google Scholar]
- Chia, H.H.; Ropelewski, C.F. The interannual variability in the genesis location of tropical cyclones in the northwest Pacific. J. Clim. 2002, 15, 2934–2944. [Google Scholar] [CrossRef]
- Harr, P.A.; Elsberry, R.L.; Hogan, T.F. Extratropical transition of tropical cyclones over the western north Pacific. Part II: The impact of midlatitude circulation characteristics. Mon. Weather Rev. 2000, 128, 2634–2653. [Google Scholar] [CrossRef]
- Zhong, Y.; Xu, M.; Wang, Y. Spatio-temporal distributive characteristics of extratropically transitioning tropical cyclones over the Northwest Pacific. Acta Meteorol. Sin. 2009, 67, 697–707. (In Chinese) [Google Scholar]
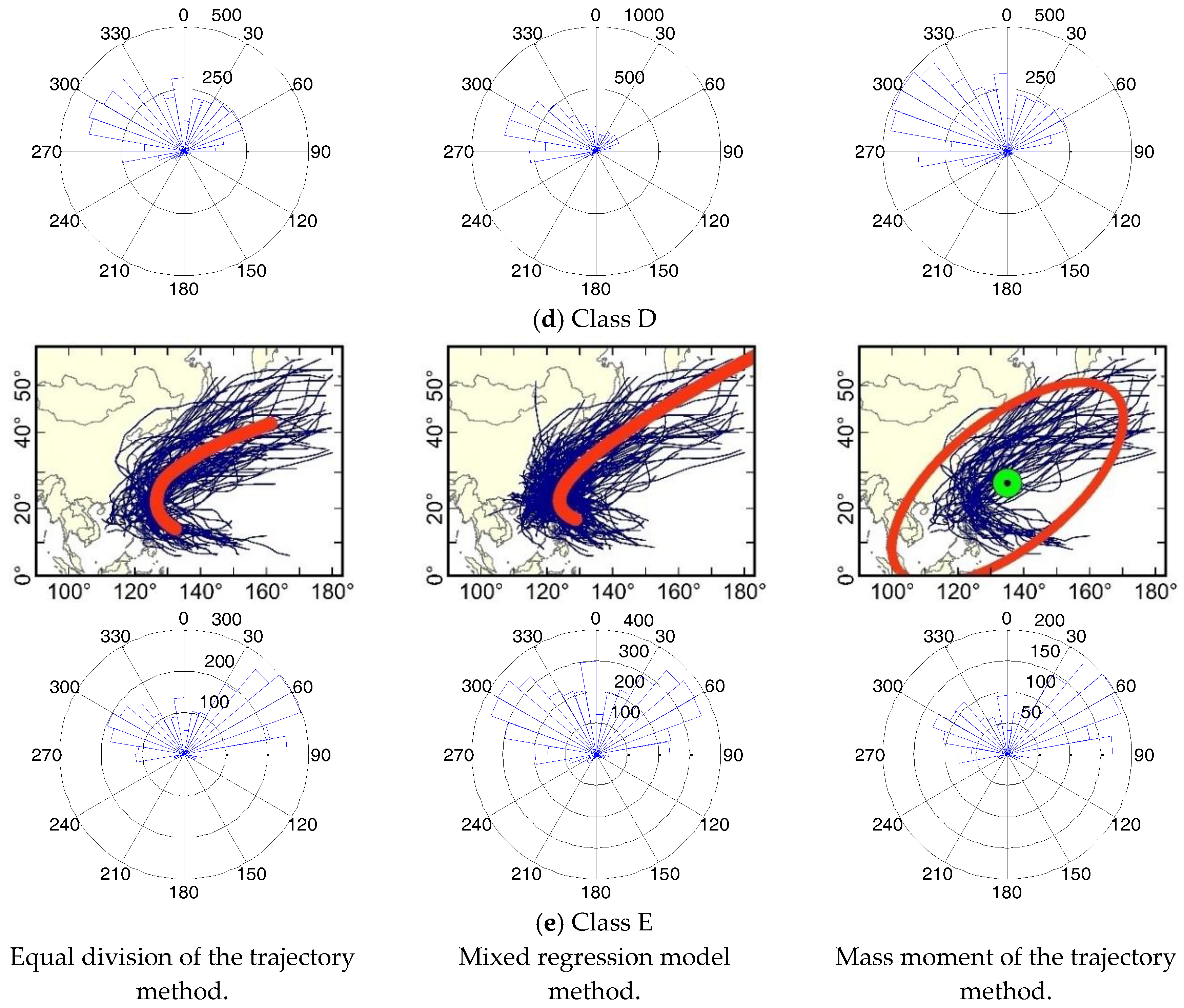
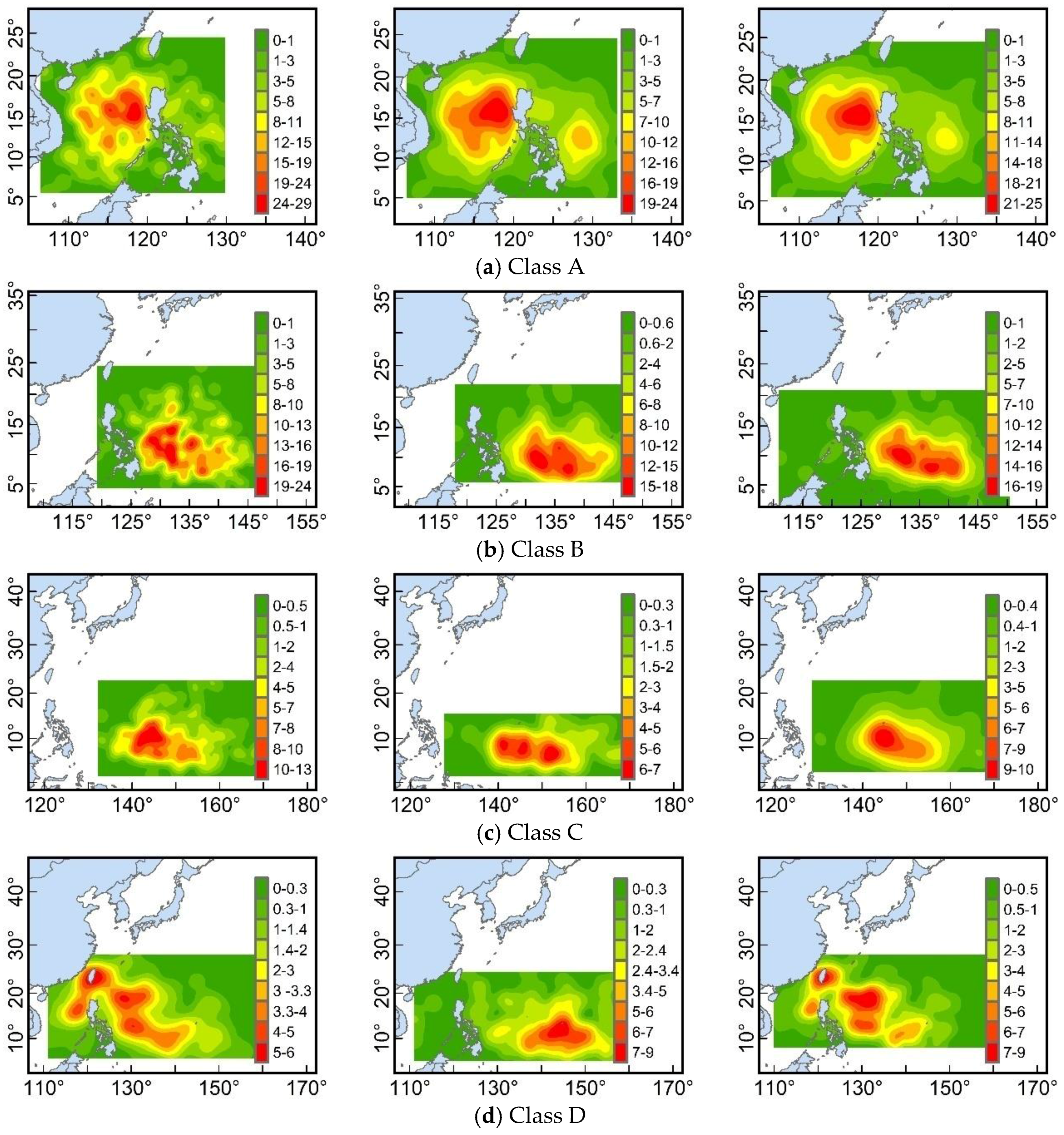
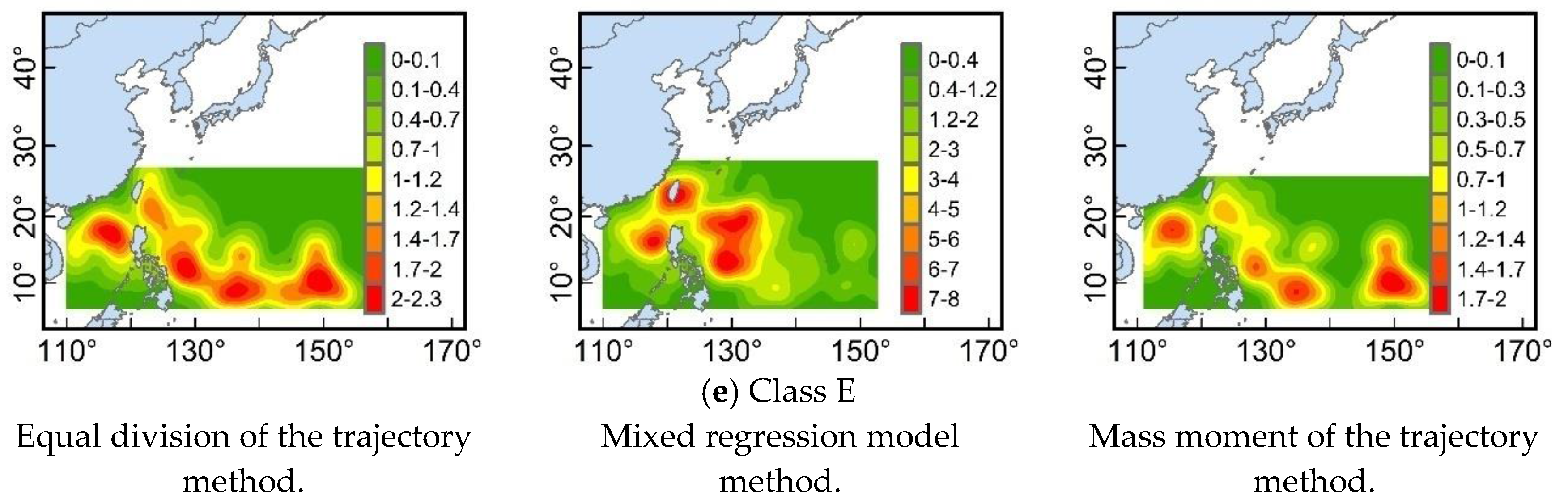
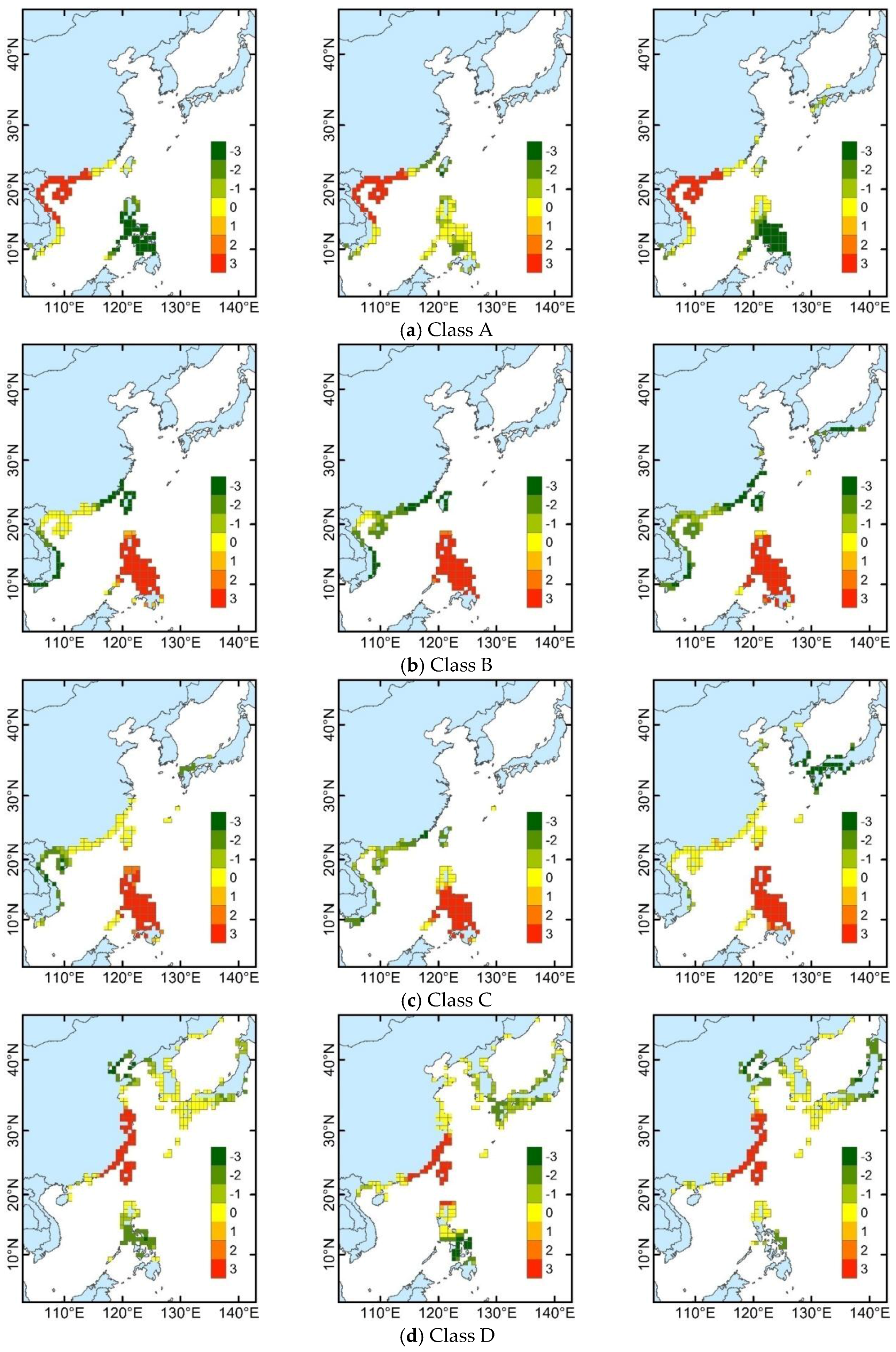
| TC Trajectory Class | Equal Division of the Trajectory Method | Mixed Regression Model Method | Mass Moment of the Trajectory Method | |||
|---|---|---|---|---|---|---|
| Average Length (km) | Standard Deviation (km) | Average Length (km) | Standard Deviation (km) | Average Length (km) | Standard Deviation (km) | |
| Class A | 1804.77 | 824.79 | 1939.48 | 900.28 | 2014.61 | 1007.87 |
| Class B | 3297.24 | 971.83 | 3429.85 | 966.40 | 3318.78 | 1066.28 |
| Class C | 4604.63 | 1297.13 | 5118.53 | 1275.13 | 5239.34 | 1416.27 |
| Class D | 4049.65 | 1846.76 | 5216.37 | 1945.33 | 3812.19 | 1529.89 |
| Class E | 7526.23 | 2210.65 | 4331.05 | 2545.40 | 8489.51 | 1930.25 |
| TC Trajectory Class | Equal Division of the Trajectory Method | Mixed Regression Model Method | Mass Moment of the Trajectory Method | |||
|---|---|---|---|---|---|---|
| Number of Trajectories in the Class | Percentage | Number of Trajectories in the Class | Percentage | Number of Trajectories in the Class | Percentage | |
| Class A | 227 | 24% | 260 | 27% | 261 | 28% |
| Class B | 266 | 28% | 208 | 22% | 243 | 26% |
| Class C | 203 | 21% | 119 | 13% | 186 | 20% |
| Class D | 166 | 18% | 163 | 17% | 204 | 21% |
| Class E | 84 | 9% | 196 | 21% | 52 | 5% |
| Overall | 946 | 100% | 946 | 100% | 946 | 100 |
| TC Trajectory Class | Equal Division of the Trajectory Method | Mixed Regression Model Method | Mass Moment of the Trajectory Method | |||
|---|---|---|---|---|---|---|
| Longitude | Latitude | Longitude | Latitude | Longitude | Latitude | |
| Class A | 117.38 | 14.914 | 118.99 | 14.47 | 118.90 | 14.72 |
| Class B | 134.01 | 11.81 | 135.94 | 10.79 | 135.09 | 10.28 |
| Class C | 148.93 | 9.78 | 150.84 | 7.87 | 150.04 | 9.62 |
| Class D | 130.67 | 16.06 | 142.38 | 12.43 | 130.66 | 17.00 |
| Class E | 132.75 | 13.75 | 127.75 | 17.05 | 132.96 | 13.89 |
| Clustering Method | Equal Division of the Trajectory Method | Mixed Regression Model Method | Mass Moment of the Trajectory Method |
|---|---|---|---|
| Type of method | Combination with the general clustering model after the transformation of the original trajectory | Cluster the original trajectory data based on the mathematical model | Combination with the general clustering model after the transformation of the original trajectory |
| Model complexity | Simple | Complicated | Relatively complicated |
| Information contained | Spatial location and shape information of the trajectory | Original complete trajectory information | Spatial location, shape information and some velocity information of the trajectory |
| Clustering results | Trajectory shape consistency is relatively good | Trajectory spatial consistency is relatively good | Essentially similar to the equal divide method |
| Class centre | Average trajectory in the class | Quadratic curve | Variance ellipse |
| Clustering Method | Equal Division of the Trajectory Method | Mixed Regression Model Method | Mass Moment of the Trajectory Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Maximum | Minimum | Mean | Maximum | Minimum | Mean | Maximum | Minimum | |
| Class A | 0.991 | 1.000 | 0.914 | 0.990 | 1.000 | 0.924 | 0.991 | 1.000 | 0.914 |
| Class B | 0.993 | 1.000 | 0.944 | 0.994 | 1.000 | 0.963 | 0.992 | 1.000 | 0.928 |
| Class C | 0.992 * | 1.000 | 0.950 | 0.991 * | 1.000 | 0.939 | 0.986 | 1.000 | 0.898 |
| Class D | 0.988 | 1.000 | 0.911 | 0.981 | 1.000 | 0.877 | 0.986 | 1.000 | 0.922 |
| Class E | 0.987 * | 1.000 | 0.940 | 0.982 | 1.000 | 0.885 | 0.987 * | 1.000 | 0.940 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Wu, G.; Du, Y.; Zhao, X. Trajectory Data Mining via Cluster Analyses for Tropical Cyclones That Affect the South China Sea. ISPRS Int. J. Geo-Inf. 2017, 6, 210. https://doi.org/10.3390/ijgi6070210
Yang F, Wu G, Du Y, Zhao X. Trajectory Data Mining via Cluster Analyses for Tropical Cyclones That Affect the South China Sea. ISPRS International Journal of Geo-Information. 2017; 6(7):210. https://doi.org/10.3390/ijgi6070210
Chicago/Turabian StyleYang, Feng, Guofeng Wu, Yunyan Du, and Xiangwei Zhao. 2017. "Trajectory Data Mining via Cluster Analyses for Tropical Cyclones That Affect the South China Sea" ISPRS International Journal of Geo-Information 6, no. 7: 210. https://doi.org/10.3390/ijgi6070210
APA StyleYang, F., Wu, G., Du, Y., & Zhao, X. (2017). Trajectory Data Mining via Cluster Analyses for Tropical Cyclones That Affect the South China Sea. ISPRS International Journal of Geo-Information, 6(7), 210. https://doi.org/10.3390/ijgi6070210






