Modified Neutral Models as Benchmarks to Evaluate the Dynamics of Land System (DLS) Model Performance
Abstract
:1. Introduction
2. Data and Methods
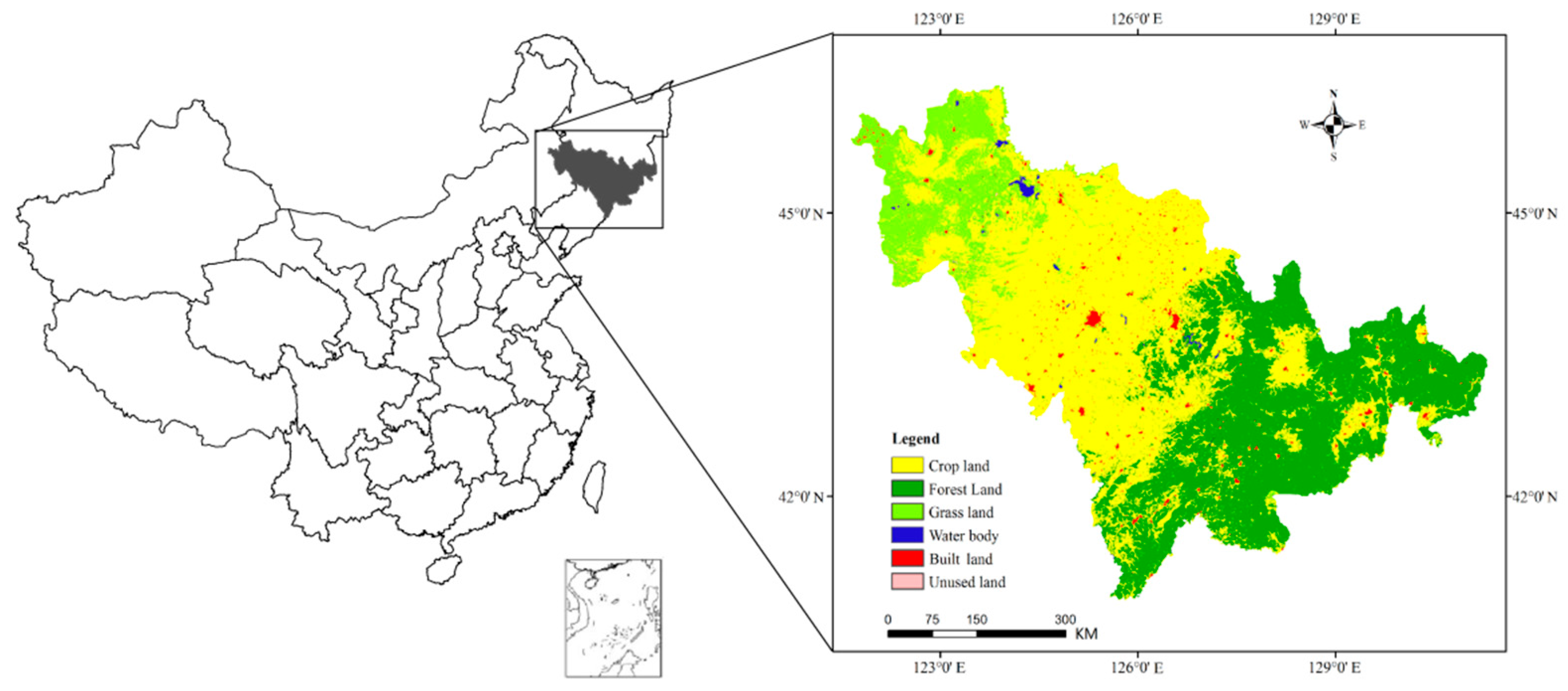
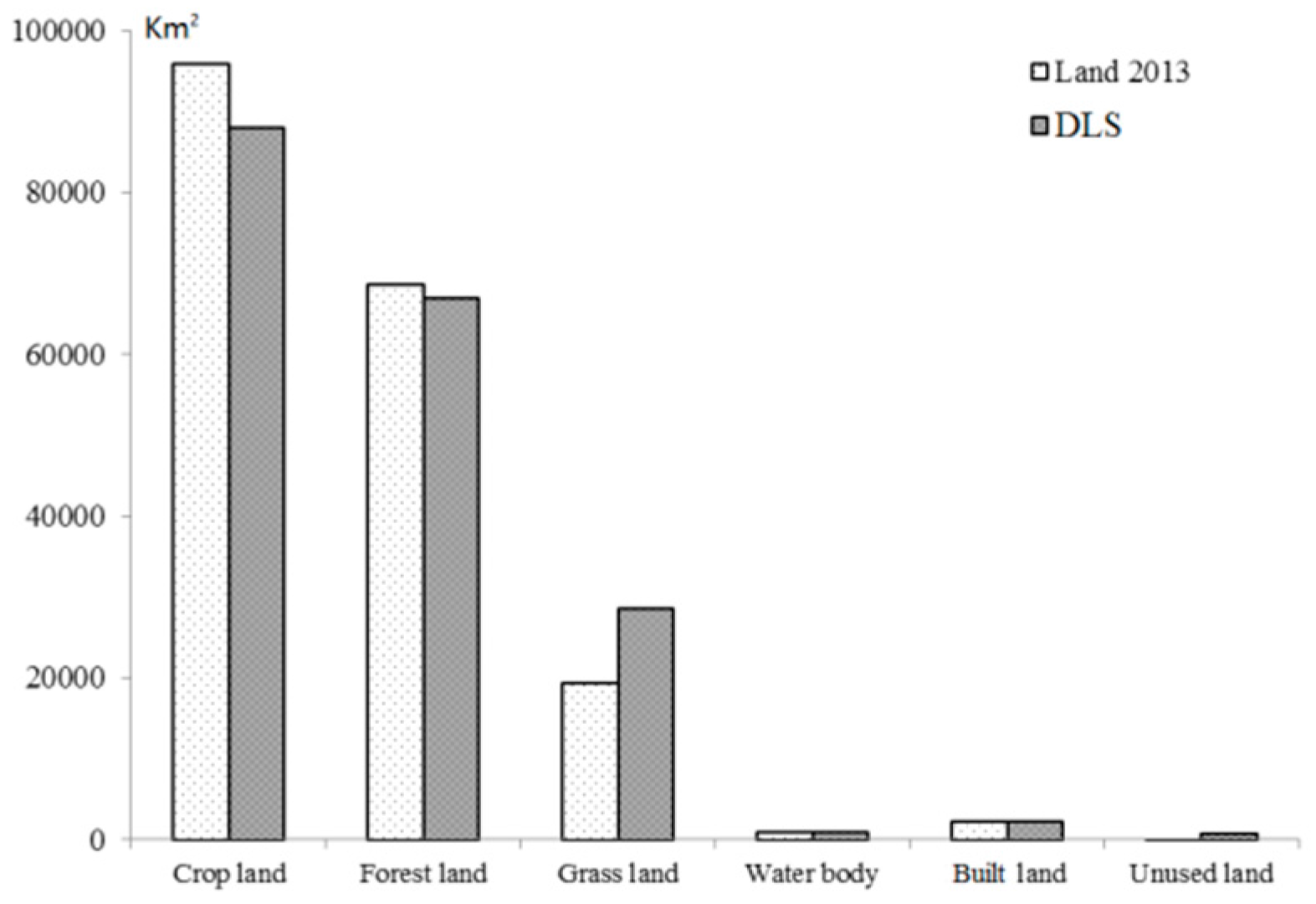
2.1. Study Area and Data Source
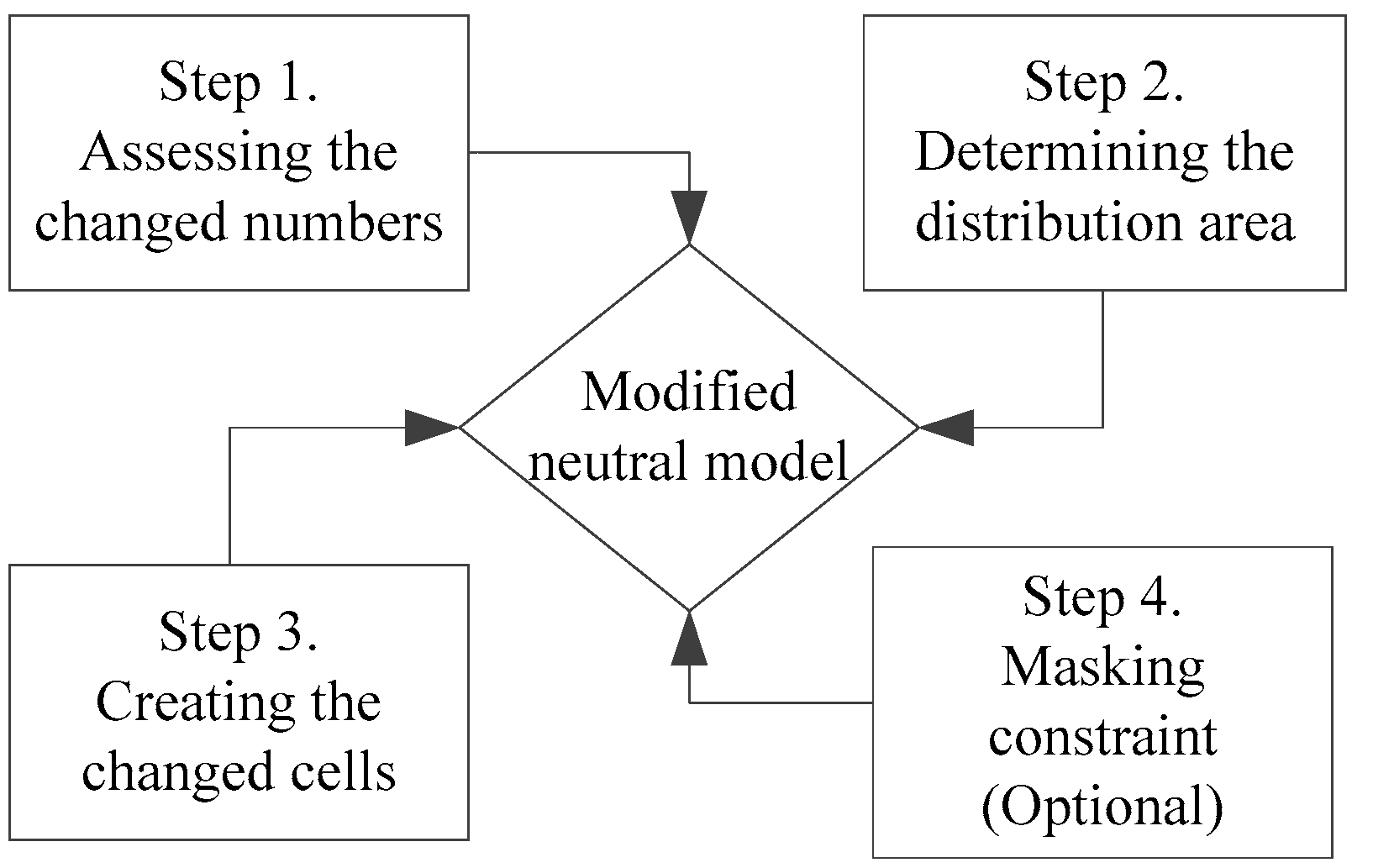
2.2. Modified Neutral Models
- Step 1: Assessing the number of changed cells.First, count the cells for all of the classes in the initial map and the final map. As one class may transform to two or more classes, based on the degree of transfer difficulty between the land use classes, we should determine the transfer probability between the different classes. Based on the probability, determine the number Nij of class i cells in the initial map that transform to class j.
- Step 2: Determining the distribution area of the changed cells.This step includes two sections. First, calculate the number of cells (Mj) that compose the distribution area using the following equation:where Nij is the number of class i cells in the initial map that transform to class j. p is the parameter that controls the degree of cell fragmentation and ranges from 0 to 1. Mi is the number of class i cells in the initial map.Mj = (Mi − Nij) × p + NijSecond, calculate the shortest distance between each cell in land class i and the patches of land class j using the neighborhood analysis tool in ArcMap 10.1 software. Place the shortest distances in ascending order, and select the top Mj cells. These selected cells compose the distribution area.
- Step 3: Creating the changed cells in the distribution area.Null neutral models are useful tools for testing the effect of a particular modeled process on observed patterns, as they create landscape patterns in the absence of those specifically processed from a blank initial map. However, they never account for the initial land use pattern. The generated landscape is not an appropriate reference map. The combination of null neutral modes and distribution area of the changed cells (generated in step 2) overcomes this shortcoming. In the distribution area, the null neutral model algorithm is applied to distribute allocations of the Nij changed cells. The algorithms of the null neutral models could include the simple random algorithm, mid-point displacement algorithm (MPD) [38], random rectangular cluster algorithm [39], modified random clusters algorithm [40], etc.In this case, the random algorithm and mid-point displacement algorithm are used to create the changed cells in the distribution area. The random algorithm is a simple and easily understood null neutral model. There is no spatial autocorrelation as each element in the array is independently assigned a value. It is usually used as a baseline for comparison. The mid-point displacement algorithm is a fractal algorithm in which the level of autocorrelation can be controlled from 0 to 1. It has been widely used in simulating landscape patterns and is integrated into standalone software such as RULE and the subsequent QRULE. When using the random algorithm, the changed cells are a series of randomly distributed cells in the distribution area. The mid-point displacement algorithm can only be applied to square arrays of specific sizes. Therefore, to enable a two dimensional array of any size to be created, we create an array that is larger than the distribution area extent, but is the minimum-sized square that will cover the desired extent, from which a slice of the required dimensions is then extracted. The two kinds of null neutral models are created by a PYTHON package of NLMpy [41]. The fragmentation degree parameter for the null neutral model algorithms is the same as parameter p in Equation (1).
- Step 4: Masking constraint (Optional).In land use models, a mask is sometimes applied to separate the changed and unchanged areas. This enables the land use model result to be subject to the same changing boundary conditions as the actual land use change. The modified neutral model is based on an existing initial land use map that minimizes change, and the masking constraint could also be applied if necessary.
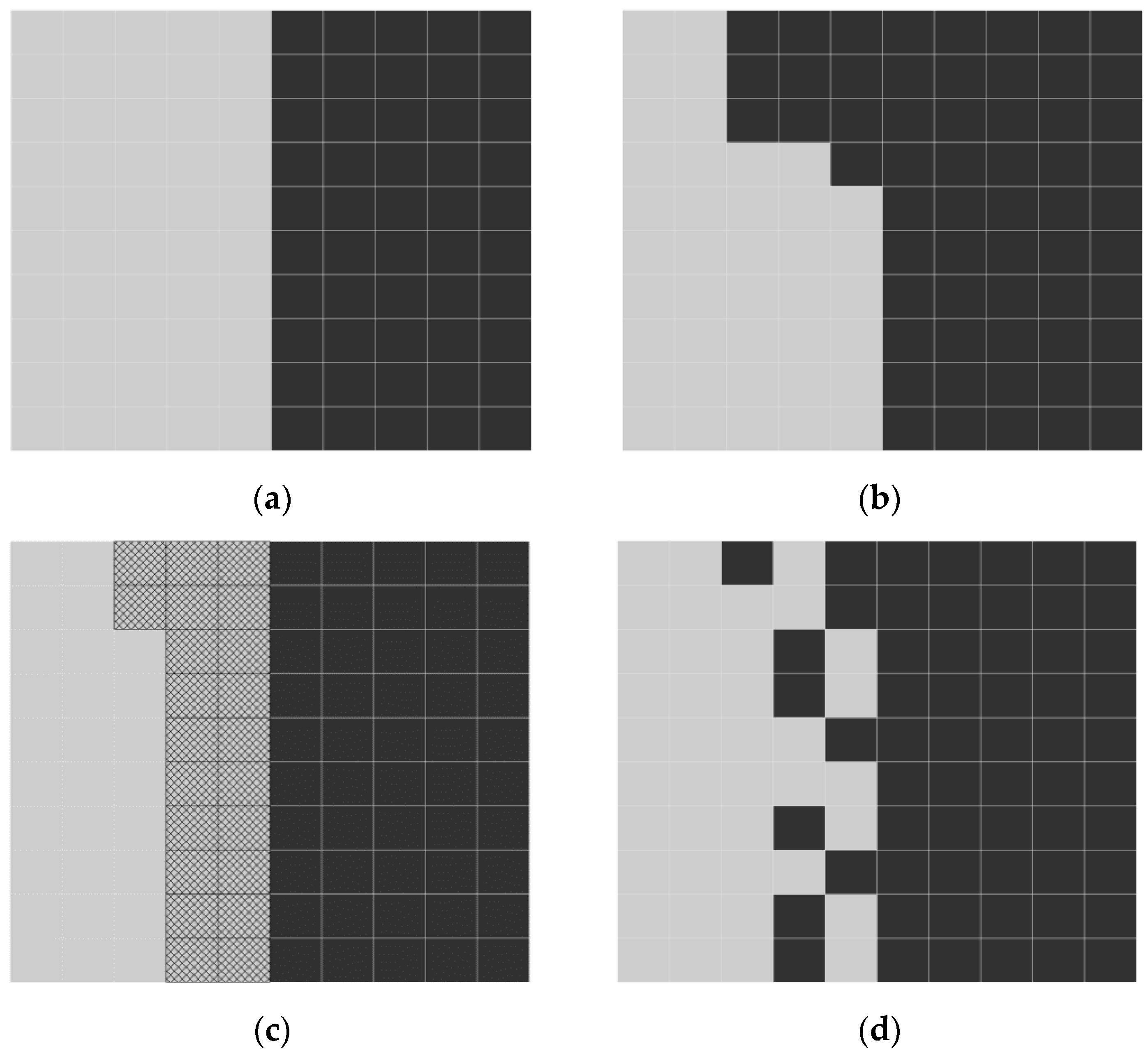
- Step 1: Assessing the number of changed cells.Class2 increased by 10 cells and class 1 decreased by 10 cells from T0 to T1.
- Step 2: Determining the distribution area.
- (1)
- Calculate the number of cells in the changed area.where 50 is the number of class 1 cells in the initial map, 10 is the number of class 1 cells in the initial map that transform to class 2, 0.3 is the parameter we set that controls the degree of cell fragmentation, and the result M = 22 is the number of cells in class 1 that compose the distribution area.M = (50 − 10) × 0.3 + 10 = 22
- (2)
- According to the shortest distance principle, select 22 cells in class 1 that are close to class 2. The selected cells compose the distribution area which is covered by the net in Figure 3c.
- Step 3: Creating the changed cells.When using the random algorithm, directly create 10 random cells in the distribution area. Then, convert these cells from class 1 to class 2 (Figure 3d). When using the mid-point displacement algorithm, the generation process is complex. First, the NLMPy produces a 10 × 10 array with a fragmentation degree parameter of 0.3 using the mid-point displacement algorithm, in which the elements of the array at each row and column position contain a value from 0 to 1. A 10 × 10 array is the minimum-sized square cover distribution area extent because the extent of netted cells is 10 × 3. Then, extract the required area from the produced patterns using the 22 netted cells as a mask. Following this, the ‘classify array’ function in NLMpy is employed to classify the 22 cells into two parts which consist of 10 cells and 12 cells, respectively. Finally, choose the 10 cells and converted them from class 1 to class 2, through which the changed cells are obtained.As we do not set the unchanged area, Step 4 is not performed. Figure 3d is the modified neutral model result based on the random algorithm for an aggregation of 0.3.
2.3. DLS Model
2.4. Metrics to Evaluate the Model
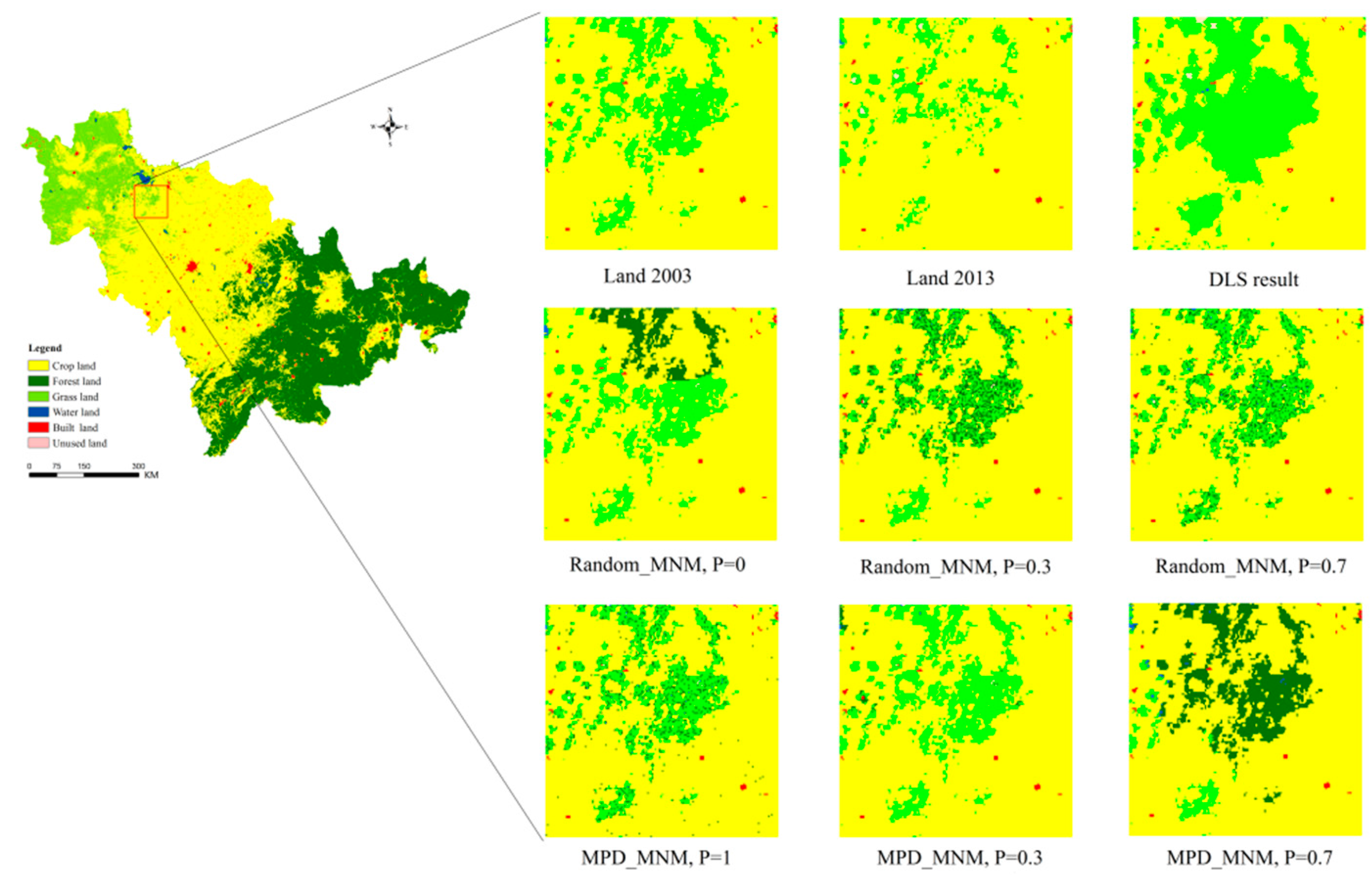
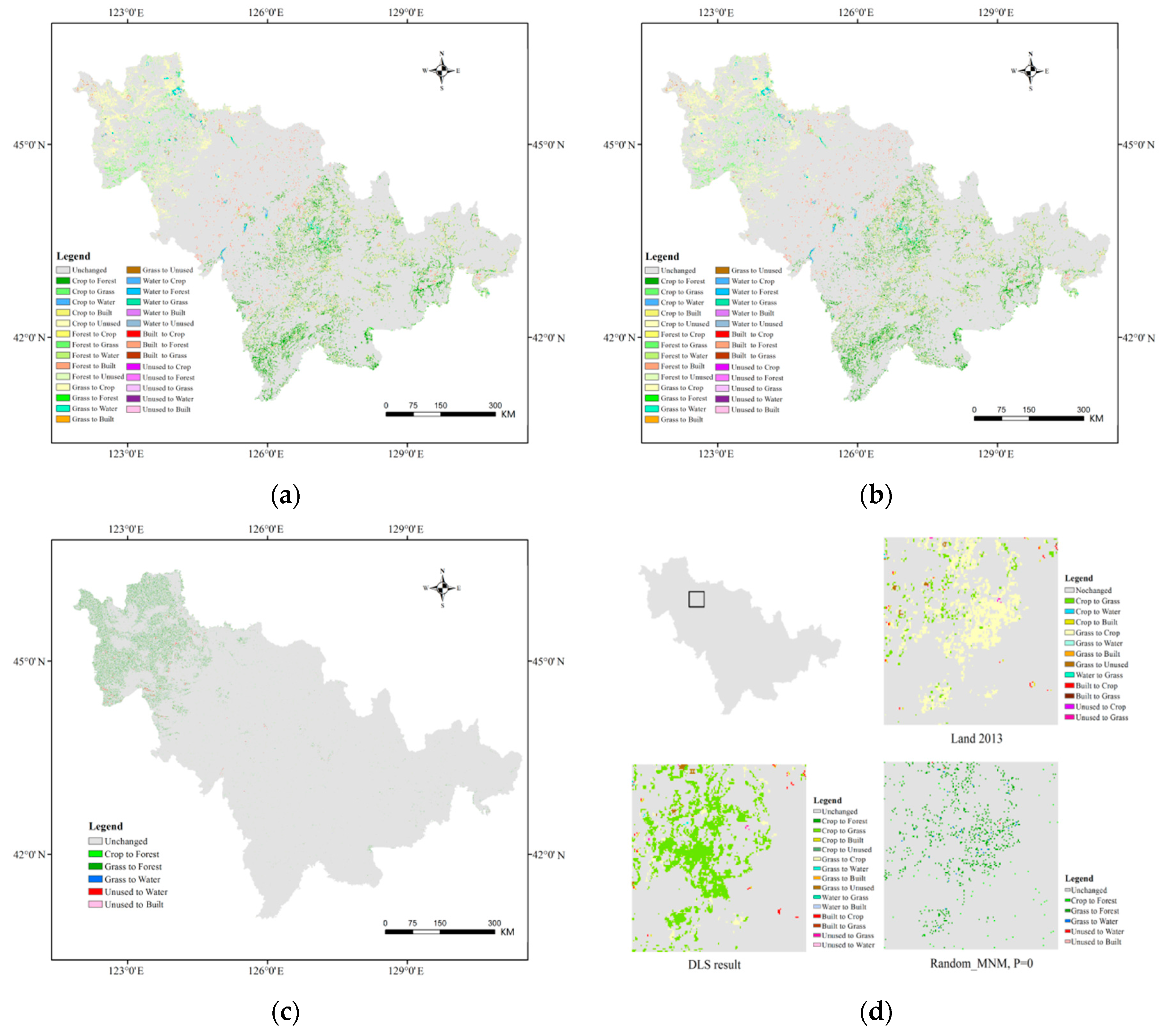
3. Results
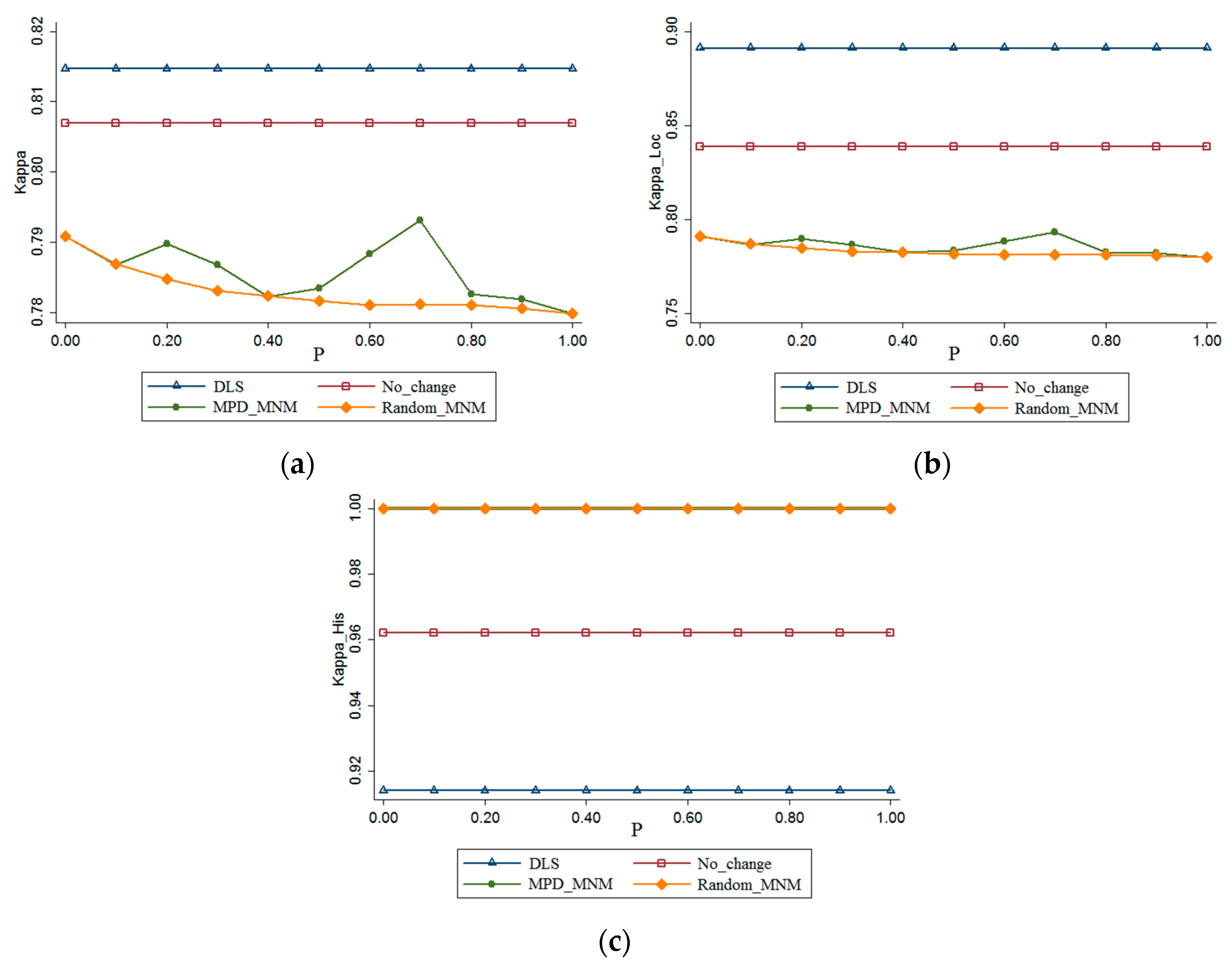
3.1. Kappa Result Comparison
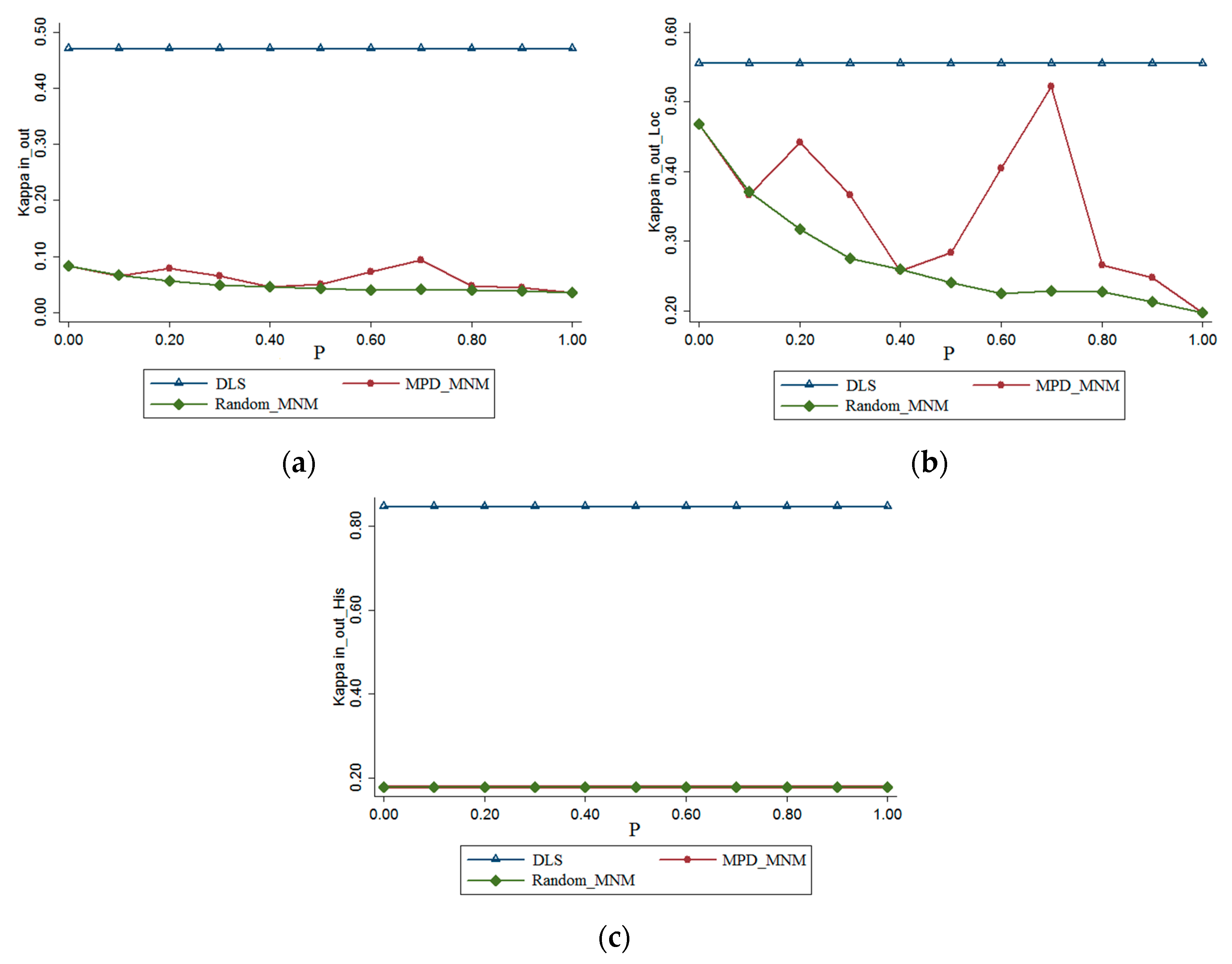
3.2. Kappain-out Result Comparison
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Turner, B.L.; Skole, D.L.; Sanderson, S.; Fischer, G.; Fresco, L.O.; Leemans, R. Land-Use and Land-Cover Change: Science/Research Plan; IGBP, 1995 (IGBP Report 35); International Geosphere-Biosphere Programme: Stockholm, Sweden, 1995; p. 132. [Google Scholar]
- Young, B.; Noone, K.; Steffen, W. Science Plan and Implementation Strategy; IGBP Report No. 53/IHDP Report No. 19; IGBP Secretariat, Global Land Project (GLP): Stockholm, Sweden, 2005; p. 64. [Google Scholar]
- Verburg, P.H.; Schot, P.P.; Dijst, M.J.; Veldkamp, A. Land use change modelling: Current practice and research priorities. GeoJournal 2004, 61, 309–324. [Google Scholar] [CrossRef]
- Ghaffarzadegan, N.; Lyneis, J.; Richardson, G.P. How small system dynamics models can help the public policy process. Syst. Dynam. Rev. 2011, 27, 22–44. [Google Scholar] [CrossRef]
- Rounsevell, M.D.A.; Pedroli, B.; Erb, K.H.; Gramberger, M.; Busck, A.G.; Haberl, H.; Kristensen, S.; Kuemmerle, T.; Lavorel, S.; Lindner, M.; et al. Challenges for land system science. Land Use Policy 2012, 29, 899–910. [Google Scholar] [CrossRef]
- Reidsma, P.; König, H.; Feng, S.; Bezlepkina, I.; Nesheim, I.; Bonin, M.; Sghaier, M.; Purushothaman, S.; Sieber, S.; van Ittersum, M.K.; et al. Methods and tools for integrated assessment of land use policies on sustainable development in developing countries. Land Use Policy. 2011, 28, 604–617. [Google Scholar] [CrossRef]
- Veldkamp, T.; Verburg, P.H.; Kok, K.; Koning, F.D.; Soepboer, W. Spatial Explicit Land Use Change Scenarios for Policy Purposes: Some Applications of the CLUE Framework. In Linking People, Place, and Policy; Walsh, S.J., Crews-Meyer, K.A., Eds.; Springer US: New York, NY, USA, 2002; pp. 317–341. [Google Scholar]
- Yang, X.; Zheng, X.; Lv, L. A spatiotemporal model of land use change based on ant colony optimization, Markov chain and cellular automata. Ecol. Model. 2012, 233, 11–19. [Google Scholar] [CrossRef]
- Verburg, P.H.; Overmars, K.P. Combining top-down and bottom-up dynamics in land use modeling: Exploring the future of abandoned farmlands in Europe with the Dyna-CLUE model. Landsc. Ecol. 2009, 24, 1167. [Google Scholar] [CrossRef]
- Chaudhuri, G.; Clarke, K. The SLEUTH land use change model: A review. Environ. Resour. Res. 2013, 1, 88–105. [Google Scholar] [CrossRef]
- Parker, D.C.; Manson, S.M.; Janssen, M.A.; Hoffmann, M.J.; Deadman, P. Multi-agent systems for the simulation of land-use and land-cover change: A review. Ann. Assoc. Am. Geogr. 2003, 93, 314–337. [Google Scholar] [CrossRef]
- Evans, T.P.; Kelley, H. Multi-scale analysis of a household level agent-based model of landcover change. J. Environ. Manag. 2004, 72, 57. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Lin, Y.; Huang, H. Simulation of land system dynamics: A review. Chin. J. Eco-Agric. 2009, 28, 2123–2129. [Google Scholar] [CrossRef]
- Dang, A.N.; Kawasaki, A. A review of methodological integration in land-use change models. Int. J. Agric. Environ. Inf. Syst. 2016, 7, 1–25. [Google Scholar] [CrossRef]
- Deng, X. Modeling the Dynamics and Consequences of Land System Change; Springer: Heidelberg/Berlin, Germany, 2011; pp. 129–157. [Google Scholar]
- Ge, Q.; Dai, J. Farming and forestry land use changes in China and their driving forces from 1900 to 1980. Sci. China Ser. D (Earth Sci China) 2005, 48, 1747–1757. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, Q.; Zhan, J.; He, S.; Lin, Y. Simulation on the dynamics of forest area changes in Northeast China. J. Geogr. Sci. 2010, 20, 496–509. [Google Scholar] [CrossRef]
- Wu, J.; Feng, Z.; Gao, Y.; Peng, J. Research on ecological effects of urban land policy based on DLS model: A case study on Shenzhen City. Acta Geogr. Sin. 2014, 69, 1673–1682. [Google Scholar]
- Jiang, Q.; Tan, B.; Xue, X.; Qi, J.; Deng, X. Quantitive modeling changes in area of reclamation and returning cultivated land to forest or pastures under representative concentration pathways (RCPs) climate scenarios. Trans. Chin. Soc. Agric. Eng. 2015, 31, 271–280. [Google Scholar] [CrossRef]
- Pontius, R.G.; Schneider, L.C. Land-cover change model validation by an ROC method for the Ipswich watershed, Massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar] [CrossRef]
- Brown, D.G.; Page, S.; Riolo, R.; Zellner, M.; Rand, W. Path dependence and the validation of agent-based spatial models of land use. Int. J. Geogr. Inf. Sci. 2005, 19, 153–174. [Google Scholar] [CrossRef]
- Couto, P. Assessing the accuracy of spatial simulation models. Ecol. Model. 2003, 167, 181–198. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Wilkinson, G.G. Results and implications of a study of fifteen years of satellite image classification experiments. IEEE Trans. Geosci. Remote Sens. 2005, 43, 433–440. [Google Scholar] [CrossRef]
- Pontius, R.G.; Shusas, E.; McEachern, M. Detecting important categorical land changes while accounting for persistence. Agric. Ecosyst. Environ. 2004, 101, 251–268. [Google Scholar] [CrossRef]
- Rutherford, G.N.; Bebi, P.; Edwards, P.J.; Zimmermann, N.E. Assessing land-use statistics to model land cover change in a mountainous landscape in the European Alps. Ecol. Model. 2008, 212, 460–471. [Google Scholar] [CrossRef]
- Riitters, K.H.; Wickham, J.D.; Wade, T.G. An indicator of forest dynamics using a shifting landscape mosaic. Ecol. Indic. 2009, 9, 107–117. [Google Scholar] [CrossRef]
- Pontius, G.R.; Malanson, J. Comparison of the structure and accuracy of two land change models. Int. J. Geogr. Inf. Sci. 2005, 19, 243–265. [Google Scholar] [CrossRef]
- Pontius, R.G.; Boersma, W.; Castella, J.C.; Clarke, K.; Nijs, T.D.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Brown, D.G.; Verburg, P.H.; Pontius, R.G., Jr.; Lange, M.D. Opportunities to improve impact, integration, and evaluation of land change models. Curr. Opin. Environ. Sustain. 2013, 5, 452–457. [Google Scholar] [CrossRef]
- Hagen-Zanker, A.; Lajoie, G. Neutral models of landscape change as benchmarks in the assessment of model performance. Landsc. Urban Plan. 2008, 86, 284–296. [Google Scholar] [CrossRef]
- With, K.A.; King, A.W. The use and misuse of neutral landscape models in ecology. Oikos 1997, 79, 219–229. [Google Scholar] [CrossRef]
- Gardner, R.H.; Urban, D.L. Neutral models for testing landscape hypotheses. Landsc. Ecol. 2007, 22, 15–29. [Google Scholar] [CrossRef]
- Wu, H.; Li, Y.; Li, N. Neutral landscape models in landscape ecology: Application and development. Chin. J. Ecol. 2012, 31, 3241–3246. [Google Scholar] [CrossRef]
- Gardner, R.H.; Milne, B.T.; Turnei, M.G.; O’Neill, R.V. Neutral models for the analysis of broad-scale landscape pattern. Landsc. Ecol. 1987, 1, 19–28. [Google Scholar] [CrossRef]
- Wu, W.; Yeager, K.M.; Peterson, M.S.; Fulford, R.S. Neutral models as a way to evaluate the Sea Level Affecting Marshes Model (SLAMM). Ecol. Model. 2015, 303, 55–69. [Google Scholar] [CrossRef]
- Palmer, M.W. The Coexistence of Species in Fractal Landscapes. Am. Nat. 1992, 139, 375–397. [Google Scholar] [CrossRef]
- Gustafson, E.J.; Parker, G.R. Relationships between landcover proportion and indices of landscape spatial pattern. Landsc. Ecol. 1992, 7, 101–110. [Google Scholar] [CrossRef]
- Saura, S.; Martínezmillán, J. Landscape patterns simulation with a modified random clusters method. Landsc. Ecol. 2000, 15, 661–678. [Google Scholar] [CrossRef]
- Etherington, T.R.; Holland, E.P.; O’Sullivan, D. Nlmpy: A python software package for the creation of neutral landscape models within a general numerical framework. Methods Ecol. Evol. 2015, 6, 164–168. [Google Scholar] [CrossRef]
- Xiu, Y.; Zhao, M.; Li, H. Simulation analysis of mid-point displacement neutral landscape model to different theme landscape. Geo. Spat. Inf. 2017, 40, 28–31. [Google Scholar]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]

| Crop Land | Forest Land | Grass Land | Water Body | Built Land | Unused Land | |
|---|---|---|---|---|---|---|
| Transition probabilities | 0.8 | 0.8 | 0.9 | 0.1 | 0.4 | 0.7 |
| T0→T1 | T0→Simulated Map | ||||||
| 0 | 1→2 | 1→3 | … | n − 1→n | Total T0 | ||
| 0 | p{0^ 0} | p{0^ (1→2)} | p{0^ (1→3)} | p{0^ (1→n)} | p{0} | ||
| 1→2 | p{(1→2)^ 0} | p{(1→2)^ (1→2)} | p{(1→2)^ (1→3)} | … | p{(1→2)^ (n − 1→n)} | p{(1→2)} | |
| 1→3 | p{(1→3)^ 0} | p{(1→3)^ (1→2)} | p{(1→3)^ (1→3)} | … | p{(1→3)^ (n − 1→n)} | p{(1→3)} | |
| … | … | … | … | … | … | … | |
| n − 1→n | p{(n − 1→n)^ 0} | p{(n − 1→n)^ (1→2)} | p{(n − 1→n)^ (1→3)} | p{ (n − 1→n)^ (n − 1→n)} | p{ (n − 1→n)} | ||
| Total T1 | p{0} | p{(1→2)} | p{(1→3)} | … | p{(n − 1→n)} | 1 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiu, Y.; Liu, W.; Yang, W. Modified Neutral Models as Benchmarks to Evaluate the Dynamics of Land System (DLS) Model Performance. ISPRS Int. J. Geo-Inf. 2017, 6, 199. https://doi.org/10.3390/ijgi6070199
Xiu Y, Liu W, Yang W. Modified Neutral Models as Benchmarks to Evaluate the Dynamics of Land System (DLS) Model Performance. ISPRS International Journal of Geo-Information. 2017; 6(7):199. https://doi.org/10.3390/ijgi6070199
Chicago/Turabian StyleXiu, Yingchang, Wenbao Liu, and Wenjing Yang. 2017. "Modified Neutral Models as Benchmarks to Evaluate the Dynamics of Land System (DLS) Model Performance" ISPRS International Journal of Geo-Information 6, no. 7: 199. https://doi.org/10.3390/ijgi6070199
APA StyleXiu, Y., Liu, W., & Yang, W. (2017). Modified Neutral Models as Benchmarks to Evaluate the Dynamics of Land System (DLS) Model Performance. ISPRS International Journal of Geo-Information, 6(7), 199. https://doi.org/10.3390/ijgi6070199





