Multi-Feature Joint Sparse Model for the Classification of Mangrove Remote Sensing Images
Abstract
:1. Introduction
2. Sparse Representation Classification
3. Multi-Feature Joint Sparse Model for Classification
3.1. Feature Selection
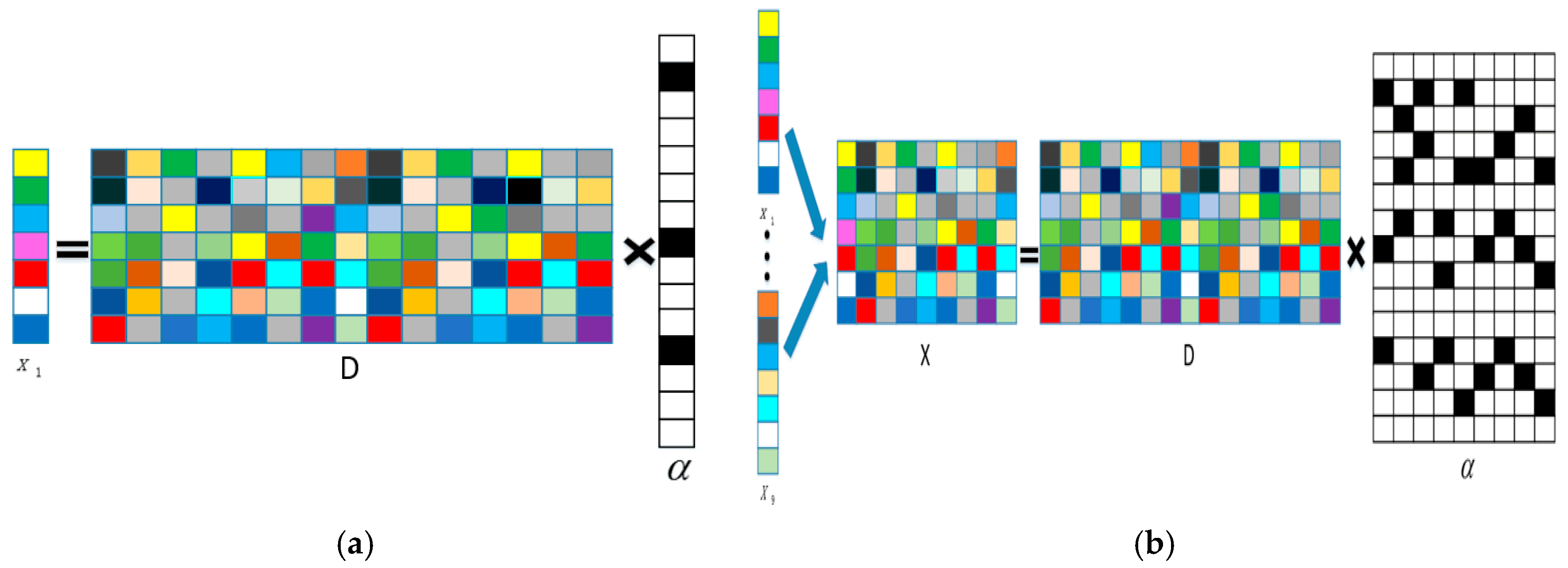
3.2. Joint Sparse Model Classification
3.3. The Procedure of the Multi-Feature Joint Sparse Model
| Algorithm 1: MF-SRU |
| Input: the set of labeled pixels , number of classes N, sparsity level L, the sub-dictionary size K, and the number of iterations to train each class sample T0. Output: matrix, which records the labels of the all pixels. (1) Use K-SVD algorithm to learn the dictionary For each pixel in the mangrove remote sensing image: (2) Construct the joint pixel , where is the target pixel at the center of the eight-pixel neighborhood; (3) Use the SOMP algorithm to obtain the sparsity representation coefficients of pixel by Equation (8); (4) Compare the reconstructed residual to classify the labels by Equation (9); (5) Continue to the next test pixel; End For |
4. Experimental Results and Analysis
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Rahman, M.M.; Ullah, M.R.; Lan, M.; Sumantyo, J.T.; Kuze, H.; Tateishi, R. Comparison of landsat image classification methods for detecting mangrove forests in sundarbans. Int. J. Remote Sens. 2013, 34, 1041–1056. [Google Scholar] [CrossRef]
- Zhao, C.; Qian, L. Comparison of remote sensing image supervision classification and unsupervised classification. J. Henan Univ. Nat. Sci. 2004, 34, 90–93. [Google Scholar]
- Gotsis, P.K.; Chamis, C.C.; Minnetyan, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar]
- Sisodia, P.S.; Tiwari, V.; Kumar, A. Analysis of Supervised Maximum Likelihood Classification for remote sensing image. In Proceedings of the IEEE Recent Advances and Innovations in Engineering, Jaipur, India, 9–11 May 2014; pp. 1–4. [Google Scholar]
- Darwish, A.; Leukert, K.; Reinhardt, W. Image Segmentation for the Purpose of Object-Based Classification. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS’03), Toulouse, France, 21–25 July 2003; pp. 2039–2041. [Google Scholar]
- Heumann, B.W. An object-based classification of mangroves using a hybrid decision tree—Support vector machine approach. Remote Sens. 2011, 3, 2440–2460. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.; Ye, M.; Zhou, J. Hyperspectral image classification based on structured sparse logistic regression and three-dimensional wavelet texture features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2276–2291. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Mei, X.; Ma, J. Hyperspectral image classification with robust sparse representation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 641–645. [Google Scholar] [CrossRef]
- Yokoya, N.; Iwasaki, A. Object detection based on sparse representation and hough voting for optical remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2053–2062. [Google Scholar] [CrossRef]
- Zhang, E.; Zhang, X.; Liu, H.; Jiao, L. Fast multifeature joint sparse representation for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1397–1401. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Xue, J.H. Joint sparse model-based discriminative K-SVD for hyperspectral image classification. Signal Process. 2016, 133, 144–155. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tropp, J.; Gilbert, A. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C.; Strauss, M.J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Process 2006, 86, 572–588. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Shi, X.; Wang, S. Monitoring mangrove forest changes using remote sensing and GIS data with decision-tree learning. Wetlands 2008, 28, 336–346. [Google Scholar] [CrossRef]
- Liao, B.W.; Zhang, Q.M. Area, Distribution and Species Composition of Mangroves in China. Wetl. Sci. 2014, 12, 435–440. [Google Scholar]
- Adame, M.F.; Neil, D.; Wright, S.F.; Lovelock, C.E. Sedimentation within and among mangrove forests along a gradient of geomorphological settings. Estuar. Coast. Shelf Sci. 2010, 86, 21–30. [Google Scholar] [CrossRef]
- Deering, D.W. Rangeland Reflectance Characteristics Measured by Aircraft and Spacecraft Sensors; Texas A & M University: College Station, TX, USA, 1978. [Google Scholar]
- Soh, L.-K.; Tsatsoulis, C. Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices. IEEE Trans. Geosci. Remote Sens. 1999, 37, 780–795. [Google Scholar] [CrossRef]
- Tetuko, J. Analysis of co-occurrence and discrete wavelet transform textures for differentiation of forest and non-forest vegetation in very-high-resolution optical-sensor imagery. Int. J. Remote Sens. 2008, 29, 3417–3456. [Google Scholar]
- Soltani-Farani, A.; Rabiee, H. When pixels team up: Spatially weighted sparse coding for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 107–111. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
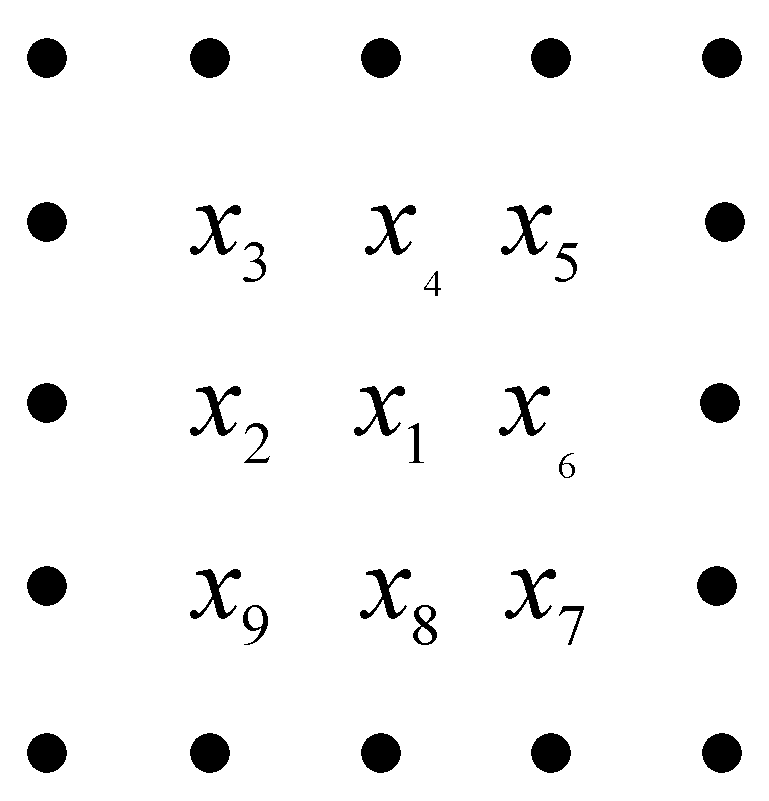

| Class Name | Land-Cover Class | Description |
|---|---|---|
| C1 | Mangroves | Mangrove forests |
| C2 | Upland vegetation | Deciduous or evergreen forest land, orchards, and tree groves |
| C3 | Urban areas | Residential, commercial, industrial and other developed land |
| C4 | Water | Permanent open water, lakes reservoirs, bays, and estuaries |
| C5 | Littoral zone | Land in the intertidal zone or the transitional zone |
| C6 | Fallow land | Fields no longer under cultivation |
| C7 | Agricultural land | Crop fields, paddy fields, and grasslands |
| Class | SRU | MF-SVM | MF-SRU | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | Total | C1 | C2 | C3 | C4 | C5 | C6 | C7 | Total | C1 | C2 | C3 | C4 | C5 | C6 | C7 | Total | |
| C1 | 180 | 20 | 0 | 0 | 0 | 0 | 19 | 219 | 182 | 0 | 0 | 0 | 0 | 0 | 63 | 245 | 183 | 0 | 0 | 0 | 0 | 0 | 36 | 219 |
| C2 | 5 | 102 | 0 | 0 | 0 | 5 | 41 | 153 | 0 | 194 | 0 | 0 | 0 | 31 | 0 | 225 | 2 | 192 | 0 | 8 | 0 | 30 | 0 | 232 |
| C3 | 0 | 12 | 192 | 0 | 0 | 14 | 0 | 218 | 0 | 0 | 170 | 0 | 0 | 15 | 0 | 185 | 0 | 0 | 192 | 0 | 0 | 9 | 0 | 201 |
| C4 | 0 | 0 | 0 | 198 | 5 | 0 | 0 | 203 | 0 | 0 | 0 | 200 | 3 | 0 | 0 | 203 | 0 | 0 | 0 | 192 | 5 | 0 | 31 | 228 |
| C5 | 1 | 0 | 0 | 2 | 195 | 0 | 25 | 223 | 0 | 0 | 0 | 0 | 197 | 0 | 2 | 199 | 0 | 0 | 0 | 0 | 195 | 0 | 1 | 196 |
| C6 | 0 | 2 | 8 | 0 | 0 | 140 | 0 | 150 | 0 | 6 | 28 | 0 | 0 | 154 | 0 | 188 | 0 | 8 | 8 | 0 | 0 | 161 | 0 | 177 |
| C7 | 14 | 64 | 0 | 0 | 0 | 41 | 115 | 234 | 18 | 0 | 2 | 0 | 0 | 0 | 135 | 155 | 15 | 0 | 0 | 0 | 0 | 0 | 132 | 147 |
| Total | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 1400 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 1400 | 200 | 200 | 200 | 200 | 200 | 200 | 200 | 1400 |
| SRU | MF-SVM | MF-SRU | |
|---|---|---|---|
| Overall/% | 80.1 | 88.0 | 89.1 |
| Kappa | 0.768 | 0.860 | 0.873 |
| SRU | MF-SVM | MF-SRU | ||||
|---|---|---|---|---|---|---|
| Class | Com/% | Omi/% | Com/% | Omi/% | Com/% | Omi/% |
| C1 | 19.5 | 10.0 | 31.5 | 9.0 | 18.0 | 8.5 |
| C2 | 25.5 | 49.0 | 15.5 | 3.0 | 20.0 | 4.0 |
| C3 | 13.0 | 4.0 | 7.5 | 15.0 | 4.5 | 4.0 |
| C4 | 2.5 | 1.0 | 1.5 | 0.0 | 18.0 | 4.0 |
| C5 | 14.0 | 2.5 | 1.0 | 1.5 | 0.5 | 2.5 |
| C6 | 5.0 | 30.0 | 17.0 | 23.0 | 8.0 | 19.5 |
| C7 | 59.5 | 42.5 | 10.0 | 32.5 | 7.5 | 34.0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.-M.; Ouyang, Y.; Zhang, R.-C.; Feng, H.-M. Multi-Feature Joint Sparse Model for the Classification of Mangrove Remote Sensing Images. ISPRS Int. J. Geo-Inf. 2017, 6, 177. https://doi.org/10.3390/ijgi6060177
Luo Y-M, Ouyang Y, Zhang R-C, Feng H-M. Multi-Feature Joint Sparse Model for the Classification of Mangrove Remote Sensing Images. ISPRS International Journal of Geo-Information. 2017; 6(6):177. https://doi.org/10.3390/ijgi6060177
Chicago/Turabian StyleLuo, Yan-Min, Yi Ouyang, Ren-Cheng Zhang, and Hsuan-Ming Feng. 2017. "Multi-Feature Joint Sparse Model for the Classification of Mangrove Remote Sensing Images" ISPRS International Journal of Geo-Information 6, no. 6: 177. https://doi.org/10.3390/ijgi6060177
APA StyleLuo, Y.-M., Ouyang, Y., Zhang, R.-C., & Feng, H.-M. (2017). Multi-Feature Joint Sparse Model for the Classification of Mangrove Remote Sensing Images. ISPRS International Journal of Geo-Information, 6(6), 177. https://doi.org/10.3390/ijgi6060177






