A Map Spectrum-Based Spatiotemporal Clustering Method for GDP Variation Pattern Analysis Using Nighttime Light Images of the Wuhan Urban Agglomeration
Abstract
:1. Introduction
2. Study Area and Data
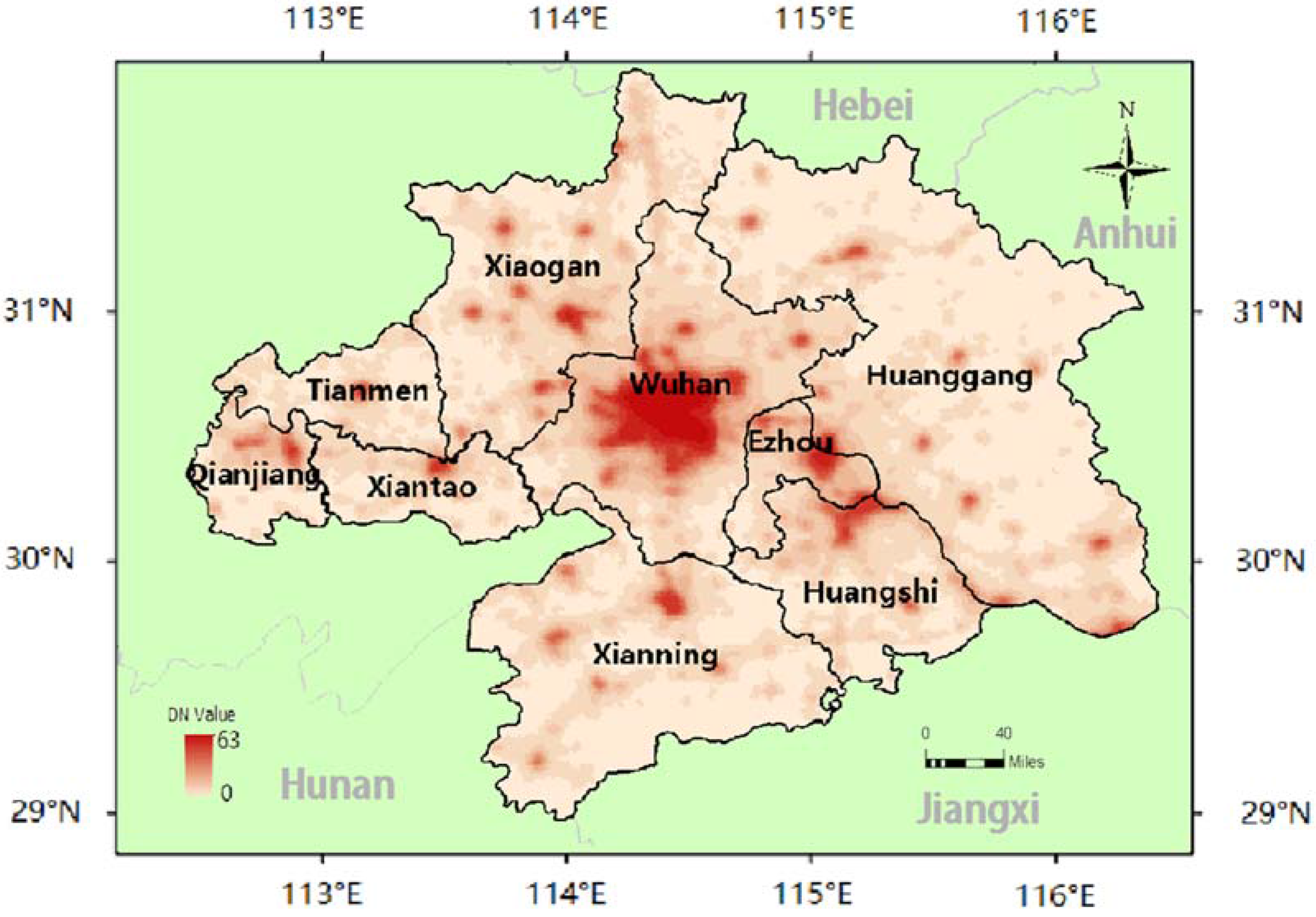
3. Dasymetric GDP Map Using Nighttime Light Images
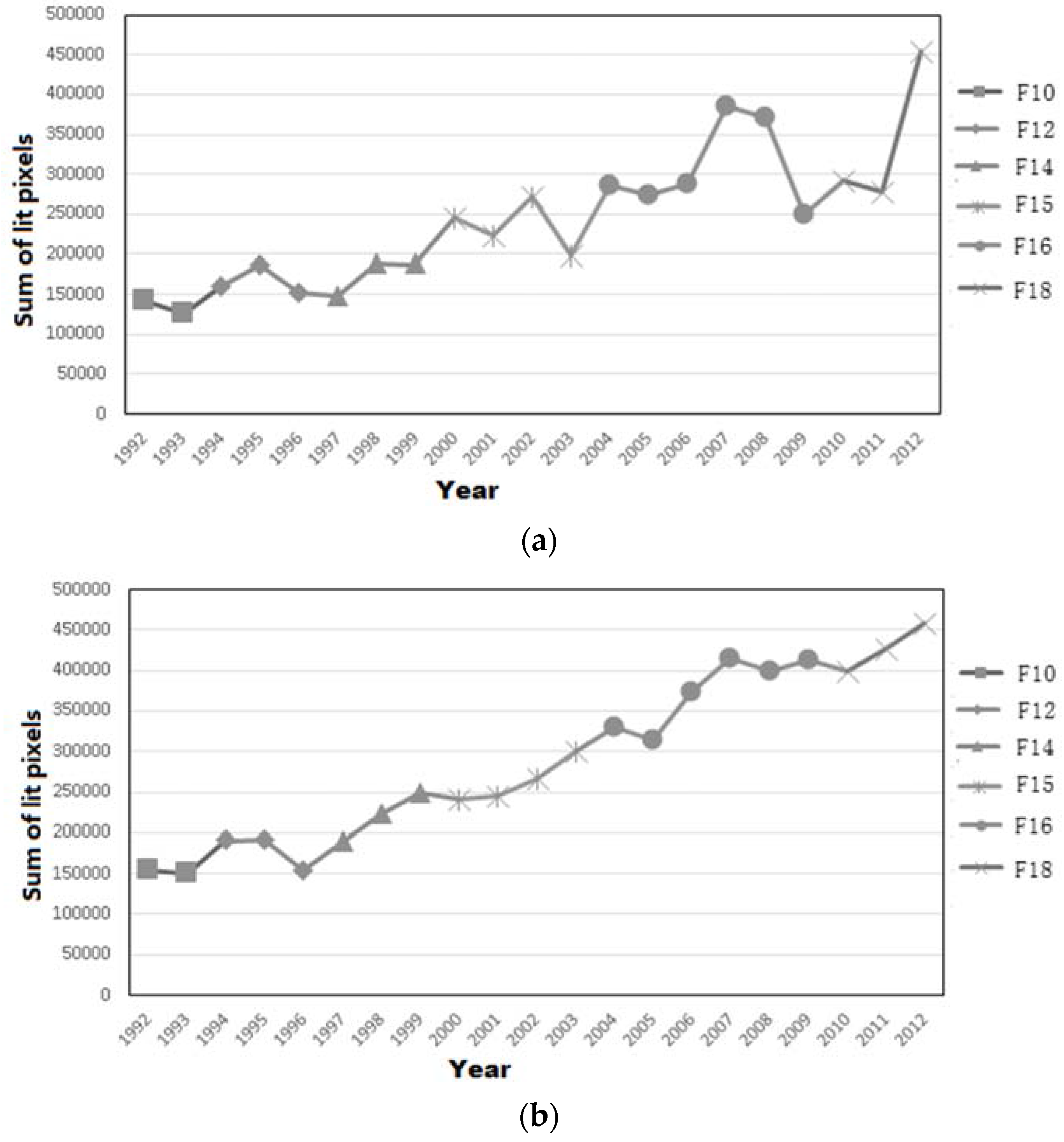
3.1. DMSP-OLS Data Preprocessing
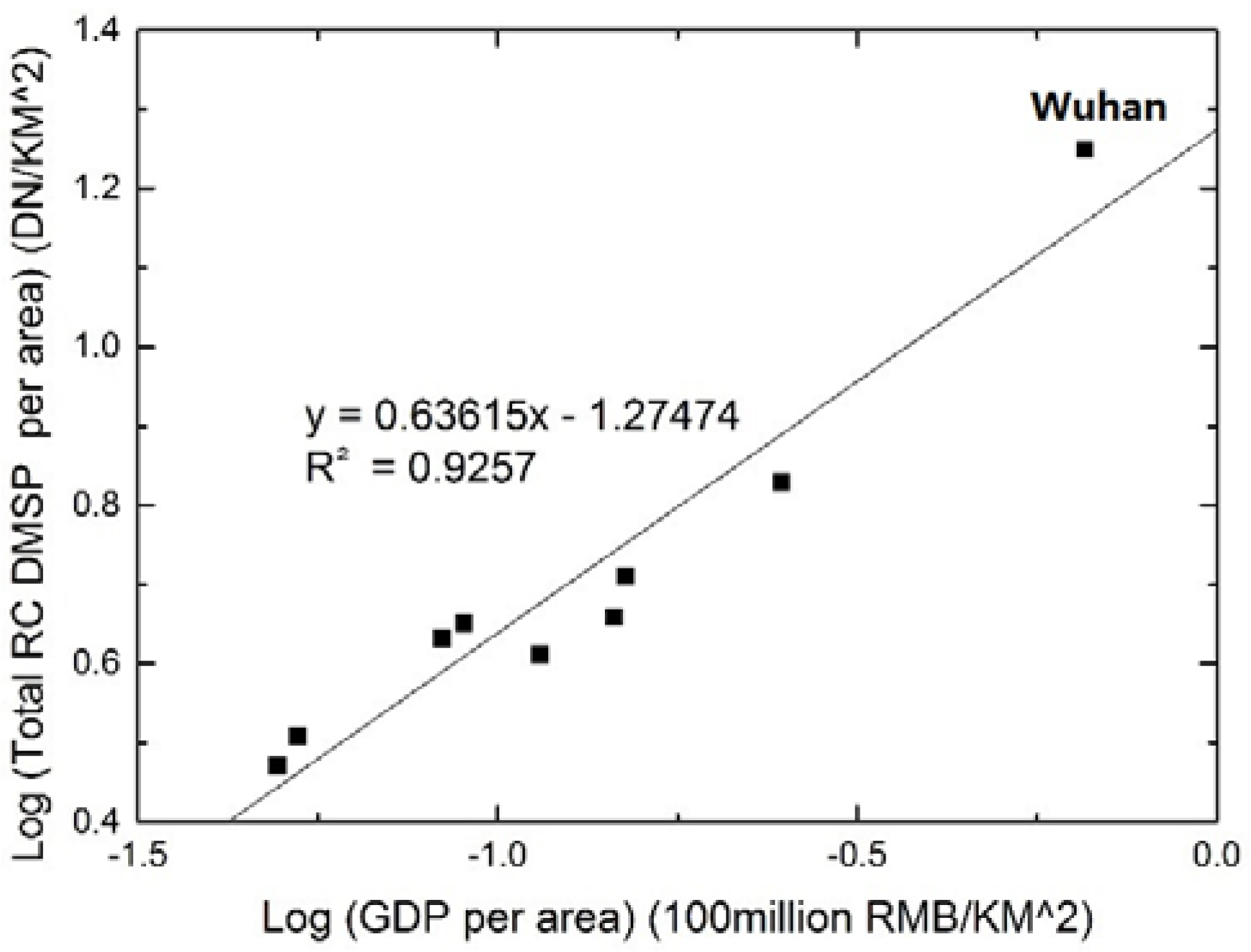
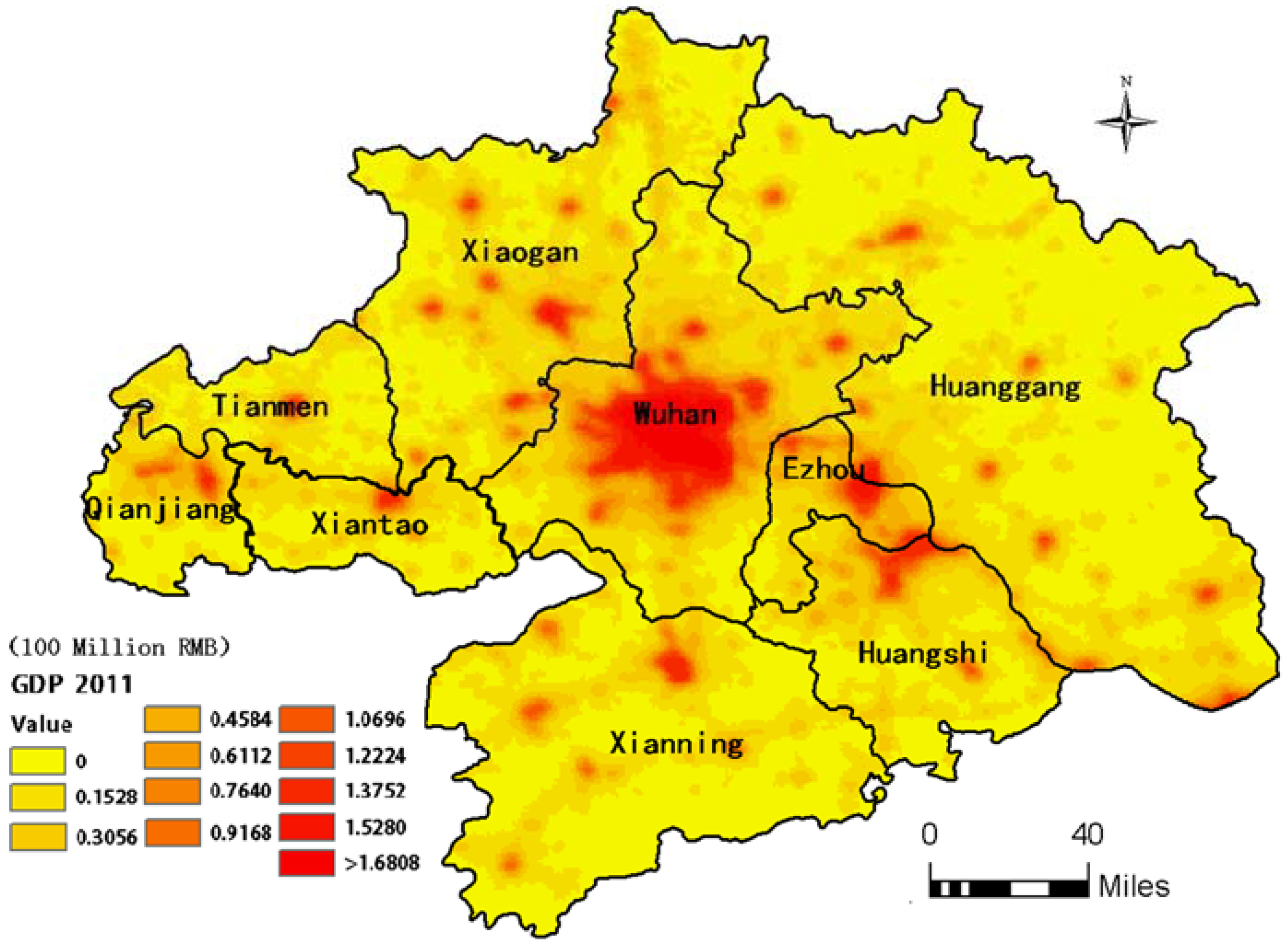
3.2. GDP Dasymetric Map
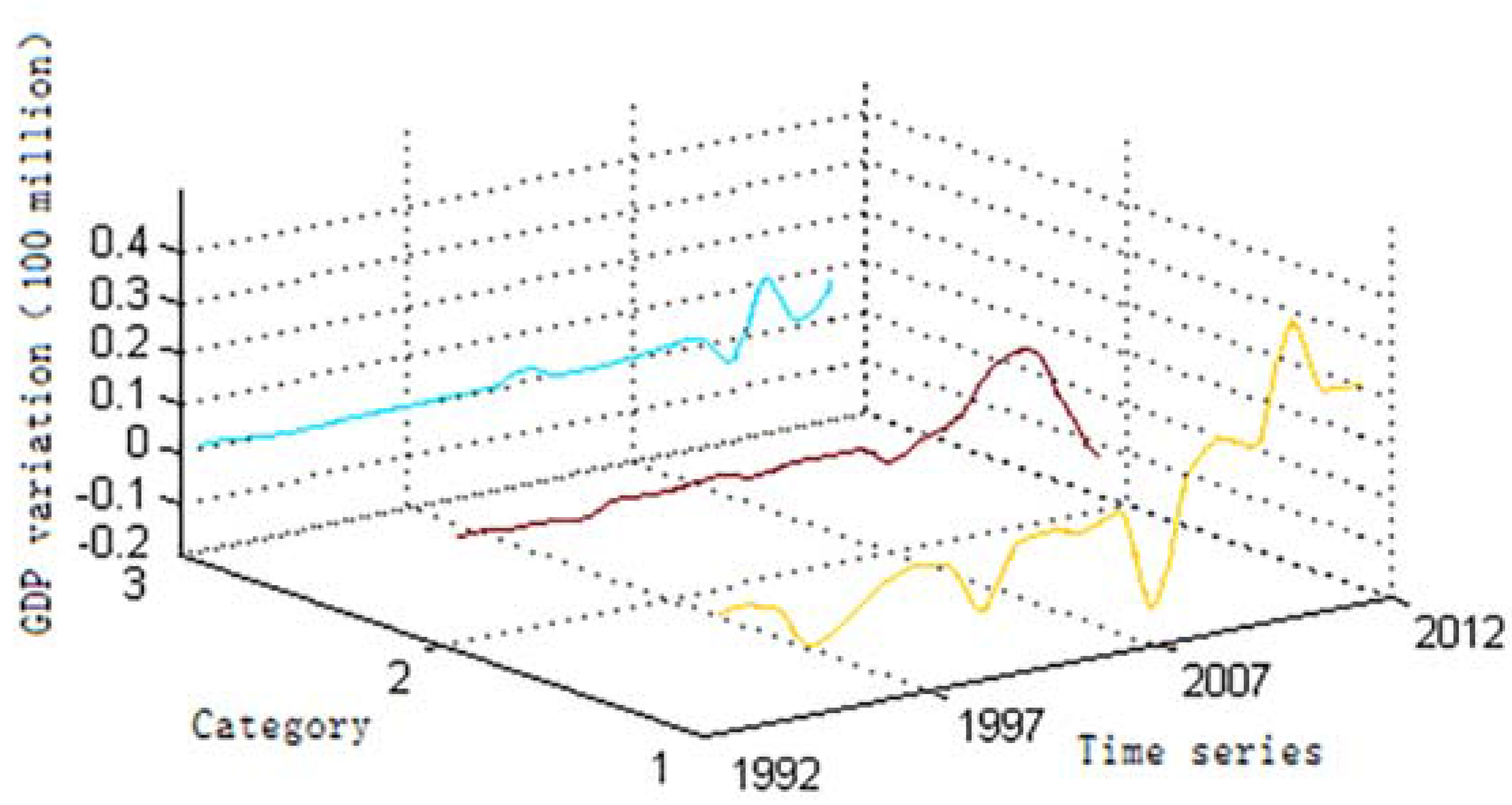
4. Map Spectrum-Based Spatiotemporal Clustering
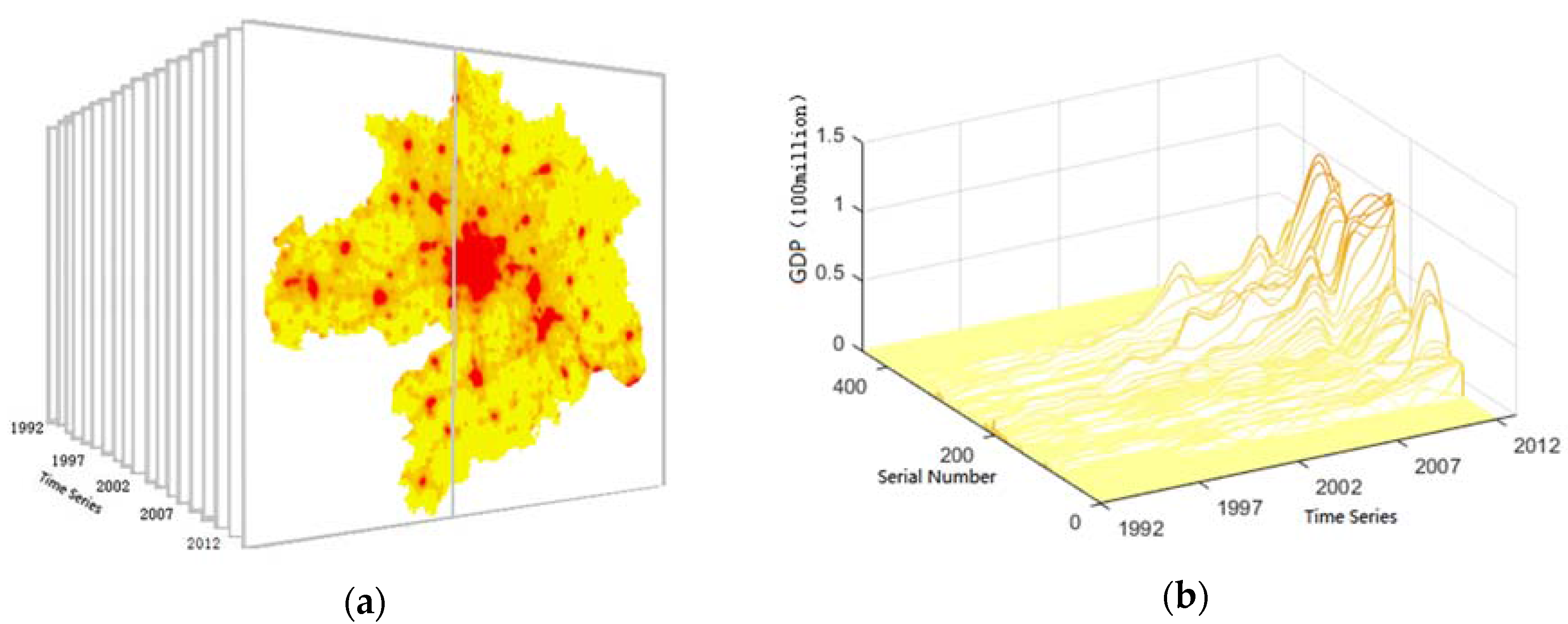
4.1. Map Spectrum-Based Spatiotemporal Representation Model
4.2. Similarity Measurement of the Map Spectrum Model
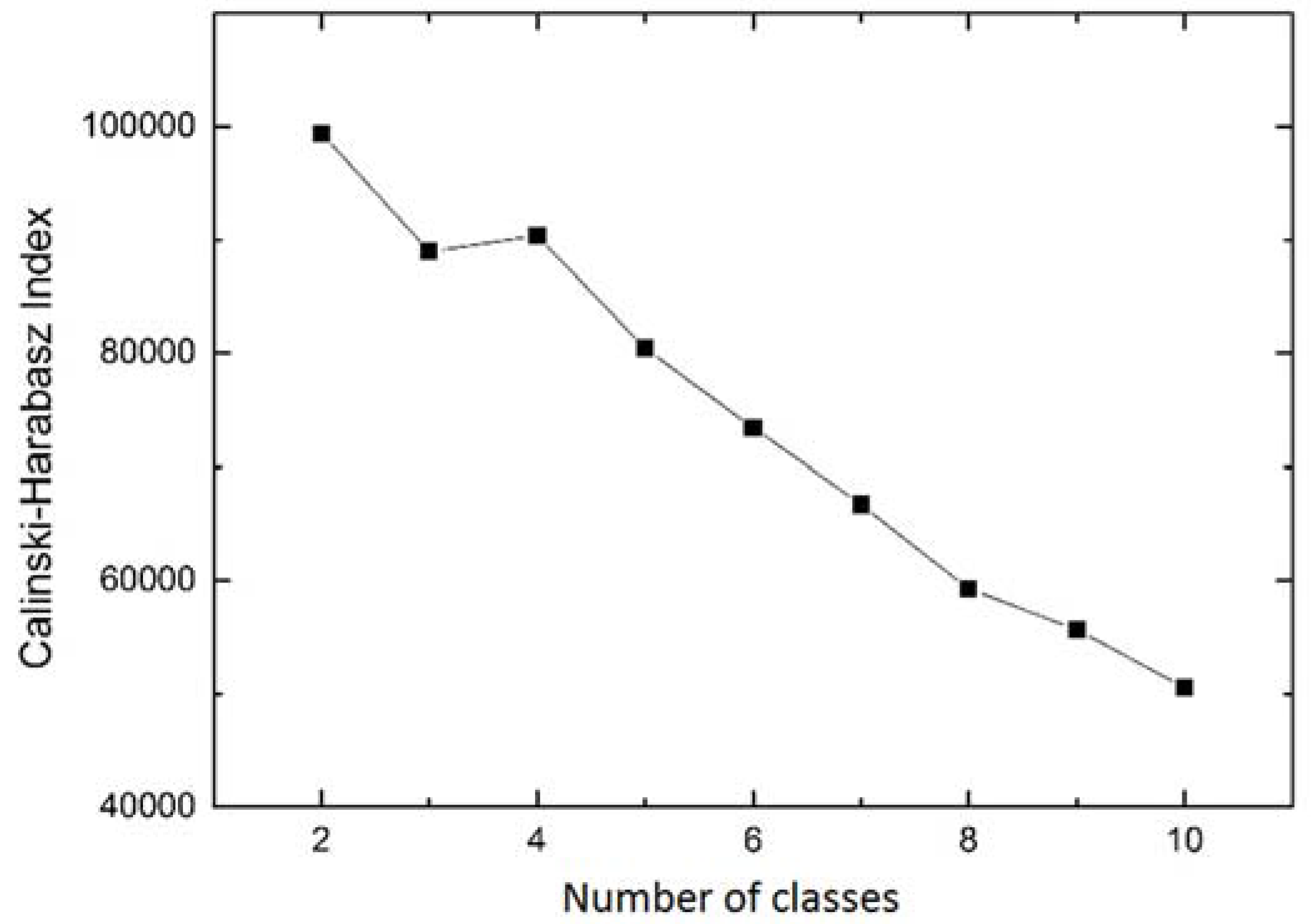
4.3. Extraction of Spatiotemporal Patterns
5. Discussion
5.1. Accuracy Assessment of the Dasymetric GDP Map based on County-Level GDP Statistics
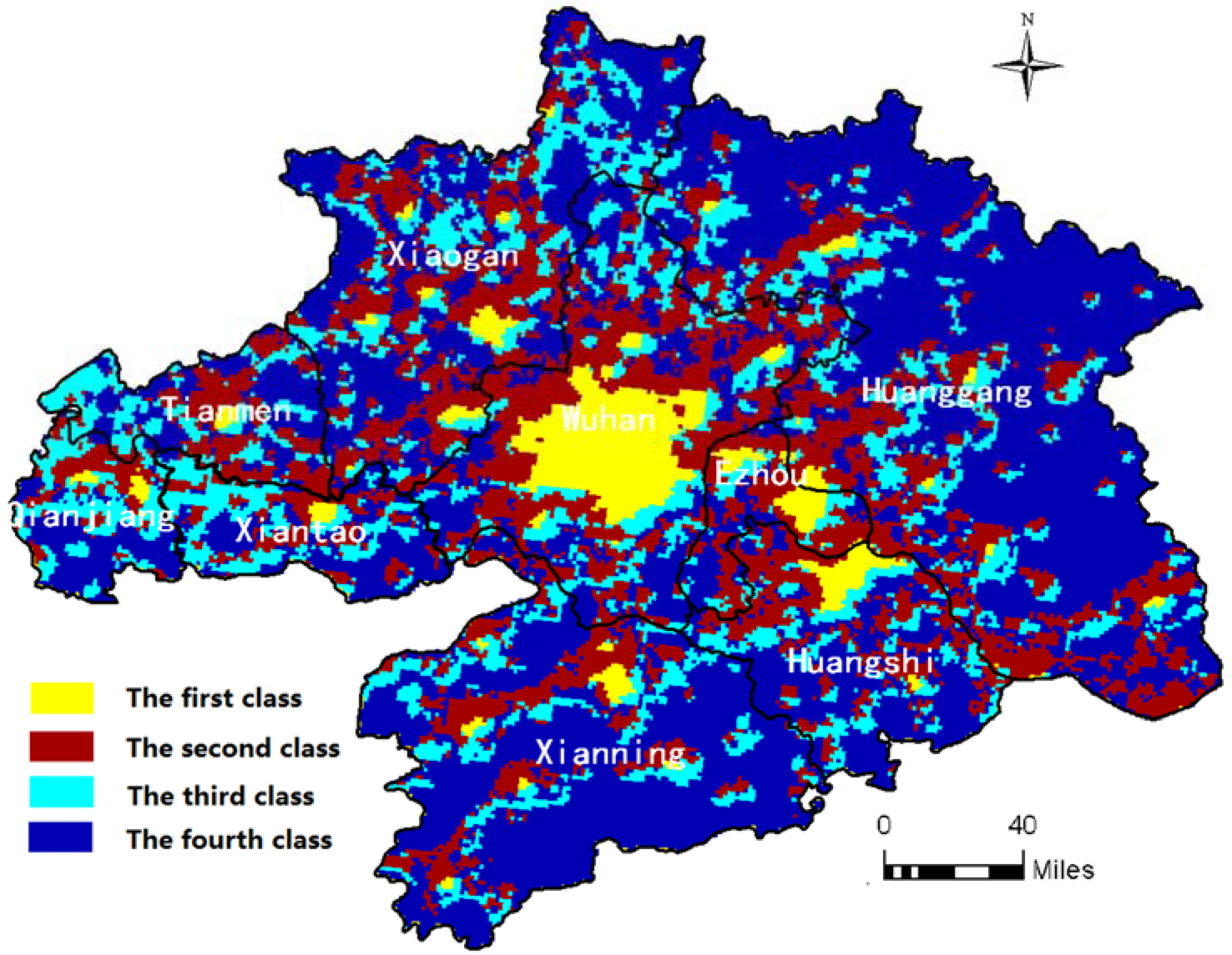
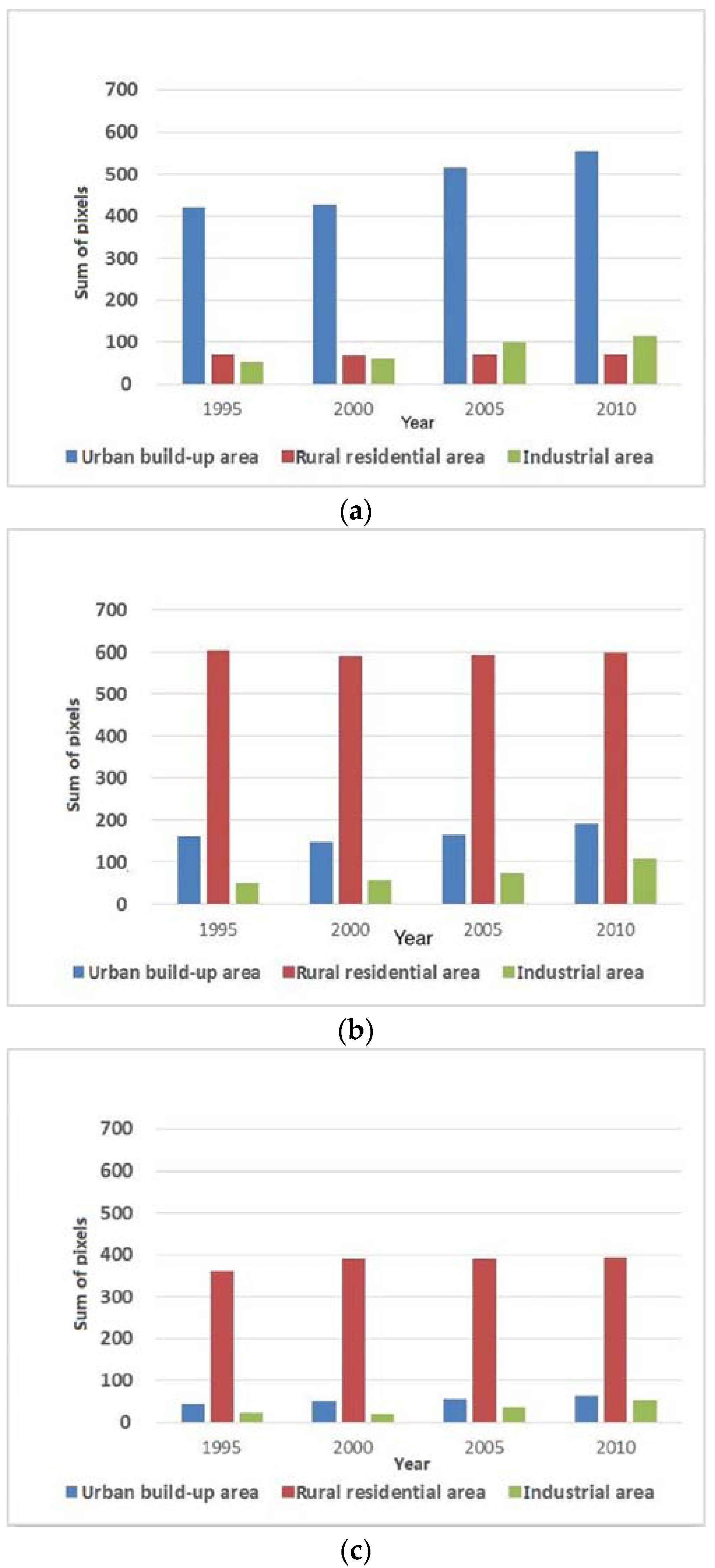
5.2. GDP Variation Pattern Analysis based on the Clustering Results
6. Conclusions
- (1)
- This study investigated the mapping of statistical GDP data based on spatial location to obtain a dasymetric GDP map using DNs from calibrated night light images. A linear regression model between DN and GDP was constructed at a prefectural level, and normalization factors between grid-level GDP and prefectural GDP statistics were used to produce accurate dasymetric GDP maps.
- (2)
- To investigate GDP growth, this study proposed a method of improved k-means clustering using a map spectrum-based, spatiotemporally integrated model. The proposed spatiotemporal representation model is a 3D model consisting of time, space, and magnitude dimensions. The model provides a solution that simultaneously considers spatial and temporal characteristics in clustering.
- (3)
- This study produced dasymetric maps and obtained the spatiotemporal patterns of GDP growth in the Wuhan urban agglomeration. These findings provide an important basis for economic development, spatial planning, decision making, and management in the region. In addition, the study provides a reference solution for spatial mapping and spatiotemporal pattern extraction using other socioeconomic data.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zeng, C.Q.; Zhou, Y.; Wang, S.X.; Yan, F.L.; Zhao, Q. Population spatialization in China based on night-time imagery and land use data. Int. J. Remote Sens. 2011, 32, 9599–9620. [Google Scholar] [CrossRef]
- Lopes, F.B.; da Silva, M.C.; Miyagi, E.S.; Fioravanti, M.C.S.; Faco, O.; Guimaraes, R.F.; Junior, O.A.D.; McManus, C.M. Spatialization of climate, physical and socioeconomic factors that affect the dairy goat production in Brazil and their impact on animal breeding decisions. Pesqui. Vet. Bras. 2012, 32, 1073–1081. [Google Scholar] [CrossRef]
- Cao, X.; Wang, J.M.; Chen, J.; Shi, F. Spatialization of electricity consumption of China using saturation-corrected DMSP-OLS data. Int. J. Appl. Earth Obs. Geoinform. 2014, 28, 193–200. [Google Scholar] [CrossRef]
- Silva, C.S.P.; Grigio, A.M.; Pimenta, M.R.C. Survey and spatialization crime urban county Mossoro-Rn. Holos 2016, 32, 352–362. [Google Scholar] [CrossRef]
- Talebi, M.; Zare, M.; Madahi-Zadeh, R.; Bali-Lashak, A. Spatial-temporal analysis of seismicity before the 2012 Varzeghan, Iran, Mw 6.5 earthquake. Turk. J. Earth Sci. 2015, 24, 289–301. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Ye, X.Y.; Tsou, M.H. Spatial, temporal, and content analysis of twitter for wildfire hazards. Nat. Hazards 2016, 83, 523–540. [Google Scholar] [CrossRef]
- Zhang, Y.; Moges, S.; Block, P. Optimal cluster analysis for objective regionalization of seasonal precipitation in regions of high spatial-temporal variability: Application to western Ethiopia. J. Clim. 2016, 29, 3697–3717. [Google Scholar] [CrossRef]
- Vogel, C.R.; Tyler, G.A.; Wittich, D.J. Spatial-temporal-covariance-based modeling, analysis, and simulation of aero-optics wavefront aberrations. J. Opt. Soc. Am. a-Opt. Image Sci. Vis. 2014, 31, 1666–1679. [Google Scholar] [CrossRef] [PubMed]
- Qian, T.N.; Bagan, H.; Kinoshita, T.; Yamagata, Y. Spatial-temporal analyses of surface coal mining dominated land degradation in Holingol, Inner Mongolia. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1675–1687. [Google Scholar] [CrossRef]
- Li, X.; Li, D.R. Can night-time light images play a role in evaluating the Syrian crisis? Int. J. Remote Sens. 2014, 35, 6648–6661. [Google Scholar] [CrossRef]
- McArdle, G.; Tahir, A.; Bertolotto, M. Interpreting map usage patterns using geovisual analytics and spatio-temporal clustering. Int. J. Digit. Earth 2015, 8, 599–622. [Google Scholar] [CrossRef]
- Chidean, M.I.; Munoz-Bulnes, J.; Ramiro-Bargueno, J.; Caamano, A.J.; Salcedo-Sanz, S. Spatio-temporal trend analysis of air temperature in Europe and western Asia using data-coupled clustering. Glob. Planet. Chang. 2015, 129, 45–55. [Google Scholar] [CrossRef]
- Wu, X.J.; Zurita-Milla, R.; Kraak, M.J. Co-clustering geo-referenced time series: Exploring spatio-temporal patterns in Dutch temperature data. Int. J. Geogr. Inf. Sci. 2015, 29, 624–642. [Google Scholar] [CrossRef]
- Damiani, M.L.; Issa, H.; Fotino, G.; Heurich, M.; Cagnacci, F. Introducing ‘presence’ and ‘stationarity index’ to study partial migration patterns: An application of a spatio-temporal clustering technique. Int. J. Geogr. Inf. Sci. 2016, 30, 907–928. [Google Scholar] [CrossRef]
- NOAA. Available online: http://ngdc.noaa.gov/eog /download.html (accessed on 24 March 2017).
- RESDC. Available online: http://www.resdc.cn (accessed on 24 March 2017).
- Liu, Z.F.; He, C.Y.; Zhang, Q.F.; Huang, Q.X.; Yang, Y. Extracting the dynamics of urban expansion in China using DMSP-OLS nighttime light data from 1992 to 2008. Landsc. Urban Plan. 2012, 106, 62–72. [Google Scholar] [CrossRef]
- Lo, C.P. Urban indicators of China from radiance-calibrated digital DMSP-OLS nighttime images. Ann. Assoc. Am. Geogr. 2002, 92, 225–240. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Ziskin, D.; Baugh, K.E.; Tuttle, B.T.; Ghosh, T.; Pack, D.W.; Erwin, E.H.; Zhizhin, M. A fifteen year record of global natural gas flaring derived from satellite data. Energies 2009, 2, 595–622. [Google Scholar] [CrossRef]
- Liu, J.; Li, W. A nighttime light imagery estimation of ethnic disparity in economic well-being in mainland China and Taiwan (2001–2013). Eurasian Geogr. Econ. 2015, 55, 691–714. [Google Scholar] [CrossRef]
- Shi, K.F.; Yu, B.L.; Huang, Y.X.; Hu, Y.J.; Yin, B.; Chen, Z.Q.; Chen, L.J.; Wu, J.P. Evaluating the ability of NPP-VIIRS nighttime light data to estimate the Gross Domestic Product and the Electric Power Consumption of China at multiple scales: A comparison with DMSP-OLS data. Remote Sens. 2014, 6, 1705–1724. [Google Scholar] [CrossRef]
- Lo, C.P. Modeling the population of china using DMSP operational linescan system nighttime data. Photogramm. Eng. Remote Sens. 2001, 67, 1037–1047. [Google Scholar]
- Wu, J.S.; Wang, Z.; Li, W.F.; Peng, J. Exploring factors affecting the relationship between light consumption and GDP based on DMSP/OLS nighttime satellite imagery. Remote Sens. Environ. 2013, 134, 111–119. [Google Scholar] [CrossRef]
- Calinski, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar] [CrossRef]
| Year | NRC DMSP-OLS | Corrected DMSP-OLS | ||
|---|---|---|---|---|
| Regression Model | R2 | Regression Model | R2 | |
| 1992 | y = 0.0045x + 9.6097 | 0.9435 | y = 0.0042x + 11.363 | 0.9630 |
| 1993 | y = 0.0072x + 5.5751 | 0.9777 | y = 0.0061x + 5.6131 | 0.9768 |
| 1994 | y = 0.0100x − 2.6774 | 0.9775 | y = 0.0084x − 2.6774 | 0.9775 |
| 1995 | y = 0.0127x − 11.919 | 0.9764 | y = 0.0123x − 11.952 | 0.9769 |
| 1996 | y = 0.0153x − 22.355 | 0.9751 | y = 0.0151x − 22.417 | 0.9757 |
| 1997 | y = 0.0150x − 25.686 | 0.9817 | y = 0.0128x − 21.877 | 0.9740 |
| 1998 | y = 0.0169x − 29.908 | 0.9810 | y = 0.0144x − 30.016 | 0.9818 |
| 1999 | y = 0.0160x − 25.013 | 0.9834 | y = 0.0122x − 25.143 | 0.9844 |
| 2000 | y = 0.0180x − 48.724 | 0.9864 | y = 0.0183x − 48.875 | 0.9873 |
| 2001 | y = 0.0185x − 49.241 | 0.9921 | y = 0.0168x − 49.412 | 0.9931 |
| 2002 | y = 0.0206x − 85.218 | 0.9850 | y = 0.0210x − 85.330 | 0.9855 |
| 2003 | y = 0.0223x − 120.66 | 0.9726 | y = 0.0148x − 120.73 | 0.9728 |
| 2004 | y = 0.0237x − 155.38 | 0.9584 | y = 0.0204x − 155.41 | 0.9585 |
| 2005 | y = 0.0248x − 189.32 | 0.9440 | y = 0.0215x − 189.33 | 0.9442 |
| 2006 | y = 0.0257x − 222.50 | 0.9301 | y = 0.0198x − 222.50 | 0.9301 |
| 2007 | y = 0.0265x − 254.98 | 0.9170 | y = 0.0246x − 254.96 | 0.9173 |
| 2008 | y = 0.0289x − 293.35 | 0.9263 | y = 0.0269x − 293.38 | 0.9263 |
| 2009 | y = 0.0298x − 336.37 | 0.9380 | y = 0.0180x − 336.37 | 0.9382 |
| 2010 | y = 0.0368x − 317.45 | 0.9517 | y = 0.0234x − 374.60 | 0.9404 |
| 2011 | y = 0.0444x − 222.38 | 0.9543 | y = 0.0228x − 400.22 | 0.9402 |
| 2012 | y = 0.0377x − 464.73 | 0.9405 | y = 0.0374x − 464.73 | 0.9405 |
| Year | RMSE | MRE | R |
|---|---|---|---|
| 1997 | 4.9614 | 4.5572% | 0.9982 |
| 1998 | 3.6867 | 3.0326% | 0.9992 |
| 1999 | 1.8850 | 1.8516% | 0.9988 |
| 2000 | 4.2335 | 3.3435% | 0.9949 |
| 2001 | 3.2224 | 2.5797% | 0.9989 |
| 2002 | 3.3361 | 2.1376% | 0.9995 |
| 2003 | 10.9458 | 6.1353% | 0.9729 |
| 2004 | 8.1877 | 4.0032% | 0.9895 |
| 2005 | 28.8478 | 11.4043% | 0.9649 |
| 2006 | 14.3577 | 5.1784% | 0.9929 |
| 2007 | 22.5479 | 7.4647% | 0.9826 |
| 2008 | 17.6268 | 4.3592% | 0.9934 |
| 2009 | 12.5426 | 2.8741% | 0.9969 |
| 2010 | 19.7350 | 3.8184% | 0.9935 |
| 2011 | 48.0933 | 7.6910% | 0.9694 |
| 2012 | 68.3982 | 9.3377% | 0.9468 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Liu, S.; Du, J. A Map Spectrum-Based Spatiotemporal Clustering Method for GDP Variation Pattern Analysis Using Nighttime Light Images of the Wuhan Urban Agglomeration. ISPRS Int. J. Geo-Inf. 2017, 6, 160. https://doi.org/10.3390/ijgi6060160
Zhang P, Liu S, Du J. A Map Spectrum-Based Spatiotemporal Clustering Method for GDP Variation Pattern Analysis Using Nighttime Light Images of the Wuhan Urban Agglomeration. ISPRS International Journal of Geo-Information. 2017; 6(6):160. https://doi.org/10.3390/ijgi6060160
Chicago/Turabian StyleZhang, Penglin, Shuaijun Liu, and Juan Du. 2017. "A Map Spectrum-Based Spatiotemporal Clustering Method for GDP Variation Pattern Analysis Using Nighttime Light Images of the Wuhan Urban Agglomeration" ISPRS International Journal of Geo-Information 6, no. 6: 160. https://doi.org/10.3390/ijgi6060160
APA StyleZhang, P., Liu, S., & Du, J. (2017). A Map Spectrum-Based Spatiotemporal Clustering Method for GDP Variation Pattern Analysis Using Nighttime Light Images of the Wuhan Urban Agglomeration. ISPRS International Journal of Geo-Information, 6(6), 160. https://doi.org/10.3390/ijgi6060160






