An Efficient Vector-Raster Overlay Algorithm for High-Accuracy and High-Efficiency Surface Area Calculations of Irregularly Shaped Land Use Patches
Abstract
:1. Introduction
2. Data and Methods
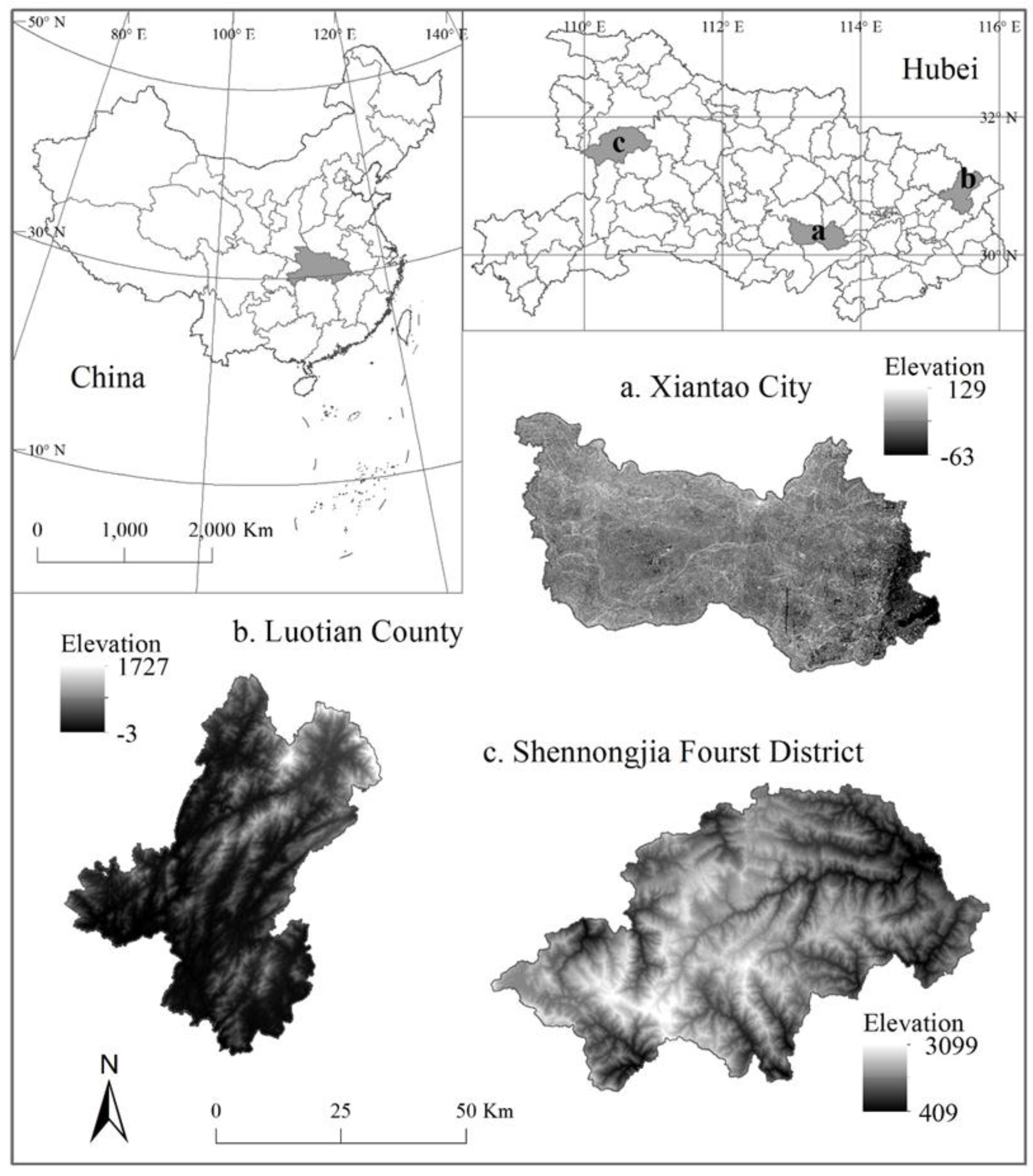
2.1. Study Area and Data
2.2. Methods
2.2.1. Generation of Raster File of Surface Area Based on the Raster-Based DEM
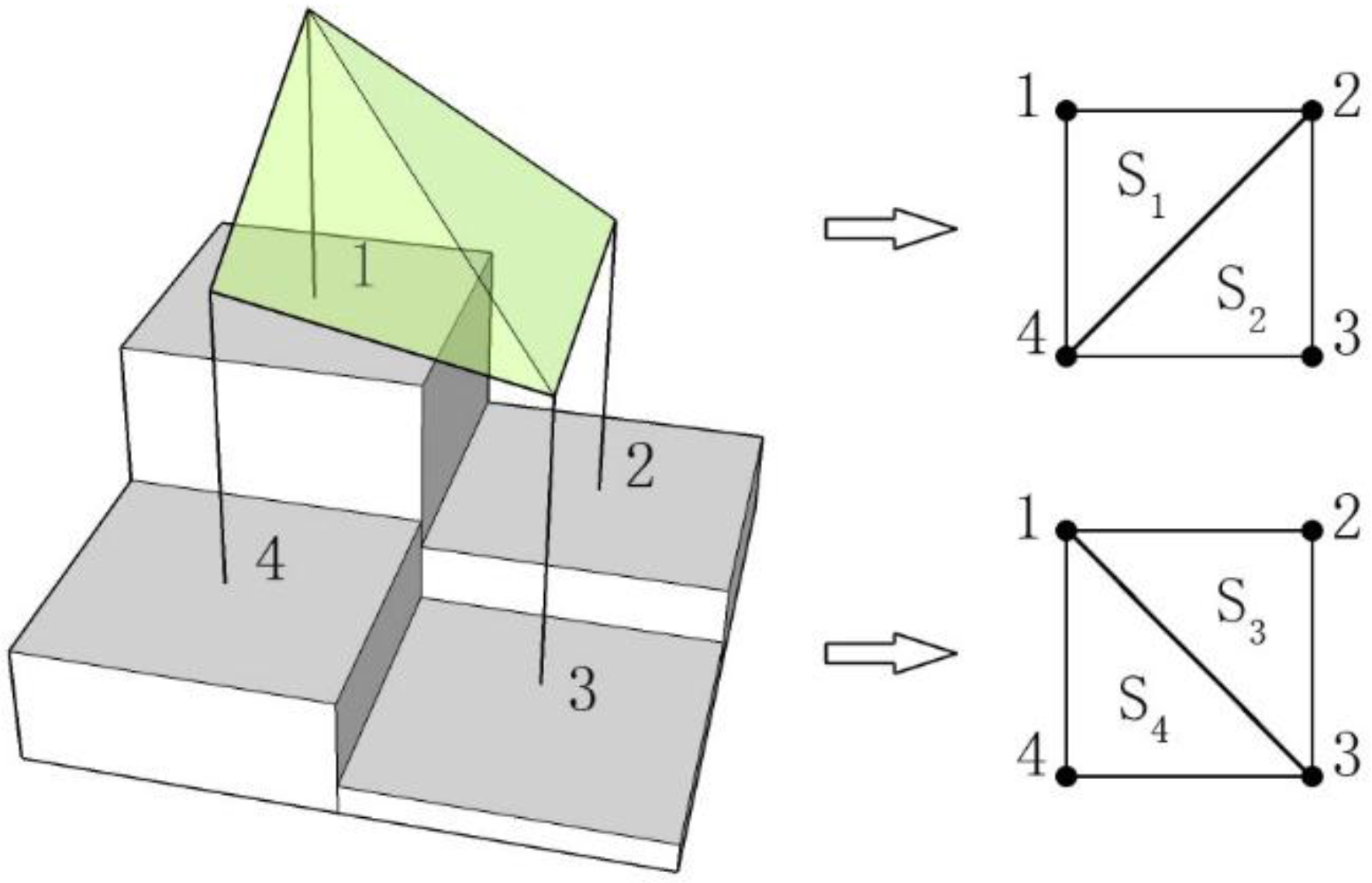
- Let be the current traversal row number, let j be the column number, and let the initial values of i and j be 2. Then, iterate the DEM raster from the second row and the second column. Label the current location of the cell as . Obtain the raster cells of locations , , and . Obtain their center points and label these points as 1, 2, 3, and 4 (Figure 2).
- Construct four triangles , and by connecting the diagonal points 1–3 and 2–4.
- Calculate the area of the four triangles as using Heron’s formula (Formula (5)).
- The surface area of zones 1-2-3-4 can be expressed by . The surface area can be written to its corresponding location, which can be identified by the row and column number of the surface area raster file. Repeat steps (1) to (4) until all rows and columns have been traversed. Each value assigned to the cells of the new raster represents the surface area of the particular cell.
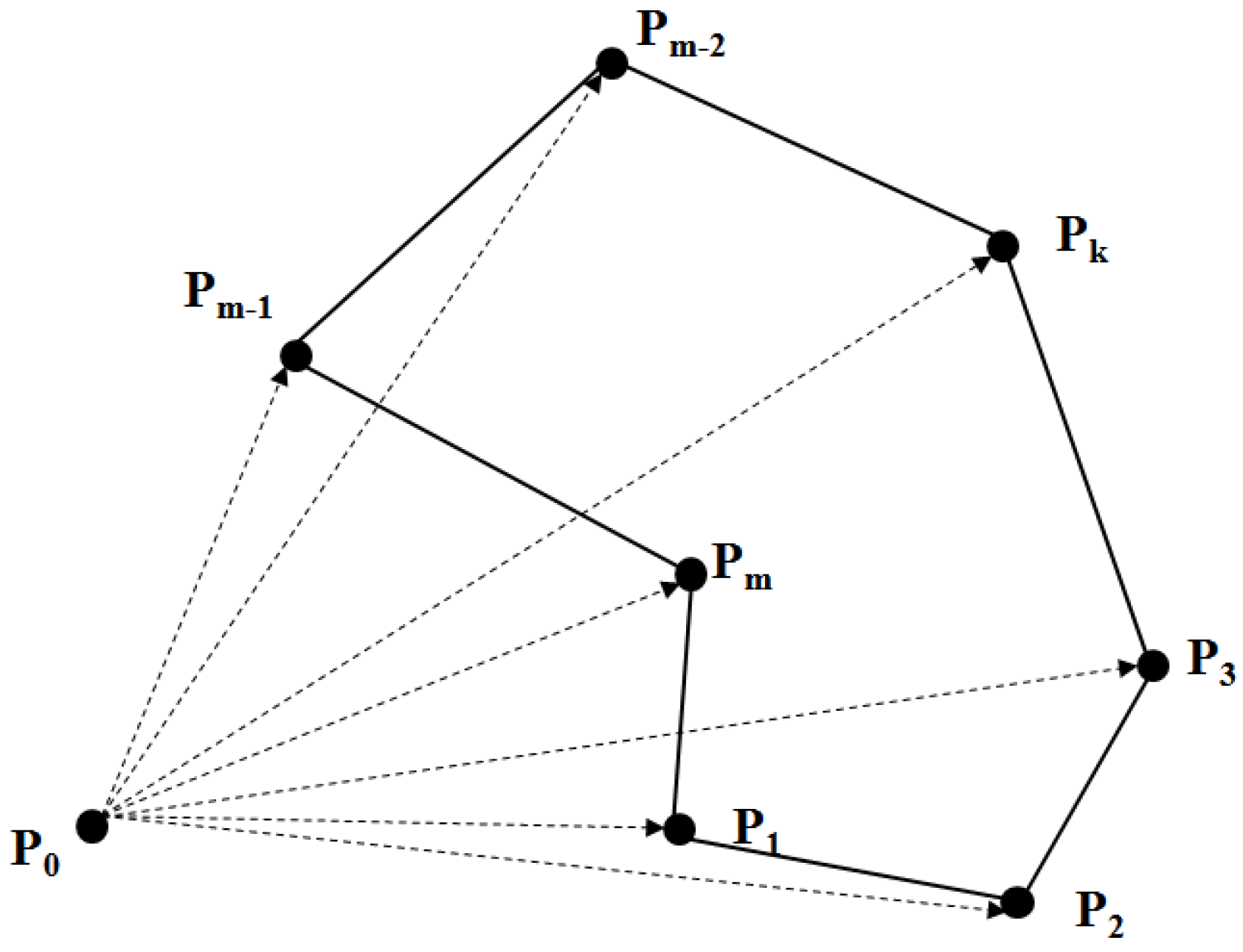
2.2.2. Vector-Raster Overlay Statistics
3. Results
4. Discussion
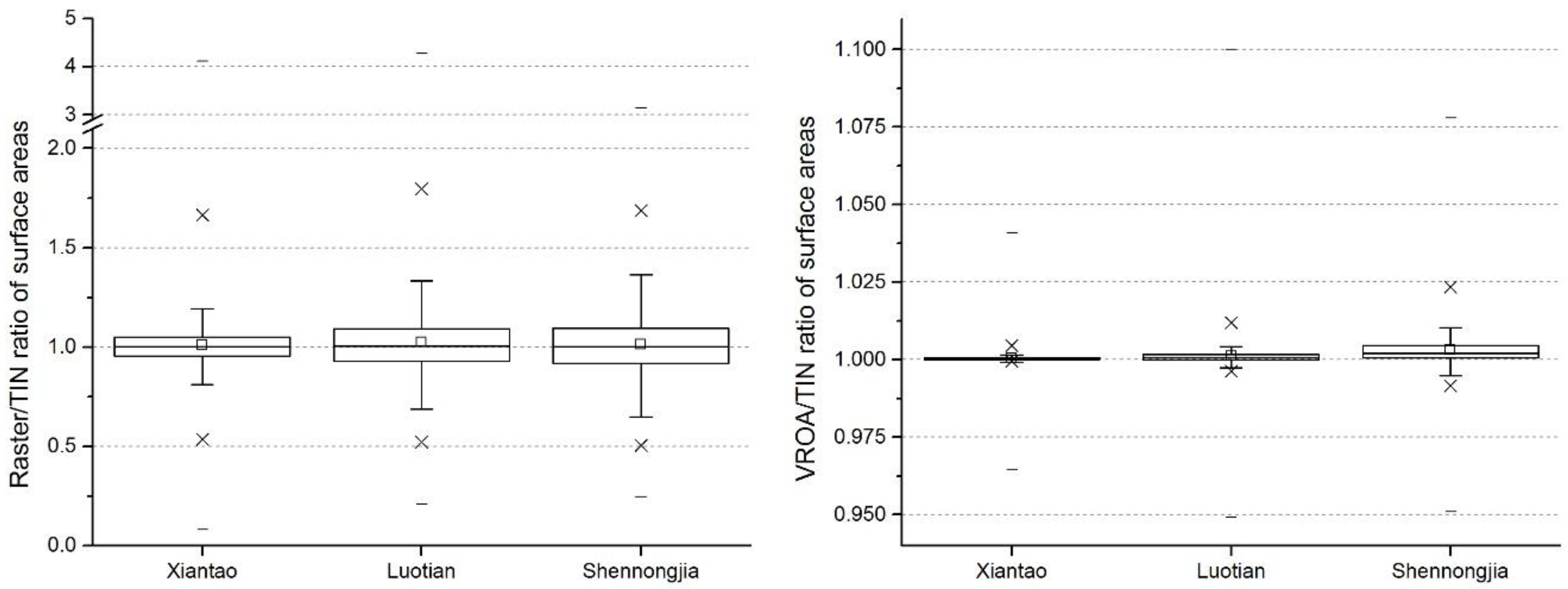
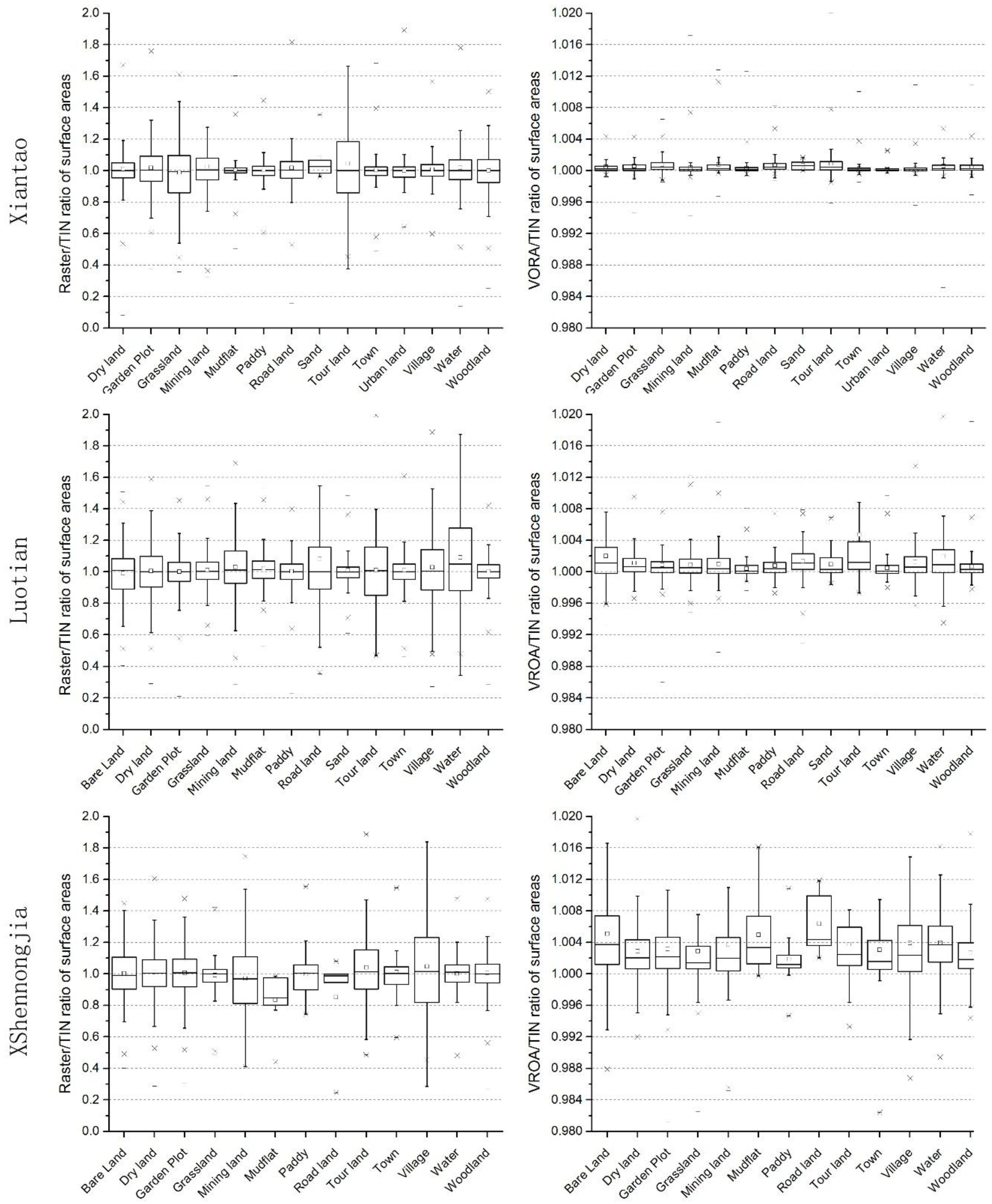
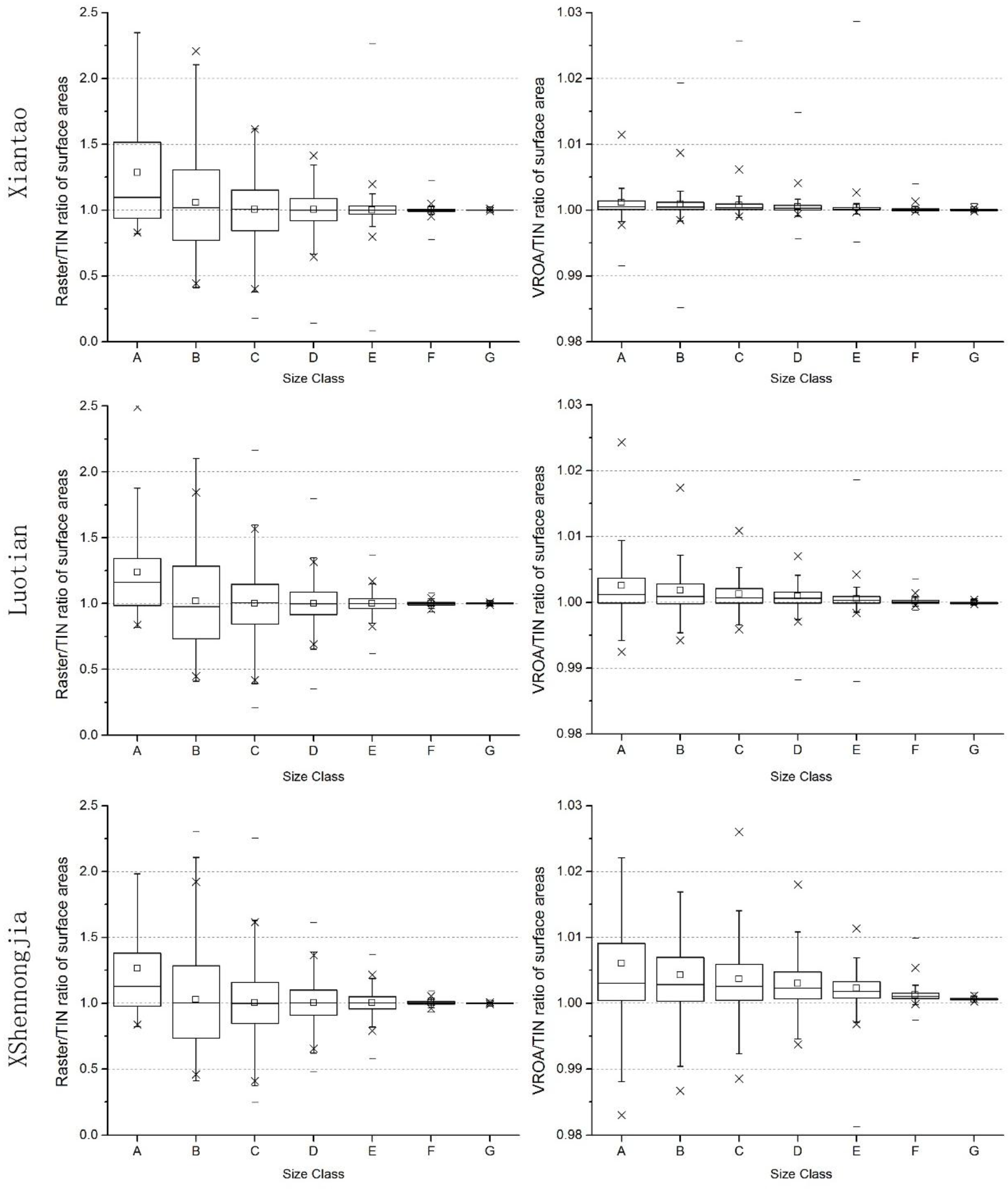
4.1. Precision Analysis
4.2. Efficiency Analysis
4.3. Compatibility Analysis
5. Conclusions
- (1)
- In vector-raster overlay statistics analysis, the proposed algorithm maintains the actual boundary of the vector polygon to clip the raster cells. Compared to the raster-based method, the results generated by the VROA-based method are closer to the results generated by the TIN-based method. Since the TIN-based method is considered to have relatively high accuracy, the VROA-based method can perform with a higher accuracy than the raster-based method.
- (2)
- The algorithm also significantly reduces the number of spatial operations and computation time compared to the TIN-based method.
- (3)
- The VROA-based method was designed based on both raster data and vector data, which avoids a loss in precision during the conversion to different data formats. The outcomes could be used in further calculation tasks.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| Algorithm A1 VROA | |
| Inputs: Surface Area Raster(SAR), Polygon Dataset(PD) | |
| Outputs: Surface Area for Each Polygon | |
| Function: VROA(SAR, PD) | |
| 1 | For each polygon(p) in PD: |
| 2 | Define pArea=0 as the surface area of cp |
| 3 | Obtain minimum enclosing rectangle (pEnv) of p |
| 4 | For each row between start and end rows of SAR covered by pEnv |
| 5 | Obtain minimum enclosing rectangle (rEnv) of row |
| 6 | Clip p by rEnv and name the clipped polygon as cp |
| 7 | Get the start point in cp and save it in a temp points array named tmpPoints |
| 8 | For each point (pT) rest in cp: |
| 9 | Define pF as the last point in tmpPoints |
| 10 | If pF and pT locate in same pixel: |
| 11 | Append pT into tmpPoints and do next |
| 12 | Else: |
| 13 | Get the intersected points(pIS) of Line(pF-pT) and the boundaries of cells |
| 14 | For each pI in pIS: |
| 15 | Append pI into tmpPoints |
| 16 | If pI.x != tmpPoints[0].x: |
| 17 | Append new point (pI.x, rEnv.minY) into tmpPoints |
| 18 | Append new point (tmpPoints[0].x, rEnv.minY) into tmpPoints |
| 19 | Append tmpPoints[0] into tmpPoints |
| 20 | Define pX as the cell tmpPoints located |
| 21 | Define pSA = CalculateArea(pX, tmpPoints, rEnv) |
| 22 | Set pArea=pArea+pSA |
| 23 | Clear tmpPoints and append pI into tmpPoints |
| 24 | If tmpPoints is not empty: |
| 25 | Define pX as the cell tmpPoints located |
| 26 | Define pSA = CalculateArea(pX, tmpPoints,rEnv) |
| 27 | Set pArea=pArea+pSA |
| 28 | Outputs pArea |
| Inputs: raster cell (pX), points array (tmpPoints), row minimum enclosing rectangle (rEnv) | |
| Outputs: surface area of the polygon presented by tmpPoints | |
| Function: CalculateArea(pX, tmpPoints, rEnv) | |
| 1 | Define pTmp as the polygon presented by tmpPoints |
| 2 | Get the ellipsoid area of pTmp as pEA |
| 3 | Get the ellipsoid area of pX as pxEA |
| 4 | Get the surface area of pX as pxSA |
| 5 | Get the surface area of pTmp (pSA) by formula pEA*pxSA/pxEA |
| 6 | Return pSA |
References
- Li, J.C.; Wang, W.L.; Hu, G.Y.; Wei, Z.H. Changes in ecosystem service values in Zoige Plateau, China. Agric. Ecosyst. Environ. 2010, 139, 766–770. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Ji, G.; Zhang, L. Changes in land use and ecosystem service values in Jinan, China. Energy Proced. 2011, 5, 1109–1115. [Google Scholar]
- Liu, Y.; Li, J.; Zhang, H. An ecosystem service valuation of land use change in Taiyuan City, China. Ecol. Model. 2012, 225, 127–132. [Google Scholar] [CrossRef]
- Chen, H.; Yang, G.; Peng, C.; Zhang, Y.; Zhu, D.; Zhu, Q.; Hu, J.; Wang, M.; Zhan, W.; Zhu, E. The carbon stock of alpine peatlands on the Qinghai–Tibetan Plateau during the Holocene and their future fate. Quat. Sci. Rev. 2014, 95, 151–158. [Google Scholar] [CrossRef]
- Cui, Q.; Wang, X.; Li, C.; Cai, Y.; Liu, Q.; Li, R. Ecosystem service value analysis of CO2 management based on land use change of Zoige alpine peat wetland, Tibetan Plateau. Ecol. Eng. 2015, 76, 158–165. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, B.M.; Liu, G.; Huang, F.F.; Liu, J.G.; Liao, W.B.; Wang, Y.Y.; Ren, S.J.; Chen, C.Q.; Peng, S.L. Biodiversity of Jinggangshan Mountain: The importance of topography and geographical location in supporting higher biodiversity. PLoS ONE 2015, 10, e0120208. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, H.; Heiskanen, J.; Maeda, E.E.; Pellikka, P.K.E. The effect of topographic normalization on fractional tree cover mapping in tropical mountains: An assessment based on seasonal Landsat time series. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 20–31. [Google Scholar] [CrossRef]
- Eisenlohr, P.V.; Alves, L.F.; Bernacci, L.C.; Mcg, P.; Torres, R.B.; Emb, P.; Fam, D.S.; Assis, M.A.; Ramos, E.; Alc, R. Disturbances, elevation, topography and spatial proximity drive vegetation patterns along an altitudinal gradient of a top biodiversity hotspot. Biodivers. Conserv. 2013, 22, 2767–2783. [Google Scholar] [CrossRef]
- Jenness, J.S. Calculating landscape surface area from digital elevation models. Wildl. Soc. Bull. 2004, 32, 829–839. [Google Scholar] [CrossRef]
- Hodgson, M.E. What cell size does the computerd slope/aspect angle represent? Photogramm. Eng. Remote Sens. 1995, 61, 513–517. [Google Scholar]
- Lopez, M.; Berry, J.K. Use surface area for realistic calculations. GeoWorld 2002, 15, 25. [Google Scholar]
- Zhang, W.; Ai-Nong, L.I. Study on calculating surface area in China based on SRTM DEM data. Geogr. Geo-Inf. Sci. 2014, 30, 51−55. [Google Scholar]
- Zhang, Y.; Zhang, L.-N.; Yang, C.-D.; Bao, W.-D.; Yuan, X.-X. Surface area processing in GIS for different mountain regions. For. Stud. China 2011, 13, 311–314. [Google Scholar] [CrossRef]
- Song, G.; Chen, Y.; Zhou, Y. Algorithm for Estimating Mountainous Surface Area Based on GPS Data. In Proceedings of the 2nd International Conference on Green Communications and Networks 2012 (GCN 2012), Chongqing, China, 12−14 December 2012; pp. 679–687. [Google Scholar]
- Zhou, Q.; Liu, X. Digital Terrain Analysis; Science Press: Beijing, China, 2006; pp. 114–122. [Google Scholar]
- Xie, C.L.; Zhao, R.; Liang, Y. Arithmetic research on computing surface area of statistic units in national geographic conditions monitoring based on geographic coordinate system. Remote Sens. Inf. 2014, 29, 47–51. [Google Scholar]
- Lu, Z.; Qu, Y.; Qiao, S. Geodesy: Introduction to Geodetic Datum and Geodetic Systems; Springer: Berlin, Germany, 2014; pp. 176–182. [Google Scholar]
- O’Rourke, J. Computational Geometry in C; Cambridge University Press: New York, NY, USA, 1994. [Google Scholar]
- Esri. ArcGIS Help 10.1—Add Surface Information (3D Analyst). Available online: http://resources.arcgis.com/en/help/main/10.1/index.html#//00q900000016000000 (accessed on 10 July 2016).



| Xiantao | Luotian | Shennongjia | |
|---|---|---|---|
| Number of land use polygons | 51,233 | 65,722 | 22,988 |
| Total surface area of TIN-based method | 2,268,766,822.94 | 2,268,766,822.94 | 3,902,985,501.19 |
| Total surface area of raster-based method | 2,270,267,464.98 | 2,270,267,464.98 | 3,905,941,441.71 |
| Total surface area of VROA-based method | 2,269,227,094.11 | 2,269,227,094.11 | 3,905,701,021.62 |
| RatioR of total surface area | 1.000433 | 1.000661 | 1.000757 |
| RatioV of total surface area | 1.000162 | 1.000203 | 1.000696 |
| Mean RatioR of patch surface areas | 1.011051 | 1.023171 | 1.013790 |
| Mean RatioV of patch surface areas | 1.000468 | 1.001099 | 1.003095 |
| Standard deviation of RatioR | 0.183528 | 0.217023 | 0.209578 |
| Standard deviation of RatioV | 0.001055 | 0.002853 | 0.005538 |
| TIN-Based Surface Areas | |||||||
|---|---|---|---|---|---|---|---|
| From value | 0 | 1000 | 2000 | 5000 | 10,000 | 100,000 | 1,000,000 |
| To value | 1000 | 2000 | 5000 | 10,000 | 100,000 | 1,000,000 | |
| Size Class | A | B | C | D | E | F | G |
| Region Name | Rows and Columns | Vector Polygon No. | Time Consumption (seconds) | ||
|---|---|---|---|---|---|
| Tin-Based | Raster-Based | Vroa-Based | |||
| Xiantao City | 3524 × 6530 | 51,732 | 4151 | 38 | 491 |
| Luotian County | 5128 × 4998 | 67,145 | 4633 | 43 | 517 |
| Shennongjia Forestry District | 4332 × 7844 | 23,244 | 3034 | 45 | 328 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, P.; Liu, Y.; He, Q.; Zhao, X.; Yang, J. An Efficient Vector-Raster Overlay Algorithm for High-Accuracy and High-Efficiency Surface Area Calculations of Irregularly Shaped Land Use Patches. ISPRS Int. J. Geo-Inf. 2017, 6, 156. https://doi.org/10.3390/ijgi6060156
Xie P, Liu Y, He Q, Zhao X, Yang J. An Efficient Vector-Raster Overlay Algorithm for High-Accuracy and High-Efficiency Surface Area Calculations of Irregularly Shaped Land Use Patches. ISPRS International Journal of Geo-Information. 2017; 6(6):156. https://doi.org/10.3390/ijgi6060156
Chicago/Turabian StyleXie, Peng, Yaolin Liu, Qingsong He, Xiang Zhao, and Jun Yang. 2017. "An Efficient Vector-Raster Overlay Algorithm for High-Accuracy and High-Efficiency Surface Area Calculations of Irregularly Shaped Land Use Patches" ISPRS International Journal of Geo-Information 6, no. 6: 156. https://doi.org/10.3390/ijgi6060156
APA StyleXie, P., Liu, Y., He, Q., Zhao, X., & Yang, J. (2017). An Efficient Vector-Raster Overlay Algorithm for High-Accuracy and High-Efficiency Surface Area Calculations of Irregularly Shaped Land Use Patches. ISPRS International Journal of Geo-Information, 6(6), 156. https://doi.org/10.3390/ijgi6060156








