Optimizing Multi-Way Spatial Joins of Web Feature Services
Abstract
:1. Introduction
2. Multi-Way SPATIAL Join of Web Feature Services
2.1. Open Geospatial Consortium (OGC) Web Feature Service
2.2. Multi-Way Spatial Join
2.3. Issues in Spatial Join Processing of Multiple Web Feature Services (WFSs)
3. The Optimization Algorithm for a Multi-Way Spatial Join of WFSs
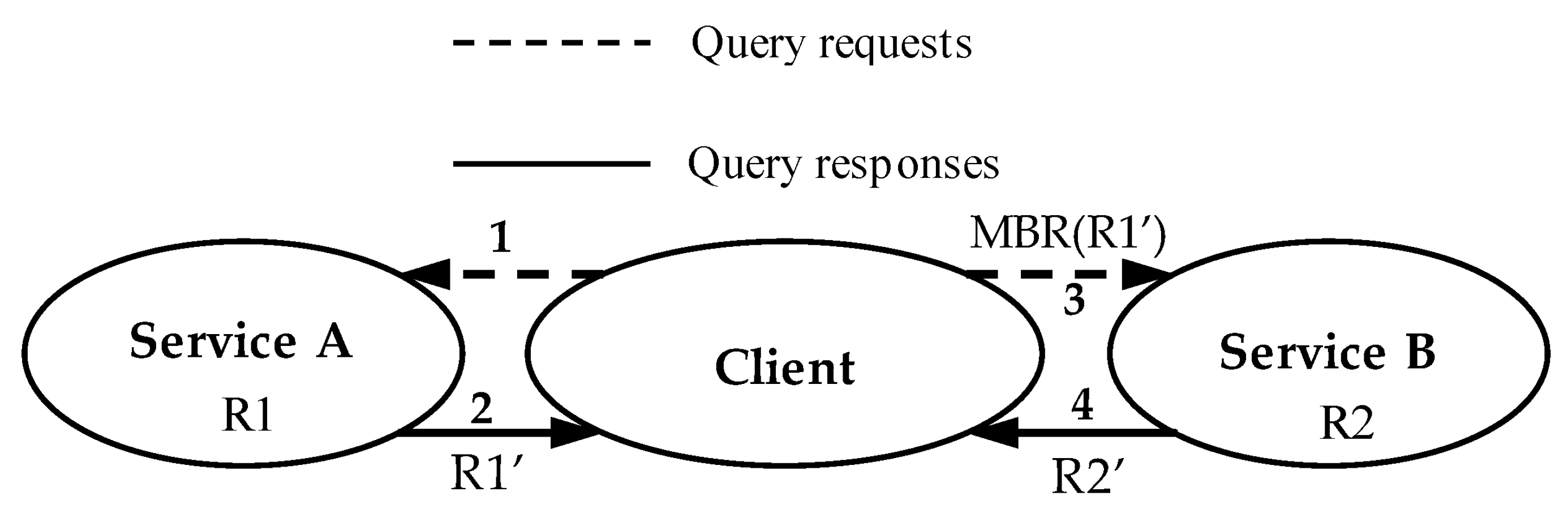
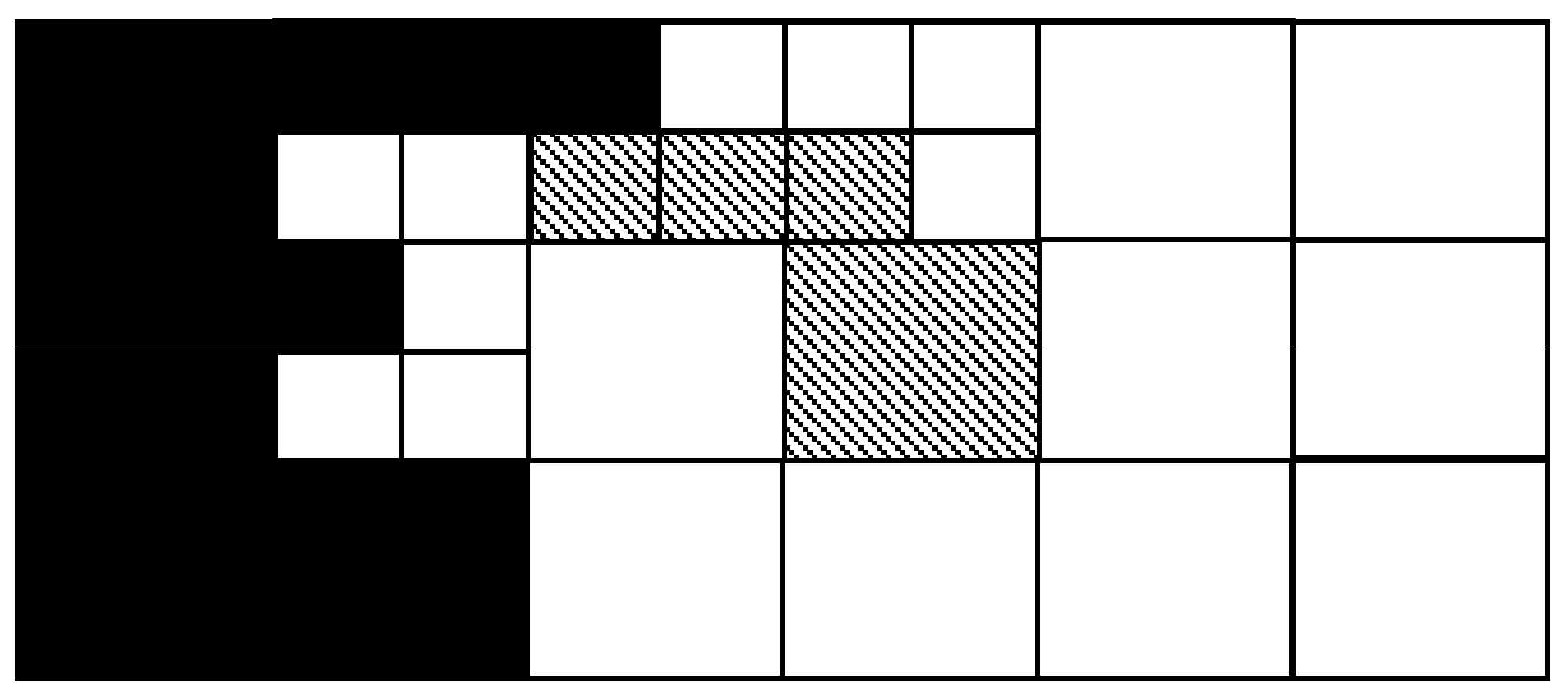
3.1. Optimizing Binary Spatial Join of Web Feature Services
- (1)
- Merge the white and diagonal sub-areas into a larger area, and send its boundary to Server A to download R1 objects contained in or crossing this boundary. Merge the black and diagonal sub-areas into a larger area, and send its boundary to Server B to download R2 objects contained in or crossing this boundary.
- (2)
- For the white sub-areas, a spatial semi-join is performed on Server B, and the candidate objects of the dataset R2 are sent to the client. For the black sub-areas, a spatial semi-join is performed on Server A and the candidate objects of the dataset R1 are sent to the client.
- (3)
- The immediate datasets are refined on the client side to obtain the final solutions of the spatial join.
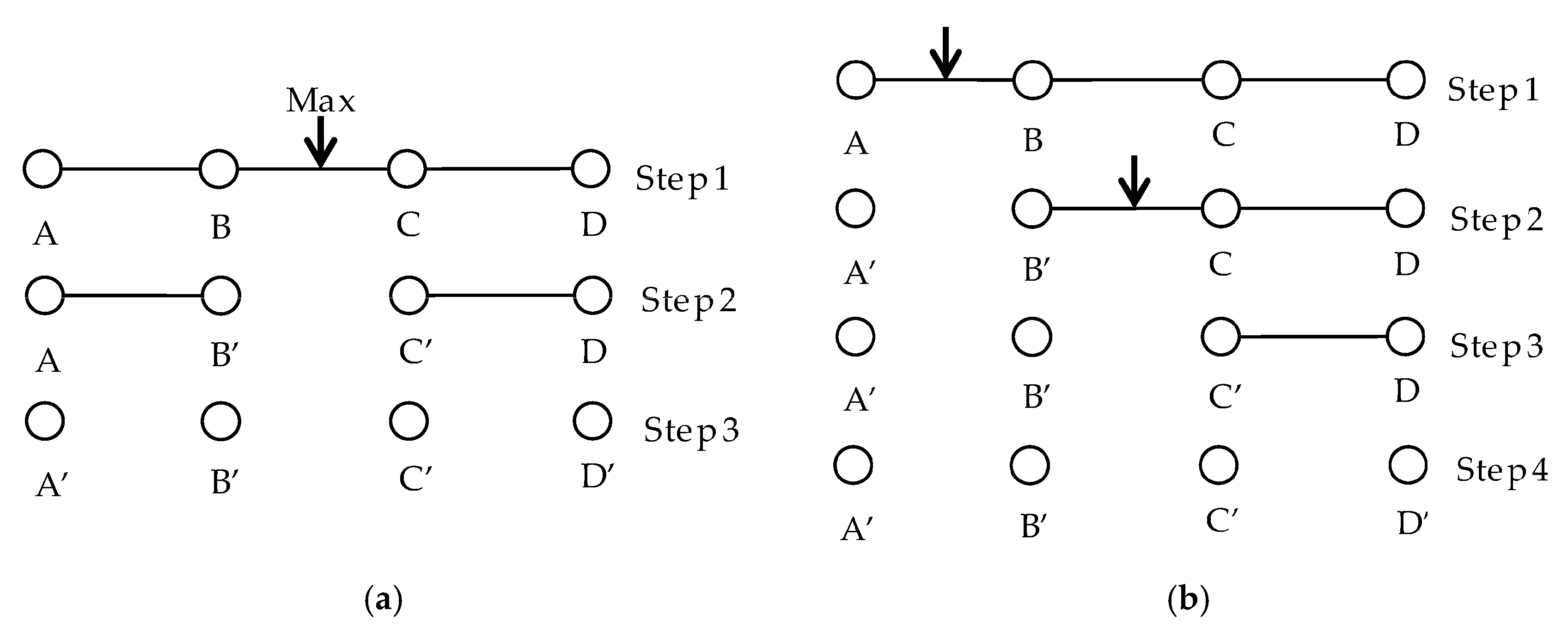
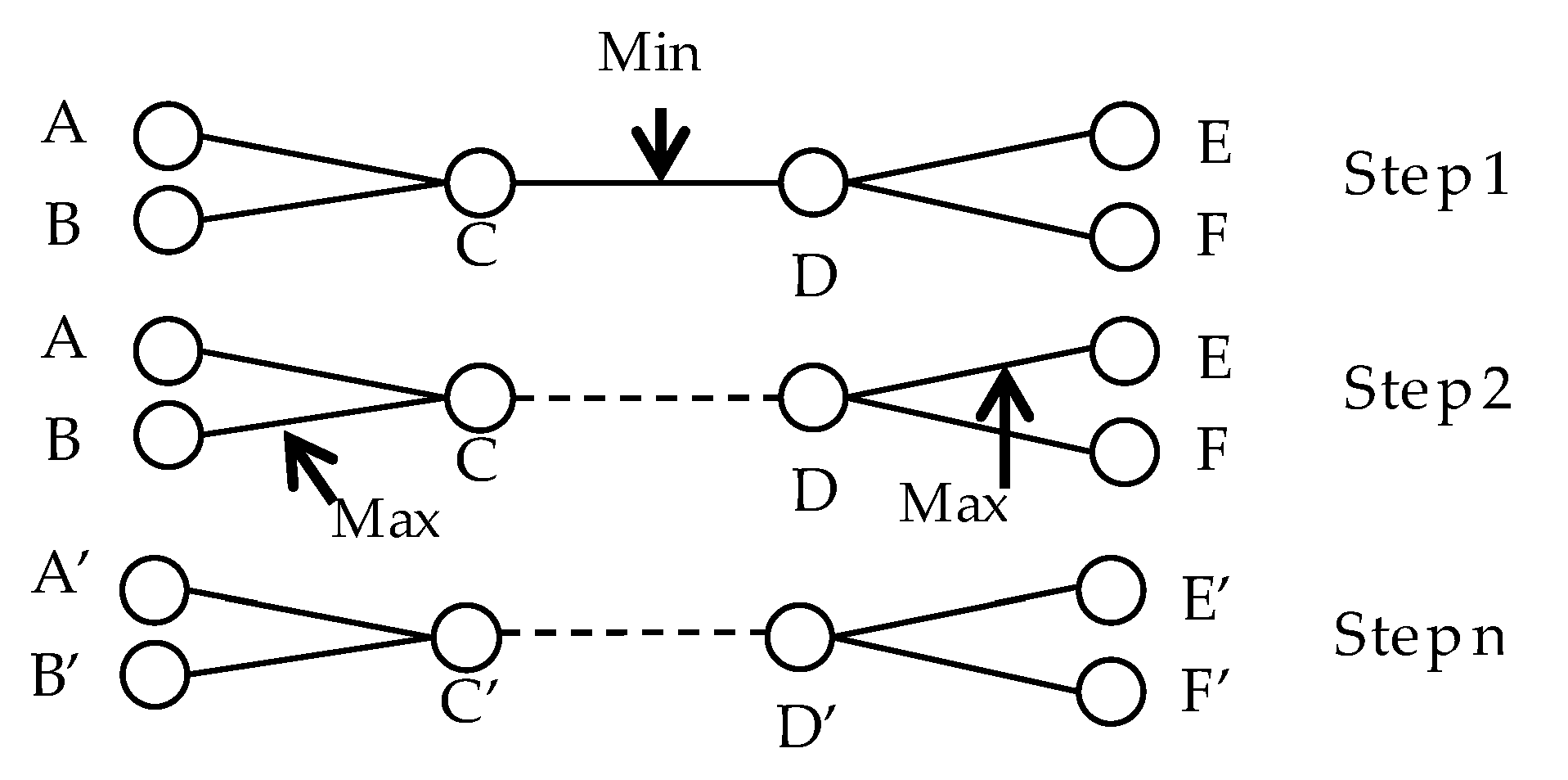
3.2. Optimizing the Multi-Way Spatial Joins of Web Feature Services
- (1)
- Estimate the filtering rates for all of the binary joins in the query graph with Equation (2).
- (2)
- Perform the join with the highest priority (usually determined by the filtering rate). After that, recalculate the filtering rate of the other binary joins with respect to the above two joined datasets, if necessary.
- (3)
- Repeatedly perform step (2) until all of the candidate objects of the related datasets have been downloaded to the client site.
| Algorithm 1: Processing multi-way spatial joins |
| Multiway-SpatialJoin(Datasets){ Foreach (Relation(i, j) in RelationSets) { /*Compute filtering rates for every binary join */ S(i, j)=ComputeFilteringRate (Datasets[i], Datasets[j]); } While (RelationSets ≠∅){ /*Stop if RelationSets is empty*/ Find the binary join with them maximum filtering rate S(n, m) or the Relation(n, m) that both datasets have a very small number of features; SpatialJoin(Datasets[n], Datasets[m]); /*Join Datasets[n] and Datasets[m]*/ Update(Datasets[n], Datasets[m]); /* Substitute Datasets[n] and Datasets[m] with the immediate solution of the previous join*/ Remove( Relation(n, m) ); /*Remove Relation(n, m) from RelationSets */ Update the filtering rates of the other joins that Datasets[n] and Datasets[m] participate in; } } |
4. Experiment Analysis
4.1. Test of Binary Spatial Join
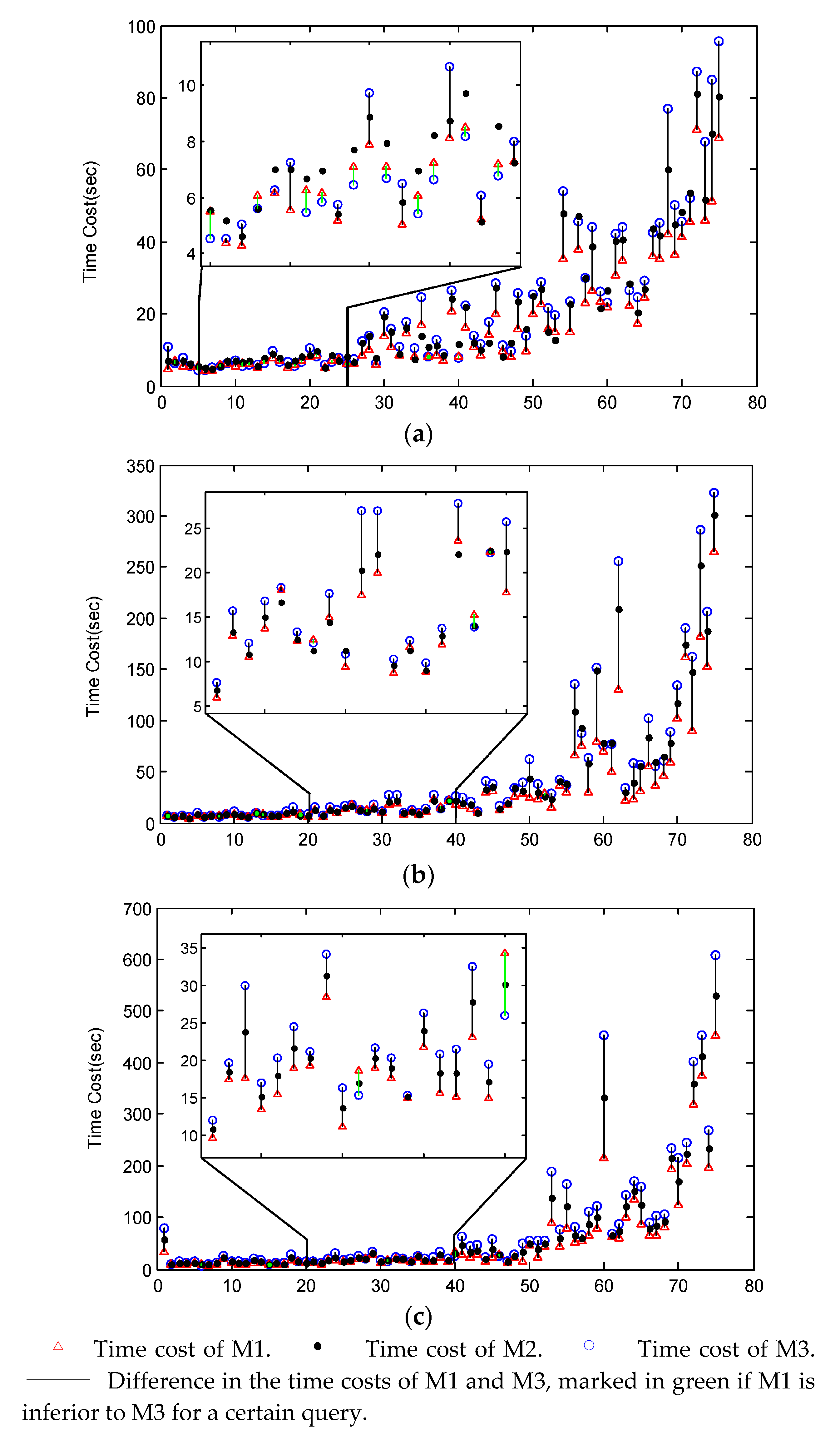
4.2. Test of Multi-Way Spatial Join
4.3. Test with Different Connection Speeds
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Farruque, N.; Osborn, W. Efficient distributed spatial semijoins and their application in multiple-site queries. In Proceedings of the 28th IEEE International Conference on Advanced Information Networking and Applications (AINA 2014), Victoria, BC, Canada, 13–16 May 2014; pp. 1089–1096. [Google Scholar]
- Open Geospatial Consortium Inc. OGC®Web Feature Service Implementation Specification. 2005. Available online: http://portal.opengeospatial.org/files/?artifact_id=8339 (accessed on 10 April 2016).
- Open Geospatial Consortium Inc. OGC®OpenGIS Web Feature Service 2.0 Interface Standard. 2010. Available online: http://portal.opengeospatial.org/files/?artifact_id=39967 (accessed on 10 April 2016).
- Gong, J.; Jia, W.; Chen, Y.; Xie, J. Development from platform GIS to cross-platform interoperable GIS. Geomat. Inf. Sci. Wuhan Univ. 2004, 29, 985–989. [Google Scholar]
- Xie, J.; Gong, J. Application of wfs in land and resources multilevel databases remote synchronization. Proc. SPIE 2005. [Google Scholar] [CrossRef]
- Zheng, W.F.; Wang, X.B.; Yin, A.T.; Kan, A.K.; Li, H.R. Application of web feature service-based data share to earthquake disaster reduction. J. Nat. Disasters 2008, 17, 1–5. [Google Scholar]
- Zhang, C.; Zhao, T.; Li, W. Towards improving query performance of web feature services (WFS) for disaster response. ISPRS Int. J. Geo-Inf. 2013, 2, 67–81. [Google Scholar] [CrossRef]
- Qi, M.Y. Research on Logistics Oriented Spatial Information Service and Its Key Techniques Issues; Institute of Remote Sensing Applications, Chinese Academy of Sciences: Beijing, China, 2006. [Google Scholar]
- Jia, W.J.; Gong, J.Y.; Li, B. Optimization method of web feature service. Acta Geod. Cartogr. Sin. 2005, 34, 168–174. [Google Scholar]
- Wu, H.; Zhe, L.; Xu, K. Cascading model of geospatial information service integration and its application. Sci. Surv. Mapp. 2010, 35, 212–214. [Google Scholar]
- Bai, Y.; Yang, C. Research on spatial information search engine. J. China Univ. Min. Technol. 2004, 33, 90–94. [Google Scholar]
- Jiang, J.; Yang, C.; Ren, Y. A spatial information crawler for OpenGIS WFS. Proc. SPIE 2008. [Google Scholar] [CrossRef]
- Mamoulis, N.; Papadias, D. Multiway spatial joins. ACM Trans. Database Syst. 2001, 26, 424–475. [Google Scholar] [CrossRef]
- Park, H.-H.; Cho, H.-J.; Chung, C.-W. Heuristic approach for early separated filter and refinement strategy in spatial query optimization. J. Syst. Softw. 2002, 62, 161–179. [Google Scholar] [CrossRef]
- Lu, H.; Shan, M.-C.; Tan, K.-L. Optimization of multi-way join queries for parallel execution. Proceessdings of the 17th International Conference on Very Large Data Bases, Barcelona, Spain, 3–9 September 1991; pp. 549–560. [Google Scholar]
- Lin, X.; Lu, H.X.; Zhang, Q. Graph partition based multi-way spatial joins. In Proceedings of the IEEE International Database Engineering and Applications Symposium (IDEAS’02), Edmonton, AB, Canada, 17–19 July 2002. [Google Scholar] [CrossRef]
- Lan, G.; Huang, Q.; Zhou, X. A spatial join strategy between ogc-compliant web feature services. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 655–658. [Google Scholar]
- Lan, G.; Wu, C.; Shi, G.; Chen, Q.; Yang, Z. Spatial join optimization among WFSs based on recursive partitioning and filtering rate estimation. Proc. SPIE 2015. [Google Scholar] [CrossRef]
- Lo, M.-L.; Ravishankar, V.C. Spatial hash-joins. In Proceedings of the ACM SIGMOD conference, Montreal, QC, Canada, 4–6 June 1996; pp. 247–258. [Google Scholar]
- Patel, J.M.; DeWitt, D.J. Partition based spatial–merge join. In Proceedings of the ACM SIGMOD conference, Montreal, QC, Canada; 1996; pp. 1–12. [Google Scholar]
- Arge, L.; Procopiuc, O. Scalable sweeping-based spatial join. In Proceedings of the International Conference on Very Large Data Bases, New York, NY, USA, 24–27 August 1998; pp. 324–335. [Google Scholar]
- Jacox, E.H.; Samet, H. Iterative spatial join. ACM Trans. Database Syst. 2003, 28, 230–256. [Google Scholar] [CrossRef]
- Papadias, D.; Mamoulis, N.; Theodoridis, Y. Constraint-based processing of multiway spatial joins. Algorithmica 2014, 30, 188–215. [Google Scholar] [CrossRef]
- Abel, D.J.; Ooi, B.C.; Tan, K.L.; Power, R.; Yu, J.X. Spatial join strategies in distributed spatial dbms. In Proceedings of the 4th International Symposium on Lame Spatial Databases, Portland, OR, USA, 6–9 August 1995; pp. 348–367. [Google Scholar]
- An, N.; Yang, Z.; Sivasubramanium, A. Selectivity estimation for spatial joins. In Proceedings of the 17th International Conference on Data Engineering, Heidelberg, Germany, 2–6 April 2001; pp. 368–375. [Google Scholar]
- Sun, C.; Agrawal, D.; Abbadi, A.E. Selectivity estimation for spatial joins with geometric selections. In Proceedings of the 8th International Conference on Extending Database Technology (EDBT 2002), Prague, Czech Republic, 25–27 March 2002; pp. 609–626. [Google Scholar]
- Karam, O. Optimizing Distributed Spatial Joins; Tulane University: New Orleans, LA, USA, 2001. [Google Scholar]
- Osborn, W.; Zaamout, S. Multiple-site distributed spatial query optimization using spatial semijoins. In Proceedings of the 10th International Baltic Conference on Databases and Information Systems (Baltic DB&IS 2012), Vilnius, Lithuania, 8–11 July 2012. [Google Scholar]
- Zhou, Q.H.; Chen, L.; Jing, N. Distributed spatial join query based on kd-tree recursive partitioning. Comput. Eng. Sci. 2011, 33, 167–172. [Google Scholar]
- U.S. Census Bureau. Census 2015 Tiger/Line Shapefiles. Available online: http://www.census.gov/ (accessed on 20 October 2016).

| No. | DS_SHF (MB) | DS_XML (KB) | ENCODE_T (s) | PARSE_T (s) | TRANS_T (s) | TOTAL (s) |
|---|---|---|---|---|---|---|
| 1 | 1 | 2472 | 0.82 | 1.14 | 0.66 | 2.62 |
| 2 | 3 | 7476 | 2.44 | 3.69 | 1.37 | 7.5 |
| 3 | 5 | 12,932 | 4.42 | 6.23 | 2.56 | 13.21 |
| 4 | 7 | 17,835 | 5.95 | 8.76 | 4.08 | 18.79 |
| 5 | 9 | 22,902 | 7.54 | 11.07 | 5.43 | 24.04 |
| 6 | 11 | 28,343 | 9.3 | 13.75 | 6.88 | 29.93 |
| 7 | 13 | 33,749 | 13.08 | 17.79 | 9.1 | 39.97 |
| 8 | 15 | 38,293 | 15.1 | 19.92 | 11.07 | 46.09 |
| 9 | 17 | 44,420 | 17 | 23.75 | 12.32 | 53.07 |
| 10 | 19 | 49,157 | 20.03 | 26.87 | 13.53 | 60.43 |
| T = 30 | T = 50 | T = 100 | Average | |
|---|---|---|---|---|
| X ≥ 1.5 | 45.0% | 60.0% | 42.0% | 49.0% |
| 1.5 > X > 1.0 | 32.0% | 20.0% | 35.0% | 29.0% |
| X ≤ 1.0 | 23.0% | 20.0% | 23.0% | 22.0% |
| T = 30 | T = 50 | T = 100 | Average | |
|---|---|---|---|---|
| X ≥ 1.5 | 53.0% | 70.0% | 51.0% | 58.0% |
| 1.5 > X >1.0 | 24.0% | 8.0% | 26.0% | 19.3% |
| X ≤ 1.0 | 23.0% | 22.0% | 23.0% | 22.7% |
| Dataset Name | Geometric Type | Number of Objects | Data Size (kb) |
|---|---|---|---|
| primary roads | polyline | 12,101 | 40,061 |
| uac10 | polygon | 3976 | 108,422 |
| place | polygon | 29,130 | 167,240 |
| rails | polyline | 180,739 | 64,872 |
| school | polygon | 6846 | 171,507 |
| Types | Number of Objects | Notably Improved | Slightly Improved | Futile | |||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M1 | M2 | M1 | M2 | ||
| Three-way | [54,1349] | 7 | 3 | 54 | 47 | 14 | 25 |
| Four-way | [196,4131] | 18 | 0 | 48 | 59 | 9 | 16 |
| Five-way | [234,4271] | 20 | 1 | 50 | 69 | 5 | 5 |
| Speed | Unlimited | 4 Mbps | 2 Mbps | 1 Mbps | 0.5 Mbps | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| NO. | M1 | M3 | M1 | M3 | M1 | M3 | M1 | M3 | M1 | M3 |
| 1 | 13.02 | 14.86 | 13.39 | 15.56 | 13.37 | 17.42 | 14.23 | 20.84 | 19.72 | 31.37 |
| 1 | 17.12 | 22.12 | 19.86 | 28.52 | 24.39 | 36.89 | 32.37 | 48.74 | 45.98 | 71.24 |
| 2 | 22.45 | 31.32 | 29.07 | 44.08 | 45.58 | 65.19 | 72.03 | 102.02 | 94.74 | 138.92 |
| 3 | 24.66 | 30.75 | 32.64 | 43.75 | 48.15 | 61.74 | 61.64 | 78.82 | 85.14 | 118.32 |
| 4 | 42.97 | 53.59 | 50.06 | 67.02 | 63.53 | 87.08 | 90.84 | 138.07 | 158.08 | 239.42 |
| 5 | 33.05 | 49.61 | 41.49 | 62.52 | 54.23 | 83.92 | 78.48 | 124.71 | 117.97 | 188.49 |
| 6 | 30.65 | 38.12 | 45.76 | 58.62 | 65.62 | 85.57 | 90.27 | 128.3 | 147.02 | 210.15 |
| 7 | 31.06 | 43.93 | 45.6 | 62.98 | 57.74 | 80.67 | 74.86 | 107.37 | 104.72 | 150.37 |
| 8 | 20.16 | 27.11 | 23.54 | 33.25 | 30.38 | 45.06 | 42.56 | 61.68 | 60.92 | 93.35 |
| 9 | 12.19 | 12.48 | 12.97 | 13.8 | 15.17 | 15.88 | 17.51 | 18.4 | 20.22 | 22.4 |
| 10 | 16.87 | 18.67 | 16.68 | 21.22 | 19.6 | 25.91 | 23.05 | 31.49 | 30.36 | 41.05 |
| 11 | 26.19 | 35.49 | 40.44 | 56.27 | 50.74 | 78.84 | 82.53 | 117.6 | 118.63 | 170.3 |
| No. | Unlimited | 4 Mbps | 2 Mbps | 1 Mbps | 0.5 Mbps |
|---|---|---|---|---|---|
| 1 | 1.14 | 1.16 | 1.30 | 1.46 | 1.59 |
| 2 | 1.29 | 1.44 | 1.51 | 1.51 | 1.55 |
| 3 | 1.40 | 1.52 | 1.43 | 1.42 | 1.47 |
| 4 | 1.25 | 1.34 | 1.28 | 1.28 | 1.39 |
| 5 | 1.25 | 1.34 | 1.37 | 1.52 | 1.51 |
| 6 | 1.50 | 1.51 | 1.55 | 1.59 | 1.60 |
| 7 | 1.24 | 1.28 | 1.30 | 1.42 | 1.43 |
| 8 | 1.41 | 1.38 | 1.40 | 1.43 | 1.44 |
| 9 | 1.34 | 1.41 | 1.48 | 1.45 | 1.53 |
| 10 | 1.02 | 1.06 | 1.05 | 1.05 | 1.11 |
| 11 | 1.11 | 1.27 | 1.32 | 1.37 | 1.35 |
| 12 | 1.36 | 1.39 | 1.55 | 1.42 | 1.44 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, G.; Zhang, Q.; Yang, Z.; Li, T. Optimizing Multi-Way Spatial Joins of Web Feature Services. ISPRS Int. J. Geo-Inf. 2017, 6, 123. https://doi.org/10.3390/ijgi6040123
Lan G, Zhang Q, Yang Z, Li T. Optimizing Multi-Way Spatial Joins of Web Feature Services. ISPRS International Journal of Geo-Information. 2017; 6(4):123. https://doi.org/10.3390/ijgi6040123
Chicago/Turabian StyleLan, Guiwen, Qiang Zhang, Zhao Yang, and Tong Li. 2017. "Optimizing Multi-Way Spatial Joins of Web Feature Services" ISPRS International Journal of Geo-Information 6, no. 4: 123. https://doi.org/10.3390/ijgi6040123
APA StyleLan, G., Zhang, Q., Yang, Z., & Li, T. (2017). Optimizing Multi-Way Spatial Joins of Web Feature Services. ISPRS International Journal of Geo-Information, 6(4), 123. https://doi.org/10.3390/ijgi6040123





